Application of Adaptive Discrete Feedforward Controller in Multi-Axial Real-Time Hybrid Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Properties of the Reference Structure
2.2. Sub-Structured System Dynamics
2.3. Transfer System
2.3.1. Coordinate Transformation for the Coupler
2.3.2. Control Plant Model Properties
2.4. MIMO Controller Application in the maRTHS Benchmark
2.4.1. Reference Controller—Linear Quadratic Gaussian (LQG) Control
2.4.2. Proposed Controller—Adaptive Discrete Feedforward Control (ADFC)
2.5. Evaluation Criteria and Performance Assessment
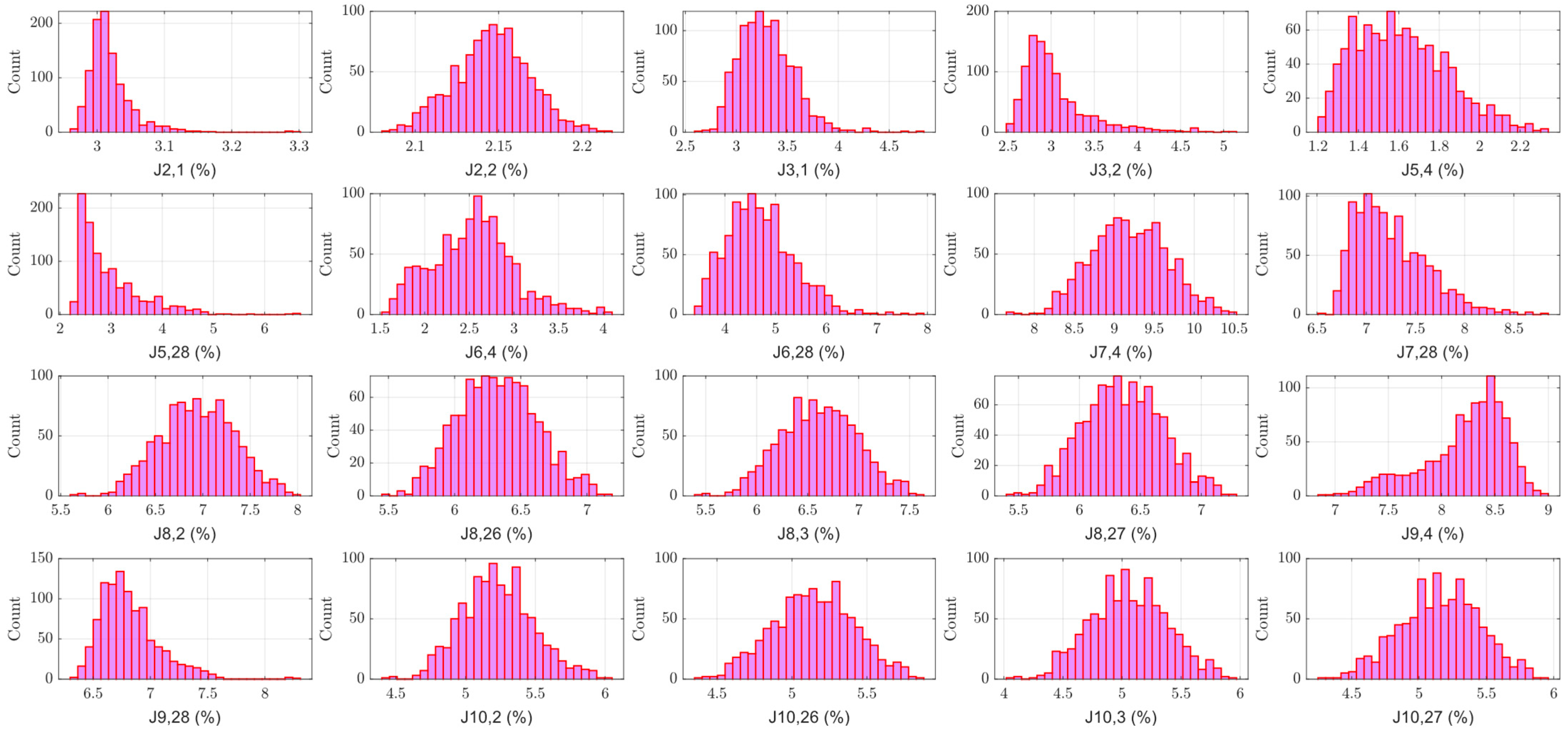
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, X.; Castaneda, N.; Dyke, S.J. Experimental validation of a generalized procedure for MDOF real-time hybrid simulation. J. Eng. Mech. 2014, 140, 04013006. [Google Scholar] [CrossRef]
- Friedman, A.; Dyke, S.J.; Phillips, B.; Ahn, R.; Dong, B.; Chae, Y.; Castaneda, N.; Jiang, Z.; Zhang, J.; Cha, Y.; et al. Large-scale real-time hybrid simulation for evaluation of advanced damping system performance. J. Struct. Eng. 2015, 141, 04014150. [Google Scholar] [CrossRef]
- Gomez, D.; Dyke, S.J.; Maghareh, A. Enabling Role of Hybrid Simulation Within the NEES Infrastructure in Advancing Earthquake Engineering Practice and Research; Intelligent Infrastructure Systems Laboratory (IISL): West Lafayette, IN, USA, 2014. [Google Scholar] [CrossRef]
- Williams, M.S.; Blakeborough, A. Laboratory testing of structures under dynamic loads: An introductory review. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2001, 359, 1651–1669. [Google Scholar] [CrossRef]
- Gao, X. Development of a Robust Framework for Real-Time Hybrid Simulation: From Dynamical System, Motion Control to Experimental Error Verification. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2012. [Google Scholar]
- Ahmadizadeh, M.; Mosqueda, G.; Reinhorn, A.M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq. Eng. Struct. Dyn. 2008, 37, 21–42. [Google Scholar] [CrossRef]
- Wallace, M.I.; Wagg, D.J.; Neild, S.A. An adaptive polynomial based forward prediction algorithm for multi-actuator real-time dynamic substructuring. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 3807–3826. [Google Scholar] [CrossRef]
- Darby, A.P.; Blakeborough, A.; Williams, M.S. Real-time substructure tests using hydraulic actuator. J. Eng. Mech. 1999, 125, 1133–1139. [Google Scholar] [CrossRef]
- Nakashima, M.; Masaoka, N. Real-time on-line test for MDOF systems. Earthq. Eng. Struct. Dyn. 1999, 28, 393–420. [Google Scholar] [CrossRef]
- Darby, A.P.; Williams, M.S.; Blakeborough, A. Stability and delay compensation for real-time substructure testing. J. Eng. Mech. 2002, 128, 1276–1284. [Google Scholar] [CrossRef]
- Zhao, J.; French, C.; Shield, C.; Posbergh, T. Considerations for the development of real-time dynamic testing using servo-hydraulic actuation. Earthq. Eng. Struct. Dyn. 2003, 32, 1773–1794. [Google Scholar] [CrossRef]
- Jung, R.Y.; Benson Shing, P.; Stauffer, E.; Thoen, B. Performance of a real-time pseudodynamic test system considering nonlinear structural response. Earthq. Eng. Struct. Dyn. 2007, 36, 1785–1809. [Google Scholar] [CrossRef]
- Chen, C.; Ricles, J.M. Analysis of actuator delay compensation methods for real-time testing. Eng. Struct. 2009, 31, 2643–2655. [Google Scholar] [CrossRef]
- Chen, C.; Ricles, J.M.; Marullo, T.M.; Mercan, O. Real-time hybrid testing using the unconditionally stable explicit CR integration algorithm. Earthq. Eng. Struct. Dyn. 2009, 38, 23–44. [Google Scholar] [CrossRef]
- Hayati, S.; Song, W. An optimal discrete-time feedforward compensator for real-time hybrid simulation. Smart Struct. Syst. 2017, 20, 483–498. [Google Scholar] [CrossRef]
- Chae, Y.; Kazemibidokhti, K.; Ricles, J.M. Adaptive time series compensator for delay compensation of servo-hydraulic actuator systems for real-time hybrid simulation. Earthq. Eng. Struct. Dyn. 2013, 42, 1697–1715. [Google Scholar] [CrossRef]
- Palacio-Betancur, A.; Gutierrez Soto, M. Adaptive tracking control for real-time hybrid simulation of structures subjected to seismic loading. Mech. Syst. Signal Process. 2019, 134, 106345. [Google Scholar] [CrossRef]
- Ning, X.; Wang, Z.; Wang, C.; Wu, B. Adaptive feedforward and feedback compensation method for real-time hybrid simulation based on a discrete physical testing system model. J. Earthq. Eng. 2022, 26, 3841–3863. [Google Scholar] [CrossRef]
- Song, W.; Dyke, S. Development of a cyber-physical experimental platform for real-time dynamic model updating. Mech. Syst. Signal Process. 2013, 37, 388–402. [Google Scholar] [CrossRef]
- Strano, S.; Terzo, M. Actuator dynamics compensation for real-time hybrid simulation: An adaptive approach by means of a nonlinear estimator. Nonlinear Dyn. 2016, 85, 2353–2368. [Google Scholar] [CrossRef]
- Huang, W.; Ning, X.; Ding, Y.; Wang, Z. A novel actuation dynamics adaptive compensation strategy for real-time hybrid simulation based on unscented Kalman filter. Int. J. Struct. Stab. Dyn. 2023, 23, 2350107. [Google Scholar] [CrossRef]
- Wang, Z.; Ning, X.; Xu, G.; Zhou, H.; Wu, B. High performance compensation using an adaptive strategy for real-time hybrid simulation. Mech. Syst. Signal Process. 2019, 133, 106262. [Google Scholar] [CrossRef]
- Ning, X.; Huang, N.W.; Xu, G.S.; Wang, Z.; Wu, B.; Zheng, L.; Xu, B. A novel model-based adaptive feedforward-feedback control method for real-time hybrid simulation considering additive error model. Struct. Control Health Monit. 2023, 2023, 5550580. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, G.; Li, Q.; Wu, B. An adaptive delay compensation method based on a discrete system model for real-time hybrid simulation. Smart Struct. Syst. 2020, 25, 569–580. [Google Scholar] [CrossRef]
- Simpson, T.; Dertimanis, V.K.; Chatzi, E.N. Towards data-driven real-time hybrid simulation: Adaptive modeling of control plants. Front. Built Environ. 2020, 6, 570947. [Google Scholar] [CrossRef]
- Li, H.W.; Wang, F.; Ni, Y.Q.; Wang, Y.W.; Xu, Z.D. An adaptive and robust control strategy for real-time hybrid simulation. Sensors 2022, 22, 6569. [Google Scholar] [CrossRef]
- Niño, A.F.; Palacio-Betancur, A.; Miranda-Chiquito, P.; Amaya, J.D.; Silva, C.E.; Gutierrez Soto, M.; Giraldo, L.F. Deep Reinforcement Learning-Based Control for Real-Time Hybrid Simulation of Civil Structures. Int. J. Robust Nonlinear Control 2025, in press. [Google Scholar] [CrossRef]
- Xu, W.; Meng, X.; Chen, C.; Guo, T.; Peng, C. Evaluation of data-driven NARX model based compensation for multi-axial real-time hybrid simulation benchmark study. Front. Built Environ. 2024, 10, 1374819. [Google Scholar] [CrossRef]
- Nakata, N.; Spencer, B.F., Jr.; Elnashai, A.S. Multi-Dimensional Mixed-Mode Hybrid Simulation Control and Applications; Newmark Structural Engineering Laboratory Report Series 005; The Newmark Structural Engineering Laboratory: Urbana, IL, USA, 2007; Available online: https://hdl.handle.net/2142/3628 (accessed on 26 October 2025).
- Chen, C.; Ricles, J.M.; Hodgson, I.C.; Sause, R. Real-Time Multi-Directional Hybrid Simulation of Building Piping Systems. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008; Available online: https://www.iitk.ac.in/nicee/wcee/article/14_S16-01-007.PDF (accessed on 26 October 2025).
- Mercan, O.; Ricles, J.M.; Sause, R.; Marullo, T. Kinematic transformations for planar multi-directional pseudodynamic testing. Earthq. Eng. Struct. Dyn. 2009, 38, 1093–1119. [Google Scholar] [CrossRef]
- Al-Mahaidi, R.; Hashemi, M.J.; Kalfat, R.; Burnett, G.; Wilson, J. Multi-Axis Substructure Testing System for Hybrid Simulation; Springer: Singapore, 2018; Available online: https://link.springer.com/book/10.1007/978-981-10-5867-7 (accessed on 26 October 2025).
- Hashemi, M.J.; Al-Ogaidi, Y.K.F.; Wilson, J.; Abdouka, K. Collapse Simulation of Multi-Story RC Buildings Through Hybrid Testing. In Proceedings of the Australian Earthquake Engineering Society Conference, Lorne, Australia, 21–23 November 2014; Available online: https://aees.org.au/wp-content/uploads/2015/06/66-Hashemi.pdf (accessed on 26 October 2025).
- Phillips, B.M.; Spencer, B.F., Jr. Model-based multiactuator control for real-time hybrid simulation. J. Eng. Mech. 2013, 139, 219–228. [Google Scholar] [CrossRef]
- Fermandois, G.A.; Spencer, B.F., Jr. Development and Implementation of a Multi-Axial Real-Time Hybrid Simulation Framework; Newmark Structural Engineering Laboratory Report Series 049; The Newmark Structural Engineering Laboratory: Urbana, IL, USA, 2018; Available online: https://hdl.handle.net/2142/101441 (accessed on 26 October 2025).
- Najafi, A.; Fermandois, G.A.; Spencer, B.F., Jr. Decoupled model-based real-time hybrid simulation with multi-axial load and boundary condition boxes. Eng. Struct. 2020, 219, 110868. [Google Scholar] [CrossRef]
- Najafi, A.; Spencer, B.F. Multiaxial real-time hybrid simulation for substructuring with multiple boundary points. J. Struct. Eng. 2021, 147, 05021007. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, T.; Zhou, H.; Du, C. Shaking-table substructure test using a MDOF boundary-coordinating device. Earthq. Eng. Struct. Dyn. 2022, 51, 3658–3679. [Google Scholar] [CrossRef]
- Elnashai, A.S.; Spencer, B.F.; Kuchma, D.A.; Yang, G.; Carrion, J.; Gan, Q.; Kim, S.J. The multi-axial full-scale sub-structured testing and simulation (MUST-SIM) facility at the University of Illinois at Urbana-Champaign. In Advances in Earthquake Engineering for Urban Risk Reduction; Springer: Dordrecht, The Netherlands, 2006; pp. 245–260. [Google Scholar] [CrossRef]
- Høgh, J.; Waldbjørn, J.; Wittrup–Schmidt, J.; Stang, H.; Berggreen, C. Quasi-Static Single-Component Hybrid Simulation of a Composite Structure with Multi-Axis Control. Strain 2015, 51, 459–473. [Google Scholar] [CrossRef]
- Tsokanas, N.; Abbiati, G.; Kanellopoulos, K.; Stojadinović, B. Multi-axial hybrid fire testing based on dynamic relaxation. Fire Saf. J. 2021, 126, 103468. [Google Scholar] [CrossRef]
- Huang, X.; Park, J.; Kwon, O.S. Network Interface Program for Actuator Controllers for Pseudo-Dynamic Hybrid Simulation. J. Earthq. Eng. 2024, 28, 266–287. [Google Scholar] [CrossRef]
- Kaufmann, W.; Beck, A.; Karagiannis, D.; Werne, D. Design, Construction and Capabilities of the Large Universal Shell Element Tester. In Proceedings of the 8th International Conference of the Spanish Association for Structural Engineering (ACHE 2022), Santander, Spain, 20–22 June 2022; Volume 73, pp. 83–88. [Google Scholar] [CrossRef]
- Mojiri, S.; Kwon, O.S.; Christopoulos, C. Development of a ten-element hybrid simulation platform and an adjustable yielding brace for performance evaluation of multi-story braced frames subjected to earthquakes. Earthq. Eng. Struct. Dyn. 2019, 48, 749–771. [Google Scholar] [CrossRef]
- Horiuchi, T.; Ohsaki, M.; Kurata, M.; Ramirez, J.A.; Yamashita, T.; Kajiwara, K. Contributions of E-Defense shaking table to Earthquake engineering and its future. J. Disaster Res. 2022, 17, 985–999. [Google Scholar] [CrossRef]
- Gomez, D.; Dyke, S.J.; Maghareh, A. Enabling role of hybrid simulation across NEES in advancing earthquake engineering. Smart Struct. Syst. 2015, 15, 913–929. [Google Scholar] [CrossRef]
- Van Den Einde, L.; Conte, J.P.; Restrepo, J.I.; Bustamante, R.; Halvorson, M.; Hutchinson, T.C.; Lai, C.T.; Lotfizadeh, K.; Luco, J.E.; Morrison, M.L.; et al. NHERI@UC San Diego 6-DOF large high-performance outdoor shake table facility. Front. Built Environ. 2021, 6, 580333. [Google Scholar] [CrossRef]
- Condori Uribe, J.W.; Salmeron, M.; Patino, E.; Montoya, H.; Dyke, S.J.; Silva, C.E.; Maghareh, A.; Najarian, M.; Montoya, A. Experimental benchmark control problem for multi-axial real-time hybrid simulation. Front. Built Environ. 2023, 9, 1270996. [Google Scholar] [CrossRef]
- Ruiz, S.; Song, W. Adaptive compensation for multi-axial real-time hybrid simulation via nonlinear parameter estimation. Front. Built Environ. 2024, 10, 1477804. [Google Scholar] [CrossRef]
- Aguila, A.J.; Li, H.; Palacio-Betancur, A.; Ahmed, K.A.; Kovalenko, I.; Gutierrez Soto, M. Conditional adaptive time series compensation and control design for multi-axial real-time hybrid simulation. Front. Built Environ. 2024, 10, 1384235. [Google Scholar] [CrossRef]
- Shangguan, Y.; Wang, Z.; Guo, Y.; Chen, Y.; Zeng, Y.; Zhou, H. Adaptive sliding-mode delay compensation for real-time hybrid simulations with multiple actuators. Front. Built Environ. 2024, 10, 1393710. [Google Scholar] [CrossRef]
- Quiroz, M.; Gálmez, C.; Fermandois, G.A. Robust decentralized adaptive compensation for the multi-axial real-time hybrid simulation benchmark. Front. Built Environ. 2024, 10, 1394952. [Google Scholar] [CrossRef]
- Tao, J.; Mercan, O. Adaptive discrete feedforward controller for tracking error compensation of servo-hydraulic actuators in real-time hybrid simulation. Struct. Control Health Monit. 2022, 29, e2895. [Google Scholar] [CrossRef]
- Tao, J.; Mercan, O.; Calayir, M. Multi-rate real-time hybrid simulation with adaptive discrete feedforward controller-based compensation strategy. Earthq. Eng. Struct. Dyn. 2024, 53, 1260–1284. [Google Scholar] [CrossRef]
- Tao, J.; Mercan, O.; Calayir, M. Improved implementation of concentrated plasticity models in real-time hybrid simulation. Structures 2024, 64, 106525. [Google Scholar] [CrossRef]
- Silva, C.E.; Gomez, D.; Maghareh, A.; Dyke, S.J.; Spencer, B.F. Benchmark control problem for real-time hybrid simulation. Mech. Syst. Signal Process. 2020, 135, 106381. [Google Scholar] [CrossRef]
- Gao, X.; Castaneda, N.; Dyke, S.J. Real time hybrid simulation: From dynamic system, motion control to experimental error. Earthq. Eng. Struct. Dyn. 2013, 42, 815–832. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB, Version: 24.2 (R2024b); The MathWorks Inc.: Natick, MA, USA, 2024. Available online: https://www.mathworks.com (accessed on 15 June 2025).
- Carrion, J.E. Model-Based Strategies for Real-Time Hybrid Testing. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2007. [Google Scholar]
- Phillips, B.M.; Spencer, B.F., Jr. Model-Based Framework for Real-Time Dynamic Structural Performance Evaluation; Newmark Structural Engineering Laboratory Report Series 031; The Newmark Structural Engineering Laboratory: Urbana, IL, USA, 2012; Available online: https://hdl.handle.net/2142/33794 (accessed on 26 October 2025).
- Fermandois, G.A.; Spencer, B.F. Model-based framework for multi-axial real-time hybrid simulation testing. Earthq. Eng. Eng. Vib. 2017, 16, 671–691. [Google Scholar] [CrossRef]
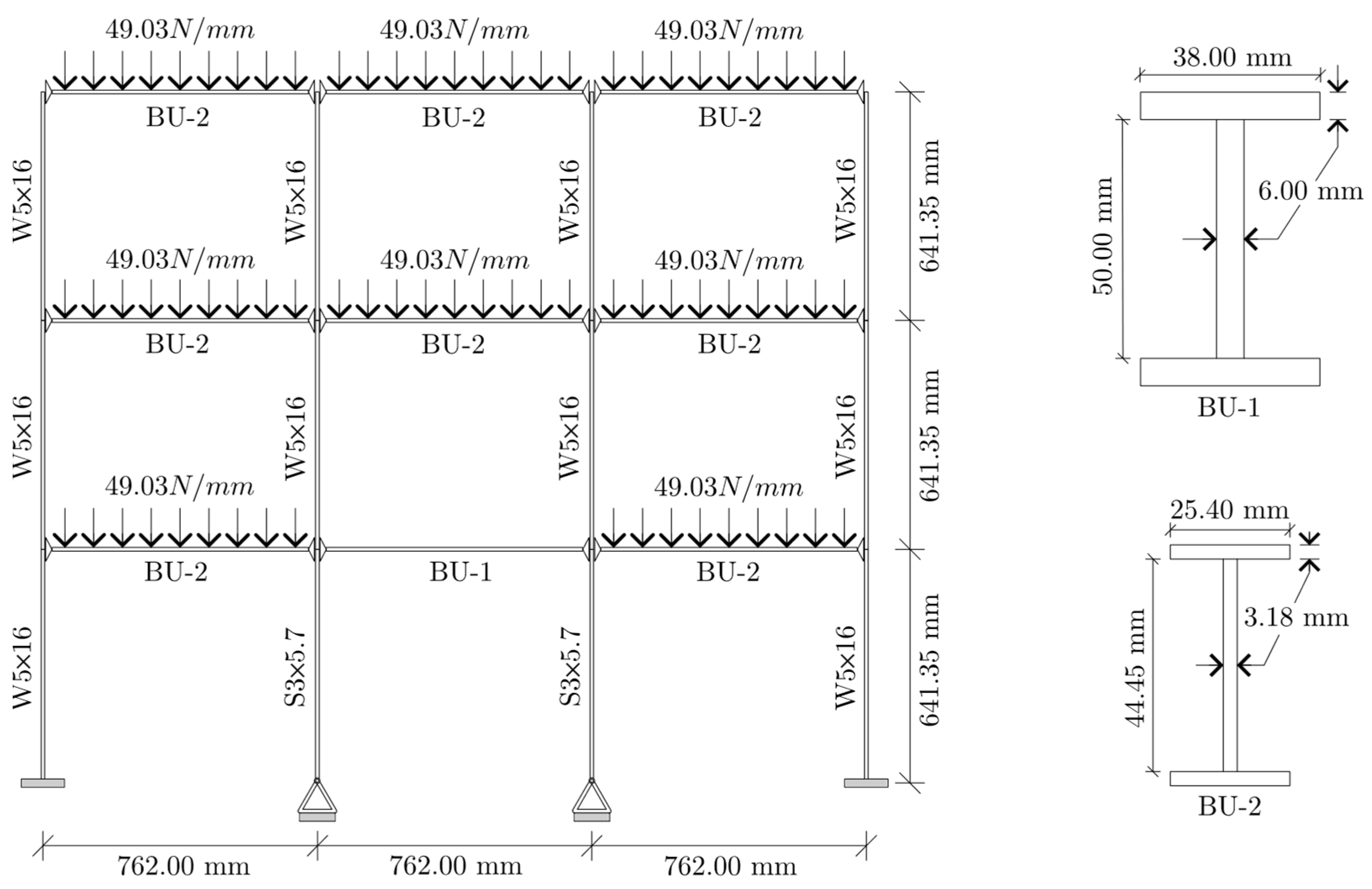

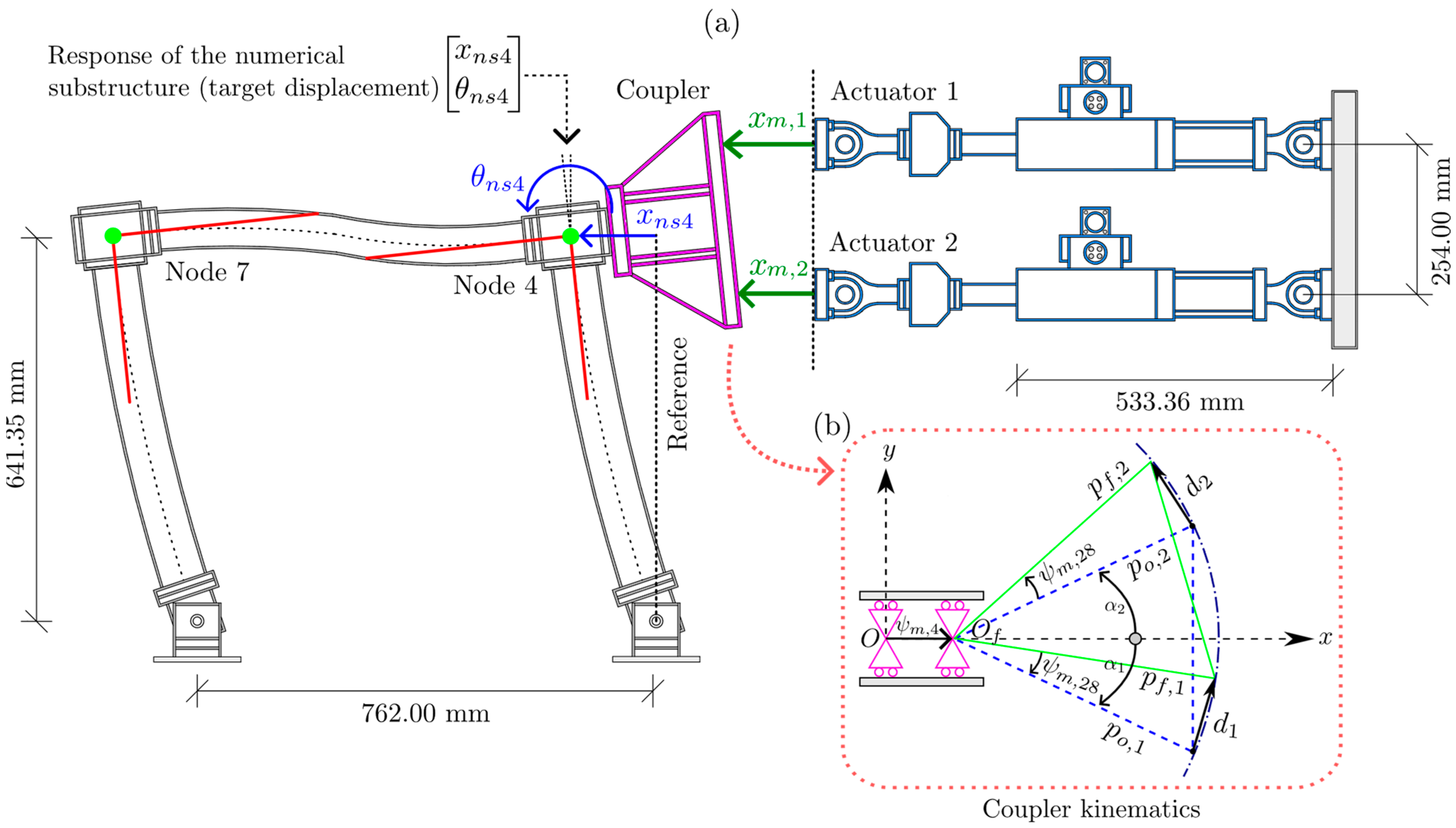

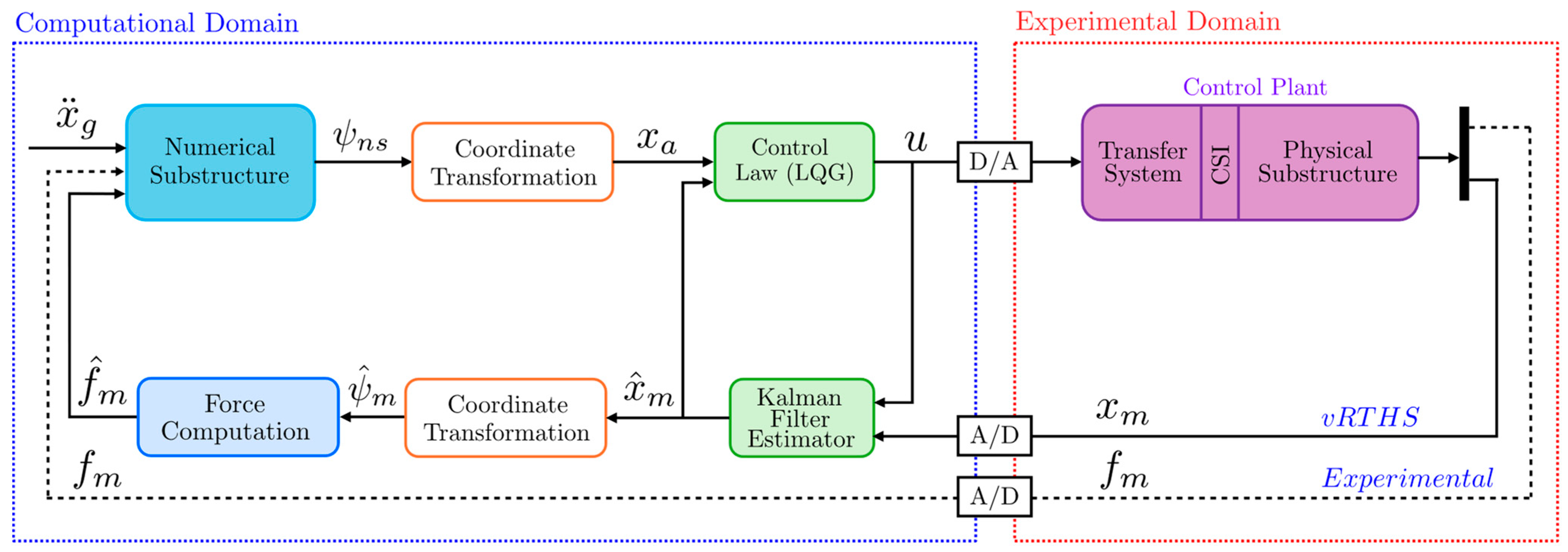
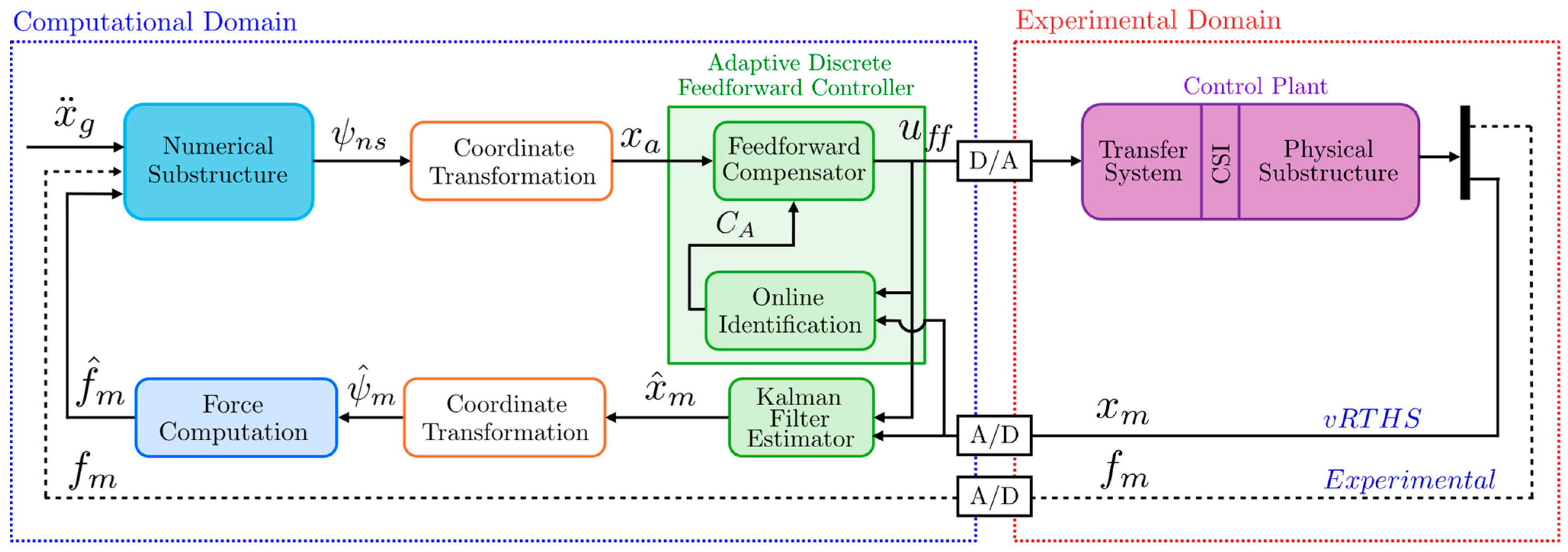

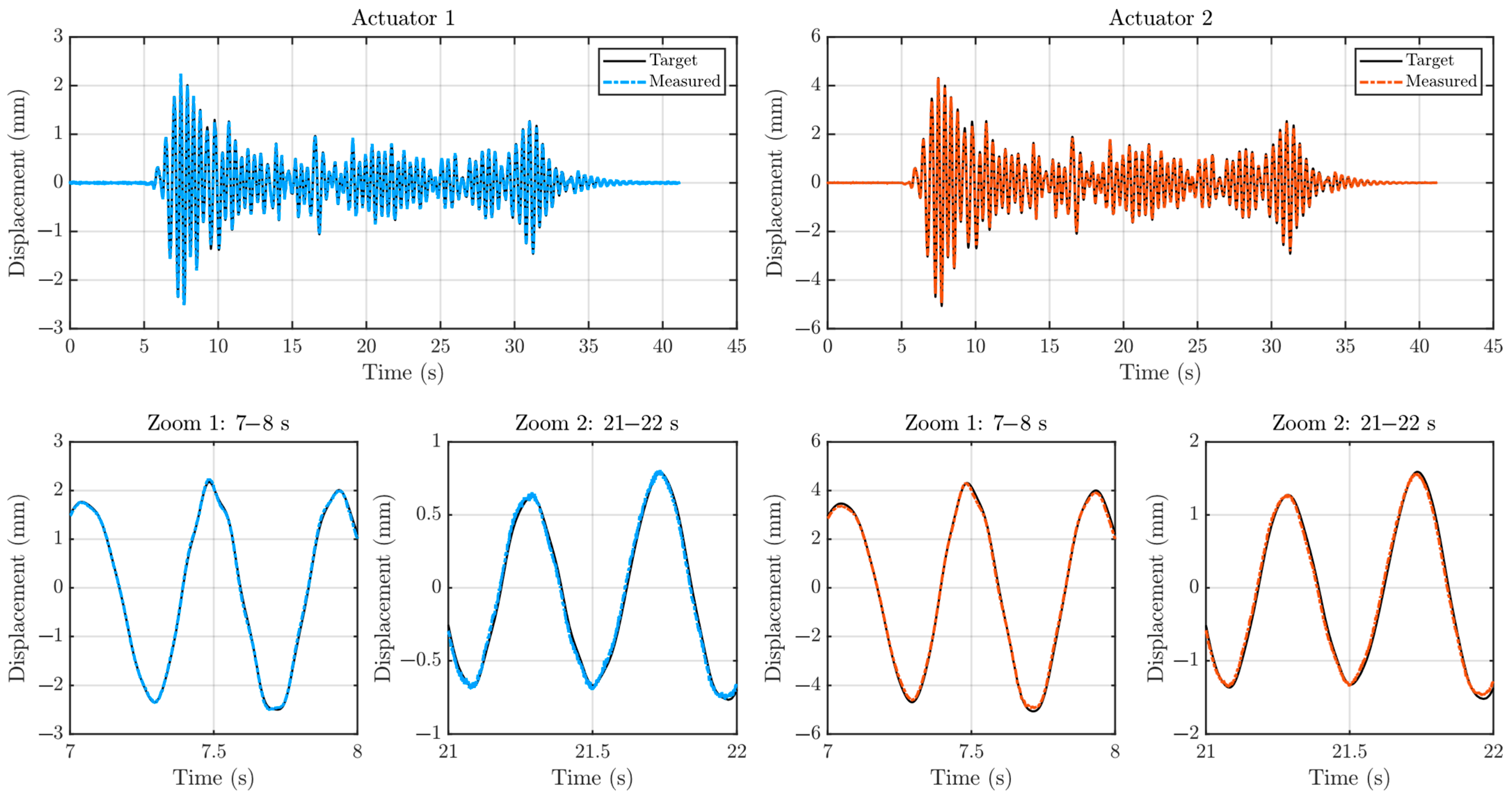
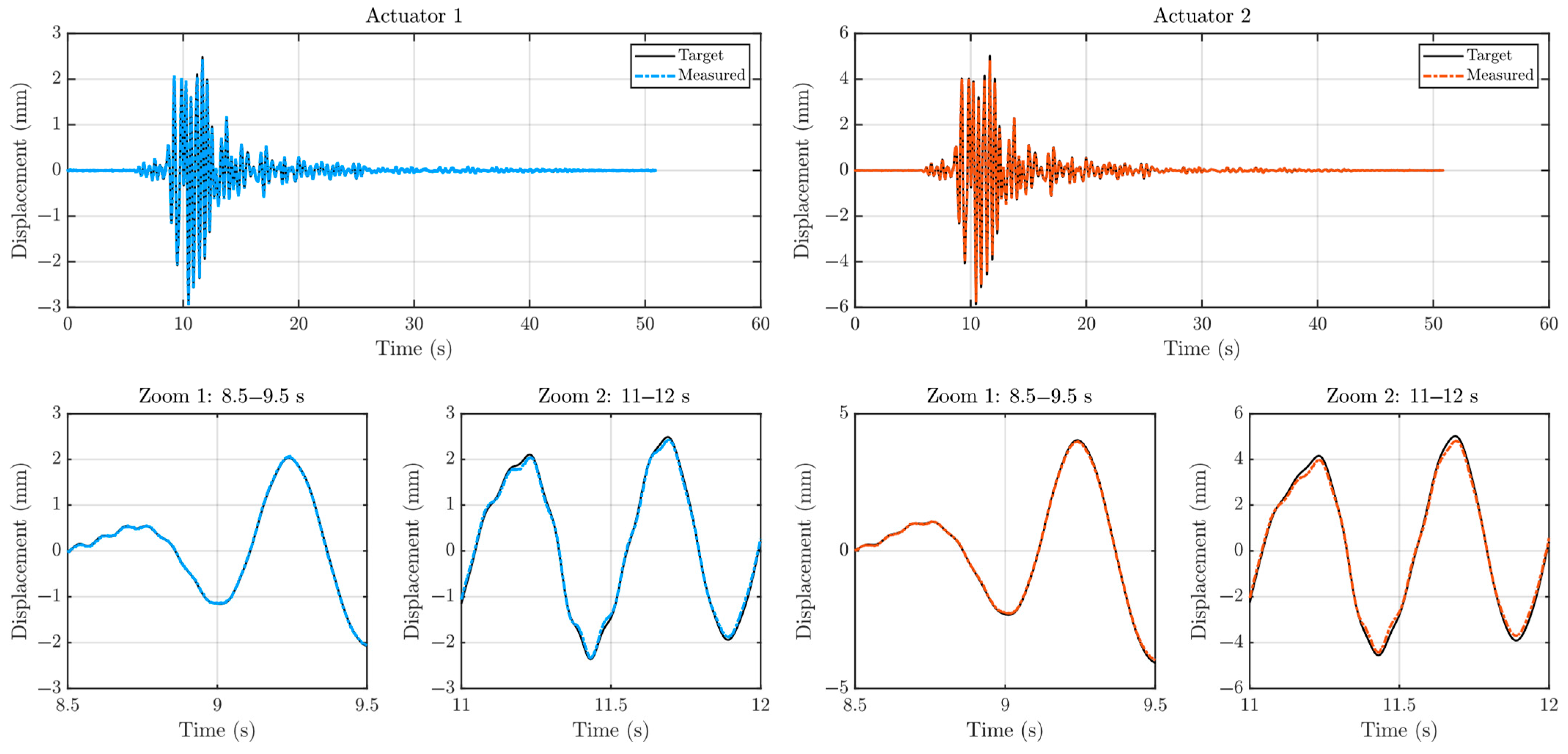
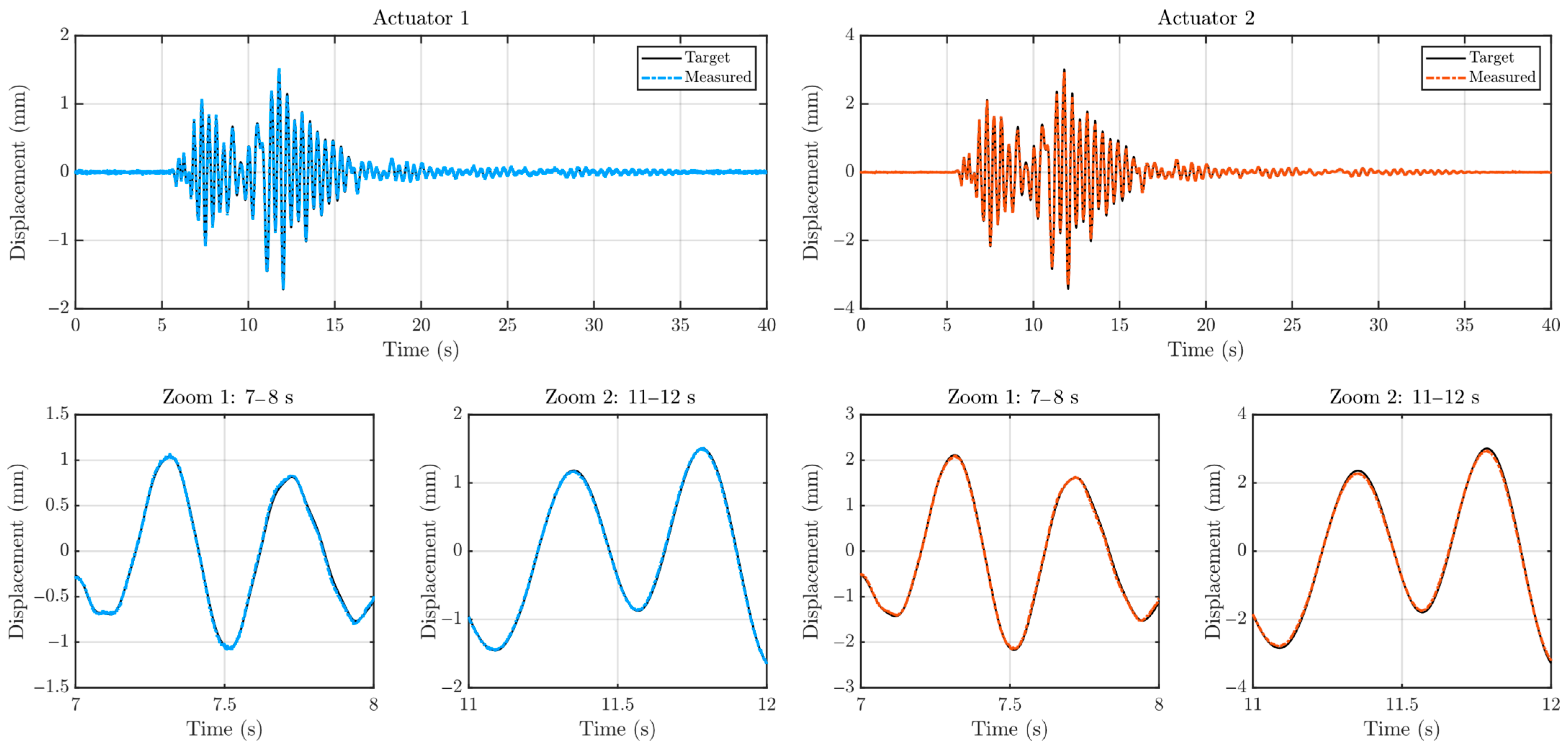
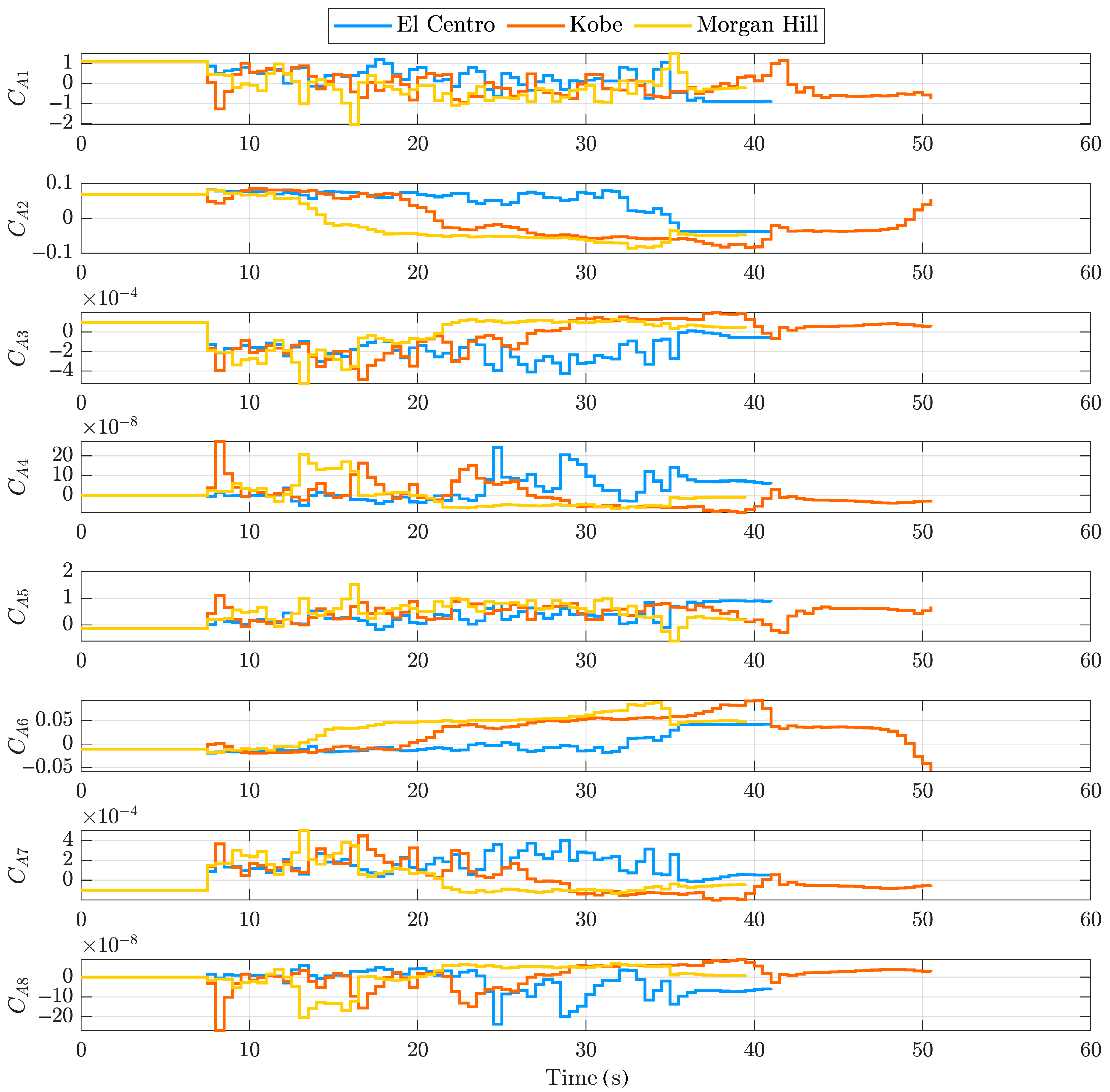
| Mode | Frequency | Effective Modal Mass—Translation | Effective Modal Mass—Rotation | ||
|---|---|---|---|---|---|
| (Hz) | (%) | (%) | (%) | (%) | |
| 1 | 2.29 | 81.05 | 81.05 | 2.37 × 10−9 | 2.37 × 10−9 |
| 2 | 12.74 | 16.60 | 97.65 | 2.11 × 10−7 | 2.13 × 10−7 |
| 3 | 26.28 | 5.33 × 10−7 | 97.65 | 61.72 | 61.72 |
| 4 | 26.53 | 8.67 × 10−3 | 97.66 | 2.89 × 10−5 | 61.72 |
| 5 | 29.91 | 2.34 | 100 | 2.42 × 10−5 | 61.72 |
| Component | Parameter | ||
|---|---|---|---|
| and | Zero 1 | −753.98 | 41.47 |
| Zero 2 | −565.48 | 31.10 | |
| Pole 1 | −16.65 | 1.00 | |
| Pole 2 | −251.32 | 15.08 | |
| and | Zero 1 | −18.85 | 0.57 |
| Zero 2 | −31.42 | 0.94 | |
| Pole 1 | −21.99 | 0.66 | |
| Pole 2 | −116.24 | −3.49 | |
| Pole 1 and 2 | −314.16 ± 395.84i | 15.71 + 19.79i |
| Performance | Index | Unit | Criterion | Equation |
|---|---|---|---|---|
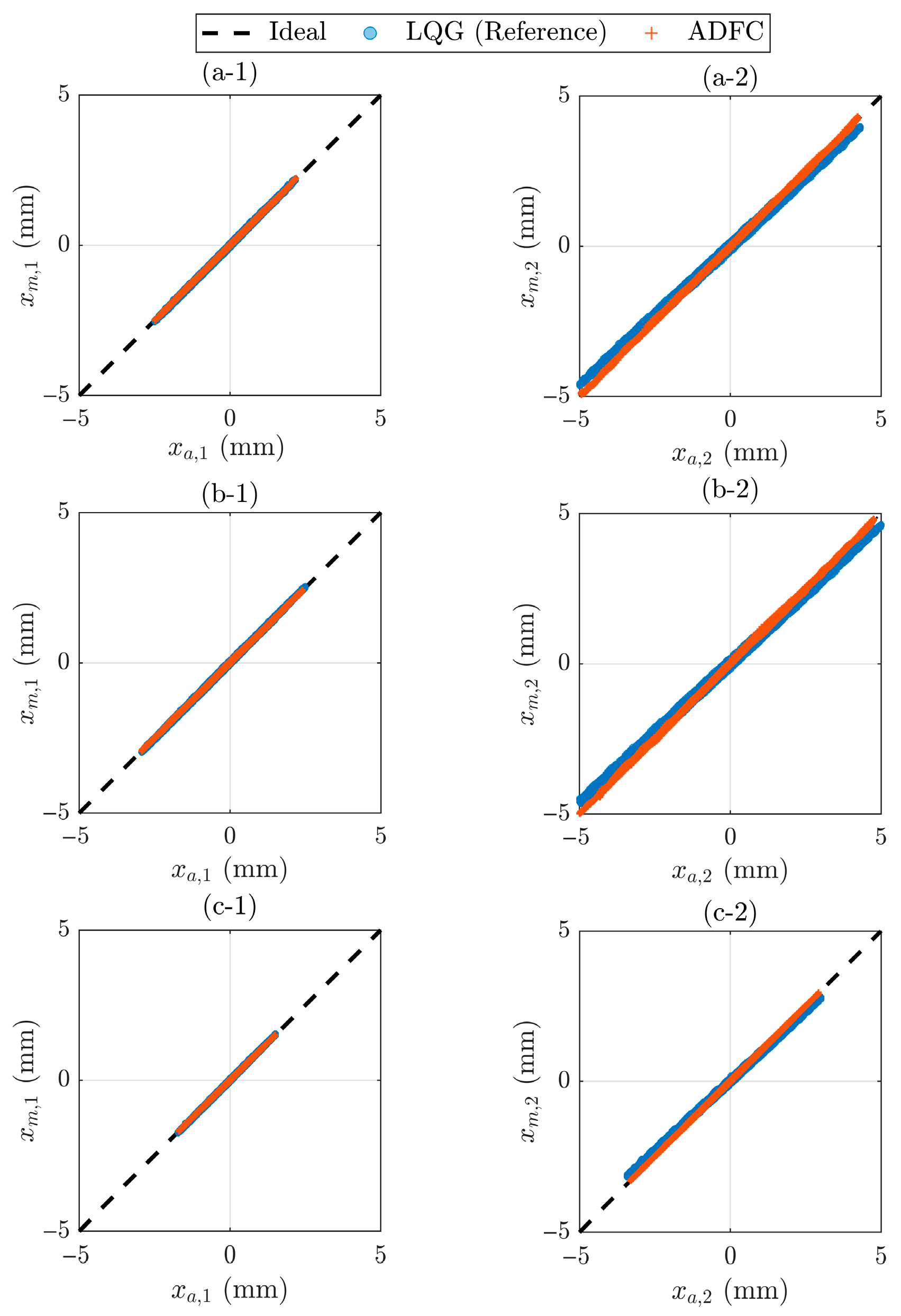
| Tracking Control | J1 | ms | Tracking time delay between desired and measured actuator displacements () | |
| J2 | % | Normalized tracking error. It represents the difference between target and measured actuator displacements () | ||
| J3 | % | Maximum peak tracking error between the instantaneous response of desired and measured actuator displacements () | ||
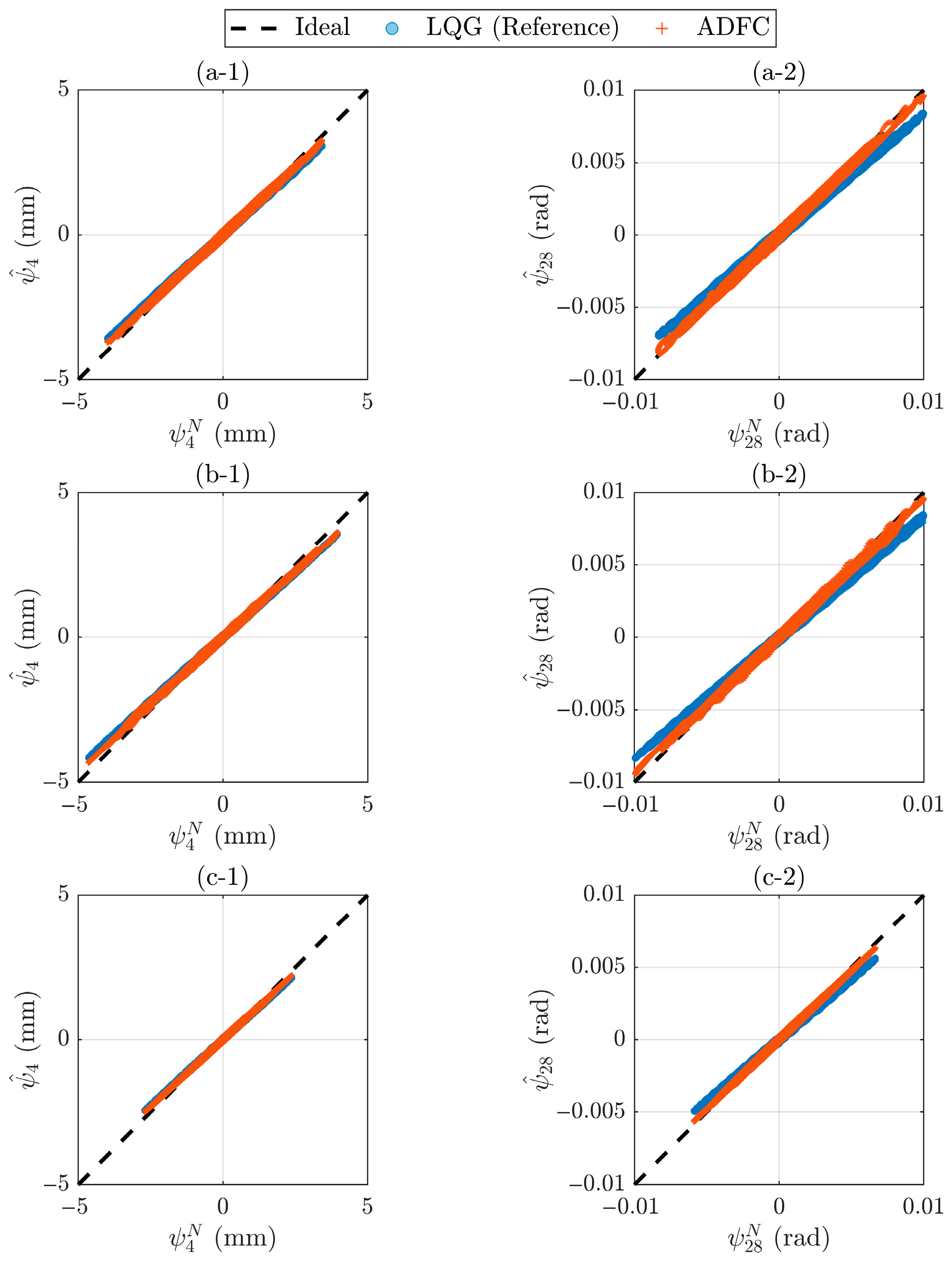
| Estimation | J4 | ms | Time delay between target and estimated interface node displacements of the frame () | |
| J5 | % | Normalized error of the difference between frame target displacements and estimated interface node displacements of the experimental frame () | ||
| J6 | % | Maximum peak error between the instantaneous response of frame target displacement and estimated interface node displacements of the experimental frame () | ||
| Global RTHS | J7 | % | Normalized error between reference and estimated measured response of the frame at the interface node () | |
| J8 | % | Normalized error between relative reference and relative numerical substructure response at upper stories () | ||
| J9 | % | Maximum peak global displacement error between reference and estimated measured response of the frame at the interface node () | ||
| J10 | % | Maximum peak global displacement error between relative reference and relative numerical substructure response at upper stories () |
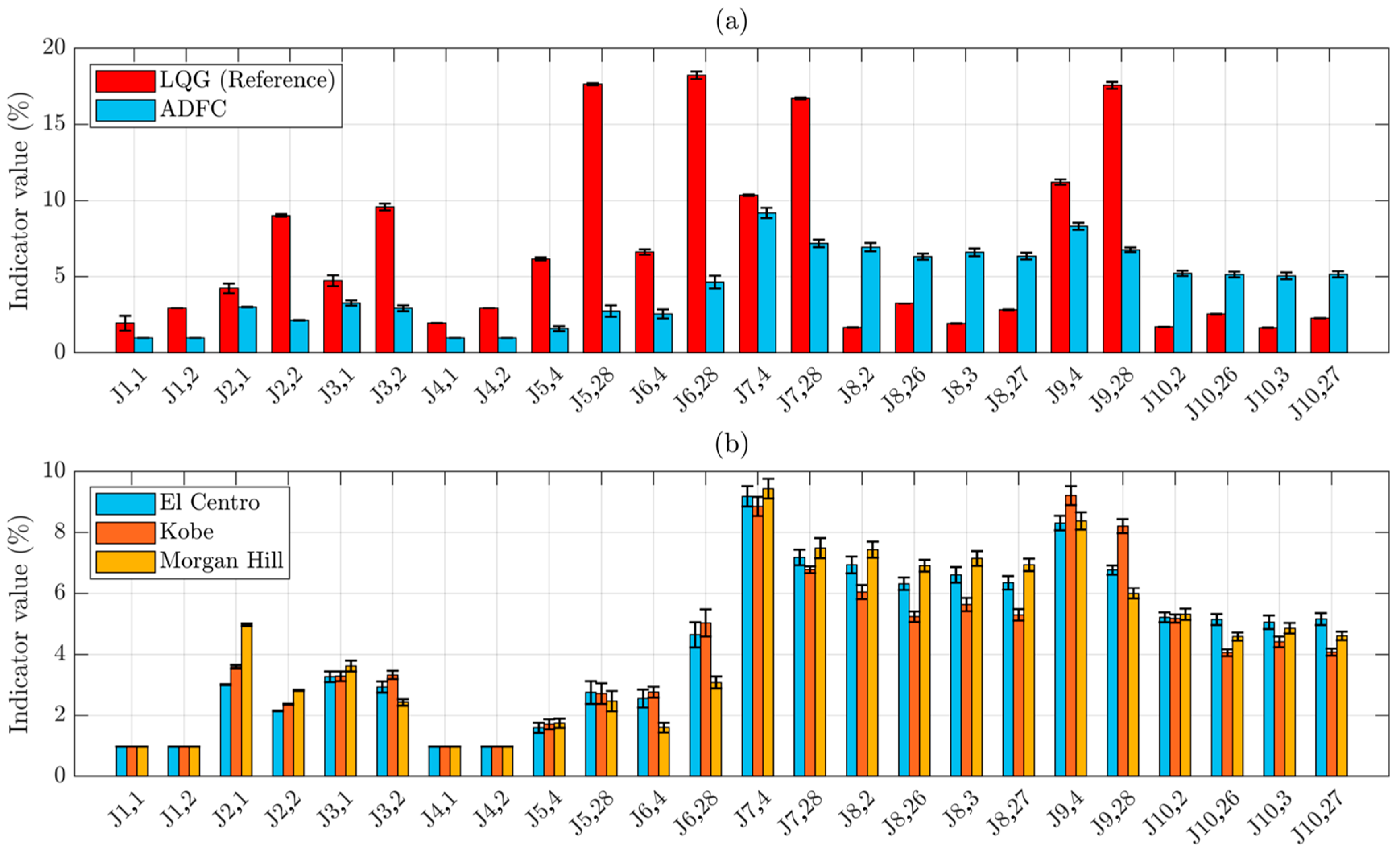
| Performance | Criterion | Index | Experimental maRTHS (with LQG) | Virtual maRTHS for Nominal Plant (with LQG) | Virtual maRTHS for Nominal Plant (with ADFC) |
|---|---|---|---|---|---|
| Tracking Control | Time delay | J1,1 | −13.7 | 2.0 | 0.98 |
| J1,2 | 2.9 | 2.9 | 0.98 | ||
| Normalized tracking error | J2,1 | 23.8 | 4.8 | 3.90 | |
| J2,2 | 13.2 | 9.4 | 2.46 | ||
| Max. peak tracking error | J3,1 | 26.9 | 5.3 | 3.39 | |
| J3,2 | 13.7 | 10.3 | 2.92 | ||
| Estimation | Time delay | J4,1 | 1.9 | 1.9 | 0.98 |
| J4,2 | 4.9 | 2.9 | 0.98 | ||
| Normalized estimation error | J5,4 | 8.1 | 6.7 | 1.69 | |
| J5,28 | 27.8 | 17.8 | 2.59 | ||
| Max. peak estimation error | J6,4 | 8.2 | 7.4 | 2.36 | |
| J6,28 | 28.6 | 18.8 | 3.88 | ||
| Global RTHS | Normalized RTHS error | J7,4 | 12.2 | 10.6 | 9.18 |
| J7,28 | 26.2 | 16.8 | 7.13 | ||
| Normalized RTHS error at upper levels | J8,2 | 12.5 | 1.8 | 6.81 | |
| J8,26 | 12.7 | 3.4 | 6.15 | ||
| J8,3 | 12.4 | 2.1 | 6.46 | ||
| J8,27 | 12.5 | 3.0 | 6.20 | ||
| Max. peak RTHS error | J9,4 | 13.2 | 11.9 | 8.61 | |
| J9,28 | 27.3 | 18.1 | 7.02 | ||
| Max. peak RTHS error at upper levels | J10,2 | 13.4 | 2.7 | 5.23 | |
| J10,26 | 13.4 | 2.7 | 4.59 | ||
| J10,3 | 12.8 | 1.8 | 4.77 | ||
| J10,27 | 13.2 | 2.4 | 4.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calayir, M.; Tao, J.; Mercan, O. Application of Adaptive Discrete Feedforward Controller in Multi-Axial Real-Time Hybrid Simulation. Actuators 2025, 14, 525. https://doi.org/10.3390/act14110525
Calayir M, Tao J, Mercan O. Application of Adaptive Discrete Feedforward Controller in Multi-Axial Real-Time Hybrid Simulation. Actuators. 2025; 14(11):525. https://doi.org/10.3390/act14110525
Chicago/Turabian StyleCalayir, Muhammet, Junjie Tao, and Oya Mercan. 2025. "Application of Adaptive Discrete Feedforward Controller in Multi-Axial Real-Time Hybrid Simulation" Actuators 14, no. 11: 525. https://doi.org/10.3390/act14110525
APA StyleCalayir, M., Tao, J., & Mercan, O. (2025). Application of Adaptive Discrete Feedforward Controller in Multi-Axial Real-Time Hybrid Simulation. Actuators, 14(11), 525. https://doi.org/10.3390/act14110525






