Robust and Non-Fragile Path Tracking Control for Autonomous Vehicles
Abstract
1. Introduction
- A robust and non-fragile path tracking controller is newly formulated using an LMI-based LQR framework. The proposed approach explicitly integrates the non-fragile property—an aspect rarely addressed in previous path tracking studies—into the controller design, thereby improving both robustness and implementation reliability under parameter perturbations.
- A systematic comparative analysis of multiple actuators (RS, 4ID, and 4IB) for yaw-moment generation is conducted. While most existing robust PTC studies have relied solely on FS or 4S, this work provides the first structured evaluation of how different actuator combinations affect path tracking robustness and overall vehicle stability.
- The comprehensive simulation results identify optimal controller–actuator configurations for practical implementation. The study demonstrates that when performance differences are minor, a simpler LQR design remains the most effective choice—offering clear design guidance for real-world autonomous vehicle control.
2. Design of a Robust Non-Fragile Path Tracking Controller
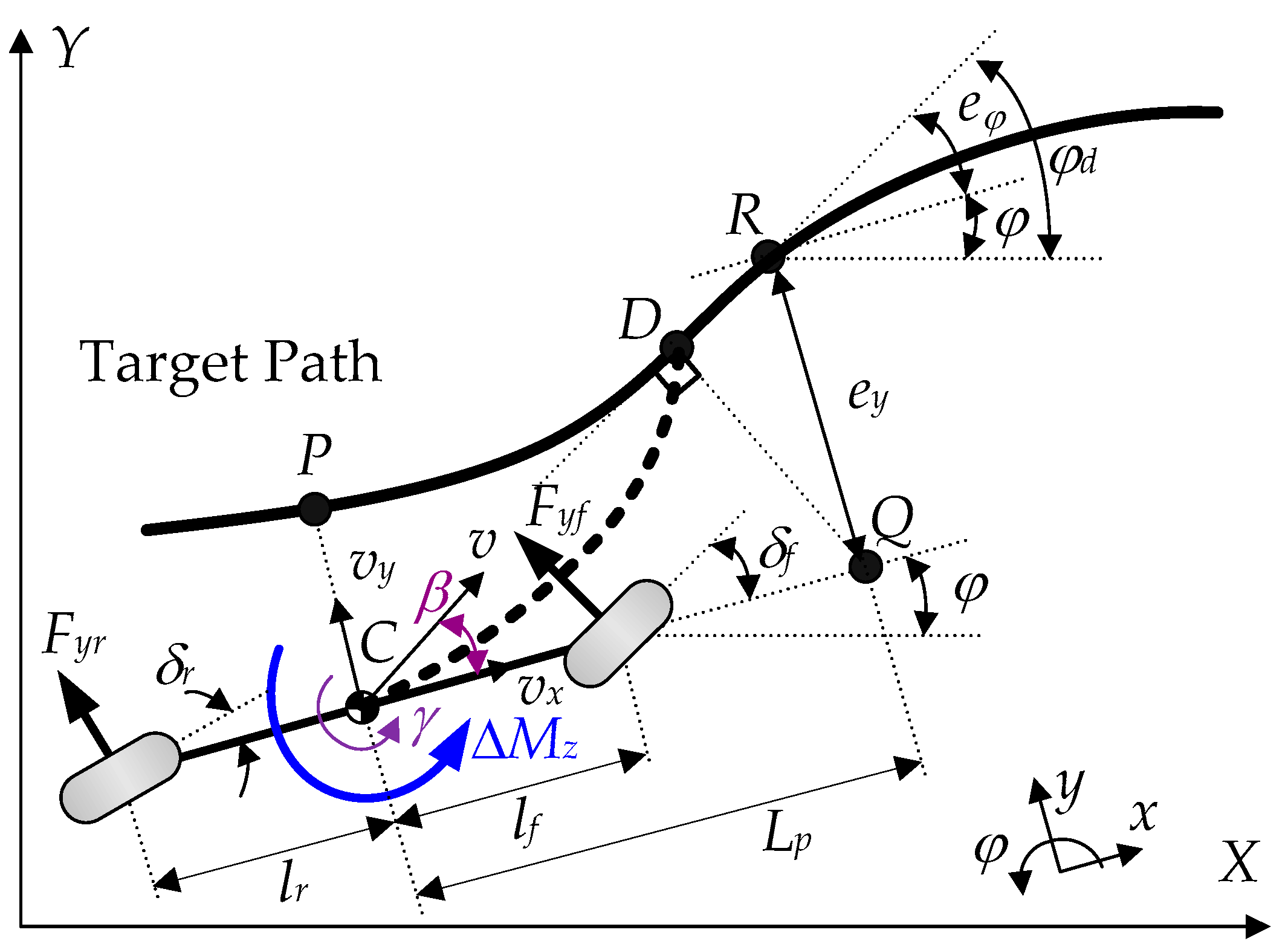
2.1. State-Space Model Formulation
2.2. Design of LQR
2.3. Design of Robust Non-Fragile LQR
2.4. Constraints Related to Tire Slip Angle
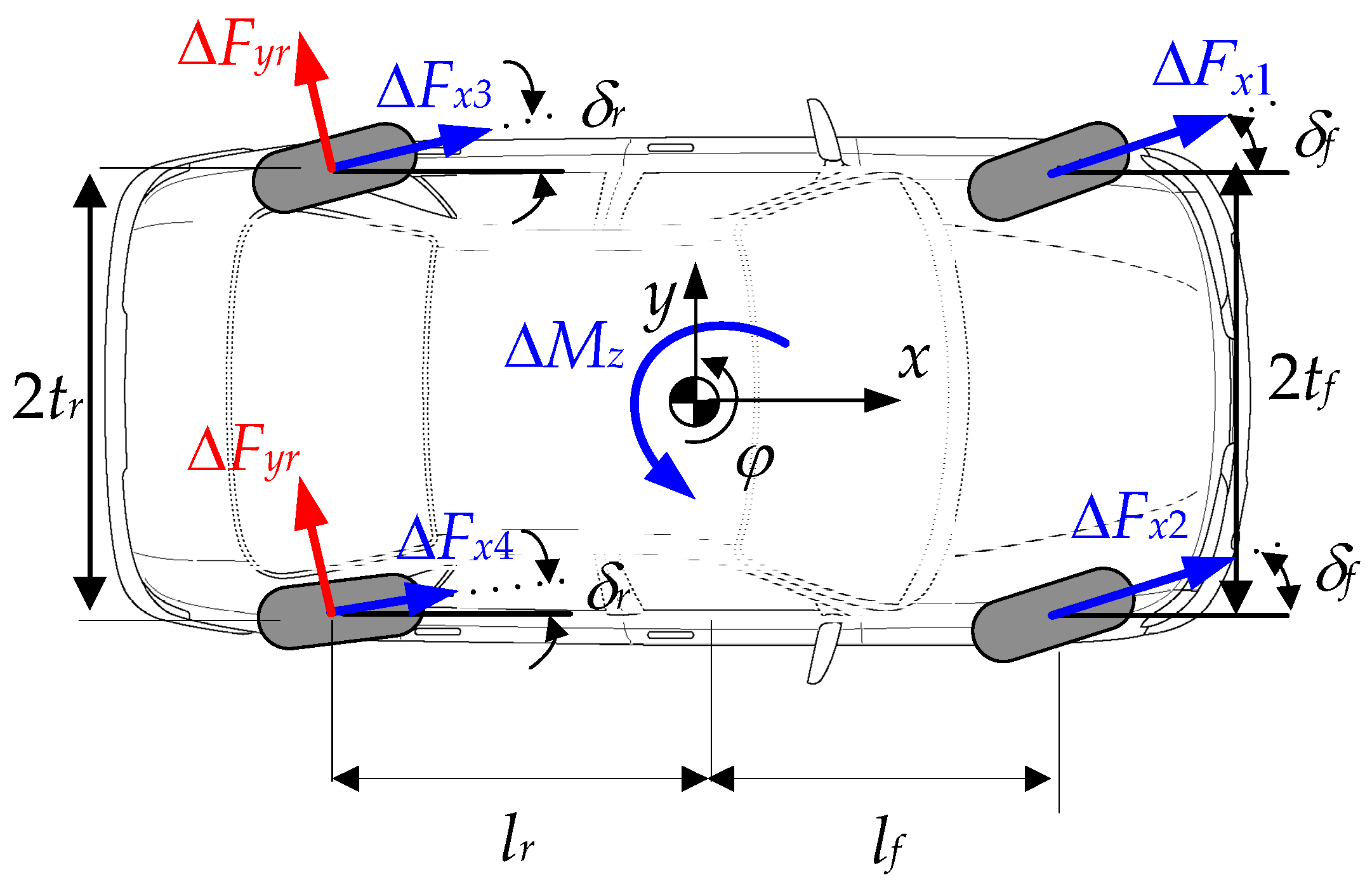
2.5. Control Allocation for LQR with CONFIG-3
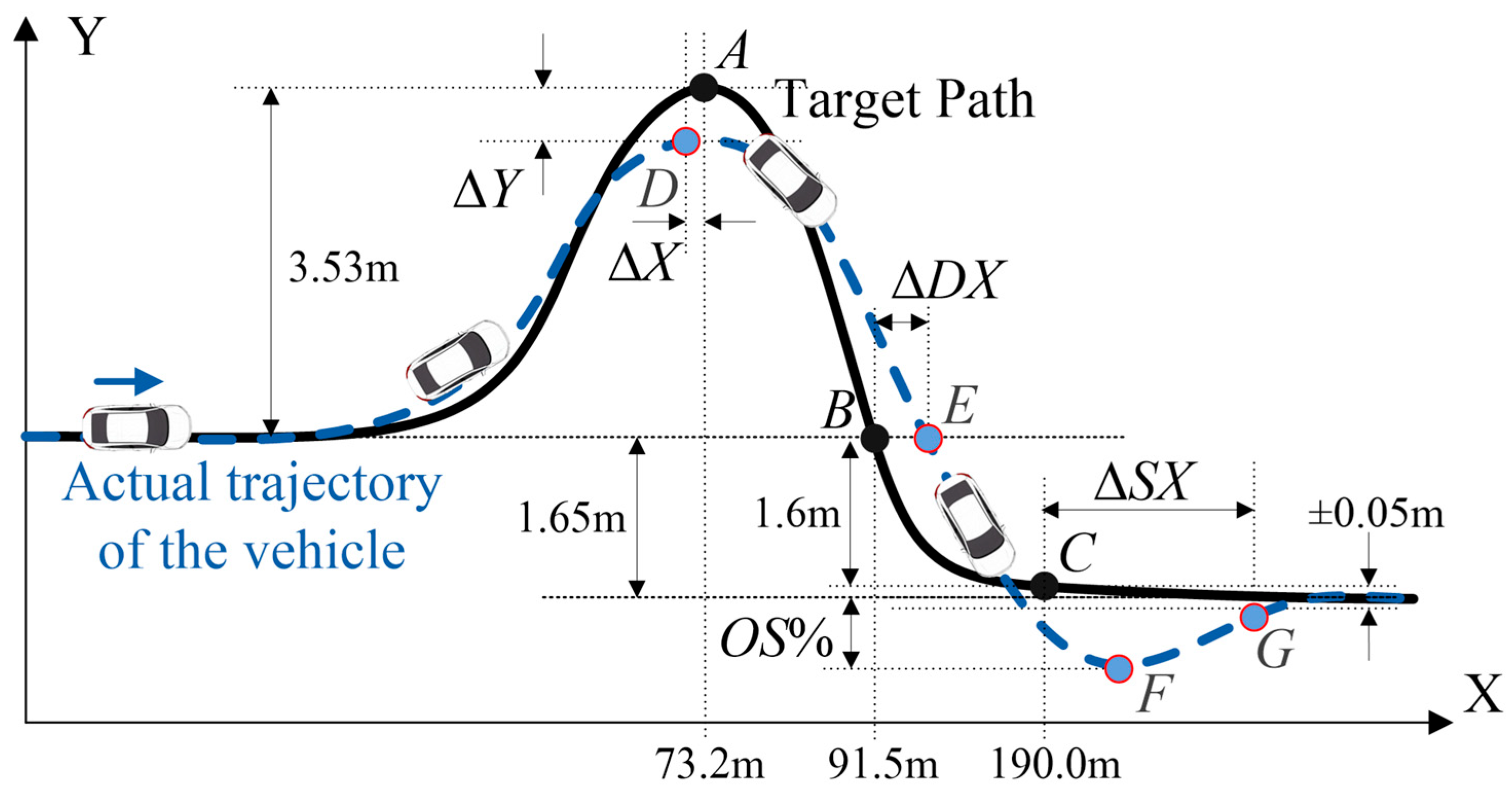
3. Performance Measures for Path Tracking Control
4. Simulation and Validation
4.1. Controller Tuning
4.2. Simulation on CarSim for the Controllers with Actuator Configurations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Actuator Combinations | kv | The Vector of MAVs, ξi | |
|---|---|---|---|
| CONFIG-1 | FS | 0.186 | [0.150 0.02 0.10 0.20 0.03] |
| CONFIG-2 | 4S | 0.182 | [0.140 0.02 0.10 0.20 0.03 0.003] |
| CONFIG-3 FS | + RS | 0.201 | [0.120 0.02 0.10 0.50 0.03 2000.0] |
| + RS + 4ID | 0.201 | [0.120 0.02 0.10 0.50 0.03 2000.0] | |
| + RS + 4IB | 0.201 | [0.120 0.02 0.10 0.50 0.03 2000.0] | |
| + RS + 4IB + 4ID | 0.198 | [0.120 0.02 0.10 0.50 0.03 2000.0] | |
| + 4ID | 0.214 | [0.100 0.02 0.10 0.50 0.03 2000.0] | |
| + 4IB | 0.203 | [0.100 0.02 0.10 0.50 0.03 2000.0] | |
| + 4IB + 4ID | 0.202 | [0.100 0.02 0.10 0.50 0.03 2000.0] |
| Actuator Combinations | kv | The Vector of MAVs, ξi | |
|---|---|---|---|
| CONFIG-1 | FS | 0.187 | [0.130 0.10 0.10 0.20 0.03] |
| CONFIG-2 | 4S | 0.177 | [0.140 0.05 0.50 0.10 0.03 0.004] |
| CONFIG-3 FS | + RS | 0.201 | [0.100 0.05 0.10 0.10 0.03 2000.0] |
| + RS + 4ID | 0.203 | [0.096 0.05 0.10 0.10 0.03 2000.0] | |
| + RS + 4IB | 0.206 | [0.110 0.05 0.10 0.10 0.03 2000.0] | |
| + RS + 4IB + 4ID | 0.206 | [0.110 0.05 0.10 0.10 0.03 2000.0] | |
| + 4ID | 0.195 | [0.074 0.02 0.10 0.10 0.03 2000.0] | |
| + 4IB | 0.197 | [0.082 0.05 0.10 0.10 0.03 2000.0] | |
| + 4IB + 4ID | 0.198 | [0.079 0.05 0.10 0.10 0.03 2000.0] |
| Actuator Combinations | kv | The Vector of MAVs, ξi | |
|---|---|---|---|
| CONFIG-1 | FS | 0.180 | [0.140 0.02 0.10 0.20 0.03] |
| CONFIG-2 | 4S | 0.153 | [0.100 0.02 0.10 0.20 0.03 0.003] |
| CONFIG-3 FS | + RS | 0.180 | [0.160 0.02 0.10 0.50 0.03 2000.0] |
| + RS + 4ID | 0.182 | [0.170 0.02 0.10 0.50 0.03 2000.0] | |
| + RS + 4IB | 0.170 | [0.120 0.02 0.10 0.50 0.03 2000.0] | |
| + RS + 4IB + 4ID | 0.179 | [0.170 0.02 0.10 0.50 0.03 2000.0] | |
| + 4ID | 0.196 | [0.140 0.02 0.10 0.50 0.03 2000.0] | |
| + 4IB | 0.181 | [0.140 0.02 0.10 0.50 0.03 2000.0] | |
| + 4IB + 4ID | 0.181 | [0.140 0.02 0.10 0.50 0.03 2000.0] |
| Actuator Combinations | kv | The Vector of MAVs, ξi | |
|---|---|---|---|
| CONFIG-1 | FS | 0.186 | [0.130 0.10 0.10 0.20 0.03] |
| CONFIG-2 | 4S | 0.174 | [0.150 0.05 0.50 0.10 0.03 0.004] |
| CONFIG-3 FS | + RS | 0.118 | [0.100 0.10 0.01 0.05 0.05 600.0] |
| + RS + 4ID | 0.102 | [0.160 0.05 0.10 0.10 0.05 800.0] | |
| + RS + 4IB | 0.088 | [0.160 0.05 0.10 0.10 0.05 500.0] | |
| + RS + 4IB + 4ID | 0.093 | [0.160 0.05 0.10 0.10 0.05 600.0] | |
| + 4ID | 0.128 | [0.160 0.10 0.01 0.05 0.02 300.0] | |
| + 4IB | 0.113 | [0.160 0.10 0.01 0.05 0.03 300.0] | |
| + 4IB + 4ID | 0.124 | [0.160 0.10 0.01 0.05 0.03 300.0] |
References
- Dudziak, A.; Stoma, M.; Kuranc, A.; Caban, J. Assessment of Social Acceptance for Autonomous Vehicles in Southeastern Poland. Energies 2021, 14, 5778. [Google Scholar] [CrossRef]
- Bartuska, L.; Hanzl, J.; Lizbetin, J. Urban traffic detectors data mining for determination of variations in traffic volumes. Arch. Motoryz. 2020, 90, 15–31. [Google Scholar] [CrossRef]
- Montanaro, U.; Dixit, S.; Fallaha, S.; Dianatib, M.; Stevensc, A.; Oxtobyd, D.; Mouzakitisd, A. Towards connected autonomous driving: Review of use-cases. Veh. Syst. Dyn. 2019, 57, 779–814. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A survey of autonomous driving: Common practices and emerging technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Omeiza, D.; Webb, H.; Jirotka, M.; Kunze, M. Explanations in autonomous driving: A survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10142–10162. [Google Scholar] [CrossRef]
- Shladover, S.E. Cooperative vehicle-highway automation systems. IEEE Intell. Transp. Syst. Mag. 2009, 1, 10–19. [Google Scholar]
- Paden, B.; Cap, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Sorniotti, A.; Barber, P.; De Pinto, S. Path tracking for automated driving: A tutorial on control system formulations and ongoing research. In Automated Driving; Watzenig, D., Horn, M., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Amer, N.H.; Hudha, H.Z.K.; Kadir, Z.A. Modelling and control strategies in path tracking control for autonomous ground vehicles: A review of state of the art and challenges. J. Intell. Robot. Syst. 2017, 86, 225–254. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Liu, L. Review and comparison of path tracking based on model predictive control. Electronics 2019, 8, 1077. [Google Scholar] [CrossRef]
- Li, D.; Du, L. AUV trajectory tracking models and control strategies: A review. J. Mar. Sci. Eng. 2021, 9, 1020. [Google Scholar] [CrossRef]
- Yao, Q.; Tian, Y.; Wang, Q.; Wang, S. Control strategies on path tracking for autonomous vehicle: State of the art and future challenges. IEEE Access 2020, 8, 161211–161222. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2022, 55, 194–236. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, J.; Xin, X.; Li, X.; Sun, C.; Huang, J.; Kong, W. A survey on learning-based model predictive control: Toward path tracking control of mobile platforms. Appl. Sci. 2022, 12, 1995. [Google Scholar] [CrossRef]
- Festl, K.; Solmaz, S.; Watzenig, D. Smooth and Robust Path-Tracking Control for Automated Vehicles: From Theory to Real-World Applications. Electronics 2025, 14, 3588. [Google Scholar] [CrossRef]
- Khosravian, A.; Masih-Tehrani, M.; Amirkhani, A.; Ebrahimi-Nejad, S. Robust autonomous vehicle control by leveraging multi-stage MPC and quantized CNN in HIL Framework. Appl. Soft Comput. 2024, 162, 111802. [Google Scholar] [CrossRef]
- Yim, S. Design of a robust controller for rollover prevention with active suspension and differential braking. J. Mech. Sci. Technol. 2012, 26, 213–222. [Google Scholar] [CrossRef]
- Kissai, M.; Monsuez, B.; Martinez, D.; Mouton, X.; Tapus, A. Robust control for over-actuated vehicles. In Proceedings of the 2019 IEEE Conference on Control Technology and Applications (CCTA), Hong Kong, China, 19–21 August 2019; pp. 822–829. [Google Scholar]
- Mustaki, S.; Chevrel, P.; Yagoubi, M.; Fauvel, F.; Kvieska, P. Robust lateral control of cars: Towards a reduction of pessimism and an easy trade-off between performance, comfort and robustness. IFAC PapersOnLine 2019, 52, 197–204. [Google Scholar] [CrossRef]
- Wang, R.; Yin, G.; Jin, X. Robust adaptive sliding mode control for nonlinear four-wheel steering autonomous vehicles path tracking systems. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016. [Google Scholar]
- Hang, P.; Chen, X.; Luo, F.; Fang, S. Robust control of a four-wheel-independent-steering electric vehicle for path tracking. SAE Int. J. Veh. Dyn. Stab. NVH 2017, 1, 307–316. [Google Scholar] [CrossRef]
- Peng, H.; Wang, W.; An, Q.; Xiang, C.; Li, L. Path tracking and direct yaw moment coordinated control based on robust MPC with the finite time horizon for autonomous independent-drive vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6053–6066. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, W.; Li, J. Gain scheduling output feedback control for vehicle path tracking considering input saturation. Energies 2020, 13, 4570. [Google Scholar] [CrossRef]
- Cong, G.; Jian, Z.; Jinxiong, L. Path Tracking Control based on adaptive control period. IFAC PapersOnLine 2020, 53, 592–597. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, J.; Yang, D.; Zhong, Z. Design and optimization of robust path tracking control for autonomous vehicles with fuzzy uncertainty. IEEE Trans. Fuzzy Syst. 2022, 30, 1788–1800. [Google Scholar] [CrossRef]
- Vo, C.P.; Lee, J.; Jeon, J.H. Robust adaptive path tracking control scheme for safe autonomous driving via predicted interval algorithm. IEEE Access 2022, 10, 124333–124344. [Google Scholar] [CrossRef]
- Li, H.; Huang, J.; Yang, Z.; Hu, Z.; Yang, D.; Zhong, Z. Adaptive robust path tracking control for autonomous vehicles with measurement noise. Int. J. Robust Nonlinear Control 2022, 32, 7319–7335. [Google Scholar] [CrossRef]
- Chen, C.; Shu, M.; Yang, Y.; Gao, T.; Bian, L. Robust H∞ path tracking control of autonomous vehicles with delay and actuator saturation. J. Control Decis. 2022, 9, 45–57. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, J.; Yang, Z.; Zhong, Z. Cooperative-game-theoretic optimal robust path tracking control for autonomous vehicles. J. Vib. Control 2022, 28, 520–535. [Google Scholar] [CrossRef]
- Li, X.; Liu, C.; Chen, B.; Jiang, J. Robust adaptive learning-based path tracking control of autonomous vehicles under uncertain driving environments. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20798–20809. [Google Scholar] [CrossRef]
- Tian, Y.; Yao, Q.; Hang, P.; Wang, S. Adaptive coordinated path tracking control strategy for autonomous vehicles with direct yaw moment control. Chin. J. Mech. Eng. 2022, 35, 1. [Google Scholar] [CrossRef]
- Tian, Y.; Yao, Q.; Hang, P.; Wang, S. A gain-scheduled robust controller for autonomous vehicles path tracking based on LPV system with MPC and H∞. IEEE Trans. Veh. Technol. 2022, 71, 9350–9362. [Google Scholar] [CrossRef]
- Hu, Z.; Yu, Z.; Yang, Z.; Hu, Z.; Bian, Y. Rendering bounded error in adaptive robust path tracking control for autonomous vehicles. IET Control Theory Appl. 2022, 16, 1259–1270. [Google Scholar] [CrossRef]
- Cai, G.; Xu, L.; Liu, Y.; Feng, J.; Liang, J.; Lu, Y.; Yin, G. Robust preview path tracking control of autonomous vehicles under time-varying system delays and saturation. IEEE Trans. Veh. Technol. 2023, 72, 8486–8499. [Google Scholar] [CrossRef]
- Chen, M.; Ren, Y.; Ou, M. Adaptive robust path tracking control for autonomous vehicles considering multi-dimensional system uncertainty. World Electr. Veh. J. 2023, 14, 11. [Google Scholar] [CrossRef]
- Ge, Z.; Man, Z.; Wang, Z.; Bai, X.; Wang, X.; Xiong, F.; Li, D. Robust adaptive sliding mode control for path tracking of unmanned agricultural vehicles. Comput. Electr. Eng. 2023, 108, 108693. [Google Scholar] [CrossRef]
- Taghavifar, H.; Shojaei, K. Adaptive robust control algorithm for enhanced path-tracking performance of automated driving in critical scenarios. Soft Comput. 2023, 27, 8841–8854. [Google Scholar] [CrossRef]
- Cao, X.; Xu, T.; Tian, Y.; Ji, X. Gain-scheduling LPV synthesis H∞ robust lateral motion control for path following of autonomous vehicle via coordination of steering and braking. Veh. Syst. Dyn. 2023, 61, 968–991. [Google Scholar] [CrossRef]
- Nam, N.N.; Han, K. Path-tracking robust model predictive control of an autonomous steering system using LMI optimization with independent constraints enforcement. Int. J. Control Autom. Syst. 2024, 22, 3352–3363. [Google Scholar] [CrossRef]
- Keel, L.H.; Bhattacharyya, S.P. Robust, fragile, or optimal? IEEE Trans. Automat. Control 1997, 42, 1098–1105. [Google Scholar] [CrossRef]
- Yang, G.; Guo, X.; Che, W.; Guan, W. Linear Systems—Non-Fragile Control and Filtering; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Park, M.; Yim, S. Comparative study on effects of input configurations of linear quadratic controller on path tracking performance under low friction condition. Actuators 2023, 12, 153. [Google Scholar] [CrossRef]
- Jeong, Y.; Yim, S. Path tracking control with four-wheel independent steering, driving and braking systems for autonomous electric vehicles. IEEE Access 2022, 10, 74733–74746. [Google Scholar] [CrossRef]
- Lee, J.; Yim, S. Comparative study of path tracking controllers on low friction roads for autonomous vehicles. Machines 2023, 11, 403. [Google Scholar] [CrossRef]
- Jilek, P.; Němec, J. System for changing adhesion conditions in experimental road vehicle. Int. J. Automot. Technol. 2021, 22, 779–785. [Google Scholar] [CrossRef]
- Dižo, J.; Blatnický, M.; Melnik, R.; Karľa, M. Improvement of steerability and driving safety of an electric three-wheeled vehicle by a design modification of its steering mechanism. LOGI Sci. J. Transp. Logist. 2022, 13, 49–60. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere: New York, NY, USA, 1975. [Google Scholar]
- Liu, K.Z. LMI approach to robust control. In Encyclopedia of Systems and Control; Baillieul, J., Samad, T., Eds.; Springer: London, UK, 2013. [Google Scholar]
- Lee, J.; Yim, S. path tracking control with constraint on tire slip angles under low-friction road conditions. Appl. Sci. 2024, 14, 1066. [Google Scholar] [CrossRef]
- Wong, H.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley and Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer: New York, NY, USA, 2006. [Google Scholar]
- Yim, S.; Choi, J.; Yi, K. Coordinated control of hybrid 4WD vehicles for enhanced maneuverability and lateral stability. IEEE Trans. Veh. Technol. 2012, 61, 1946–1950. [Google Scholar] [CrossRef]
- Yim, S. Coordinated control with electronic stability control and active steering devices. J. Mech. Sci. Technol. 2015, 29, 5409–5416. [Google Scholar] [CrossRef]
- Rezaeian, A.; Zarringhalam, R.; Fallah, S.; Melek, W.; Khajepour, A.; Chen, S.-K.; Moshchuck, N.; Litkouhi, B. Novel tire force estimation strategy for real-time implementation on vehicle applications. IEEE Trans. Veh. Technol. 2015, 64, 2231–2241. [Google Scholar] [CrossRef]
- Yim, S. Comparison among active front, front independent, 4-wheel and 4-wheel independent steering systems for vehicle stability control. Electronics 2020, 9, 798. [Google Scholar] [CrossRef]
- Park, M.B.; Yim, S. Design of Static Output Feedback Integrated Path Tracking Controller for Autonomous Vehicles. Processes 2025, 13, 1335. [Google Scholar] [CrossRef]
- Nah, J.; Yim, S. Vehicle stability control with four-wheel independent braking, drive and steering on in-wheel motor-driven electric vehicles. Electronics 2020, 9, 1934. [Google Scholar] [CrossRef]
- Kim, H.H.; Ryu, J. Sideslip angle estimation considering short-duration longitudinal velocity variation. Int. J. Automot. Technol. 2011, 12, 545–553. [Google Scholar] [CrossRef]
- Mechanical Simulation Corporation. VS Browser: Reference Manual, the Graphical User Interfaces of BikeSim, CarSim, and TruckSim; Mechanical Simulation Corporation: Ann Arbor, MI, USA, 2009. [Google Scholar]
- Ben Hazem, Z.; Guler, N.; Altaif, A.H. Model-free trajectory tracking control of a 5-DOF mitsubishi robotic arm using deep deterministic policy gradient algorithm. Discov. Robot. 2025, 1, 4. [Google Scholar] [CrossRef]

| Actuator Combinations | Vector of Virtual Weights | ||
|---|---|---|---|
| CONFIG-1 | SET-1 | FS | |
| CONFIG-2 | SET-2 | 4S | |
| CONFIG-3 FS | SET-3 | +RS | |
| SET-4 | +RS + 4ID | ||
| SET-5 | +RS + 4IB | ||
| SET-6 | +RS + 4ID + 4IB | ||
| SET-7 | +4ID | ||
| SET-8 | +4IB | ||
| SET-9 | +4ID + 4IB | ||
| Parameter | Value | Unit |
|---|---|---|
| ms | 1823 | kg |
| lf | 1.27 | m |
| lr | 1.90 | m |
| Iz | 6286 | kg-m2 |
| tr | 0.80 | m |
| tf | 0.80 | m |
| Cf | 42,000 | N/rad |
| Cr | 62,000 | N/rad |
| Actuator Combinations | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | FS | 0.39 | −0.020 | 0.5 | 0.69 | −2.29 | 1.5 | 5.1 |
| CONFIG-2 | SET-2 | 4S | 0.39 | −0.020 | 0.5 | 0.67 | −2.32 | 2.0 | 6.4 |
| CONFIG-3 FS | SET-3 | +RS | 0.31 | −0.021 | 0.4 | 0.54 | −2.53 | 1.9 | 6.2 |
| SET-4 | +RS + 4ID | 0.34 | −0.020 | 0.6 | 0.59 | −3.08 | 1.8 | 6.2 | |
| SET-5 | +RS + 4IB | 0.36 | −0.020 | 0.6 | 0.57 | −2.76 | 2.0 | 6.4 | |
| SET-6 | +RS + 4ID + 4IB | 0.35 | −0.020 | 0.6 | 0.54 | −3.13 | 2.0 | 6.4 | |
| SET-7 | +4ID | 0.33 | −0.020 | 0.7 | 0.88 | −4.19 | 1.2 | 6.0 | |
| SET-8 | +4IB | 0.29 | −0.021 | 0.4 | 0.47 | −2.51 | 1.7 | 5.2 | |
| SET-9 | +4ID + 4IB | 0.28 | −0.020 | 0.3 | 0.48 | −2.79 | 1.5 | 5.6 | |
| Actuator Combinations | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | FS | 0.59 | −0.020 | 0.9 | 0.95 | −3.04 | 1.5 | 4.9 |
| CONFIG-2 | SET-2 | 4S | 0.57 | −0.021 | 0.9 | 0.89 | −2.83 | 2.5 | 7.7 |
| CONFIG-3 FS | SET-3 | +RS | 0.39 | −0.021 | 0.6 | 0.63 | −3.07 | 1.9 | 6.1 |
| SET-4 | +RS + 4ID | 0.41 | −0.021 | 0.9 | 0.75 | −3.67 | 1.7 | 6.0 | |
| SET-5 | +RS + 4IB | 0.49 | −0.020 | 0.9 | 0.75 | −3.41 | 2.0 | 6.2 | |
| SET-6 | +RS + 4ID + 4IB | 0.49 | −0.021 | 0.9 | 0.74 | −3.54 | 1.9 | 6.2 | |
| SET-7 | +4ID | 0.34 | −0.021 | 0.8 | 0.98 | −4.52 | 1.1 | 7.7 | |
| SET-8 | +4IB | 0.31 | −0.021 | 0.3 | 0.52 | −2.79 | 1.7 | 5.5 | |
| SET-9 | +4ID + 4IB | 0.28 | −0.021 | 0.2 | 0.52 | −2.76 | 1.5 | 5.6 | |
| Actuator Combinations | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | FS | 0.32 | −0.021 | 0.4 | 0.59 | −2.03 | 1.5 | 5.2 |
| CONFIG-2 | SET-2 | 4S | 0.12 | −0.020 | 0.1 | 0.30 | −0.94 | 2.2 | 7.4 |
| CONFIG-3 FS | SET-3 | +RS | 0.39 | −0.020 | 0.5 | 0.67 | −1.79 | 1.9 | 6.5 |
| SET-4 | +RS + 4ID | 0.43 | −0.021 | 0.7 | 0.72 | −2.64 | 1.9 | 6.3 | |
| SET-5 | +RS + 4IB | 0.23 | −0.021 | 0.3 | 0.41 | −1.96 | 2.0 | 6.7 | |
| SET-6 | +RS + 4ID + 4IB | 0.44 | −0.020 | 0.8 | 0.68 | −2.76 | 2.0 | 6.3 | |
| SET-7 | +4ID | 0.43 | −0.020 | 0.9 | 1.04 | −3.52 | 1.2 | 5.5 | |
| SET-8 | +4IB | 0.35 | −0.020 | 0.5 | 0.59 | −2.41 | 1.7 | 5.3 | |
| SET-9 | +4ID + 4IB | 0.35 | −0.020 | 0.5 | 0.61 | −2.65 | 1.6 | 5.6 | |
| Actuator Combinations | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | ||
|---|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | FS | 0.57 | −0.021 | 0.9 | 0.95 | −3.01 | 1.5 | 4.9 |
| CONFIG-2 | SET-2 | 4S | 0.59 | −0.020 | 0.9 | 0.92 | −2.75 | 2.5 | 7.7 |
| CONFIG-3 FS | SET-3 | +RS | 0.39 | −0.020 | 0.5 | 0.67 | −1.79 | 1.9 | 6.5 |
| SET-4 | +RS + 4ID | 0.14 | −0.021 | 0.3 | 0.53 | −1.62 | 1.7 | 19.3 | |
| SET-5 | +RS + 4IB | 0.13 | −0.021 | 0.1 | 0.31 | −0.53 | 2.0 | 7.1 | |
| SET-6 | +RS + 4ID + 4IB | 0.12 | −0.021 | 0.0 | 0.34 | 0.14 | 1.9 | 7.2 | |
| SET-7 | +4ID | 0.30 | −0.020 | 0.5 | 1.16 | −2.45 | 1.1 | 21.7 | |
| SET-8 | +4IB | 0.27 | −0.020 | 0.1 | 0.55 | −0.89 | 1.7 | 6.3 | |
| SET-9 | +4ID + 4IB | 0.28 | −0.021 | 0.1 | 0.65 | −0.31 | 1.5 | 6.0 | |
| AC’s | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | |
|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | 0.56 ± 0.40 | −0.023 ± 0.021 | 0.9 ± 0.6 | 1.79 ± 1.17 | 8.44 ± 4.91 | 1.5 ± 0.4 | 7.7 ± 1.9 |
| CONFIG-2 | SET-2 | 0.56 ± 0.38 | −0.022 ± 0.021 | 1.5 ± 1.1 | 1.75 ± 1.15 | 9.57 ± 5.97 | 2.0 ± 0.3 | 8.3 ± 2.0 |
| CONFIG-3 FS | SET-3 | 0.65 ± 0.40 | −0.006 ± 0.025 | 2.3 ± 1.7 | 1.82 ± 1.16 | 9.18 ± 5.62 | 1.5 ± 0.3 | 7.5 ± 1.8 |
| SET-4 | 0.65 ± 0.40 | −0.006 ± 0.025 | 2.3 ± 1.7 | 1.82 ± 1.16 | 9.18 ± 5.62 | 1.5 ± 0.3 | 7.5 ± 1.8 | |
| SET-5 | 0.65 ± 0.40 | −0.006 ± 0.025 | 2.3 ± 1.7 | 1.82 ± 1.16 | 9.18 ± 5.62 | 1.5 ± 0.3 | 7.5 ± 1.8 | |
| SET-6 | 0.69 ± 0.41 | −0.001 ± 0.026 | 2.4 ± 1.8 | 1.85 ± 1.17 | 9.27 ± 5.74 | 1.5 ± 0.3 | 7.5 ± 1.8 | |
| SET-7 | 0.36 ± 0.33 | −0.037 ± 0.023 | 3.4 ± 3.0 | 1.48 ± 1.01 | 7.81 ± 5.73 | 1.5 ± 0.3 | 7.7 ± 1.9 | |
| SET-8 | 0.47 ± 0.36 | −0.019 ± 0.026 | 3.7 ± 3.2 | 1.57 ± 1.07 | 7.85 ± 6.09 | 1.5 ± 0.3 | 7.8 ± 1.9 | |
| SET-9 | 0.48 ± 0.37 | −0.017 ± 0.026 | 3.7 ± 3.2 | 1.58 ± 1.08 | 7.84 ± 6.12 | 1.5 ± 0.3 | 7.8 ± 1.9 |
| AC’s | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | |
|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | 0.74 ± 0.46 | −0.028 ± 0.022 | 1.1 ± 0.6 | 2.06 ± 1.25 | 10.71 ± 5.45 | 1.5 ± 0.4 | 8.1 ± 2.5 |
| CONFIG-2 | SET-2 | 0.72 ± 0.43 | −0.027 ± 0.020 | 1.8 ± 1.1 | 1.97 ± 1.20 | 11.89 ± 6.47 | 2.5 ± 0.2 | 9.4 ± 2.5 |
| CONFIG-3 FS | SET-3 | 0.78 ± 0.45 | −0.003 ± 0.028 | 3.4 ± 2.5 | 1.96 ± 1.20 | 9.63 ± 5.88 | 1.5 ± 0.4 | 8.0 ± 2.3 |
| SET-4 | 0.71 ± 0.43 | −0.010 ± 0.027 | 3.5 ± 2.7 | 1.87 ± 1.16 | 9.60 ± 5.71 | 1.5 ± 0.4 | 8.1 ± 2.3 | |
| SET-5 | 0.87 ± 0.46 | −0.002 ± 0.026 | 2.6 ± 1.6 | 2.09 ± 1.22 | 9.48 ± 5.94 | 1.5 ± 0.4 | 7.8 ± 2.2 | |
| SET-6 | 0.87 ± 0.46 | −0.002 ± 0.026 | 2.6 ± 1.6 | 2.09 ± 1.22 | 9.48 ± 5.94 | 1.5 ± 0.4 | 7.8 ± 2.2 | |
| SET-7 | 0.33 ± 0.35 | −0.045 ± 0.025 | 4.3 ± 3.8 | 1.44 ± 1.01 | 8.78 ± 5.96 | 1.5 ± 0.4 | 8.5 ± 2.4 | |
| SET-8 | 0.57 ± 0.41 | −0.016 ± 0.029 | 4.7 ± 3.9 | 1.69 ± 1.11 | 9.49 ± 5.66 | 1.5 ± 0.4 | 8.4 ± 2.4 | |
| SET-9 | 0.51 ± 0.39 | −0.022 ± 0.028 | 4.8 ± 4.1 | 1.63 ± 1.09 | 9.29 ± 5.66 | 1.5 ± 0.4 | 8.4 ± 2.4 |
| AC’s | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | |
|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | 0.50 ± 0.39 | −0.022 ± 0.022 | 1.4 ± 1.0 | 1.70 ± 1.15 | 8.77 ± 5.79 | 1.5 ± 0.4 | 7.9 ± 1.9 |
| CONFIG-2 | SET-2 | 0.39 ± 0.40 | −0.013 ± 0.030 | 4.2 ± 3.8 | 1.47 ± 1.15 | 9.76 ± 7.73 | 2.3 ± 0.2 | 9.8 ± 2.5 |
| CONFIG-3 FS | SET-3 | 0.73 ± 0.43 | −0.007 ± 0.023 | 1.3 ± 0.8 | 1.97 ± 1.23 | 10.04 ± 5.57 | 1.5 ± 0.4 | 7.8 ± 1.9 |
| SET-4 | 0.76 ± 0.43 | −0.008 ± 0.022 | 0.9 ± 0.5 | 2.03 ± 1.24 | 8.39 ± 5.09 | 1.5 ± 0.4 | 7.7 ± 1.9 | |
| SET-5 | 0.60 ± 0.42 | −0.000 ± 0.029 | 3.2 ± 2.5 | 1.74 ± 1.18 | 10.52 ± 6.13 | 1.5 ± 0.4 | 8.3 ± 2.1 | |
| SET-6 | 0.79 ± 0.44 | −0.004 ± 0.023 | 1.0 ± 0.5 | 2.05 ± 1.26 | 8.56 ± 5.32 | 1.5 ± 0.4 | 7.7 ± 1.9 | |
| SET-7 | 0.41 ± 0.37 | −0.040 ± 0.021 | 1.6 ± 1.3 | 1.60 ± 1.09 | 8.73 ± 5.48 | 1.5 ± 0.4 | 7.8 ± 2.0 | |
| SET-8 | 0.55 ± 0.40 | −0.018 ± 0.024 | 2.0 ± 1.5 | 1.73 ± 1.16 | 10.27 ± 5.65 | 1.5 ± 0.4 | 8.0 ± 2.0 | |
| SET-9 | 0.55 ± 0.40 | −0.018 ± 0.024 | 2.0 ± 1.5 | 1.73 ± 1.16 | 10.24 ± 5.65 | 1.5 ± 0.4 | 8.0 ± 2.0 |
| AC’s | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | |
|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | 0.74 ± 0.46 | −0.029 ± 0.022 | 1.1 ± 0.7 | 2.06 ± 1.25 | 10.81 ± 5.48 | 1.5 ± 0.4 | 8.1 ± 2.5 |
| CONFIG-2 | SET-2 | 0.73 ± 0.43 | −0.027 ± 0.019 | 1.6 ± 1.0 | 1.99 ± 1.21 | 12.04 ± 6.52 | 2.5 ± 0.2 | 9.4 ± 2.5 |
| CONFIG-3 FS | SET-3 | 0.97 ± 0.63 | 0.009 ± 0.034 | 1.1 ± 0.6 | 2.35 ± 1.54 | 12.35 ± 5.96 | 1.5 ± 0.4 | 12.6 ± 4.1 |
| SET-4 | 0.54 ± 0.52 | −0.008 ± 0.032 | 2.4 ± 2.0 | 1.75 ± 1.32 | 14.30 ± 6.82 | 1.5 ± 0.4 | 12.6 ± 4.0 | |
| SET-5 | 0.78 ± 0.58 | 0.017 ± 0.036 | 2.3 ± 1.7 | 2.03 ± 1.44 | 14.53 ± 7.24 | 1.5 ± 0.4 | 12.8 ± 4.2 | |
| SET-6 | 0.70 ± 0.56 | 0.009 ± 0.034 | 2.3 ± 1.8 | 1.94 ± 1.40 | 14.49 ± 7.04 | 1.5 ± 0.4 | 12.8 ± 4.1 | |
| SET-7 | 0.22 ± 0.43 | −0.049 ± 0.025 | 2.0 ± 1.8 | 1.42 ± 1.16 | 11.64 ± 7.13 | 1.5 ± 0.4 | 12.0 ± 3.7 | |
| SET-8 | 0.74 ± 0.60 | −0.002 ± 0.035 | 1.3 ± 0.9 | 2.07 ± 1.48 | 13.17 ± 5.66 | 1.5 ± 0.4 | 12.7 ± 4.2 | |
| SET-9 | 0.58 ± 0.55 | −0.022 ± 0.030 | 1.2 ± 0.8 | 1.90 ± 1.39 | 12.82 ± 5.13 | 1.5 ± 0.4 | 12.7 ± 4.1 |
| Controller | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) |
|---|---|---|---|---|---|---|---|
| LQR | 0.56 ± 0.12 | −0.015 ± 0.007 | 2.5 ± 0.7 | 1.72 ± 0.34 | 8.70 ± 1.71 | 1.5 ± 0.1 | 7.7 ± 0.5 |
| LMI.R | 0.68 ± 0.13 | −0.017 ± 0.008 | 3.2 ± 0.8 | 1.87 ± 0.35 | 9.81 ± 1.75 | 1.6 ± 0.1 | 8.3 ± 0.7 |
| LMI.NF | 0.59 ± 0.12 | −0.014 ± 0.008 | 1.9 ± 0.6 | 1.78 ± 0.35 | 9.48 ± 1.75 | 1.6 ± 0.1 | 8.1 ± 0.6 |
| LMI.RNF | 0.67 ± 0.16 | −0.011 ± 0.010 | 1.7 ± 0.4 | 1.95 ± 0.41 | 12.91 ± 1.91 | 1.6 ± 0.1 | 11.8 ± 1.2 |
| AC’s | ΔX (m) | ΔY (m) | OS% (%) | ΔDX (m) | ΔSX (m) | (deg) | (deg/s) | |
|---|---|---|---|---|---|---|---|---|
| CONFIG-1 | SET-1 | 0.63 ± 0.19 | −0.026 ± 0.010 | 1.1 ± 0.3 | 1.90 ± 0.54 | 9.68 ± 2.45 | 1.5 ± 0.2 | 7.9 ± 1.0 |
| CONFIG-2 | SET-2 | 0.60 ± 0.19 | −0.022 ± 0.010 | 2.3 ± 1.0 | 1.79 ± 0.53 | 10.81 ± 3.02 | 2.3 ± 0.1 | 9.2 ± 1.1 |
| CONFIG-3 FS | SET-3 | 0.78 ± 0.22 | −0.002 ± 0.013 | 2.0 ± 0.7 | 2.02 ± 0.58 | 10.30 ± 2.60 | 1.5 ± 0.2 | 9.0 ± 1.3 |
| SET-4 | 0.66 ± 0.20 | −0.008 ± 0.012 | 2.3 ± 0.9 | 1.87 ± 0.55 | 10.37 ± 2.69 | 1.5 ± 0.2 | 9.0 ± 1.3 | |
| SET-5 | 0.72 ± 0.21 | 0.002 ± 0.013 | 2.6 ± 0.9 | 1.92 ± 0.56 | 10.93 ± 2.86 | 1.5 ± 0.2 | 9.1 ± 1.3 | |
| SET-6 | 0.76 ± 0.21 | 0.000 ± 0.012 | 2.1 ± 0.7 | 1.98 ± 0.57 | 10.45 ± 2.77 | 1.5 ± 0.2 | 9.0 ± 1.3 | |
| SET-7 | 0.33 ± 0.17 | −0.043 ± 0.011 | 2.8 ± 1.2 | 1.49 ± 0.48 | 9.24 ± 2.76 | 1.5 ± 0.2 | 9.0 ± 1.3 | |
| SET-8 | 0.58 ± 0.20 | −0.014 ± 0.013 | 2.9 ± 1.2 | 1.77 ± 0.55 | 10.19 ± 2.63 | 1.5 ± 0.2 | 9.2 ± 1.3 | |
| SET-9 | 0.53 ± 0.19 | −0.020 ± 0.012 | 3.0 ± 1.3 | 1.71 ± 0.53 | 10.05 ± 2.57 | 1.5 ± 0.2 | 9.2 ± 1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, I.; Nah, J. Robust and Non-Fragile Path Tracking Control for Autonomous Vehicles. Actuators 2025, 14, 510. https://doi.org/10.3390/act14110510
Lee I, Nah J. Robust and Non-Fragile Path Tracking Control for Autonomous Vehicles. Actuators. 2025; 14(11):510. https://doi.org/10.3390/act14110510
Chicago/Turabian StyleLee, Ilhan, and Jaewon Nah. 2025. "Robust and Non-Fragile Path Tracking Control for Autonomous Vehicles" Actuators 14, no. 11: 510. https://doi.org/10.3390/act14110510
APA StyleLee, I., & Nah, J. (2025). Robust and Non-Fragile Path Tracking Control for Autonomous Vehicles. Actuators, 14(11), 510. https://doi.org/10.3390/act14110510







