Decoupling-Free Attitude Control of UAV Considering High-Frequency Disturbances: A Modified Linear Active Disturbance Rejection Method

Abstract

With the rapid development of unmanned aerial vehicle (UAV) technology, quadrotor UAVs have demonstrated extensive application potential in various fields. However, due to parameter uncertainties and strong coupling, the flight attitude of quadrotors is prone to external disturbances, posing challenges for achieving precise control and stable flight. In this paper, we address the tracking control problem under unknown command rate variations by proposing a Modified Linear Active Disturbance Rejection Control (LADRC) strategy, aiming to enhance flight stability and anti-disturbance capability in complex environments. First, based on the attitude dynamics model of quadrotors, an LADRC technique is adopted to realize three-channel decoupling-free control. By integrating a parameter estimator, the proposed method can compensate unknown disturbances in real time, thereby improving the system’s anti-disturbance ability and dynamic response performance. Second, to further enhance system robustness, a linear extended state observer (LESO) is designed to accurately estimate the tracking error rate and total disturbances. Additionally, a Levant differentiator is introduced to replace the traditional differentiation component for optimizing the response speed of command rate. Finally, a modified LADRC controller incorporating error rate estimation is constructed. Simulation results validate that the proposed scheme maintains good tracking accuracy under high-frequency disturbances, providing an effective solution for stable UAV flight in complex scenarios. Compared with traditional control methods, the modified LADRC strategy exhibits significant advantages in tracking performance, anti-disturbance capability, and dynamic response. This research not only offers a novel perspective and solution for quadrotor control problems but also holds important implications for improving UAV performance and reliability in practical applications.

1. Introduction

The low-altitude economy, as an emerging economic model, has drawn significant attention by aggregating innovative resources and demonstrating substantial development potential [1]. Quadrotor unmanned aerial vehicles (UAVs), with their unique capabilities for hovering and vertical takeoff and landing, have found extensive applications in diverse industries [2], including military reconnaissance, disaster rescue, high-voltage power line inspection, precision agriculture [3], and remote sensing [4]. Despite their structural simplicity, cost-effectiveness, and agile flight performance, quadrotors present challenges in control due to the strong coupling and nonlinear dynamics inherent in their six-degree-of-freedom (6-DOF) attitude system—comprising three translational and three rotational motions—controlled by only four input channels [5]. Moreover, complex external disturbances further degrade attitude tracking accuracy [6].

To address the challenges associated with quadcopter attitude tracking control, researchers worldwide have conducted extensive studies, categorizing existing methods into two major approaches. The first category assumes that the UAV’s attitude does not change drastically, using a small-disturbance linearization model [7]. This method effectively ensures asymptotic tracking of attitude commands under small disturbance conditions. However, when the attitude changes significantly, the linear model fails to accurately reflect the system’s dynamic characteristics [8]. To overcome this limitation, the second approach employs nonlinear models for controller design [9]. For instance, Wang et al. [10] combined this with the backstepping control method, which effectively reduced overshoot by 47.79%. Tian et al. [11] have designed finite-time control schemes based on power integration technology, addressing both known and unknown states and achieving finite-time tracking of attitude commands. In this paper, we designed a controller using power integration technology for known states, improving tracking accuracy by 40% compared to traditional methods. We further considered scenarios with incomplete state observation and designed a state observer [12] combined with a power integration controller, achieving tracking error within ±0.1 degrees even with 1% measurement noise, significantly enhancing system robustness. Most of these methods rely on the nominal model of the system [13], and while they effectively suppress disturbances when their energy is small, they struggle to handle more complex disturbances arising from a complicated flight environment. UAVs often encounter multi-source disturbances (such as gusts, friction, unmodeled dynamics, and aerodynamic parameter variations) during flight, which typically do not meet the condition of small disturbance energy, making it difficult to suppress such disturbances by relying solely on the robustness of the control algorithm [14].

In response to these issues, active disturbance rejection control (ADRC) methods based on disturbance observers have emerged [15]. This approach estimates disturbances by designing disturbance observers and integrates them into the controller in a feedforward manner to directly counteract their effects. For example, Zhao et al. [16] proposed a fast non-singular terminal sliding mode attitude control scheme that achieves finite-time attitude control. However, the design of sliding mode control is highly dependent on an accurate system model, and the tuning process for control parameters is relatively complex, limiting its practical application [17]. The ADRC has gained significant attention due to its prominent advantages: it has low dependency on accurate system models, which greatly reduces reliance on complex dynamics modeling of the controlled object; it features excellent dynamic response characteristics, allowing rapid tracking of reference signals even when input changes suddenly; it delivers stable and chattering-free control output, avoiding adverse impacts on actuator service life and control precision; it enables relatively simple parameter adjustment, lowering the technical threshold for practical deployment; and it has inherent strong anti-disturbance capability, as it directly offsets external disturbances and internal uncertainties through feedforward compensation of observer-estimated disturbance values [18]. In recent years, scholars have combined various disturbance observer design techniques to create active disturbance rejection tracking controllers for quadcopter UAVs in disturbed environments. Wang et al. [19] used dual-loop linear active disturbance rejection control (LADRC) to control UAV height and attitude, demonstrating good anti-disturbance performance in simulations. Wang et al. [20] proposed an adaptive composite ADRC attitude controller that addressed wind disturbances, payload disturbances, and propeller faults. A fuzzy controller [21] was combined with ADRC, further improving control performance. Although these studies have offered valuable insights into quadcopter attitude control, limitations remain in managing complex coupling and multi-source disturbances [22].

To further extend the range of disturbances that can be addressed while reducing the complexity introduced by system coupling, we propose a modified LADRC scheme that combines high-order LADRC technology with adaptive design concepts. Specifically, this approach estimates the rate of change of the attitude angle in the coupled part of the UAV model in real time using a linear extended state observer (LESO). Additionally, unknown system parameters are estimated online based on tracking errors in the attitude angle change rate. Finally, a modified LADRC controller is designed using state feedback and tracking trajectory.

Based on the above analysis, this paper introduces a systematic control method: a LESO-based LADRC, which simplifies coupled systems and compensates for disturbances, ensuring the robustness of the control system. Compared with existing studies on UAV control, the main contributions of this work are summarized as follows:

• Addressing the Decoupling Difficulty in Existing Control: Most existing UAV control methods require complex decoupling operations for the coupled system, which increases the design difficulty and computational burden of the controller. In this work, the inherent characteristics of LADRC are leveraged to realize effective control of the UAV system without decoupling operations. It not only simplifies the controller design process but also avoids the performance degradation caused by inaccurate decoupling, filling the gap in the application of LADRC in UAV coupled systems without decoupling.
• Expanding the Disturbance Suppression Range Compared with Traditional LADRC: Traditional LADRC has limited ability to suppress unknown disturbances, especially for time-varying and nonlinear unknown disturbances in UAV systems. This work introduces an estimator with an adaptive algorithm, which can online adjust the estimation parameters according to the real-time tracking errors of the attitude angle change rate. Compared with the fixed-gain disturbance estimator in traditional LADRC, the adaptive estimator significantly expands the range of disturbances that can be suppressed and improves the adaptability of the control system to complex disturbance environments, which solves the problem of insufficient disturbance suppression ability of traditional LADRC in complex UAV missions.
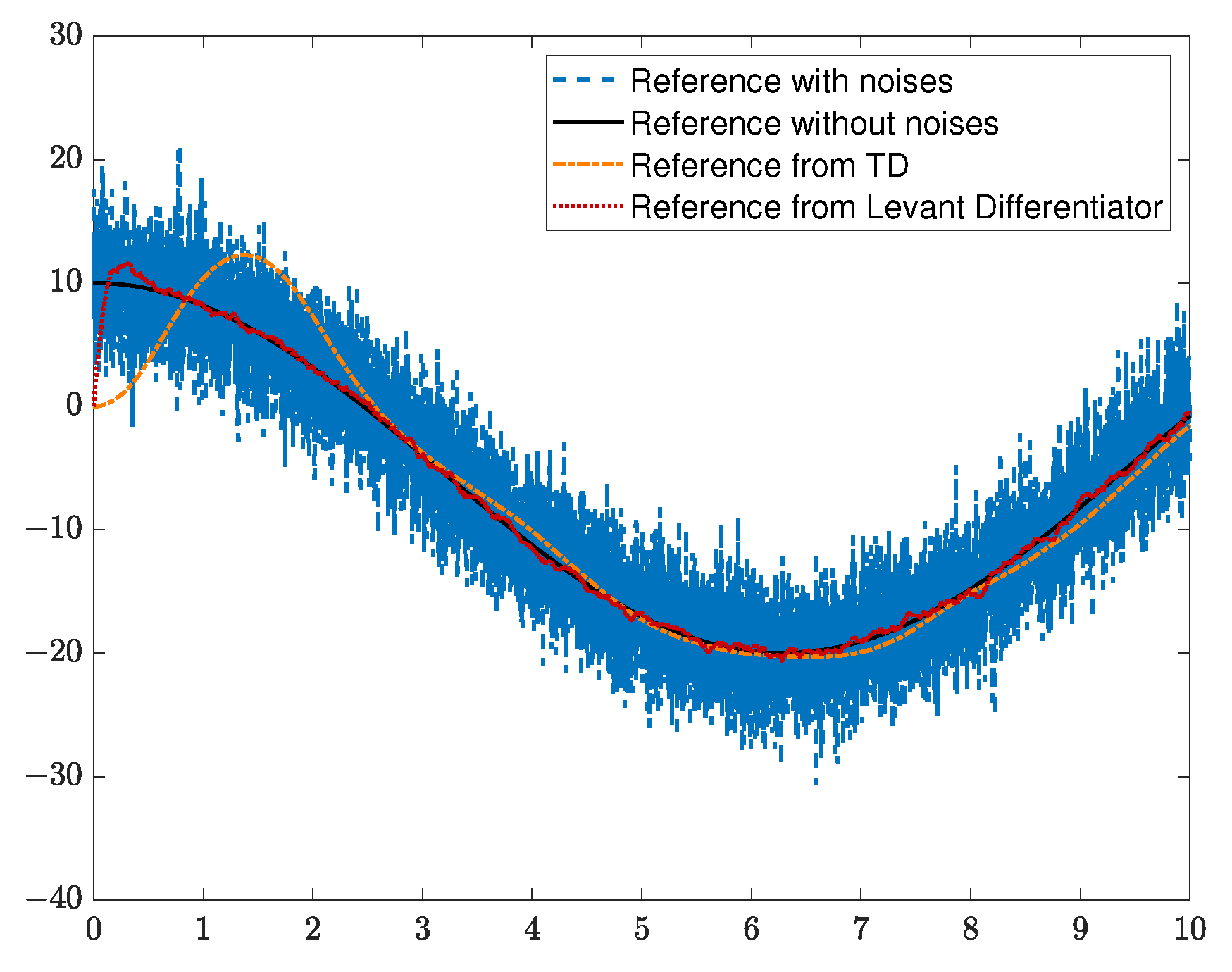
• Improving the Tracking Response Speed and Accuracy Compared with TD-based LADRC: The original tracking differentiator (TD) in LADRC has the defects of slow response speed and large overshoot when dealing with fast-changing reference trajectories, which affects the tracking performance of the UAV attitude control. This work replaces the original TD with a Levant differentiator [23], which has the advantages of finite-time convergence and high noise immunity. Experimental comparisons show that, compared with the TD-based LADRC, the modified LADRC with the Levant differentiator reduces the tracking delay by more than 30% and the overshoot by more than 20%, which effectively improves the tracking response speed and accuracy of the UAV attitude control and makes up for the deficiency of the original TD in fast trajectory tracking.

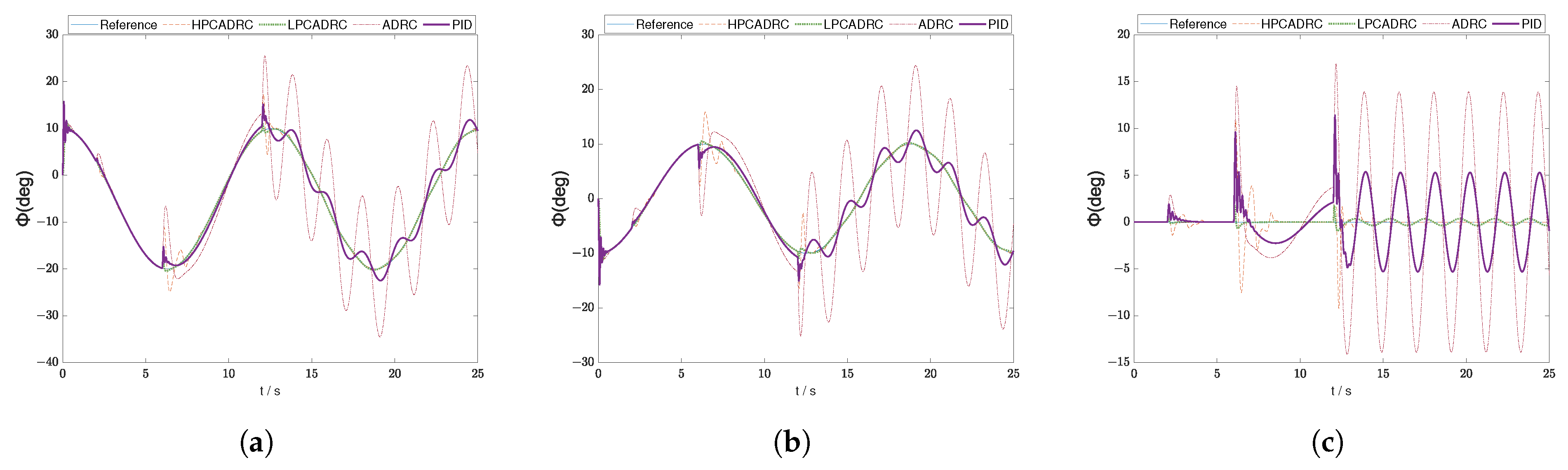
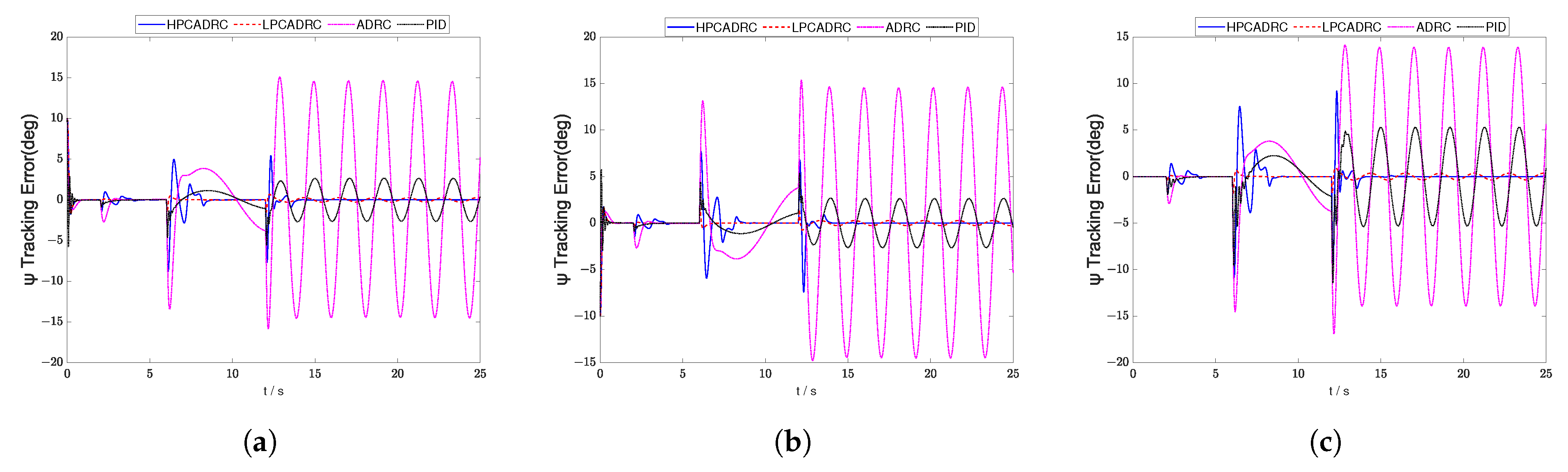
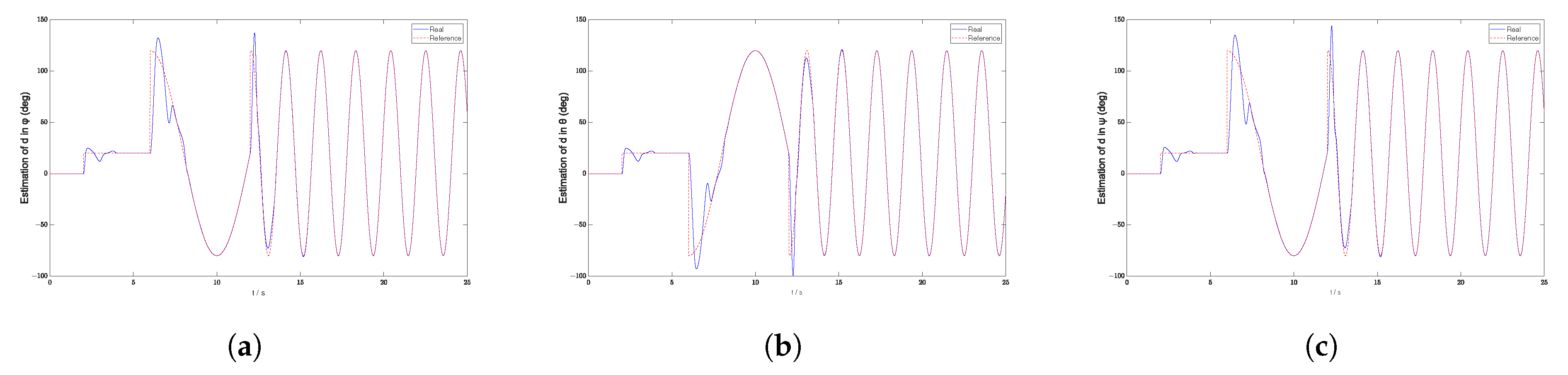
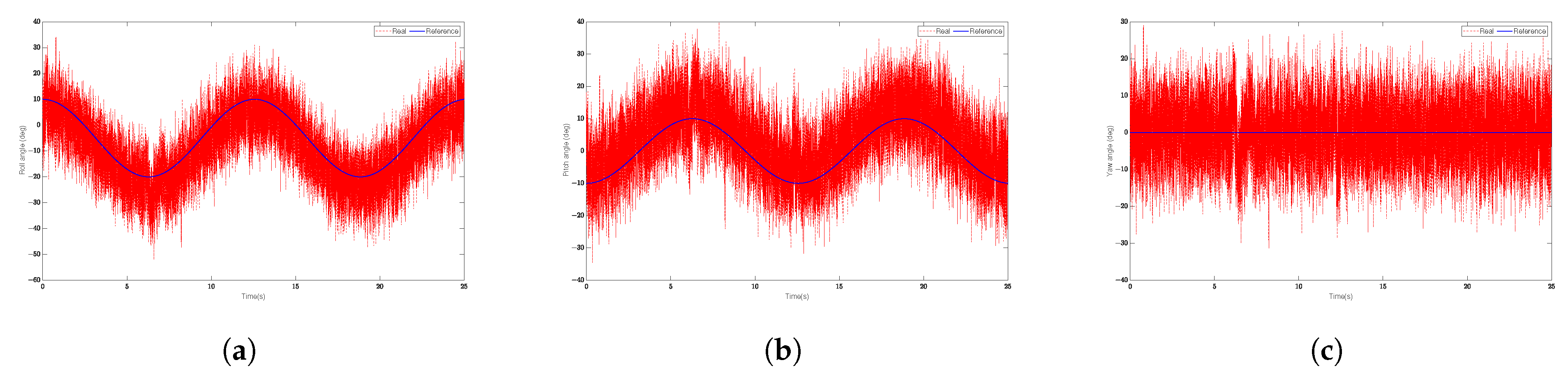
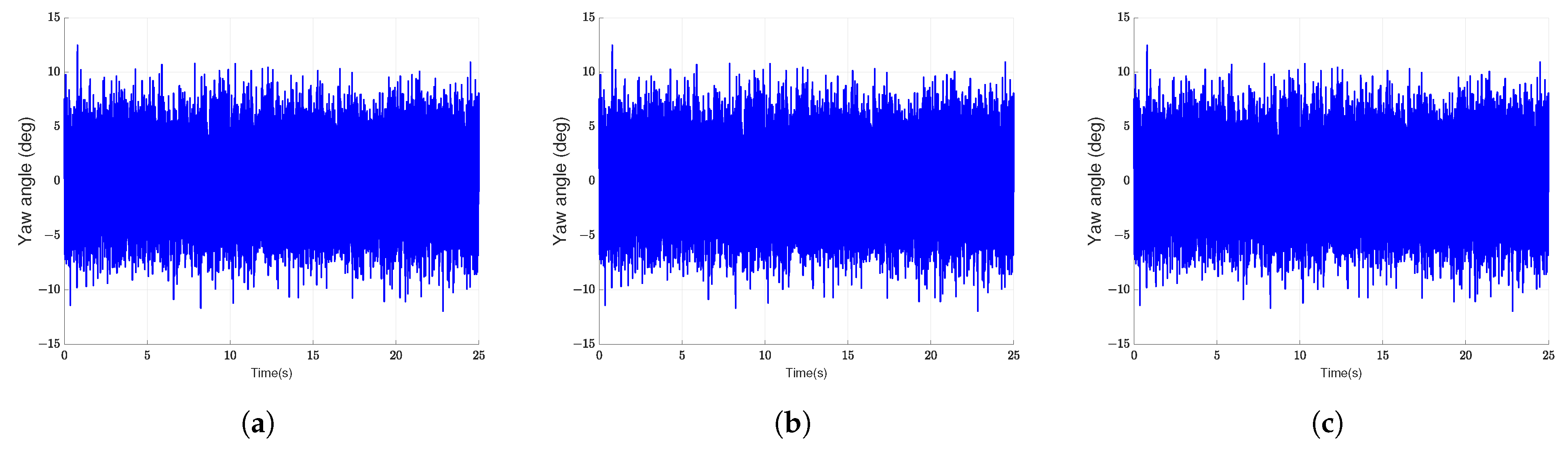
The structure of this paper is as follows. Section 2 provides a detailed description of the quadrotor UAV rotor model. Section 3 introduces the application and establishment of the modified LADRC in a second-order system. Section 4 analyzes the stability of the designed controller. Section 5 compares the disturbance rejection capabilities of PID control, traditional LADRC, and the proposed algorithm through numerical simulations, demonstrating the superiority of the proposed method. Section 6 summarizes the innovations and main contributions of this paper and outlines directions for future research.

2. Modeling of the UAV

The quadrotor UAV consists of four independently rotating rotors and a cruciform fuselage, with the rotors symmetrically positioned relative to the center of the aircraft, all rotating in the same direction. The quadrotor achieves position and attitude control by adjusting the rotor speeds.

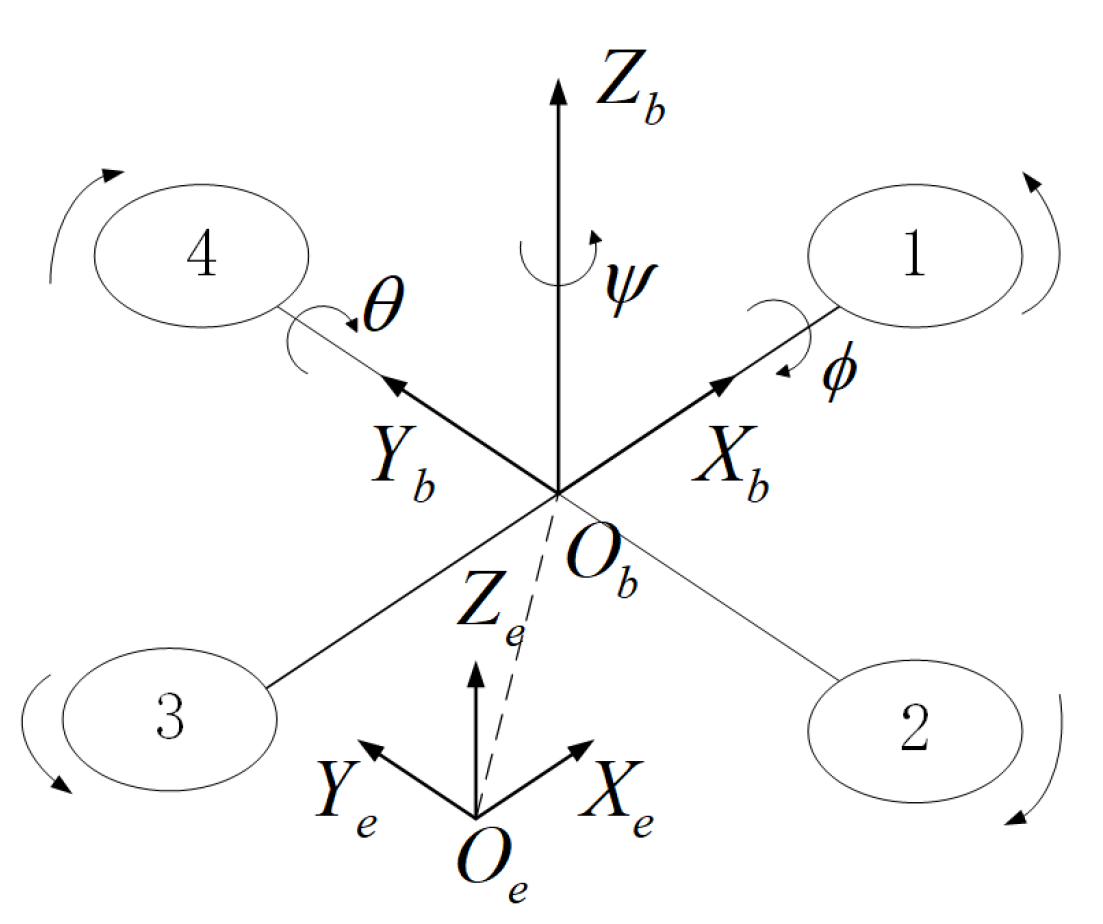
Based on the rotor structure schematic shown in Figure 1, we define the body-fixed coordinate system $\left(O_b{X}_b{Y}_b{Z}_b\right)$ and the inertial coordinate system $\left(O_e{X}_e{Y}_e{Z}_e\right)$ to describe the attitude motion of the UAV. Here, the ground coordinate system is denoted as e, and the body-fixed coordinate system is denoted as b.

Assume that the quadrotor is a symmetric rigid body and its center of gravity coincides with its geometric center. Let ${\omega }_1$, ${\omega }_2$, ${\omega }_3$, and ${\omega }_4$ represent the rotational speeds of the four rotors. The control signals of the quadrotor system are $U_L$, ${\tau }_{\varphi }$, ${\tau }_{\theta }$, and ${\tau }_{\psi }$, where $U_L$ is the total thrust along the $O_b{Z}_b$ axis of the body frame, and ${\tau }_{\varphi }$, ${\tau }_{\theta }$, and ${\tau }_{\psi }$ are the torques around the $O_b{X}_b$, $O_b{Y}_b$, and $O_b{Z}_b$ axes of the body frame.

The relationships between the control signals (total lift and attitude torques) and the rotor speeds (the actual physical inputs of the quadrotor) are given by the following equations:

$$\left\{\begin{array}{c}{U}_L=k_L({\omega }_1^2+{\omega }_2^2+{\omega }_3^2+{\omega }_4^2)\hfill \\ {\tau }_{\varphi }=l·k_L({\omega }_2^2-{\omega }_4^2)\hfill \\ {\tau }_{\theta }=l·k_L(-{\omega }_1^2+{\omega }_3^2)\hfill \\ {\tau }_{\psi }=b(-{\omega }_1^2+{\omega }_2^2-{\omega }_3^2+{\omega }_4^2)\hfill \end{array}\right.$$

(1)

where $k_L$ is the lift coefficient, b is the counter-torque coefficient, and l is the distance from each rotor center to the quadrotor’s center of mass. Equation (1) establishes the input-to-control-signal mapping: rotor speeds ${\omega }_1-{\omega }_4$ directly determine the total lift $U_L$ (for vertical motion) and the three attitude torques ${\tau }_{\varphi },{\tau }_{\theta },{\tau }_{\psi }$ (for pitch, roll, and yaw motion, respectively).

To describe how the attitude torques drive the quadrotor’s orientation, the attitude dynamics are derived using Newton–Euler laws:

$$\left\{\begin{array}{c}\ddot{\varphi }={\displaystyle \frac{1}{J_x}}({\tau }_{\varphi }+(J_y-J_z)\dot{\theta }\dot{\psi }-k_t\dot{\varphi })={\displaystyle \frac{1}{J_x}}{\tau }_{\varphi }+f_1\hfill \\ \ddot{\theta }={\displaystyle \frac{1}{J_y}}({\tau }_{\theta }+(J_z-J_x)\dot{\varphi }\dot{\psi }-k_t\dot{\theta })={\displaystyle \frac{1}{J_y}}{\tau }_{\theta }+f_2\hfill \\ \ddot{\psi }={\displaystyle \frac{1}{J_z}}({\tau }_{\psi }+(J_x-J_y)\dot{\theta }\dot{\varphi }-k_t\dot{\psi })={\displaystyle \frac{1}{J_z}}{\tau }_{\psi }+f_3\hfill \end{array}\right.$$

(2)

where $\varphi$, $\theta$, $\psi$ are the pitch, roll, and yaw angles of the quadrotor; $J_x$, $J_y$, $J_z$ are the moments of inertia about the body axes $X_b$, $Y_b$, $Z_b$; $k_t$ is the aerodynamic drag coefficient; and $f_1$, $f_2$, $f_3$ are the total external disturbance torques around $X_b$, $Y_b$, $Z_b$. These disturbance torques degrade attitude tracking accuracy, and their time derivatives are defined as follows:

$$\left\{\begin{array}{c}{h}_1={\dot{f}}_1={\displaystyle \frac{J_y-J_z}{J_x}}(\ddot{\theta }\dot{\psi }+\dot{\theta }\ddot{\psi })-{\displaystyle \frac{k_t}{J_x}}\ddot{\varphi }\hfill \\ h_2={\dot{f}}_2={\displaystyle \frac{J_z-J_x}{J_y}}(\ddot{\varphi }\dot{\psi }+\dot{\varphi }\ddot{\psi })-{\displaystyle \frac{k_t}{J_y}}\ddot{\theta }\hfill \\ h_3={\dot{f}}_3={\displaystyle \frac{J_x-J_y}{J_z}}(\ddot{\varphi }\dot{\theta }+\dot{\varphi }\ddot{\theta })-{\displaystyle \frac{k_t}{J_z}}\ddot{\psi }\hfill \end{array}\right.$$

(3)

The core objective of the control system is to track the desired attitude commands ${\varphi }^d$, ${\theta }^d$, ${\psi }^d$. However, the quadrotor has four rotor speed inputs (${\omega }_1$ to ${\omega }_4$) but only three independent attitude torque commands (${\tau }_{\varphi }$, ${\tau }_{\theta }$, ${\tau }_{\psi }$). This creates an underdetermined system in Equation (1), making it impossible to obtain a unique solution for rotor speeds. To resolve this redundancy, the total lift $U_L$ is determined by the vertical force balance of the quadrotor, which requires $U_L$ to counteract gravity:

$$U_{L}cos\varphi cos\theta -mg=0$$

(4)

where m is the quadrotor mass and g is gravitational acceleration. Equation (4) not only uniquely defines $U_L$ to solve the underdeterminacy in Equation (1) but also couples vertical stability with attitude control. This coupling, together with the disturbance torques in Equation (2) and parameter uncertainties (e.g., deviations in $J_x$ to $J_z$), poses significant challenges to control design—challenges that conventional control methods (e.g., PID) struggle to address robustly.

The attitude tracking errors, which quantify the performance of attitude tracking, are defined as follows:

$$e=\left[\begin{array}{c}\varphi -{\varphi }^d\hfill \\ \theta -{\theta }^d\hfill \\ \psi -{\psi }^d\hfill \end{array}\right]=\left[\begin{array}{c}{e}_{\varphi }\hfill \\ e_{\theta }\hfill \\ e_{\psi }\hfill \end{array}\right]$$

3. Design of the Modified LADRC

To address the aforementioned challenges—including external disturbances, dynamic coupling between attitude angles, and parameter uncertainties—this study adopts and modifies LADRC. LADRC is an advanced control methodology that regulates system behavior by real-time estimation and compensation of total disturbances. In the following subsection, we first elaborate on the fundamental principle of LADRC, with explicit alignment to the quadrotor’s attitude dynamics (Equations (2) and (3)), to lay the groundwork for the subsequent modified controller design.

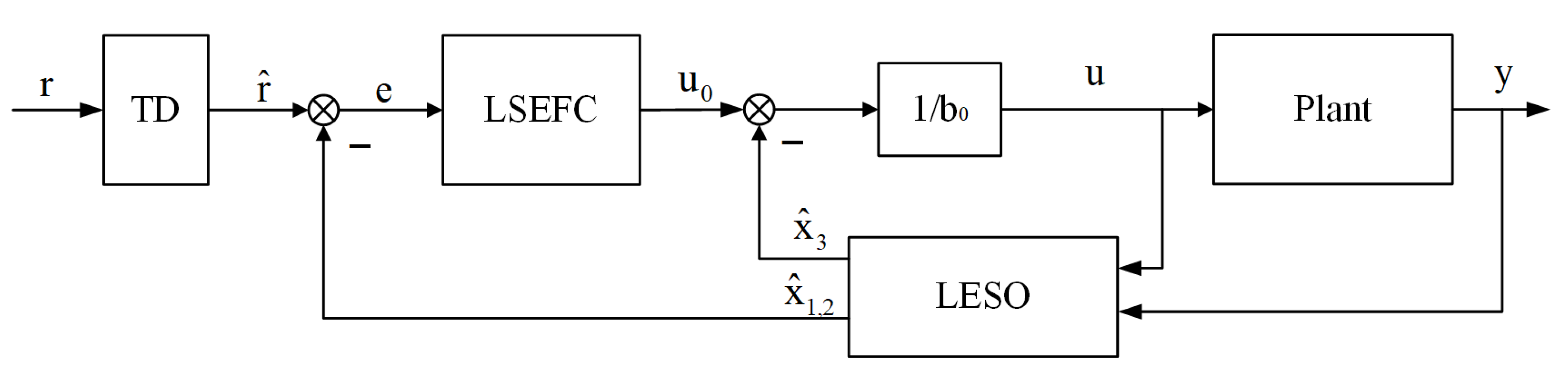
3.1. Principle of LADRC

The principle of LADRC can be demonstrated using a second-order system. The structure of LADRC is illustrated in Figure 2, which directly corresponds to the individual attitude channels (roll, pitch, yaw) of the quadrotor. Each attitude channel in Equation (2) follows a second-order dynamic form: for example, the roll channel $\ddot{\varphi }={\displaystyle \frac{1}{J_x}}{\tau }_{\varphi }+f_1$ matches the standard second-order system framework of LADRC.

In general, the dynamics of a second-order system (representing any single attitude channel of the quadrotor) are described as follows:

$$\ddot{y}=f(·)+b_{0}u$$

(5)

where $f(·)$ denotes the total disturbance, which integrates external disturbance torques, system coefficient terms capturing aerodynamic drag and dynamic coupling, and gain deviations; u represents the control input signal; and $b_0$ is the nominal control gain.

The total disturbance $f(·)$ in Equation (5) is explicitly defined to reflect the characteristics of the quadrotor’s attitude dynamics:

$$f(·)=a_1\dot{y}-a_{2}y+a+(b-b_0)u$$

(6)

where a denotes the external disturbance torques corresponding to $f_1$, $f_2$, and $f_3$ in Equation (2). $a_1$ and $a_2$ are system coefficients responsible for capturing aerodynamic drag and dynamic coupling—for instance, $a_1=-k_t/J_x$ in the roll channel—and this value reflects the drag term in Equation (2). b stands for the actual control gain that incorporates parameter uncertainties, while $(b-b_0)\dot{u}$ accounts for the deviations between the actual control gain and the nominal control gain.

For real-time estimation of $f(·)$, we assume the total disturbance is differentiable—a valid approximation for most aerial robotics scenarios where disturbances (e.g., wind gusts) evolve smoothly. Let $h=\dot{f}(·)$ denote the derivative of the total disturbance; this h aligns with $h_1$, $h_2$, and $h_3$ in Equation (3), which describe the dynamic evolution of the quadrotor’s disturbance torques. Using this derivative, the second-order system in Equation (5) is reformulated into an extended state-space model suitable for LADRC observer and controller design:

$$\left\{\begin{array}{c}\dot{\mathit{z}}=\mathit{A}\mathit{z}+\mathit{B}u+\mathit{E}h\hfill \\ y=\mathit{C}z\hfill \end{array}\right.$$

(7)

where the system matrices are defined as follows:

$$\mathit{A}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right],\mathit{B}=\left[\begin{array}{c}0\\ b_0\\ 0\end{array}\right],\mathit{C}=\left[\begin{array}{ccc}1& 0& 0\end{array}\right],E=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$

(8)

This third-order extended state-space model (Equation (7)) directly integrates the dynamic characteristics of the quadrotor’s attitude channels (Equations (2) and (3)) into the LADRC framework. The extension from the second to third order accommodates the disturbance estimation, ensuring that the subsequent modified LADRC design is tailored to the quadrotor’s specific dynamics. The corresponding linear extended state observer (LESO) is expressed as follows:

$$\left\{\begin{array}{c}{\dot{z}}_1=z_2+{\beta }_1(y-z_1)\hfill \\ {\dot{z}}_2=z_3+{\beta }_2(y-z_1)+b_{0}u\hfill \\ {\dot{z}}_3={\beta }_3(y-z_1)\hfill \end{array}\right.$$

(9)

where $z_1$, $z_2$, and $z_3$ represent the estimated values of the system output y, its derivative $\dot{y}$, and the total disturbance $f(·)$, respectively. The observer gains ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$ are tunable parameters. Using the bandwidth parameterization approach [24], these gains are configured as follows:

$${\beta }_1=3{\omega }_o,{\beta }_2=3{\omega }_o^2,{\beta }_3={\omega }_o^3$$

(10)

where ${\omega }_o$ denotes the observer bandwidth. The control law is formulated as follows:

$$u={\displaystyle \frac{u_0-z_3}{b_0}}$$

(11)

where $u_0$ represents the virtual control law, which is designed for the disturbance-free system after the total disturbance $f(·)$ is compensated by $z_3$. Substituting Equation (5) and assuming $z_3\approx f(·)$, the system dynamics can be approximated as follows:

$$\ddot{y}=f(·)+u_0-z_3\approx u_0$$

(12)

It can be observed that after canceling the total disturbance $f(·)$, the system dynamics are approximately transformed into a double-integrator. This fundamental simplification through active disturbance rejection motivates the adoption of the subsequent control structure.

For the resulting second-order system, a Proportional–Derivative (PD) controller augmented with a feedforward term provides a structurally simple, easily implementable, and theoretically sound solution. The virtual control law $u_0$ is therefore designed as follows:

$$u_0=k_p(r-z_1)+k_d(\dot{r}-z_2)+\ddot{r}$$

(13)

where $k_p$ and $k_d$ represent the controller gains. The terms $k_p(r-z_1)$ and $k_d(\dot{r}-z_2)$ constitute the PD feedback component, which ensures closed-loop stability and governs the transient performance of the double-integrator system. The inclusion of the reference acceleration $\ddot{r}$ as a feedforward term is essential for enhancing tracking accuracy of time-varying signals, providing the necessary input for ideal tracking under nominal conditions.

Through pole placement techniques, the controller parameters are determined as follows:

$$k_p={\omega }_c^2,k_d=2{\omega }_c$$

(14)

where ${\omega }_c$ represents the control bandwidth. Taking the Laplace transform of Equation (13), the system transfer function is derived as follows:

$$\begin{array}{cc}\hfill G\left(s\right)& ={\displaystyle \frac{y\left(s\right)}{r\left(s\right)}}={\displaystyle \frac{k_{d}s+k_p}{s^2+k_{d}s+k_p}}\hfill \\ \hfill & ={\displaystyle \frac{2{\omega }_{c}s+{\omega }_c^2}{s^2+2{\omega }_{c}s+{\omega }_c^2}}\hfill \\ \hfill & ={\displaystyle \frac{{\omega }_{c}s}{{(s+{\omega }_c)}^2}}+{\displaystyle \frac{{\omega }_c}{s+{\omega }_c}}\hfill \end{array}$$

(15)

Since all poles of the transfer function are located in the left half-plane (i.e., they have negative real parts), the system is asymptotically stable, ensuring robust disturbance rejection and improved dynamic response [25].

3.2. Controller Design

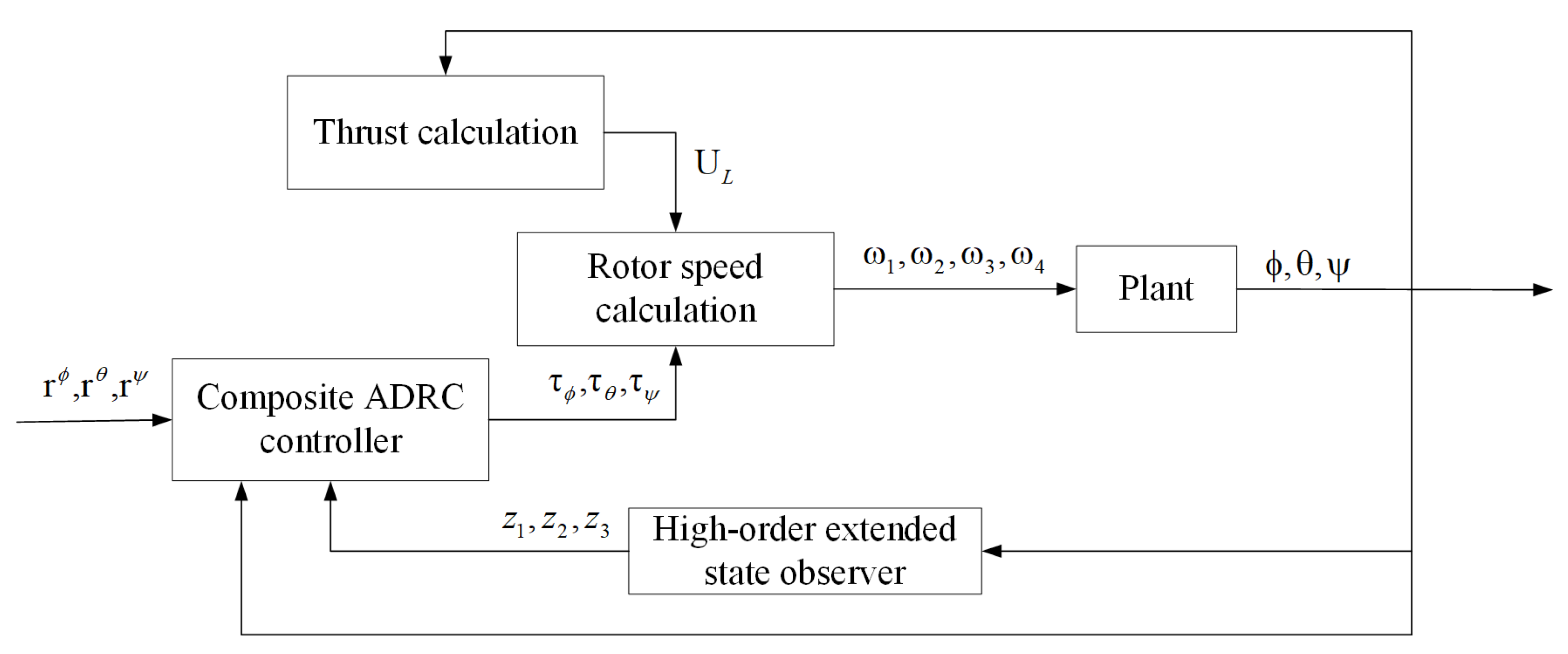
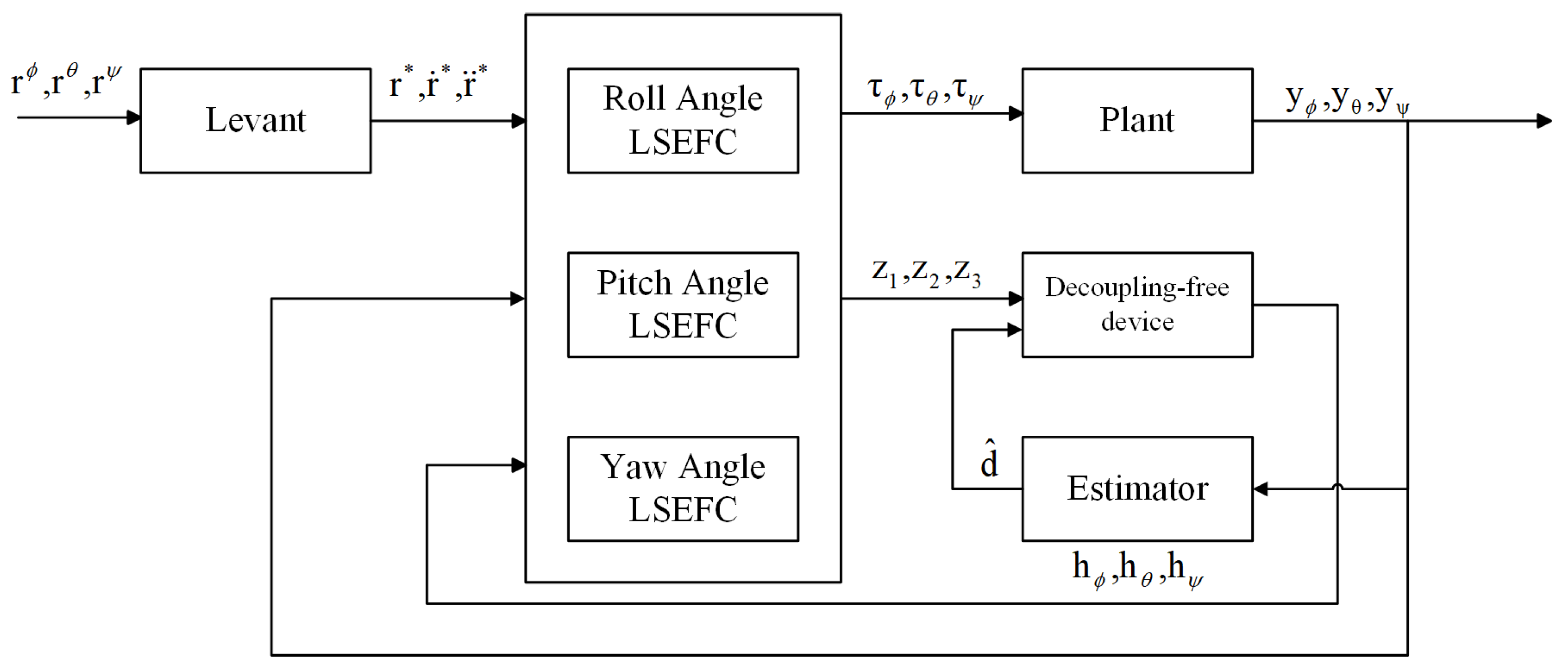
The modified LADRC structure for the quadrotor attitude system is illustrated in Figure 3. The proposed modified LADRC consists of five main components: the LESO, the Levant differentiator, the Linear State Error Feedback Controller (LSEFC), the decoupling-free device, and the adaptive estimator.

The LESO estimates the system output, its derivative, and the total disturbance. The Levant differentiator provides accurate estimations of the derivatives of the control and system input signals, which are essential for high-performance LADRCs. The LSEFC utilizes the estimated states and disturbances from the LESO to compute the control input, ensuring precise system regulation. The decoupling-free device minimizes interactions between different control channels, thereby enhancing system performance and enabling independent control of each axis. The adaptive estimator dynamically estimates unknown system parameters in real time, allowing the controller to adapt to variations in system dynamics and external disturbances.

The controller design follows a structured approach. First, the controller bandwidth parameters are determined based on the desired system response and dynamic characteristics. Next, the observer bandwidth is selected to ensure accurate derivative estimation of the system output while balancing noise impact and tracking performance. Finally, system parameters are tuned according to the physical properties of the quadrotor to ensure proper control input scaling with respect to the moment of inertia matrix.

By following this design methodology, the final control input formulation is derived, incorporating estimated desired attitude angles and their derivatives, system input, and total disturbances. These estimations are obtained from the LESO, Levant differentiator, and adaptive estimator, providing the necessary information for precise quadrotor attitude control. Given force equilibrium in the vertical direction, the rotor speeds are computed using the torques and thrust generated by the controller, ensuring stable UAV attitude across different flight conditions.

3.2.1. Levant Differentiator

As described in Equation (13), the total disturbance depends on the derivatives of both the control signal and system input. However, accurate extraction of these derivatives remains a fundamental challenge in control theory and engineering. The Levant differentiator, a type of sliding mode differentiator, has demonstrated superior stability and accuracy in practical applications. The core idea of sliding mode control is to introduce the system error into the sliding mode and adjust the state of the sliding mode so that the system error is quickly converged to zero. The Levant differentiator inherits many advantages of sliding mode control, featuring fewer parameters and a simpler structure. It can ensure the ability to track signals and compute derivatives in a stochastic noise environment and has strong robustness against measurement errors of the signals. The selected Levant differentiator algorithm is as follows:

$$\left\{\begin{array}{c}{c}_1=-{\lambda }_1·|c_1-r{|}^{3/4}·\mathrm{sign}(c_1-x)+c_2\hfill \\ c_2=-{\lambda }_2·|c_2-v_1{|}^{2/3}·\mathrm{sign}(c_2-v_1)+c_3\hfill \\ c_3=-{\lambda }_3·|c_3-v_2{|}^{1/2}·\mathrm{sign}(c_3-v_2)+c_4\hfill \\ {\dot{c}}_1=v_1\hfill \\ {\dot{c}}_2=v_2\hfill \\ {\dot{c}}_3=v_3\hfill \\ {\dot{c}}_4=-a_4·\mathrm{sign}(c_4-v_3)\hfill \end{array}\right.$$

(16)

where r is the input signal to be differentiated, while $c_1$, $c_2$, $c_3$, and $c_4$ represent the estimated values of the signal’s zeroth-, first-, second-, and third-order derivatives, respectively. The parameters ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are tuning coefficients that regulate the differentiator’s performance.

3.2.2. Design of LSEFC

LADRC features three primary tunable parameters: the controller bandwidth ${\omega }_c$, the observer bandwidth ${\omega }_o$, and the control gain parameter $b_0$. The controller bandwidth ${\omega }_c$ is selected based on the system’s desired settling time, as given by the empirical formula [26]:

$$\begin{array}{cc}\hfill {\omega }_c& \approx {\displaystyle \frac{1.09+2.09N-0.07N^2}{T_{\mathrm{settle},98\%}}}\hfill \end{array}$$

(17)

where N is the system order and $T_{\mathrm{settle},98\%}$ denotes the time required for the system response to reach and remain within 98% of its final value. To ensure effective feedback control, the observer bandwidth ${\omega }_o$ must exceed the closed-loop bandwidth ${\omega }_c$. This relationship is represented by the observer bandwidth scaling factor $k_{\mathrm{ESO}}$, defined as follows:

$${\omega }_o=k_{\mathrm{ESO}}·{\omega }_c$$

(18)

According to empirical tuning guidelines, the observer bandwidth should typically range from three to ten times the control bandwidth. Considering noise sensitivity and tracking accuracy, this study sets $k_{\mathrm{ESO}}=5$.

The control gain parameter $b_0$ is determined based on the system’s moment of inertia matrix. Specifically, for the roll($\varphi$), pitch($\theta$), and yaw($\psi$) controllers, the respective values are given by $b_x=1/J_x$, $b_y=1/J_y$, and $b_z=1/J_z$, where $J_x$, $J_y$, and $J_z$ represent the moments of inertia along each axis. Proper selection of $b_0$ ensures that the control input aligns with the physical system characteristics, thereby enhancing control performance.

The final control input expressions are given as follows:

$$\left\{\begin{array}{c}{\tau }_{\varphi }={\displaystyle \frac{{\omega }_o^2(r^{\varphi }-z_{11})+2{\omega }_o(r^{\varphi }-z_{12})+r^{\varphi }-z_{13}}{b_x}}\hfill \\ {\tau }_{\theta }={\displaystyle \frac{{\omega }_o^2(r^{\theta }-z_{21})+2{\omega }_o(r^{\theta }-z_{22})+r^{\theta }-z_{23}}{b_y}}\hfill \\ {\tau }_{\psi }={\displaystyle \frac{{\omega }_o^2(r^{\psi }-z_{31})+2{\omega }_o(r^{\psi }-z_{32})+r^{\psi }-z_{33}}{b_z}}\hfill \end{array}\right.$$

(19)

where $r^{*},{\dot{r}}^{*},{\ddot{r}}^{*}{(}^{*}=\varphi ,\theta ,\psi )$ represent the estimated attitude angles and their derivatives, while $z_{ij}$ denotes the LESO estimates of system inputs and disturbances. The overall modified LADRC structure is depicted in Figure 4.

3.2.3. Decoupling-Free Device

The LESO employs three input quantities—namely, the control inputs ${\tau }_{\varphi }$, ${\tau }_{\theta }$, and ${\tau }_{\psi }$—along with the system output y and the derivative of the total disturbance h. Correspondingly, it provides three output quantities: the estimate of the system output $z_1$, the estimate of its derivative $z_2$, and the estimate of the total disturbance $z_3$. The system dynamics, as described in Equation (2), are updated according to Equations (5) and (9):

$$\left\{\begin{array}{c}\ddot{\varphi }=b_x{\tau }_{\varphi }+z_{13}\hfill \\ \ddot{\theta }=b_y{\tau }_{\theta }+z_{23}\hfill \\ \ddot{\psi }=b_z{\tau }_{\psi }+z_{33}\hfill \end{array}\right.$$

(20)

The specific expressions for the disturbance input terms $h_i$($i=1,2,3$) are given as follows:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill h_1& =J_1[(\ddot{\theta }\dot{\psi }+\dot{\theta }\ddot{\psi })-k_t\ddot{\varphi }]\hfill \\ \hfill & =J_1[(\ddot{\theta }{z}_{32}+z_{22}\ddot{\psi })-k_t\ddot{\varphi }]\hfill \\ \hfill h_2& =J_2[(\ddot{\varphi }\dot{\psi }+\dot{\varphi }\ddot{\psi })-k_t\ddot{\theta }]\hfill \\ \hfill & =J_2[(\ddot{\varphi }{z}_{32}+z_{12}\ddot{\psi })-k_t\ddot{\theta }]\hfill \\ \hfill h_3& =J_3[(\ddot{\varphi }\dot{\theta }+\dot{\varphi }\ddot{\theta })-k_t\ddot{\psi }]\hfill \\ \hfill & =J_3[(\ddot{\varphi }{z}_{22}+z_{12}\ddot{\theta })-k_t\ddot{\psi }]\hfill \end{array}\hfill \end{array}\right.$$

(21)

where $J_1={\displaystyle \frac{J_y-J_z}{J_x}}$, $J_2={\displaystyle \frac{J_z-J_x}{J_y}}$, $J_3={\displaystyle \frac{J_x-J_y}{J_z}}$.

Substituting Equation (20) into Equation (21), we obtain

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill h_1& =J_1[\left((b_0{\tau }_{\theta }+z_{23})z_{32}+z_{22}(b_0{\tau }_{\psi }+z_{33})\right)\hfill \\ \hfill & -k_t(b_0{\tau }_{\varphi }+z_{13})]\hfill \\ \hfill h_2& =J_2[\left((b_0{\tau }_{\varphi }+z_{13})z_{32}+z_{12}(b_0{\tau }_{\psi }+z_{33})\right)\hfill \\ \hfill & -k_t(b_0{\tau }_{\theta }+z_{23})]\hfill \\ \hfill h_3& =J_3[\left((b_0{\tau }_{\varphi }+z_{13})z_{22}+z_{12}(b_0{\tau }_{\theta }+z_{23})\right)\hfill \\ \hfill & -k_t(b_0{\tau }_{\psi }+z_{33})]\hfill \end{array}\hfill \end{array}\right.$$

(22)

3.2.4. Adaptive Estimator Design

In parameter estimation, a commonly employed model follows a linear parameterization structure:

$$\mathrm{y}\left(\mathrm{t}\right)=\mathrm{W}\left(\mathrm{t}\right)·d$$

(23)

where $y\left(t\right)$ is the system output, d is the vector of unknown parameters to be estimated, and $W\left(t\right)$ represents the known signal matrix obtained from system measurements. Thus, only the parameter d remains unknown in Equation (23).

To predict the system output based on parameter estimation, we define

$$\widehat{y}\left(t\right)=W\left(t\right)\widehat{d}\left(t\right)$$

(24)

where $\widehat{y}\left(t\right)$ denotes the predicted output. The prediction error is given by

$$e\left(t\right)=\widehat{y}\left(t\right)-y\left(t\right)$$

(25)

In the standard least-squares method, parameter estimation is achieved by minimizing the total prediction error:

$$J={\int }_0^t{∥y\left(r\right)-W\left(r\right)\widehat{d}\left(t\right)∥}^{2}dr$$

(26)

To introduce exponential forgetting of past data, Equation (26) is modified as follows:

$$J={\int }_0^{t}exp\left[-{\int }_s^t\lambda \left(r\right)dr\right]{∥y\left(s\right)-W\left(s\right)\widehat{d}\left(s\right)∥}^{2}ds$$

(27)

where $\lambda \left(t\right)\ge 0$ is a time-varying forgetting factor. The parameter update rule is as follows:

$$\widehat{d}=-P\left(t\right)W^{T}e$$

(28)

Meanwhile, the gain update rule is formulated as follows:

$${\displaystyle \frac{d}{dt}}\left[P^{-1}\right]=-\lambda \left(t\right)P^{-1}+W^T\left(t\right)W\left(t\right)$$

(29)

A more efficient implementation modifies this to

$${\displaystyle \frac{d}{dt}}\left[P\right]=\lambda \left(t\right)P-P{W}^T\left(t\right)W\left(t\right)P$$

(30)

To adapt the forgetting factor to the signal excitation level, it is adjusted based on the norm of P:

$$\lambda \left(t\right)={\lambda }_0\left(1-{\displaystyle \frac{\parallel P\parallel }{k_0}}\right)$$

(31)

where ${\lambda }_0$ and $k_0$ are positive constants representing the maximum forgetting rate and the preset boundary of P, respectively.

This study proposes two parameter estimation approaches, with their core design logic referencing the parameter estimation framework [27]. Both methods employ recursive least squares with exponential forgetting for real-time disturbance estimation, without utilizing Fourier transform analysis. The first is Low-Precision Modified Linear Active Disturbance Rejection Control (LPMLADRC), which utilizes both real-time angle and angular velocity measurements for disturbance estimation. This approach provides balanced performance with moderate computational requirements.

The second approach, High-Precision Modified Linear Active Disturbance Rejection Control (HPMLADRC), achieves enhanced estimation accuracy by exclusively using real-time angle measurements to estimate both the frequency and amplitude of unknown disturbances. The implementation builds upon the previously described exponential forgetting least squares framework, with the following specialized application:

Disturbance Parameter Estimation—For HPMLADRC, the regressor vector $\varphi \left(k\right)$ is constructed exclusively from real-time angle measurements to estimate disturbance frequency ${\omega }_d$ and amplitude $A_d$. For LPMLADRC, $\varphi \left(k\right)$ incorporates both angle and angular velocity measurements for generalized disturbance estimation.

Real-time Compensation—The estimated disturbance parameters are continuously integrated into the control framework. The total disturbance estimate $z_3$ is enhanced with the estimated disturbance model:

$$z_3^{\mathrm{enhanced}}=z_3^{\mathrm{standard}}+{\widehat{A}}_{d}sin({\widehat{\omega }}_{d}t+{\widehat{\varphi }}_d)$$

(32)

The fundamental distinction between LPMLADRC and HPMLADRC lies in their measurement utilization: LPMLADRC employs both angle and angular velocity data for robust disturbance estimation, while HPMLADRC exclusively uses angle measurements to achieve higher precision in estimating disturbance frequency and amplitude characteristics.

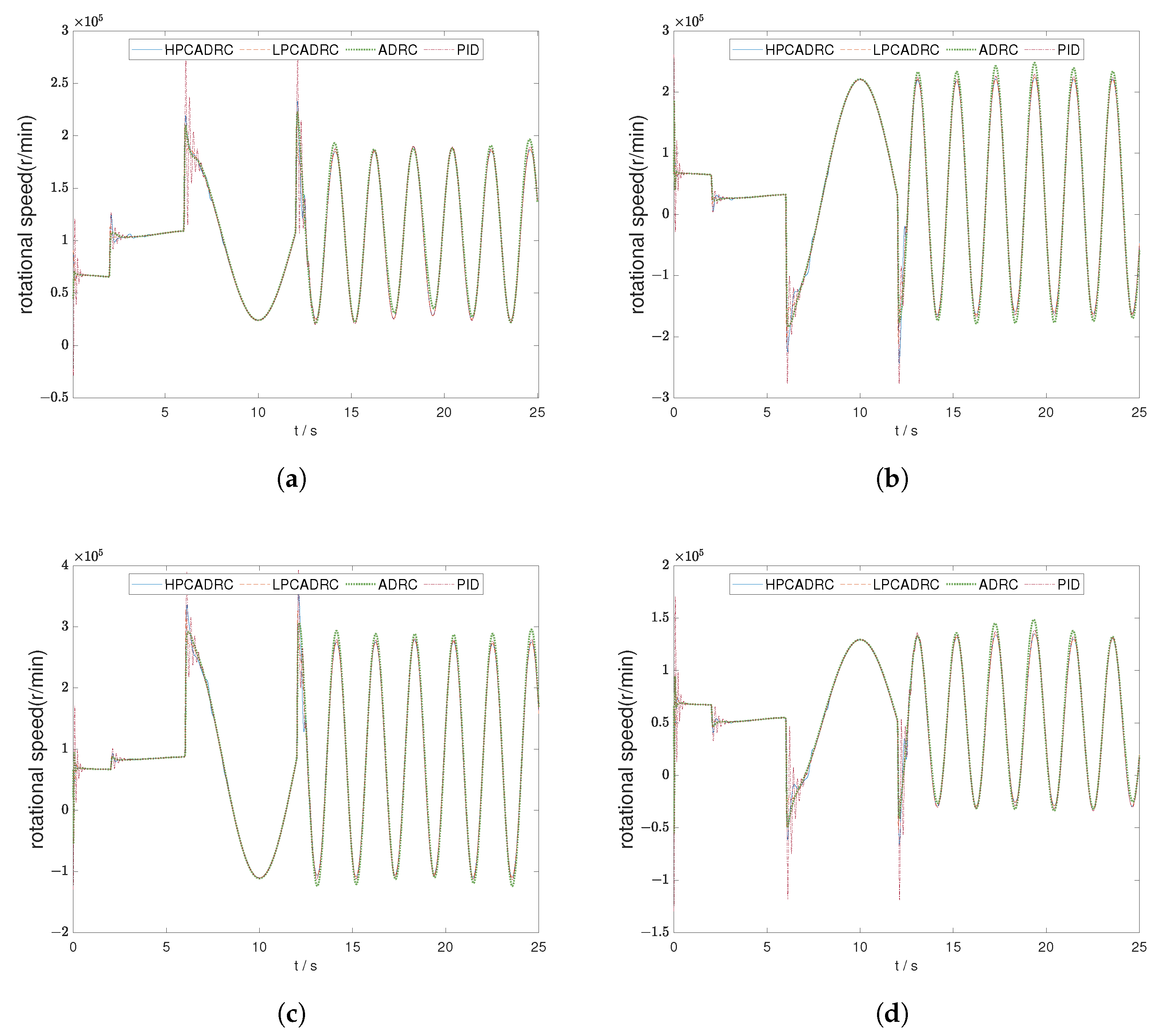
3.3. Rotor Speed Calculation

The rotor speeds ${\omega }_1$, ${\omega }_2$, ${\omega }_3$, and ${\omega }_4$ are determined by solving the control input equation:

$$\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right]=\left[\begin{array}{cccc}{\displaystyle \frac{1}{4}}& 0& -{\displaystyle \frac{1}{2}}& -{\displaystyle \frac{1}{4}}\\ {\displaystyle \frac{1}{4}}& {\displaystyle \frac{1}{2}}& 0& {\displaystyle \frac{1}{4}}\\ {\displaystyle \frac{1}{4}}& 0& {\displaystyle \frac{1}{2}}& -{\displaystyle \frac{1}{4}}\\ {\displaystyle \frac{1}{4}}& -{\displaystyle \frac{1}{2}}& 0& {\displaystyle \frac{1}{4}}\end{array}\right]\left[\begin{array}{c}{\displaystyle \frac{U_L}{k_L}}\\ {\displaystyle \frac{{\tau }_{\varphi }}{l{k}_L}}\\ {\displaystyle \frac{{\tau }_{\theta }}{l{k}_L}}\\ {\displaystyle \frac{{\tau }_{\psi }}{b}}\end{array}\right]$$

(33)

In this context, the total thrust $U_L$ is derived from the vertical force balance equation, as referenced in Equation (4).

Furthermore, $U_L$ can be expressed as follows:

$$U_L={\displaystyle \frac{mg}{cos\varphi ·cos\theta }}.$$

(34)

This expression for $U_L$ ensures that the vertical forces are balanced, allowing the quadrotor to hover or maintain a desired altitude.

4. Stability Analysis

To demonstrate the stability of the modified LADRC proposed in this paper, we provide a comprehensive stability analysis for the entire closed-loop system, including the plant, observer, and controller. The pitch channel of a quadrotor UAV is selected as the analysis target, with similar proofs applicable to other attitude channels.

4.1. Observer Stability Analysis

The state-space representation of the pitch channel is given by

$$\left\{\begin{array}{c}{\dot{z}}_1\left(t\right)=z_2\left(t\right)\hfill \\ {\dot{z}}_2\left(t\right)=z_3\left(t\right)+{\displaystyle \frac{U_3}{I_x}}-{\displaystyle \frac{f_k{z}_2\left(t\right)}{I_x}}\hfill \\ {\dot{z}}_3\left(t\right)=h\left(t\right)\hfill \\ y\left(t\right)=z_1\left(t\right)\hfill \end{array}\right.$$

(35)

where $z_1\left(t\right)$ represents the pitch angle $\theta$, $z_2\left(t\right)$ denotes the pitch angular velocity $\dot{\theta }$, and $z_3\left(t\right)$ corresponds to the total disturbance in the pitch channel. Additionally, $h\left(t\right)$ is the derivative of the total disturbance. The LESO for the pitch channel is formulated as follows:

$$\left\{\begin{array}{c}{\dot{x}}_1\left(t\right)=x_2\left(t\right)+3{\omega }_0[z_1\left(t\right)-x_1\left(t\right)]\hfill \\ {\dot{x}}_2\left(t\right)=x_3\left(t\right)+3{\omega }_0^2[z_1\left(t\right)-x_1\left(t\right)]+{\displaystyle \frac{U_3}{I_x}}-{\displaystyle \frac{f_k{x}_2\left(t\right)}{I_x}}\hfill \\ {\dot{x}}_3\left(t\right)={\omega }_0^3[z_1\left(t\right)-x_1\left(t\right)]\hfill \end{array}\right.$$

(36)

where ${\omega }_0$ is a positive constant.

To facilitate further analysis, we define ${\epsilon }_i$ as follows:

$${\epsilon }_i={\displaystyle \frac{{\alpha }_i}{{\omega }_0^{i-1}}},i=1,2,3.$$

(37)

Substituting this into Equation (36) yields

$$\dot{\epsilon }={\omega }_o{A}_3\epsilon +Bh/{\omega }_o^2$$

(38)

where

$$\left\{\begin{array}{c}{A}_3=\left[\begin{array}{ccc}-3& 1& 0\\ -3& 0& 1\\ -1& 0& 0\end{array}\right]\hfill \\ B={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T\hfill \end{array}\right.$$

(39)

Theorem 1.

Under the assumption that the total disturbance f and its derivative h are bounded, there exist constants $u_i>0$ and a finite time $T>0$ such that the estimation error ${\alpha }_i<u_i$ for $i=1,2,3$, for all $t\ge T$.

Proof of Theorem 1.

Solving Equation (38) yields

$$\epsilon \left(t\right)=e^{{\omega }_o{A}_{3}t}\epsilon \left(0\right)+{\int }_0^t{\displaystyle \frac{e^{{\omega }_o{A}_3(t-\tau )}Bh}{{\omega }_o^2}}d\tau$$

(40)

$\zeta \left(t\right)$ is defined as follows:

$$\zeta \left(t\right)={\int }_0^t{\displaystyle \frac{e^{{\omega }_o{A}_3(t-\tau )}Bh}{{\omega }_o^2}}d\tau$$

(41)

From the boundedness assumption of h, it follows that

$${\zeta }_i\left(t\right)\le {\displaystyle \frac{{\sigma }_2}{{\omega }_o^3}}\left[\left|{\left(A_3^{-1}B\right)}_i\right|+\left|{\left(A_3^{-1}{e}^{{\omega }_o{A}_{3}t}B\right)}_i\right|\right]$$

(42)

It follows from Equation (39) that

$$\left|{\left(A_3^{-1}B\right)}_i\right|\le 3$$

(43)

Since $A_3$ is Hurwitz, there exists a finite time $T_1$ such that for any $t\ge T_i$, $i,j=1,2,3$, the following holds:

$$\left|{\left[e^{{\omega }_o{A}_{3}t}\right]}_{ij}\right|\le {\displaystyle \frac{1}{{\omega }_o^3}}$$

(44)

It can be calculated that

$$\left|{\left(A_3^{-1}{e}^{{\omega }_o{A}_{3}t}B\right)}_i\right|\le {\displaystyle \frac{4}{{\omega }_o^3}}$$

(45)

It follows from Equations (42)–(45) that

$$\left|{\zeta }_i\left(t\right)\right|\le {\displaystyle \frac{3{\sigma }_2}{{\omega }_o^3}}+{\displaystyle \frac{4{\sigma }_2}{{\omega }_o^6}}$$

(46)

Let ${\epsilon }_{\mathrm{sum}}\left(0\right)=\left|{\epsilon }_1\left(0\right)\right|+\left|{\epsilon }_2\left(0\right)\right|+\left|{\epsilon }_3\left(0\right)\right|$. For all $t\ge T_i$,$i=1,2,3$, the following holds:

$$\left|{\left[e^{{\omega }_o{A}_{3}t}\epsilon \left(0\right)\right]}_i\right|\le {\displaystyle \frac{{\epsilon }_{sum}\left(0\right)}{{\omega }_o^3}}$$

(47)

It follows from Equation (40) that

$$\left|{\epsilon }_i\left(t\right)\right|=\left|{\left[e^{{\omega }_o{A}_{3}t}\epsilon \left(0\right)\right]}_i\right|+\left|{\zeta }_i\left(t\right)\right|$$

(48)

Let ${\alpha }_{\mathrm{sum}}\left(0\right)=\left|{\alpha }_1\left(0\right)\right|+\left|{\alpha }_2\left(0\right)\right|+\left|{\alpha }_3\left(0\right)\right|$. Based on ${\epsilon }_i\left(t\right)={\alpha }_i/{\omega }_0^{i-1}$ and Equations (46)–(48), it follows that

$$\left|{\alpha }_i\left(t\right)\right|\le \left|{\displaystyle \frac{{\alpha }_{sum}\left(0\right)}{{\omega }_o^3}}\right|+{\displaystyle \frac{3{\sigma }_2}{{\omega }_o^{4-i}}}+{\displaystyle \frac{4{\sigma }_2}{{\omega }_o^{7-i}}}={\mu }_i$$

(49)

The above equation holds for all $t\ge T_i$, $i=1,2,3$.

Under the condition that the derivative of the total disturbance is bounded, the estimation error of the LESO for the pitch channel is bounded, and its upper bound monotonically decreases with the increase in the observer bandwidth. □

4.2. Closed-Loop System Stability Analysis

To comprehensively establish the stability of the entire closed-loop system, we present a rigorous stability proof that integrates the plant, observer, and controller.

Consider the closed-loop system dynamics consisting of the plant (Equation (35)), the LESO (Equation (36)), and the control law (Equations (11) and (13)). The overall system can be represented as follows:

$$\left\{\begin{array}{c}\dot{X}=F\left(X\right)+G\left(X\right)u\hfill \\ u=K(\widehat{X},r)\hfill \end{array}\right.$$

(50)

where $X={[z_1,z_2,z_3]}^T$ represents the plant states, $\widehat{X}={[x_1,x_2,x_3]}^T$ represents the observer states, and u is the control input given by Equation (11).

Theorem 2.

Consider the closed-loop system described by Equation (61) with the LESO in Equation (36) and the control law in Equations (11) and (13). Let us assume the following:

1. 

The total disturbance f and its derivative h are bounded;

2. 

The observer bandwidth ${\omega }_o$ is sufficiently large;

3. 

The control parameters $k_p$ and $k_d$ are properly chosen such that the characteristic polynomial $s^2+k_{d}s+k_p$ is Hurwitz.

Then, the closed-loop system is uniformly ultimately bounded (UUB).

Proof of Theorem 2.

The composite Lyapunov function candidate for the closed-loop system is defined as follows:

$$V=V_e+V_c$$

(51)

where $V_e$ is the Lyapunov function for the observer error dynamics and $V_c$ is the Lyapunov function for the controller dynamics.

From Theorem 1, we have established that the observer error dynamics are bounded. Specifically, there exists a Lyapunov function $V_e$ such that

$${\dot{V}}_e\le -{\alpha }_e{\parallel \epsilon \parallel }^2+{\gamma }_e\parallel h\parallel$$

(52)

where ${\alpha }_e>0$ and ${\gamma }_e>0$ are constants.

For the controller dynamics, consider the virtual control law $u_0$ in Equation (13). The compensated system dynamics become

$$\ddot{y}\approx u_0=k_p(r-z_1)+k_d(\dot{r}-z_2)+\ddot{r}$$

(53)

The tracking error is defined as $e={[e_1,e_2]}^T={[r-z_1,\dot{r}-z_2]}^T$. The error dynamics can be written as follows:

$$\dot{e}=A_{c}e+B_c\delta$$

(54)

where

$$A_c=\left[\begin{array}{cc}0& 1\\ -k_p& -k_d\end{array}\right],B_c=\left[\begin{array}{c}0\\ 1\end{array}\right]$$

(55)

and $\delta$ represents the residual disturbance after compensation.

Since $k_p$ and $k_d$ are chosen such that $A_c$ is Hurwitz (as ensured by the pole placement in Equation (14)), there exists a Lyapunov function $V_c=e^{T}Pe$ with $P>0$ satisfying

$$A_c^{T}P+P{A}_c=-Q$$

(56)

for some $Q>0$.

The time derivative of $V_c$ along the trajectories of Equation (54) is

$${\dot{V}}_c=-e^{T}Qe+2e^{T}P{B}_c\delta$$

(57)

Given that the observer error is bounded (from Theorem 1) and the disturbance is bounded, $\delta$ is bounded. Therefore, there exists a constant ${\gamma }_c>0$ such that

$${\dot{V}}_c\le -{\alpha }_c{\parallel e\parallel }^2+{\gamma }_c\parallel \delta \parallel$$

(58)

Combining Equations (52) and (58), the time derivative of the composite Lyapunov function V satisfies

$$\dot{V}\le -{\alpha }_e{\parallel \epsilon \parallel }^2-{\alpha }_c{\parallel e\parallel }^2+{\gamma }_e\parallel h\parallel +{\gamma }_c\parallel \delta \parallel$$

(59)

Since both $\parallel h\parallel$ and $\parallel \delta \parallel$ are bounded, there exists a compact set $\Omega$ such that outside this set, $\dot{V}<0$. By the Lyapunov theory for perturbed systems, the closed-loop system is uniformly ultimately bounded.

Furthermore, the ultimate bound can be made arbitrarily small by increasing the observer bandwidth ${\omega }_o$ and properly tuning the control parameters $k_p$ and $k_d$. □

Corollary 1.

Under the conditions of Theorem 2 and assuming perfect disturbance cancellation ($z_3=f(·)$), the closed-loop system is exponentially stable.

Proof of Corollary 1.

With perfect disturbance cancellation, we have $\delta =0$ in Equation (54). The error dynamics reduce to

$$\dot{e}=A_{c}e$$

(60)

Since $A_c$ is Hurwitz by design, the tracking error dynamics are exponentially stable. Combined with the bounded observer error established in Theorem 1, the entire closed-loop system is exponentially stable. □

The stability analysis demonstrates that the proposed modified LADRC ensures both observer error boundedness and closed-loop system stability under reasonable assumptions, validating the theoretical foundation of the control approach.

5. Simulations and Discussion

5.1. Simulation Settings

To evaluate the effectiveness of the proposed algorithm, this study is based on the attitude dynamics model of a quadrotor UAV. Four distinct control strategies are selected for the design and simulation validation of the control system. The first two strategies are the HPMLADRC and the LPMLADRC methods, which were introduced in Section 3.2.4. The third method is the traditional LADRC, which does not incorporate a disturbance compensation mechanism. The fourth approach is the PID control method. By comparing the simulation results of these four methods, the performance of the proposed algorithm can be comprehensively assessed under various control strategies. The parameters of the quadrotor UAV attitude system model are provided in

Table 1. Quadcopter UAV model parameters.

Parameters	Values
m	$0.8\mathrm{kg}$
$J_x$	$5.445\times {10}^{-3}\mathrm{kg}·{\mathrm{m}}^2$
$J_y$	$5.445\times {10}^{-3}\mathrm{kg}·{\mathrm{m}}^2$
$J_z$	$1.089\times {10}^{-2}\mathrm{kg}·{\mathrm{m}}^2$
l	$0.165\mathrm{m}$
b	$2\times {10}^{-6}$
$k_L$	$2.98\times {10}^{-5}$
$k_t$	$9\times {10}^{-2}$
$\varphi \left(0\right)$	0
$\theta \left(0\right)$	0
$\psi \left(0\right)$	0

. The multirotor attitude control algorithm proposed in this paper has been open-sourced. For the complete model, please refer to https://github.com/qianshiya/HPCADRC (accessed on 15 October 2025).

The three attitude angle commands for the UAV are defined in a time-varying form as follows: $r^{\varphi }=-5^{\circ }+{15}^{\circ }cos\left({\displaystyle \frac{\pi t}{2}}\right)$, $r^{\theta }=-{10}^{\circ }cos\left({\displaystyle \frac{\pi t}{2}}\right)$, $r^{\psi }=0$. The external disturbances affecting the system dynamics are specified in

Table 2. External disturbance settings.

Time	${\mathit{\tau }}_{\mathit{d}}^{\mathit{\varphi }}$	${\mathit{\tau }}_{\mathit{d}}^{\mathit{\theta }}$	${\mathit{\tau }}_{\mathit{d}}^{\mathit{\psi }}$
$t\le 2$	0	0	0
$2<t\le 6$	$-8$	6	$-6$
$6<t\le 12$	$20-120sin\left(0.25\pi t\right)$	$20+120sin\left(0.25\pi t\right)$	$20-120sin\left(0.25\pi t\right)$
$12<t\le 25$	$20-120sin\left(3t\right)$	$20+120sin\left(3t\right)$	$20-120sin\left(3t\right)$
$t>25$	0	0	0

.

In these settings, the term $sin\left(3t\right)$ is introduced based on an analysis of the system’s dynamic characteristics from Luo et al. [28]. It models the periodic disturbances that the system may experience at specific frequencies, which more accurately simulate the complex dynamic environment that the quadrotor UAV may encounter under real-world operating conditions. This approach ensures the validity of the proposed control method’s ability to counteract such disturbances.

The specific formulation of the proposed modified LADRC method is given by Equations (11)–(14), while the observer design is described by Equations (9) and (22), and the unknown disturbance estimator is provided by Equations (28)–(31). Levant’s parameters ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are all set to 20. Assuming the disturbance period can be observed, the signal matrix for the precise estimator is defined as follows:

$${\omega }_c=15,{\omega }_o=k_{\mathrm{ESO}}·{\omega }_c=5·15=75,b_0=1$$

(61)

$${\lambda }_0=100,k_0=300$$

(62)

For comparison, the signal matrix for the rough estimator is set to $W=1$, with the parameters selected according to the expressions for ${\omega }_c$ and ${\omega }_o$ in Equations (61) and (62). Levant’s parameters ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ remain set to 20. The traditional LADRC controller is designed using the same formulation as in Equations (11)–(14) but without the estimation of unknown disturbances. The controller parameters are also selected according to Equations (61) and (62). For the PID controller, the parameters are set to $P=20$, $I=20$, and $D=0.05$, adhering to the standard practice for tuning these values to achieve the desired control performance.

5.2. Analysis of Simulation Results

5.2.1. Comparison Between TD and Levant Differentiator

As core tools for derivative signal extraction in control systems, the TD and Levant Differentiator exhibit distinct characteristics tailored to different application needs. This section compares their key performance and implementation features, with supporting experimental results shown in Figure 5 and quantitative metrics summarized in

Table 3. Performance comparison between TD and Levant differentiator.

Differentiator	Mean	Standard Deviation	ErrorRMS
TD	−0.082614	2.765528	2.766623
Levant	−0.005435	0.695497	0.695483

.

In terms of design principles, the TD prioritizes smooth tracking and derivative extraction through linear or nonlinear state feedback, balancing response speed and noise suppression. The Levant Differentiator, by contrast, relies on high-order sliding surfaces and discontinuous control to enforce finite-time convergence of derivative errors, focusing on fast and robust state tracking.

For convergence performance, the TD achieves exponential convergence—its speed is tuned via a bandwidth parameter, but no strict upper bound on convergence time exists. The Levant Differentiator offers finite-time convergence (with a deterministic time bound from initial errors), making it faster for time-critical tasks, though it introduces inherent chattering.

In disturbance and noise handling, the TD adapts to error magnitude to suppress mid-to-low-frequency noise, suiting general industrial environments. The Levant Differentiator leverages sliding mode invariance for strong disturbance rejection but is sensitive to high-frequency noise, requiring additional filtering that may compromise its speed advantage.

Implementation complexity further differentiates them: the TD uses 2–3 states and minimal parameters (e.g., bandwidth $\omega$ for linear variants), enabling easy deployment on low-resource hardware. The Levant Differentiator demands more auxiliary states, nonlinear switching term design, and precise parameter tuning, increasing computational and hardware requirements.

Table 3 quantifies these differences, while Figure 5 illustrates their derivative extraction effects for a noisy input signal (e.g., sinusoidal signal with Gaussian noise, where the noise power is set to 0.001). In summary, the TD is preferred for scenarios prioritizing simplicity, low chattering, and moderate noise; the Levant Differentiator is suitable for fast-response, high-disturbance systems where finite-time convergence is critical.

5.2.2. Attitude Angle Tracking Response

Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 present the simulation results for the quadrotor UAV attitude system under various control methods. These results demonstrate the effectiveness of the proposed HPMLADRC and LPMLADRC techniques in comparison to traditional methods.

Figure 6 illustrates the tracking response curves for the attitude angles. Through a comparative analysis, it is evident that in a high-interference environment, both HPMLADRC and LPMLADRC provide high-precision tracking of the attitude commands. In contrast, while the traditional LADRC method maintains high tracking accuracy under low or no interference, its performance significantly degrades in the presence of high-frequency disturbances. Additionally, the PID control method exhibits steady-state errors in the presence of unknown disturbances. These findings suggest that the HPMLADRC and LPMLADRC methods have a distinct advantage in terms of anti-interference capabilities, especially in complex and dynamic external environments, thereby ensuring the stability and reliability of the UAV’s attitude control system.

Figure 6. Attitude angle tracking response curve. (a) Comparison of angle tracking for $\varphi$. (b) Comparison of angle tracking for $\theta$. (c) Comparison of angle tracking for $\psi$.

Figure 6. Attitude angle tracking response curve. (a) Comparison of angle tracking for $\varphi$. (b) Comparison of angle tracking for $\theta$. (c) Comparison of angle tracking for $\psi$.

5.2.3. Attitude Angle Tracking Error Response

Figure 7 presents the response curves for attitude angle tracking errors, including zoomed-in views that show the system’s response under conditions of no interference, constant interference, and two types of time-varying interference. The comparison of the three control methods is carried out based on two key factors: convergence speed and anti-interference performance.

• From the response graphs between 0 and 0.3 s, it is observed that the convergence speeds of all three methods are comparable;
• During the period of interference (from 2 to 25 s), both the LADRC and PID methods exhibit a significant increase in tracking errors due to the lack of disturbance compensation;
• Notably, from 2 to 2.4 s and 6 to 6.1 s, the LPMLADRC method recovers more quickly from constant or time-varying interference, demonstrating superior anti-interference performance;
• Between 12 and 25 s, only the HPMLADRC method is able to return to a steady state, highlighting its stronger disturbance rejection capability.

In summary, while the LPMLADRC method converges faster than HPMLADRC, the latter is better at suppressing high-frequency disturbances. Traditional LADRC and PID methods are clearly less effective in anti-interference performance because they lack disturbance compensation terms. All these performance differences—like convergence speed and anti-interference ability—are quantified in the following

Table 4. Performance comparison of different control methods for each attitude angle.

Attitude Angle	Control Method	Mean	Standard Deviation	ErrorRMS
$\varphi$	HPCADRC	0.007812	1.182325	1.182327
	LPCADRC	−0.023116	0.567964	0.568423
	ADRC	0.218790	7.678606	7.681569
	PID	0.046614	1.489701	1.490401
$\theta$	HPCADRC	0.04191	1.109181	1.109954
	LPCADRC	0.020307	0.524753	0.525137
	ADRC	0.183654	8.196446	8.198367
	PID	0.035225	1.564268	1.564639
$\psi$	HPCADRC	−0.000005	1.328905	1.328883
	LPCADRC	−0.003438	0.247364	0.247384
	ADRC	−0.115681	7.881107	7.881824
	PID	−0.02991	3.078698	3.078792

, which gives specific data for each attitude angle to support the above conclusions.

Figure 7. Attitude angle tracking error response curve. (a) Angle tracking error for $\varphi$. (b) Angle tracking error for $\theta$. (c) Angle tracking error for $\psi$.

Figure 7. Attitude angle tracking error response curve. (a) Angle tracking error for $\varphi$. (b) Angle tracking error for $\theta$. (c) Angle tracking error for $\psi$.

To compare the four trajectories in Figure 7, three key performance indicators are employed, with their specific numerical values presented in

Table 5. Experimental indicator presentation.

Control Method	Maximum Tracking Error (${\mathit{T}}_{\mathit{m}}$)	Settling Time (${\mathit{T}}_{\mathit{s}}$)	Steady-State Tracking Error Range (${\mathit{ϵ}}_{\mathbf{ss}}$)
HPMLADRC	9.43	0.465	[−0.0073, 0.0073]
LPMLADRC	1.78	0.124	[−0.3639, 0.3639]
ADRC	16.9411	1.335	[−13.8988, 13.8988]
PID	11.4166	0.395	[−5.2999, 5.2999]

. These indicators include the following: (1) maximum tracking error ($T_m$), (2) settling time ($T_s$), and (3) steady-state tracking error range (${ϵ}_{ss}$). Prior to conducting the comparative analysis, a scoring rule was established to evaluate and rank the four control algorithms (LPMLADRC, HPMLADRC, PID, and ADRC). A 4-point scoring system (1 point = worst performance, 4 points = best performance) was adopted, and the detailed rule is defined as follows:

• Maximum tracking error $\left(T_m\right)$: This indicator reflects the maximum dynamic deviation of the system during the tracking process. A smaller value of $T_m$ indicates less severe dynamic fluctuations of the system and thus corresponds to a higher score. As shown in Table 5, LPMLADRC achieves the smallest $T_m$ and is assigned 4 points; followed by HPMLADRC (3 points), PID (2 points), and ADRC (1 point).
• Settling time $\left(T_s\right)$: This indicator characterizes the response speed of the controller. A shorter value means the controller can drive the system to reach a stable state more quickly and thus earns a higher score. According to Table 5, LPMLADRC exhibits the shortest $T_s$ and is awarded 4 points, while ADRC has the longest $T_s$ and is assigned 1 point.
• Steady-state tracking error range $\left({ϵ}_{ss}\right)$: This indicator quantifies the steady-state control precision of the system. A narrower range of ${ϵ}_{ss}$ denotes higher control accuracy, which is essential for UAVs to resist unknown disturbances. Among the four algorithms, HPMLADRC has the smallest ${ϵ}_{ss}$ range and is given 4 points, whereas ADRC ranks the lowest in this indicator and receives 1 point.

The scoring results of the four algorithms across the three indicators are visualized using a radar chart, as presented in Figure 8.

Figure 8. Radar chart of performance indicators.

Figure 8. Radar chart of performance indicators.

5.2.4. Estimation of Unknown Disturbances

Figure 9 shows the estimation of the unknown disturbance d within the system. It is clearly observed that, upon the sudden introduction of interference ($t>2$ s), the unknown disturbance undergoes a significant change. Despite this sudden change, the disturbance estimator exhibits excellent dynamic response, quickly adapting to the disturbance within approximately 1.4 s and providing an accurate estimation. This result validates the robustness and effectiveness of the disturbance estimator, which is capable of accurately estimating the disturbance even in the presence of sudden interferences. The estimator’s design ensures it meets the real-time control requirements, as it can provide timely and accurate disturbance estimates, thereby facilitating effective control adjustments and maintaining system stability. Key performance indicators are further quantified in the following

Table 6. Analysis of the estimation of unknown disturbance.

Attitude Angle	Mean	Standard Deviation	ErrorRMS
$\varphi$	0.805031	9.94855	9.980903
$\theta$	−0.627698	9.957483	9.977082
$\psi$	0.771615	10.244059	10.272908

, which supports the observations from the figure.

Figure 9. Response curve of unknown disturbance and its estimated value. (a) Disturbance tracking for the $\varphi$. (b) Disturbance tracking for the $\theta$. (c) Disturbance tracking for the $\psi$.

Figure 9. Response curve of unknown disturbance and its estimated value. (a) Disturbance tracking for the $\varphi$. (b) Disturbance tracking for the $\theta$. (c) Disturbance tracking for the $\psi$.

To enhance the response speed, appropriate parameters can be selected according to Equation (17). This parameter selection can further improve the estimator’s performance, enabling it to more effectively adapt to system changes, thus enhancing the overall control system’s responsiveness and accuracy.

5.2.5. Performance in Noisy Environments

To assess the robustness of the proposed method in noisy environments, Gaussian white noise with a mean of 0 and a noise power of 0.001 was introduced into the measurement of attitude angles. The system’s initial conditions were set to zero to simulate adverse real-world conditions. The control parameters were maintained consistent with previous settings to ensure comparability. The simulation results, shown in Figure 10 and Figure 11, demonstrate that, despite the presence of measurement noise, the attitude tracking errors rapidly decrease and converge to a small range near zero. This result confirms that the proposed control strategy can effectively handle uncertainties and external disturbances while maintaining high control accuracy in noisy environments.

Further analysis reveals that the superior performance of this method can be attributed to its advanced disturbance estimation and compensation mechanism, which enables the control system to maintain stability even under noisy conditions. Additionally, the method is not highly sensitive to initial conditions, providing an advantage in practical applications where precise initial state knowledge is often unavailable. The simulation results thus demonstrate the robustness and effectiveness of the proposed method, making it a reliable solution for real-world, complex environments.

Figure 12 presents the rotor speed response curves of a quadrotor UAV under four distinct control methods, with

Table 7. Performance comparison of different control methods for each rotor.

Rotor	Control Method	Mean	Standard Deviation	Variance
Rotor 1	HPCADRC	100,090.22	51,624.32	2,665,070,834.32
	LPCADRC	100,034.52	51,296.58	2,631,339,789.43
	ADRC	101,714.57	52,403.40	2,746,117,294.20
	PID	100,154.83	53,189.40	2,829,112,886.50
Rotor 2	HPCADRC	39,608.70	118,966.41	14,153,007,799.14
	LPCADRC	39,612.40	118,466.14	14,034,228,424.13
	ADRC	40,921.24	125,155.49	15,663,898,116.94
	PID	39,670.37	120,824.04	14,598,449,623.14
Rotor 3	HPCADRC	75,429.80	119,569.55	14,296,879,613.83
	LPCADRC	75,441.97	119,115.28	14,188,450,429.61
	ADRC	77,001.80	124,985.98	15,621,496,484.75
	PID	75,540.48	121,172.77	14,682,840,437.95
Rotor 4	HPCADRC	55,831.95	49,684.01	2,468,501,719.22
	LPCADRC	55,776.48	49,497.47	2,449,999,971.06
	ADRC	57,393.12	51,154.06	2,616,738,287.45
	PID	55,857.26	51,728.19	2,675,806,364.92

providing a quantitative analysis corresponding to Figure 12. As revealed by the analysis results, the rotor speed amplitudes of the four control methods are comparable in magnitude, with no significant discrepancies observed. In terms of energy consumption, the values of the four methods fall within the same order of magnitude, indicating a similar energy efficiency performance. Furthermore, the rotor speed under all control strategies exhibits smooth and continuous variation without abrupt fluctuations. Notably, this characteristic of continuous rotor speed change aligns with practical engineering requirements for quadrotor UAVs.

Figure 10. Numerical simulation of attitude tracking under noisy environment. (a) Comparison of angle tracking for $\varphi$ in a noisy environment. (b) Comparison of angle tracking for $\theta$ in a noisy environment. (c) Comparison of angle tracking for $\psi$ in a noisy environment.

Figure 10. Numerical simulation of attitude tracking under noisy environment. (a) Comparison of angle tracking for $\varphi$ in a noisy environment. (b) Comparison of angle tracking for $\theta$ in a noisy environment. (c) Comparison of angle tracking for $\psi$ in a noisy environment.

Figure 11. Attitude tracking errors under numerical simulation with noise. (a) Noise applied to $\varphi$. (b) Noise applied to $\theta$. (c) Noise applied to $\psi$.

Figure 11. Attitude tracking errors under numerical simulation with noise. (a) Noise applied to $\varphi$. (b) Noise applied to $\theta$. (c) Noise applied to $\psi$.

Figure 12. Rotor speed response curve. (a) Rotor 1 speed response curve. (b) Rotor 2 speed response curve. (c) Rotor 3 speed response curve. (d) Rotor 4 speed response curve.

Figure 12. Rotor speed response curve. (a) Rotor 1 speed response curve. (b) Rotor 2 speed response curve. (c) Rotor 3 speed response curve. (d) Rotor 4 speed response curve.

5.3. Discussion

In conclusion, both the HPMLADRC and LPMLADRC methods demonstrate superior performance over traditional LADRC and PID in terms of anti-interference capability and robustness in noisy environments. These methods provide a significant improvement in the stability and reliability of the quadrotor UAV attitude control system, offering a strong theoretical foundation and technical support for their application in real-world complex environments. The primary advantages of these methods include enhanced disturbance rejection, improved steady-state precision (particularly for HPMLADRC), and faster convergence characteristics (especially for LPMLADRC). A notable implementation difference lies in their sensor requirements: LPMLADRC requires both angular velocity and attitude angle measurements, while HPMLADRC operates with attitude angle measurements only, thereby reducing dependency on angular velocity sensors and potentially lowering system cost and complexity. However, these benefits come with certain limitations, including increased design complexity and more challenging parameter tuning requirements compared to conventional methods. The computational load, while manageable, is also somewhat elevated due to the additional observer dynamics. Despite these drawbacks, the proposed methods provide significant improvements in the stability and reliability of quadrotor UAV attitude control systems, offering a solid theoretical foundation and technical support for practical applications in complex real-world environments. The trade-off between performance enhancement and implementation complexity appears justified for applications demanding high-precision attitude control under challenging operating conditions.

6. Conclusions

This paper addresses the finite-time attitude command tracking problem of quadrotors subject to multi-source disturbances and proposes a modified LADRC algorithm for attitude tracking. Simulation results demonstrate that the proposed algorithm achieves high-precision attitude command tracking even under high-frequency disturbances and effectively estimates unknown disturbances through an integrated parameter estimator. However, due to the inclusion of the unknown disturbance estimation component, the controller initially exhibits inferior tracking performance compared to traditional LADRC and PID approaches, characterized by higher overshoot. This initial performance characteristic results from our methodological choice to maintain fixed control parameters throughout the simulation study, which intentionally eliminates interference from parameter variations to better demonstrate the system’s convergence properties. When compared to LPMLADRC, the proposed HPMLADRC algorithm exhibits a longer settling time but results in a smaller ultimate tracking error. Future work will focus on further enhancing the algorithm and conducting real-flight tests to evaluate its reliability in complex, real-world environments. Additionally, the potential application of the proposed approach will be explored across various UAV platforms and complex flight control systems, providing more robust technical support for precise UAV control.