Dynamic Parameter Identification Method for Space Manipulators Based on Hybrid Optimization Strategy

Abstract

High-precision identification of dynamic parameters is crucial for the on-orbit performance of space manipulators. This paper investigates dynamic modeling and parameter identification under special environmental conditions such as microgravity and vacuum. First, a dynamic model of the manipulator incorporating a nonlinear friction term is established using the Newton-Euler method, and an improved Stribeck friction model is proposed to better characterize high-speed conditions and space environmental effects. On this basis, a hybrid parameter identification method combining Particle Swarm Optimization (PSO) and Levenberg–Marquardt (LM) algorithms is proposed to balance global search capability and local convergence accuracy. To enhance identification performance, Fourier series are used to design excitation trajectories, and their harmonic components are optimized to improve the condition number of the observation matrix. Experiments conducted on a ground test platform with a six-degree-of-freedom (6-DOF) manipulator show that the proposed method effectively identifies 108 dynamic parameters. The correlation coefficients between predicted and measured joint torques all exceed 0.97, with root mean square errors below 5.1 N·m, demonstrating the high accuracy and robustness of the method under limited data samples. The results provide a reliable model foundation for high-precision control of space manipulators.

1. Introduction

Space manipulators play a critical role in on-orbit servicing missions, including satellite maintenance, space station assembly, and space debris removal [1,2,3,4]. The dynamic parameters of a manipulator system are pivotal determinants of its control accuracy and dynamic performance. Consequently, high-precision parameter identification serves as the foundation for robust and adaptive control of space manipulators. Furthermore, the uncertainty bounds derived from the identification process can directly quantify the modeling uncertainties required for robust controller design. In the space microgravity environment, the influence of the gravity term is significantly reduced, making joint friction and nonlinear damping effects the dominant factors affecting system performance. An accurate dynamic model is essential for trajectory planning, force control, and energy consumption optimization [5,6,7]. Dynamic parameter identification refers to the process of determining unknown parameters in the manipulator’s dynamic model (such as mass, center of mass position, inertia tensor, and friction coefficients) through experimental or simulation data [8,9]. However, the space environment possesses unique characteristics such as vacuum, microgravity, and extreme temperature variations, making it difficult to fully simulate actual on-orbit conditions in ground experiments, leading to significant deviations in identified dynamic parameters [10,11]. Therefore, research on dynamic parameter identification methods suitable for the special environment of space manipulators is of great theoretical and practical importance.

Dynamic modeling is the foundation of parameter identification. Common modeling methods in robotics include the Newton-Euler method and the Lagrange method. The Newton-Euler method, based on force and torque balance principles, analyzes the forces on each link of the manipulator to establish the dynamic equations [12]. The Lagrange method, based on energy conservation principles, describes the dynamic behavior of the manipulator by establishing the Lagrange equations [13]. In terms of computational efficiency and clarity of physical interpretation, the Newton-Euler method is generally preferred over the Lagrange method and is easier to implement.

The goal of parameter identification is to estimate the parameter values of the manipulator’s dynamic model from experimental data. Common parameter identification methods include least squares, Kalman filtering, neural networks, and intelligent optimization algorithms. The least squares method is a classical parameter identification approach that estimates parameters by minimizing the sum of squared errors between model outputs and actual outputs [14]. The Kalman filter is a recursive parameter estimation method that utilizes the system’s state and observation equations to approximate the true values through continuous state estimation updates [15]. Neural network methods are nonlinear parameter identification techniques that leverage the powerful learning ability of neural networks to approximate the manipulator’s dynamic model [16]. The Particle Swarm Optimization (PSO) algorithm, as a global optimization method, can be used for dynamic parameter identification and to improve identification accuracy by optimizing excitation trajectories [17,18]. Additionally, some studies explore the use of Deep Reinforcement Learning (DRL) methods for parameter identification, optimizing parameters such as friction coefficients through imitation learning [19]. It should be noted that common parameter identification methods have their own advantages and disadvantages. The least squares method is computationally simple and easy to implement but is sensitive to noise. The Kalman filter has strong noise suppression capabilities but requires knowledge of the system’s precise state-space model. Neural network methods can handle complex nonlinear systems but typically require large amounts of training data and are prone to falling into local optima.

To improve the accuracy of manipulator dynamic parameter identification, optimizing the design of the excitation trajectory is key. Using the Fourier series method to design excitation trajectories, through optimization of harmonic components, can simultaneously meet the requirements of trajectory smoothness and sufficient parameter excitation, significantly improving identification accuracy and convergence speed [18,20] This method achieves optimal excitation of the system’s dynamic characteristics by adjusting the amplitude, frequency, and phase relationships of each harmonic.

Friction is a critical factor limiting the control accuracy of manipulators, and its accurate modeling and identification are essential for improving system performance. Typical friction models include: the Coulomb friction model (considering only normal pressure effects), the viscous friction model (linearly related to velocity), and the comprehensive Stribeck friction model. Research shows that the Stribeck model can more accurately characterize friction characteristics in ground environments by integrating static friction, velocity-dependent friction, and boundary lubrication effects [21,22]. However, the space environment significantly influences friction characteristics, necessitating adaptations to traditional models.

Although significant progress has been made in the research of dynamic parameter identification for space manipulators, numerous challenges remain in the special environment of space. Firstly, the joint friction characteristics under microgravity conditions are fundamentally different from those in ground environments (e.g., preload changes due to lubricant migration), limiting the applicability of traditional friction models. Secondly, limited by on-orbit experimental conditions and energy constraints, the amount of experimental data available is extremely limited. Furthermore, extreme temperature variations and the vacuum environment in space significantly affect joint friction characteristics, further increasing the complexity of parameter identification. To address these issues, this paper proposes a hybrid identification strategy integrating dynamic parameter identification, excitation trajectory optimization, and friction characteristic modification, focusing on the influence mechanism of the space environment on joint friction characteristics and developing corresponding on-orbit parameter modification methods. The main contributions of this paper are as follows:

• A dynamic parameter identification method combining PSO and LM algorithms is proposed, balancing global search capability and local optimization accuracy. This method uses PSO for initial parameter estimation and then refines them with the LM algorithm, significantly improving identification accuracy while ensuring computational efficiency, making it particularly suitable for small-sample optimization problems in space missions.
• A nonlinear friction model incorporating Stribeck effects adapted to the space environment is established, revealing the influence mechanisms of vacuum, microgravity, and temperature variations on joint friction. Studies show that the space environment significantly alters friction parameter characteristics, leading to the proposal of an adaptive on-orbit modification method based on environmental monitoring, effectively enhancing the model’s environmental adaptability.
• To validate the effectiveness of the proposed dynamic parameter identification method, a 6-DOF space manipulator experimental platform without additional torque sensors was designed and built. By fusing joint current signals and motion state data, combined with an improved dynamic modeling method, high-precision parameter identification under conditions without direct torque measurement was achieved.

The structure of this paper is as follows: Section 2 establishes a nonlinear dynamic model of the space manipulator incorporating an improved Stribeck friction term and completes the model linearization; Section 3 designs parameter excitation trajectories based on Fourier series to reduce the ill-conditioning of the observation matrix; Section 4 proposes the PSO-LM hybrid optimization algorithm for high-precision global identification of dynamic parameters; Section 5 verifies the effectiveness and engineering practicality of the proposed method through experiments on a 6-DOF manipulator; Section 6 presents conclusions and future work.

2. Space Manipulator Dynamic Modeling and Model Linearization

Dynamic modeling of space manipulators is the theoretical foundation for achieving high-precision motion control and parameter identification [23]. Given the particularity of the space microgravity environment, this paper uses the Newton-Euler method to establish a nonlinear dynamic equation including joint friction effects, performs linearization processing, and finally establishes regression matrices describing the rigid body dynamics term and the nonlinear friction term separately.

2.1. Rigid Body Dynamic Model

The manipulator dynamic equation (Newton-Euler method) describes the relationship between joint torque τ and motion variables ($q,\dot{q},\ddot{q}$):

$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+G(q)+F_{friction}(\dot{q})=\tau$$

(1)

where:

$\tau \in {ℝ}^n$ is the joint drive torque vector ($n$ is the number of degrees of freedom);

$q,\dot{q},\ddot{q}\in {ℝ}^n$ are the joint position, velocity, and acceleration vectors, respectively;

$M(q)\in {ℝ}^{n\times n}$ is the symmetric positive definite inertia matrix;

$C(q,\dot{q})\in {ℝ}^{n\times n}$ is the Coriolis/centrifugal force matrix;

$G(q)\in {ℝ}^n$ is the gravity term;

$F_{friction}(\dot{q})\in {ℝ}^n$ is the nonlinear friction term.

In the space microgravity environment, the magnitude of the gravity term $G(q)$ is significantly reduced, its impact is much smaller than in the ground environment, while the friction term ${\tau }_f$ and nonlinear dynamic effects become relatively prominent, becoming the dominant factors affecting control accuracy.

It should be noted that the dynamic model established in this work is based on the assumptions of rigid links and rigid joints. This assumption simplifies the preliminary problem of parameter identification and is applicable to the current target platform. However, for future large-scale and lightweight space manipulators, flexible effects—including elastic deformations of the links and torsional compliance in the joint transmission chains—will become significant, potentially degrading the model’s predictive accuracy under high-dynamic or heavy-load conditions. Future work will focus on developing an integrated technological chain, encompassing rigid-flexible coupled dynamic modeling, on-orbit parameter identification, and active vibration suppression.

2.2. Space Manipulator Friction Model

The joint friction characteristics of space manipulators directly affect their trajectory tracking accuracy and energy efficiency. Unlike the ground environment, space manipulators face challenges such as lubricant migration due to microgravity, dry friction dominance in vacuum, and parameter drift caused by extreme temperatures. The traditional Stribeck model only includes a linear viscous term ($k_{v1}\dot{q}$), making it difficult to describe nonlinear friction effects in high-speed conditions and the influence of the space environment. This study extends higher-order velocity terms to establish an improved model suitable for the full speed range and provides a parameter identification strategy for the space environment.

2.2.1. Improved Stribeck Friction Model

The classical Stribeck model is too idealized, while space manipulators face complex environments such as microgravity, extreme temperatures, and high vacuum, resulting in complex friction behavior. This paper proposes the following improved Stribeck friction model for each joint:

$$F_{friction,i}=\left[f_c+(f_b-f_c)e^{-{(\left|{\dot{q}}_i\right|/v_b)}^2}\right]\mathrm{sgn}(\dot{q})+k_{v1}\dot{q}+k_{v2}{\dot{q}}^2+k_{v3}{\dot{q}}^3$$

(2)

where:

$F_{friction,i}$ is the friction torque for the $i$-th joint;

$f_c$ is the Coulomb friction coefficient (N·m);

$f_b$ is the static friction coefficient (N·m);

$v_s$ is the Stribeck characteristic velocity (rad/s);

$k_{v1}$, $k_{v2}$, $k_{v3}$ are velocity-dependent friction coefficients (units N·m·s/rad, N·m·s²/rad², N·m·s³/rad³, respectively).

This model decomposes the friction torque into several parts:

• $\left[f_c+(f_b-f_c)e^{-{(\left|{\dot{q}}_i\right|/v_b)}^2}\right]\mathrm{sgn}(\dot{q})$ characterizes the Stribeck transition effect from static to Coulomb friction;
• $k_{v1}\dot{q}$ represents linear viscous friction;
• $k_{v2}{\dot{q}}^2$ and $k_{v3}{\dot{q}}^3$ are used to describe nonlinear velocity-dependent friction.

The inclusion of this higher-order term ($k_{v2}$,$k_{v3}$) is physically justified by the fact that under high-speed conditions, phenomena such as shear thinning of lubricants, turbulent damping, and subtle yet non-negligible aerodynamic effects in the space vacuum environment can cause the friction torque to exhibit a nonlinear relationship with velocity. Existing theories [24,25,26] suggest that higher-order terms are better able to capture these nonlinear effects, particularly in the high-speed regime.

The friction characteristics of the model in different speed regions are as follows:

Low-speed region ($‖\dot{q}‖\approx 0.1v_s$): Static friction dominates, torque peak approaches $f_b$.

Transition region ($0.1v_s\le ‖\dot{q}‖\le 10v_s$): Stribeck effect is significant.

High-speed region ($‖\dot{q}‖\gg 10v_s$): The proportion of nonlinear velocity-dependent terms ($k_{v2}$, $k_{v3}$) increases significantly.

The improved model has nonlinear damping and state-dependent parameters, making it more suitable for practical space applications.

2.2.2. Space Environment Adaptability Analysis

Space manipulators face special environments such as microgravity, vacuum, and temperature variations during on-orbit service. These factors significantly affect joint friction characteristics, causing model parameters to drift or change nonlinearly. To ensure the accuracy of the friction model, parameter adaptability modifications for different environmental factors are necessary [9].

• Microgravity environment: The disappearance of gravity leads to changes in gear preload distribution within the gearbox, causing the static friction coefficient $f_b$ to drift. The strategy is to calibrate $f_b$ in real-time on orbit using adaptive update algorithms based on joint torque feedback.
• Vacuum environment: The disappearance of air resistance causes higher-order friction terms related to air damping (especially $k_{v2}{{\dot{q}}_i}^2$ and $k_{v3}{\dot{q}}^3$) to decrease significantly or even approach zero. In this environment, especially $k_{v2}{{\dot{q}}_i}^2$ and $k_{v3}{\dot{q}}^3$ can be ignored or set to zero. Under such conditions, $k_{v2}{{\dot{q}}_i}^2$ and $k_{v3}{\dot{q}}^3$ may be neglected or set to zero. Their corresponding coefficients can be initially estimated through ground-based vacuum chamber experiments or derived from aerodynamic theory, with final calibration performed using on-orbit data.
• Temperature variation environment: Lubricant viscosity changes with temperature, causing nonlinear shifts in parameters such as the Coulomb friction coefficient $f_c$ and Stribeck characteristic velocity $v_s$. Therefore, temperature compensation functions can be introduced into the friction model. For example, the relationship between the Coulomb friction coefficient $f_c$ and temperature T can be expressed as follows:

  $$f_c(T)=f_{c0}+\alpha (T-T_0)$$

  (3)

  where: $f_{c0}$ is the reference Coulomb friction value at reference temperature $T_0$; $\alpha$ is the friction-temperature sensitivity coefficient (reflecting the rate of change in $f_c$ with temperature); $T$ is the current ambient temperature; $T_0$ is the reference temperature (e.g., 20 °C).

It is essential to calibrate the key parameters in this compensation model, such as the temperature–friction sensitivity coefficient α, through systematic and controlled environmental experiments. The specific experimental and identification procedure is as follows: Inside a temperature-controlled chamber, the joint is maintained at a constant velocity to decouple the effects of speed and temperature, while the ambient temperature (T) is systematically varied in steps or sweeps. The corresponding joint friction torque is recorded synchronously. By applying parameter estimation techniques, such as the least squares method, to fit the steady-state friction torque data across different temperatures, an accurate estimate of coefficient α in Equation (3) can be obtained.

This study proposes this compensation framework to establish a parametric modeling approach capable of adapting to variations in the space environment. The validity of the framework relies on the feasibility of conducting ground-based experiments that isolate influencing factors, while the accurate calibration of its parameters depends on subsequent systematic validation in specialized environmental simulation facilities. This step is essential for transitioning the method from theory to engineering application.

2.3. Model Linearization

2.3.1. Linearization Objective

Parameter identification usually requires transforming the nonlinear dynamic equation into a linear form concerning the dynamic parameters [27]. Considering the characteristics of the space microgravity environment, the gravity term $\widehat{G}(q)$ can be treated as a known prior or independently compensated term, allowing the dynamic equation to be rewritten as follows:

$$\tau -\widehat{G}(q)=Y_r(q,\dot{q},\ddot{q}){\mathrm{\Phi }}_r+Y_f(\dot{q}){\mathrm{\Phi }}_f$$

(4)

where:

$Y_r(q,\dot{q},\ddot{q})\in {ℝ}^{n\times p_r}$ is the regression matrix of the rigid body dynamics term;

${\mathrm{\Phi }}_r\in {ℝ}^{p_r}$ is the set of rigid body dynamic parameters (linear combinations of basic parameters such as mass, center of mass position, and moment of inertia);

$Y_f(\dot{q})\in {ℝ}^{n\times p_f}$ is the regression matrix of the friction term;

${\mathrm{\Phi }}_f\in {ℝ}^{p_f}$ is the friction parameter vector;

$\widehat{G}(q)$ is the estimated value of the gravity term based on prior knowledge (can be set to zero in on-orbit applications or compensated via an on-board model).

2.3.2. Parameter Linearization

The regression matrix $Y_r$ for the rigid body dynamics term can be constructed by partial differentiation of the dynamic equation with respect to each dynamic parameter:

$$Y_r(q,\dot{q},\ddot{q}){\mathrm{\Phi }}_r=M(q)\ddot{q}+C(q,\dot{q})\dot{q}$$

(5)

Due to the significantly reduced magnitude of the gravity term $\widehat{G}(q)$ in the space microgravity environment, its parameter sensitivity is low, so it can be treated as an independent term or incorporated into prior compensation during linearization.

The regression matrix ${\mathrm{\Phi }}_f$ for the nonlinear friction term can be constructed according to the improved model proposed in Equation (2). For each joint, its friction torque ${\tau }_{f,i}$ can be linearized as follows:

$$Y_{f,i}({\dot{q}}_i){\mathrm{\Phi }}_{f,i}={\tau }_{f,i}$$

(6)

where ${\mathrm{\Phi }}_{f,i}={[f_{c,i},f_{s,i},v_{b,i},k_{v1,i},k_{v2,i},k_{v3,i}]}^T$ is the friction parameter vector for the i-th joint, and $Y_{f,i}({\dot{q}}_i)$ is the corresponding regression row vector, whose elements are composed of the partial derivatives of Equation (2) with respect to each parameter in ${\mathrm{\Phi }}_{f,i}$.

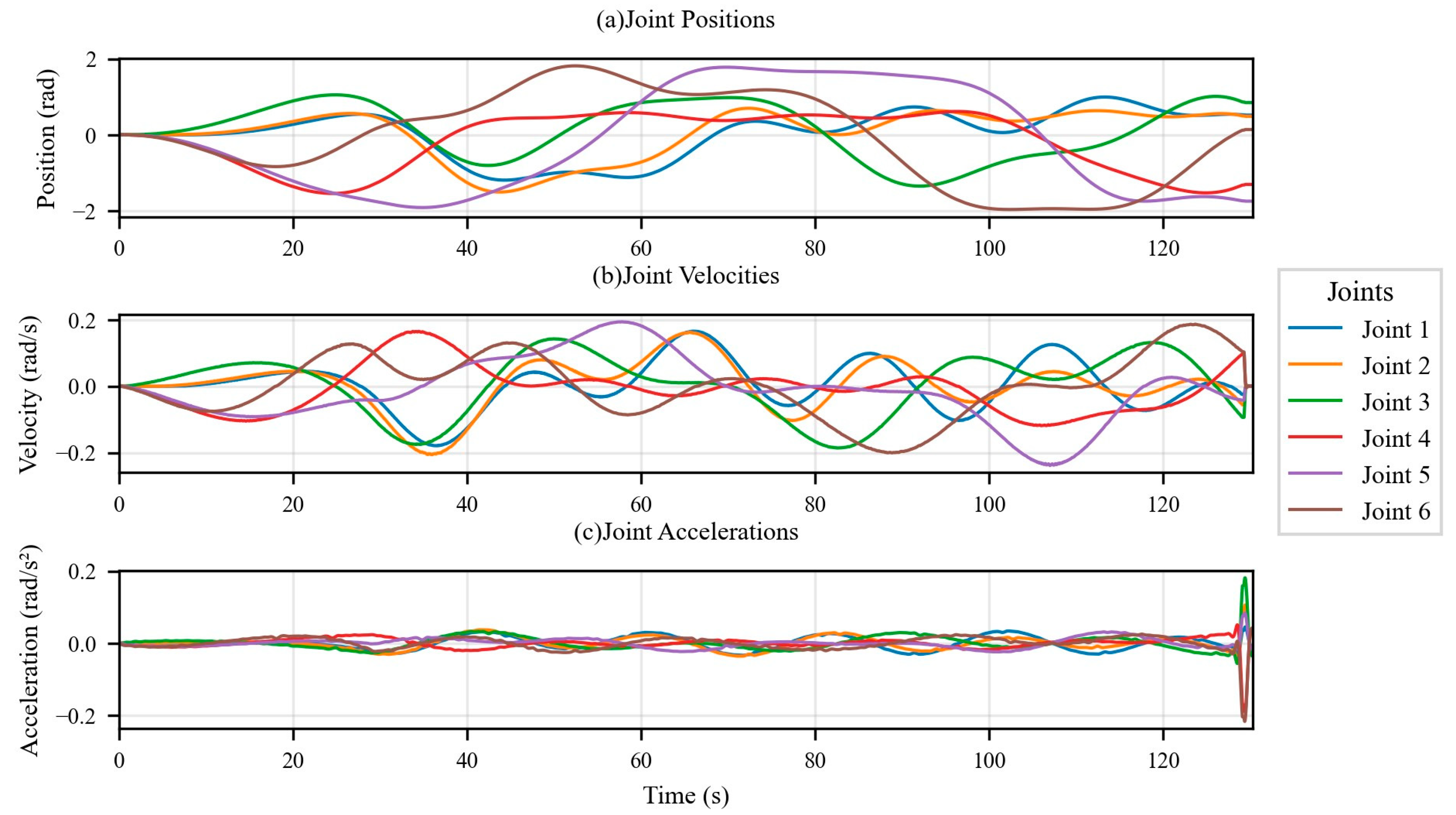
3. Excitation Trajectory Optimization Design

In the process of robot dynamic parameter identification, the design of the excitation trajectory is decisive for the accuracy of parameter identification. Poorly designed trajectories can lead to an ill-conditioned observation matrix, amplifying the impact of sensor noise and modeling errors on the identification results. To reduce the impact of sensor errors and improve parameter identification accuracy, the excitation trajectory must be optimized [28].

3.1. Optimization Objectives and Theoretical Basis

In robot dynamic parameter identification, the design of the excitation trajectory directly affects the ill-conditioning of the observation matrix $Y_N$. According to error propagation theory, when the observation matrix $Y_N$ and the torque measurement vector ${\tau }_N$ have disturbances $\delta Y_N$ and $\delta {\tau }_N$, respectively, the parameter estimation error $\delta \mathrm{\Phi }$ satisfies the inequality:

$${\displaystyle \frac{‖\delta \mathrm{\Phi }‖}{‖\mathrm{\Phi }‖}}\le {\displaystyle \frac{\kappa (Y_N)}{1-\kappa (Y_N)\frac{‖\delta Y_N‖}{‖Y_N‖}}}({\displaystyle \frac{‖\delta {\tau }_N‖}{‖{\tau }_N‖}}+{\displaystyle \frac{‖\delta Y_N‖}{‖Y_N‖}})$$

(7)

where:

$\kappa (Y_N)$ is the spectral condition number of the observation matrix $Y_N$.

${\displaystyle \frac{‖\delta {\tau }_N‖}{‖{\tau }_N‖}}$ and ${\displaystyle \frac{‖\delta Y_N‖}{‖Y_N‖}}$ represent the relative errors of the observation matrix and torque measurements, respectively.

From Equation (7), it can be seen that the relative error of parameter estimation is mainly affected by the condition number $\kappa (Y_N)$ of the observation matrix. The larger $\kappa (Y_N)$ is, the more ill-conditioned the observation matrix, and the more sensitive the parameter identification results are to noise. Therefore, a core objective of excitation trajectory optimization is to minimize the condition number of the observation matrix:

$$\min \kappa (Y(\xi ))=\min ({\displaystyle \raisebox{1ex}{${\sigma }_{\max (Y(\xi ))}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{\min (Y(\xi ))}$}\right.})$$

(8)

where $\xi$ represents the parameterized vector of the excitation trajectory (e.g., coefficients of the Fourier series), and ${\sigma }_{\max (Y(\xi ))}$ and ${\sigma }_{\min (Y(\xi ))}$ represent the maximum and minimum singular values of the matrix, respectively.

3.2. Fourier Series Excitation Trajectory Design

Among various excitation trajectory forms (such as polynomial curves, spline curves, finite-order Fourier series), this paper selects the finite-order Fourier series as the excitation trajectory, mainly based on the following three key advantages:

• Periodicity: Periodic trajectories allow for repeated experiments. Time-domain averaging of sampled data can significantly improve the signal-to-noise ratio of the data.
• Analytical Differentiation: Velocity and acceleration signals can be obtained directly through analytical differentiation of the position trajectory, avoiding additional noise introduced by numerical differentiation.
• Bandwidth Control: By limiting the highest frequency component of the Fourier series, the bandwidth of the excitation trajectory can be effectively controlled, avoiding excitation of the robot’s unmodeled high-frequency dynamics or natural frequencies and preventing resonance phenomena.

The selection of the fundamental frequency $f_0$ is based on the bandwidth of the manipulator and the servo capability of the joints, typically set within a range of 1/5 to 1/10 of the maximum joint velocity. The number of harmonics $N_h$ is chosen through a trade-off between adequately exciting the dynamic parameters and avoiding the excitation of unmodeled high-frequency modes. A typical value lies between 3 and 5, with the final selection optimized by monitoring the variation in the condition number of the observation matrix with respect to $N_h$.

The position trajectory for the $i$-th joint is designed in the form of a finite-order Fourier series:

$$q_i(t)=q_{i,0}+{\displaystyle \sum _{k=1}^{N_h}\left[\frac{a_{i,k}}{{\omega }_k}\sin ({\omega }_{k}t)-\frac{b_{i,k}}{{\omega }_k}\cos ({\omega }_{k}t)\right]}$$

(9)

where ${\omega }_k=2\pi k{f}_0$, and $f_0$ is the fundamental frequency (Hz). By differentiating Equation (9), the analytical expressions for joint velocity and acceleration can be directly obtained:

Joint velocity:

$${\dot{q}}_i(t)={\displaystyle \sum _{k=1}^{N^h}\left[a_{i,k}\cos ({\omega }_{k}t)+b_{i,k}\sin ({\omega }_{k}t)\right]}$$

(10)

Joint acceleration:

$${\ddot{q}}_i(t)={\displaystyle \sum _{k=1}^{N_h}{\omega }_k\left[-a_{i,k}\sin ({\omega }_{k}t)+b_{i,k}\cos ({\omega }_{k}t)\right]}$$

(11)

where:

$a_{i,k}$, $b_{i,k}$: Fourier series coefficients (optimization variables), determining the shape of the trajectory.

$f_0$: fundamental frequency (Hz), determining the trajectory period $T$ ($T=1/f_0$).

$N_h$: number of harmonics (usually 3–5), determining the frequency bandwidth of the trajectory.

$q_{i,0}$: initial position offset of the joint.

The design of the excitation trajectory must satisfy the physical constraints of the manipulator, including joint position limits, velocity limits, acceleration limits, and avoiding excitation of structural resonance frequencies. To avoid resonance, the frequency band of the trajectory $N_h{f}_0$ should be designed to remain well below the lowest known structural natural frequency of the manipulator (obtained through modal analysis), with a sufficient safety margin. Therefore, the trajectory parameter optimization problem needs to be solved under the following constraints:

Joint position constraint: $q_{\min }\le q_i(t)\le q_{\max }$.

Joint velocity constraint: $\left|{\dot{q}}_i(t)\right|\le {\dot{q}}_{\max }$.

Joint acceleration constraint: $\left|{\ddot{q}}_i(t)\right|\le {\ddot{q}}_{\max }$.

Frequency constraint $N_h{f}_0\le f_{avoid}$(where $f_{avoid}$ denotes the frequency threshold to be avoided).

Thus, based on the actual performance and workspace of the robot, the position, velocity, and acceleration ranges of the excitation trajectory can be determined. The optimization problem can be solved using improved genetic algorithms to obtain the optimal excitation trajectory.

It should be noted that the smooth Fourier-series trajectory adopted in this study effectively excites the robot’s workspace while ensuring the continuous differentiability of the excitation signal, which provides favorable conditions for the stable identification of dynamic parameters. However, such a trajectory may not adequately excite the system’s dynamic response under non-smooth operating conditions, such as sudden acceleration changes or impact loads. Discontinuous trajectories (e.g., step commands) can excite unmodeled high-frequency dynamic modes (e.g., structural flexibility and resonance) and the transient characteristics of nonlinear friction, potentially leading to degraded prediction accuracy of the model under these boundary conditions.

The identification results based on smooth excitation establish a high-fidelity performance benchmark for the model under quasi-steady-state and continuous smooth motion conditions. Future research will focus on exploring composite excitation trajectory optimization strategies. This involves introducing controlled, spectrally characterized non-smooth elements into the existing Fourier basis functions to actively excite and identify the aforementioned transient and high-frequency dynamic characteristics while ensuring system safety. This work will be a critical step toward constructing high-fidelity, highly robust dynamic models suitable for complex on-orbit operations such as collision, docking, and rapid maneuvers.

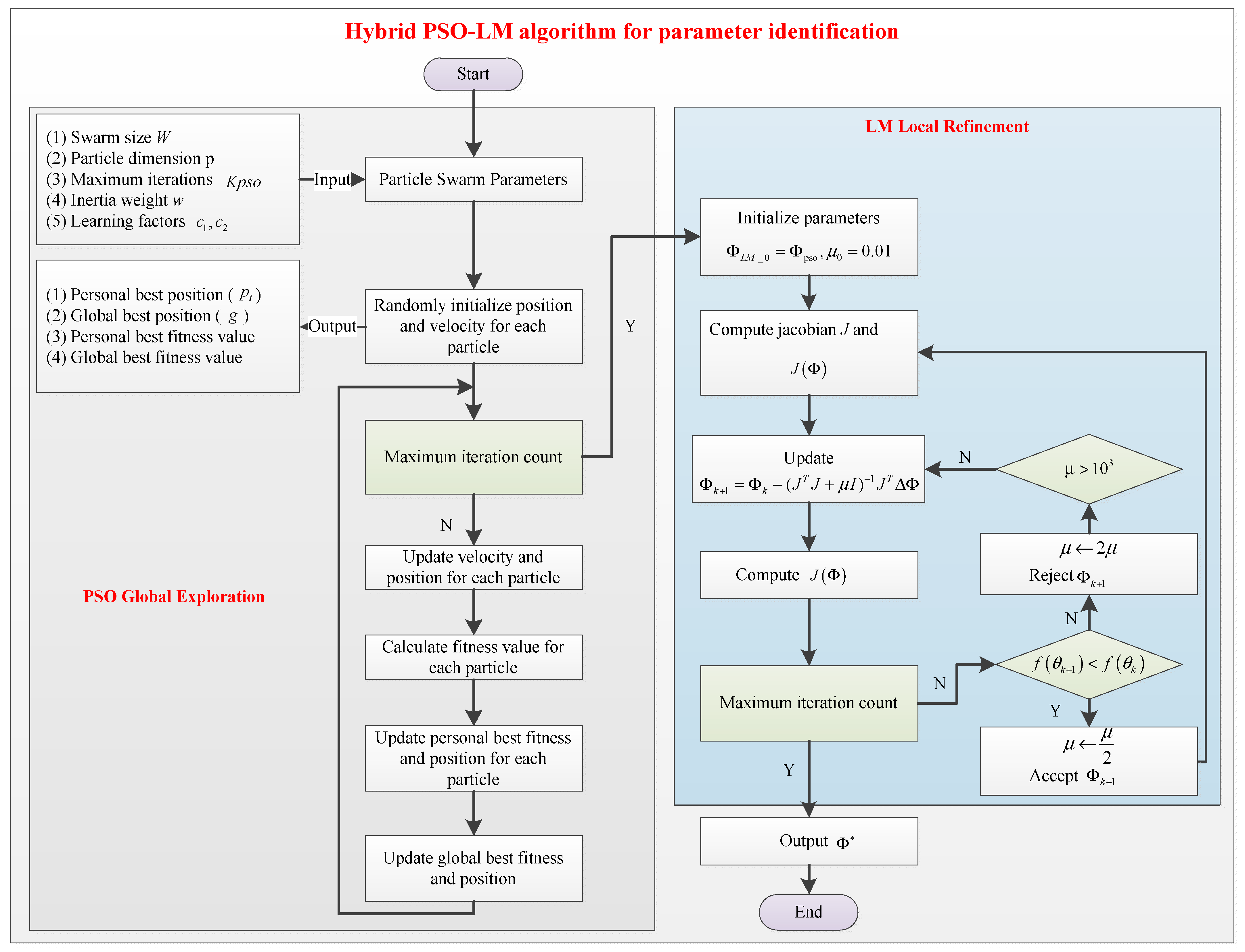
4. Hybrid PSO-LM Algorithm for Dynamic Parameter Identification

4.1. PSO-LM Algorithm

The Particle Swarm Optimization (PSO) algorithm achieves global optimization in multi-dimensional parameter space by simulating the collective foraging behavior of bird flocks or fish schools. The algorithm has good global exploration ability and can effectively avoid local optima traps; however, it often suffers from slow convergence speed in the later stages of search [29]. In contrast, the Levenberg–Marquardt (LM) algorithm, as a numerical method widely used for nonlinear least squares problems, combines the robustness of the gradient descent method with the fast convergence characteristics of the Gauss-Newton method. When the initial parameter settings are within the neighborhood of the true parameters, the LM algorithm can exhibit nearly second-order convergence speed [30]. However, the main limitation of this algorithm is that its optimization performance depends heavily on the quality of the initial parameter selection; inappropriate initial values can easily lead to convergence failure or entrapment in suboptimal solutions.

This study adopts a PSO-LM cooperative optimization strategy, which significantly improves the accuracy and computational efficiency of parameter identification by organically integrating the global search capability of the PSO algorithm and the local convergence characteristics of the LM algorithm. In this algorithm, each particle position vector represents a set of candidate dynamic parameter solutions Φ, transforming the complex dynamic parameter identification problem into an objective function optimization problem.

In the proposed algorithm, the position vector $\mathrm{\Phi }$ of each particle represents a candidate solution for the dynamic parameters. All parameters to be identified are consolidated into a high-dimensional parameter vector $\mathrm{\Phi }\in {ℝ}^{n_p}$, defined as follows:

$$\mathrm{\Phi }={\left[{\mathrm{\Phi }}_r^T,{\mathrm{\Phi }}_f^T\right]}^T$$

(12)

where:

${\mathrm{\Phi }}_r\in {ℝ}^{n_r}$ comprises all base rigid-body dynamic parameters (e.g., link mass, center of mass position, inertia tensor) after linearization.

${\mathrm{\Phi }}_f\in {ℝ}^{n_f}$ contains all joint friction parameters (e.g., Coulomb friction coefficient $f_c$, static friction coefficient $f_b$, viscous friction coefficient $k_{v1},k_{v2},k_{v3}$ for each joint).

$n_p=n_r+n_f$ denotes the total dimension of the parameter vector. For the 6-DoF manipulator considered in this work, $n_p=108$.

The core goal of the algorithm is to find a set of parameters ${\mathrm{\Phi }}^{\ast }$ that minimizes the error between the theoretical model predicted torque and the actual measured torque. For this purpose, the following objective function is constructed:

$$F\left(\mathrm{\Phi }\right)={\displaystyle \frac{1}{2}}{\displaystyle \sum _{l=1}^{N_s}{‖{\tau }_{\mathrm{meas}}^{(l)}-{\tau }_{\mathrm{model}}\left(q^{(l)},{\dot{q}}^{(l)},{\ddot{q}}^{(l)};\mathrm{\Phi }\right)‖}^2}$$

(13)

where:

$N_s$ is the total number of sampling points.

${\tau }_{\mathrm{meas}}^{(l)}$ is the measured joint torque vector at the $l$-th sampling point.

${\tau }_{\mathrm{model}}(\cdot )$ is the predicted joint torque vector calculated based on the dynamic model.

$q^{(l)},{\dot{q}}^{(l)},{\ddot{q}}^{(l)}$ are the joint position, velocity, and acceleration vectors at the l-th sampling point, respectively.

${\left|\cdot \right|}_2$ denotes the L2 norm of the vector.

Central to this objective function is the Jacobian matrix $J(\mathrm{\Phi })\in {ℝ}^{(L\cdot n)\times n_p}$, whose elements are the partial derivatives of the model residuals with respect to each parameter. Defining the residual vector $r(\mathrm{\Phi })\in {ℝ}^{L\times n}$ as follows:

$$r(\mathrm{\Phi })={\left[{({\tau }_{\mathrm{meas}}{}^{(1)}-{\tau }_{\mathrm{model}}{}^{(1)})}^T,\dots ,{({\tau }_{\mathrm{meas}}{}^{(L)}-{\tau }_{\mathrm{model}}{}^{(L)})}^T\right]}^T$$

(14)

the Jacobian matrix is given by:

$$J(\mathrm{\Phi })={\displaystyle \frac{\partial r(\mathrm{\Phi })}{\partial \mathrm{\Phi }}}=\left(\begin{array}{ccc}{\displaystyle \frac{\partial r_1(\mathrm{\Phi })}{\partial {\mathrm{\Phi }}_1}}& \dots & {\displaystyle \frac{\partial r_1(\mathrm{\Phi })}{\partial {\mathrm{\Phi }}_{n_p}}}\\ ⋮& \ddots & ⋮\\ {\displaystyle \frac{\partial r_m(\mathrm{\Phi })}{\partial {\mathrm{\Phi }}_1}}& \dots & {\displaystyle \frac{\partial r_m(\mathrm{\Phi })}{\partial {\mathrm{\Phi }}_{n_p}}}\end{array}\right)$$

(15)

where $J_{ij}(\mathrm{\Phi })={\displaystyle \frac{\partial r_i(\mathrm{\Phi })}{\partial {\mathrm{\Phi }}_j}}$ denotes the sensitivity of the $i$-th residual to the $j$-th parameter. In the Levenberg–Marquardt algorithm, this Jacobian matrix guides the parameter update direction $\mathrm{\Delta }\mathrm{\Phi }$.

The objective function $F\left(\mathrm{\Phi }\right)$ is the fitness value that each particle needs to evaluate. The goal of the algorithm is to find the optimal parameter ${\mathrm{\Phi }}^{\ast }$ such that:

$${\mathrm{\Phi }}^{\ast }=\arg \min F(\mathrm{\Phi })$$

(16)

The hybrid algorithm proceeds in two stages:

Stage 1: PSO Global Search

The PSO algorithm initializes a population of N particles, each representing a possible solution ${\mathrm{\Phi }}_i$ in the parameter space. The particle swarm explores the parameter space by iteratively updating its velocity and position. The velocity and position update rules for particle i are as follows:

$$v_i{}^{k+1}=w{v}_i^k+c_1{r}_1(p_i-{\mathrm{\Phi }}_i^k)+c_2{r}_2(g-{\mathrm{\Phi }}_i^k)$$

(17)

where:

$v_i$ is the velocity vector of particle $i$.

$w$ represents a linearly decreasing inertia weight.

$c_1$ and $c_2$ are cognitive and social learning factors, respectively.

$p_i$ denotes the historical best solution of particle $i$.

$r_1$ and $r_2$ are drawn independently from $U\left(0,1\right)$.

$g$ represents the global historical best solution.

The position update rule governing particle motion is formulated as follows:

$${\mathrm{\Phi }}_i^{k+1}={\mathrm{\Phi }}_i^k+{{\mathrm{\Phi }}_i}^{k+1}$$

(18)

where:

${\mathrm{\Phi }}_i^{k+1}$ represents the updated position vector of particle $i$ at iteration $k+1$.

${\mathrm{\Phi }}_i^k$ denotes the current position of particle.

${v_i}^{k+1}$ is the velocity vector computed from Equation (17). The termination criteria are triggered when the maximum iteration count $K_{PSO}$ is reached.

The optimal solution ${\mathrm{\Phi }}_{\mathrm{pso}}$ output from PSO serves as the initial parameter vector ${\mathrm{\Phi }}_{LM\_0}$ for subsequent LM refinement.

$${\mathrm{\Phi }}_{LM\_0}={\mathrm{\Phi }}_{\mathrm{pso}}$$

(19)

Phase 2: LM Local Refinement

The LM algorithm then refines the parameters via Jacobian matrix computation and adaptive damping factor adjustment to achieve rapid local convergence.

The LM update rule is:

$${\mathrm{\Phi }}_{k+1}={\mathrm{\Phi }}_k-{(J^{T}J+\mu I)}^{-1}{J}^T\mathrm{\Delta }\mathrm{\Phi }$$

(20)

where:

$J$ is the Jacobian matrix of residuals.

$I$ denotes the identity matrix.

The damping factor $\mu$ is adaptively regulated:

if $f\left({\mathrm{\Phi }}_{k+1}\right)<f\left({\mathrm{\Phi }}_k\right)$, update $\mu$ to ${\displaystyle \frac{\mu }{2}}$.

if $f\left({\mathrm{\Phi }}_{k+1}\right)\ge f\left({\mathrm{\Phi }}_k\right)$, update $\mu$ to $2\mu$, then recompute the step size. The termination criteria are triggered when the maximum iteration count $K_{LM}$ is reached.

The proposed PSO-LM hybrid optimization framework employs a dual-stage architecture, as schematically depicted in Figure 1. In the first stage, the Particle Swarm Optimization module (indicated in gray) conducts comprehensive exploration within the p-dimensional parameter domain. The algorithm initializes a population of candidate solutions and progressively refines their positions through iterative velocity and position updates. Throughout this global search phase, both personal optimal positions ($p_i$) and the swarm’s global optimum ($g$) are continuously updated through fitness evaluation until reaching the maximum iteration count $K_{PSO}$ is met.

Following the completion of PSO exploration, the algorithm enters the Levenberg–Marquardt refinement stage (shown in blue), where the optimal solution identified by PSO serves as the initial parameter estimate. This second stage leverages second-order convergence characteristics through precise computation of the residual Jacobian matrix ($J$) while employing an adaptive damping coefficient μ to regulate optimization stability. Should the LM phase demonstrate insufficient improvement ($\mathrm{\mu }>$10³), the algorithm automatically reactivates the PSO module for renewed global exploration. The optimization process concludes when the LM phase reaches its iteration limit, producing the final optimized parameter set ${\mathrm{\Phi }}^{\ast }$.

To enhance algorithmic robustness, a safeguard mechanism is incorporated wherein suboptimal solutions from the current optimization cycle serve as enhanced initial estimates for subsequent optimization rounds. This iterative refinement strategy ensures progressive convergence toward the globally optimal solution while maintaining computational efficiency.

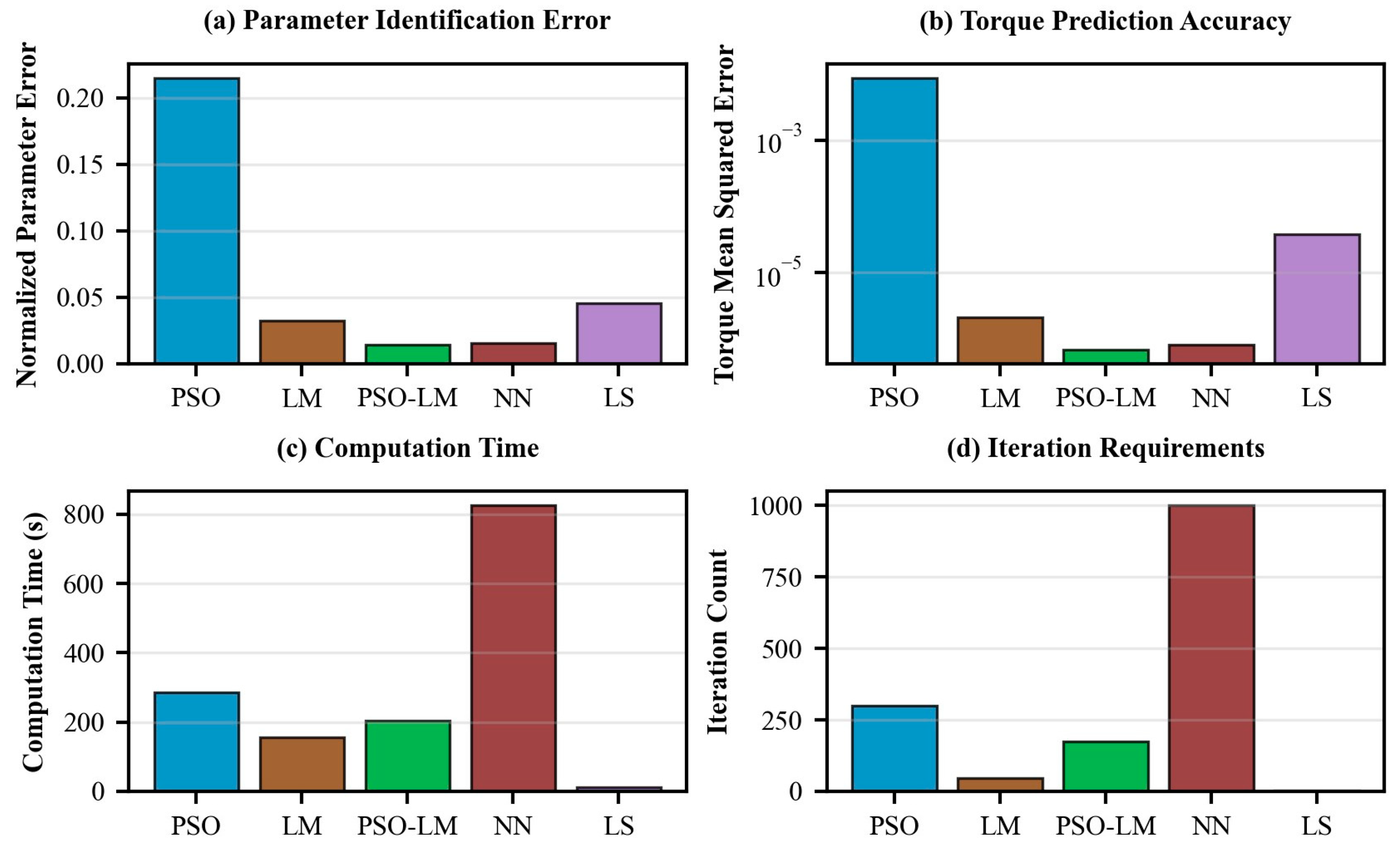
4.2. Evaluation of Dynamics Parameter Identification Algorithms Based on Simulation

This study establishes a Python-based (version 3.12) evaluation platform for dynamics parameter identification algorithms. The platform systematically assesses the capability of various algorithms to recover the true parameters from noise-corrupted data by comparing the nominal dynamic parameters of the manipulator with the actual parameters (considered as the ground truth). It utilizes the nominal parameters to generate theoretical joint torque data, while the actual torque values are computed based on perturbed actual parameters. The identification performance of different algorithms is quantitatively evaluated by systematically processing these numerical experiments.

Through numerical simulations, a comprehensive evaluation of six parameter identification methods was conducted. The comparative analysis covers multiple performance dimensions, including convergence accuracy, computational efficiency, and robustness. The detailed results are presented in Figure 2.

In terms of convergence accuracy, the proposed PSO-LM hybrid algorithm demonstrates superior performance, exhibiting significantly lower joint torque prediction errors compared to all benchmark algorithms. Specifically, the torque prediction accuracy is improved by 21.2% compared to the conventional LM algorithm and by 47.4% compared to the standard PSO method. The average parameter estimation error for the total set of 108 dynamic parameters (including 72 rigid-body parameters and 36 nonlinear friction parameters) across all 6 joints is reduced to a very low level, confirming that the identified dynamic parameters are closer to the true values.

Regarding computational efficiency, the PSO-LM algorithm achieves an excellent balance between accuracy and time cost. Although its computation time is slightly longer than that of the LM algorithm, it reduces the runtime by 57.6% compared to the standalone PSO algorithm. Furthermore, compared to computationally intensive neural network methods, which require substantially longer times, the proposed method achieves an efficiency improvement exceeding 86%, effectively addressing the real-time application bottleneck of such methods in practical engineering scenarios.

Simulation results indicate that the PSO-LM algorithm effectively handles strong nonlinearities and complex coupling effects within the high-dimensional parameter space, demonstrating particularly outstanding performance in identifying the higher-order term parameters of the Stribeck friction model. The algorithm shows good identification capability for inertial parameters, Coriolis force parameters, and complex nonlinear friction parameters.

In summary, the PSO-LM algorithm is not merely a compromise solution but rather a synergistic enhancement strategy: it retains the fast local convergence characteristics of the LM algorithm while effectively mitigating its sensitivity to initial conditions through the global exploration capability of PSO, thereby achieving comprehensive performance advantages over all standalone algorithms. It is crucial to emphasize that parameter estimation constitutes the core of the dynamic identification process. Although dynamic modeling and data measurement provide the necessary input conditions, the final accuracy of dynamic parameter identification fundamentally depends on the performance of the optimization algorithm under fixed experimental settings.

5. Experimental Verification

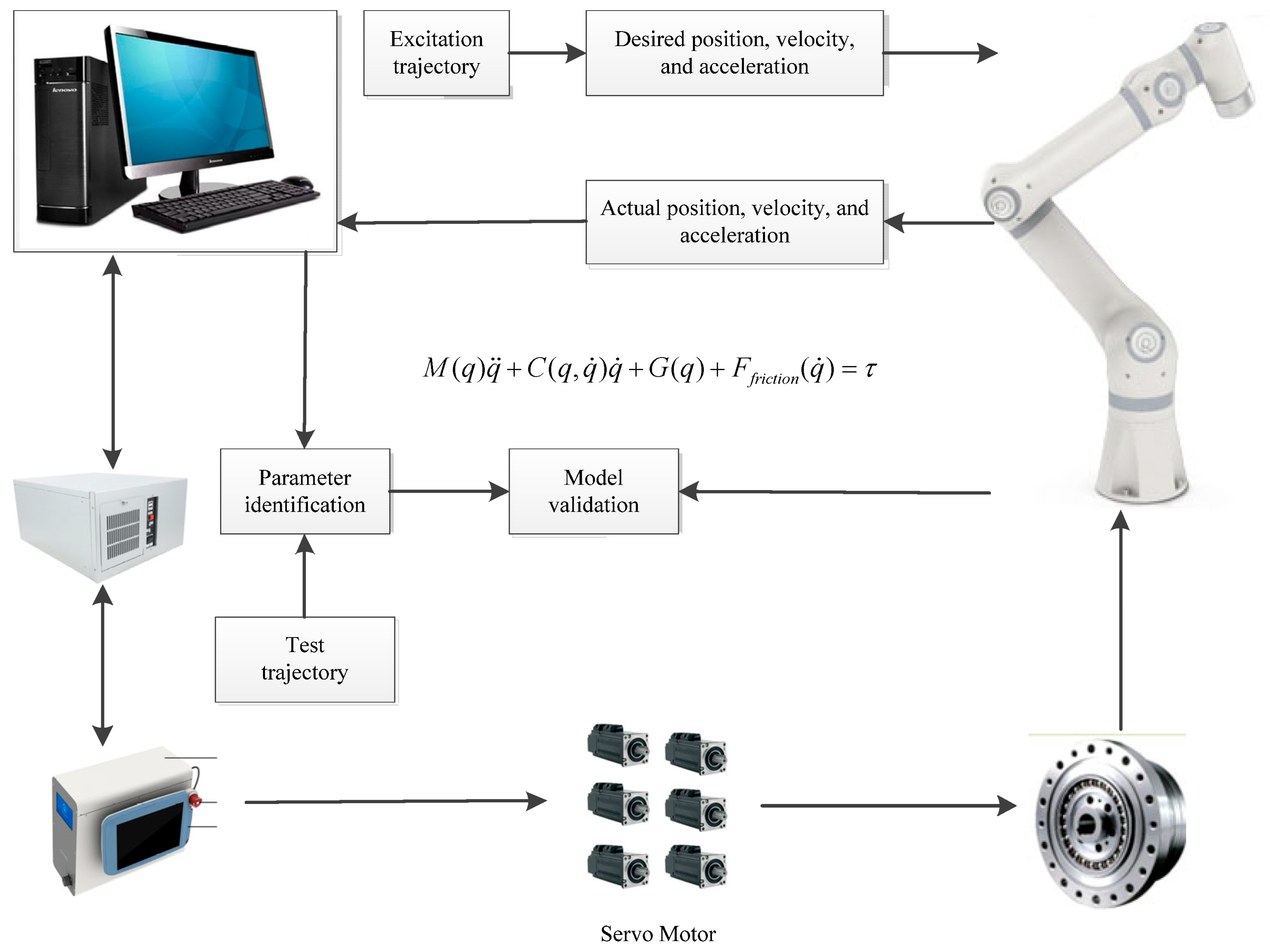
5.1. Experimental Setup

5.1.1. Experimental Platform Construction

To verify the effectiveness of the proposed dynamic parameter identification method, a complete experimental verification platform was built. The system uses a six-degree-of-freedom space manipulator prototype. Each joint is driven by a permanent magnet synchronous servo motor and integrates a high-precision optical encoder for joint position feedback. Joint torque information is obtained by acquiring the motor armature current and combining it with a pre-calibrated torque constant. The data acquisition system uses an NI real-time controller with a sampling frequency set to 1 kHz to ensure accurate capture of system dynamic characteristics. The experimental platform system is shown in Figure 3.

5.1.2. Validation Method

Since the true values of the robot’s dynamic parameters cannot be directly measured, traditional true value comparison verification methods are not applicable. Therefore, this study adopts a cross-validation strategy: a feasible trajectory different from the excitation trajectory used for identification is selected as the validation trajectory, the robot is controlled to track this trajectory, and the joint input torque signals are synchronously collected.

Based on the identified dynamic parameters and the desired motion trajectory, the predicted joint torques are calculated. The identification accuracy is evaluated by comparing the predicted values with the measured values.

For the dynamic parameter identification problem of the six-degree-of-freedom space manipulator, a systematic identification strategy was adopted, successfully identifying a total of 108 dynamic parameters. This parameter set includes 72 rigid body dynamic parameters and 36 nonlinear friction parameters. The main identification results are summarized in

Table 1. Identified dynamic parameters table.

Parameter	Joint 1	Joint 2	Joint 3	Joint 4	Joint 5
$J_m$	4.9695	7.2326	2.0867	1 × 10−6	3.7425
$k_{v1}$	19.7469	37.8161	14.1530	7.3522	5.3967
$k_{v2}$	0.0574	0.4232	−0.3233	0.7128	0.2969
$k_{v3}$	−0.1671	−0.1859	−0.0090	−0.0300	0.2570
$f_c$	14.8791	12.0478	15.5775	4.0419	4.5851
$v_b$	1 × 10−3	1 × 10−3	0.0055	1 × 10−3	0.0011
$f_b$	20.1409	12.3278	18.3598	6.0389	7.3202
$k_1$	0.02258	1 × 10−6	1 × 10−6	1 × 10−6	1 × 10−6
$m_i$	6.0683	6.4725	4.2054	2.7177	2.6093
$x_c$	−1 × 10−5	−2 × 10−5	0	0	0
$y_c$	0.0464	−0.2869	0.2762	−0.0454	0.0425
$z_c$	−0.2781	−0.1292	0.0584	−0.1970	−0.1680
$I_{xx}$	0.5006	0.8002	0.4125	0.1163	0.0829
$I_{xy}$	−3 × 10−5	−4 × 10−5	0	0	0
$I_{xz}$	2 × 10−5	−2 × 10−5	0	0	0
$I_{yy}$	0.4833	0.1253	0.0241	0.1081	0.0761
$I_{yz}$	−0.0798	0.2242	0.0780	0.0245	−0.0188
$I_{zz}$	0.0309	0.6887	0.3941	0.0108	0.0093

.

The identification process is based on the linearized dynamic model established in Section 2. The regression matrix ${\mathrm{\Phi }}_r$ for the rigid body dynamics term is obtained from the linearized relationship of the Newton-Euler equations with respect to the standard base inertia parameters, and the regression matrix ${\mathrm{\Phi }}_f$ for the friction term is derived from the improved Stribeck friction model proposed in Section 2.2.1. Key steps include, first, using the optimized fifth-order Fourier series from Section 3 as the excitation trajectory to fully excite the system dynamics and ensure a good condition number of the observation matrix ($\kappa (Y_N)$), followed by applying the PSO-LM hybrid optimization algorithm proposed in Section 4, where the PSO stage performs preliminary positioning in the global parameter space through swarm intelligence search (the swarm size $N=100$, with cognitive factor $c_1=1.5$, social factor $c_2=1.5$, and inertia weight $\omega$ linearly decreasing from 0.9 to 0.4, the maximum iteration number $K_{pso}$ = 300). The optimal solution ${\mathrm{\Phi }}_{\mathrm{pso}}$ output from PSO serves as the initial parameter vector ${\mathrm{\Phi }}_{LM\_0}$ for subsequent LM refinement. The LM stage performs (iteration count $K_{LM}$ = 100), achieving fast convergence through adaptive adjustment of the damping factor $\mu$. The identification accuracy was verified through multiple indicators: the root mean square error of predicted torque for each joint was less than 5.1 N·m, the correlation coefficient exceeded 0.97, and the parameters were physically meaningful (e.g., positive definite inertia matrix, decreasing friction coefficients, etc.). The results show that this method can effectively handle the challenges of high dimensionality, strong nonlinearity, and parameter coupling in the dynamic parameter identification of space manipulators, providing a reliable model foundation for subsequent high-precision control.

5.2. Dynamic Parameter Identification Verification and Analysis

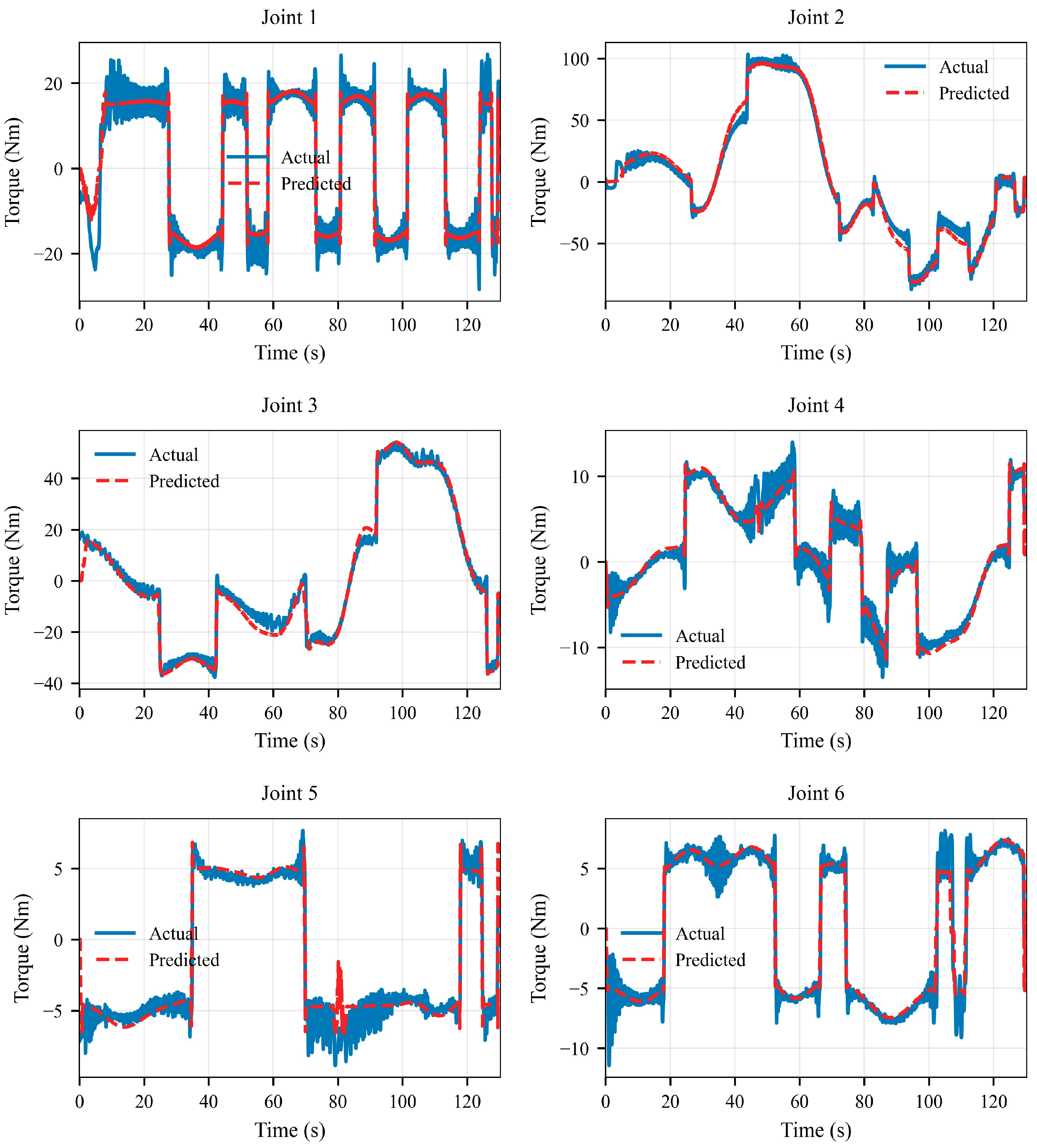
5.2.1. Validation Trajectory and Torque Prediction

To meet the continuity requirements of the motion trajectory at the position, velocity, and acceleration levels, the validation trajectory adopts the same parameterized form as the excitation trajectory design criterion, namely the finite-order Fourier series described by Equation (9). This trajectory form can strictly satisfy the boundary conditions of zero position, velocity, and acceleration at the start and end points through the linear superposition of harmonic components, thereby ensuring the smoothness and stability of the manipulator motion and avoiding additional excitation or impact caused by sudden trajectory changes.

In contrast to the excitation trajectory, the validation trajectory employs a completely independent set of Fourier coefficients. Its fundamental frequency and harmonic amplitudes are redesigned, resulting in significant differences from the excitation trajectory in terms of frequency-domain energy distribution and time-domain dynamic range. As shown in Figure 4, the validation trajectories for each joint of the robot are continuous and smooth at the position, velocity, and acceleration levels. Moreover, their amplitudes are strictly constrained within the physical motion limits of each joint, covering the entire workspace and dynamic range of the manipulator. These characteristics fully demonstrate the suitability and reliability of this parameterized trajectory form for the experimental validation phase.

The validation trajectory was applied as the position command input to each joint. The corresponding joint torque predictions were computed based on the identified dynamic parameters, while the actual output torques of each joint were synchronously recorded. A comparison between the measured and predicted torques is presented in Figure 5, which shows close agreement between the predicted torques and the experimental measurements. This result validates the accuracy of the identified dynamic parameters across the global workspace and under varying dynamic conditions, thereby demonstrating the effectiveness and robustness of the proposed method.

5.2.2. Quantitative Accuracy Analysis

To quantitatively evaluate the identification accuracy, this study calculated the root mean square error (RMSE), mean absolute error (MAE), maximum absolute error, and correlation coefficient (R) between the predicted torque and the measured torque for each joint. The results are summarized in

Table 2. Statistical accuracy of dynamic parameter identification for each joint of the 6-DOF space manipulator.

Joint No.	RMSE (N·m)	Max Error (N·m)	MAE (N·m)	Correlation Coefficient (R)
Joint 1	3.9462	22.8779	2.5430	0.9737
Joint 2	5.0670	21.3276	3.9640	0.9953
Joint 3	3.2432	19.0617	2.2192	0.9941
Joint 4	1.4322	7.7453	1.0329	0.9740
Joint 5	1.0583	8.3433	0.6640	0.9753
Joint 6	1.1699	8.1504	0.6278	0.9815

.

Based on a comparative analysis, the relative contributions of coupling effects and load inertia to the errors in joints J1–J3 are estimated to be approximately 60% and 40%, respectively. Although the identification model includes coupling terms, its modeling accuracy under high-dynamic operating conditions still requires further improvement. Future work will explore the incorporation of more sophisticated coupling model terms to enhance prediction accuracy.

5.2.3. Discussion and Analysis for Space Applications

All experiments in this study were conducted on a six-degree-of-freedom ground-based platform. It must be explicitly emphasized that extrapolating the experimental results directly to space applications is subject to limitations due to physical differences between terrestrial and orbital environments, particularly in terms of gravity conditions, lubrication mechanisms, and structural stiffness. Microgravity significantly affects joint preload and friction characteristics; high vacuum can shift lubrication regimes from fluid-film to boundary lubrication; and extreme thermal cycling may induce dimensional changes in structural components. These factors collectively influence the on-orbit validity of the identified dynamic parameters.

To partially address these challenges, this study introduces an environmentally sensitive friction model (Equations (2) and (3)) and emphasizes the necessity of on-orbit recalibration. In terms of excitation trajectory, a smooth fifth-order Fourier series trajectory is employed, which is suitable for adequately exciting the dynamic characteristics of the current system. It should be noted, however, that if the trajectory contains torque discontinuities or high dynamic frequency components, unmodeled dynamic behaviors may be excited, thereby compromising parameter identification accuracy. Future work will investigate trajectory design strategies incorporating non-smooth excitation components, such as steps or pulses, to enhance model robustness under complex dynamic conditions.

Despite the aforementioned environmental limitations, the excitation trajectory optimization method and hybrid parameter identification framework proposed in this study retain general methodological value. The results establish an effective benchmark for high-precision dynamic parameter calibration of robots in ground-based environments. Future efforts will focus on developing algorithms capable of online adaptive updates of model parameters—particularly friction parameters—and plan to validate and refine the model through microgravity simulation platforms, such as air-bearing tables, or via in-orbit experiments, thereby improving its reliability and extrapolability for real-world space applications.

6. Conclusions

This paper addresses the need for high-precision on-orbit control of space manipulators by systematically investigating dynamics modeling and parameter identification under special environmental conditions such as microgravity and vacuum. The main contributions are as follows:

• A nonlinear dynamic model for space manipulators incorporating an improved Stribeck friction term is established. This model elucidates the influence mechanisms of vacuum, microgravity, and temperature variations on joint friction, and an adaptive on-orbit correction method based on environmental monitoring is proposed.
• A hybrid parameter identification method integrating Particle Swarm Optimization (PSO) and the Levenberg–Marquardt (LM) algorithm is proposed. This method leverages the global search capability of PSO and the fast local convergence of LM, achieving significant improvements in identification accuracy while maintaining computational efficiency.
• Excitation trajectories are designed using Fourier series. By optimizing the harmonic components, the condition number of the observation matrix is significantly improved, effectively enhancing parameter identifiability.
• The effectiveness of the proposed method is validated on a six-degree-of-freedom ground-based manipulator test platform. All 108 dynamic parameters are successfully identified, with the correlation coefficients between predicted and measured joint torques exceeding 0.97, and the root mean square errors remaining below 5.1 N·m.

The identified high-fidelity model provides a reliable foundation for advanced control strategies such as robust and adaptive control. The quantified parameter uncertainty ranges can also be utilized for robustness design in controller synthesis. Future research will focus on developing dynamics modeling and identification techniques for rigid-flexible coupled systems; introducing advanced friction models capable of describing complex nonlinearities like hysteresis; investigating composite excitation trajectories incorporating non-smooth elements to enhance model robustness under extreme operating conditions; exploring adaptive parameter update algorithms based on on-orbit data; and validating model effectiveness in real space environments through ground-based simulations and in-orbit experiments.