Observer-Based Volumetric Flow Control in Nonlinear Electro-Pneumatic Extrusion Actuator with Rheological Dynamics
Abstract
1. Introduction
- Nonlinear Dynamic Modeling: A comprehensive nonlinear model of the motor–screw–syringe system is formulated, incorporating the physical dynamics of the actuator and the rheological characteristics of the printed material. This model enables the prediction of volumetric flow behavior under varying process conditions.
- Observer-Based State Estimation: An unknown input observer (UIO) is implemented to estimate unmeasurable internal states such as chamber pressure or nozzle force. These estimated variables are essential for real-time feedback and control in systems where direct sensing is infeasible.
- Closed-Loop Volumetric Flow Regulation: A proportional–integral–derivative (PID) controller is applied to the estimated flow rate to regulate extrusion output. This approach enables real-time compensation for variations in material viscosity, actuation lag, and dynamic disturbances, enhancing extrusion stability and consistency.
- Simulation and Experimental Validation: The control architecture is evaluated through both numerical simulations and experimental trials. Validation results confirm the effectiveness of the proposed approach in achieving stable, accurate flow control and improving deposition quality compared to baseline methods.
2. Materials and Methods
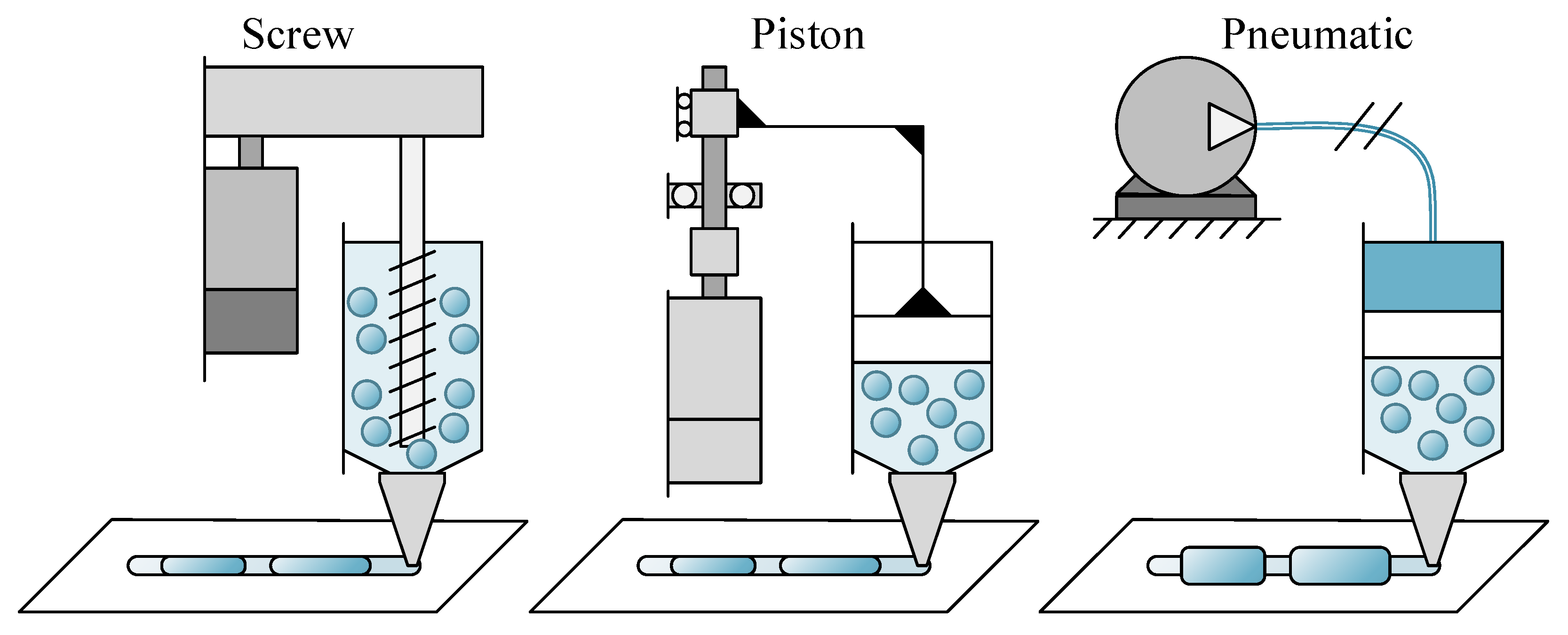
2.1. Extrusion Mechanism Overview and Proposed Actuation Design
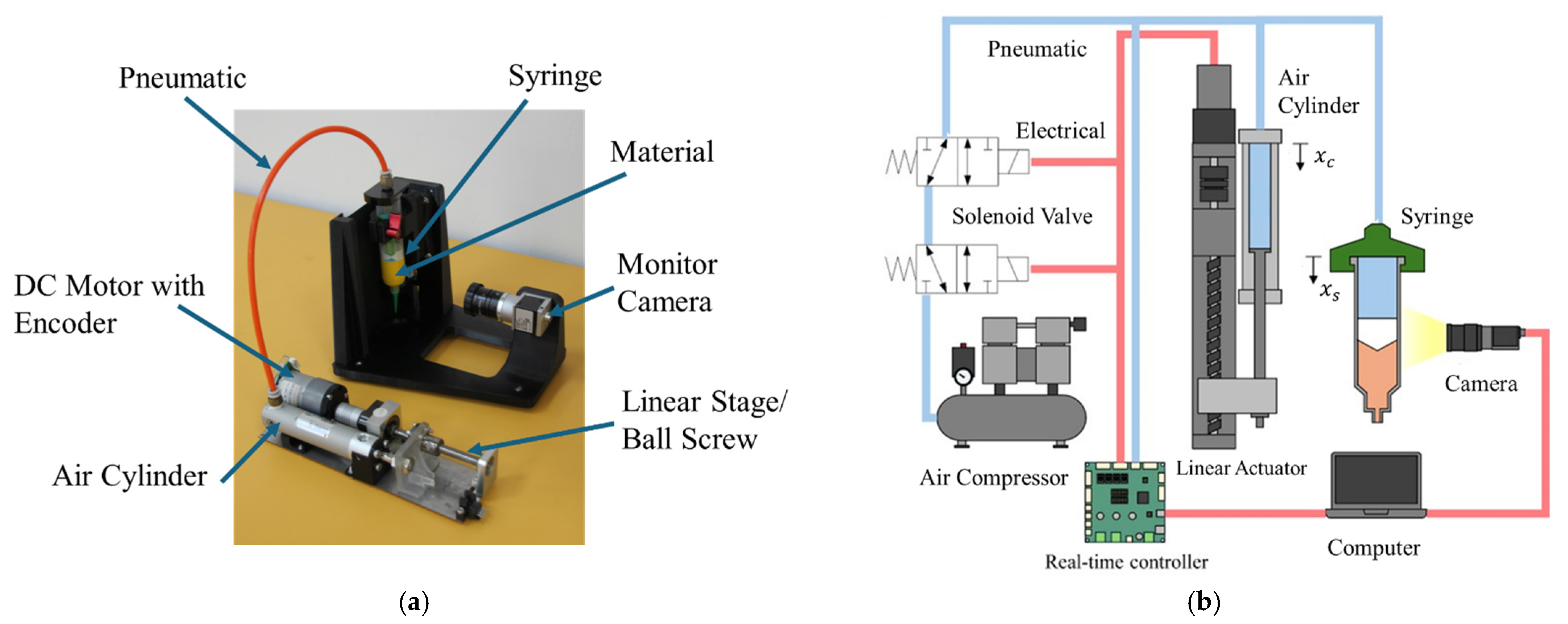
2.2. The System Architecture of Electro-Pneumatic Extrusion Actuator
2.3. Dynamic Modeling and Control Design
2.3.1. Dynamic Model of the System
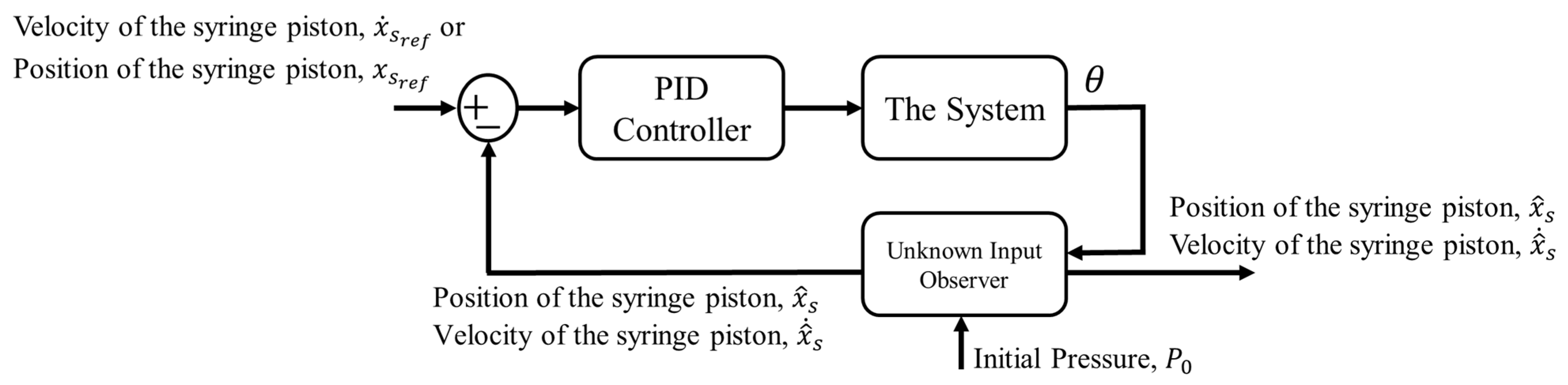
2.3.2. Unknown Input Observer Design and Flow Control Strategy
2.3.3. Control Technique
3. Experimental Results and Discussions
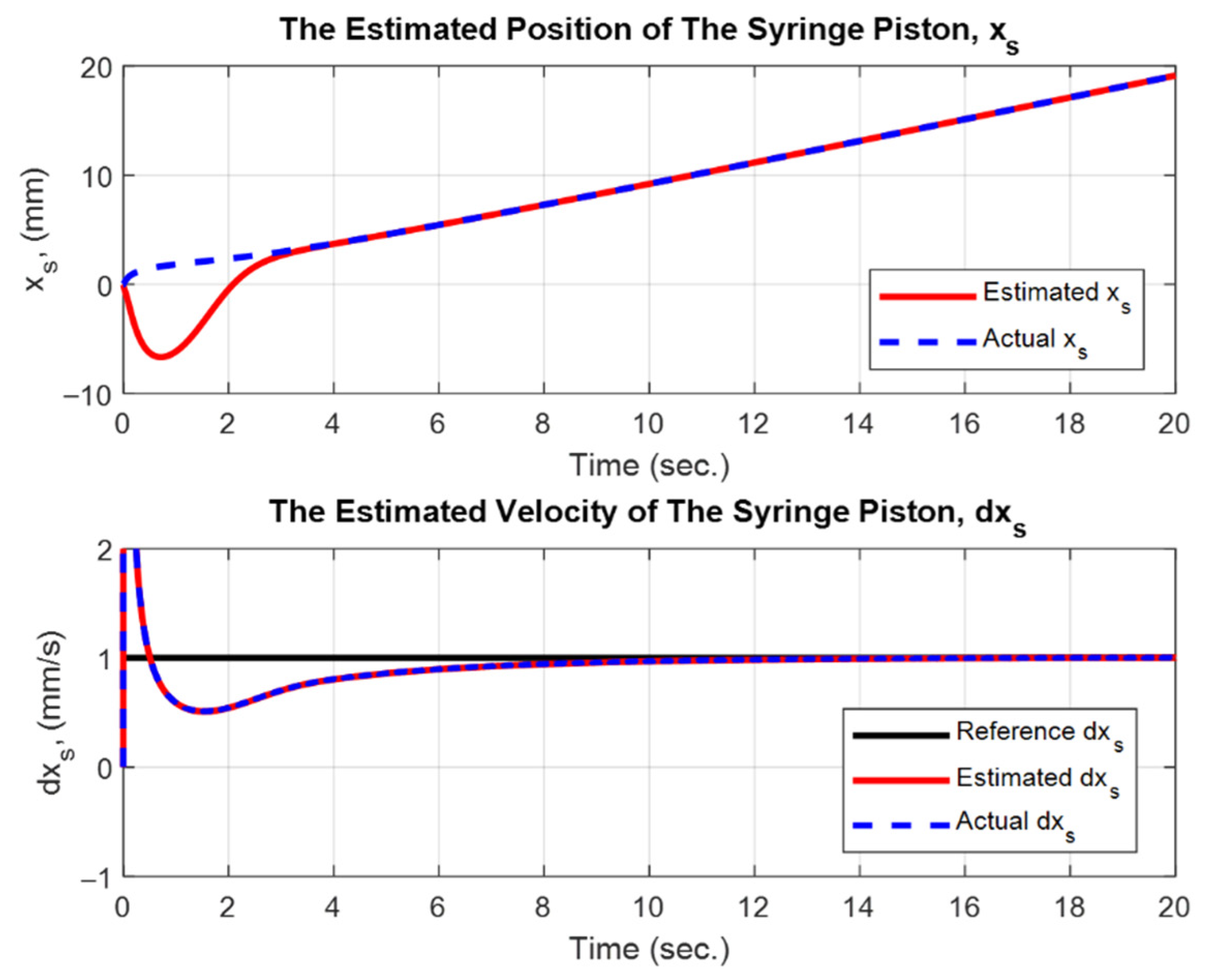
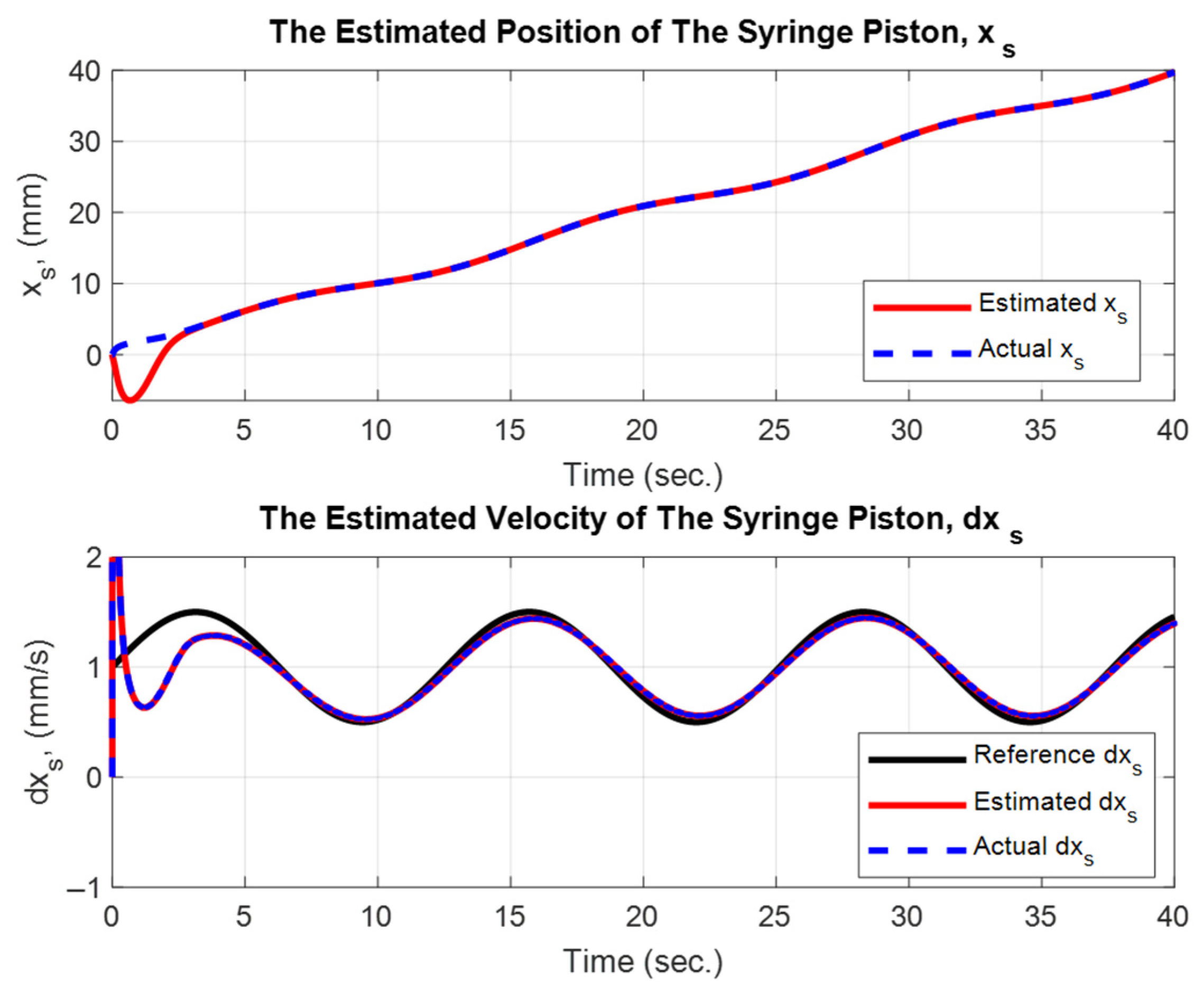
3.1. Simulation Results of the Unknown Input Observer
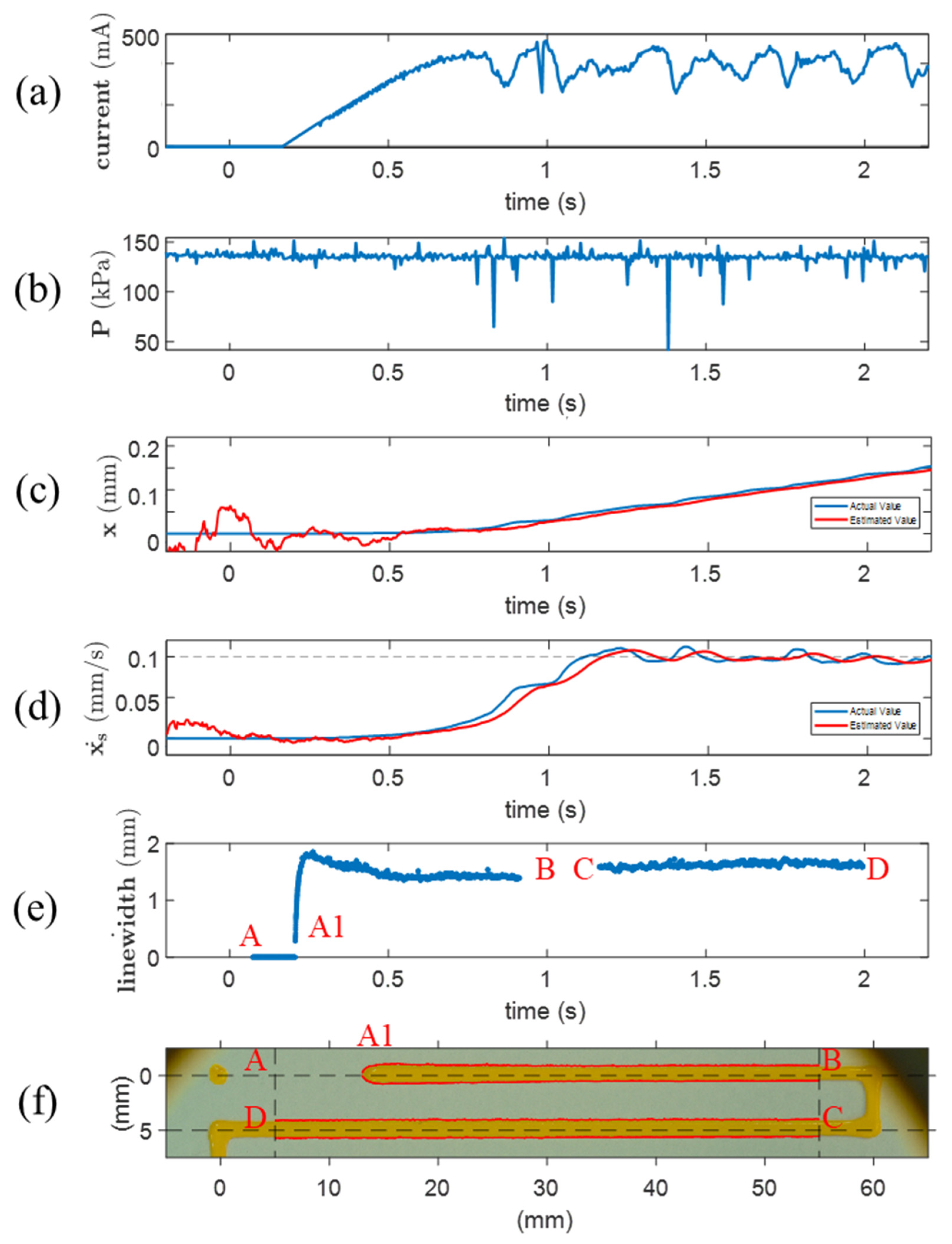
3.2. Experimental Results of the System
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bakrani Balani, S.; Mokhtarian, H.; Salmi, T.; Coatanéa, E. An investigation of the influence of viscosity and printing parameters on the extrudate geometry in the material extrusion process. Polymers 2023, 15, 2202. [Google Scholar] [CrossRef]
- Schuller, T.; Jalaal, M.; Fanzio, P.; Galindo-Rosales, F.J. Optimal shape design of printing nozzles for extrusion-based additive manufacturing. Addit. Manuf. 2024, 84, 104130. [Google Scholar] [CrossRef]
- Jang, J.W.; Min, K.E.; Kim, C.; Wern, C.; Yi, S. Rheological properties and 3D printing behavior of PCL and DMSO2 composites for bio-scaffold. Materials 2024, 17, 2459. [Google Scholar] [CrossRef]
- del-Mazo-Barbara, L.; Ginebra, M.P. Rheological characterisation of ceramic inks for 3D direct ink writing: A review. J. Eur. Ceram. Soc. 2021, 41, 18–33. [Google Scholar] [CrossRef]
- Gharraei, R.; Bergstrom, D.; Chen, X.D. Extrusion bioprinting from a fluid mechanics perspective. Int. J. Bioprint. 2024, 10, 3973. [Google Scholar] [CrossRef]
- Guidetti, X.; Mingard, N.; Cruz-Oliver, R.; Nagel, Y.; Rueppel, M.; Rupenyan, A.; Balta, E.C.; Lygeros, J. Force controlled printing for material extrusion additive manufacturing. Addit. Manuf. 2024, 89, 104297. [Google Scholar] [CrossRef]
- Marnot, A.; Koube, K.; Jang, S.; Thadhani, N.; Kacher, J.; Brettmann, B. Material extrusion additive manufacturing of high particle loaded suspensions: A review of materials, processes and challenges. Virtual Phys. Prototyp. 2023, 18, e2279149. [Google Scholar] [CrossRef]
- Cooke, M.E.; Rosenzweig, D.H. The rheology of direct and suspended extrusion bioprinting. APL Bioeng. 2021, 5, 011502. [Google Scholar] [CrossRef] [PubMed]
- Lukhi, M.; Mittermeier, C.; Kiendl, J. Multi-physics simulation of a material extrusion-based additive manufacturing process: Towards understanding stress formation in the printed strand. Prog. Addit. Manuf. 2025, 10, 6839–6853. [Google Scholar] [CrossRef]
- Bernagozzi, G.; Battegazzore, D.; Arrigo, R.; Frache, A. Optimizing the rheological and thermal behavior of polypropylene-based composites for material extrusion additive manufacturing processes. Polymers 2023, 15, 2263. [Google Scholar] [CrossRef]
- Khan, I.; Barsoum, I.; Abas, M.; Al Rashid, A.; Koç, M.; Tariq, M. A review of extrusion-based additive manufacturing of multi-materials-based polymeric laminated structures. Compos. Struct. 2024, 349–350, 118490. [Google Scholar] [CrossRef]
- Altıparmak, S.C.; Yardley, V.A.; Shi, Z.; Lin, J. Extrusion-based additive manufacturing technologies: State of the art and future perspectives. J. Manuf. Process. 2022, 83, 607–636. [Google Scholar] [CrossRef]
- Moretti, M.; Rossi, A.; Senin, N. In-process simulation of the extrusion to support optimisation and real-time monitoring in fused filament fabrication. Addit. Manuf. 2021, 38, 101817. [Google Scholar] [CrossRef]
- McAfee, M.; Kariminejad, M.; Weinert, A.; Huq, S.; Stigter, J.D.; Tormey, D. State estimators in soft sensing and sensor fusion for sustainable manufacturing. Sustainability 2022, 14, 3635. [Google Scholar] [CrossRef]
- Youssef, S.M.; Soliman, M.; Saleh, M.A.; Mousa, M.A.; Elsamanty, M.; Radwan, A.G. Modeling of soft pneumatic actuators with different orientation angles using echo state networks for irregular time series data. Micromachines 2022, 13, 216. [Google Scholar] [CrossRef]
- Brown, D.F.; Xie, S.Q. Model Predictive Control with Optimal Modelling for Pneumatic Artificial Muscle in Rehabilitation Robotics: Confirmation of Validity Though Preliminary Testing. Biomimetics 2025, 10, 208. [Google Scholar] [CrossRef]
- Cao, G.; Liu, Y.; Zhu, Z. Observer-based adaptive robust control of soft pneumatic network actuators. Int. J. Control Autom. Syst. 2022, 20, 1695–1705. [Google Scholar] [CrossRef]
- Oleff, A.; Küster, B.; Stonis, M.; Overmeyer, L. Process monitoring for material extrusion additive manufacturing: A state-of-the-art review. Prog. Addit. Manuf. 2021, 6, 705–730. [Google Scholar] [CrossRef]
- Liu, Y.-C. Disturbance-Observer-Based Sliding-Mode Speed Control for Synchronous Reluctance Motor Drives via Generalized Super-Twisting Algorithm. Actuators 2024, 13, 233. [Google Scholar] [CrossRef]
- Jiang, C.; Yang, Z.; Zheng, J.; Fu, B.; Bai, Y. Research on Active Disturbance Rejection Control of Rigid–Flexible Coupled Constant Force Actuator. Actuators 2025, 14, 325. [Google Scholar] [CrossRef]
- Chaiprabha, K.; Sithiwichankit, C.; Chungsangsatiporn, W.; Phanomchoeng, G.; Chancharoen, R. Digital Twin-Enabled Extrusion Control for High-Fidelity Printing of Polymers. Polymers 2025, 17, 2215. [Google Scholar] [CrossRef] [PubMed]
- Epaarachchi, J.A. The effect of viscoelasticity on fatigue behaviour of polymer matrix composites. In Creep and Fatigue in Polymer Matrix Composites; Woodhead Publishing: Cambridge, UK, 2010; pp. 492–513. [Google Scholar]
- Justino Netto, J.M.; Idogava, H.T.; Frezzatto Santos, L.E.; Silveira, Z.C.; Romio, P.; Alves, J.L. Screw-assisted 3D printing with granulated materials: A systematic review. Int. J. Adv. Manuf. Technol. 2021, 115, 2711–2727. [Google Scholar] [CrossRef]
- Estelle, K.T.; Gozen, B.A. Precision flow rate control during micro-scale material extrusion by iterative learning of pressure-flow rate relationships. Addit. Manuf. 2024, 82, 104031. [Google Scholar] [CrossRef]
- Fanucci, S.; Prinsloo, E. Development of a low-cost hydrogel microextrusion printer based on a Kossel delta 3D printer platform. Eng. Rep. 2023, 5, e12615. [Google Scholar] [CrossRef]
- Miri, A.K.; Nieto, D.; Iglesias, L.; Goodarzi Hosseinabadi, H.; Maharjan, S.; Ruiz-Esparza, G.U.; Khoshakhlagh, P.; Manbachi, A.; Dokmeci, M.R.; Chen, S.; et al. Microfluidics-Enabled Multimaterial Maskless Stereolithographic Bioprinting. Adv. Mater. 2018, 30, e1800242. [Google Scholar] [CrossRef]
- Malik, S.; Hagopian, J.; Mohite, S.; Lintong, C.; Stoffels, L.; Giannakopoulos, S.; Beckett, R.; Leung, C.; Ruiz, J.; Cruz, M.; et al. Robotic Extrusion of Algae-Laden Hydrogels for Large-Scale Applications. Glob. Chall. 2020, 4, 1900064. [Google Scholar] [CrossRef]
- Phanomchoeng, G.; Chancharoen, R. Hybrid motor system for high precision position control of a heavy load plant. Eng. J. 2019, 23, 161–173. [Google Scholar] [CrossRef]
- Jintanawan, T.; Phanomchoeng, G.; Suwankawin, S.; Kreepoke, P.; Chetchatree, P.; U-viengchai, C. Design of Kinetic-Energy Harvesting Floors. Energies 2020, 13, 5419. [Google Scholar] [CrossRef]
- Łukaszewicz, G.; Kalita, P. Navier–Stokes Equations: An Introduction with Applications; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Phanomchoeng, G.; Rajamani, R. Real-Time Estimation of Rollover Index for Tripped Rollovers with a Novel Unknown Input Nonlinear Observer. IEEE/ASME Trans. Mechatron. 2014, 19, 743–754. [Google Scholar] [CrossRef]
- Phanomchoeng, G.; Zemouche, A.; Jeon, W.; Rajamani, R.; Mazenc, F. H∞ Observer for Descriptor Nonlinear Systems with Nonlinear Output Equations. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 5952–5956. [Google Scholar] [CrossRef]
- The MathWorks Inc. Matlab. Available online: https://www.mathworks.com (accessed on 23 June 2024).

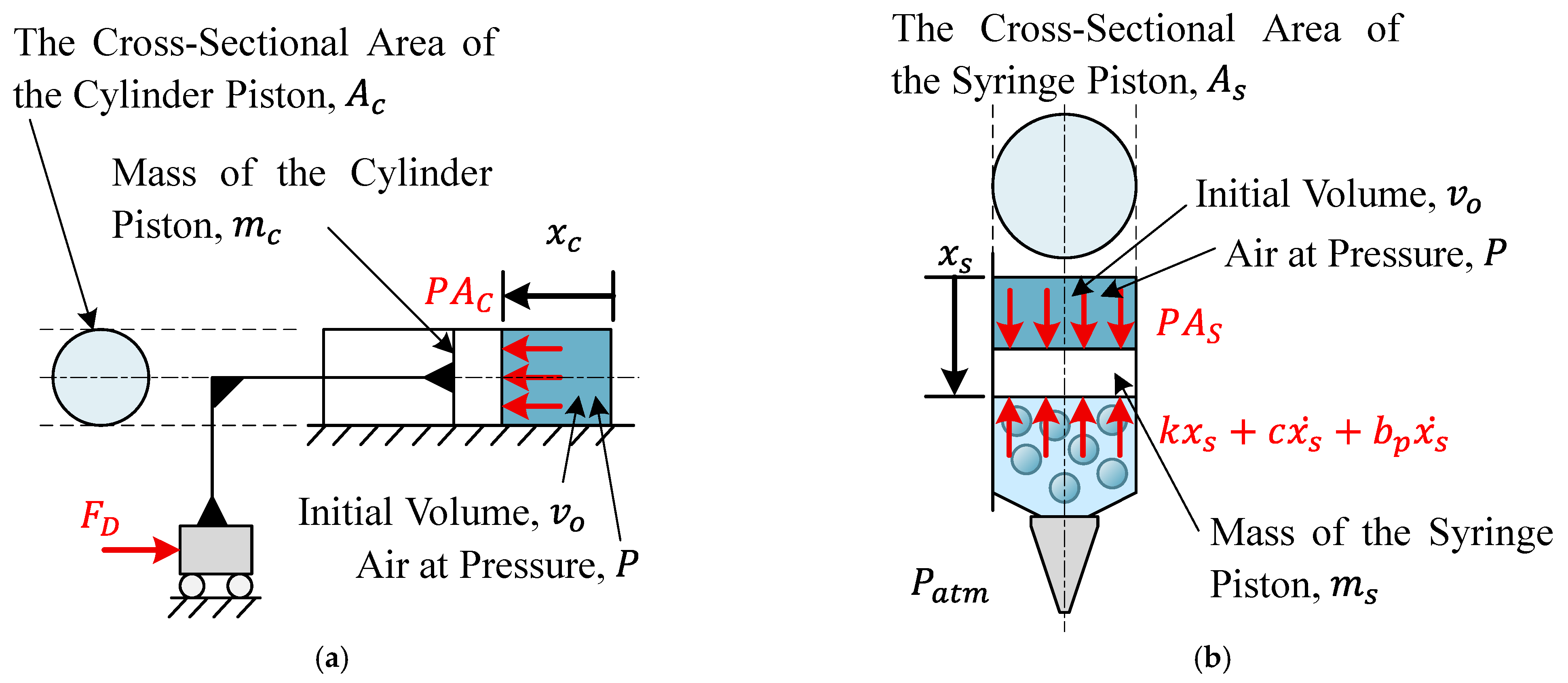


| Components | Parameters | Value | Unit |
|---|---|---|---|
| Pneumatic Cylinder | Initial Volume, | 25.5 | |
| Cross-Section Area of the Piston, | 201 | ||
| Mass of the Piston, | 0.736 | ||
| Stroke Length | 153 | ||
| Syringe | Cross-Section Area of the Syringe, | 397.25 | |
| Mass of the Syringe, | 0.1 | kg | |
| DC Motor | Moment of Inertia of the Rotor, | ||
| Electric Resistance, | 0.9 | ||
| Electric Inductance, | |||
| Electromotive Force Constant, | |||
| Motor Torque Constant, | |||
| Linear Stage | Pitch of the Ball Screw, | 2 | |
| Efficiencies of the Thread of Ball Screw, | 0.9 | ||
| Efficiencies of the Thrust Bearing of Ball Screw, | 0.9 | ||
| Encoder | Pulse per Revolution | 4000 | |
| 1 Pulse of Encoder | 0.006375 | ||
| The System | Atmospheric Pressure | 101.325 | kPa |
| Initial temperature | 300 | K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chancharoen, R.; Sithiwichankit, C.; Chaiprabha, K.; Suthithanakom, S.; Phanomchoeng, G. Observer-Based Volumetric Flow Control in Nonlinear Electro-Pneumatic Extrusion Actuator with Rheological Dynamics. Actuators 2025, 14, 496. https://doi.org/10.3390/act14100496
Chancharoen R, Sithiwichankit C, Chaiprabha K, Suthithanakom S, Phanomchoeng G. Observer-Based Volumetric Flow Control in Nonlinear Electro-Pneumatic Extrusion Actuator with Rheological Dynamics. Actuators. 2025; 14(10):496. https://doi.org/10.3390/act14100496
Chicago/Turabian StyleChancharoen, Ratchatin, Chaiwuth Sithiwichankit, Kantawatchr Chaiprabha, Setthibhak Suthithanakom, and Gridsada Phanomchoeng. 2025. "Observer-Based Volumetric Flow Control in Nonlinear Electro-Pneumatic Extrusion Actuator with Rheological Dynamics" Actuators 14, no. 10: 496. https://doi.org/10.3390/act14100496
APA StyleChancharoen, R., Sithiwichankit, C., Chaiprabha, K., Suthithanakom, S., & Phanomchoeng, G. (2025). Observer-Based Volumetric Flow Control in Nonlinear Electro-Pneumatic Extrusion Actuator with Rheological Dynamics. Actuators, 14(10), 496. https://doi.org/10.3390/act14100496








