1. Introduction
Brushless doubly fed reluctance machine (BDFRM) has been extensively investigated over the past few years, and several research studies have been conducted in the field of BDFRM operation [
1]. Particularly, it allows the use of a partially rated inverter in many variable-speed applications. The machine incorporates a uniquely designed rotor alongside a stator equipped with two distinct windings, each characterized by a different number of poles. The stator assembly comprises conventional laminated steel and two separate stationary winding sets. Magnetic coupling between these stator winding sets is facilitated by the rotor’s inherent ferromagnetic saliency, making the rotor geometry a critical factor in determining the degree of mutual magnetic interaction [
2]. This BDFRM maintains the economic benefits associated with Doubly Fed Induction Generators by enabling the employment of a power converter sized at approximately 30% of the machine’s rated capacity. Moreover, the BDFRM offers the advantage of brushless construction, eliminating the need for maintenance-related brush components [
3].
The two sets of stator windings, i.e.,
-pole power and
-pole control windings, have their own independent three-phase connection. The power winding is grid-connected, and the control winding may be fed from a bi-directional converter [
4].
If the control winding is supplied with a power converter, the doubly-fed adjustable-speed mode of the BDFRM can be achieved through appropriate control strategies [
5]. The basic condition for electromechanical energy conversion for this machine is that the reluctance rotor must satisfy the following condition [
6]:
where
is the number of rotor poles;
and
are the power and control winding pole pairs, respectively. Only the positive sign case in Equation (1) will be considered in this study. Thus, the machine steady-state doubly fed synchronous speed is as follows [
6]:
where
(in rad/s) is the angular speed; the indexes
and
refer, respectively, to the power and control windings;
is related to the rotor.
Detailed knowledge of the magnetic field distribution in electrical machines is essential for the design and analysis of their performance prior to the manufacturing process. Moreover, the precise knowledge of parameters is of critical importance for correct performance prediction and design optimization.
Numerical techniques enable very accurate prediction of the machine’s electromagnetic performances. However, the numerical approach requires a longer computational time for analyzing the characteristics of the machines. On the other hand, analytical methods can provide accurate solutions with less computational effort. In fact, analytical calculations have the advantages of being flexible for initial performance evaluation and optimization of electrical machines.
A technique using the concept of winding functions has been utilized for developing inductance expressions of the BDFRM [
7]. In [
8], the transient model of the BDFRM is presented by using the winding function principles in order to evaluate the BDFRM model for different modes of operation. Reference [
9] introduces an analytical approach for the analysis and design of a brushless doubly fed reluctance generator, which combines both equivalent electrical and magnetic circuit representations. Additionally, a semi-analytical framework incorporating an equivalent electric circuit alongside a Reluctance Network Model for the purpose of size optimization in novel BDFRM designs is presented in [
10]. The validity and effectiveness of this modeling approach have been substantiated through comprehensive experimental testing on prototype machines.
Subdomain modeling is a rigorous analytical technique that entails partitioning the electromagnetic problem into distinct physical regions, or subdomains, within which Maxwell’s equations are solved analytically [
11]. Utilizing this approach with the incorporation of hyperbolic functions, the magnetic vector potential distribution has been computed for surface-mounted permanent magnet (PM) machines as demonstrated in [
12], and for PM machines featuring surface-inset magnets with an outer rotor configuration, as detailed in [
13]. In these analyses, magnetic saturation effects were not considered. Furthermore, an exact two-dimensional subdomain method tailored for switched reluctance machines fed by sinusoidal current inputs is developed in [
14].
In this study, the subdomain method is employed to analytically determine both the magnetic field distribution and inductance characteristics of a brushless doubly fed reluctance machine featuring a smooth stator and salient pole rotor. The organization of the paper is as follows: first, the development of the two-dimensional subdomain model for the investigated machine is described; next, the derivation of key parameters—including the flux density components, electromagnetic torque, and inductances—is detailed. Subsequently, the analytical findings from a case study are presented and validated through comparison with results obtained via numerical simulation. The study concludes with a summary of the main outcomes.
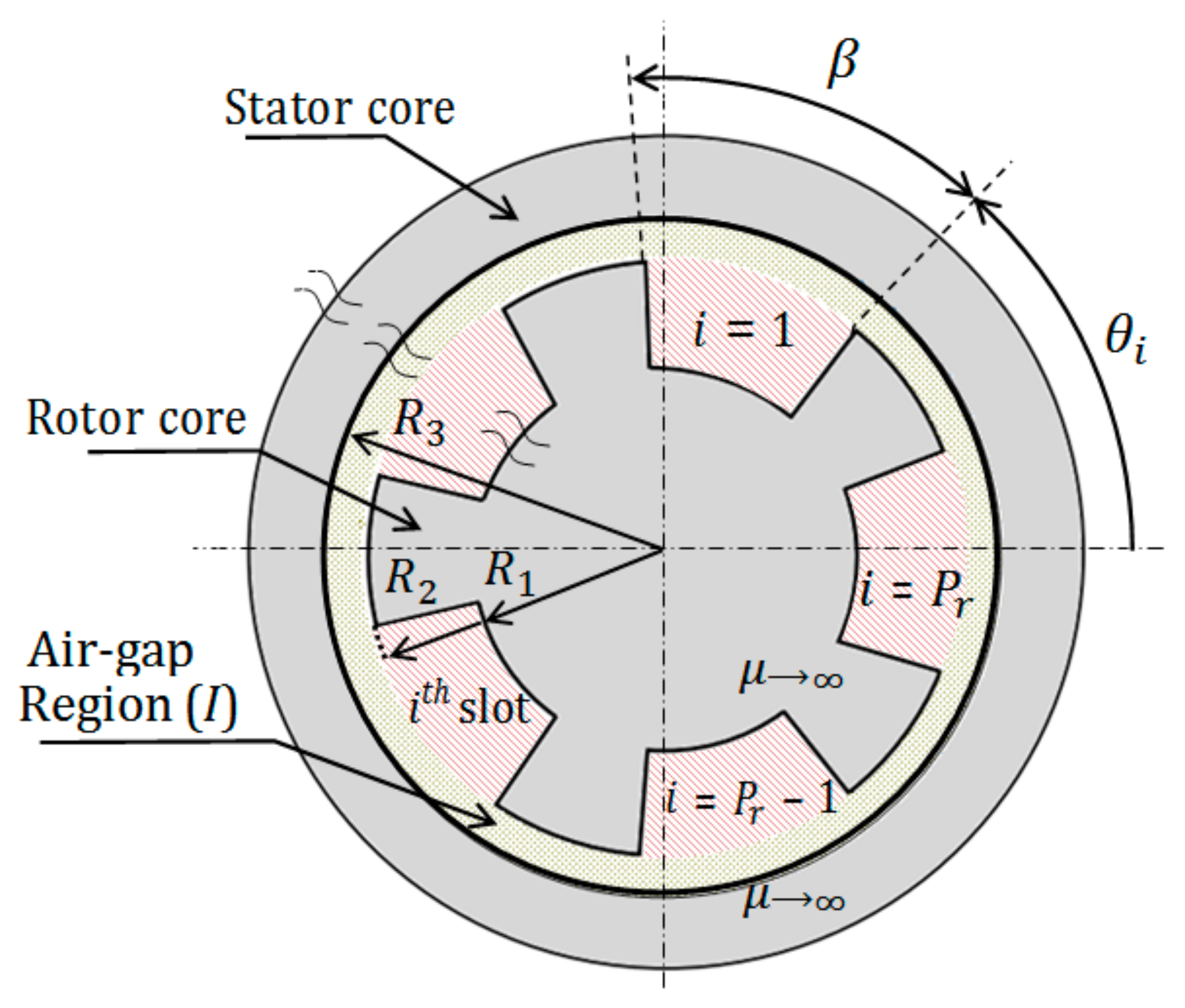
2. Motor Geometry and Assumptions
The basic configuration of the BDFRM considered for this work is represented in
Figure 1. The machine has a smooth stator and a simple salient laminated rotor with
saliencies. The geometrical parameters are the inner and outer radii of the rotor, the inner radius of the stator, and the rotor slot opening.
The slot opening angle is
. The angular position of the
rotor slot is defined as
where
is the angular position of the rotor and
is the number of rotor poles.
As shown in
Figure 1, this machine has been partitioned into two regions: Region
for the air-gap and Region
for the rotor slots.
The model is formulated in magnetic vector potential in 2D polar coordinates with the following main assumptions:
The stator and rotor cores are assumed to be infinitely permeable, with the stator core considered slotless.
A two-dimensional magnetic vector potential formulation is adopted, and end effects are neglected (infinitely long machine).
Eddy-current effects within the materials are neglected.
The rotor operates at constant angular velocity,
Both stator windings are supplied by balanced sinusoidal currents, each represented by an equivalent current sheet.
The results obtained from the proposed model are valid under the stated simplifying assumptions, which provide an approximate analytical framework. They are appropriate for qualitative analysis and initial design exploration, quick estimations, or long laminated machines. For advanced design, each assumption must be revisited to correct or refine the predictions.
3. Magnetic Field Calculation
According to the 2D problem assumption, the magnetic vector potential only has one component along the -direction and only depends on and coordinates. As mentioned previously, the entire domain of the magnetic field is divided into two subdomains, so that, in polar coordinates, in the air-gap (Region ) and in the rotor slot (Region ), with being the unit vector along the -axis.
For the sake of clarity and simplicity of the general solutions in the different subdomains, the following notations are defined as follows:
3.1. Equivalent Current Sheet Distribution
The stator windings are considered as an equivalent current sheet distributed over the stator inner radius for simpler analysis. In addition, the surface current density is limited to the fundamental term. Therefore, in the presence of an infinitely permeable stator iron, the expressions, with respect to time, of the sinusoidal current densities
and
, corresponding to the power and control winding currents, respectively, are
Here,
denotes the angular position along the stator core. The parameters
and
are the phase shifts with respect to an arbitrary reference of each winding (phase-
axis of the power and control winding, respectively). The variables
and
indicate the angular frequencies of the electrical supplies to the two stator windings. The amplitudes of the current densities in the power and control windings are denoted by
and
, respectively, and are determined as described in [
15]:
where
is the number of series turns per phase,
is the three-phase stator current amplitude, and
is the fundamental winding factor of the power (or control) winding.
is the inner stator radius.
The resultant current sheet acting along the stator interior surface is the superposition of the two current densities produced by the power and control windings, such as
If the rotor rotates with a constant angular velocity
given by Equation (2), the current sheet expression (Equation (9)) can be transformed from the stator reference frame to the rotor reference frame (angle
) using Equation (10), and the result is given by Equation (11):
Reference [
16] presents an analysis to identify the field characteristics and discusses their impact on the analysis and design of the brushless doubly fed induction machine, which has similar stator doubly fed windings. The characteristics are determined from an analysis of the sum of two rotating sinusoidal field waveforms with different angular frequencies and pole pairs. It is concluded that the form of the field distribution depends on the relative amplitude of the two field components, excitation frequencies, and their relative angular offset. In this particular case, the stator windings meet the following condition related to the angular frequencies and pole pairs:
The spatial profile of the magnetic field remains invariant over time and rotates synchronously with the machine, given that the angular velocities of the two underlying flux density distributions are identical. However, the instantaneous angular position and the respective peak (positive and negative) values of the resultant flux density are governed by the relative angular displacement between the two component flux distributions. This relative offset is fundamentally determined by the machine’s operating conditions [
16]. Consequently, when the condition expressed in Equation (12) is satisfied, the rotor achieves synchronous rotation with respect to the resultant stator surface current density, as specified in Equation (13):
Under these conditions, the electromagnetic field problem is reduced to a magnetostatic analysis. The subsequent study will be confined to this specific synchronous operating regime. As a result, the expression describing the current density, as observed from the rotor reference frame (cf. Equation (11)), is given by:
It should be noted that, in real operation, the synchronization condition (Equation (12)) is often not exactly satisfied. When a small slip exists—either in steady asynchronous regimes or during transients—the electromagnetic model must include time-dependent terms. In this case, the equivalent current sheet no longer appears as a constant distribution but instead carries frequency components shifted by the slip frequency. This leads to fields that vary in both space and time, and to additional induced currents in the conductors. Although such an extension increases the complexity of the formulation, it allows the model to capture essential physical effects such as torque oscillations, additional losses, and dynamic interactions between the stator and rotor.
3.2. General Solution of Laplace’s Equation in Rotor Slots (Region i)
The field behavior in the
rotor slot is governed by the following Laplace’s equation:
The tangential component of the magnetic field at both the sides and the base of each rotor slot vanishes, reflecting the idealization of an infinitely permeable iron core. In addition to the continuity condition enforced at the interface between the slot and the air-gap regions, the
slot subdomain (refer to
Figure 2) is thus subject to the following boundary conditions:
Considering the Neumann boundary condition described in Equation (17), the solution can be sought in the form detailed in references [
17,
18,
19]:
By using the boundary conditions at the bottom of the
rotor slot from Equation (18) and the continuity condition at the top of the slot from Equation (16), the solution for
in Equation (19) can be simplified to Equation (20):
where
is a positive integer and
is defined by Equation (4).
The constant terms
and
are coefficients to be determined. For this purpose, condition (16) is considered. The air-gap magnetic vector potential is expanded into a Fourier series over the
rotor slot opening at
=
. It is obtained for the mean value as
and for the
harmonic, we can write the following:
The expression for the coefficient
is given in
Appendix A.
3.3. General Solution of Laplace’s Equation in Air-Gap (Region I)
The Laplace’s equation governing the field in the air-gap subdomain, which is an annular domain delimited by the external radius of the rotor
and the stator internal radius
, is given by:
where
is the magnetic vector potential in the air-gap region.
The air-gap subdomain and the associated boundary conditions are shown in
Figure 3.
In the case of an ideal stator iron core with infinite magnetic permeability, the boundary condition at the interface between the air-gap and the current sheet can be expressed as follows:
where
is the magnetic permeability of free space.
Following the formulation of [
17,
18], the function
is introduced as
where
is the magnetic vector potential in the
-rotor slot region, which is given by Equation (20).
The boundary condition at
is
The general solution of Equation (23) can be found by separating the variables
and
. By taking into account the boundary conditions in Equations (24) and (26), the solution can be written as [
17,
18]:
where
is a positive integer,
and
are defined by Equations (4) and (5). The Fourier coefficients
,
,
, and
are determined using a Fourier series expansion of
and Equation (25) over the air-gap interval, such as
where
: it is the boundary function defined at the slot upper surface, representing the spatial distribution of the magnetic potential along the angular coordinate.
, : , and are the Fourier coefficients of the magnetic potential in the air-gap region, which is used to describe the circumferential field distribution.
, : and are the Fourier coefficients in the slot-opening region, ensuring the continuity of the potential and field at the slot boundaries.
The expressions of these coefficients are given in
Appendix A.
3.4. Magnetic Flux Density and Torque Calculation
Knowing the solutions of the vector potential in the air-gap domain, the radial and tangential components of the magnetic flux density
and
are, respectively, determined according to Equations (32) and (33):
Rearranging Equations (32) and (33), the components of the flux density distribution in the air-gap domain can also be expressed through Equations (34) and (35):
Radial and tangential components of air-gap magnetic fields are employed to find the electromagnetic torque using the Maxwell stress tensor method. To evaluate the electromagnetic torque in two-dimensional cylindrical geometries, the integration path is chosen as a circular contour enclosing the rotor within the air-gap. The torque is then expressed by integrating the Maxwell stress tensor over this path, represented as follows:
where
is the mid-air-gap radius of the circle taken as the integration path, and
is the machine axial length.
By substituting the expressions given in Equations (34) and (35) into Equation (36), the resulting analytical formula for the electromagnetic torque takes the following form:
with
3.5. Windings Self and Mutual Inductances
Three-phase self-inductances
,
and mutual inductance between the two sets of primary and secondary windings
, can be calculated from the magnetic energy [
20] as
where
,
and
are, respectively, the magnetic energies when only the power winding, the control winding, and both windings are fed with their respective three-phase currents
.
For a linear material, the magnetostatic energy
contained in a field in a volume
can be expressed in terms of the magnetic vector potential
and the current density
as
In the case of a surface current distribution, the expression of
reduces to
where
is the axial length of the machine,
is the magnetic permeability of free space,
is the normal unit vector, and
is an elementary curvilinear displacement.
At
, the elementary linear element is
To evaluate the magnetic energy due to the stator current sheets, Equations (42) and (43) are used. The integration path is chosen as a circular contour, with
varying from 0 to
, defined on the inner radius of the stator and therefore encompassing all the poles enclosing the rotor.
4. Analytical Results and Comparison with Finite Element Analysis
As a case study, a BDFRM having a two-pole power winding, a six-pole control winding, and a simple salient rotor composed of four saliencies is investigated under unsaturated conditions. The air-gap flux density, the static torque, and the three-phase inductances are calculated on the basis of the proposed model and verified by a two-dimensional FE model using “Femm version 4.2” software [
21].
The main design parameters of the investigated machine are shown in
Table 1. The analytical solutions in the domains of the air-gap (of harmonic order
) and in the rotor slots (of harmonic order
) have been computed with a finite number of harmonic terms
and
, respectively. Using values of
, the field solution is predicted with good accuracy.
The 2D FEM model is created on the basis of the geometric parameters given in
Table 1. As the sketch in
Figure 4 highlights, the rotor has four salient poles, and the stator is represented by a circle of radius
. Moreover, the entire cross-section of the machine is modeled.
A circular boundary representing the inner radius of the stator is established. This boundary is discretized into multiple circular arcs, each subjected to a Neumann boundary condition to enforce the tangential component of the magnetic field. This segmentation into circular arcs is performed with an angle of 1°, which is an optimal value that ensures an accurate representation of the current density distribution, which is intended to replicate the analytical model’s prescribed conditions, specifically, the superposition of two sinusoidal current densities with distinct amplitudes and pole pair numbers. Furthermore, a reference frame aligned with the stator is defined. The reference axis is chosen consistently with that used in the analytical formulation, for the phase shifts and . In addition, the relative permeability of the iron core in the FE model is set equal to , which is a large value that is used to simulate infinite permeability.
4.1. Magnetic Vector Potential, Flux Density, and Torque Calculations
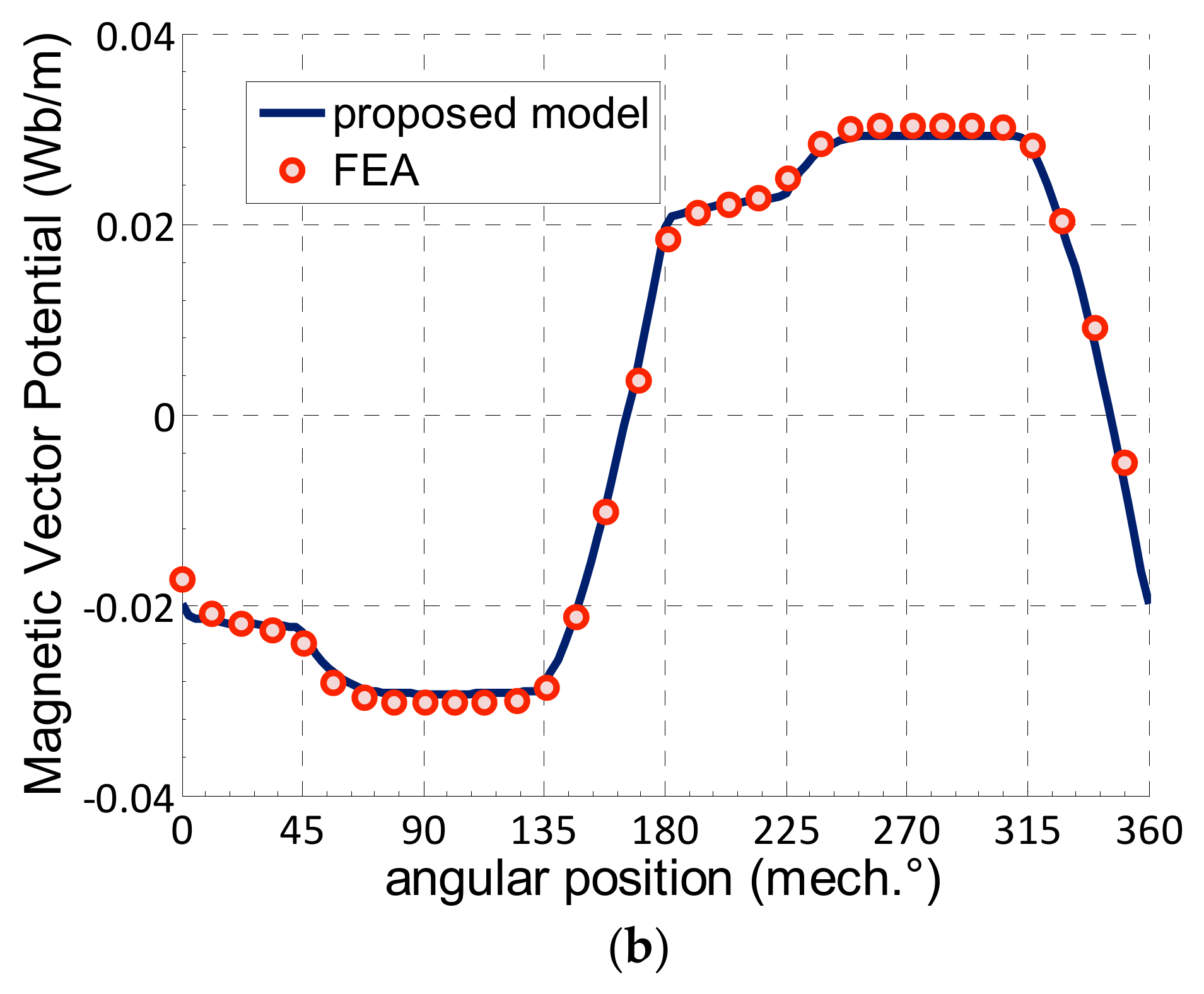
The predicted magnetic vector potential variation in the middle of the air-gap is shown in
Figure 5 for two rotor initial positions. The comparison shows that there is a good agreement between the FEA results and those predicted using the analytical model.
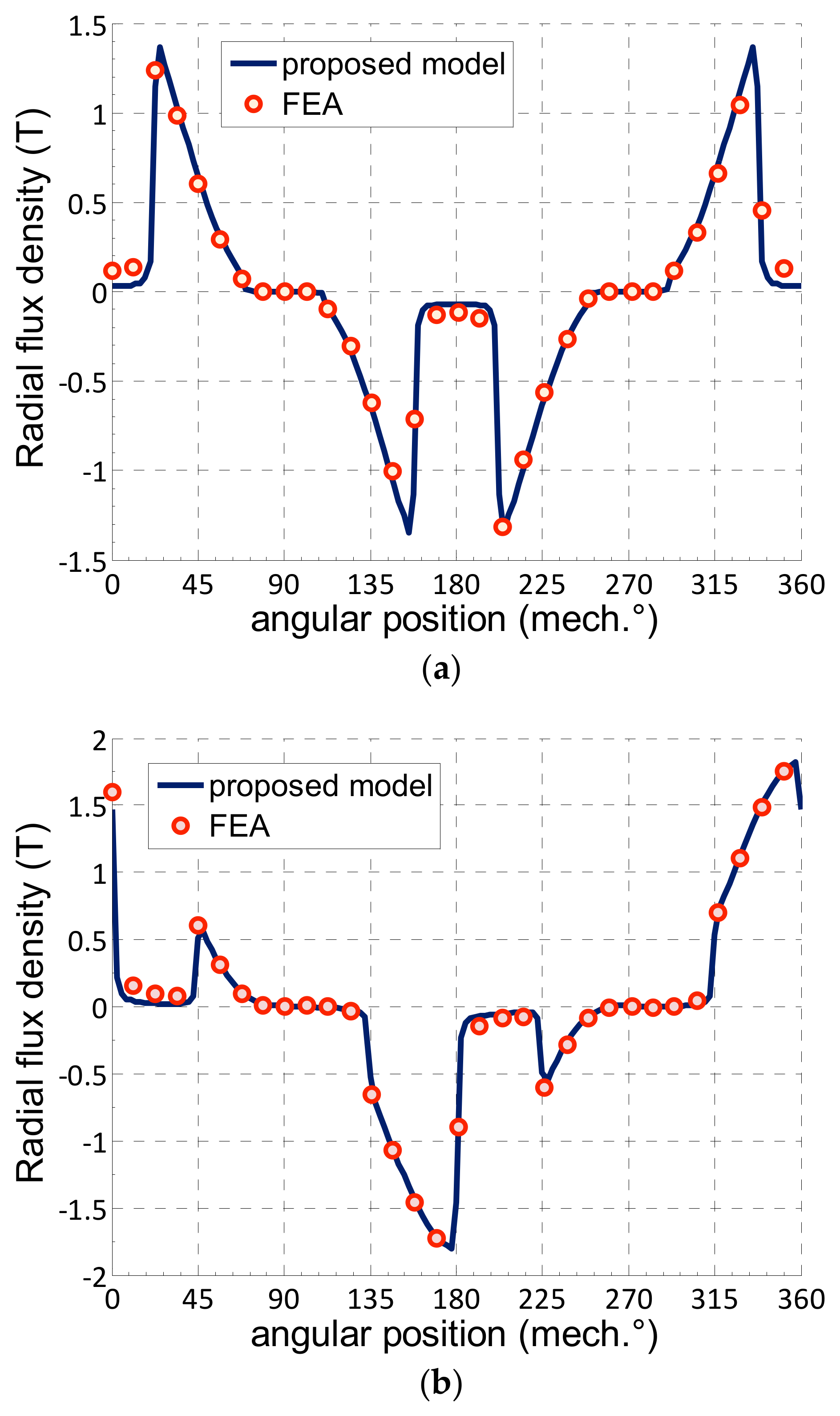
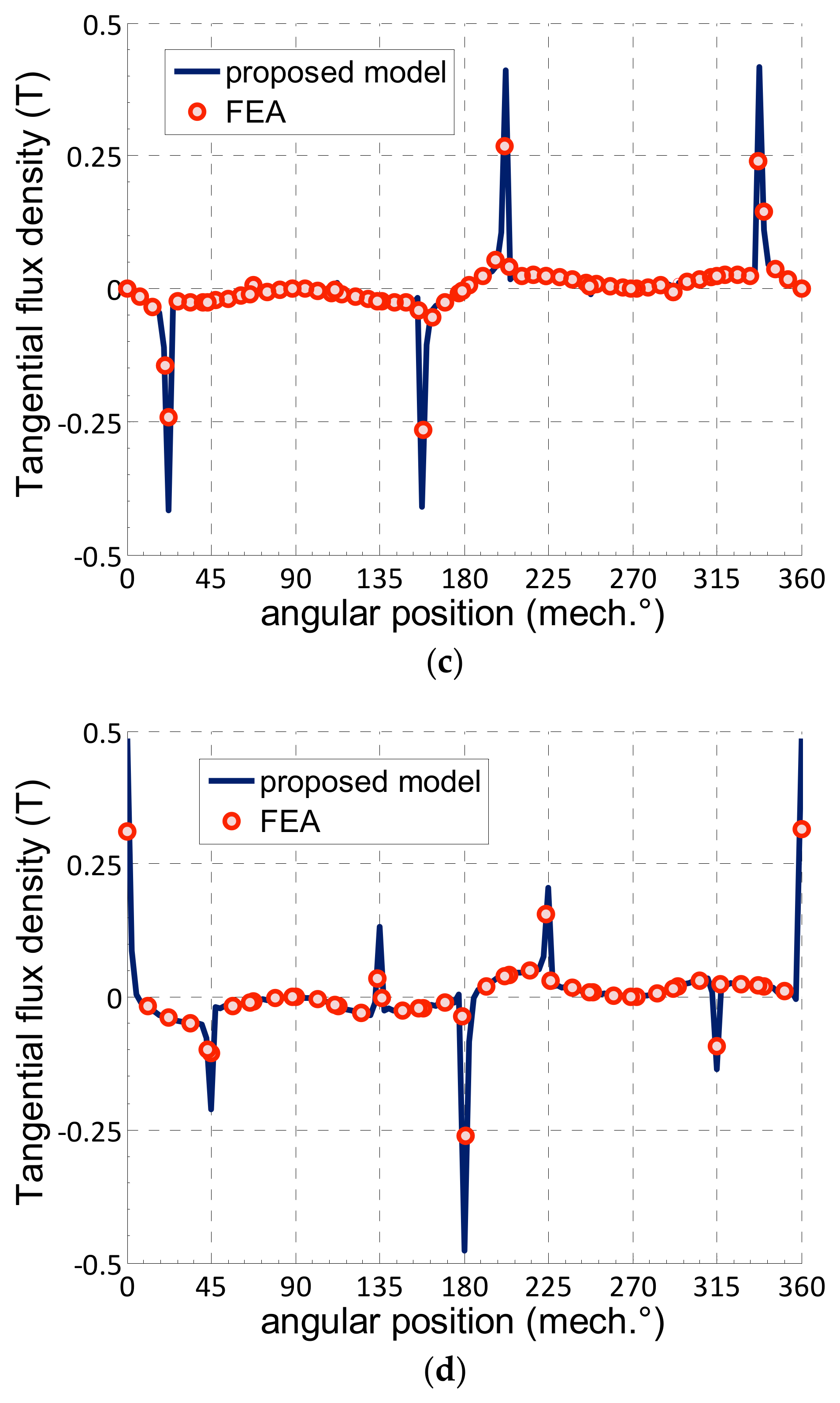
In addition, the flux density distributions in the whole air-gap region are analyzed and compared. As illustrated in
Figure 6, the radial and tangential flux density waveforms at the mid air-gap, obtained from both FEA and the analytical approach, are in very good agreement, further demonstrating the high accuracy of the proposed analytical model.
In a brushless doubly fed machine (BDFM), the power winding is typically connected directly to the power grid, while the control winding is connected through a power electronic converter. Torque control is achieved by adjusting the magnitude and angle of the control winding’s current. Thus, in the present analysis, torque is computed by maintaining the phase shift
of the power winding to zero, while the machine can be controlled by varying the control winding current angle
for a given current sheet amplitude of the respective winding. For two sets of windings current densities,
Figure 7 shows the torque waveform as a function of the control winding current angle. In both cases, it can be seen that the analytical results show good agreement with the FEA results.
Table 2 presents the relative error in the maximum developed torque obtained from finite element simulations for different permeabilities and magnetic materials. The data show that for relative permeabilities around 5000, the relative error remains within acceptable limits for predicting machine performance. However, the error increases significantly when the magnetic material experiences saturation. Additionally, it is observed that the critical control angle at which the pull-out torque occurs is slightly higher than the theoretical value of 30°, as predicted by the analytical model.
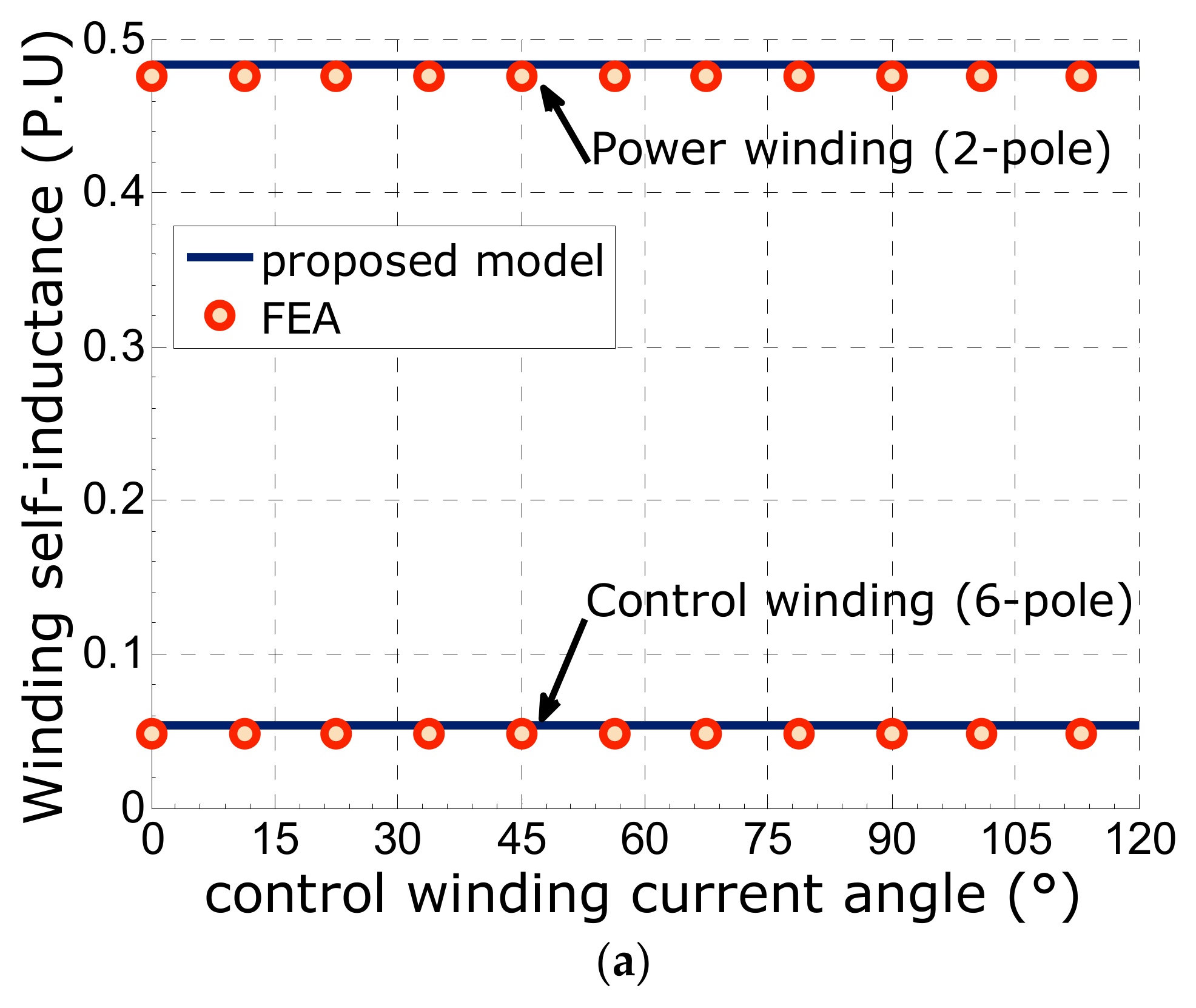
4.2. Inductance Calculation
The three-phase self-inductances are obtained from the total energy associated with only the imposed current sheet with respect to the considered winding, while the mutual-inductance between the two windings is obtained similarly by superimposing the current sheets of the two windings.
The magnetic energy is analytically evaluated using the energy relationship given in Equation (44). For the finite element analysis (FEA), the built-in magnetic energy calculation feature within the “femm” software post-processor is utilized to obtain the corresponding values.
The inductance values are expressed in per unit (p.u.), as they are derived from magnetic energy calculations. Specifically, the different values of electromagnetic energy have been normalized by dividing them by the maximum magnetic energy obtained from a reference machine. This reference pertains to a machine with an identical stator current sheet and air-gap, but fitted with a cylindrical rotor. Both analytically derived and finite element analysis (FEA) model results have been normalized in this manner, ensuring a consistent basis for comparison across models.
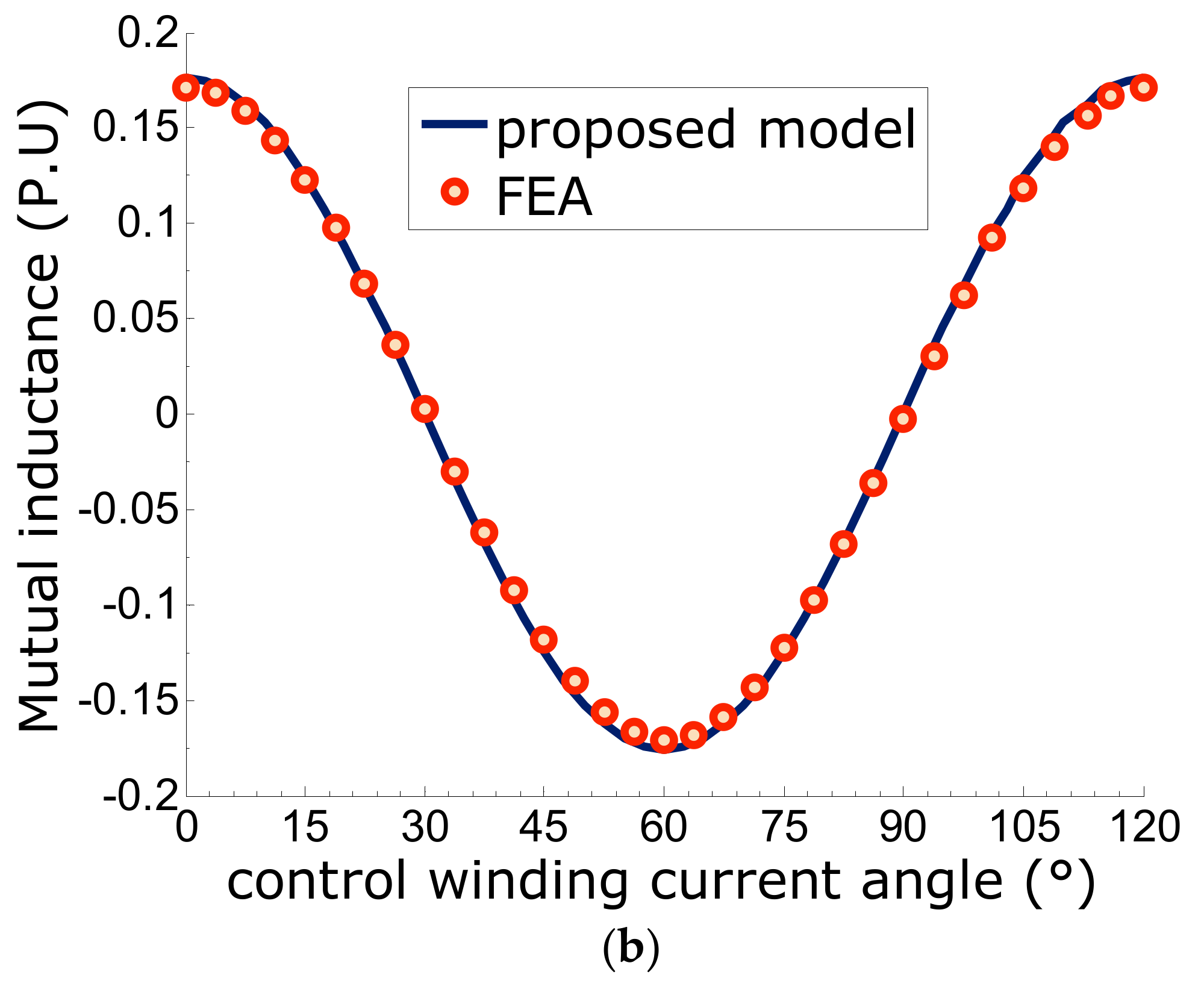
Figure 8 shows the evolution of self and mutual inductances, as a function of control winding current angle, obtained by analytical model and finite element simulations. In
Figure 8b, it can be seen that the variation in the mutual inductance expresses the reluctance nature of the BDFRM.
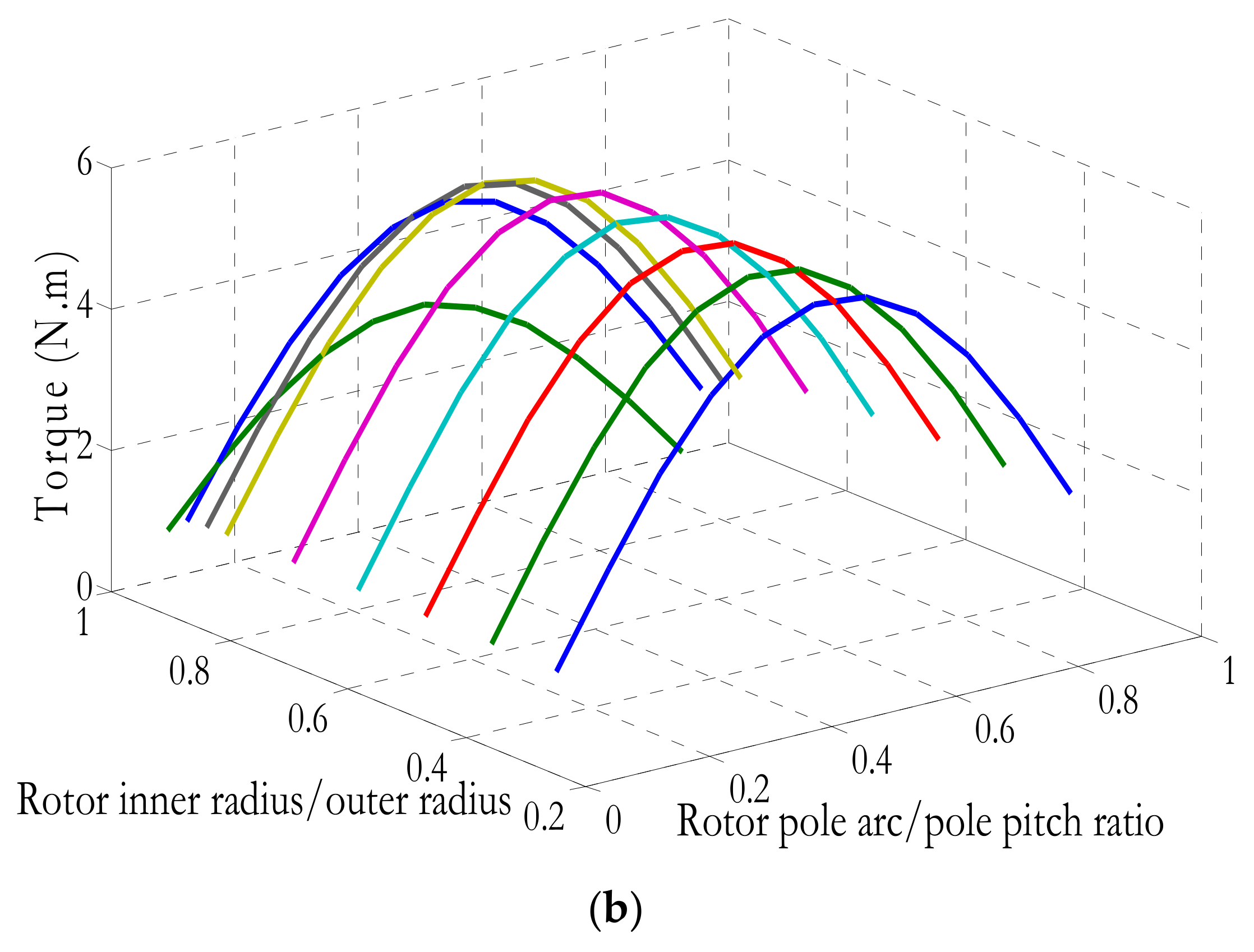
4.3. Design Parameters Sensitivity
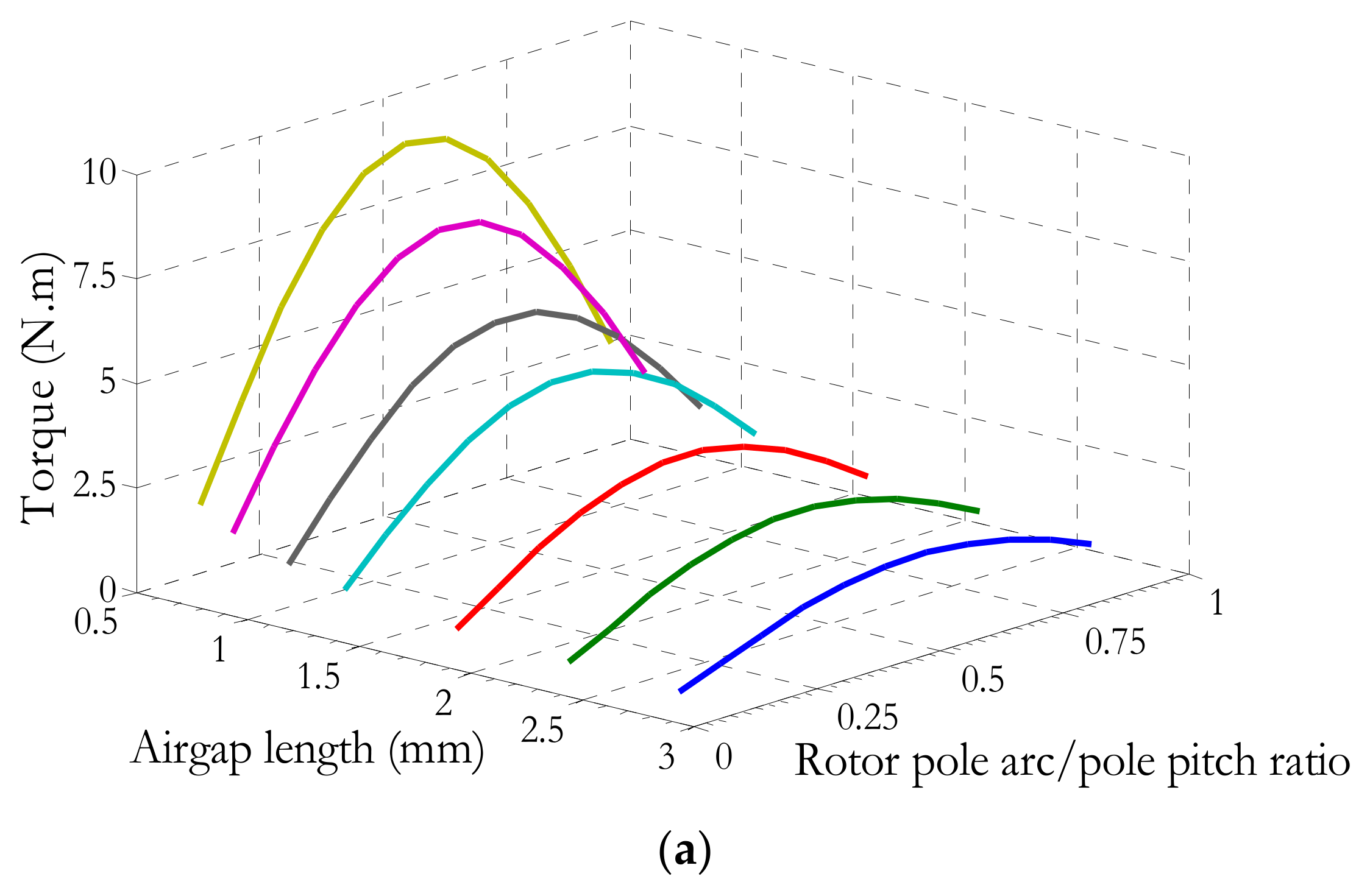
The analytical model is employed to evaluate the sensitivity of torque performance to key geometric parameters, namely the rotor pole arc-to-pole pitch ratio, the air-gap length, and the rotor inner-to-outer radius ratio. The obtained results are presented in
Figure 9. It can be seen from
Figure 9a that, like the synchronous reluctance machine equipped with a simple salient rotor, the rotor pole arc angle, in the studied machine, is one of the most influential design parameters (
Figure 9a). On the other hand, it is noticed in
Figure 9b that rotor slot depth is a less influential design parameter.