A Bilevel Optimization Framework for Adversarial Control of Gas Pipeline Operations
Abstract
1. Introduction
2. Literature Review
2.1. Cybersecurity in Critical Infrastructure Systems
2.2. Pipeline Network Modeling and Control
2.3. Cyber–Physical Modeling of Pipeline Attacks
2.4. Limitation of Existing Research and Motivation
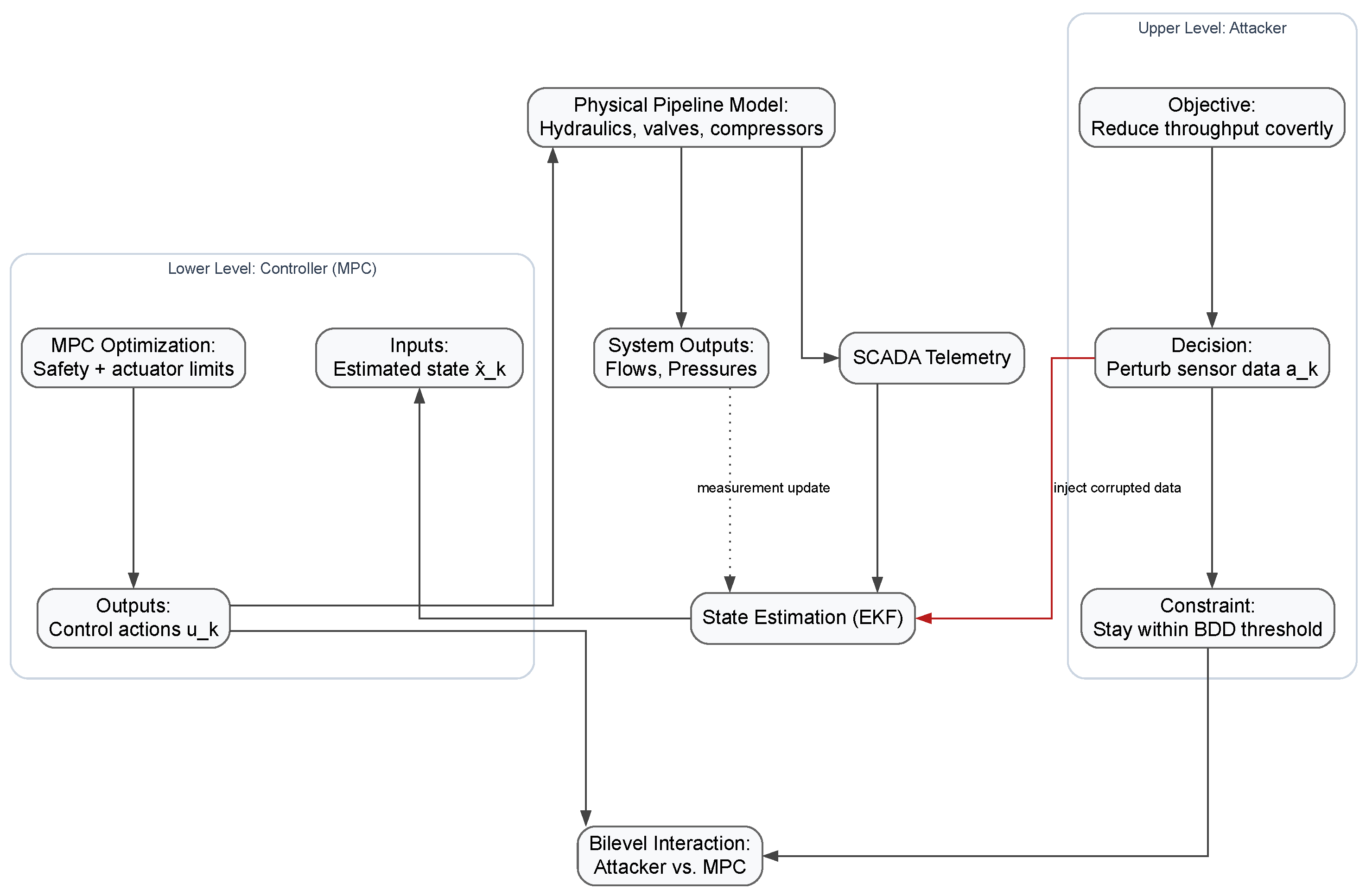
3. Methodology
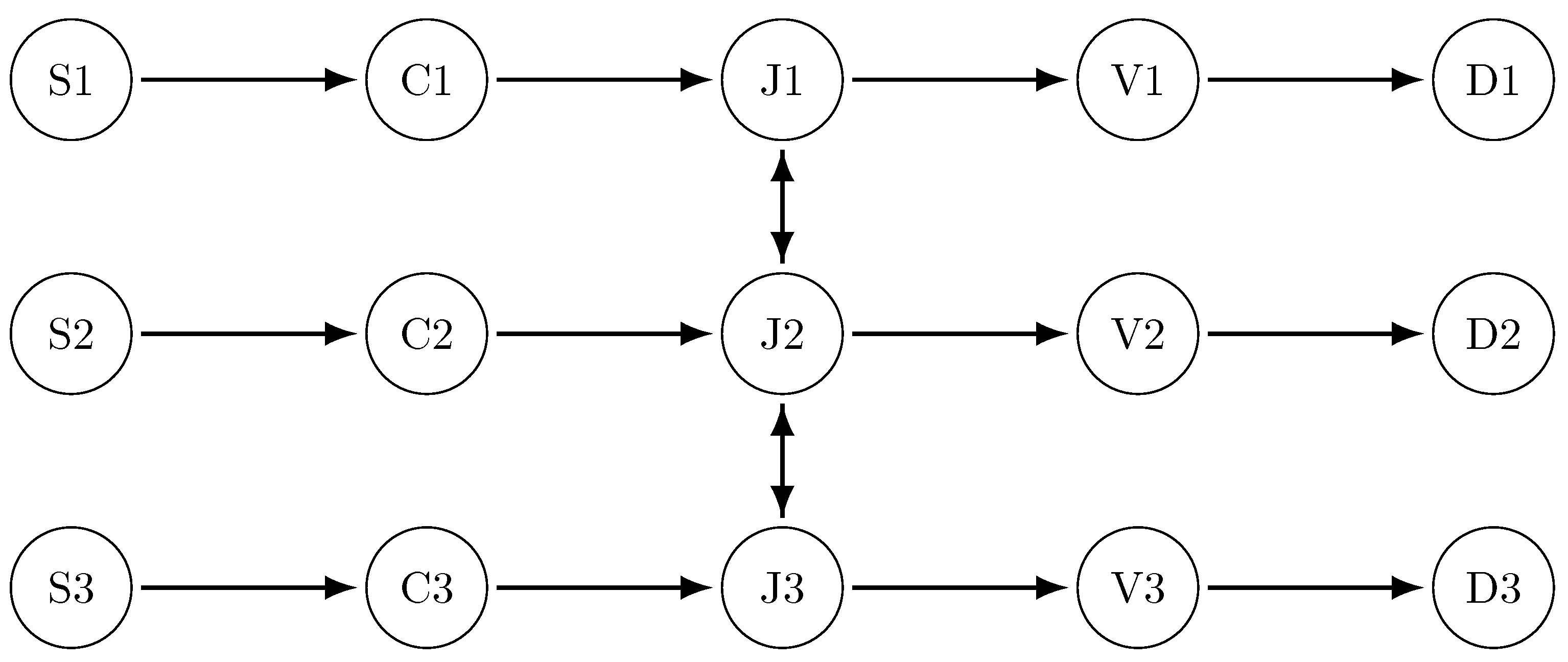
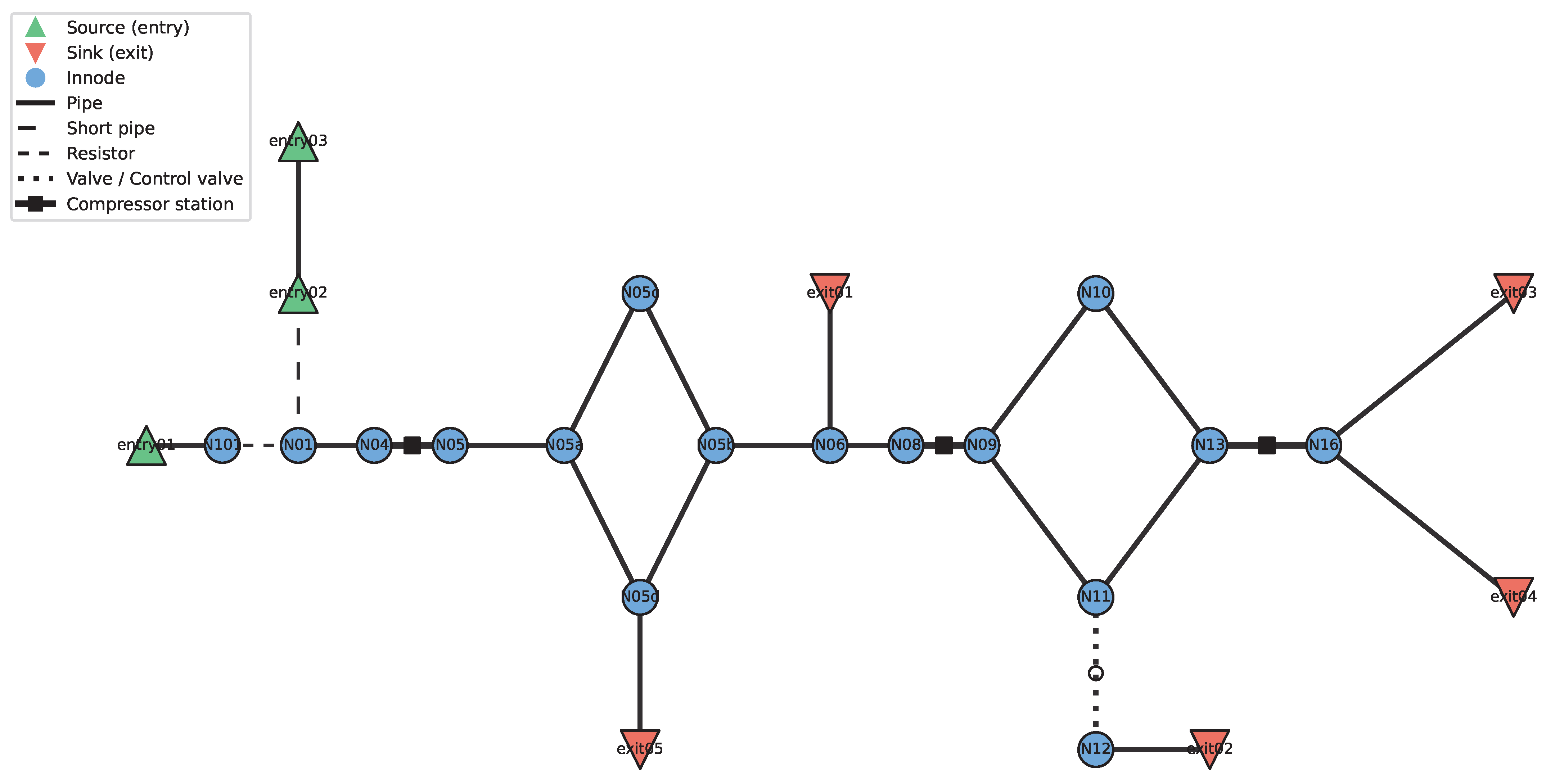
3.1. Network Topology and Hydraulic Modeling
3.1.1. Network Representation
3.1.2. Edge Flow Models
- = the mass (or standard volumetric) flow rate along edge e;
- , = the pressures at the upstream and downstream nodes, respectively.
- = symbol ensures that flow is directed from higher to lower pressure;
- = the composite hydraulic resistance, given by , where is the Darcy–Weisbach friction factor, is the internal diameter of the pipe, is the pipe length, and c is the isothermal speed of sound in the transported gas.
3.1.3. Nodal Pressure Dynamics
3.2. Control and Monitoring Mechanisms
3.2.1. Measurement Model
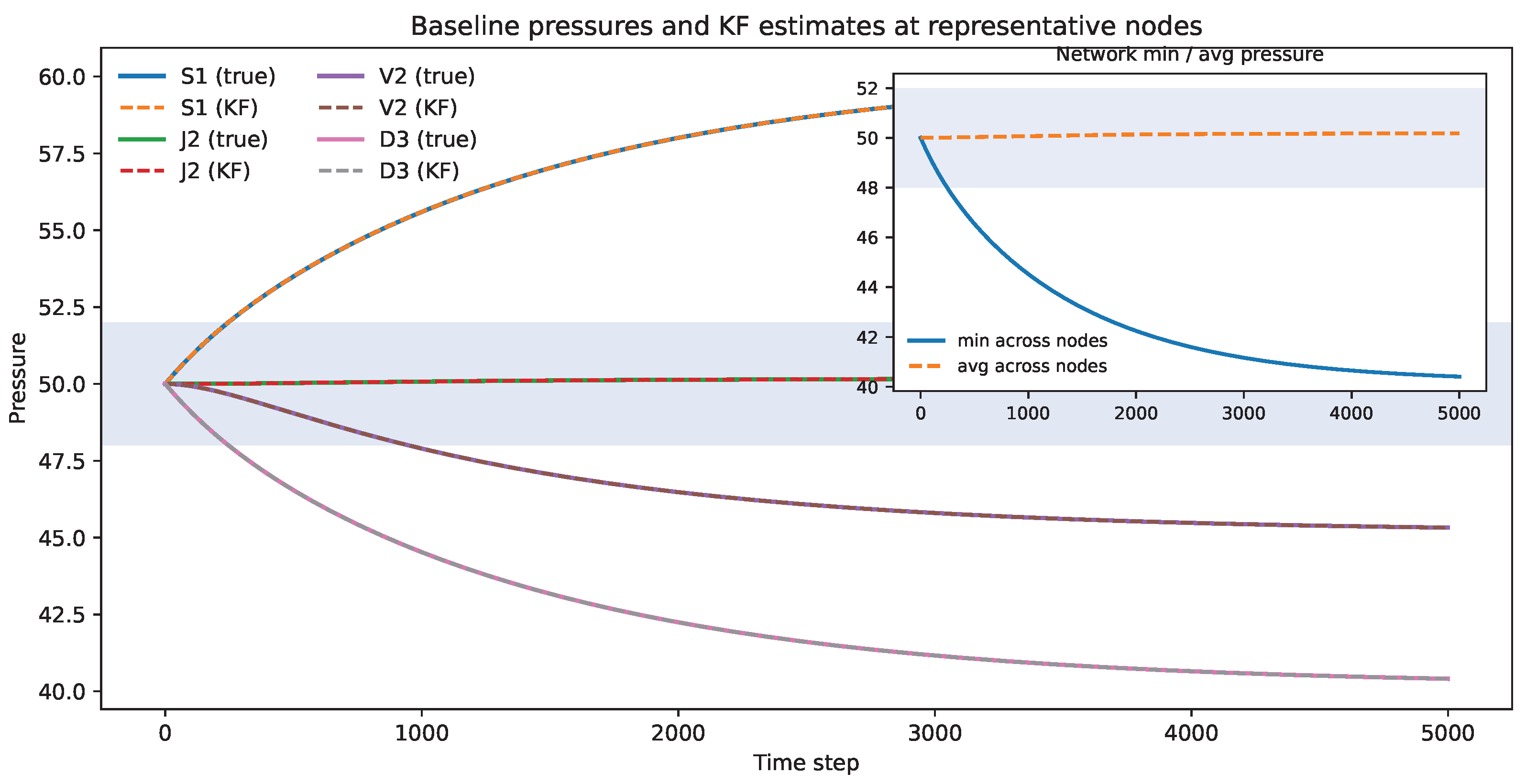
3.2.2. State Estimation
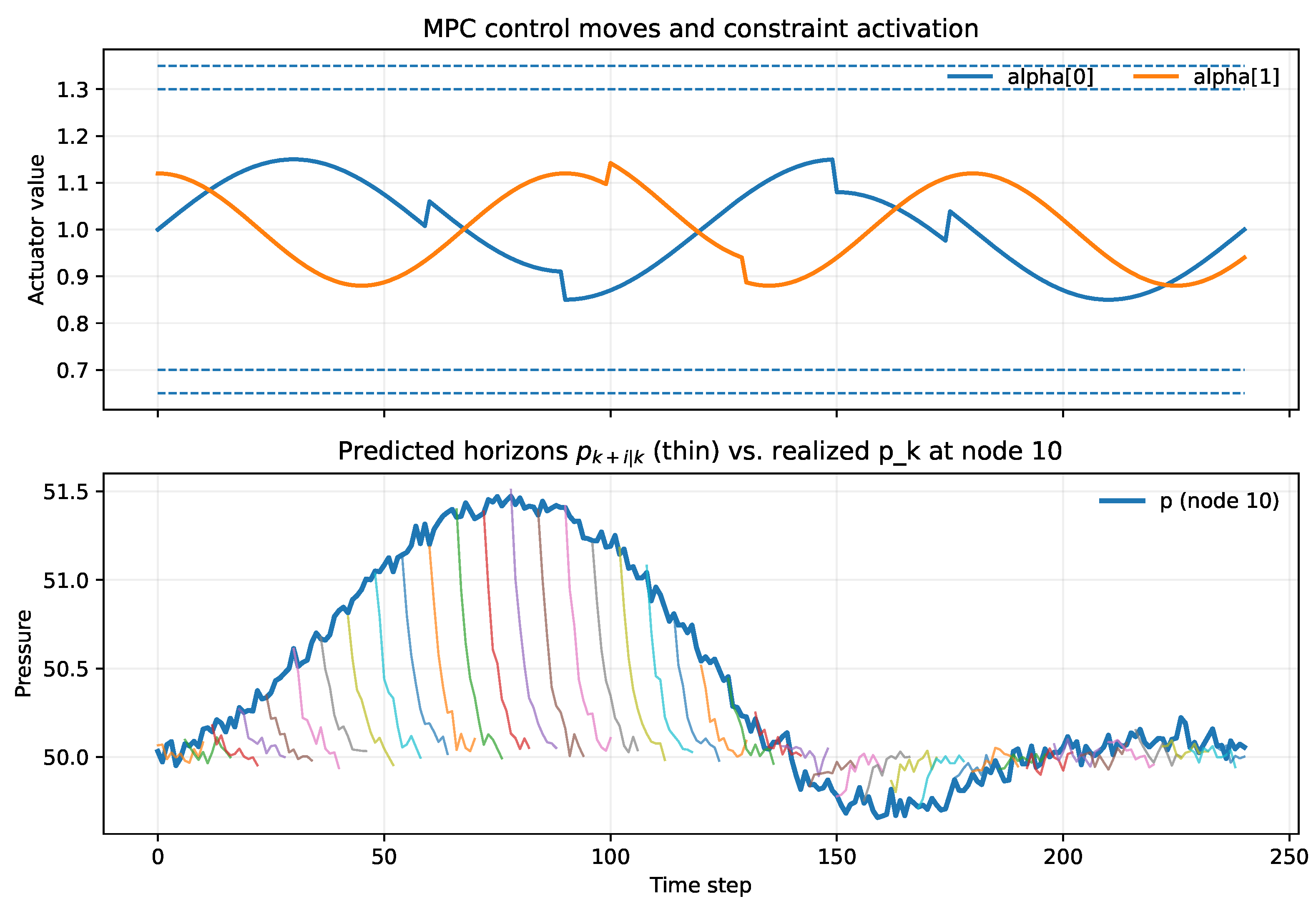
3.2.3. Control Strategy
3.3. Bilevel Attack–Control Formulation
3.4. Solving the Bilevel Attack and Control Problem
4. Case Studies
4.1. Case Study 1
4.1.1. Network Configuration and Parameter Settings
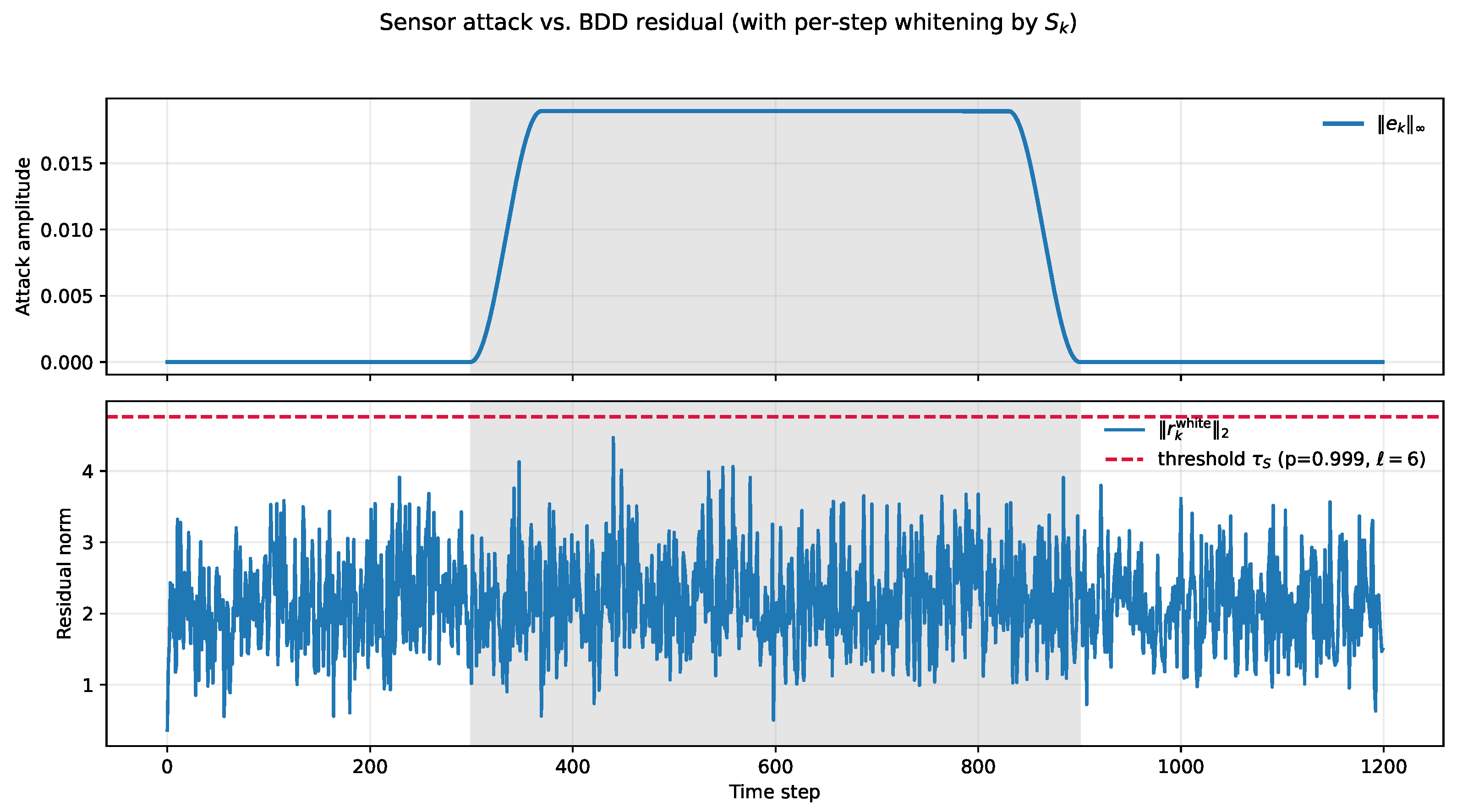
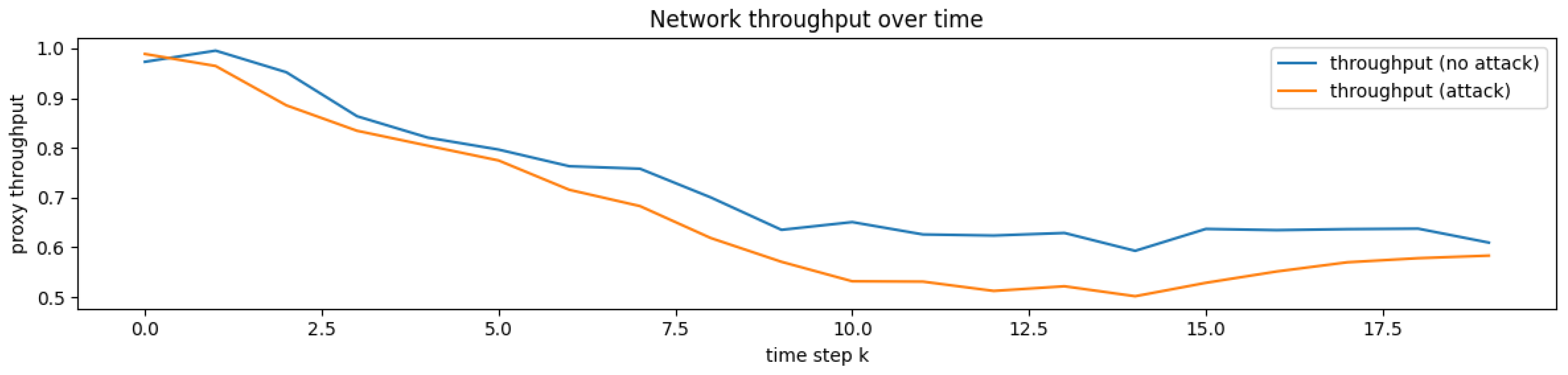
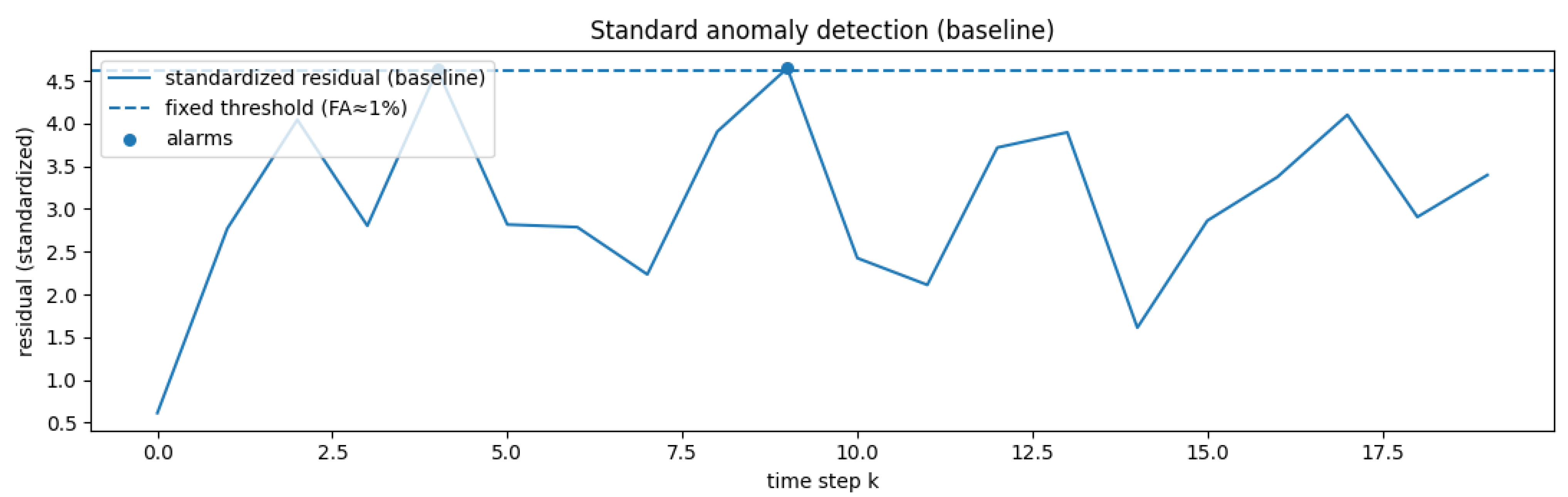
4.1.2. Results
4.2. Case Study 2
Network Configuration and Parameter Settings
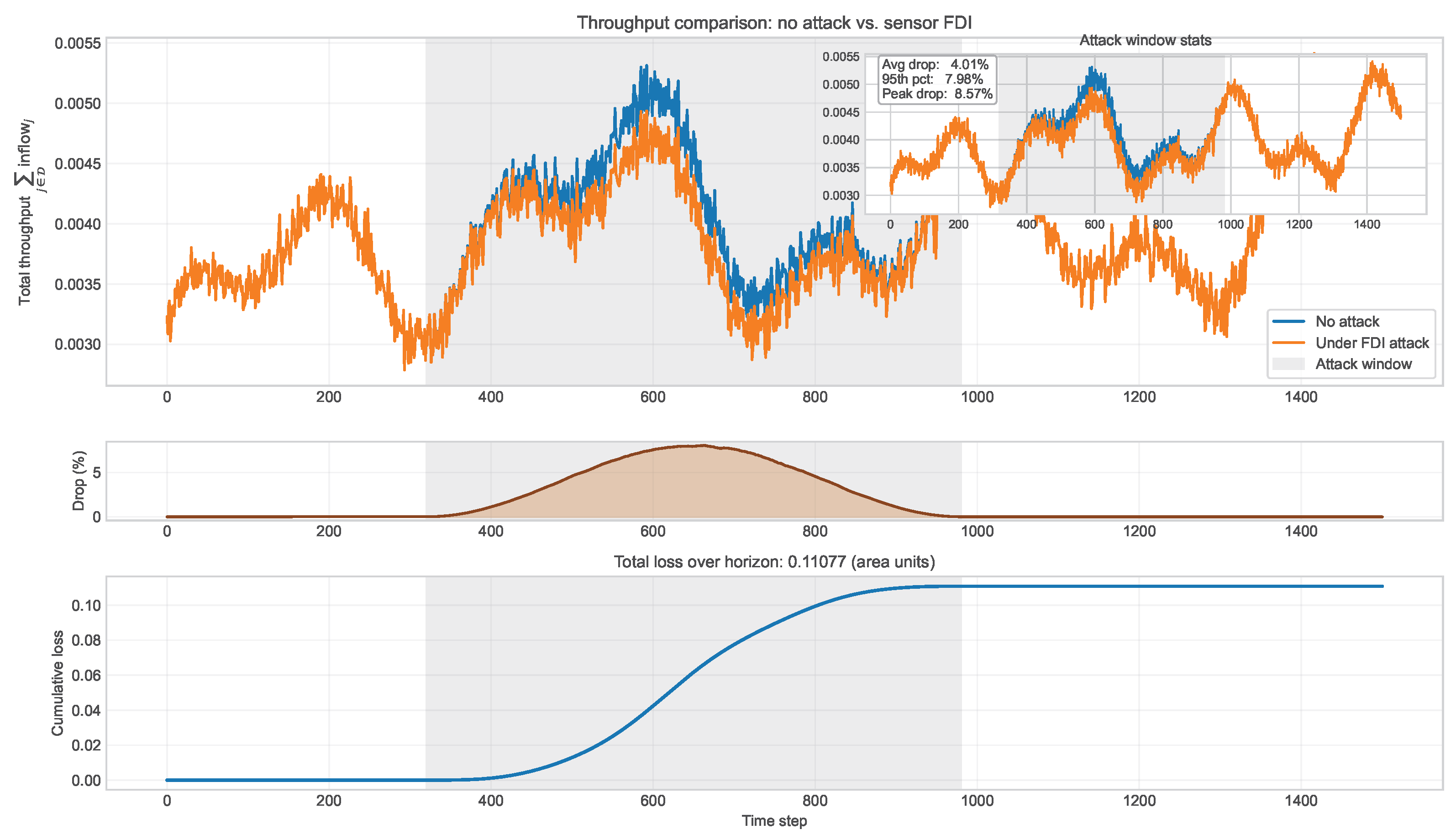
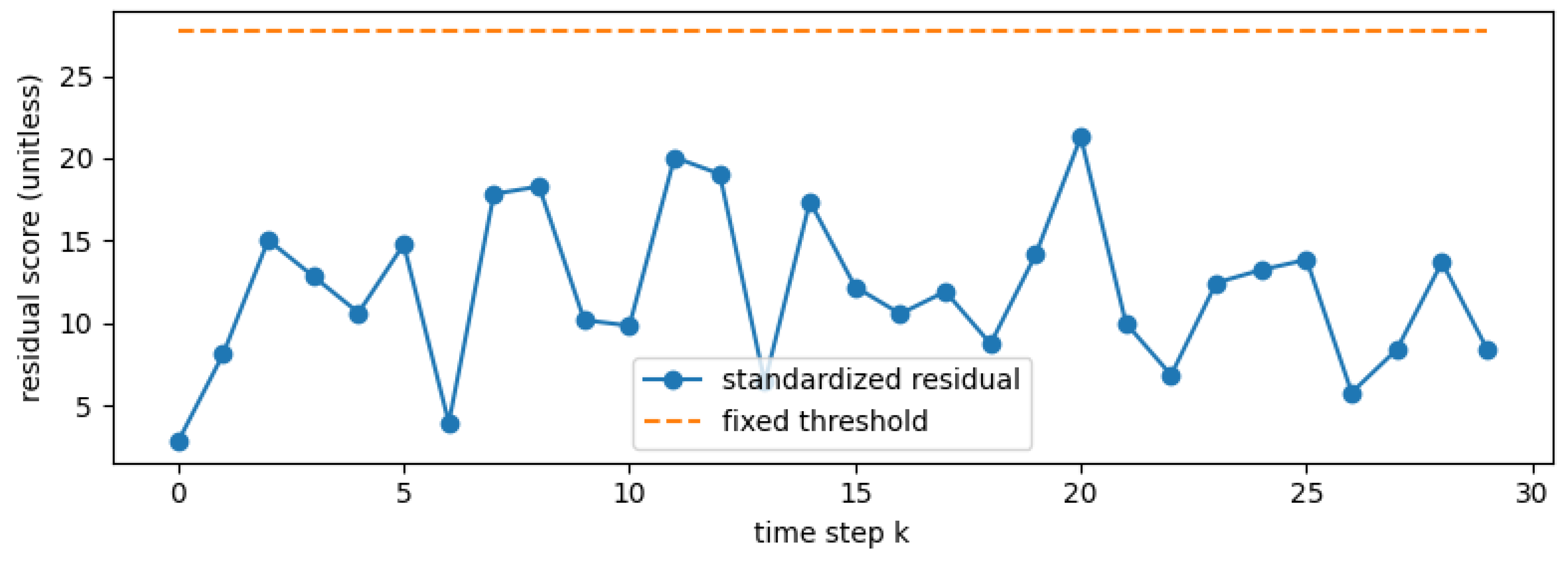
4.3. Results
4.4. Computational Performance and Scalability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, C.; Li, C.; Reniers, G.; Yang, F. Safety and security of oil and gas pipeline transportation: A systematic analysis of research trends and future needs using WoS. J. Clean. Prod. 2021, 279, 123583. [Google Scholar] [CrossRef]
- Enemosah, A.; Ifeanyi, O.G. SCADA in the Era of IoT: Automation, Cloud-driven Security, and Machine Learning Applications. Int. J. Sci. Res. Arch. 2024, 13, 3417–3435. [Google Scholar] [CrossRef]
- Kayan, H.; Nunes, M.; Rana, O.; Burnap, P.; Perera, C. Cybersecurity of Industrial Cyber-Physical Systems: A Review. arXiv 2021, arXiv:2101.03564. [Google Scholar] [CrossRef]
- Tsvetanov, T.; Slaria, S. The effect of the Colonial Pipeline shutdown on gasoline prices. Econ. Lett. 2021, 209, 110122. [Google Scholar] [CrossRef]
- Song, H.; Srinivasan, R.; Sookoor, T.; Jeschke, S. Smart Cities: Foundations, Principles, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Cybersecurity and Infrastructure Security Agency. Cybersecurity Best Practices for Smart Cities. U.S. Department of Homeland Security, 2023. Available online: https://www.cisa.gov/sites/default/files/2023-04/cybersecurity-best-practices-for-smart-cities_508.pdf (accessed on 1 August 2025).
- Alonso, R.; Haber, R.E.; Castaño, F.; Recupero, D.R. Interoperable software platforms for introducing artificial intelligence components in manufacturing: A meta-framework for security and privacy. Heliyon 2024, 10, e26446. [Google Scholar] [CrossRef]
- BBC News. San Francisco Transit System Hacked, Free Rides for All, 2016. Available online: https://www.bbc.com/news/technology-38127096 (accessed on 11 August 2025).
- Cybersecurity and Infrastructure Security Agency. DarkSide Ransomware: Best Practices for Preventing Business Disruption from Ransomware Attacks, 2021. Available online: https://www.cisa.gov/news-events/cybersecurity-advisories/aa21-131a (accessed on 11 August 2025).
- U.S. Department of Health and Human Services, Office for Civil Rights. Vermont Medical Center Ransomware Incident Report, 2020. Available online: https://ocrportal.hhs.gov/ocr/breach/breach_report.jsf (accessed on 11 August 2025).
- Reuters. Minnesota Calls in National Guard After St. Paul Slammed by ‘Digital Attack’, July 2025. Available online: https://www.reuters.com/world/us/minnesota-calls-national-guard-after-st-paul-slammed-by-digital-attack-2025-07-29/ (accessed on 11 August 2025).
- Sridhar, S.; Hahn, A.; Govindarasu, M. Cyber–Physical System Security for the Electric Power Grid. Proc. IEEE 2012, 100, 210–224. [Google Scholar] [CrossRef]
- Knowles, W.; Prince, D.D.C.; Hutchison, D.; Disso, J.F.P.; Jones, K. A Survey of Cyber Security Management in Industrial Control Systems. Int. J. Crit. Infrastruct. Prot. 2015, 9, 52–80. [Google Scholar] [CrossRef]
- Kosut, O.; Jia, L.; Thomas, R.J.; Tong, L. Malicious Data Attacks on the Smart Grid. IEEE Trans. Smart Grid 2011, 2, 645–658. [Google Scholar] [CrossRef]
- Teixeira, A.; Shames, I.; Sandberg, H.; Johansson, K.H. A Secure Control Framework for Resource-Limited Adversaries. Automatica 2015, 51, 135–148. [Google Scholar] [CrossRef]
- Langner, R. Stuxnet: Dissecting a Cyberwarfare Case. IEEE Secur. Priv. 2011, 9, 49–51. [Google Scholar] [CrossRef]
- Dibaji, S.M.; Pirani, M.; Flamholz, D.B.; Annaswamy, A.M.; Johansson, K.H.; Chakrabortty, A. A Systems and Control Perspective of Cyber–Physical Systems Security: A Survey of Recent Advances. Annu. Rev. Control 2019, 47, 394–411. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Dörfler, F.; Bullo, F. Attack Detection and Identification in Cyber–Physical Systems. IEEE Trans. Autom. Control 2013, 58, 2715–2729. [Google Scholar] [CrossRef]
- Osiadacz, A. Simulation of transient gas flows in networks. Int. J. Numer. Methods Fluids 1984, 4, 13–24. [Google Scholar] [CrossRef]
- Thorley, A.R.D.; Tiley, C.H. Unsteady and transient flow of compressible fluids in pipelines—A review of theoretical and some experimental studies. Int. J. Heat Fluid Flow 1987, 8, 3–15. [Google Scholar] [CrossRef]
- Osiadacz, A.J. Simulation and Analysis of Gas Networks; E. & F.N. Spon: London, UK, 1987. [Google Scholar]
- Chaczykowski, M. Transient flow in natural gas pipeline—The effect of pipeline thermal model. Appl. Math. Model. 2010, 34, 1051–1067. [Google Scholar] [CrossRef]
- Durgut, İ.; Leblebicioğlu, K. State estimation of transient flow in gas pipelines by a Kalman filter-based estimator. J. Nat. Gas Sci. Eng. 2016, 35, 189–196. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, Q.; Xie, W.; Wang, S. Enhanced Leak Detection and Localization in Liquid Pipelines Using an Improved Extended Kalman Filter. Processes 2025, 13, 1447. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Chaczykowski, M.; Sund, F.; Zarodkiewicz, P.; Hope, S.M. Gas composition tracking in transient pipeline flow. J. Nat. Gas Sci. Eng. 2018, 55, 321–330. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; Wiley-Interscience: Hoboken, NJ, USA, 2001. [Google Scholar]
- Bu, Y.; Swartz, C.L.E.; Wu, C. A two-level MPC method for the operation of a gas pipeline system under demand variation. Comput. Chem. Eng. 2024, 183, 108597. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, J.; Dubljevic, S. Tracking model predictive control and moving horizon estimation design of distributed parameter pipeline systems. Comput. Chem. Eng. 2023, 178, 108381. [Google Scholar] [CrossRef]
- Ghilardi, L.M.P.; Naik, S.; Martelli, E.; Casella, F.; Biegler, L.T. Economic Nonlinear Model Predictive Control for cyclic gas pipeline operation. Comput. Chem. Eng. 2025, 196, 109039. [Google Scholar] [CrossRef]
- Moetamedzadeh, H.R.; Khanmirza, E.; Pourfard, A.; Madoliat, R. Intelligent nonlinear model predictive control of gas pipeline networks. Trans. Inst. Meas. Control 2019, 41, 4569–4589. [Google Scholar] [CrossRef]
- Yadav, P.; Paul, K.; Shukla, S.; Panchal, H.; Tyagi, V.K. Architecture and security of SCADA systems: A review. Int. J. Crit. Infrastruct. Prot. 2021, 34, 100433. [Google Scholar] [CrossRef]
- Lu, Z.; She, Y.; Loewen, M. A Sensitivity Analysis of a Computer Model-Based Leak Detection System for Oil Pipelines. Energies 2017, 10, 1226. [Google Scholar] [CrossRef]
- Choubineh, A.; Wood, D.A.; Choubineh, Z. Applying separately cost-sensitive learning and Fisher’s discriminant analysis to address the class imbalance problem: A case study involving a virtual gas pipeline SCADA system. Int. J. Crit. Infrastruct. Prot. 2020, 29, 100357. [Google Scholar] [CrossRef]
- Alanazi, M.; Mahmood, A.; Chowdhury, M.J.U. SCADA vulnerabilities and attacks: A review of the state-of-the-art and open issues. Comput. Secur. 2023, 125, 103028. [Google Scholar] [CrossRef]
- Adegboye, M.A.; Fung, W.K.; Karnik, A. Recent Advances in Pipeline Monitoring and Oil Leakage Detection Technologies: Principles and Approaches. Sensors 2019, 19, 2548. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, C.; Liang, Y.; Liao, Q.; Li, Z.; Wang, B. Deeppipe: A Deep-Learning Method for Anomaly Detection of Multi-Product Pipelines. Energy 2022, 259, 125025. [Google Scholar] [CrossRef]
- Xu, L.; Xu, K.; Qin, Y.; Li, Y.; Huang, X.; Lin, Z.; Ye, N.; Ji, X. TGAN-AD: Transformer-Based GAN for Anomaly Detection of Time Series Data. Appl. Sci. 2022, 12, 8085. [Google Scholar] [CrossRef]
- Altaha, M.; Hong, S. Anomaly Detection for SCADA System Security Based on Unsupervised Learning and Function Codes Analysis in the DNP3 Protocol. Electronics 2022, 11, 2184. [Google Scholar] [CrossRef]
- Kim, B.; Alawami, M.A.; Kim, E.; Oh, S.; Park, J.; Kim, H. A Comparative Study of Time Series Anomaly Detection Models for Industrial Control Systems. Sensors 2023, 23, 1310. [Google Scholar] [CrossRef] [PubMed]
- An, L.; Yang, G.H. Secure State Estimation Against Sparse Sensor Attacks With Adaptive Switching Mechanism. IEEE Trans. Autom. Control 2018, 63, 2596–2603. [Google Scholar] [CrossRef]
- Nakahira, Y.; Mo, Y. Attack-Resilient H2, H∞, and ℓ1 State Estimator. IEEE Trans. Autom. Control 2018, 63, 4353–4360. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, D.; Johansson, K.H.; Shi, L. Optimal Linear Cyber-Attack on Remote State Estimation. IEEE Trans. Control Netw. Syst. 2017, 4, 4–13. [Google Scholar] [CrossRef]
- Isom, J.D.; Stamps, A.T.; Esmaili, A.; Mancilla, C. Two Methods of Data Reconciliation for Pipeline Networks. Comput. Chem. Eng. 2018, 115, 487–503. [Google Scholar] [CrossRef]
- Marino, A.; Zio, E. A Framework for the Resilience Analysis of Complex Natural Gas Pipeline Networks from a Cyber-Physical System Perspective. Comput. Ind. Eng. 2021, 162, 107727. [Google Scholar] [CrossRef]
- Rezazadeh, A.; Talarico, L.; Reniers, G.; Cozzani, V.; Zhang, L. Applying Game Theory for Securing Oil and Gas Pipelines Against Terrorism. Reliab. Eng. Syst. Saf. 2019, 191, 106140. [Google Scholar] [CrossRef]
- Fawzi, H.; Tabuada, P.; Diggavi, S. Secure Estimation and Control for Cyber–Physical Systems Under Adversarial Attacks. IEEE Trans. Autom. Control 2014, 59, 1454–1467. [Google Scholar] [CrossRef]
- Menon, E.S. Gas Pipeline Hydraulics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Schmidt, M.; Aßmann, D.; Burlacu, R.; Humpola, J.; Joormann, I.; Kanelakis, N.; Koch, T.; Oucherif, D.; Pfetsch, M.E.; Schewe, L.; et al. GasLib—A Library of Gas Network Instances. Data 2017, 2, 40. [Google Scholar] [CrossRef]
- de França Freire, J.L.; Gomes, M.R.R.; Gomes, M.G. Handbook of Pipeline Engineering; Springer Nature: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
| Physics and Network | ||
|---|---|---|
| Isothermal sound speed | c | 380 m s−1 |
| Friction factor (uniform) | 0.012 | |
| Pipe diameter (uniform) | 0.50 m | |
| Pipe length | 10 to 30 km | |
| Initial pressure (all nodes) | 3.5 MPa | |
| Limits | ||
| Pressure bounds | 2.0 MPa, 5.0 MPa | |
| Control bounds | compressor ratio ; valve opening | |
| Ramp limit (per step) | 0.05 | |
| Sensing and detection | ||
| Pressure sensors (count) | 6 | |
| Measurement noise (pressure) | , | |
| Process noise (pressure) | ||
| BDD residual threshold | 0.075 MPa | |
| Exogenous profiles and attack | ||
| External injections/withdrawals | piecewise constant, ∼10 kg s−1 | |
| Attack horizon | h | 32 steps (8 h) |
| Case | Baseline Mean [Units/s] | Attacked Mean [Units/s] | Mean Drop [%] | Peak Drop [%] | Median Drop [%] | Cumulative Loss [Area] |
|---|---|---|---|---|---|---|
| FDI | 0.004044 | 0.003876 | 4.15 | 8.57 | 4.02 | 0.110773 |
| Physics and Network | ||
|---|---|---|
| Isothermal sound speed | c | 350 ms−1 |
| Friction factor (typical) | 0.010–0.012 | |
| Pipe diameter (range) | 0.50–2.10 m | |
| Pipe length (range) | 10 m–100 km | |
| Initial pressure (all nodes) | 5.0 MPa | |
| Limits | ||
| Pressure bounds | 3.0 MPa, 7.0 MPa | |
| Control bounds | compressor ratio ; valve opening | |
| Ramp limit (per step) | 0.10 | |
| Sensing and detection | ||
| Pressure sensors (count) | 12 | |
| Measurement noise (pressure) | , | |
| Process noise (pressure) | (0.02 MPa)2 | |
| BDD residual threshold | 0.005 MPa | |
| Exogenous profiles and attack | ||
| External injections/withdrawals | piecewise constant, ∼5–15 kgs−1 | |
| Attack horizon | h | 20 steps |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katale, T.S.; Gao, L.; Zhang, Y.; Senouci, A. A Bilevel Optimization Framework for Adversarial Control of Gas Pipeline Operations. Actuators 2025, 14, 480. https://doi.org/10.3390/act14100480
Katale TS, Gao L, Zhang Y, Senouci A. A Bilevel Optimization Framework for Adversarial Control of Gas Pipeline Operations. Actuators. 2025; 14(10):480. https://doi.org/10.3390/act14100480
Chicago/Turabian StyleKatale, Tejaswini Sanjay, Lu Gao, Yunpeng Zhang, and Alaa Senouci. 2025. "A Bilevel Optimization Framework for Adversarial Control of Gas Pipeline Operations" Actuators 14, no. 10: 480. https://doi.org/10.3390/act14100480
APA StyleKatale, T. S., Gao, L., Zhang, Y., & Senouci, A. (2025). A Bilevel Optimization Framework for Adversarial Control of Gas Pipeline Operations. Actuators, 14(10), 480. https://doi.org/10.3390/act14100480






