Prescribed Performance Tracking Control for Nonlinear Stochastic Time-Delay Systems with Multiple Constraints
Abstract
1. Introduction
2. Problem Description and Preliminaries
2.1. Problem Description
2.2. Preliminaries
3. Solutions to Constraints
3.1. Input Saturation Constraint
3.2. Prescribed Performance Constraint
3.3. Asymmetric Time-Varying State Constraints
4. Adaptive Control Design and Stability Analysis
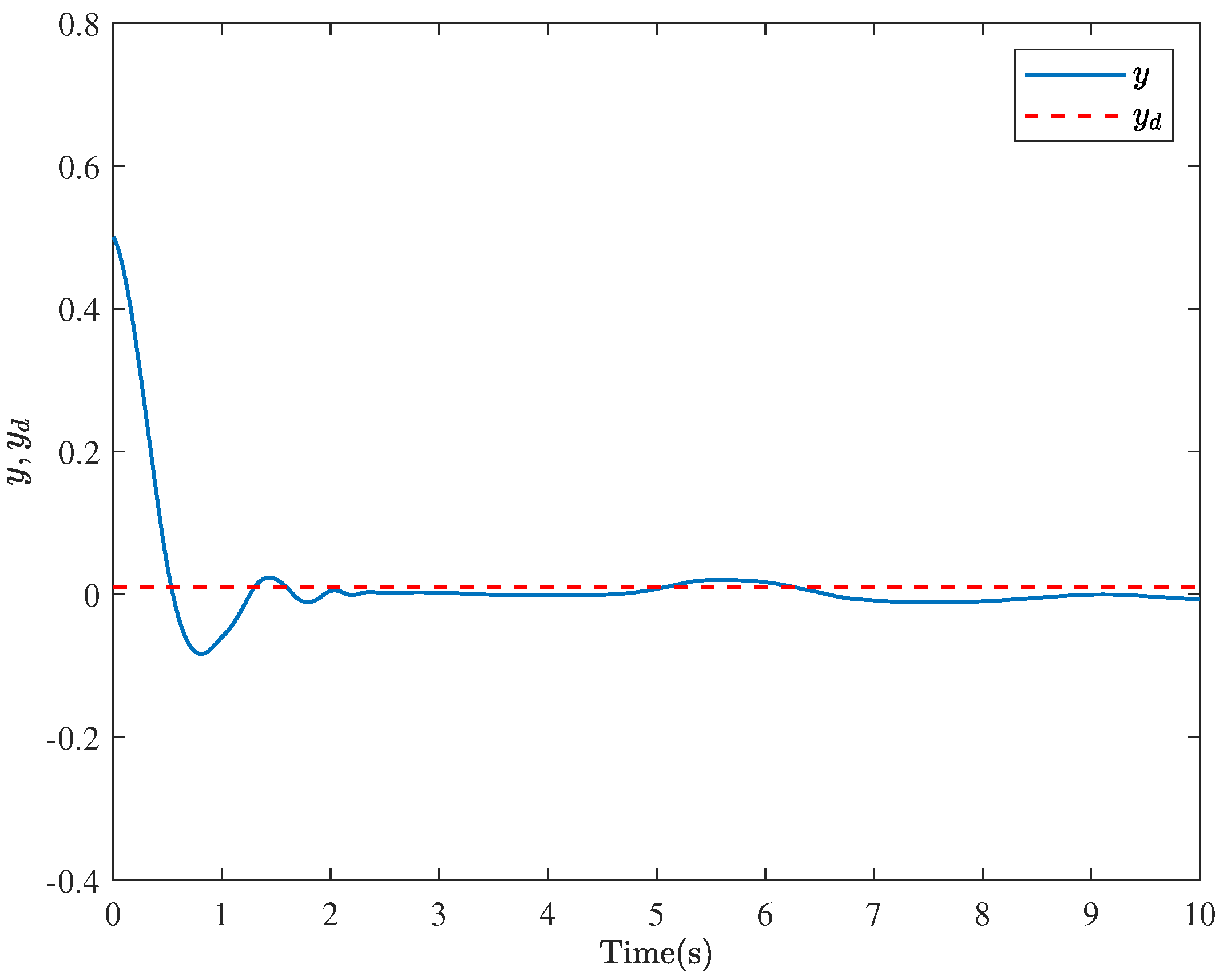
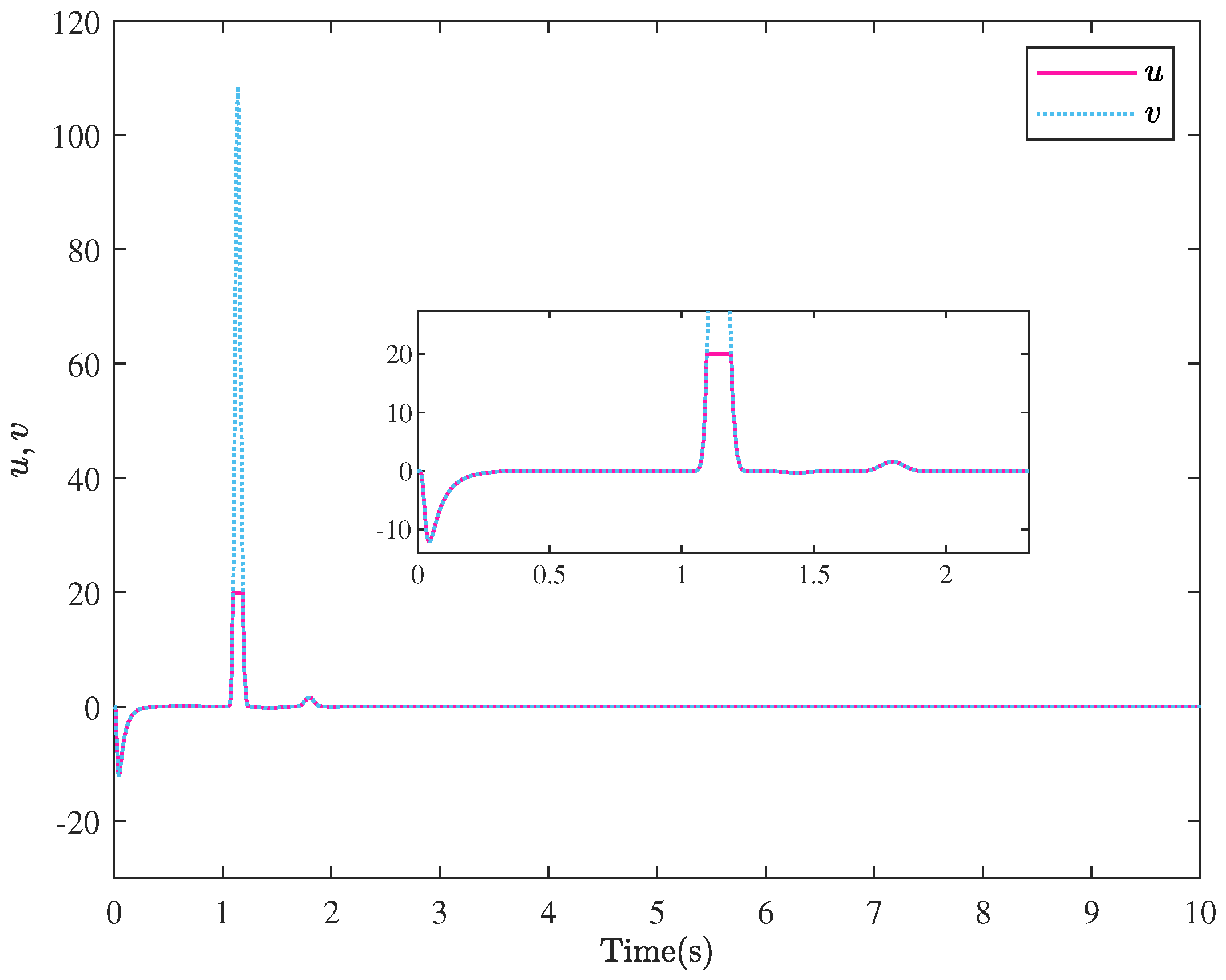
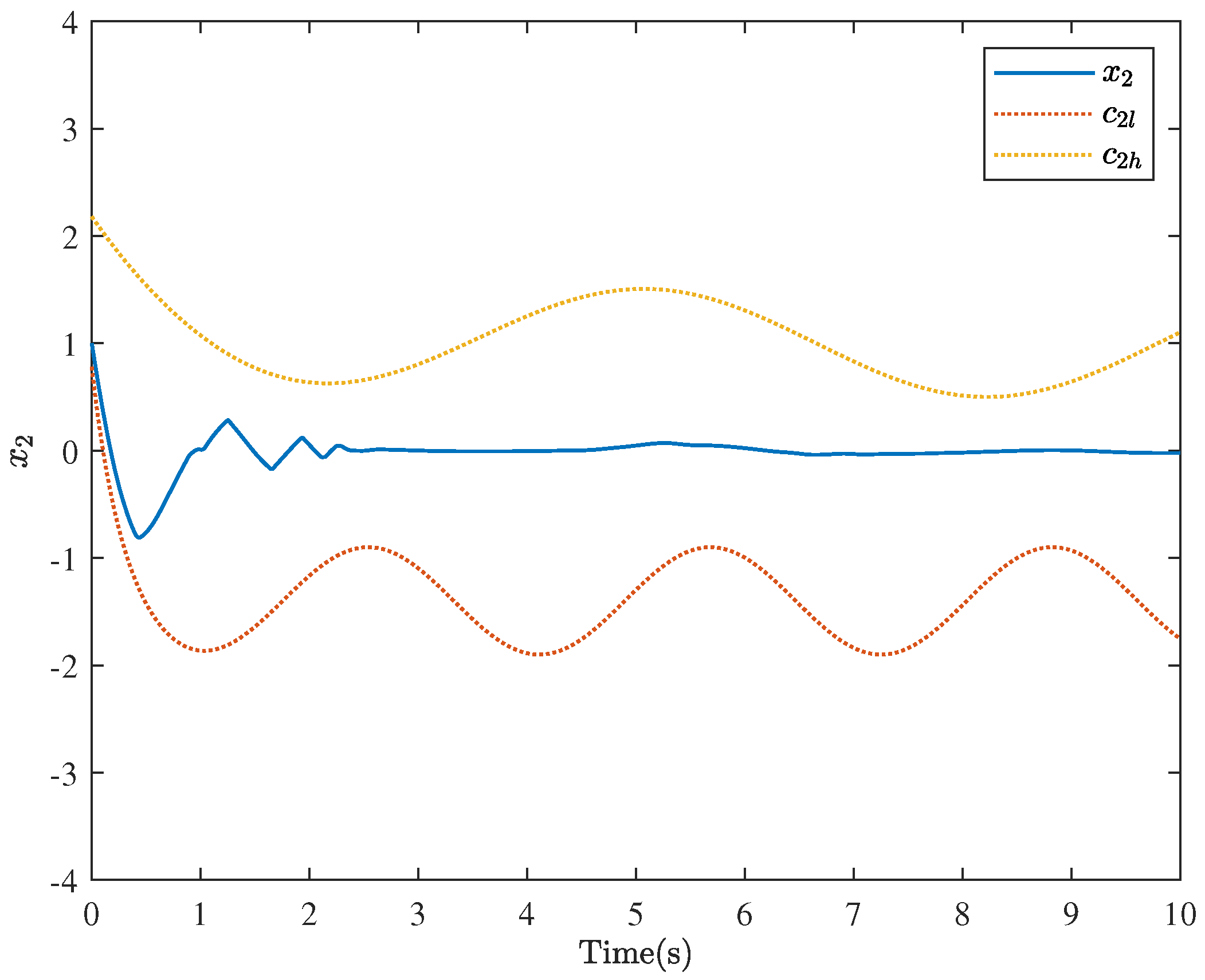
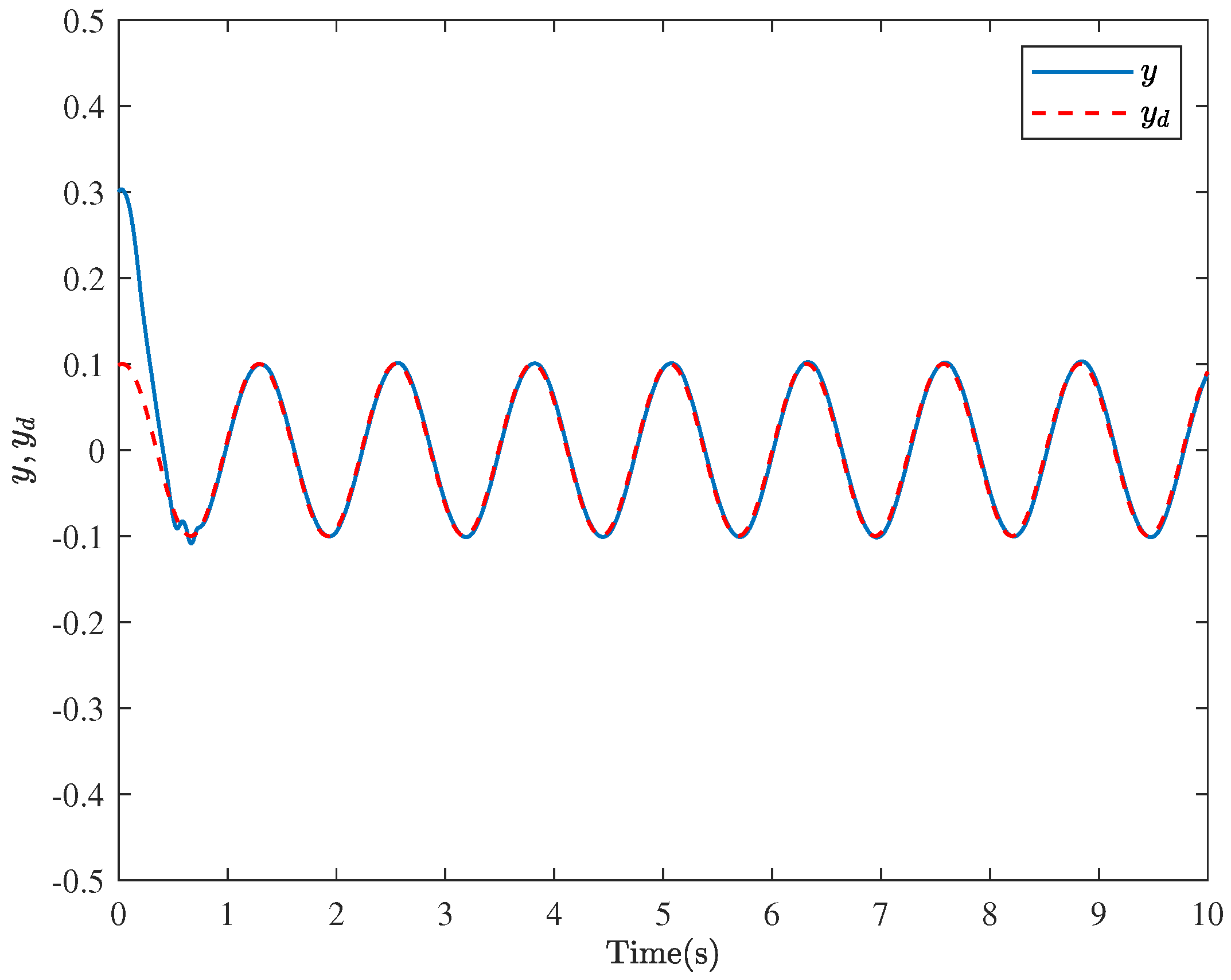
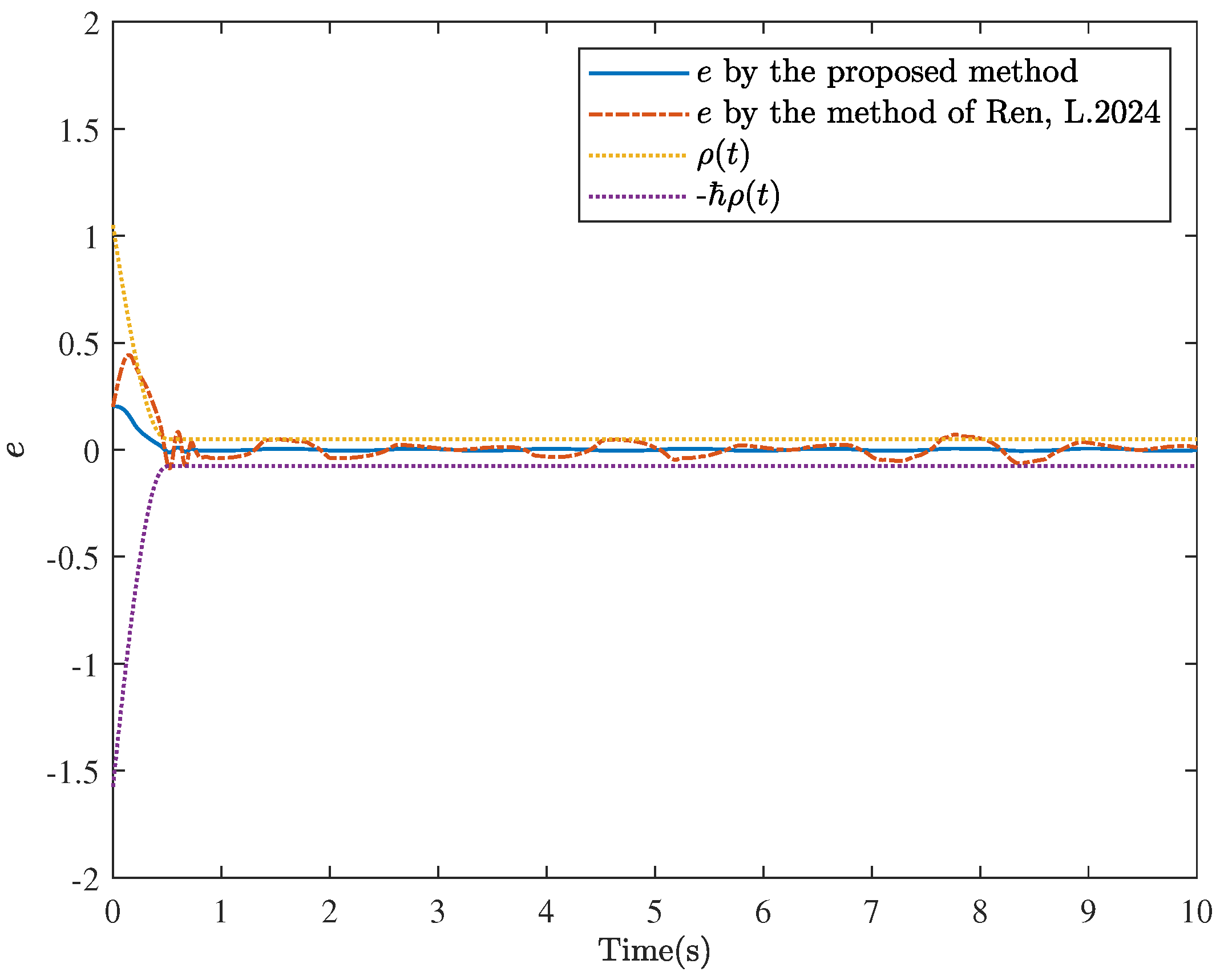
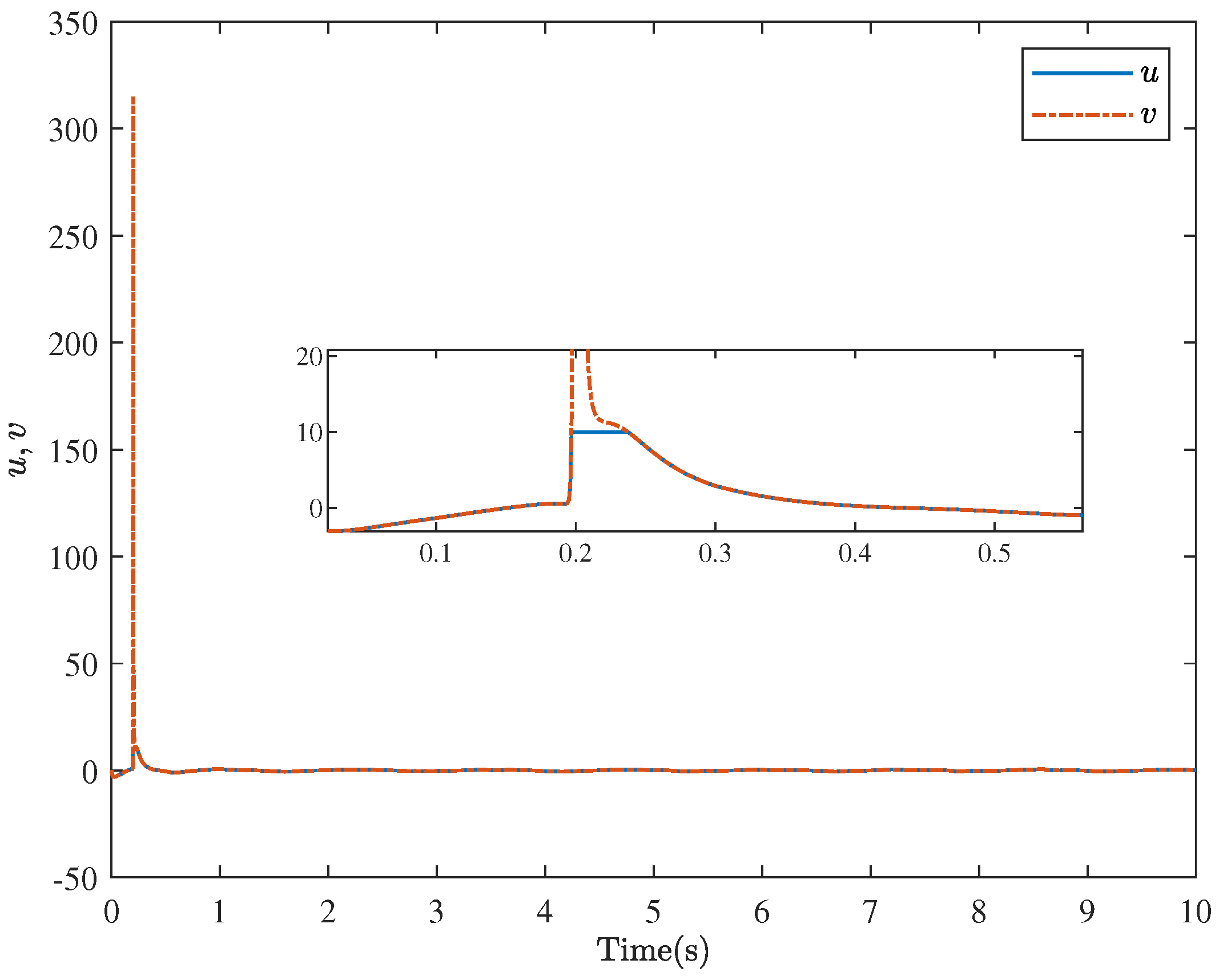
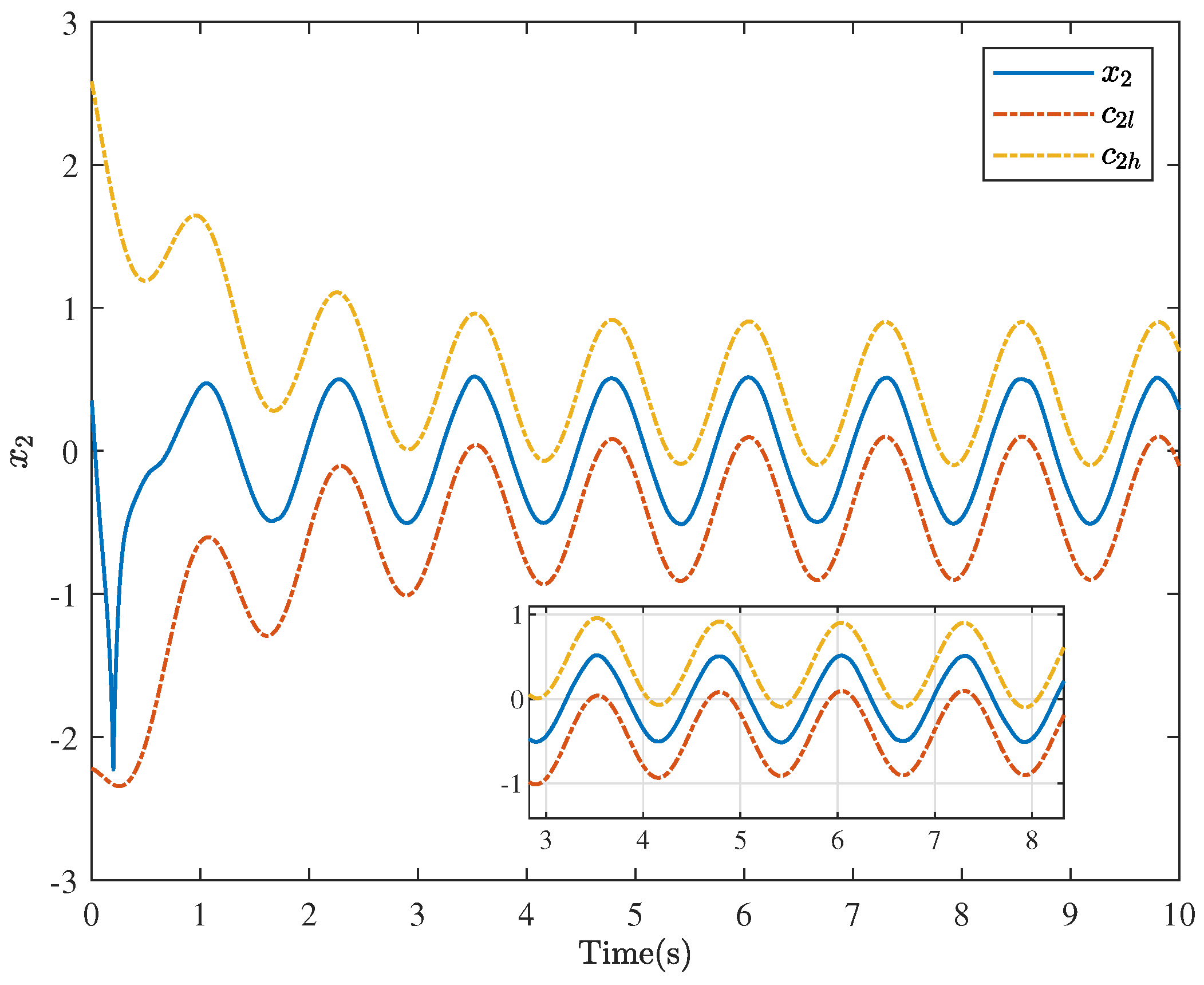
5. Simulation Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AlNemer, G.; Hosny, M.; Udhayakumar, R.; Elshenhab, A.M. Existence and hyers–ulam stability of stochastic delay systems governed by the rosenblatt process. Mathematics 2024, 12, 1729. [Google Scholar] [CrossRef]
- Zhu, Q.X. Stability analysis of stochastic delay differential equations with Lévy noise. J. Frankl. Inst. 2018, 118, 62–68. [Google Scholar] [CrossRef]
- Chen, H.; Shi, P.; Lim, C. Stability analysis for nonautonomous impulsive hybrid stochastic delay systems. Syst. Control. Lett. 2024, 187, 105785. [Google Scholar] [CrossRef]
- Min, H.; Xu, S.; Zhang, B.; Ma, Q. Globally adaptive control for stochastic nonlinear time-delay systems with perturbations and its application. Automatica 2019, 102, 105–110. [Google Scholar] [CrossRef]
- Fan, L.; Zhu, Q.; Zheng, W. Stability analysis of switched stochastic nonlinear systems with state-dependent delay. IEEE Trans. Autom. Control 2024, 69, 2567–2574. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, H.; Zhang, J.; Yu, L.; Sun, J. Multiple delay-dependent robust H∞ finite-time filtering for uncertain itô stochastic takagi–sugeno fuzzy semi-markovian jump systems with state constraints. IEEE Trans. Fuzzy Syst. 2020, 30, 321–331. [Google Scholar] [CrossRef]
- Ding, K.; Zhu, Q.; Zheng, W. Disturbance-observer-based finite-time antidisturbance control for Markov switched descriptor systems with multi-disturbances and intermittent measurements. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 2968–2981. [Google Scholar] [CrossRef]
- Ding, L.; Li, S.; Liu, Y.; Gao, H.; Chen, C.; Deng, Z. Adaptive neural network-based tracking control for full-state constrained wheeled mobile robotic system. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2410–2419. [Google Scholar] [CrossRef]
- Gao, H.; Song, X.; Ding, L.; Deng, Z. Adaptive tracking control of nonholonomic systems based on feedback error learning. Int. J. Robot. Autom. 2013, 28, 371–378. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Kang, Y. Adaptive robust coordinated control of multiple mobile manipulators interacting with rigid environments. Automatica 2010, 46, 2028–2034. [Google Scholar] [CrossRef]
- Jakobsen, H.A. Chemical Reactor Modeling, Multiphase Reactive Flows; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Mhaskar, P.; Kennedy, A.B. Robust model predictive control of nonlinear process systems: Handling rate constraints. Chem. Eng. Sci. 2008, 63, 366–375. [Google Scholar] [CrossRef]
- Tee, K.; Ge, S.; Tay, E. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Ren, B.; Ge, S.; Tee, K.; Lee, T. Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar] [PubMed]
- Guo, T.; Wu, X. Backstepping control for output-constrained nonlinear systems based on nonlinear mapping. Neural Comput. Appl. 2014, 25, 1665–1674. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, L.; Liu, L.; Tong, S.; Chen, C.P. Adaptive neural network learning controller design for a class of nonlinear systems with time-varying state constraints. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 66–75. [Google Scholar] [CrossRef]
- Liu, X.; Gao, C.; Wang, H.; Wu, L.; Yang, Y. Adaptive neural tracking control of full-state constrained nonstrict-feedback time-delay systems with input saturation. Int. J. Control. Autom. Syst. 2020, 18, 2048–2060. [Google Scholar] [CrossRef]
- Fang, L.; Ma, L.; Ding, S.; Park, J. Finite-time stabilization of high-order stochastic nonlinear systems with asymmetric output constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7201–7213. [Google Scholar] [CrossRef]
- Shu, Y. BLF-based neural dynamic surface control for stochastic nonlinear systems with time delays and full-state constraints. Int. J. Control 2024, 97, 982–998. [Google Scholar] [CrossRef]
- Vo, A.; Truong, T.; Kang, H.J.; Le, T. A fixed-time sliding mode control for uncertain magnetic levitation systems with prescribed performance and anti-saturation input. Eng. Appl. Artif. Intell. 2024, 133, 108373. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Y.; Zhang, O.; Chen, W.; Wang, J.; Gao, Y.; Liu, J. A novel faster fixed-time adaptive control for robotic systems with input saturation. IEEE Trans. Ind. Electron. 2024, 71, 5215–5223. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zhang, O.; Zhao, Y.; Chen, W.; Gao, Y. Adaptive disturbance observer-based fixed-time tracking control for uncertain robotic systems. IEEE Trans. Ind. Electron. 2024, 71, 14823–14831. [Google Scholar] [CrossRef]
- Hao, Y.; Fang, Z.; Liu, H. Adaptive T-S fuzzy synchronization for uncertain fractional-order chaotic systems with input saturation and disturbance. Inf. Sci. 2024, 666, 120423. [Google Scholar] [CrossRef]
- Shen, X.; Liu, J.; Liu, G.; Zhang, J.; Leon, J.; Wu, L.; Franquelo, L.G. Finite-time sliding mode control for NPC converters with enhanced disturbance compensation. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 1–10. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, S.; Chen, X.; Zhang, B. Fast finite-time control for a class of stochastic low-order nonlinear system with uncertainties. J. Frankl. Inst. 2024, 361, 106788. [Google Scholar] [CrossRef]
- Wang, D.; Ge, S.; Liang, X.; Li, D. Time-synchronized formation control of unmanned surface vehicles. IEEE Trans. Intell. Veh. 2024, 1–9. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, H.; Sun, Y.; Qin, H. Adaptive prescribed performance second-order sliding mode tracking control of autonomous underwater vehicle using neural network-based disturbance observer. Ocean Eng. 2022, 260, 111939. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Cabecinhas, D.; Pascoal, A.M.; Zhang, W. Prescribed performance path following control of USVs via an output-based threshold rule. IEEE Trans. Veh. Technol. 2024, 73, 6171–6182. [Google Scholar] [CrossRef]
- Lin, X.; Xu, R.; Yao, W.; Gao, Y.; Sun, G.; Liu, J.; Wu, L. Observer-Based prescribed performance speed control for PMSMs: A data-driven RBF neural network approach. IEEE Trans. Ind. Inform. 2024, 20, 7502–7512. [Google Scholar] [CrossRef]
- Chang, R.; Bai, Z.; Zhang, B.; Sun, C. Adaptive finite-time prescribed performance tracking control for unknown nonlinear systems subject to full-state constraints and input saturation. Int. J. Robust Nonlinear Control 2022, 32, 9347–9362. [Google Scholar] [CrossRef]
- Chang, R.; Hou, T.; Bai, Z.; Sun, C. Event-triggered adaptive tracking control for nonlinear systems with input saturation and unknown control directions. Int. J. Robust Nonlinear Control 2024, 34, 3891–3911. [Google Scholar] [CrossRef]
- Chang, R.; Liu, Y.; Chi, X.; Sun, C. Event-based adaptive formation and tracking control with predetermined performance for nonlinear multi-agent systems. Neurocomputing 2025, 611, 128660. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, G. Prescribed performance fault-tolerant control of nonlinear systems via actuator switching. IEEE Trans. Fuzzy Syst. 2024, 32, 1013–1022. [Google Scholar] [CrossRef]
- Shen, L.; Wang, H.; Yue, H. Prescribed performance adaptive fuzzy control for affine nonlinear systems with state constraints. IEEE Trans. Fuzzy Syst. 2022, 30, 5351–5360. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, J.; Lu, J.; Gui, W. Stability of stochastic time-delay systems involving delayed impulses. Automatica. 2023, 152, 110955. [Google Scholar] [CrossRef]
- Zhang, M.; Zhu, Q. Stability of stochastic delayed differential systems with average-random-delay impulses. J. Frankl. Inst. 2024, 361, 106777. [Google Scholar] [CrossRef]
- Li, Z.; Song, Y.; Li, X.; Zhou, B. On stability analysis of stochastic neutral-type systems with multiple delays. Automatica 2025, 171, 111905. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Cui, G.; Li, Z.; Hao, W. Finite-time distributed control of non-triangular stochastic nonlinear multi-agent systems with input constraints. Actuators 2023, 12, 28. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, B. Adaptive predefined time control for strict-feedback systems with actuator quantization. Actuators 2024, 13, 366. [Google Scholar] [CrossRef]
- Long, Z.; Zhou, W.; Fang, L.; Zhu, D. Fixed-Time stabilization of a class of stochastic nonlinear systems. Actuators 2023, 13, 3. [Google Scholar] [CrossRef]
- Ren, L.; Wu, J.; Liu, J. Dynamic event-triggered adaptive fixed-time fuzzy tracking control for stochastic nonlinear systems under asymmetric time-varying state constraints. Int. J. Fuzzy Syst. 2024, 26, 73–86. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Q. Event-triggered adaptive neural network control for stochastic nonlinear systems with state constraints and time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 1932–1944. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yin, S.; Zhang, L.; Yin, X.; Yan, H. Improved results on asymptotic stabilization for stochastic nonlinear time-delay systems with application to a chemical reactor system. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 195–204. [Google Scholar] [CrossRef]
- Hua, C.; Liu, P.X.; Guan, X. Backstepping control for nonlinear systems with time delays and applications to chemical reactor systems. IEEE Trans. Ind. Electron. 2009, 56, 3723–3732. [Google Scholar]
- Bolin, D.; Kovács, M.; Kumar, V.; Simas, A. Regularity and numerical approximation of fractional elliptic differential equations on compact metric graphs. Math. Comput. 2024, 93, 2439–2472. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Q.; Fan, X. Event-triggered adaptive fuzzy control for stochastic nonlinear time-delay systems. Fuzzy Sets Syst. 2023, 452, 42–60. [Google Scholar] [CrossRef]
- Lin, W.; Qian, C. Adaptive control of nonlinearly parameterized systems: The smooth feedback case. IEEE Trans. Autom. Control. 2002, 47, 1249–1266. [Google Scholar] [CrossRef]
- Wang, H.; Chen, B.; Lin, C. Adaptive neural tracking control for a class of stochastic nonlinear systems. Int. J. Robust Nonlinear Control 2014, 24, 1262–1280. [Google Scholar] [CrossRef]
- Ai, Z.; Wang, H.; Niu, B.; Zhao, X. Fuzzy adaptive fixed-time output feedback tracking control for stochastic nonlinear systems with unmodeled dynamics. IEEE Trans. Fuzzy Syst. 2024, 32, 4074–4085. [Google Scholar] [CrossRef]
- Shao, S.; An, Z.; Chen, M.; Zhao, Q. Resilient neural control based on event-triggered extended state observers and the application in unmanned aerial vehicles. IEEE Trans. Intell. Veh. 2023, 9, 930–943. [Google Scholar] [CrossRef]
- Kanellakopoulos, I.; Kokotovic, P.V.; Morse, A.S. Systematic design of adaptive controllers for feedback linearizable systems. In Proceedings of the 1991 American Control Conference, Boston, MA, USA, 26–28 June 1991; pp. 649–654. [Google Scholar]
- Wang, H.; Liu, K.; Liu, X.; Chen, B.; Lin, C. Neural-based adaptive output-feedback control for a class of nonstrict-feedback stochastic nonlinear systems. IEEE Trans. Cybern. 2015, 45, 1977–1987. [Google Scholar] [CrossRef]

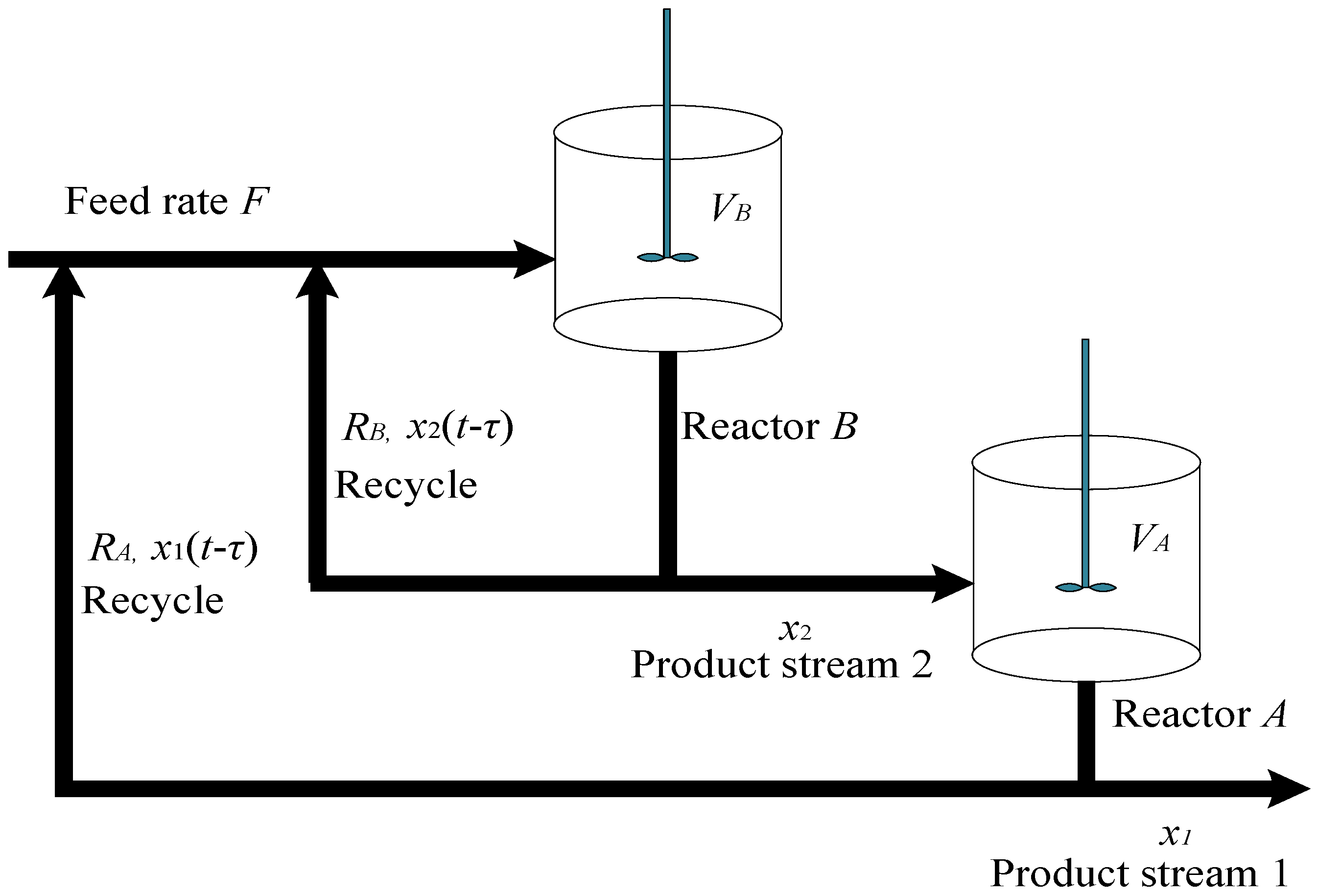

| Parameter | The Practical Significance | Value |
|---|---|---|
| Recirculation flow | 0.5 m3/s | |
| Recirculation flow | 0.6 m3/s | |
| Reactor residence time | 2 s | |
| Reactor residence time | 2 s | |
| Reaction constant | ||
| Reaction constant | ||
| Reaction volume | ||
| Reaction volume | 1 | |
| F | Feed rate | 0.5 m3/s |
| Different Methods | TMTE | TMSSE | TECT |
|---|---|---|---|
| The proposed method | 0.2 | 0.005 | 0.6 |
| The method of [41] | 0.442 | 0.05 | 1.525 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Chang, R.; Wang, Y. Prescribed Performance Tracking Control for Nonlinear Stochastic Time-Delay Systems with Multiple Constraints. Actuators 2025, 14, 19. https://doi.org/10.3390/act14010019
Zhang M, Chang R, Wang Y. Prescribed Performance Tracking Control for Nonlinear Stochastic Time-Delay Systems with Multiple Constraints. Actuators. 2025; 14(1):19. https://doi.org/10.3390/act14010019
Chicago/Turabian StyleZhang, Man, Ru Chang, and Ying Wang. 2025. "Prescribed Performance Tracking Control for Nonlinear Stochastic Time-Delay Systems with Multiple Constraints" Actuators 14, no. 1: 19. https://doi.org/10.3390/act14010019
APA StyleZhang, M., Chang, R., & Wang, Y. (2025). Prescribed Performance Tracking Control for Nonlinear Stochastic Time-Delay Systems with Multiple Constraints. Actuators, 14(1), 19. https://doi.org/10.3390/act14010019





