A Novel Design of Soft Corrugated Actuator for Creating Precise Head and Neck Positioning System
Abstract
1. Introduction
- A corrugated actuator design that can produce linear displacement in response to applied pressure, which can aid in the implementation of accurate closed-loop control.
- The development of a multi-actuator system that provides 4 DoF for head positioning during cancer treatment.
2. Materials and Methods
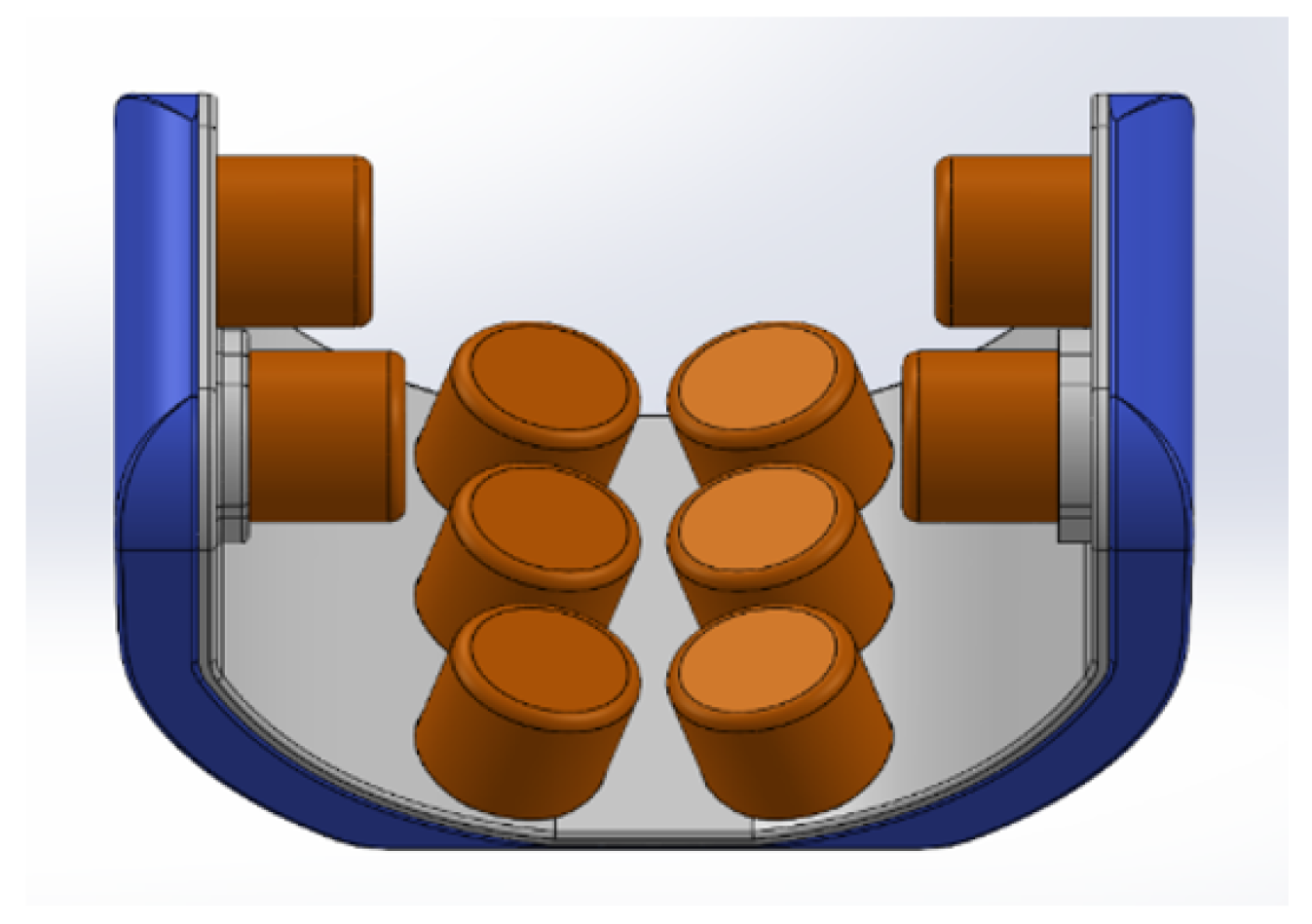
2.1. System Design
2.2. Single Actuator Design and Simulation Studies
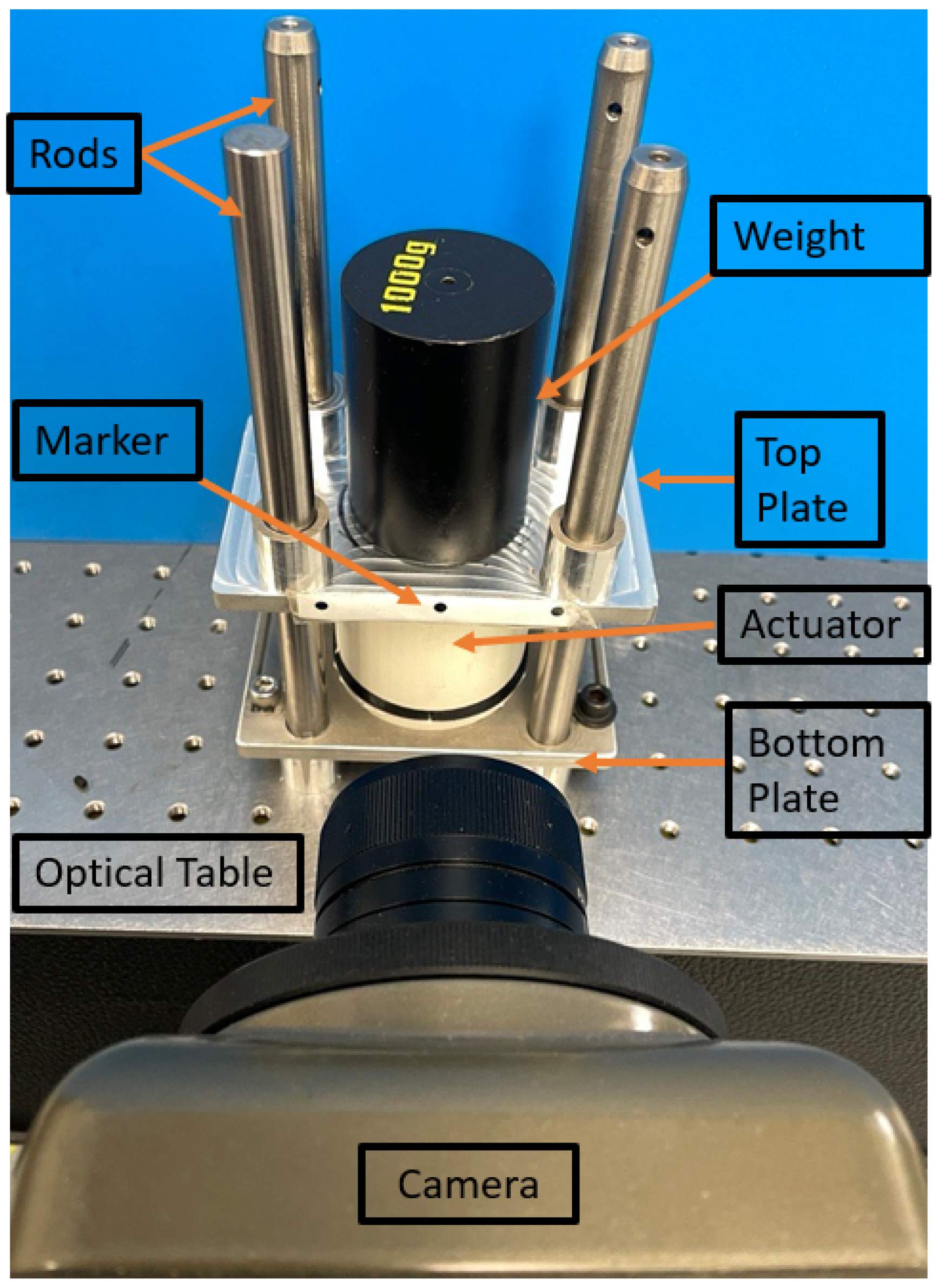
2.3. Single Actuator Fabrication and Experimental Setup
2.4. Single Actuator Modeling
- Data Collection;
- Exploratory Data Analysis and Data Pre-Processing;
- ML Model for Single Actuator.
2.4.1. Data Collection
2.4.2. Exploratory Data Analysis and Data Pre-Processing
- Statistical Overview: One fundamental metric examined is the Std Dev, which is used to measure the skewness of the dataset. This could affect the modeling of distance-based methods, such as K-Nearest Neighbor (KNN), discussed in Section 2.4.3. Notably, the weight parameter exhibits a relatively high Std Dev (605.619 g), indicating substantial dispersion among the collected data points. To address this, statistical log transformation is applied to the weight feature, which effectively reduced its Std Dev (1.626 g) [21].Here, denotes transformed weight, log denotes natural logarithm function, W denotes original weight values, and constant value 1 handles 0 g weight. Equation (1) shows statistical log transformation.
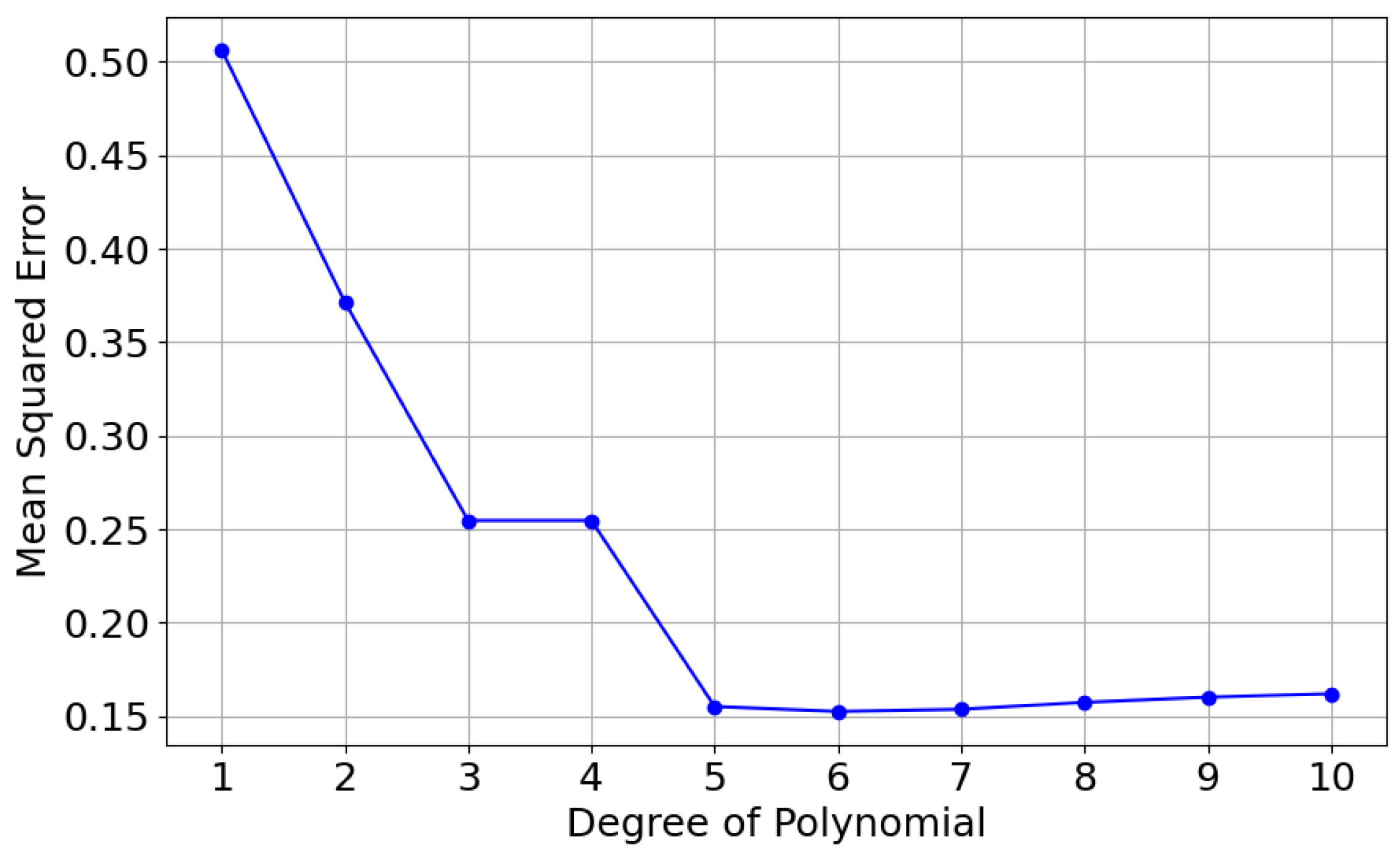
- Feature Analysis: The selection of the regression model and appropriate feature transformation is determined based on the relationship between each feature and the target variable. In our case, the two features (weight and displacement) and the target variable (pressure) are analyzed for their correlations to select the most suitable model.This analysis provides the basis for applying strategic polynomial feature transformation [22], which allows us to derive the interaction effects of weight and displacement features on pressure, leading to a better fit for the regression model.The optimal degree of the polynomial features is chosen using a grid search with cross-validation (GridSearchCV) [23] and regression modeling [24], with respect to weight and displacement, to find the degree with the least Mean Squared Error (MSE) in pressure prediction. Regression modeling is further substantiated in Section 2.4.3.From Figure 5, we can infer that polynomial degree 6 is the optimal degree for our model with the least MSE.
- Data Augmentation: To handle insufficient sample size that could lead to overfitting, in which the model performs well on the training set but poorly on unseen data, we employ the following techniques:
- (a)
- Bootstrapping: We augment the dataset to generate an additional 1619 records by iteratively selecting random samples from the original dataset and adding these samples back as new data, which expands the overall dataset size to the desired length [25].
- (b)
- Gaussian Noise: During model validation with unseen data, we observe instances where the model predicted identical pressure values for static weights that only differed in displacement. This behavior indicated overfitting. Gaussian noise [26] is introduced, thereby enabling model generalization, while preserving the statistical properties of the original dataset.
By applying Bootstrapping and introducing Gaussian noise, we are able to improve data quality and quantity, which will help produce effective actuator pressure predictions.
2.4.3. ML Model for Single Actuator
2.4.4. Model Evaluation
3. Application: Multi-Actuator H&N Positioning System
3.1. System Fabrication and Experimental Setup
3.2. Multi-Actuator System Model
4. Results
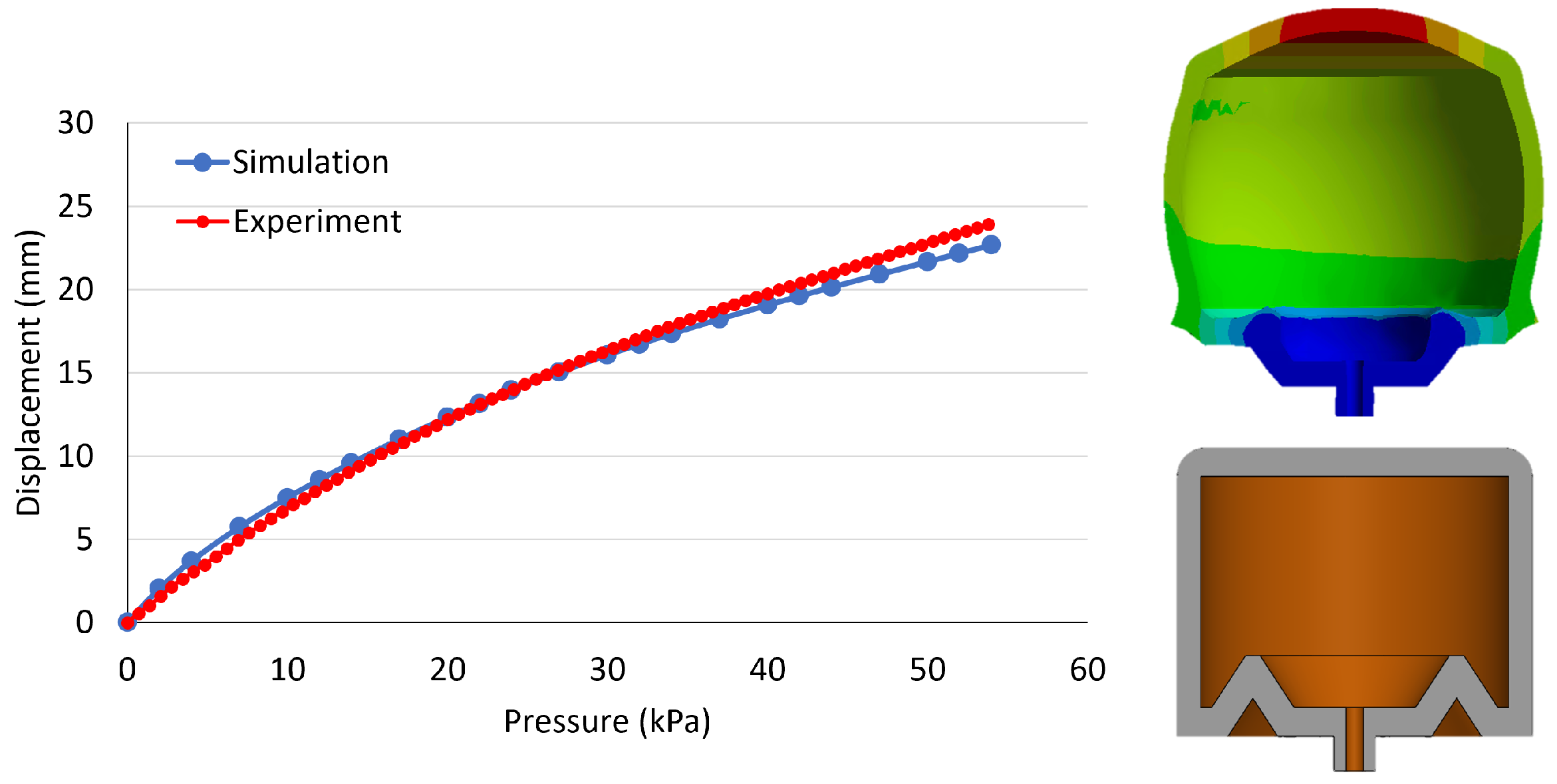
4.1. Single Actuator Simulation Validation
4.2. Single Actuator Model Validation
4.3. Multi-Actuator System Model Validation
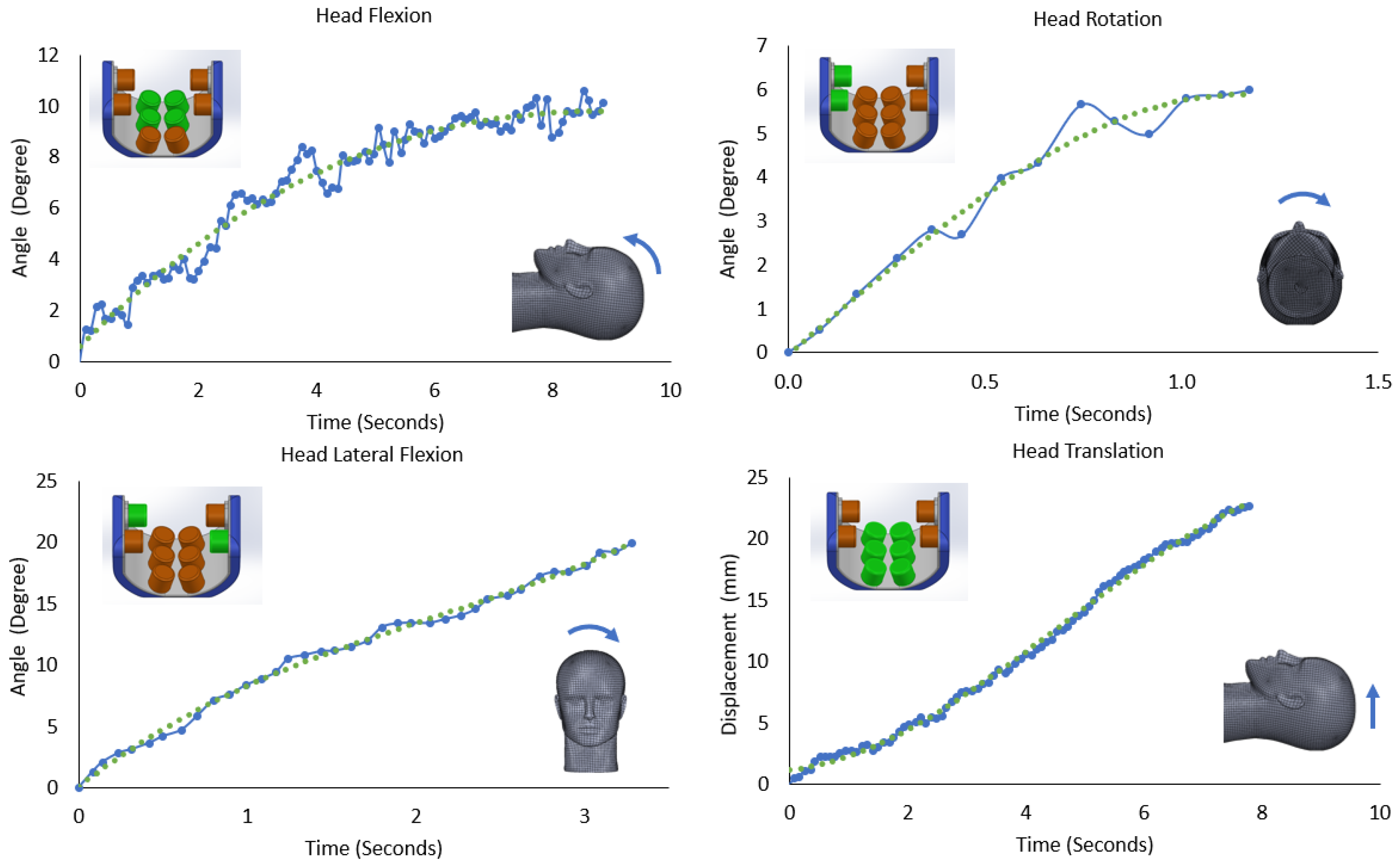
4.4. 4-DoF Multi-Actuator H&N Positioning System
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| DoF | Degrees of Freedom |
| H&N | Head and Neck |
| Std Dev | Standard Deviation |
| MSE | Mean Squared Error |
| KNN | K-Nearest Neighbor |
| SVD | Singular Value Decomposition |
| PCA | Principal Component Analysis |
References
- Skorina, E.H.; Onal, C.D. Soft Pneumatic Actuators: Modeling, Control, and Application. In Smart Materials: Considerations on Earth and in Space; Springer: Cham, Germany, 2022; pp. 129–219. [Google Scholar]
- Erel, V.; Singh, I.; Lindsay, A.R.; Shi, W.Y.; Wijesundara, M.B. Development and Characterization of a Modular Soft Actuator Enabled Elbow Exoskeleton for Assistive Movements. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85444, p. V08AT08A046. [Google Scholar]
- Singh, I.; Erel, V.; Gu, Y.; Lindsay, A.R.; Patterson, R.M.; Swank, C.; Wijesundara, M.B. Development of Soft Pneumatic Actuator Based Wrist Exoskeleton for Assistive Motion. In Proceedings of the 2023 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Seattle, WA, USA, 27 June–1 July 2023; pp. 359–366. [Google Scholar]
- Runciman, M.; Darzi, A.; Mylonas, G.P. Soft robotics in minimally invasive surgery. Soft Robot. 2019, 6, 423–443. [Google Scholar] [CrossRef] [PubMed]
- Xavier, M.S.; Tawk, C.D.; Zolfagharian, A.; Pinskier, J.; Howard, D.; Young, T.; Lai, J.; Harrison, S.M.; Yong, Y.K.; Bodaghi, M.; et al. Soft pneumatic actuators: A review of design, fabrication, modeling, sensing, control and applications. IEEE Access 2022, 10, 59442–59485. [Google Scholar] [CrossRef]
- Peng, Y.; Nabae, H.; Funabora, Y.; Suzumori, K. Peristaltic transporting device inspired by large intestine structure. Sens. Actuators A Phys. 2024, 365, 114840. [Google Scholar] [CrossRef]
- Peng, Y.; Sakai, Y.; Nakagawa, K.; Funabora, Y.; Aoyama, T.; Yokoe, K.; Doki, S. Funabot-Suit: A bio-inspired and McKibben muscle-actuated suit for natural kinesthetic perception. Biomim. Intell. Robot. 2023, 3, 100127. [Google Scholar] [CrossRef]
- Erel, V.; Lindsay, A.R.; Singh, I.; Wijesundara, M.B. Corrugated Diaphragm Actuator for Soft Robotic Applications. J. Mech. Des. 2022, 144, 045001. [Google Scholar] [CrossRef]
- Facing Cancer Head-On NIH. Available online: https://www.nidcr.nih.gov/news-events/nidcr-news/2024/facing-cancer-head (accessed on 5 August 2024).
- 2024 Head & Neck Cancer Data and Resources. Available online: https://www.nevadacancercoalition.org/blog/2024-head-neck-cancer-data-and-resources (accessed on 5 August 2024).
- Xing, L.; Lin, Z.X.; Donaldson, S.S.; Le, Q.T.; Tate, D.; Goffinet, D.R.; Wolden, S.; Ma, L.; Boyer, A.L. Dosimetric effects of patient displacement and collimator and gantry angle misalignment on intensity modulated radiation therapy. Radiother. Oncol. 2000, 56, 97–108. [Google Scholar] [CrossRef] [PubMed]
- Manning, M.A.; Wu, Q.; Cardinale, R.M.; Mohan, R.; Lauve, A.D.; Kavanagh, B.D.; Morris, M.M.; Schmidt-Ullrich, R.K. The effect of setup uncertainty on normal tissue sparing with IMRT for head-and-neck cancer. Int. J. Radiat. Oncol. Biol. Phys. 2001, 51, 1400–1409. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Akpati, H.C.; Li, J.G.; Liu, C.R.; Amdur, R.J.; Palta, J.R. An immobilization system for claustrophobic patients in head-and-neck intensity-modulated radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 2004, 59, 1531–1539. [Google Scholar] [CrossRef] [PubMed]
- Cerviño, L.I.; Detorie, N.; Taylor, M.; Lawson, J.D.; Harry, T.; Murphy, K.T.; Mundt, A.J.; Jiang, S.B.; Pawlicki, T.A. Initial clinical experience with a frameless and maskless stereotactic radiosurgery treatment. Pract. Radiat. Oncol. 2012, 2, 54–62. [Google Scholar] [CrossRef] [PubMed]
- Cervino, L.I.; Pawlicki, T.; Lawson, J.D.; Jiang, S.B. Frame-less and mask-less cranial stereotactic radiosurgery: A feasibility study. Phys. Med. Biol. 2010, 55, 1863. [Google Scholar] [CrossRef] [PubMed]
- Wiersma, R.D.; Wen, Z.; Sadinski, M.; Farrey, K.; Yenice, K.M. Development of a frameless stereotactic radiosurgery system based on real-time 6D position monitoring and adaptive head motion compensation. Phys. Med. Biol. 2009, 55, 389. [Google Scholar] [CrossRef] [PubMed]
- Ogunmolu, O.; Kulkarni, A.; Tadesse, Y.; Gu, X.; Jiang, S.; Gans, N. Soft-NeuroAdapt: A 3-DOF neuro-adaptive patient pose correction system for frameless and maskless cancer radiotherapy. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3661–3668. [Google Scholar]
- Ogunmolu, O.; Liu, X.; Gans, N.; Wiersma, R.D. Mechanism and model of a soft robot for head stabilization in cancer radiation therapy. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4609–4615. [Google Scholar]
- Available online: https://www.smooth-on.com/products/pmc-724/ (accessed on 10 September 2024).
- Blaber, J.; Adair, B.; Antoniou, A. Ncorr: Open-source 2D digital image correlation matlab software. Exp. Mech. 2015, 55, 1105–1122. [Google Scholar] [CrossRef]
- Benoit, K. Linear regression models with logarithmic transformations. Lond. Sch. Econ. Lond. 2011, 22, 23–36. [Google Scholar]
- Deprez, M.; Robinson, E.C. Machine Learning for Biomedical Applications: With Scikit-Learn and PyTorch; Elsevier Science: Amsterdam, The Netherlands, 2023. [Google Scholar]
- VanderPlas, J. Python Data Science Handbook: Essential Tools for Working with Data; O’Reilly Media: Sebastopol, CA, USA, 2017. [Google Scholar]
- Ostertagová, E. Modelling using polynomial regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Overfitting, model tuning, and evaluation of prediction performance. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Cham, Germany, 2022; pp. 109–139. [Google Scholar]
- Arslan, M.; Guzel, M.; Demirci, M.; Ozdemir, S. SMOTE and gaussian noise based sensor data augmentation. In Proceedings of the 2019 4th International Conference on Computer Science and Engineering (UBMK), Samsun, Turkey, 11–15 September 2019; pp. 1–5. [Google Scholar]
- Fonti, V.; Belitser, E. Feature selection using lasso. Amst. Res. Pap. Bus. Anal. 2017, 30, 1–25. [Google Scholar]
- Hackeling, G. Mastering Machine Learning with Scikit-Learn; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]




| Dimensions | Actuator |
|---|---|
| (mm) | 50 |
| (mm) | 14 |
| (mm) | 60 |
| (mm) | 30 |
| (mm) | 4 |
| (mm) | 5 |
| (degree) | 65° |
| Model | Mean Squared Error | R2 Score |
|---|---|---|
| Polynomial Regression | 0.1538 | 0.9050 |
| KNN-CV | 0.1015 | 0.9914 |
| Weight (g) | Expansion from Experiment (mm) | Expansion from Simulation (mm) | Expansion Deviation (mm) |
|---|---|---|---|
| 0 | 22.66 | 22.05 | 0.61 |
| 500 | 21.22 | 20.68 | 0.54 |
| 1000 | 19.98 | 19.67 | 0.31 |
| 1500 | 18.89 | 18.35 | 0.54 |
| 2000 | 17.40 | 17.13 | 0.27 |
| Input Weight (g) | Input Displacement (mm) | Predicted Pressure (kPa) | Experimentally Measured Displacement (mm) | Displacement Deviation (mm) |
|---|---|---|---|---|
| 300 | 6 | 16.88 | 6 | 0 |
| 600 | 10 | 33.14 | 11 | 1 |
| 700 | 4 | 15.02 | 3 | 1 |
| 950 | 2 | 16.81 | 2 | 0 |
| 1000 | 2.5 | 33.27 | 2 | 0.5 |
| 1500 | 7.5 | 15.02 | 7 | 0.5 |
| 1800 | 4 | 16.95 | 3 | 1 |
| 2000 | 10 | 15.09 | 9 | 1 |
| Predicted P1 (kPa) | Predicted P2 (kPa) | Target Angle (degree) | Measured Angle (degree) |
|---|---|---|---|
| 17.01 | 24.52 | 2.00° | 1.79° |
| 32.52 | 35.96 | 4.00° | 3.78° |
| 35.75 | 53.32 | 6.00° | 5.50° |
| 51.88 | 62.01 | 8.00° | 7.62° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erel, V.; Suresh, S.; Singh, I.; Palomino, A.; Tafannum, F.; Hosseini Nami, S.; Jiang, S.; Peng, H.; Gans, N.; Wijesundara, M.B.J. A Novel Design of Soft Corrugated Actuator for Creating Precise Head and Neck Positioning System. Actuators 2024, 13, 351. https://doi.org/10.3390/act13090351
Erel V, Suresh S, Singh I, Palomino A, Tafannum F, Hosseini Nami S, Jiang S, Peng H, Gans N, Wijesundara MBJ. A Novel Design of Soft Corrugated Actuator for Creating Precise Head and Neck Positioning System. Actuators. 2024; 13(9):351. https://doi.org/10.3390/act13090351
Chicago/Turabian StyleErel, Veysel, Sanjana Suresh, Inderjeet Singh, Allison Palomino, Faiza Tafannum, Seyedehhelya Hosseini Nami, Steve Jiang, Hao Peng, Nicholas Gans, and Muthu B. J. Wijesundara. 2024. "A Novel Design of Soft Corrugated Actuator for Creating Precise Head and Neck Positioning System" Actuators 13, no. 9: 351. https://doi.org/10.3390/act13090351
APA StyleErel, V., Suresh, S., Singh, I., Palomino, A., Tafannum, F., Hosseini Nami, S., Jiang, S., Peng, H., Gans, N., & Wijesundara, M. B. J. (2024). A Novel Design of Soft Corrugated Actuator for Creating Precise Head and Neck Positioning System. Actuators, 13(9), 351. https://doi.org/10.3390/act13090351










