Research on the Control Method of a 2DOF Parallel Platform Based on Electromagnetic Drive

Abstract

In this paper, a spatial two-degree-of-freedom (2DOF) parallel platform based on electromagnetic redundant drive and its control method are investigated. The platform is redundantly driven by three electromagnetic-spring conforming branched chains, and the design provides better flexibility and responsiveness than conventional parallel structures. The introduction of the electromagnetic drive alleviates the stresses within the conventional rigid redundant drive structure and reduces the detrimental effects associated with rigid redundancy. In this paper, the structure and equivalent SPU model of the platform are first introduced, with S referring to the kinematic sub, P to the spherical sub, and U to the universal joint. The degrees of freedom of the platform are analyzed, and the inverse kinematic model and velocity Jacobi matrix are derived, so as to derive the relationship between the pitch, roll angles, and length of the gimbal chain, and the relational equation between the angle and the current is further established to realize the electromagnetic control of the parallel redundant platform. The control part is realized as follows. Firstly, the angle information of the platform is obtained from the gyroscope to the microcontroller, the filtered angle is derived through the Untraceable Kalman Filter (UKF), and the angle value can be fused with data by both the mathematical model and PID algorithm to introduce the current value required to achieve the balance and realize the balance. In the simulation part, this paper uses Simulink and Simscape in MATLAB for joint simulation, and by giving the simulated trajectory and the desired trajectory of the joints, the driving force diagrams of the three branched chains based on the Least-Second Paradigm method are derived, and the trajectory error and driving force error are given to validate the reliability of the method of this paper.

1. Introduction

With the rapid development of modern manufacturing and robotics, parallel platforms have been widely used in precision machining, assembly, medical, and aerospace fields due to their advantages of high accuracy, high rigidity, and high load capacity [1]. The background of its development can be traced back to the 1960s when researchers began to explore the possibility of parallel structures in order to improve the precision and rigidity of mechanical systems. Compared with traditional series-connected robots, parallel-connected platforms are able to achieve higher rigidity and better load capacity by combining multiple branched chains in parallel and evenly distributing the motion errors and loads over multiple branched chains, thus improving the stability and reliability of the system.

However, conventional parallel platforms still face a number of challenges in practical applications, especially those related to redundant drives. First, in the traditional rigid-redundant drive structure, the introduction of redundant drive mechanisms, while enhancing the flexibility and fault tolerance of the system, often leads to an increase in internal stresses, which may result in unnecessary rigid constraints when dealing with complex motions, limiting the system’s suppleness and responsiveness.

Second, the complexity of the dynamic model and the presence of signal drift and environmental noise in the sensors make it more difficult for redundant parallel platforms to achieve an accurate and efficient control balance [2]. For example, maintaining the camera balance at all times is an important factor in an environment-exploring spherical robot that needs to carry a camera; a stable picture is crucial for environment exploration and observation, and the spherical robot needs to face various uneven terrains while keeping the camera stable [3,4,5].

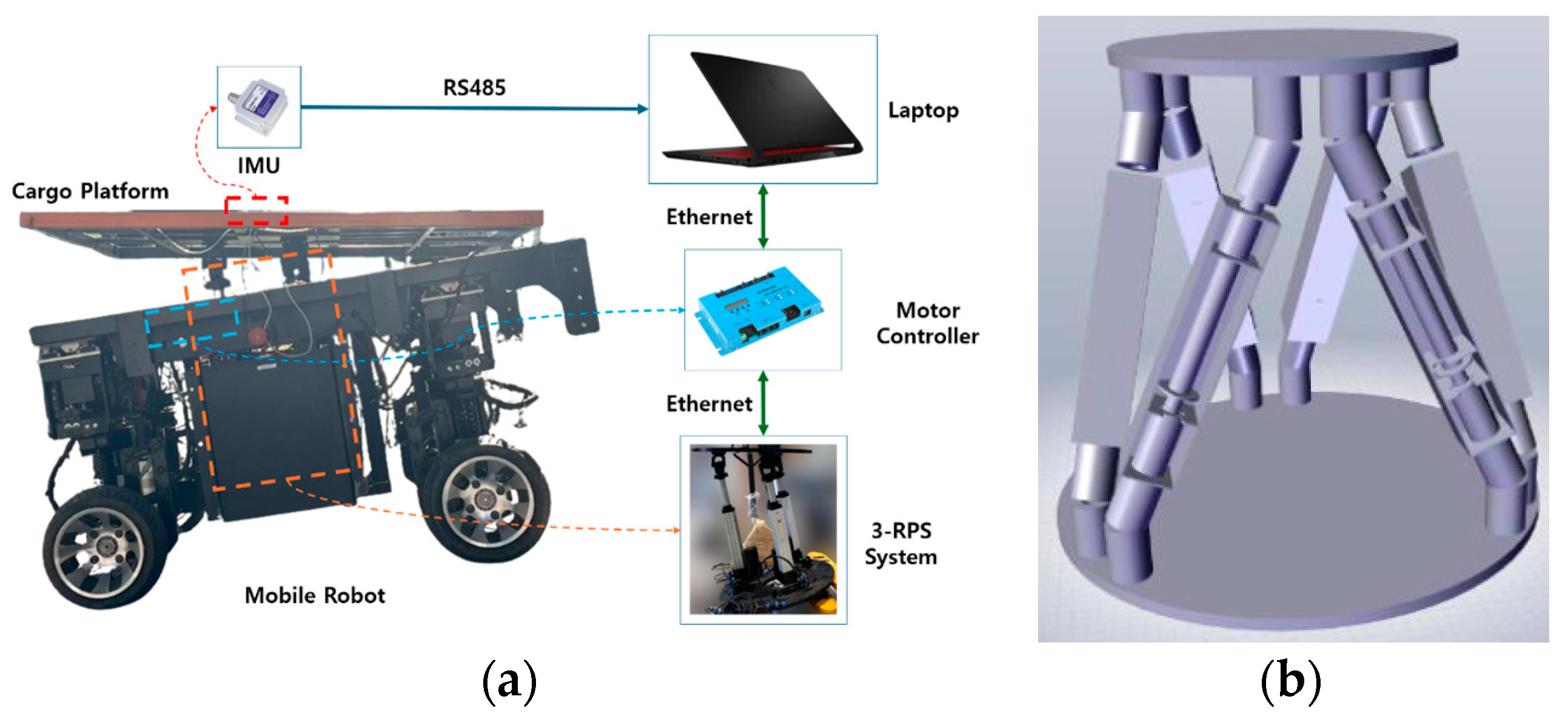
An-Dong Hwang and Woo-Young Kim from Chonnam National University have investigated the control of an agricultural mobile robot cargo platform with a 3-RPS parallel mechanism [6]. By establishing a kinematic model, inverse kinematic calculation, and PID controller adjustment, combined with real-time feedback IMU data, the length of the robot’s three drive rods was precisely adjusted to dynamically maintain the level of the agricultural mobile robot’s cargo platform during transportation on uneven ground, effectively reducing the tilt angle and ensuring the stability of agricultural products transportation [7]. In this article, each drive rod is connected to a servo motor, and these motors are responsible for adjusting the length of the drive rods. The mechanical structure is shown in Figure 1a.

Qiu Xiang Gu and Jiawei Tian, from the University of Electronic Science and Technology (UEST), studied a six-degree-of-freedom parallel platform structure based on Stewart [8]. The control chip of this structure is a S32K144 microcontroller. The manufacturer of the S32K144 is NXP, headquartered in Eindhoven, the Netherlands, and it is designed, developed and manufactured by NXP. Six parallel-connected robotic arms are controlled by the MCU program, and the servo motors of each group of robotic arms are brushless direct current (BLDC) motors [9,10], the manufacturer of this BLDC motor is DJI, a company based in Shenzhen, China; the length of each robotic arm is adjusted according to the real-time feedback data by using a PI control algorithm in order to realize the attitude adjustment of the platform in the workspace. In addition, the kinematic positive and negative solution algorithm calculation and trajectory planning are carried out through the control center program on the PC, as well as the real-time synchronous control of each drive using the CAN bus to ensure that the platform reaches the set target attitude, so as to complete the leveling process. This structure can come to test the effectiveness of the control algorithm, but its nature is still a rigid structure driven by brushless DC (BLDC) motors, which will have the problems of internal force wear and rigidity constraints. The structure of the six-degree-of-freedom parallel platform is shown in Figure 1b.

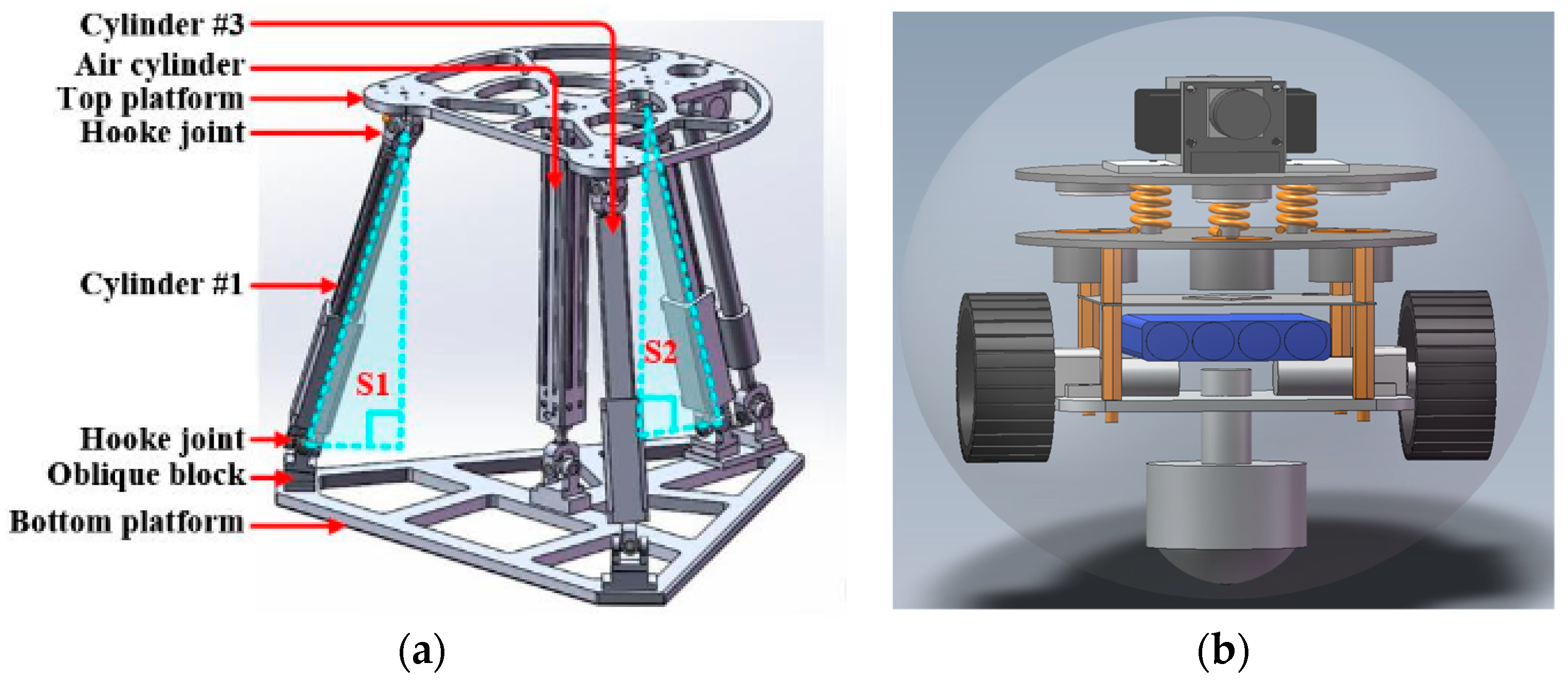
Jiang Shuo and Wang Junzheng et al. from the School of Automation, Beijing Institute of Technology (BIT) investigated a 3-degree-of-freedom (3-DOF) parallel stabilized platform with high vibration isolation performance [11]. Its working principle is, firstly, that a compliance control framework is established through the mass-spring-damper model and combined with a 3D striving solution, filtering, and online estimation of environmental stiffness and secondly, the flexibility of the electric cylinder is adjusted in real time to correct the reference trajectory, so as to keep the platform balanced and stabilized under the complex perturbation, but its core drive is still realized through the electric cylinder controlled by the motor. The electric cylinder is controlled by the motor, and its telescopic length is adjusted according to the adaptive active compliance control strategy, so as to adjust the platform’s attitude and position. The structure is shown in Figure 2a.

As can be seen from the above study, parallel platforms are used in a wide range of applications, and they have different modeling and control methods. In order to achieve the balance of the platform, drive rods and motors are often used, which are rigid mechanical drives. Because of this, there are problems of slow response and large internal forces in redundant drives; the former is not suitable for high-speed dynamic control, while the latter can cause structural deformation, losses, and a low energy conversion rate. These parallel platform mechanisms receive the effects of rigidity and internal forces, and there is a risk of wear and tear.

Therefore, it is crucial to develop a more efficient and stable control method. Electromagnetic drive, as an efficient and responsive drive method, provides new possibilities to solve this challenge [12,13]. Compared with traditional servomotor and hydraulic actuator drives, the electromagnetic drive has obvious advantages in terms of response speed and control accuracy, and structurally it is also free from wear and rigidity constraints caused by internal forces compared with traditional control methods. These advantages provide new ideas for the control of parallel redundant platforms.

In this paper, we propose a spatial two-degree-of-freedom parallel platform based on an electromagnetic redundant drive and its control method, which is redundantly driven by three electromagnetic-spring composite struts, which provides higher responsiveness and better flexibility than the traditional parallel structure and mitigates the adverse effects of the internal forces and rigid constraints on the structure of the traditional rigid redundant drive method. In terms of application, the driving method of the parallel platform proposed in this paper is seldom seen in the open literature and applications, so we apply the proposed parallel platform to an environment-detecting spherical robot with lidar and camera piggybacking so that the spherical robot can always maintain the lidar and the camera to keep a stable attitude during its movement, which is of better innovation and practical value. Parallel platform application on a spherical robot equipped with a camera and LiDAR 3D diagram is shown in Figure 2b.

In this paper, the structure of the platform and the equivalent SPU model are firstly introduced, the degrees of freedom of the redundant parallel platform are calculated, and the inverse kinematic equations and Jacobi matrix of the platform are analyzed. According to the analyzed results, the relationship between the rotation angle and the length of the branched chain is given and the relational equation between the angle and the current is deduced through the equations of dynamics and electromagnetism, which establishes the foundation for the later control. In order to solve the problems of noise and zero drift of the gyroscope sensor in practical applications, this paper introduces the untraceable Kalman filter (UKF), the processed angle information is passed to the controller, and the solved feedback signal is given to the current controller, so as to change the magnetic force of the electromagnet and realize the balance. In addition, we can also launch the angle and current relationship equation to solve the required current value, and the feedback signal together with the electromagnet, to realize the fusion of the two data and to achieve more accurate control. In the electromagnetic control process, how to efficiently distribute the magnetic force so that the power can be minimized is also a problem worth discussing. Based on this paper, we use MATLAB2023b to establish Simulink and Simscape models and use a driving force allocation strategy based on the minimum two-paradigm number method, through the design of the three-dimensional motion trajectory of the joint point at the end of the branched chain, to calculate the force of each branched chain. We also join the traditional hybrid driving force allocation for simulation and comparison, and the results show that the proposed method is smaller than the traditional method in terms of the consumption of power and deviation. The results show that the method proposed in this paper is smaller than the traditional method in terms of power consumption and deviation.

The paper is organized as follows: Section 1 is the introduction, which summarizes the latest research and applications of parallel platforms and gives an application of the electromagnetic redundantly driven parallel platform proposed in this paper. In Section 2, we analyze the electromagnetic redundant drive parallel platform structure, give the equivalent model, and analyze the degrees of freedom, inverse kinematics, Jacobi matrix, and platform offset angle of the parallel platform. In Section 3, this paper continues the analysis of the branched chain model and the dynamics model of the parallel platform and gives the equations for the relation between the length of the branched chain and the angle as well as the current and the angle. Section 4 presents the data fusion algorithm using UKF and describes the establishment of the equations of state and measurement as well as the process of traceless variation. Section 5 discusses the branched chain drive allocation, MATLAB simulation, and trajectory planning verification for the electromagnetic redundant drive parallel platform. In Section 6, the paper is summarized.

2. Parallel Platform Analysis of the Electromagnetic Drive

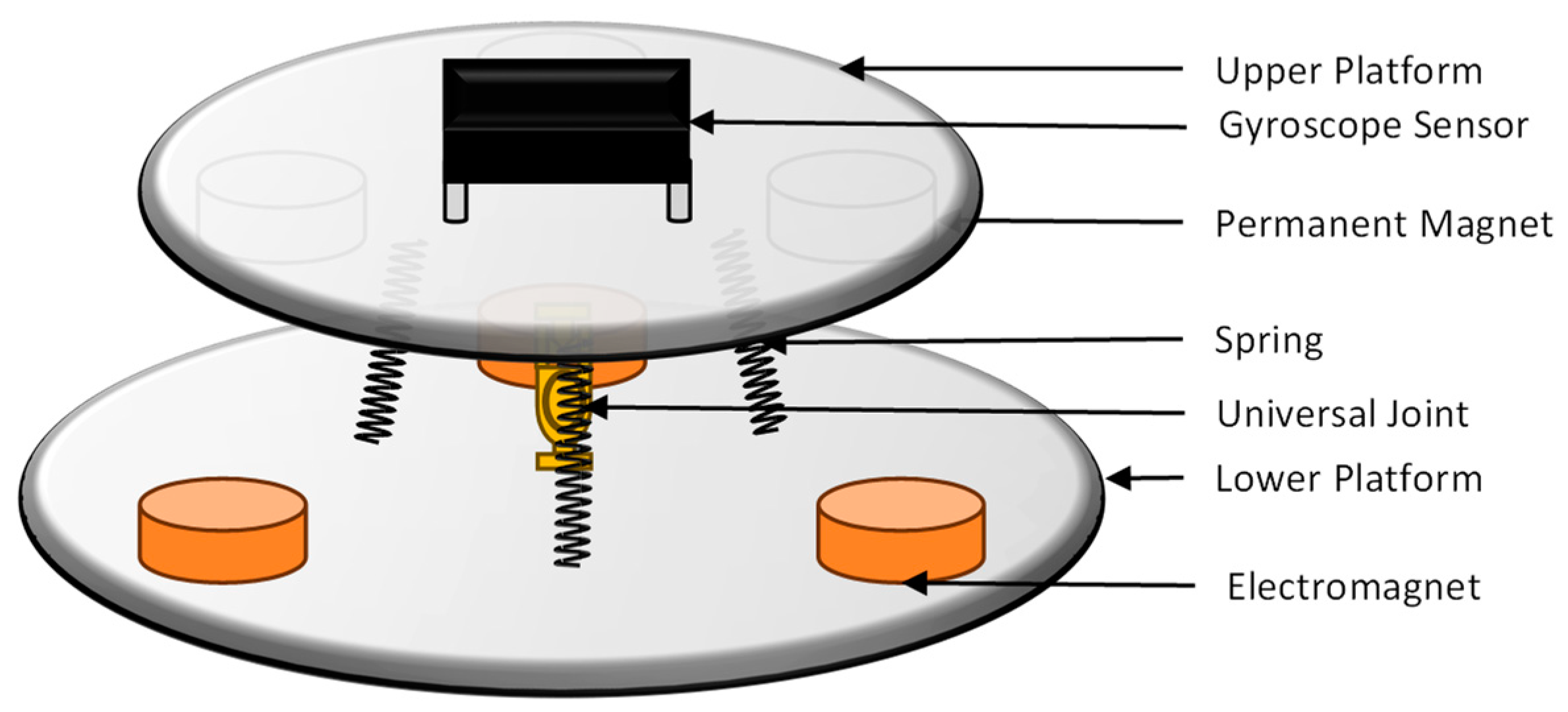
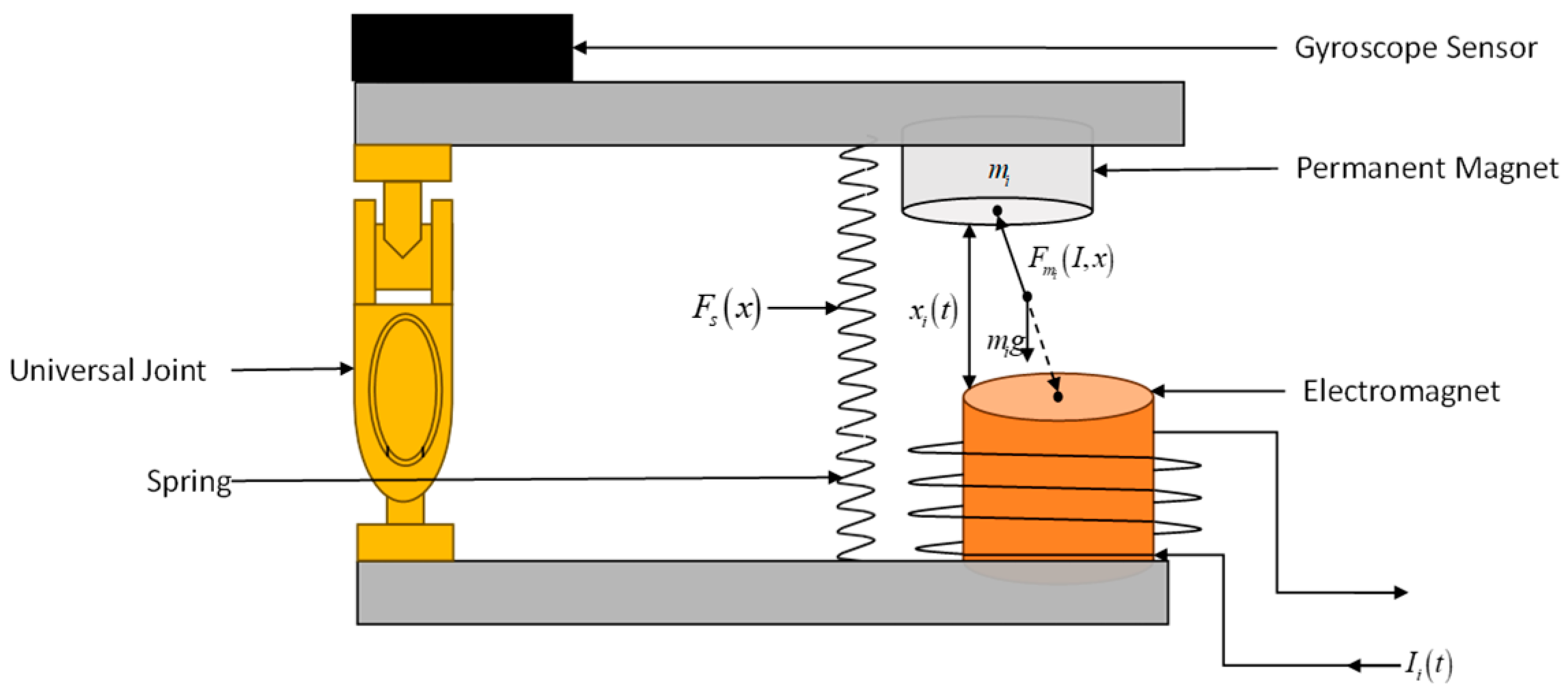
The object analyzed in this paper is a 2DOF parallel platform mechanism, and the control method is an electromagnetic drive. The structure is divided into a circular upper platform and a lower platform, in which the top surface of the upper platform is equipped with a gyroscope sensor, the bottom surface is uniformly distributed with three permanent magnets of the same specification, the top surface of the lower platform is distributed with three electromagnets of the same specification, and the middle of the platform has a universal hinge in the center of the circle as well as three springs of the same specification uniformly distributed, the three permanent magnets, and the three electromagnets that form three electromagnetic-spring composite drive struts together.

The three-branched-chain two-degree-of-freedom platform forms a redundant drive control. The three-branched-chain structure can effectively improve the stability of the system by sharing the loads and moments through the redundant degrees of freedom [14], especially when responding to external perturbations and load variations. The system can be automatically adjusted to maintain equilibrium to adapt to the dynamically changing working environment, which is very important for application scenarios that require rapid adjustment and precise control. The schematic of the electromagnetically driven 2DOF parallel platform is shown in Figure 3.

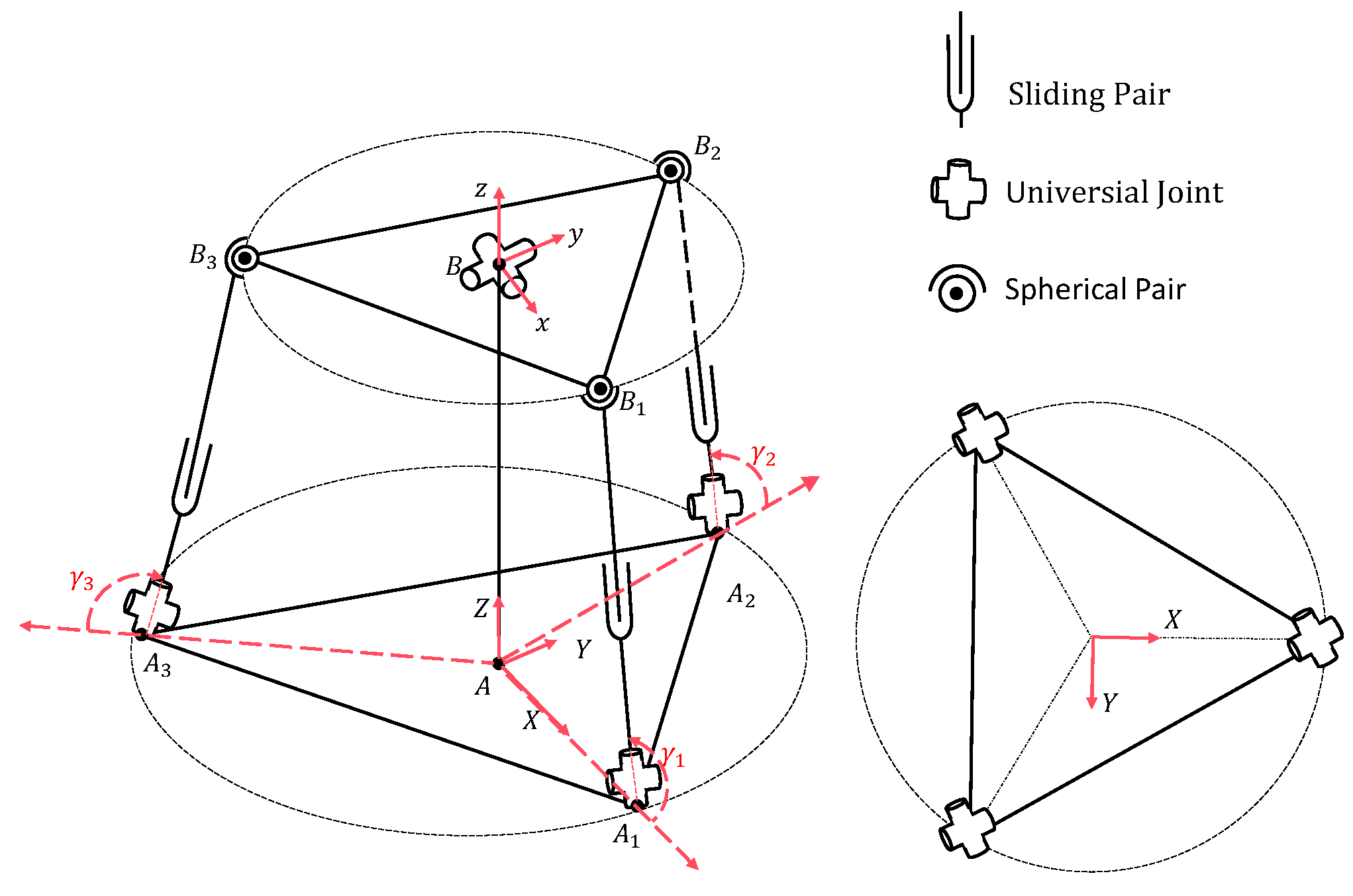
In order to simplify the mechanism analysis, the parallel platform is designed for equivalent analysis. Then, the parallel platform has three electromagnetic-spring composite drive pivot chains. This mechanism includes a fixed lower platform A₁A₂A₃, a movable upper platform B₁B₂B₃, universal joints connecting the platforms, and three legs A_iB_i (i = 1, 2, 3). Both platforms are circular, as shown in Figure 4. Among them, each strut chain has a spherical sub (S) at the top, a moving sub (P) in the middle, and a universal joint (U) at the bottom. A fixed coordinate system A-xyz is established on the lower platform, and a moving coordinate system B-xyz is established on the upper platform. The origins of both coordinate systems are located at the centers of the respective platforms, with the Y axis and y axis parallel to A₂A₃ and B₂B₃, respectively, and the Z axis and z axis perpendicular to the planes A₁A₂A₃ and B₁B₂B₃, respectively.

2.1. Degree of Freedom Analysis of Parallel Platform

As shown in Figure 4, this mechanism consists of three SPU legs. According to the modified Grubler–Kutzbach (G–K) formula [15], the degree of freedom (DOF) of the system is 6. Due to the constraint forces exerted by the intermediate universal joint (U) in the z-direction of the moving platform and along the coordinate axes of the moving platform, the end-effector can only rotate about the x and y axes, resulting in two DOFs for the end-effector. Moreover, there are no common constraints or redundant constraints in this mechanism. Based on the aforementioned analysis, the overall DOF of the mechanism can be calculated as follows:

$$M=6(n-g-1)+{\displaystyle \sum _{i=1}^g{f}_i}+v-\zeta =2$$

(1)

where $n$ is the total number of links in the system, including all moving and fixed components, $g$ is the total number of joints in the system, f_i is the DOF of the i-th joint, representing the number of independent movements the joint can provide, v is the number of independent input motions in the system, the active DOFs of the system, and $\zeta$ is the number of redundant constraints in the system.

2.2. Inverse Solution Model and Jacobian Matrix Analysis of the Parallel Platform

The electromagnet is equivalent to the prime A₁A₂A₃, then the triangle formed by the vertices of the upper and lower planes of this mechanism is equilateral, the distance from the center of the upper plane to the vertex BB_i = $2b$, the distance from the center of the lower plane to the vertex AA_i = $2a$, and the distance between the upper and lower planes $AB$ = $h_0$. The length of the prismatic joint P is ${\mathrm{x}}_i$ = ${\mathrm{A}}_i{\mathrm{B}}_i$ for (i = 1, 2, 3). Then, according to the inverse solution model of the mechanism, we can obtain the relationship equation between the $\alpha$ and $\beta$ angle changes caused by the X—Y rotation sequence of the moving platform and the length of the chain ${\mathrm{x}}_i$ as

$$\left\{\begin{array}{l}{x}_1=A{B}_1=\left(\begin{array}{c}2b\cos \beta +h_0\sin \beta -2a\\ 2b\sin \alpha \sin \beta -h_0\sin \alpha \cos \beta \\ -2b\cos \alpha \sin \beta +h_0\cos \alpha \cos \beta \end{array}\right)\hfill \\ x_2=A{B}_2=\left(\begin{array}{c}{h}_0\sin \beta +\sqrt{3}b\sin \beta -b\cos \beta +a\\ \sqrt{3}b\cos \alpha +K_{11}-\sqrt{3}a\\ \sqrt{3}b\sin \alpha +K_{22}\end{array}\right)\hfill \\ x_3=A{B}_3=\left(\begin{array}{c}-b\cos \beta +\sqrt{3}b\sin \beta +h_0\sin \beta +a\\ -\sqrt{3}b\cos \alpha +K_{11}+\sqrt{3}a\\ -\sqrt{3}b\sin \alpha +K_{22}\end{array}\right)\hfill \end{array}\right.$$

(2)

In the above formula, the following applies:

$$\left\{\begin{array}{c}{K}_{11}=-b\sin \alpha \sin \beta -h_0\sin \alpha \cos \beta \\ K_{22}=b\cos \alpha \sin \beta +h_0\cos \alpha \cos \beta \end{array}\right.$$

(3)

To perform kinematic analysis for the design of a more efficient control algorithm, we need to analyze the Jacobian matrix of the mechanism to simulate its actual motion [16]. Then, the first order fully differential equation for the length of the strut with respect to the angle is given by

$$\left\{\begin{array}{l}d{x}_1=\left[\begin{array}{cc}0& -2D_{88}+h_0\cos \alpha \\ 2b{D}_{44}-h_0{D}_{22}& 2b{D}_{33}+h_0{D}_{11}\\ 2b{D}_{11}-h_0{D}_{33}& -2b{D}_{22}-h_0{D}_{44}\end{array}\right]\left[\begin{array}{c}d\alpha \\ d\beta \end{array}\right]\hfill \\ d{x}_2=\left[\begin{array}{cc}0& D_{99}+D_{77}+D_{88}\\ -D_{55}-b{D}_{44}-h_0{D}_{22}& -b{D}_{33}+h_0{D}_{11}\\ D_{66}-b{D}_{11}-h_0{D}_{33}& b{D}_{22}-h_0{D}_{44}\end{array}\right]\left[\begin{array}{c}d\alpha \\ d\beta \end{array}\right]\hfill \\ d{x}_3=\left[\begin{array}{cc}0& D_{88}+D_{77}+D_{99}\\ D_{55}-b{D}_{44}-h_0{D}_{22}& -b{D}_{33}+h_0{D}_{11}\\ -D_{66}-b{D}_{11}-h_0{D}_{33}& b{D}_{22}-h_0{D}_{44}\end{array}\right]\left[\begin{array}{c}d\alpha \\ d\beta \end{array}\right]\hfill \end{array}\right.$$

(4)

In the above formula, the following applies:

$$\left\{\begin{array}{c}{D}_{11}=\sin \alpha \sin \beta \hfill \\ D_{22}=\cos \alpha \cos \beta \hfill \\ D_{33}=\sin \alpha \cos \beta \hfill \\ D_{44}=\cos \alpha \sin \beta \hfill \\ D_{55}=\sqrt{3}b\sin \alpha \hfill \\ D_{66}=\sqrt{3}b\cos \alpha \hfill \\ D_{77}=\sqrt{3}b\cos \beta \hfill \\ D_{88}=b\sin \beta \hfill \\ D_{99}=h_0\cos \beta \hfill \end{array}\right.$$

(5)

In simplified form, this can be expressed as

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\end{array}\right]=J\left[\begin{array}{c}\dot{\alpha }\\ \dot{\beta }\end{array}\right]\to \left[\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right]=J\left[\begin{array}{c}{\omega }_{\alpha }\\ {\omega }_{\beta }\end{array}\right]$$

(6)

where $v_i$ (for i = 1, 2, 3) represents the velocity of the chain length changes, ${\omega }_n$ (for n = α, β) denotes the angular velocities of points on the moving platform, and $J$ is the velocity Jacobian matrix of the mechanism. The relationship can be represented as

$$J=\left[\begin{array}{cc}0& -2D_{88}+h_0\cos \alpha \\ 2b{D}_{44}-h_0{D}_{22}& 2b{D}_{33}+h_0{D}_{11}\\ 2b{D}_{11}-h_0{D}_{33}& -2b{D}_{22}-h_0{D}_{44}\\ 0& D_{99}+D_{77}+D_{88}\\ -D_{55}-b{D}_{44}-h_0{D}_{22}& -b{D}_{33}+h_0{D}_{11}\\ D_{66}-b{D}_{11}-h_0{D}_{33}& b{D}_{22}-h_0{D}_{44}\\ 0& D_{88}+D_{77}+D_{99}\\ D_{55}-b{D}_{44}-h_0{D}_{22}& -b{D}_{33}+h_0{D}_{11}\\ -D_{66}-b{D}_{11}-h_0{D}_{33}& b{D}_{22}-h_0{D}_{44}\end{array}\right]$$

(7)

This Jacobian matrix analysis allows us to understand the velocity and angular velocity relationships within the mechanism, which is crucial for designing accurate and responsive control algorithms.

2.3. Calculation of an Offset Angle of the Moving-Fixed Platform

In electromagnetic systems, accurate calculation of the interaction force between the electromagnet and the permanent magnet is important for optimizing the design and improving the system performance. Since the sizes of the moving and fixed platforms are different (a ≠ b), the angular deviation between the permanent magnet and the electromagnet will be generated. In order to accurately control the magnetic force of the mechanism, we need to calculate the directional cosine $\cos {\gamma }_i$ (for i = 1, 2, 3) between the points of the moving and fixed platforms, between $B_i$ and $A_i$, then their directional cosines can be expressed as

$$\left\{\begin{array}{c}\cos {\gamma }_1={\displaystyle \frac{B_1•A_1}{‖B_1‖‖A_1‖}}\\ \cos {\gamma }_2={\displaystyle \frac{B_2•A_2}{‖B_2‖‖A_2‖}}\\ \cos {\gamma }_3={\displaystyle \frac{B_3•A_3}{‖B_3‖‖A_3‖}}\end{array}\right.$$

(8)

By calculating the directional cosines between electromagnets and permanent magnets, we are able to accurately characterize their relative positional relationship and calculate the interaction force based on this. This is important for the design and optimization of electromagnetic systems.

3. Electromagnetic-Spring Composite Pivot Chain Model and Dynamic Analysis of the Parallel Platform

The electromagnetic-spring composite pivot chain in a 2-DOF parallel platform is modeled as shown in Figure 5.

In Figure 5, let the sum of the interaction force between the electromagnet and the permanent magnets be $F_{m_i}\left(I,x\right)$, the elastic force of the spring be $F_s\left(x\right)$, the mass of the permanent magnets be $m_i$ (for i = 1, 2, 3), $x_i\left(t\right)$ (for i = 1, 2, 3) be the amount of the change in length of each strut chain induced in the course of the motion, the excitation current of the electromagnet be $I_i\left(t\right)$, and the air resistance be neglected. In the initial state, since the three permanent magnets are uniformly distributed in the upper plane of the three equidistant lines, it is an equilibrium state, and the force point is at the center of the circle. The mathematical model of the electromagnetic drive system can be described by the equations of electromagnetism, kinematics, and circuitry, as follows:

$$\left\{\begin{array}{l}{F}_{m_i}(I,x)={\displaystyle \frac{{\mu }_{0}NSMV{I}_i(t)}{4\pi x_i^3(t)}}\cos {\gamma }_i\hfill \\ F_s(t)=k_s{x}_i(t)\hfill \\ m_i{\ddot{x}}_i(t)=m_{i}g+F_{m_i}(I,x)+F_s(t)\hfill \end{array}\right.$$

(9)

In the above equation, ${\mu }_0$ is the air permeability, $S$ is the magnetic pole area of the electromagnet, $N$ is the number of turns of the coil, $M$ is the magnetization strength of the permanent magnet, $V$ is the volume of the permanent magnet, and $K$ is the elasticity coefficient of the spring. The electromagnetic and elastic formulas of the Equation (9) are obtained by substituting them into the kinematic equations:

$$m_i{\ddot{x}}_i(t)=m_{i}g+{\displaystyle \frac{{\mu }_{0}NSMV{I}_i(t)}{4\pi x_i^3(t)}}\cos {\gamma }_i+k_s{x}_i(t)$$

(10)

The simplified transformation leads to the equation for the variation in the current $I_i\left(t\right)$ with respect to the length of the branched chain $x_i\left(t\right)$ as

$$I_i(t)={\displaystyle \frac{4\pi x_i^3(t)}{{\mu }_{0}NSMV\cos {\gamma }_i}}\left[m_i\left({\ddot{x}}_i(t)-g\right)-k_s{x}_i(t)\right]$$

(11)

Thus, we have

$$\left\{\begin{array}{c}{I}_1(t)={\displaystyle \frac{4\pi x_1^3(t)}{{\mu }_{0}NSMV\cos {\gamma }_i}}\left[m_1\left({\ddot{x}}_1(t)-g\right)-k_s{x}_1(t)\right]\\ I_2(t)={\displaystyle \frac{4\pi x_2^3(t)}{{\mu }_{0}NSMV\cos {\gamma }_i}}\left[m_2\left({\ddot{x}}_2(t)-g\right)-k_s{x}_2(t)\right]\\ I_3(t)={\displaystyle \frac{4\pi x_3^3(t)}{{\mu }_{0}NSMV\cos {\gamma }_i}}\left[m_3\left({\ddot{x}}_3(t)-g\right)-k_s{x}_3(t)\right]\end{array}\right.$$

(12)

The relationship between the current and the angle is

$$\left\{\begin{array}{l}{I}_1(t)=K_{m_1}{x}_1^3(t)\left[m_1\left({\displaystyle \frac{d^2\left(x_1\right)}{d{t}^2}}-g\right)-k_s\left(x_1\right)\right]\hfill \\ I_2(t)=K_{m_2}{x}_2^3(t)\left[m_2\left({\displaystyle \frac{d^2\left(x_2\right)}{d{t}^2}}-g\right)-k_s\left(x_2\right)\right]\hfill \\ I_3(t)=K_{m_3}{x}_3^3(t)\left[m_3\left({\displaystyle \frac{d^2\left(x_3\right)}{d{t}^2}}-g\right)-k_s\left(x_3\right)\right]\hfill \end{array}\right.$$

(13)

Let $t_1$ = $\cos \alpha$ and $t_2$ = $\cos \beta$, then the coefficients in Equation (13) are given by

$$\left\{\begin{array}{l}{K}_{m_i}={\displaystyle \frac{4\pi }{{\mu }_{0}NSMV\cos {\gamma }_i}}\hfill \\ k_0=4\left(a^2+b^2\right)\hfill \\ k_1=-6ab{t}_1+2ab{t}_2\hfill \\ k_2=2\sqrt{3}ab\sqrt{1-t_1^2}\sqrt{1-t_2^2}\hfill \end{array}\right.$$

(14)

Based on the analysis above, we can implement a simplified control of the parallel platform mechanism. The control process is as follows:

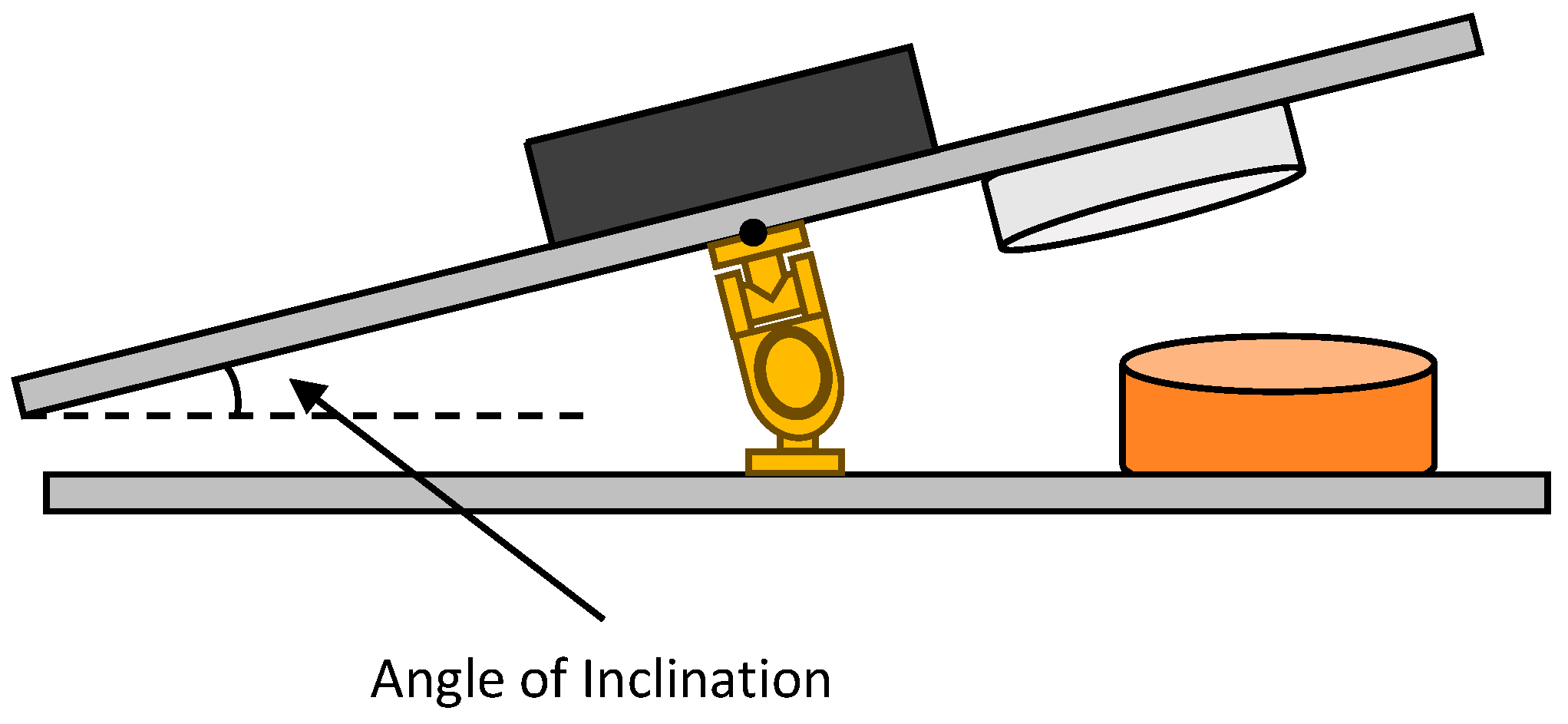
In the initial state, the system does not receive external interference; at this time, the center of gravity of the mechanism is in the center position, the mechanism is in a state of equilibrium, and the gyroscope measurement shows that $\alpha$ = $\beta$ = 0. In the process of movement, the platform will be tilted, as shown in Figure 6. In order to maintain the balance of the upper platform, the gyroscope sensor needs to measure the actual tilt angle $\alpha$ and $\beta$ of the upper platform in real time. These measured angles are compared with the target angle, and the error value is calculated. The error value is processed to generate the control signals, which are used as the pulse signals of the actuator, and by adjusting the magnetic force generated by the electromagnet, these signals correct the attitude of the upper platform, thus realizing the dynamic balance control.

However, if filtering is not applied, sensor noise and measurement errors may significantly affect the accuracy and stability of the control system. This may lead to incorrect error calculations and unstable platform motion. To address these issues, the Unscented Kalman Filter (UKF) can be introduced. The UKF is an advanced filtering technique that provides more accurate state estimation by taking into account the nonlinear characteristics of the system. By applying the UKF, we can reduce the effects of noise and measurement errors, thus improving the stability and performance of the dynamic balance control system [17].

4. Data Fusion Algorithm Based on the Unscented Kalman Filter

In the actual operation of the mechanism, relying solely on gyroscope sensors to detect angles for real-time control may encounter issues such as noise and drift, leading to inaccurate angle measurements and compromised control performance. The noise and cumulative drift of the gyroscope can cause error accumulation, resulting in significant deviations during long-term operation [18,19,20].

To address this, the Unscented Kalman Filter (UKF) can be introduced. By considering the tilt angles of the platform as the state equation and the angles measured by the gyroscope sensor as the observation equation, the UKF can perform data fusion. This method effectively combines sensor data with the mathematical model, significantly reducing the noise and drift errors of the gyroscope. Consequently, it provides more accurate and stable angle estimations, allowing for precise system state estimation and control. This enhances the robustness and reliability of the control system. The process of data fusion between the gyroscope sensor and the mathematical model is illustrated in Figure 7.

Based on Figure 6, it is understood that the equilibrium state of the upper platform is primarily determined by the variables $\alpha$ and $\beta$. Therefore, the state vector of the platform’s position is

$$X_k=\left[\begin{array}{c}{\alpha }_k\\ {\beta }_k\end{array}\right]$$

(15)

Assuming the system is driven by process noise, the state transition equation of the system is

$$X_{k+1}=X_k+W_k$$

(16)

The observation vector obtained from the gyroscope sensor is

$$Z_k=\left[\begin{array}{c}\Delta {\alpha }_k\\ \Delta {\beta }_k\end{array}\right]$$

(17)

Based on the angular variations measured by the gyroscope, the measurement equation can be expressed as

$$Z_k=H{X}_k+V_k$$

(18)

In the equations above, $W_k$ represents the process noise, which describes the random perturbations or uncertainties within the system at each time step. It is assumed to be zero-mean Gaussian noise with a covariance matrix Q. $\Delta {\alpha }_k$ and $\Delta {\beta }_k$ denote the angular variations in the dynamic platform at time step $k$. $V_k$ represents the measurement noise, assumed to be zero-mean Gaussian noise with a covariance matrix R.

Due to the uncertainty in the motion state of the mechanism, the angle variation exhibits nonlinearity. Therefore, we employ the Unscented Transform (UT) to handle the state estimation of nonlinear systems. The process involves calculating a set of Sigma points based on the state mean and covariance matrix. Each Sigma point is assigned a weight, and the Sigma points are transformed through a nonlinear function to obtain a new set of Sigma points. These transformed Sigma points are then used to estimate the mean and covariance of the transformed variables, thereby providing updated filter values. The transformation process is as follows [21]:

• Calculate Sigma Points

To capture the statistical characteristics of the state variables, a set of sample points called Sigma points is chosen. These points are generated based on the mean and covariance matrix. Denote the number of Sigma points by $n$ and the state dimension of the system by N. From the Equation (15), it is known that the system’s state dimension is N = 2. Set the state vector mean as X and the initial covariance matrix as P. The Sigma points are then calculated as

$$\left\{\begin{array}{ll}{\chi }_0=X,\hfill & i=0\hfill \\ {\chi }_i=X+{\left(\sqrt{\left(n+\lambda \right)P}\right)}_i,\hfill & i=1,2,\dots ,n\hfill \\ {\chi }_{i+n}=X-{\left(\sqrt{\left(n+\lambda \right)P}\right)}_i,\hfill & i=1,2,\dots ,n\hfill \end{array}\right.$$

(19)

$$\lambda ={\sigma }^2\left(n+\kappa \right)-n$$

(20)

In this context, $\lambda$ is the scaling parameter and $\sigma$ typically ranges from (0.001, 1). A smaller $\sigma$ will make the Sigma points more concentrated. Generally, $\sigma$ is set to 10⁻³. $\kappa$ is a secondary scaling parameter used to further adjust the distribution of Sigma points, generally set to 0.

2.

Calculate the Weights of Sigma Points

The weights are used to calculate the weighted mean and covariance of the transformed Sigma points, as follows:

$$\left\{\begin{array}{l}{W}_0^{\left(m\right)}={\displaystyle \frac{\lambda }{(n+\lambda )}}\hfill \\ W_0^{\left(c\right)}={\displaystyle \frac{\lambda }{(n+\lambda )}}+\left(1-{\sigma }^2+\eta \right)\hfill \\ W_i^{\left(m\right)}=W_i^{\left(c\right)}={\displaystyle \frac{1}{2(n+\lambda )}},i=1,2,\dots ,2N\hfill \end{array}\right.$$

(21)

Here, $\eta$ is used to adjust for known distribution biases, typically set to 2 for Gaussian distributions.

3.

Initialize the State Vector and Covariance Matrix

$$P_0=E\left[\left(X_0-{\widehat{X}}_0\right){\left(X_0-{\widehat{X}}_0\right)}^T\right]$$

(22)

4.

Prediction Step

$$\left\{\begin{array}{ll}{\chi }_{i,t-1}={\widehat{X}}_{t-1},\hfill & i=0\hfill \\ {\chi }_{i,t-1}={\widehat{X}}_{t-1}+{\left(\sqrt{\left(n+\lambda \right)P_{t-1}}\right)}_i,\hfill & i=1,2,\dots ,n\hfill \\ {\chi }_{i+n,t-1}={\widehat{X}}_{t-1}-{\left(\sqrt{\left(n+\lambda \right)P_{t-1}}\right)}_i,\hfill & i=1,2,\dots ,n\hfill \end{array}\right.$$

(23)

Using the system model to predict the transformation of the Sigma points and employing the state transition equation ${\chi }_{i,t|t-1}$ = f(${\chi }_{i,t-1}$) [22], the predicted values at the next time step for each Sigma point are calculated. The predicted mean and covariance are then computed using the transformed Sigma points and their corresponding weights, as follows:

$${\widehat{X}}_{t|t-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{\left(m\right)}{X}_{t|t-1}}$$

(24)

$${\mathit{P}}_{t|t-1}=\sum _{i=0}^{2n}{W}_i^{(c)}\left({\widehat{X}}_{t|t-1}-X_{t|t-1}\right){\left({\widehat{X}}_{t|t-1}-X_{t|t-1}\right)}^T$$

(25)

5.

Correct Step

$$\left\{\begin{array}{ll}{\delta }_{i,t|t-1}={\widehat{X}}_{t|t-1},\hfill & i=0\hfill \\ {\delta }_{i,t|t-1}={\widehat{X}}_{t|t-1}+{\left(\sqrt{\left(n+\lambda \right)P_{t|t-1}}\right)}_i,\hfill & i=1,2,\dots ,n\hfill \\ {\delta }_{i+n,t|t-1}={\widehat{X}}_{t|t-1}-{\left(\sqrt{\left(n+\lambda \right)P_{t|t-1}}\right)}_i,\hfill & i=1,2,\dots ,n\hfill \end{array}\right.$$

(26)

Using the current predicted Sigma points ${\delta }_{i,t|t-1}$, calculate the Sigma points ${{\rm Z}}_{i,t|t-1}$ in the measurement space, as follows:

$$Z_{i,t|t-1}=HX\left({\delta }_{i,t|t-1}\right)$$

(27)

Next, compute the mean, covariance, and cross-covariance matrices using the transformed Sigma points ${{\rm Z}}_{i,t|t-1}$ in the measurement space and their corresponding weights $W_i^{\left(m\right)}$, as follows:

$$\left\{\begin{array}{l}{\widehat{Z}}_{i,t|t-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{\left(m\right)}{Z}_{i,t|t-1}}\hfill \\ {\mathit{S}}_t={\displaystyle \sum _{i=0}^{2n}}{W}_i^{(c)}\left({\widehat{Z}}_{i,t|t-1}-{\mathit{Z}}_{i,t|t-1}\right){\left({\widehat{Z}}_{i,t|t-1}-{\mathit{Z}}_{i,t|t-1}\right)}^T\hfill \\ {\mathit{P}}_{XZ}={\displaystyle \sum _{i=0}^{2n}}{W}_i^{(c)}\left({\widehat{X}}_{t|t-1}-X_{t|t-1}\right){\left({\widehat{Z}}_{i,t|t-1}-{\mathit{Z}}_{i,t|t-1}\right)}^T\hfill \end{array}\right.$$

(28)

Using the calculated cross-covariance matrix ${\mathit{P}}_{XZ}$ and measurement covariance matrix ${\mathit{S}}_t$, the Kalman gain $K_t$ is computed as

$$K_t={\mathit{P}}_{XZ}{\mathit{S}}_t^{-1}$$

(29)

6.

Update the State Estimate

Using the Kalman gain K_t and the measurement residual ($Z_t$ − ${\widehat{Z}}_{t-1}$), update the state estimate ${\widehat{X}}_t$ as follows:

$${\widehat{X}}_t={\widehat{X}}_{t|t-1}+K_t\left(Z_t-{\widehat{Z}}_{t|t-1}\right)$$

(30)

$$P_t=P_{t|t-1}-K_t{\mathit{S}}_t{K}_t^T$$

(31)

With the above calculations, we can obtain the updated ${\widehat{X}}_t$ angle data. The updated angle value can be solved by the PID algorithm, which solves the feedback signal to the current controller to be converted into the corresponding current value; the angle value is then transmitted to the mathematical model of the mechanism, which solves the current value required by each branch chain at time $t$. By fusing the current data solved by the mathematical model with the current data solved by the PID controller with weights, we can change the magnetism of the electromagnet more accurately to keep the platform balanced.

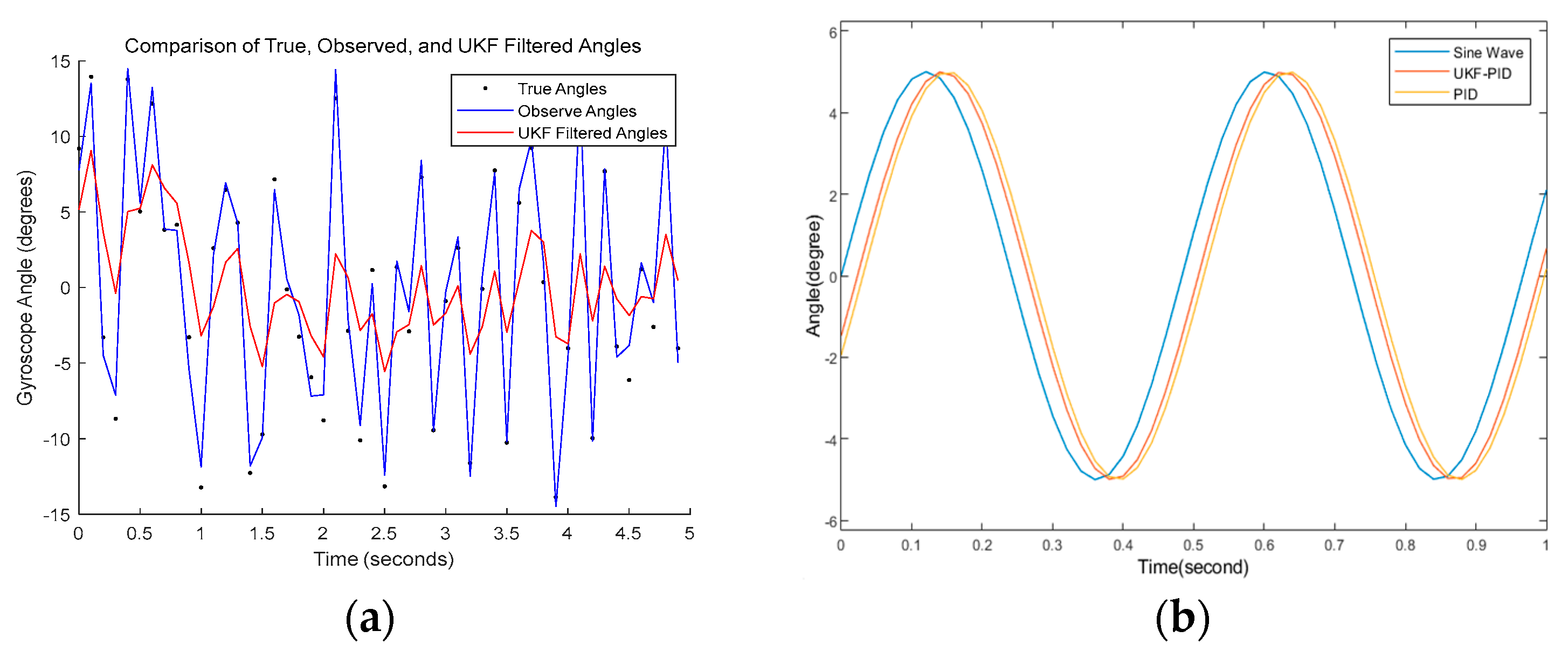
In order to show the filtering effect of UKF on the angle, the nonlinearly varying angle is given to compare with the observed value, where the angle range is (−14°, 14°), as shown in Figure 8. In addition, we added a sine wave and compared it with the PID algorithm without UKF, and it can be concluded that the following effect of this paper is better, the result is shown in Figure 8b.

5. Verification of Drive Distribution and Simulation in Redundant Platforms

In electromagnetic redundant drive parallel mechanisms, it is crucial to address the coordinated distribution of drive forces as the number of actuators exceeds the degrees of freedom [23]. Effective force distribution not only minimizes energy consumption but also enhances system stability. The following section discusses the drive assignment methodology for electromagnetically redundant parallel platforms.

Since the model in this paper is a three-branched two-degree-of-freedom structure, the number of actuators exceeds the degrees of freedom. A key issue is how to appropriately allocate the driving forces to effectively reduce energy consumption and enhance system stability [24]. This paper proposes a strategy based on the minimum two-norm method for optimizing force allocation in such mechanisms.

According to Equation (7), we can learn that the relationship between the length change velocity and the angle change velocity of each branched chain is derived from the Jacobian matrix $J$. In order to realize the minimum two-paradigm number allocation strategy for the driving torque [25], it is necessary to first compute the transpose matrix $J^T$ of the Jacobian matrix $J$ and then derive the pseudo-inverse $J^{+}$ of the Jacobian matrix. We first compute the transpose of the Jacobian matrix $J^T$, as shown in Equation

$$J^T=\left[\begin{array}{ccccc}0& 2b{D}_{44}-h_0{D}_{22}& \dots & D_{55}-b{D}_{44}-h_0{D}_{22}& -D_{66}-b{D}_{11}-h_0{D}_{33}\\ -2D_{88}+h_0\cos \alpha & 2b{D}_{33}+h_0{D}_{11}& \dots & -b{D}_{33}+h_0{D}_{11}& b{D}_{22}-h_0{D}_{44}\end{array}\right]$$

(32)

Then, we can obtain this Equation

$$J^{T}J=\left[\begin{array}{cc}\begin{array}{c}A\\ B^T\end{array}& \begin{array}{c}B\\ C\end{array}\end{array}\right]$$

(33)

where $A$, $B$, and $C$ are matrices, and the pseudo-inverse is given by

$$J^{+}={\left(J^{T}J\right)}^{-1}{J}^T$$

(34)

To implement the force allocation strategy, we define the platform velocity vector $\dot{x}$, which can be derived from the velocity Jacobi matrix mentioned above, and solve the joint velocity vector $\dot{q}$ through the pseudo-inverse matrix, as follows:

$$\dot{q}=J^{+}\dot{x}$$

(35)

Then, the driving forces $\tau$ are calculated using the dynamics equation, as follows:

$$\tau =M\left(\dot{q}\right)\ddot{q}+C\left(\dot{q},q\right)\dot{q}+G\left(q\right)$$

(36)

where $M$ is the inertia matrix, $C$ is the Coriolis matrix, and $G$ is the gravity matrix. To minimize the input forces $\tau$, the minimum two-norm method can be used. This problem can be expressed as

$$\min {‖\tau ‖}_2$$

(37)

Under these circumstances, the use of the pseudo-inverse matrix $J^{+}$ ensures the minimum two-norm solution. Specifically, this means that when solving for the force distribution $\tau$, the solution with the minimum two-norm of the input force is selected [26].

5.1. Trajectory Planning and Simulation Verification of Parallel Platforms Using MATLAB

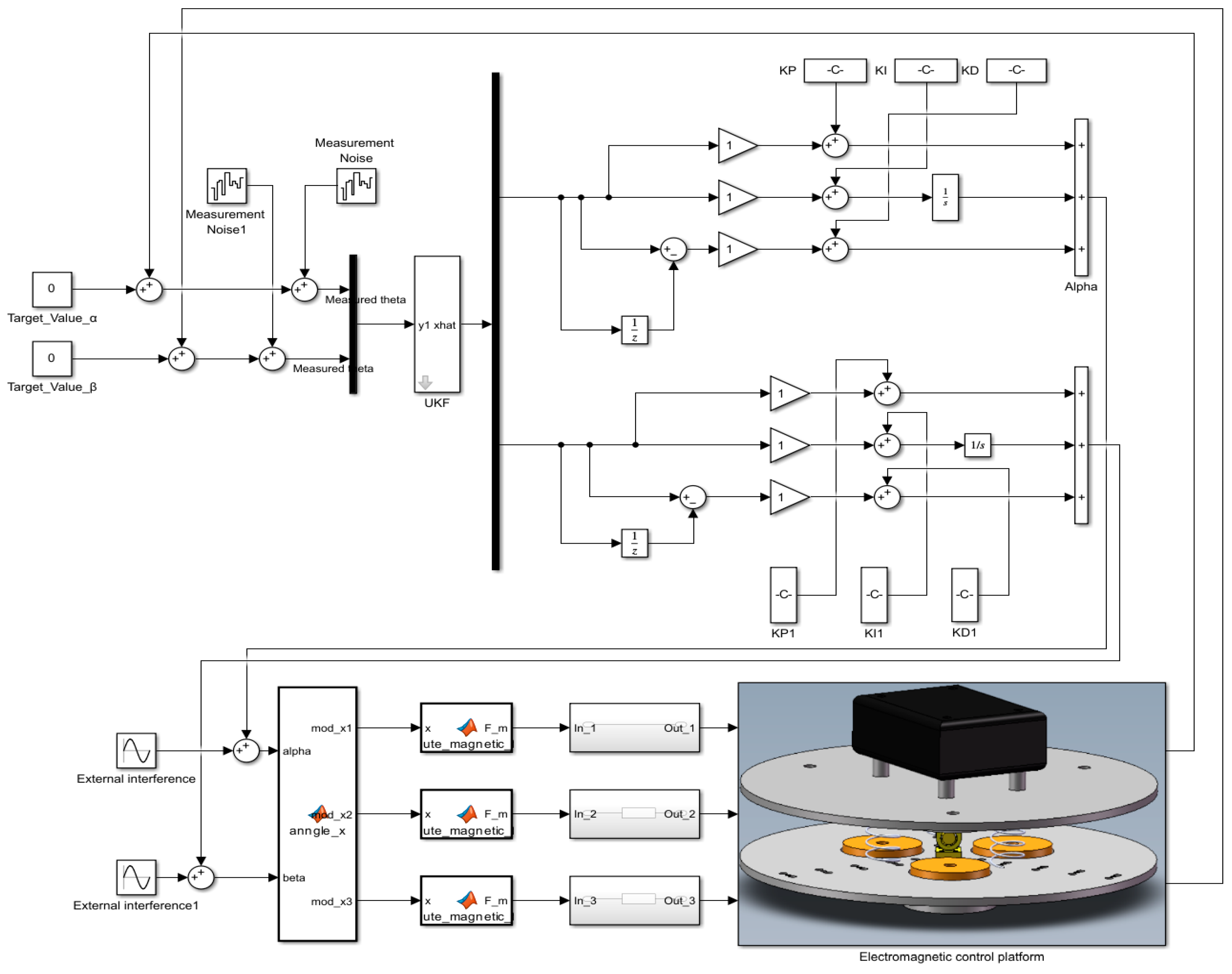
In this section, we simulate and analyze the electromagnetic redundant drive parallel platform model by using Simulink and Simscape tools in MATLAB. The Simulink model is used to design and implement the control system, including input signal generation, control algorithms (PID controllers), and output signal processing, in which we will also add modules such as Simulink-PS converter to convert the signals, so that the control signals can be transmitted to the model, and Simscape is used to build a three-dimensional model of the electromagnetic redundant drive parallel platform. Through the joint simulation of the two, we can describe the dynamic behavior of the system to achieve efficient simulation and verification of complex systems. Figure 9 shows the joint simulation model of the electromagnetic redundant drive parallel platform.

In order to verify the effectiveness of the minimum two-paradigm method of the driving force, this paper simulates the simulated and desired three-dimensional motion trajectories of the joint points at the end of the branched chain by a given change in angle, and the displacement deviation of the motion trajectories is given. The parameter settings are shown in

Table 1. Parallel redundant mechanism scale parameters.

Scale Parameter	Numerical Value	Unit
Moving platform radius Rb	0.06	m
Fixed platform radius Ra	0.04	m
Fore-aft angle range α	±14	(°)
Left-right angle range β	±14	(°)
Time range t	0~5	s
Frequency ω	2π/5	Hz

.

The variations in the pose of the moving platform (in degrees) and the motion trajectory at the end joint of the branched chain (in meters) are described by the following equations:

$$\left\{\begin{array}{c}\alpha =14\times \sin \left({\displaystyle \frac{2\pi }{5}}t\right)\\ \beta =14\times \sin \left({\displaystyle \frac{2\pi }{5}}t\right)\end{array}\right.$$

(38)

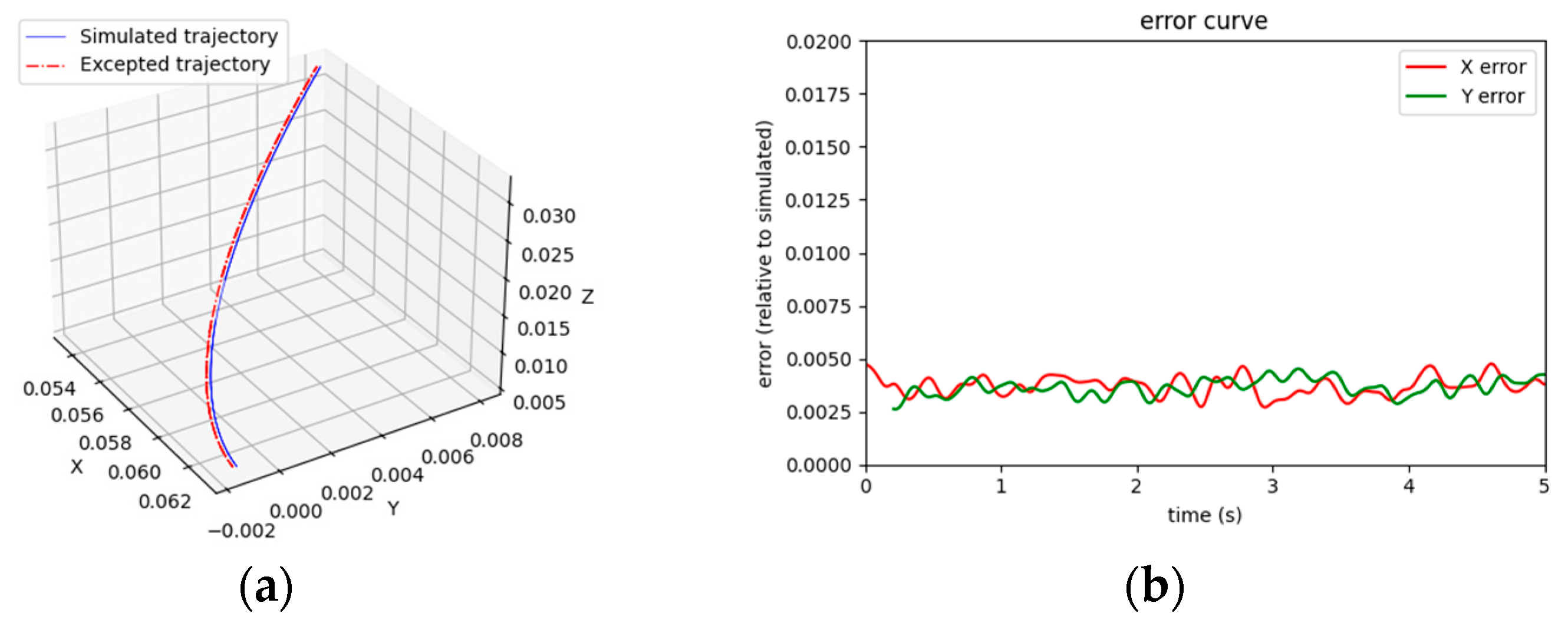
The simulated and desired 3D trajectories of the joint points at the end of the branched chain are derived from the variation of angles $\alpha$ and $\beta$ within the reachable range of the platform motion, as shown in Figure 10a. The simulated and desired trajectory errors of the joint points at the end of the branched chain are shown in Figure 10b.

From the figure, we can see the simulated and desired trajectories and their displacement deviations, and it can be seen that the deviation values are all within a reasonable range of 1%.

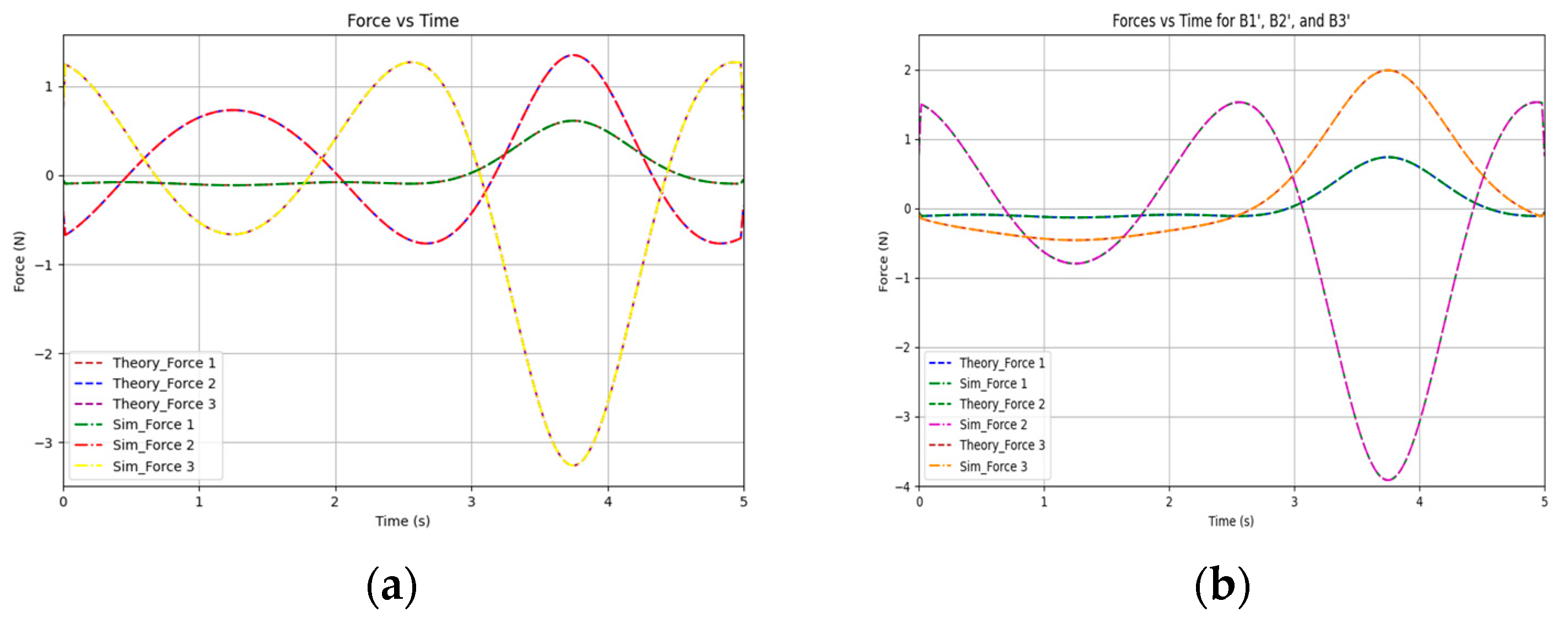
Next, based on the trajectory designed in Figure 10 for the parallel mechanism, the theoretical drive forces for each branch obtained using the minimum two-norm method are compared with the simulated drive forces for each branch [27]. In order to verify the efficiency of the drive force assignment based on the least two-paradigm method used in this paper, we include the traditional hybrid drive force assignment for comparison, and the results show that the proposed method in this paper requires less force and deviation than the traditional method for the same trajectory. The comparison chart is shown in Figure 11.

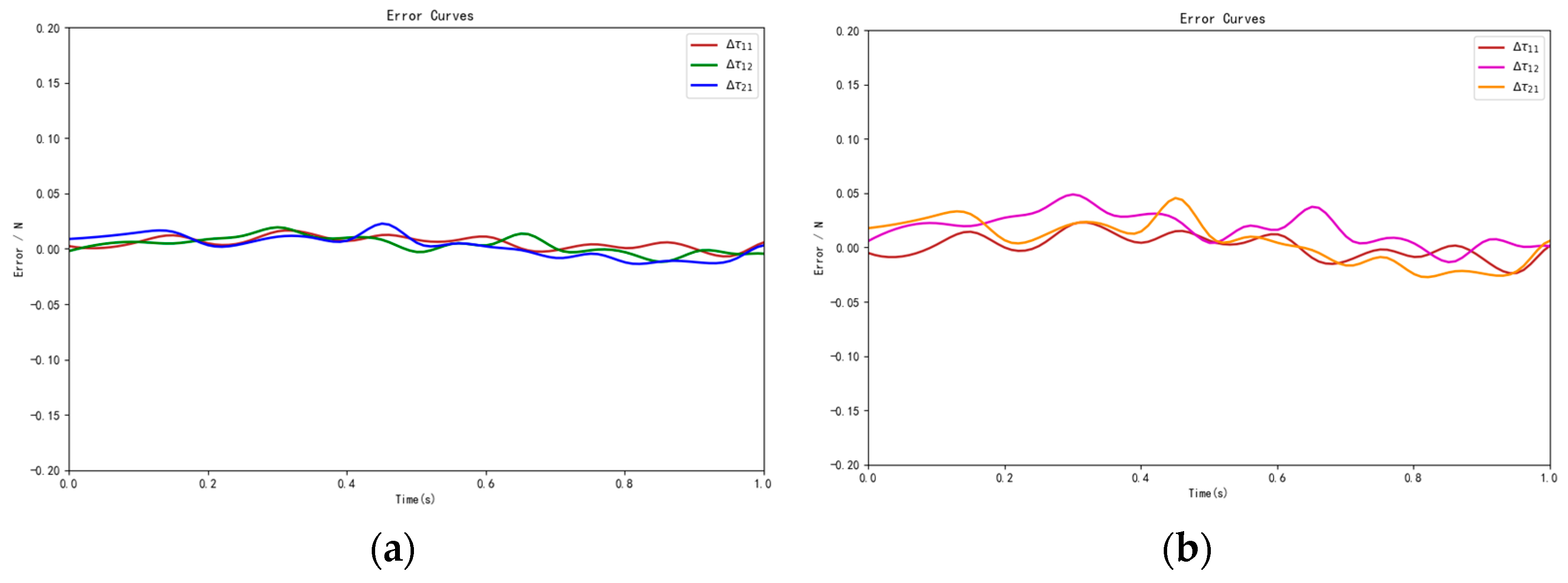
The offset graph between the simulated and theoretical driving force can be seen in Figure 12, it can be seen that the error of the least-square-paradigm-based driving force allocation method used in this paper is at 0.7%, while the error of the traditional hybrid force drive is at 8%, and the effect used in this paper is better. The method used in this paper also uses less force for the same trajectory.

5.2. Evaluation of Interference Immunity, Response, and Load Capacity of Parallel Platforms

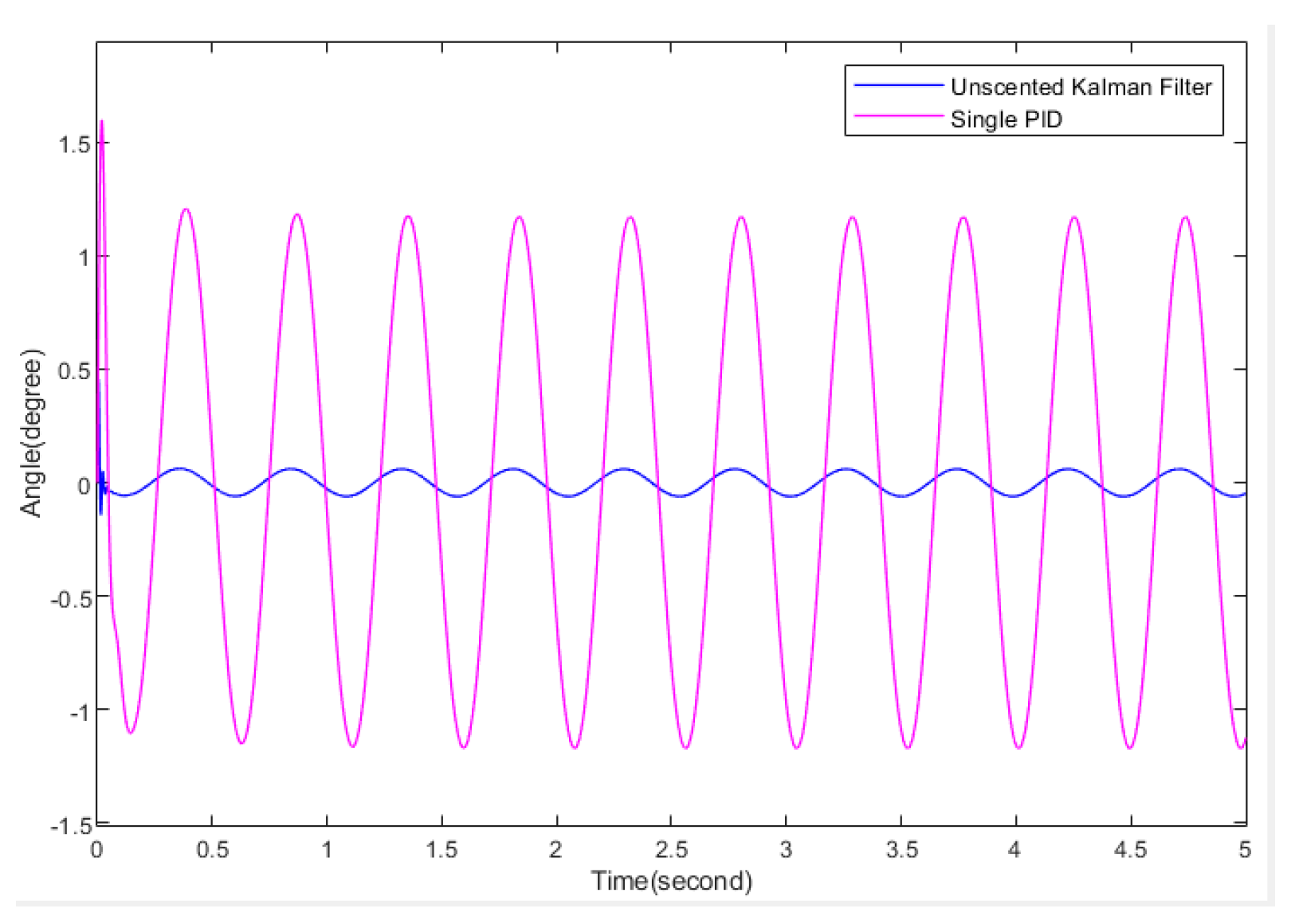
In order to evaluate the performance of the control algorithm, we tested a parallel platform driven by electromagnetic redundancy by adding a periodic sine wave with a peak value of 10 degrees. We performed comparative simulations using a single PID controller versus a PID controller containing a traceless Kalman filter, as shown in Figure 13.

The results show that the PID controller containing the UKF is able to suppress the influence of external disturbances more effectively.

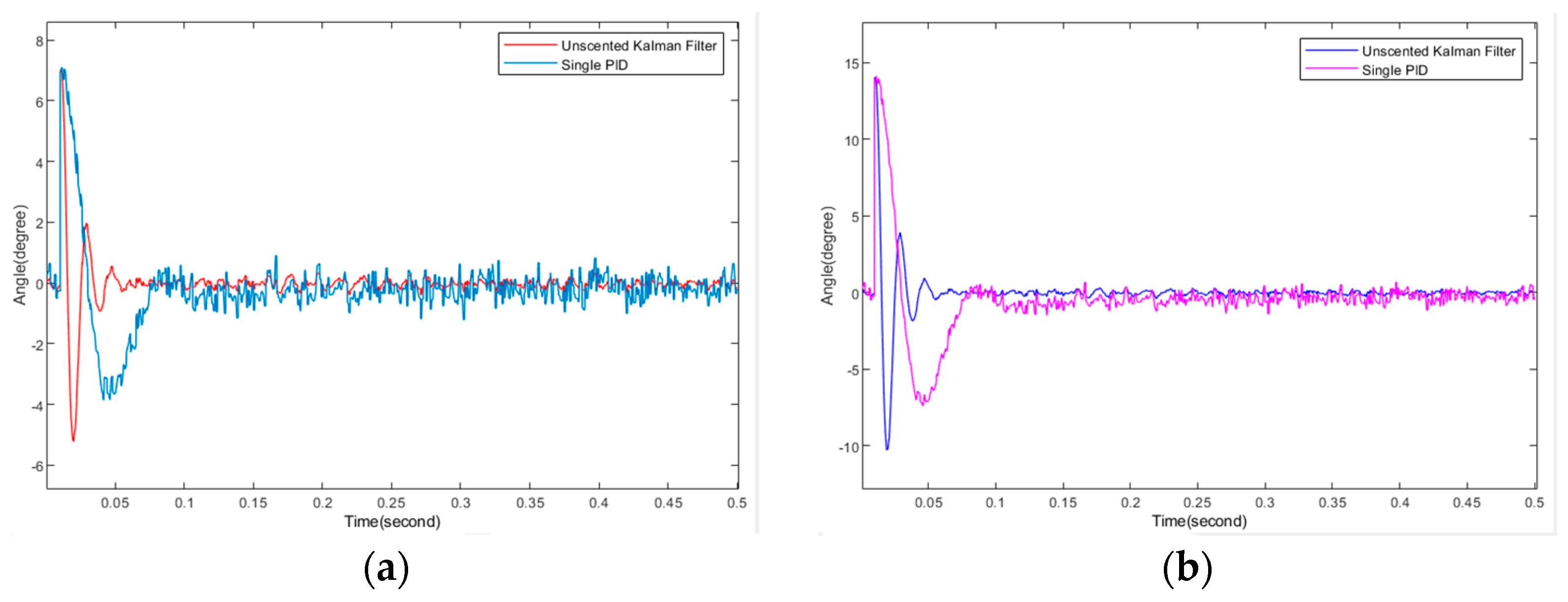
For electromagnetic redundant drive parallel platforms, another very important thing is the response-ability. The response capability can show a platform’s anti-interference ability and control ability. Therefore, we test the platform’s responsiveness by inputting different angle values to the platform, as shown in Figure 14.

The specific condition is to input 7-degree and 14-degree angles to the platform as external interference and add some noise. In the parameterization, we are given K_p = 88,614, K_i = 652,500, and K_d = 130. By comparing the graphs, we can see that the PID controller with UKF used in this paper is better than just the PID controller in terms of response-ability.

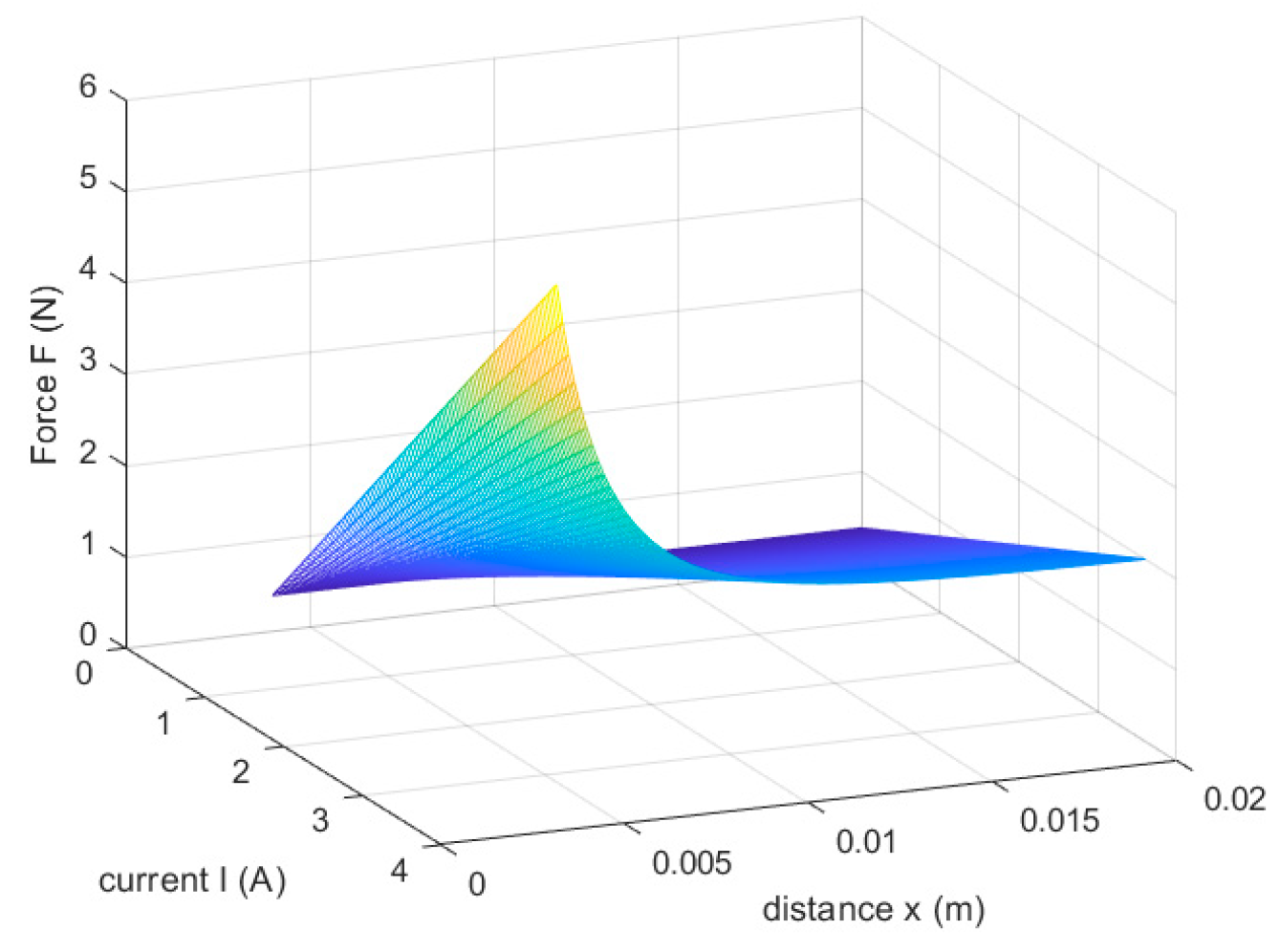
The next step is to evaluate the load capacity of the EM-driven parallel redundant platforms, as the load capacity is directly related to the performance and reliability of the platforms under different operating conditions. Evaluating the load capacity determines whether the platform is able to maintain stable accuracy and motion performance when subjected to varying weights and external forces. This is critical to ensure that the platform is still able to perform accurately in applications with high load and dynamic requirements. Therefore, we used MATLAB to make a 3D plot of the load force of the parallel platform as a function of the length of the branched chain and the current, as shown in the following Figure 15.

From the figure, we can see that with the parameters given in this paper, the load force can reach up to 5.8 N, which can provide loads for some small cameras and so on. Of course, the size of the load force is very much related to the specifications of the electromagnet and permanent magnet, as well as the elasticity coefficient of the spring, so different scenarios and loads, electromagnets, permanent magnets, springs, etc., with different parameters, can be used.

6. Conclusions

In this paper, the control method of a spatial two-degree-of-freedom parallel platform driven by electromagnetic redundancy is investigated. Firstly, the latest research and applications of parallel platforms are analyzed, and a background of the application of this platform on spherical robots is given with a three-dimensional diagram. Then, the platform with an electromagnetic-spring composite pivot chain is equivalent to the SPU parallel platform [28], and the degrees of freedom, inverse kinematics, Jacobian matrix, and offset angle of the platform are analyzed to build a mathematical model of the platform [29].

Next, we derived the relationship between the current and the length and angle of the branched chain through the mathematical model, laying the foundation for the next step of data fusion. By introducing the Unscented Kalman Filter (UKF) [30], we have filtered the angle information well, and the processed angle information can be solved by both PID and mathematical modeling to fuse the current values to achieve more accurate control.

Due to the redundancy of actuators in parallel redundant mechanisms exceeding the number of degrees of freedom, optimally distributing forces to reduce energy consumption and improve system stability is crucial [31]. Then, we used MATLAB to build the simulation model, and according to the input trajectory, we compared the drive force allocation based on the Least-Second Paradigm method used in this paper with the traditional hybrid drive force allocation [32,33], and the method in this paper is better than the traditional both in terms of the error and the use of force allocation. Finally, using simulation software, the response curves and load capacity curves of the platform under different external disturbance conditions are given to further verify the response and load capacity of the design.