A Data-Driven Comprehensive Evaluation Method for Electromagnetic Suspension Maglev Control System

Abstract

As new advanced vehicles, the safety and stability of electromagnetic suspension maglev trains have always been a subject of concern. This study introduces the improved R index and τ-distance index into the performance evaluation of the suspension control system, respectively assessing the stability of the suspension gap and the smoothness of train operation, combining them with grey relational analysis to achieve data-driven comprehensive evaluation. Furthermore, feasibility tests on the Fenghuang Maglev Express validate the effectiveness and superiority of the comprehensive evaluation method based on measured data. Experimental results demonstrate that the data-driven comprehensive evaluation method, through designing specialized evaluation metrics and increasing assessment dimensions, effectively evaluates the performance of the suspension system control loop. Compared to a traditional error integral comprehensive performance index, it offers greater comprehensiveness and accuracy, along with real-time state-monitoring capabilities.

1. Introduction

As a new type of transportation, the maglev train uses non-adhesive magnetic action to separate the maglev vehicle from the track. It has the advantages of low vibration and noise, a friendly environment, strong climbing ability, a small turning radius, etc. Compared with traditional wheel-rail system rail transit, it is more advanced and lower cost. At present, in Germany, Japan, China, and the Republic of Korea, the main research direction is focused on the development of electromagnetic suspension (EMS) maglev vehicles. Among them, the maximum operating speed of most maglev trains is 100 to 160 km/h, which mainly solves the traffic and transportation problems within the city, and the cost is comparable to that of light rail [1].

Because the electromagnetic force is inversely proportional to the square of the suspension gap, the open-loop electromagnetic suspension system is an inherently unstable system with strong nonlinearity and instability, and reliable active control must be applied. In the EMS suspension system, the suspension sensor monitors and feeds back the real-time signal to the suspension controller [2]. The pre-designed control algorithm processes the feedback signal and adjusts the excitation current of the suspension electromagnet to ensure that the suspension gap is stable near the set value so as to achieve stable suspension control.

However, the performance of the control system depends on the accurate identification and parameter setting of the electromagnetic force model. With the extension of the running time, the performance will often degrade due to the mismatch of the model and external disturbance, resulting in poor control effects and even endangering traffic safety in serious cases. Safety is the most important attribute of public transport. The fundamental principle to ensure the safe operation of the EMS maglev system is to strictly ensure that the train does not hit the rail during operation, and at the same time, it must have a certain level of stability. However, the running condition of the EMS maglev train is complicated; the track is not smooth, and the sudden braking of the train and the passengers moving in the train will affect the stable suspension of the train, which is far from the preset value under the impact vibration. Therefore, the comprehensive and accurate performance evaluation of the suspension control system is particularly important [3,4,5]. This can not only guide the parameter tuning of the controller but also monitor the real-time operating status of the maglev train and avoid disastrous consequences in advance. However, most of the existing evaluation methods are one-dimensional evaluations with a single index, which inevitably lacks objectivity and can not measure the state of the suspension control system comprehensively and accurately. In this paper, based on the industry-recognized stationary index, a new data-driven evaluation index is proposed, and a comprehensive evaluation method is designed by using grey correlation analysis [6,7].

2. EMS Maglev Suspension Control System

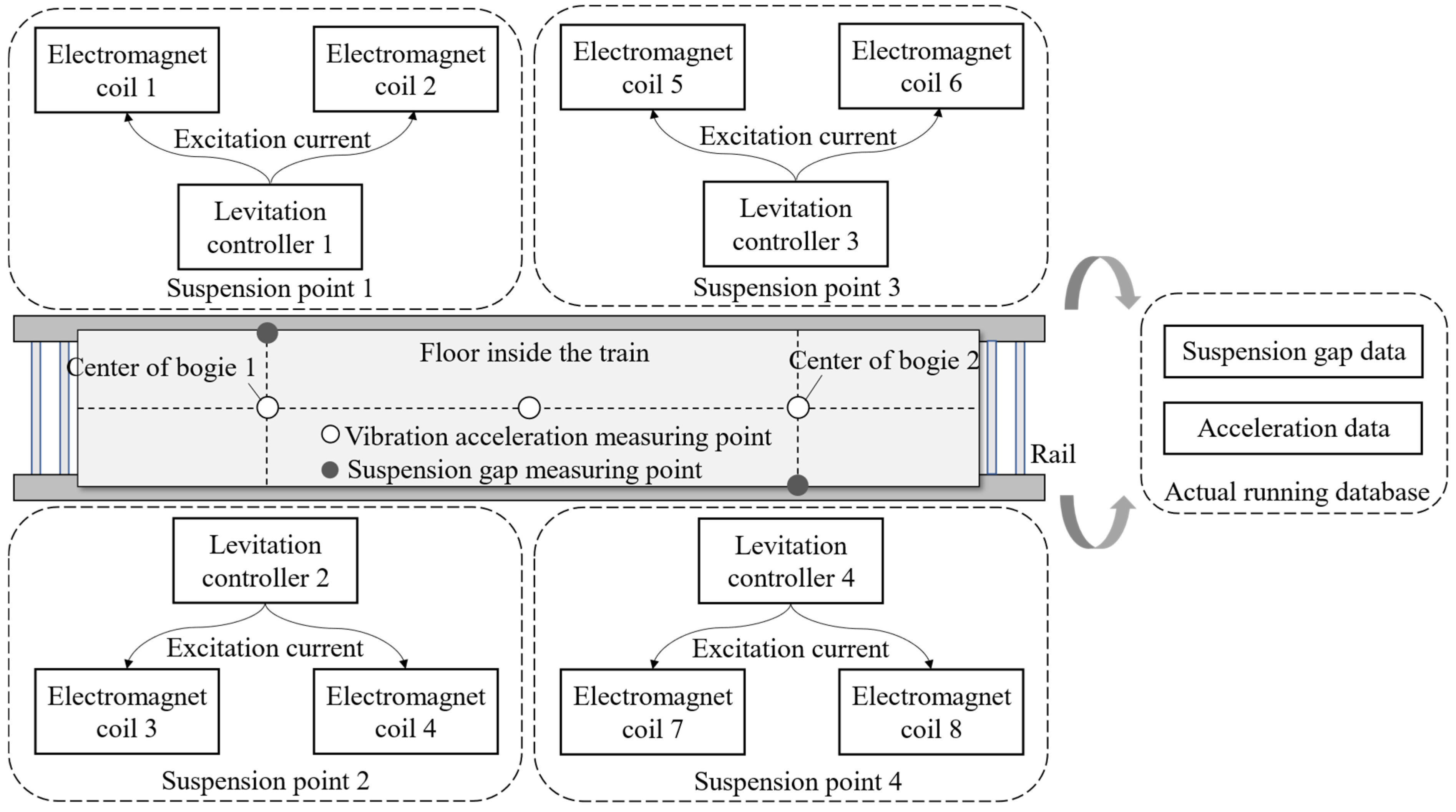
EMS maglev trains are supported by multiple suspension points. Typically, one bogie constitutes a suspension module supported by four suspension points. The electromagnetic coil set at each suspension point generates electromagnetic induction with the track through the input excitation current or voltage, providing an upward suspension force to maintain the suspension gap between the vehicle and the track. Under external disturbances, when the suspension gap increases, the electromagnetic force provided by the electromagnet decreases [8]. If this force is insufficient to support the vehicle’s weight, a track collision incident occurs; when the suspension gap decreases, the electromagnetic force increases, and if it exceeds the vehicle’s weight, a locking phenomenon occurs. Therefore, the suspension system is an open-loop, non-self-stabilizing system that requires a suspension controller to form a closed-loop control circuit for adjustment. The suspension system is equipped with real-time monitoring devices such as gap sensors, acceleration sensors, and current sensors. The signals obtained by these devices serve as feedback for the suspension controller, adjusting the real-time excitation current to create a dynamic balance between electromagnetic force and gravity [9,10,11]. The typical configuration of an EMS maglev train suspension module is shown in Figure 1.

3. Performance Evaluation Method

3.1. Classical Performance Evaluation Methods

Generally, deterministic index and stochastic index are used to evaluate the performance of the control system. In the suspension control system, the deterministic index can better characterize the ability of the suspension control system to track and set the suspension gap, aiming at the time domain performance evaluation of the system response (such as step response, slope response, acceleration response, etc.) under the determined input signal [12]. The randomness index aims at the ability of the suspension control system to resist external random interference such as track irregularity, noise and crosswind. The deterministic performance and the stochastic performance of the suspension control system are evaluated by the error integral comprehensive performance index and the minimum variance index, respectively [13,14].

However, the minimum variance index must learn the prior knowledge of the expected output probability distribution before it can be used, which is very difficult to achieve for some complex systems. Moreover, the minimum variance index has the problem of model mismatch in the performance evaluation of nonlinear systems and time-varying systems, which may not be accurate. In comparison, the data-driven performance evaluation method is more practical and generalized. The error integral comprehensive performance index and Sperling stability index introduced below are both data-driven performance evaluation methods that do not involve complex system modeling and are widely used in the industry [15].

3.1.1. Error Integral Comprehensive Performance Index

The integrated performance index of error integral uses the integral form of the deviation value between the actual output data and the set output data to express the performance of the system, which is related to the dynamic performance index and the steady-state performance index of the control system, and reflects the performance of the whole response transition process of the system through a unified mathematical description. The smaller the index value, the higher the precision of the control system.

The deviation between the actual output data and the set output data at time $t$ is generally represented by $e\left(t\right)$. Subsequently, various indexes can be expressed in the following form:

• Integral of Absolute Error (IAE)

$$IAE={\int }_0^{\infty }\left|e\left(t\right)\right|\mathrm{d}t$$

(1)

The IAE index is an integral of the absolute value of the error. The index reflects well the accumulation of small deviations of the system output, and the smaller the value, the better the damping and transient response characteristics of the system. It can represent the performance of the whole transition process of the system, but the response speed of the system is weak.

2.

Integral of Squared Error (ISE)

$$ISE={\int }_0^{\infty }{e\left(t\right)}^2\mathrm{d}t$$

(2)

The ISE index is the integral of the squared error and time. Compared with IAE, this index can more prominently reflect the large deviation and response speed of the system output. The ISE index is related to the energy consumption of the system and the smaller the value, the smaller the consumption, but it may cause a large oscillation of the system, thus affecting the stability.

3.

Integral of Time-Weighted Absolute Error (ITAE)

$$ITAE={\int }_0^{\infty }t\left|e\left(t\right)\right|\mathrm{d}t$$

(3)

The ITAE index is the integral of the product of time and the absolute value of the error. In addition to reflecting the deviation of the system, this index can better reflect the adjustment time of the system response. Since this index considers the time term, it can better reflect the response time of the system while reflecting the deviation.

4.

Integral of Time-Weighted Squared Error (ITSE)

$$ITSE={\int }_0^{\infty }t{\left(e\right(t\left)\right)}^2\mathrm{d}t$$

(4)

The ITSE index is the integral of error squared over time. This criterion mainly considers the errors in the late stage of the transient response and less considers the initial errors in the response, which is more suitable for evaluating the performance of the system with long-term fluctuations. The smaller the value of this index, the smaller the error in the later phase of the transient response.

3.1.2. Sperling Index

Many railway-developed countries have their own operational stability evaluation system, such as China’s GB/T 5599 [16], Europe’s UIC 513 [17], ISO 2631−1 [18] of the International Organization for Standardization, Britain’s EN 12299/EN 14363 [19,20], Russia’s GOST/R 55495 [21], and the United States’ FRA [22]. The calculation methods of various operational smoothness and running quality evaluation indicators, such as data length and frequency weighting coefficients, differ, and each has its own advantages, disadvantages, and suitability. Since the research object of EMS maglev trains is mainly conducted in China, the train smoothness indicators adopted in GB/T 5599, which was revised in 2019 in China, are used as the calculation standard for Sperling’s smoothness index [23,24,25].

The Sperling index is expressed as follows:

$$W=3.57\sqrt[10]{{\displaystyle \frac{A^3}{f}}F\left(f\right)}$$

(5)

where $A$ is the vibration acceleration in meters per second ($\mathrm{m}/{\mathrm{s}}^2$). $f$ is the vibration frequency expressed in hertz (Hz). $F\left(f\right)$ is the frequency correction factor, as shown in

Table 1. Frequency correction factor.

Vertical Vibration		Transverse Vibration
$\mathit{f}$/Hz	$\mathit{F}\left(\mathit{f}\right)$	$\mathit{f}$/Hz	$\mathit{F}\left(\mathit{f}\right)$
$0.5 \le f<5.9$	$0.325f^2$	$0.5 \le f<5.4$	$0.8f^2$
$5.9 \le f<20.0$	$400/f^2$	$5.4 \le f<26.0$	$600/f^2$
$f \ge 20.0$	1	$f \ge 26.0$	1

.

During calculation, the Sperling index component $W_i$ is calculated according to vibration frequency $f_i(i=\mathrm{1,2},3,......)$, and the final Sperling index is as follows:

$$X_i=\sqrt[10]{W_1^{10}{+W}_2^{10}+\cdots \cdots {+W}_n^{10}}=\sqrt[10]{\sum _{i=1}^n{W}_i^{10}}$$

(6)

3.2. Improved R Index

The R index is derived from a system steady-state detection method proposed by Cao et al. in 1995 [26]. The basic idea is to compare the values of the two variance estimation forms of the continuous variables of the system. The closer the values are, the better the system stability will be. The mathematical form can be expressed as:

$$S_1^2={\displaystyle \frac{1}{n-1}}\sum _{i=1}^n{(y_i-\overline{y})}^2,$$

(7)

$$S_2^2={\displaystyle \frac{1}{2(n-1)}}\sum _{i=1}^n{(y_i-y_{i-1})}^2.$$

(8)

Here, $\overline{y}$ is the average of $y_i$. Under steady-state conditions, the ratio of the two estimated values $R=S_1^2/S_2^2$ is approximately equal to 1, and the distance from 1 means that the system stability becomes worse.

The traditional R index essentially measures the deviation of a given dataset from its average value, while the control performance evaluation focuses more on the deviation between actual and set values. This paper proposes an improved R index that addresses the requirements of practicality, applicability, and real-time performance evaluation. It incorporates the set value into the calculation to meet the performance evaluation requirements and significantly reduces computational complexity by utilizing the exponentially weighted moving average (EWMA) method [27]. This improvement allows for improved computational speed while retaining the trend of the index variations.

For a general control system, under ideal conditions, the optimal performance of the control system ensures that the controller output satisfies the following relationship:

$$y_i=y_{sp}-e_i$$

(9)

Here, $y_i$ and $y_{sp}$ represent the real-time suspension gap and the set ideal gap, respectively, and $e_i$ is the deviation between the suspension gap and the set value. The mean output of the suspension controller $\overline{y}$ is improved to match the set value $y_{sp}$ of the suspension control system, thereby enabling the R index to measure the deviation between the actual value and the set value.

After improvement, the R index of the i point:

$$R_i={\displaystyle \frac{S_{1, i}^2}{S_{2, i}^2}}={\displaystyle \frac{\alpha \times e_i^2+(1-\alpha )\times S_{1,i-1}^2}{\frac{1}{2}\times \alpha \times {(e_i-e_{i-1})}^2+(1-\alpha )\times S_{2,i-1}^2}}$$

(10)

Here $\alpha$ represents the forgetting factor, which denotes the weighting coefficient for the current value. A larger value of $\alpha$ results in smoother data and stronger suppression of noise, while a smaller value approaches the actual data more closely. As a result, the sequence of $R$ values can be obtained, which, combined with some simple data processing techniques, allows for a direct assessment of control performance. For instance, the running process can be divided into multiple segments based on its characteristics and the average value $\overline{R}$ or the median value $R_{\mathrm{M}}$ of each segment’s $R$ value can be determined. By measuring the proximity of these values to the ideal value of 1, an intuitive evaluation of control performance can be achieved.

3.3. τ-Distance Index

Passenger comfort is a crucial factor to consider for the commercial operation of EMS maglev trains. It primarily depends on the vibration acceleration experienced by passengers inside the train. The lower the acceleration value and the smaller its rate of change, the higher the passenger comfort. In this study, a five-dimensional feature extraction approach is proposed for vibration acceleration signals. After standardization, the τ-distance index is introduced to indirectly assess the performance of the suspension control system. The calculation of the τ-distance index involves feature value block computation, feature normality test/normalization, and feature standardization. Then, the average τ-distance index is obtained by averaging the standardized five-dimensional features distributed in a hypersphere, as shown in Figure 2 [28].

3.3.1. Five-Dimensional Feature Introduction

The selected five-dimensional data features include standard deviation ($\sigma$), root mean square ($X_{rms}$), mean value ($\overline{X}$), range (Range) and variance (Var). The calculation formula is as follows:

1.

Standard Deviation. It can reflect the degree of dispersion of a set of data. $\overline{X}$ represents the mean of a set of data, $n$ represents the number of data, and $X_i$ represents the $i$-th number.

$$\sigma =\sqrt{{\displaystyle \frac{1}{n-1}}\sum _{i=1}^n{(X_i-\overline{X})}^2}$$

(11)

2.

Root Mean Square. Also known as effective value, it can represent the discreteness of a set of data.

$$X_{rms}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{X_i}^2}$$

(12)

3.

Average Value. One of the most common statistical indicators that reflects the overall picture of a set of data.

$$\overline{X}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{X}_i$$

(13)

4.

Range. A measure of variation in a set of data.

$$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}=\max \left(X_i\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(X_i\right)$$

(14)

5.

Variance. It is the square of the standard deviation.

$$\mathrm{v}\mathrm{a}\mathrm{r}={\displaystyle \frac{1}{n-1}}\sum _{i=1}^n{(X_i-\overline{X})}^2$$

(15)

3.3.2. Feature Standardization

To make the comfort evaluation results more reliable and accurate, this paper extracts multidimensional data features and constructs a multidimensional feature distribution space. It is necessary to standardize the features; otherwise, the feature distribution space will be a hyper-ellipsoid. A hyper-ellipsoid distribution will cause certain features to have a larger weight in the distance calculation. After standardization, the data features should be distributed in a hypersphere.

Before standardization, it is necessary to clarify the distribution of features. Only features that satisfy a normal distribution can be standardized. The Jarque–Bera method can be used for normality testing: if the feature values of each group satisfy a normal distribution, then set H = 0, and the feature values can be directly standardized; otherwise, if the feature values do not satisfy a normal distribution, set H = 1, and the features need to undergo normal transformation. At this point, the Box–Cox method, based on generalized power transformation, is used to convert the non-normal distribution of features into a normal distribution [29]. The Box–Cox transformation model is as follows:

$$y^{(\partial )}=\left\{\begin{array}{c}{\displaystyle \frac{y^{\partial }-1}{\partial }},\partial \ne 0\\ \ln y,\partial =0\end{array},\right.$$

(16)

In the above formula, $\beta$ is an undetermined transformation parameter, different $\beta$, the transformation is different, so the above formula is a transformation family. Applying the above transformation to the observed values of the dependent variable $y_1,y_2,\cdots ,y_n$, the transformed variable is:

$$y^{\left(\beta \right)}=\left(y_1^{\left(\beta \right)},y_2^{\left(\beta \right)},\dots ,y_n^{\left(\beta \right)}\right)$$

(17)

By appropriately selecting the parameter $\beta$, the Box–Cox transformation can be used to convert feature data into data that satisfies a normal distribution. Further, the z-score method is used to standardize the feature data that meet the normal distribution criteria. The standardized data have the same scale, making comparisons between different features fairer. Additionally, the z-score method does not alter the shape of the data distribution. If the original data are approximately normally distributed, the standardized data will have a mean of 0 and a standard deviation of 1 but will still maintain their original distribution shape. The z-score standardization formula is as follows:

$$X_k^{\prime }={\displaystyle \frac{X_k-{\overline{X}}_k}{\sqrt{\frac{1}{n-1}\sum _{i=1}^n{(X_k-{\overline{X}}_k)}^2}}}$$

(18)

Here, $X_k^{\prime }$ represents the normalized value of the k-th feature, $X_k$ represents the value of the k-th feature and ${\overline{X}}_k$ represents the mean value of the k-th feature.

3.3.3. Define the τ-Distance Index

When the features of the data are standardized, they are distributed within a hypersphere. According to the characteristics of hypersphere distribution, the Euclidean distance to the center of the sphere is used as an indicator of comfort, denoted as $\tau$-distance. The formula is shown below, where $N$ represents the number of features. The smaller the values of these five feature values, the higher the comfort index. Therefore, the smaller the τ-distance, the higher the passenger comfort.

$$\tau ={\displaystyle \frac{\sum _{j=1}^N{X}_j^{\prime 2}}{N}}$$

(19)

4. Data-Driven Comprehensive Evaluation Method

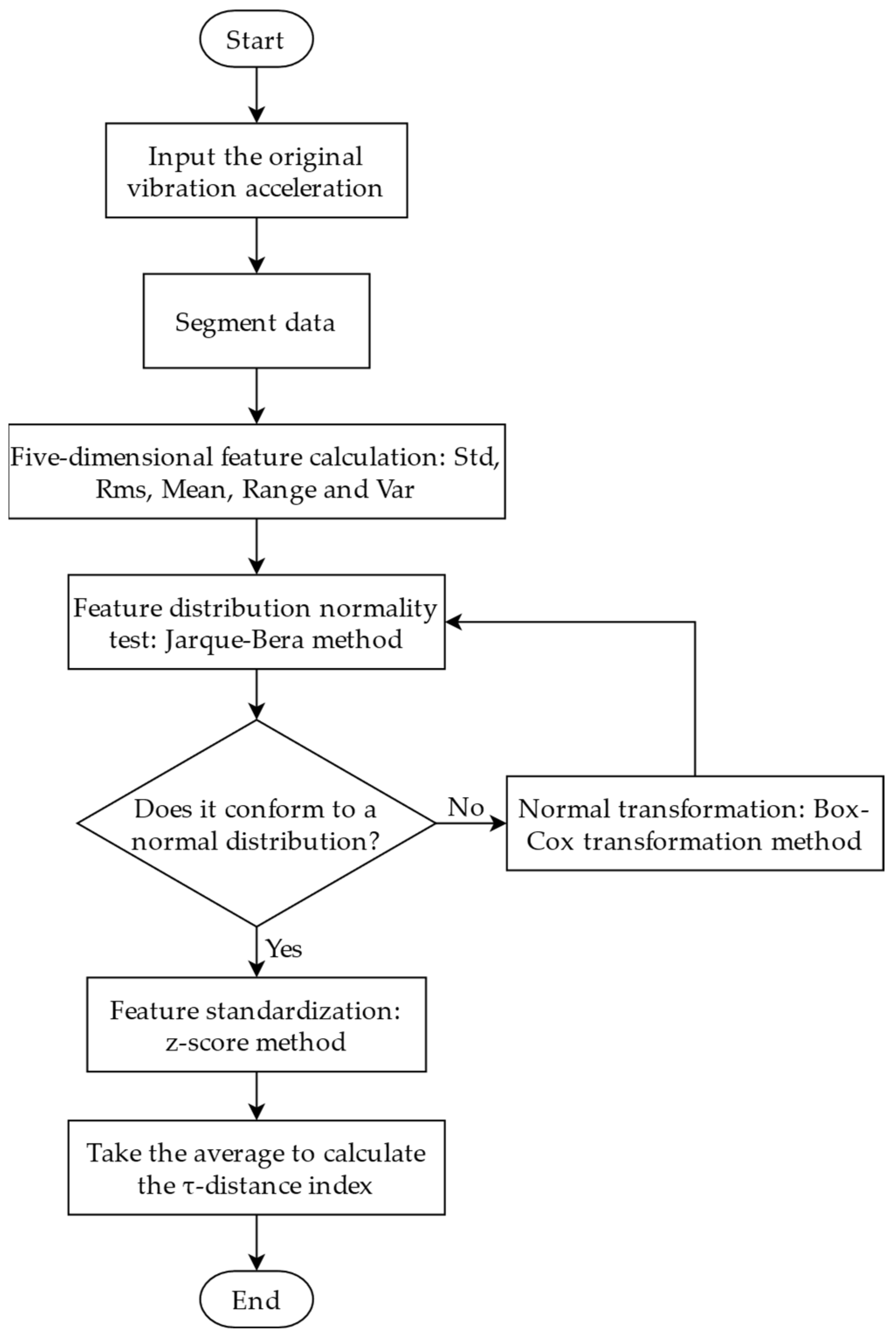
In this paper, industry-recognized stability indicators are used as a reference. Based on the proposed data-driven new evaluation indicators, a comprehensive evaluation method is designed using grey relational analysis.

The improved R index and τ-distance index proposed above can complete performance evaluation using only operational data without affecting system operation since they are non-intrusive. According to their respective characteristics, the improved R index is used to evaluate the fluctuation degree of the suspension gap, thereby monitoring state changes; the τ-distance index is used to evaluate the stability of vertical acceleration, thus analyzing passenger comfort and enhancing the dimensions for performance evaluation. For comprehensive and accurate assessment, industry-recognized stability indicators are used as standards. After calculating each indicator, grey relational analysis is employed to derive indicator weights, leading to the comprehensive evaluation results.

The basic idea of grey relational analysis is to judge the closeness of relationships by determining the similarity of the geometric shapes between the reference data series and several comparison data series, reflecting the degree of association between curves. Its core is to establish a parent sequence that changes over time according to certain rules and treat the changes of each evaluation object over time as subsequences, calculating the degree of correlation between each subsequence and the parent sequence and deriving conclusions based on the correlation size. The specific calculation steps are as follows:

1.

Determine parent and subseries. First, determine the reference series reflecting the characteristics of system behavior and the comparison series affecting the system behavior. This method uses the Sperling stability index as the reference series (parent sequence) and the improved R index and τ-distance index as the comparison series (subsequence).

2.

Normalization of variables. Since the data in the factors series within the system may have different dimensions, making comparison difficult or leading to incorrect conclusions. Data normalization is generally required for grey relational analysis. This method employs mean normalization.

3.

Calculate the grey relational coefficients. Let $x_i\left(k\right)$ be the standardized subsequence, and $y\left(k\right)$ be the standardized parent sequence ($k =\mathrm{1,2},\dots ,n$, $i =\mathrm{1,2},\dots ,m$, $n$ is the data volume of the sequence, and $m$ is the number of subsequences). Then, the correlation coefficient can be expressed as:

$${\xi }_i\left(k\right)={\displaystyle \frac{\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}\underset{k}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|y\left(k\right)-x_i\left(k\right)\right|+\rho \underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}\underset{k}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|y\left(k\right)-x_i\left(k\right)\right|}{\left|y\left(k\right)-x_i\left(k\right)\right|+\rho \underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}\underset{k}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|y\left(k\right)-x_i\left(k\right)\right|}}$$

(20)

where $\rho$ presents the resolution coefficient, $\rho \in (0,\infty )$. When $\rho \le 0.5463$, the resolution is best. The resolution coefficient is usually set to 0.5.

Let ${\mathsf{\Delta }}_i\left(k\right)=\left|y\right(k)-x_i(k\left)\right|$, then:

$${\xi }_i(k)={\displaystyle \frac{\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}\underset{k}{\mathrm{m}\mathrm{i}\mathrm{n}}{\mathsf{\Delta }}_i(k)+\rho \underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}\underset{k}{\mathrm{m}\mathrm{a}\mathrm{x}}{\mathsf{\Delta }}_i(k)}{{\mathsf{\Delta }}_i(k)+\rho \underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}}\underset{k}{\mathrm{m}\mathrm{a}\mathrm{x}}{\mathsf{\Delta }}_i(k)}}$$

(21)

4.

Calculate the grey correlation degree. The grey relational coefficients represent the degree of correlation between each parent sequence and subsequences at each time point. Since these coefficients are numerous and dispersed, it is necessary to aggregate them into a single value for comprehensive comparison. The average value of these coefficients is used to represent the degree of association between the parent sequence and subsequences. The formula for the correlation degree $r_i$ is as follows:

$$r_i={\displaystyle \frac{1}{n}}{\sum }_{k=1}^n{\xi }_i\left(k\right),k=\mathrm{1,2},\dots ,n$$

(22)

After the relational coefficient is calculated, the suspension control system can be comprehensively evaluated. The comprehensive evaluation process is shown in Figure 3.

5. Experiment and Analysis

This paper uses actual operating data from maglev trains on the Hunan Fenghuang Maglev Express to test the effectiveness and accuracy of the comprehensive evaluation method proposed above for assessing the performance of electromagnetic suspension control system loops. The train’s operational stability is tested using both the integrated performance indicators of error integration and the comprehensive evaluation method proposed in this paper. A single normal conducting magnetic levitation car has a running gear that includes five suspension frames, totaling 20 suspension points. The data acquisition system is also equipped with 20 acquisition points per car, capable of simultaneously collecting key data such as suspension gaps, vertical acceleration, and lateral acceleration, with a sampling rate of 1 kSa/s.

5.1. Performance Evaluation of Suspension Control System Based on Error Integral Comprehensive Performance Index

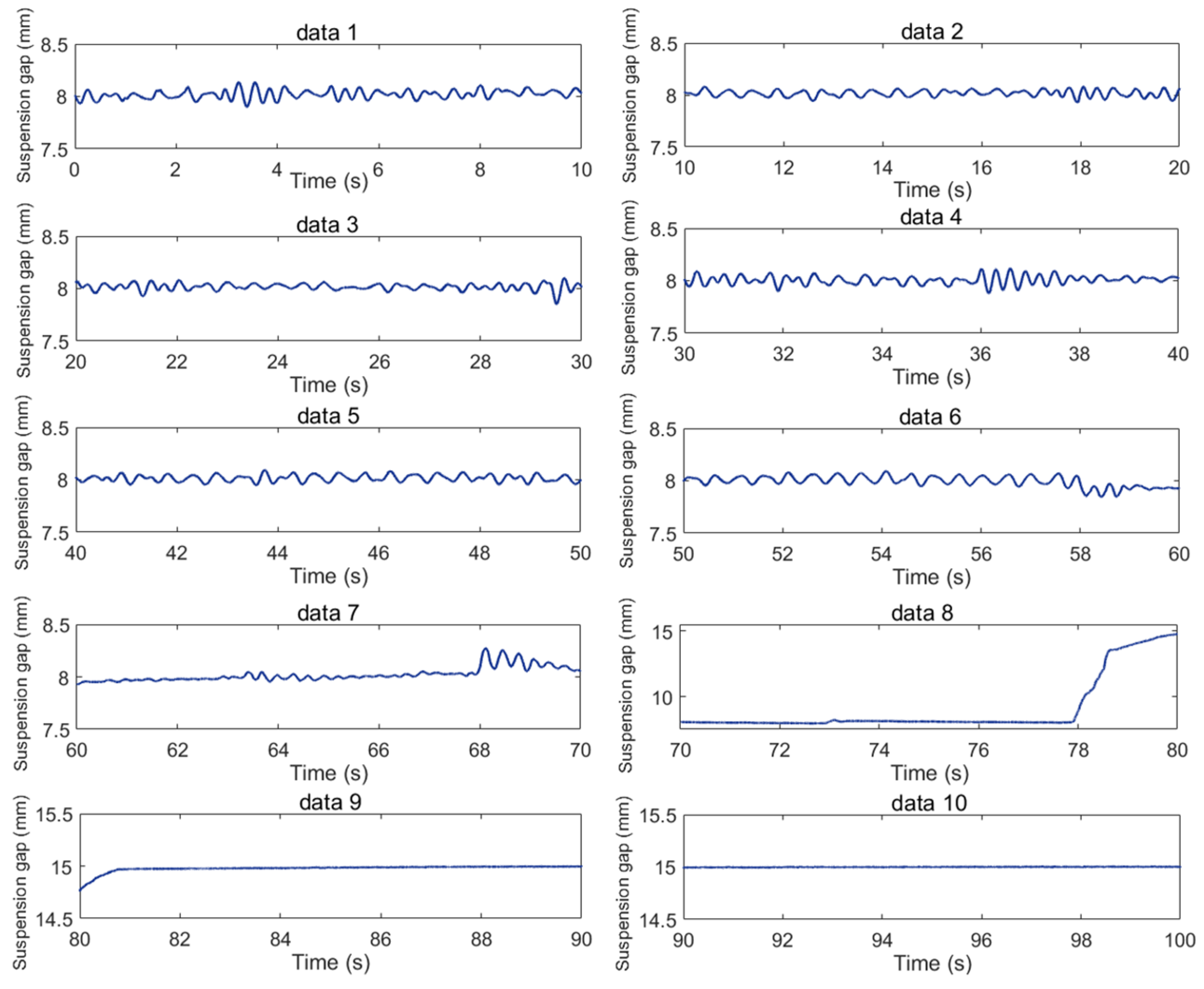
The error integral comprehensive performance index has significant advantages in comprehensiveness and robustness, relying on the precise solution of integrals. The commonly used trapezoidal method for solving numerical integrals approximates the area of small segments with trapezoids, improving accuracy with increased segmentation. However, for raw suspension gap data in Figure 4 with severe fluctuations and poor smoothness, the trapezoidal method introduces significant errors. This paper employs the adaptive Simpson method, which dynamically adjusts the subdivision of subintervals, significantly enhancing the adaptability and accuracy of numerical integration.

The duration of the raw suspension gap data is 100 s. In order to evaluate the controller performance, the data is divided into 10 sections with significant stationarity differences; each section of data lasts 10 s. The segmentation suspension gap is shown in Figure 5. Data 1 to Data 7 correspond to the normal operation phases, Data 10 represents the stopping phase of the train that stops suspension, and Data 8 to Data 9 indicate the intermediate transition phases. It is evident that even trains operating under normal conditions exhibit significant fluctuations in operational gaps, and the state of the suspension controller displays variabilities that do not maintain absolute stability.

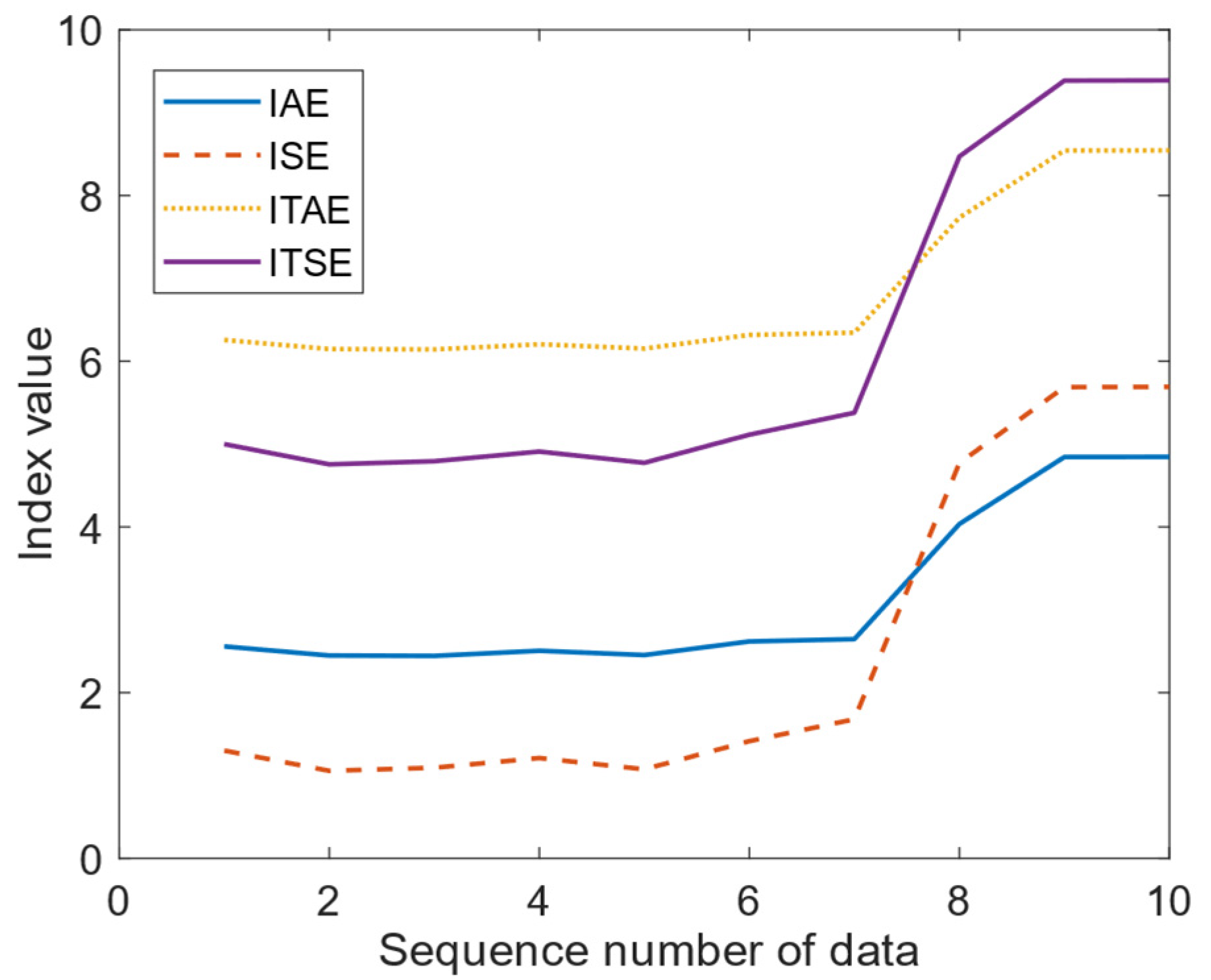
The comprehensive performance index of the error integral was calculated for these ten pieces of data, and the obtained results were recorded in

Table 2. Error integral comprehensive performance index of actual data.

Performance Index Value	IAE	ISE	ITAE	ITSE
data 1	3.61 × 102	2.00 × 101	1.81 × 106	9.99 × 104
data 2	2.80 × 102	1.14 × 101	1.40 × 106	5.69 × 104
data 3	2.78 × 102	1.24 × 101	1.39 × 106	6.20 × 104
data 4	3.20 × 102	1.62 × 101	1.60 × 106	8.12 × 104
data 5	2.84 × 102	1.19 × 101	1.42 × 106	5.94 × 104
data 6	4.15 × 102	2.60 × 101	2.07 × 106	1.30 × 105
data 7	4.42 × 102	4.77 × 101	2.21 × 106	2.39 × 105
data 8	1.08 × 104	5.91 × 104	5.42 × 107	2.96 × 108
data 9	6.98 × 104	4.87 × 105	3.49 × 108	2.43 × 109
data 10	7.00 × 104	4.90 × 105	3.50 × 108	2.45 × 109

. At the same time, for the convenience of plotting, the values of the four indicators are all taken as logarithms to the base of 10, and the curve variations of the four indicators are presented in Figure 6.

Obviously, the error integral comprehensive performance index can reflect the variation trend of the suspension gap accurately. However, the index value itself lacks reference value and is difficult to evaluate quantitatively between different operating speeds and test routes. When the data change is not significant, the variation trends of the four indexes may also conflict with each other. For example, there is a divergence in the changes of the four indices from Data 2 to Data 3. Moreover, the high computational complexity, sensitivity to initial conditions, and ability to handle nonlinear problems all present certain limitations.

5.2. Comprehensive Evaluation of Suspension Control System Performance

5.2.1. Calculation of the Sperling Index W

Selecting the vertical vibration acceleration as the subject, perform Fourier transform on each 10-s segment, and extract the target frequency spectrum data within the range of 0.5 to 40 Hz. Subsequently, calculate the W index for each segment using correction coefficients for the segmented frequencies of 0.5 to 5.9 Hz, 5.9 to 20 Hz, and 20 to 40 Hz, resulting in

Table 3. Sperling index W of actual data.

data 1	data 2	data 3	data 4	data 5
2.07	1.85	2.02	1.89	2.10
data 6	data 7	data 8	data 9	data 10
2.09	1.84	4.01	2.09	2.17

.

5.2.2. Calculation of the Improved R Index

The suspension gap of EMS maglev trains stabilizes at around 8 mm, so a set value of 8 mm is used to calculate the suspension gap deviation. The choice of the forgetting factor $\alpha$ affects the index value and evaluation effect. Based on debugging experience, $\alpha$ is set to 0.05, which can reduce the computational load and improve real-time performance without deviating significantly from the current control effect to the ideal effect. Hence, the improved R index is independently calculated for each 10-s segment. The average values $R_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ and the median values $R_{\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}}$ are obtained, resulting in

Table 4. Improved R index of actual data.

	${\mathit{R}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{n}}$	${\mathit{R}}_{\mathbf{m}\mathbf{e}\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{n}}$
data 1	4.51 × 102	2.22 × 102
data 2	3.13 × 102	1.63 × 102
data 3	3.09 × 102	1.35 × 102
data 4	3.39 × 102	1.67 × 102
data 5	2.75 × 102	1.55 × 102
data 6	8.12 × 102	3.40 × 102
data 7	1.53 × 103	2.28 × 102
data 8	5.93 × 105	1.48 × 103
data 9	6.50 × 106	5.42 × 106
data 10	3.89 × 106	3.80 × 106

.

5.2.3. Calculation of the $\tau$

Before calculating the $\tau$-distance index, it is necessary to perform a normal distribution test on the vertical acceleration data. Using the Jarque–Bera method, the 8th, 9th, and 10th groups of data do not conform to the characteristics of a normal distribution. After the Box–Cox transformation, the feature quantities of 10 segments of data are calculated and standardized. Further, the average $\tau$-distance index is calculated, resulting in

Table 5. Standardized five-dimensional features and $\tau$-distance index of actual data.

	$\mathit{\sigma }$	${\mathit{X}}_{\mathit{r}\mathit{m}\mathit{s}}$	$\overline{\mathit{X}}$	Range	Var	$\mathit{\tau }$-Distance
data 1	−0.32	−0.28	−0.45	1.49	−0.58	0.59
data 2	−0.32	−0.29	−0.45	1.58	−0.58	0.65
data 3	−0.29	−0.26	−0.46	1.73	−0.58	0.74
data 4	−0.32	−0.28	−0.45	1.40	−0.58	0.54
data 5	−0.31	−0.28	−0.45	1.63	−0.58	0.67
data 6	−0.43	−0.37	−0.45	1.18	−0.59	0.45
data 7	−0.37	−0.32	−0.45	1.22	−0.58	0.45
data 8	−0.30	−0.27	−0.44	4.80	−0.58	4.74
data 9	−0.51	−0.46	−0.49	1.18	−0.59	0.49
data 10	−0.53	−0.47	−0.49	1.16	−0.59	0.49

.

5.2.4. Comprehensive Evaluation Index Calculation

Using the Sperling index as the parent sequence, the improved R index and $\tau$-distance index as subsequences, and taking the resolution $\rho =0.5$, the grey relational coefficients are calculated and resulting in

Table 6. Subsequence Grey Relational Coefficients.

The improved R index	0.7062
$\mathrm{The} \tau$-distance index	0.8930

.

It can be seen that the $\mathsf{\tau }$-distance index has a stronger correlation with the stationarity index and should be given a higher weight in the comprehensive evaluation. After weighting the standardized subsequences, a comprehensive evaluation value can be obtained. The final comprehensive evaluation value is compared with the above indices, as shown in

Table 7. Comparison of index values.

Comparison of Index Values	IAE	ISE	ITAE	ITSE	Sperling Index	${\mathit{R}}_{\mathbf{m}\mathbf{e}\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{n}}$	$\mathit{\tau }$-Distance	Comprehe-Nsive Evaluation Value
data 1	3.61 × 102	2.00 × 101	1.81 × 106	9.99 × 104	2.07	2.22 × 102	0.59	0.60
data 2	2.80 × 102	1.14 × 101	1.40 × 106	5.69 × 104	1.85	1.63 × 102	0.65	0.47
data 3	2.78 × 102	1.24 × 101	1.39 × 106	6.20 × 104	2.02	1.35 × 102	0.74	0.49
data 4	3.20 × 102	1.62 × 101	1.60 × 106	8.12 × 104	1.89	1.67 × 102	0.54	0.55
data 5	2.84 × 102	1.19 × 101	1.42 × 106	5.94 × 104	2.10	1.55 × 102	0.67	0.57
data 6	4.15 × 102	2.60 × 101	2.07 × 106	1.30 × 105	2.09	3.40 × 102	0.45	0.69
data 7	4.42 × 102	4.77 × 101	2.21 × 106	2.39 × 105	1.84	2.28 × 102	0.45	0.57
data 8	1.08 × 104	5.91 × 104	5.42 × 107	2.96 × 108	4.01	1.48 × 103	4.74	2.25
data 9	6.98 × 104	4.87 × 105	3.49 × 108	2.43 × 109	2.09	5.42 × 106	0.49	2.45
data 10	7.00 × 104	4.90 × 105	3.50 × 108	2.45 × 109	2.17	3.80 × 106	0.49	1.40

.

5.2.5. Analysis of Experimental Results

Based on the comparison of the values of various evaluation indicators presented in Table 6, it can be seen that the comprehensive evaluation index demonstrates a strong integrative capability and closely aligns with the actual performance of the suspension control system. Taking Data 5 and Data 6 as examples, the suspension gap graph shows that Data 6 exhibits more severe fluctuations in the latter half, deviating further from the set value. This is reflected in the four indexes of the integral error performance and the comprehensive evaluation index, all of which show higher values for Data 6 compared to Data 5. Focusing on Data 2, Data 3, and Data 5, the error integral comprehensive performance index for these three datasets is very close, making the evaluation inconclusive. However, the comprehensive evaluation index suggests that the suspension control system performance corresponding to Data 5 is the worst, while Data 2 has the best performance. This aligns with the Sperling index results, where Data 5 shows the most intense vibration and Data 2 the smoothest. Moreover, the comprehensive evaluation index can accurately identify the operational state of the suspension control system. For instance, the comprehensive evaluation index value for Data 8 is significantly higher than that for Data 7, indicating a sudden change in the index value. Conversely, the index value for Data 10 is suddenly much lower compared to Data 9. This suggests that the suspension control system abruptly left its stable suspension state and then became slightly stable but could not return to its usual stable level. This corresponds to the suspension frame descending during the Data 8 period (around 70 to 80 s) and stabilizing during the Data 10 period (around 90 to 100 s). The comprehensive evaluation results match the actual state very well.

6. Conclusions

Based on the data-driven performance evaluation method for EMS maglev control systems it is of significant importance for the performance monitoring, evaluation, and diagnosis of maglev train operations. The comprehensive evaluation method proposed in this paper is based on the classical Sperling index, the proposed improved R index, and the $\tau$-distance index, utilizing the grey relational analysis method to achieve a comprehensive and accurate evaluation of the suspension control system performance and simulation was conducted using actual operation data. The experimental simulation results show that, compared with the traditional error integral comprehensive performance index, the comprehensive evaluation method proposed in this paper ensures usability and achieves evaluation from more dimensions, improving comprehensiveness and accuracy, with evaluation results aligning well with the real-time state of the suspension control system. In practical applications, there is no need to obtain a complex model of the control system; performance can be accurately assessed, and state changes of the control system can be obtained based solely on operational data, thus achieving real-time monitoring and online evaluation, laying the foundation for improving the performance of EMS maglev control systems.

It should be noted that some deficiencies still exist in this study. For example, the reference sequence in grey relational analysis is derived from the industry’s classical evaluation system, which limits the transferability of this method. Future research may consider enhancing the general applicability of the comprehensive evaluation method, allowing more industrial applications to reference this method.