Abstract
The electromagnet module, as a fundamental component providing levitation force for maglev trains, plays a crucial role in ensuring the stability of train operation. However, vibrations can easily occur due to the mechanical coupling between the two suspension points of the electromagnet module. To reveal the inherent instability of the system and the coupling relationship between the state variables, a state-space equation that considers the mechanical coupling between the two suspension points is established. Furthermore, a differential control algorithm based on geometric feature transformation is proposed to mitigate the structural coupling vibration. Simulation experiments are conducted to compare the dynamic characteristics of the system before and after implementing the improvement algorithm under complex conditions. At the same time, the influence of control parameters on electromagnetic vibration was analyzed, focusing particularly on vibrations resulting from parameter mismatch, offering crucial insights for enhancing system stability. Additionally, suspension tests are carried out on the high-speed double bogie test platform in the Key Laboratory of Hunan Province to further validate the effectiveness of the proposed algorithm. The proposed control framework is both effective and concise, making it easy to implement in engineering applications. This research holds significant practical value in improving the stability of maglev trains.
1. Introduction
Normal conductive maglev trains achieve stable contactless suspension between the vehicle and the track by utilizing the electromagnetic force generated by conventional magnets. This innovative mode of rail transit provides various advantages over traditional urban rail transit systems, such as subways and light rails. Specifically, it offers low vibration and noise levels, strong climbing ability, small turning radius, and environmental friendliness, making it a highly promising means of transportation in the modern era [1,2,3].
The special nature of its technology also introduces unique issues. Unlike wheeled trains, maglev trains may experience vehicle–track coupled vibration even when statically suspended on the guideway [4]. Maglev trains require high-precision tracks to maintain smooth and high-speed operations, and bridge structures are more conducive to meeting these requirements compared to ground-level tracks. Therefore, most of the maglev lines that have been constructed in China are primarily composed of bridges. To address the issue of coupled vibrations, one potential solution is to enhance the bridge’s stiffness, damping, and track installation accuracy. However, such an approach would substantially escalate construction and maintenance expenses. Hence, a more optimal approach involves mitigating coupled vibrations through optimized suspension control strategies, thereby ensuring economic viability. Along these lines, numerous domestic and international scholars have conducted extensive analyses on the matter of vehicle–track coupling. Based on a vector-based finite element method, a magnetic coupling system model for medium- and low-speed maglev trains was constructed [5]. Additionally, the stability criterion for Hopf bifurcation in magnetic levitation systems was proposed, and coupled vibrations between maglev trains and tracks were analyzed utilizing the Hopf bifurcation criterion [6,7]. According to some scholars, the mismatch between control parameters and track parameters can result in vehicle–track coupling vibrations. Consequently, a comprehensive analysis has been conducted to examine the stability of the vehicle–track coupling system and the impact of control parameter adjustments. The findings reveal that modifying controller parameters can effectively mitigate coupling vibrations to a certain extent.
When trains travel on flexible structures like switches, this can result in coupling vibrations between the high-speed maglev train and the track, which in turn leading to increased fluctuations in the suspension air gap, directly impacting the safety and comfort of train operations. The Shanghai high-speed maglev line in China, for instance, experiences excessive vibration when vehicles pass through switches. To address the issue of coupling vibration, one approach is to increase the stiffness and damping of the structures. However, this significantly raises the overall system cost. As a result, experts have reached a consensus on mitigating coupling vibration through the optimization of suspension control strategies. The impact of control parameters on the dynamic characteristics of the maglev system was investigated through numerical studies on the maglev train–track coupling system. Additionally, the elastic deformation characteristics of the track and the conditions for dynamic Hopf bifurcation of the maglev control system were analyzed [6,7]. According to some scholars, the mismatch between control parameters and track parameters can result in vehicle–track coupling vibrations. Consequently, a comprehensive analysis has been conducted to examine the stability of the vehicle–track coupling system and the impact of control parameter adjustments. The findings reveal that modifying controller parameters can effectively mitigate coupling vibrations to a certain extent. A simulation analysis was conducted to investigate the impact of PID control parameters on the medium–low-speed train–track coupled vibrations. Additionally, coupling vibration characteristic tests were performed on the maglev operational line in Changsha [8]. The influence of control parameters on the dynamic characteristics of the maglev system is explored through numerical analysis [9,10]. In response to vehicle–track self-excited vibrations during static suspension or low-speed operation, some scholars have proposed methods such as adaptive virtual dampers, band-stop filters, and adaptive notch filters to suppress vibrations. These methods are employed due to the concentrated vibration frequencies in such scenarios [11,12,13,14]. Furthermore, Wang and Song, et al. [15,16,17,18] have conducted in-depth analyses of the vehicle–track coupling issue.
However, most of the current research has predominantly focused on the interaction between the vehicle and the track, overlooking the coupling effect between the two suspension points of the electromagnetic suspension module. Furthermore, existing studies tend to treat the two suspension control units as separate systems and regard their mutual influence as interference force. A multi-point suspension control optimization algorithm is proposed to address the issue of suboptimal performance resulting from the independent control of two points in electromagnetic suspension [19]. While this method falls short in considering the mechanical coupling effect between the electromagnetic suspension modules, it was pointed out that the electromagnetic module serves as a fundamental component for providing the levitation force in maglev trains.The motion of the electromagnetic module directly influences the stability of train operations [20,21]. In-depth research was conducted, and a feedback decoupling controller was designed, yielding promising results through simulation analysis. The mutual interference between the two suspension units can effectively be eliminated by this control scheme. However, it should be noted that the algorithm relies on models and presents a relatively complex implementation process in the engineering practice. The dynamic response of the vehicle–track coupled system under motion was investigated, while simultaneously analyzing the factors contributing to coupled vibrations [22].
In summary, extensive research has been conducted by domestic scholars on the vibration problems of vehicle–track coupling systems from various perspectives. However, the focus has been on the vehicle–track relationship, with more emphasis on the independent control of each suspension point. There has been limited consideration of the vehicle–track coupling vibrations caused by the structural coupling of the electromagnetic module at both ends, and the designed algorithms face challenges in practical implementation. A crucial requirement is to propose control algorithms that are both easily implemented in engineering and effective in reducing vibrations to tackle the issue of mechanical structural coupling.
In this research, the motion equations for an electromagnetic module considering the coupling between two suspended structures were established and the state-space equations were derived to reveal the coupling relationships among the state variables. To address the coupled vibrations caused by structural coupling, we proposed a differential control algorithm based on geometric feature transformation. The effectiveness of the algorithm under complex conditions was verified through simulations and experimental validation. In summary, the main contributions of this paper can be summarized as follows:
- (1)
- Regarding vehicle–track coupled vibration due to the mechanical structure, a differential control algorithm is proposed based on geometric feature transformation to address the vibration caused by mechanical coupling. This algorithm is an improvement upon the existing independent control algorithm and is easily implementable in engineering practice.
- (2)
- The influence of control parameters on suppressing non-mechanical coupling vibrations is examined, and the effectiveness of the proposed approach in mitigating vehicle–track coupling vibrations has been verified through a simulation.
- (3)
- In response to non-ideal conditions such as installation precision and external force disturbance commonly encountered in engineering practice, a comparative analysis was conducted on the dynamic response of the system before and after the improved algorithm. The results demonstrate the continued effectiveness of the proposed algorithm under these non-ideal conditions, while also providing guidance for engineering design.
- (4)
- The effectiveness of the control strategy has been experimentally verified, providing valuable insights for magnetic levitation control and holding significant engineering practical applications.
The rest of this paper is organized as follows. In Section 2, we introduce the modeling of the electromagnetic module–track coupling system and explore the open-loop stability of the coupling system. The coupling relationships between variables are revealed through the state-space equations. In Section 3, we propose a differential control algorithm based on geometric feature transformation. In Section 4, a comparative analysis of the algorithm before and after improvement under various scenarios is conducted. Section 5 gives the experimental results and analysis. The paper ends with conclusions and future work in Section 6.
2. Establishment of Electromagnet Module Suspension Modeling by Accounting for Mechanical Coupling
The electromagnetic module comprises left and right suspension points, which are interconnected as a unified entity through a steel structure, as depicted in Figure 1. According to the simplified schematic diagram of the electromagnetic module, the corresponding dynamic equations are as follows.
where J is the moment of inertia of an electromagnet, represents the force exerted by the left metal spring, represents the force exerted by the right metal spring, and represents the rotation angle of the center of mass. Moreover, the physical meanings of other letters are given in Table 1. According to the geometric positional relationship, it can be obtained that
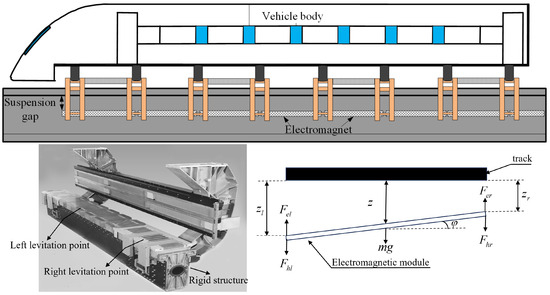
Figure 1.
Illustration of structure coupling for electromagnetic module suspension system.

Table 1.
Physical meaning of system parameters.
Since the inclination angle is very small, it can be assumed that . Substituting Equation (2) into Equation (1), the following can be obtained:
The physical meanings represented by each symbol in the figure are as shown in Table 1.
A metal spring can be modeled as a damped spring system. The expression for the force can be described as
where and represents the stiffness coefficient of the left and the right metal spring. and represents the damping of the left and the right metal spring. The expression for the electromagnetic circuit is as follows:
where A represents the effective area of the electromagnet. The expression for the electromagnetic force at both ends of the module is defined by the following equation:
To summarize, the nonlinear mathematical model of the suspension module is given by
The nonlinear model can be Taylor-expanded around the equilibrium point.
where, to make it look concise, the incremental symbol is omitted. The state variables are defined as . Near the equilibrium point, . After simplification, the state-space equations are as follows.
where
According to the state-space equation, the model described above can be identified as a coupled system. The dynamic characteristics of the left suspension point are influenced by the gap and current of the right suspension point’s state variables, while the dynamic characteristics of the right suspension point are influenced by the gap and current of the left suspension point’s state variables. There is a mutual influence between the dynamic characteristics of the left and right suspension points. Furthermore, it should be noted that the system is inherently unstable and necessitates designing a controller.
By substituting the values in Table 1, the root of the open-loop system of the electromagnetic module can be calculated as follows. The system has positive eigenvalues, and a controller needs to be designed for an unstable system.
On the other hand, substituting the values from Table 1, the roots of the electromagnetic module system are as follows. The presence of positive eigenvalues in the system requires the design of a controller to stabilize it.
3. A Differential Control Algorithm Based on Geometric Feature Transformation
Currently, in practical engineering, magnetic levitation control systems primarily utilize a current and position loop with PID controllers. The control framework is depicted in Figure 2, marked as Method 1.

Figure 2.
The describtion of independent control framework based on dual-loop PID.
The adoption of this control scheme results in a coupling relationship between the two suspension points. Each suspension point perceives the influence of the other as external interference, causing suboptimal control performance and the occurrence of coupling vibration. Therefore, improving the dual closed-loop PID controller to achieve decoupled control is a practical and significant approach.
The left suspension point and right suspension point are connected by a rigid structure, but the center of mass motion and rotation around the center of mass of the rigid structure are two independent movements. By controlling the position of the center of mass and the rotation angle, it is possible to achieve position control of the electromagnetic module. Based on this, we can derive the following control law:
where and , respectively, represent the angle error and gap error of the electromagnet barycenter. In the engineering project, due to the existence of sensors and actuators only related to the left and right suspension points in the physical system, it is not possible to directly control the angle and center of mass. However, there is a geometric relationship between , , z, and . z and can be obtained from and through a nonsingular transformation. Therefore, the following control law is designed, using differential control, and the control framework is designed as shown in Figure 3, marked as Method 2.
where
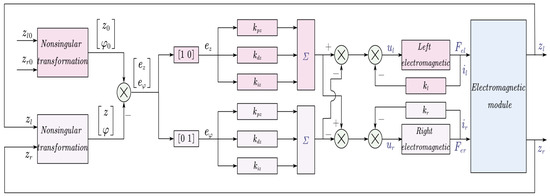
Figure 3.
The description of the differential control framework based on nonsingular transformation.
4. Vibration Control of a Maglev Train–Track Coupling System
A nonlinear model was built using simulation software, and closed-loop control was implemented using Method 1 and Method 2, respectively. The simulation results are shown in the figure. Under ideal conditions with no disturbances, both algorithms have demonstrated excellent control performance, as shown in Figure 4a–c. The left and right suspension points can quickly track the target gap with the rotation angle maintained at 0. The levitation process is relatively smooth, and the dynamic performance of the electromagnetic module is not affected by mechanical structure coupling.
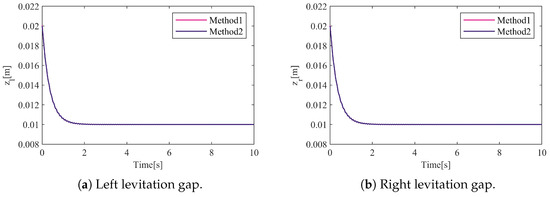
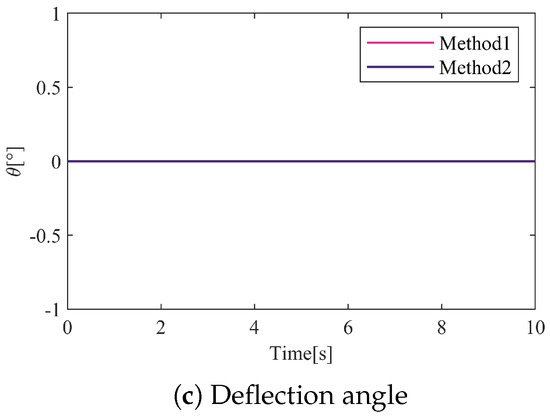
Figure 4.
Respose of system under ideal conditions with no disturbances.
During train operations, deviations in the installation of an electromagnetic module can affect the initial working conditions of the suspension points, ultimately affecting their overall performance. To simulate such deviations in engineering, the initial gap of the left and right suspension points is set as 21 mm and 19 mm, respectively. Through a simulation, the dynamic response curves of the system are obtained, as illustrated in Figure 5 and Figure 6. Both control methods tend to stabilize the system. However, Method 1 exhibits significant fluctuations in the suspension gap during the approach to the set value. Method 2, on the other hand, shows a quick attainment of 0 degrees in angle, indicating no coupling effect between the left and right suspension points. Consequently, the suspension gap curve is smoother than when using Method 1. Under Method 1 and Method 2, the closed-loop system exhibits distinct primary vibration frequencies from the Figure 7. Notably, the amplitude at the primary vibration frequency for Method 1 is greater than that for Method 2.
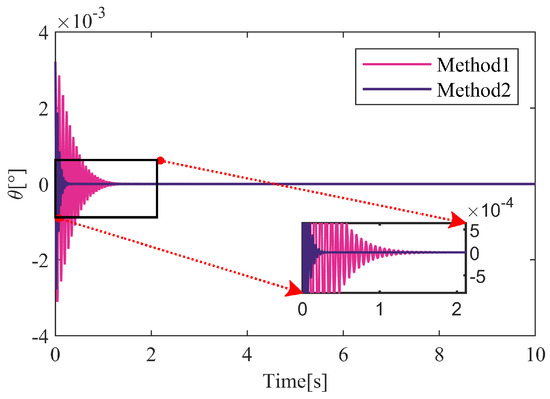
Figure 5.
Dynamic response for deflection angle under different methods when an initial deviation exists.

Figure 6.
Dynamic response for levitation gap under different methods when an initial deviation exists.

Figure 7.
Frequency response for angle data under different methods when an initial deviation exists.
With an increase in deviation to 1.5 mm, Figure 8 and Figure 9 show the curve of the dynamic response. The gap fluctuation is more significant with Method 1. However, after applying Method 2, the system response is obviously improved and effectively suppresses the coupling vibration.

Figure 8.
Dynamic response for deflection angle under different methods when initial deviation is 1.5 mm.

Figure 9.
Dynamic response for levitation gap under different methods when initial deviation is 1.5 mm.
To observe the impact of deviation on the system more intuitively, we can gather the dynamic response curves of the system under different deviations in Figure 10 and Figure 11. From the graph, it is evident that as the deviation increases, the dynamic characteristics of the system gradually deteriorate. Therefore, enhancing the installation accuracy of the electromagnet holds great significance in improving the dynamic performance of the system.

Figure 10.
Dynamic response for levitation gap under different initial deviations using Method 1.
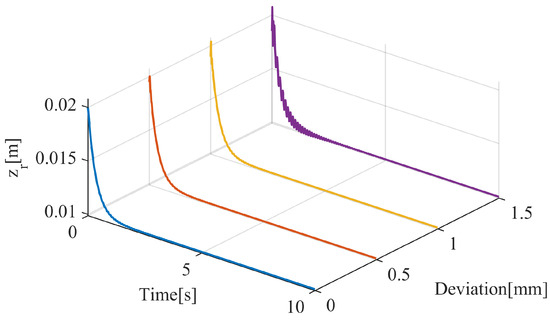
Figure 11.
Dynamic response for levitation gap under different initial deviations using Method 2.
During the train’s operation, the electromagnetic module is prone to external interference or unbalanced forces. To simulate this scenario, a constant force of 500 N is applied to the suspension point on the right side in the simulation. The dynamic response curve of the system is observed thereafter in Figure 12 and Figure 13. In Method 2, the electromagnetic module exhibits a smaller angle fluctuation and rapidly decreases, whereas in Method 1, the angle fluctuation is larger and convergence to 0 takes longer. Coupled vibration occurs with the electromagnetic module. Similarly, Figure 14 presents the results of the frequency domain analysis of the angle data. The amplitude at the primary vibration frequency for Method 1 is clearly greater than that for Method 2. The larger amplitude at zero frequency is due to the presence of a DC offset.

Figure 12.
Dynamic response for deflection angle under different methods when subjected to external perturbation.

Figure 13.
Dynamic response for levitation gap under different methods when subjected to external perturbation.

Figure 14.
Frequency response for levitation gap under different methods when subjected to external perturbation.
During the process of train levitation, it is common for the left and right suspension points of the electromagnetic module to become unsynchronized. To simulate this situation, we have introduced a 1-millimeter delay in the levitation command for the left suspension point. As shown in Figure 15 and Figure 16, during the levitation process, the suspension module exhibits significant coupled vibration. In contrast, the improved control framework proposed in this paper can better suppress this vibration. Figure 17 presents the frequency domain analysis results of the angle data. The amplitude within the frequency range of interest is clearly smaller for Method 2 compared to Method 1.

Figure 15.
Dynamic response for deflection angle under different methods when suspension points work asynchronously.

Figure 16.
Dynamic response for levitation gap under different methods when suspension points work asynchronously.

Figure 17.
Frequency response for levitation gap under different methods when suspension points work asynchronously.
The above analysis is aimed at the gap fluctuation caused by the mechanical coupling between the left and right suspension points. In practical engineering, parameter coupling vibration exists that is caused by mismatched control parameters and system parameters. When the control parameters , , and , the dynamic response curve is obtained in the absence of other external disturbances, as shown in Figure 18 and Figure 19. Although the module’s rotation angle remains at 0, there is significant fluctuation in the suspension gap, indicating that there is no structural coupling between the left and right suspension points of the system, but vibration occurs. When adjusting the differential feedback coefficient from 6 to 9, it can be observed in Figure 20 that as the control parameter increases, the vibration is effectively suppressed. During long-term service, the system’s structural parameters may change, resulting in a mismatch between the control parameters and the structural parameters. In this case, appropriately increasing kdz is beneficial to improving the dynamic performance of the system.

Figure 18.
Dynamic response for deflection angle under different methods without mechanical coupling.

Figure 19.
Dynamic response for levitation gap under different methods without mechanical coupling.

Figure 20.
Dynamic response for the electromagnetic module when increases.
5. Experimental Verification
To further validate the effectiveness of the improved control algorithm, this paper conducted a suspension test on the 18 m line high-speed double bogie test platform at the Key Laboratory of Hunan Province, as shown in Figure 21. The double maglev frame comprises two bogies, each with two suspension modules or four suspension points. The sensors, deployed in the test platform, include gap sensors, current sensors, and accelerometer sensors. The gap sensor is installed on the electromagnet, while the acceleration sensor and current sensor are installed inside the controller enclosure. Gap sensors are employed to measure the distance between the suspension point and track, while current sensors collect the current of the electromagnet coil at the suspension point. Accelerometer sensors, on the other hand, gather acceleration data of the suspension point. It is important to note that the system algorithm lacks a corresponding sensor for gap differential signals, and the gap signal tends to have a high level of noise, which makes it challenging to implement in practical engineering. Consequently, the acceleration integral signal is often used instead of the gap differential signal to enhance the control effectiveness.

Figure 21.
The test platform for high-speed double bogie.
Implementing both control methods in the test platform, the dynamic response curve of the system is obtained in Figure 22 and Figure 23. The results showed that without the improved algorithm control, there was a significant fluctuation in the electromagnets during the levitation process, and noticeable vibration near the rated air gap. However, with the improved algorithm control, the train levitation process was relatively stable, and the vibration near the rated air gap was reduced. The experimental data fully demonstrated the effectiveness of the improved algorithm framework proposed in this paper, which can effectively suppress structural coupling vibrations. Due to the absence of angle sensors, we did not directly collect angle data during the experiment. Instead, we conducted a frequency domain analysis on the suspension gap data. As shown in Figure 24, the dual magnetic suspension system, being quite complex, exhibits multiple frequency peaks, which aligns with our expectations. However, within the frequency range of interest, the system’s vibration amplitude under Method 2 is consistently smaller than under Method 1.
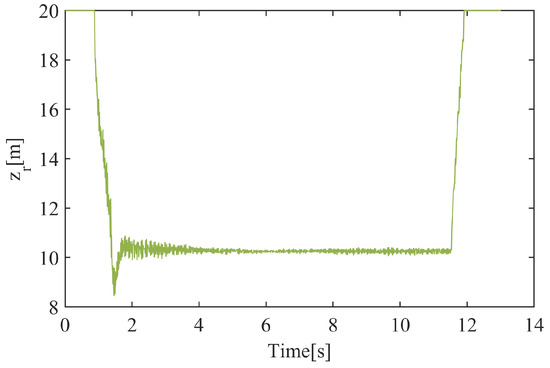
Figure 22.
Dynamic response for levitation gap under Method 1.
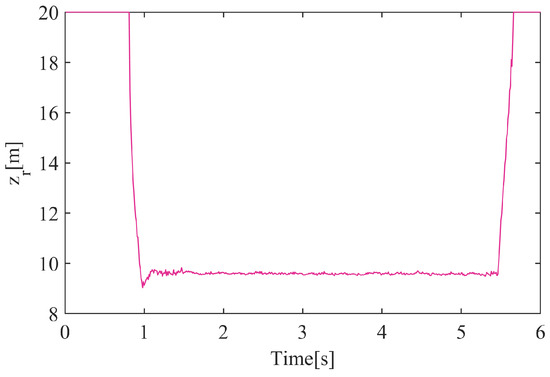
Figure 23.
Dynamic response for levitation gap under Method 2.
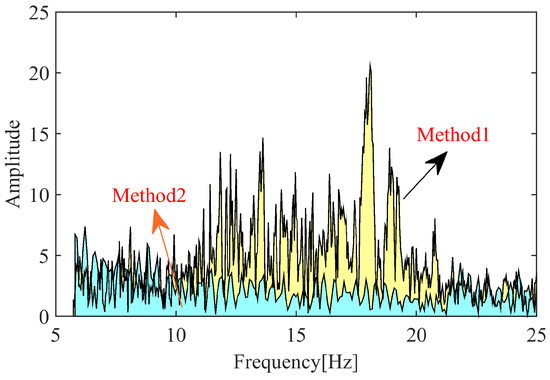
Figure 24.
The comparison of frequency response for levitation gap under Method 1 and Method 2.
6. Conclusions
This research provides a comprehensive analysis of the coupled vibration problem caused by the mechanical structure of electromagnetic modules. By establishing the state-space equations for the coupled system, the inherent instability of the system and the coupling relationship between the state variables are revealed. Additionally, a differential control algorithm based on nonsingular transformation is proposed. The effectiveness of the proposed algorithm under complex conditions is verified through simulations, and experimental validation is conducted as well. The conclusions are listed as follows:
- (1)
- Through a simulation and theoretical analysis, there are two types of vibrations during the operation of maglev trains: parameter mismatch vibration and structural coupling vibration.
- (2)
- For parameter mismatch vibration, appropriately increasing is beneficial for improving the dynamic performance of the system. For structural coupling vibration, the method proposed in this article has shown good results.
- (3)
- The inconsistency of the initial conditions of the two suspension points has a significant impact on the dynamic performance of the suspension module.
This research has significant practical implications for improving the smoothness of train operations. The proposed control framework is both effective and concise, making it easy to implement in engineering. In future work, we will focus on the study of vibration caused by track irregularities during operation.
Author Contributions
Conceptualization, S.L.; methodology, S.L.; software, S.L.; validation, S.L. and C.D.; formal analysis, S.L.; investigation, S.L.; resources, S.L.; data curation, S.L.; writing—original draft preparation, S.L.; writing—review and editing, C.D.; visualization, C.D.; supervision, C.D.; project administration, Z.L.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 52332011).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, X.M. Maglev Train; Shanghai Scientific & Technical Publishers: Shanghai, China, 2003. [Google Scholar]
- Long, Z.Q.; Zhai, M.D.; Wang, Z.Q. Condition Monitoring, Fault Diagnosis, and Fault-Tolerant Control of the Maglev Trains; Shanghai Scientific & Technical Publishers: Shanghai, China, 2023. [Google Scholar]
- Long, Z.Q.; Li, X.L.; Chen, H. Research on Permanent-Electromagnetic Levitation Technology and Application; Shanghai Scientific & Technical Publishers: Shanghai, China, 2023. [Google Scholar]
- Liang, S.; Wang, Z.Q.; Li, X.L.; Long, Z.Q. Research on vehicle-track coupling vibration control based on feedforward compensation and full-state feedback control. J. Tongji Univ. (Nat. Sci.) 2023, 3, 321–331. [Google Scholar]
- Sun, Y.G.; Xu, J.Q.; Wang, S.M. Modeling and numerical analysis of magnetic-force coupling system of maglev train based on vector FEM. J. Tongji Univ. (Nat. Sci.) 2021, 49, 1635–1641. [Google Scholar]
- Sun, Y.G.; Xu, J.Q.; Wang, W.J.; Lin, G.B. Hopf bifurcation analysis of maglev vehicle-guideway interaction vibration system and stability control based on fuzzy adaptive theory. Comput. Ind. 2019, 108, 197–209. [Google Scholar] [CrossRef]
- Sun, Y.G.; He, Z.Y.; Xu, J.Q.; Lin, G.B. Dynamic analysis and vibration control for a maglev vehicle-guideway coupling system with experimental verification. Mech. Syst. Signal Process 2023, 188, 109954. [Google Scholar] [CrossRef]
- Zeng, J.W.; Xia, W.T.; Xiang, X.G.; Long, Z.Q. Research on the mechanism and control characteristics of vehicle-track beam coupling vibration for medium-speed maglev vehicle. IEEE Trans. Transp. Electrific. 2022, 8, 3236–3246. [Google Scholar] [CrossRef]
- Xia, W.T.; Zeng, J.W.; Dou, F.S. Method of combining theoretical calculation with numerical simulation for analyzing effects of parameters on the maglev vehicle-bridge system. IEEE Trans. Veh. Technol. 2021, 70, 2250–2257. [Google Scholar] [CrossRef]
- Wu, J.J.; Zheng, X.J.; Zhou, Y.H. Dynamic stability analysis of maglev vehicle body-single span elastic track coupling control system. J. Lanzhou Univ. (Nat. Sci.) 2003, 39, 22–26. [Google Scholar]
- Zhou, D.F.; Hansen, C.H.; Li, J. Suppression of maglev vehiclegirder self-excited vibration using a virtual tuned mass damper. J. Sound Vib. 2011, 5, 883–901. [Google Scholar] [CrossRef]
- Zhou, D.F.; Yu, P.C.; Wang, L. An adaptive vibration control method to suppress the vibration of the maglev train caused by track irregularities. J. Sound Vib. 2017, 408, 331–350. [Google Scholar] [CrossRef]
- Li, J.H.; Li, J.; Zhou, D.; Peng, C. The active control of maglev stationary self-excited vibration with a virtual energy harvester. IEEE Trans. Ind. Electron. 2015, 62, 2942–2951. [Google Scholar] [CrossRef]
- Wang, Y.J.; Yan, J.D.; Shi, J.; Urushadze, S. Vibration reduction for interaction response of a maglev vehicle running on guideway girders. Struct. Eng. Mech. 2020, 76, 163–173. [Google Scholar]
- Wang, L.C.; Li, J.H.; Zhou, D.F. Mechanism analysis and simulation verification of coupled self-excited vibration of maglev train-bridge. Vib. Shock 2017, 36, 13–19. [Google Scholar]
- Song, Y.; Lin, G.; Ni, F. Study on coupled vertical vehicle-bridge dynamic performance of medium and low-speed maglev train. Appl. Sci. 2021, 11, 5898. [Google Scholar] [CrossRef]
- Wang, D.; Li, X.; Liang, L.; Qiu, X. Influence of the track structure on the vertical dynamic interaction analysis of the low-to-medium-speed maglev train-bridge system. Adv. Mech. Eng. 2019, 22, 2937–2950. [Google Scholar] [CrossRef]
- Wang, D.; Li, X.; Liang, L.; Qiu, X. Dynamic interaction analysis of bridges induced by a low-to-medium-speed maglev train. J. Vib. Contr. 2020, 26, 2013–2025. [Google Scholar] [CrossRef]
- Xu, J.Q.; Lin, G.B.; Chen, C. Modeling and control of multi-point suspension of maglev vehicles under load disturbance. J. Tongji Univ. (Nat. Sci) 2020, 48, 1353–1363. [Google Scholar]
- Liu, D.S.; Li, J.; Chang, W.S. Research on motion coupling of EMS type maglev train module. J. Railways 2006, 28, 22–26. [Google Scholar]
- Liu, D.S.; Li, J.; Kun, Z. Design of nonlinear decoupling controller for double-electromagnet suspension system. J. Autom. 2006, 3, 321–328. [Google Scholar]
- Wang, S.M.; Ni, Y.Q.; Sun, Y.G.; Lu, Y.; Duan, Y.F. Modelling dynamic interaction of maglev train-controller-rail-bridge system by vector mechanics. J. Sound Vib. 2022, 533, 117023–117045. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).