Distributed Event-Triggered Optimal Algorithm Designs for Economic Dispatching of DC Microgrid with Conventional and Renewable Generators: Actuator-Based Control and Optimization
Abstract
1. Introduction
1.1. Distributed Optimization Algorithm
1.2. Event-Triggered Control
1.3. Contributions
- Inspired by [29], a distributed optimization control mechanism is proposed to reduce the production cost of DC microgrids and solve the DC microgrid economic dispatch problem. The mechanism ensures the maximum energy utilization rate of RGs and the minimum cost of CGs. In addition, it realizes the optimal synergy between conventional energy and renewable energy.
- To reduce the communication and sampling frequency of DC microgrid systems, a novel event-triggered optimization algorithm is designed. The algorithm takes advantage of the event-triggered control to reduce the frequency of communication and current sampling and improves the communication efficiency, as well as the lifetime of the system.
- The optimization algorithm proposed in this paper is based on the discrete time domain. This improvement avoids the instability caused by the discretization of the partial continuous control algorithm and the Zeno phenomenon. In addition, the algorithm is fully distributed, requiring only limited information about neighboring cells to achieve the update iterations of the optimal controller.
2. Preliminaries and Problem Formulation
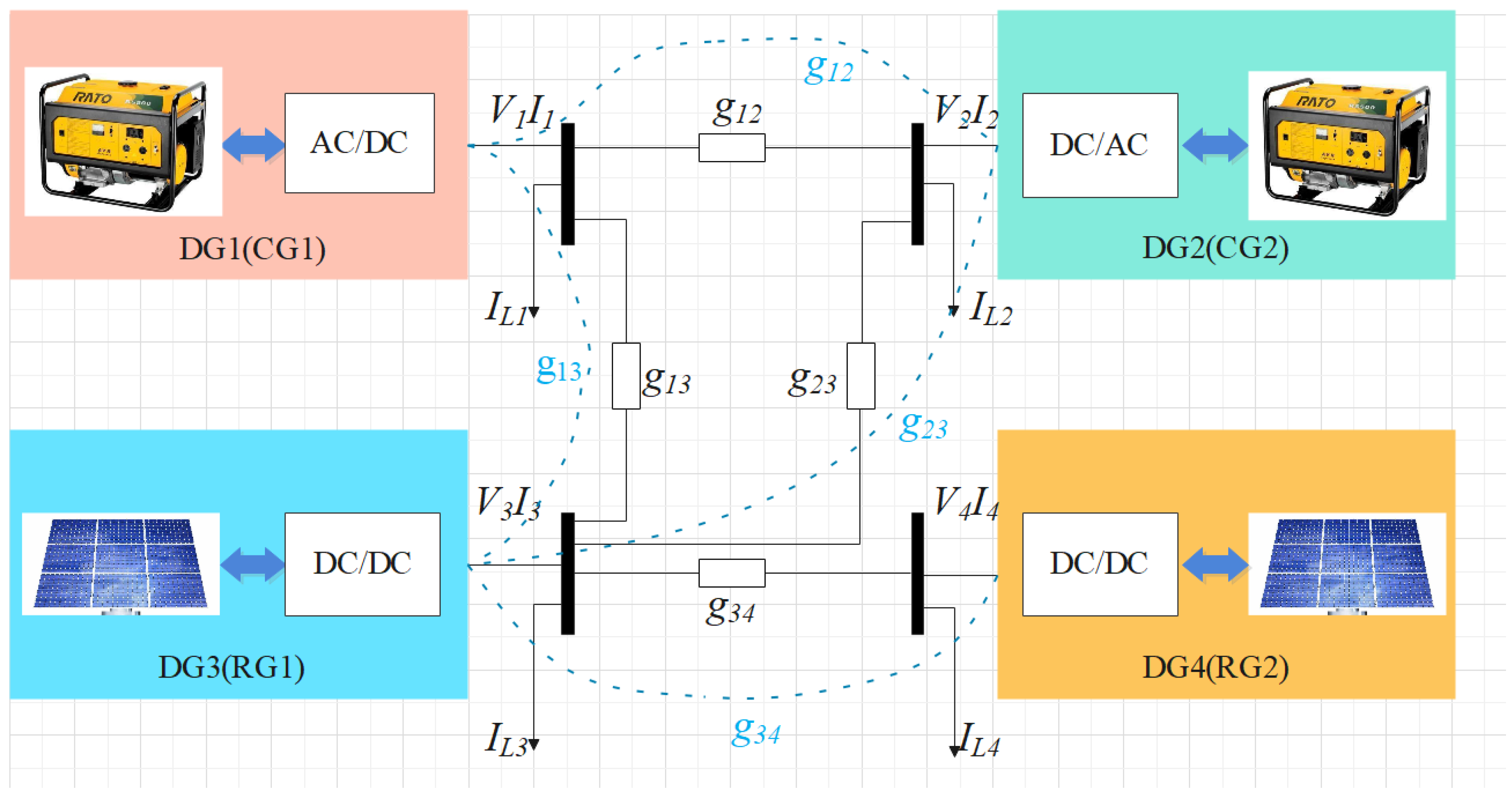
2.1. DC Microgrid Model
2.2. Electrical Network Model
3. Distributed Event-Triggered Optimization Algorithm
3.1. Convex Optimization Solving Conditions
3.2. Distributed Event-Triggered Optimization Algorithm
4. The Convergence and Stability of the Algorithm
5. Simulation Experiments
5.1. Parameters Setup
5.2. Case 1: Constant RG
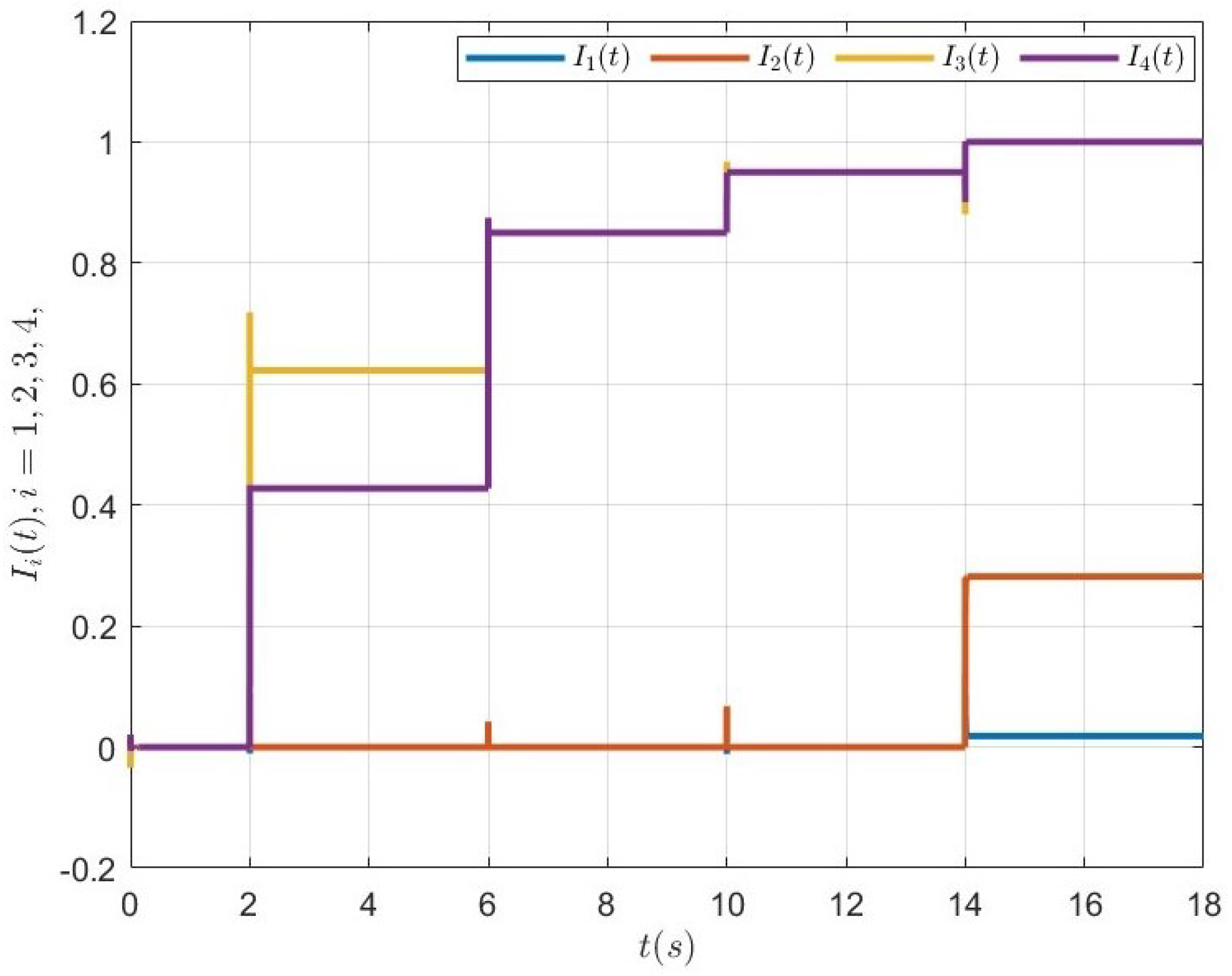
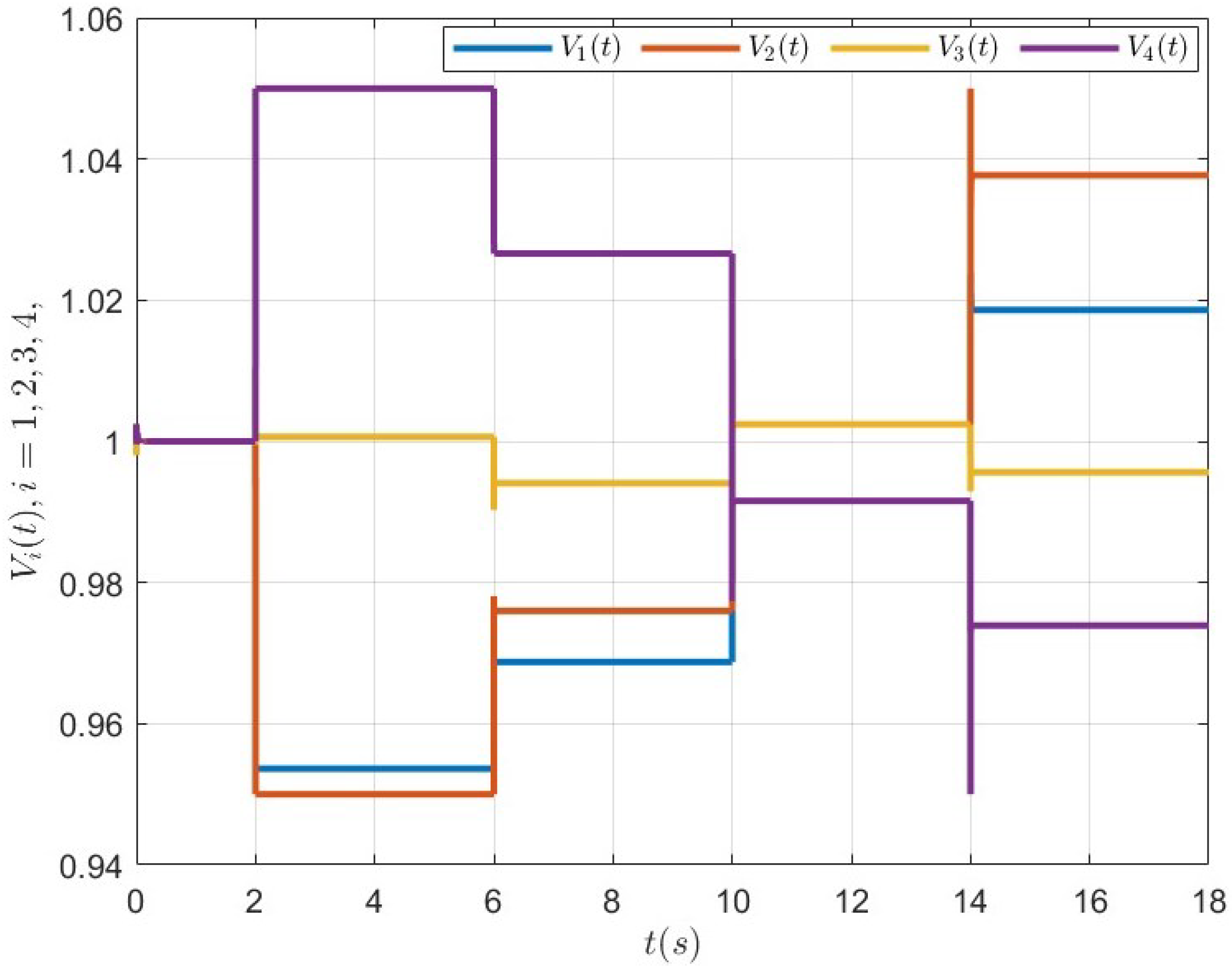
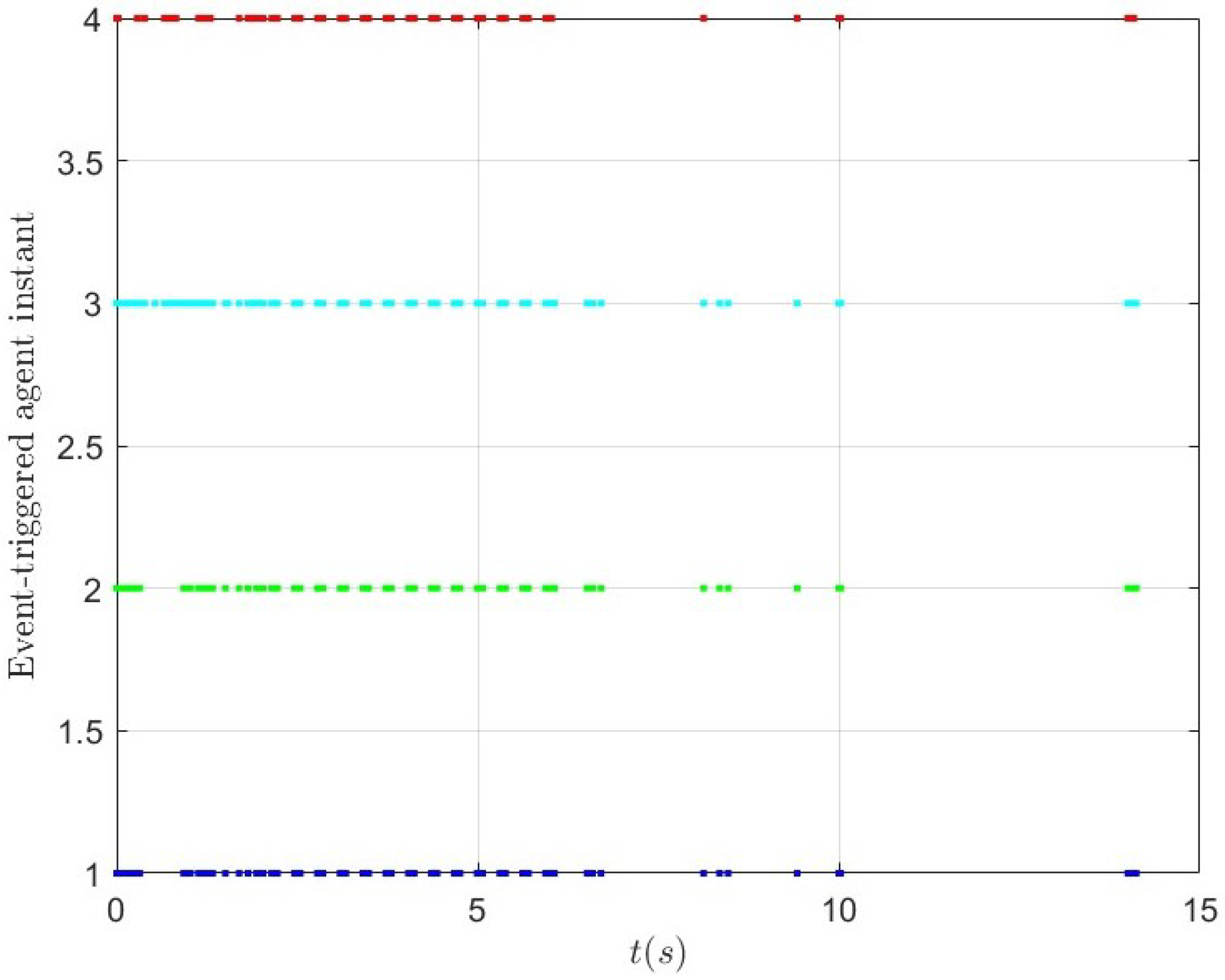
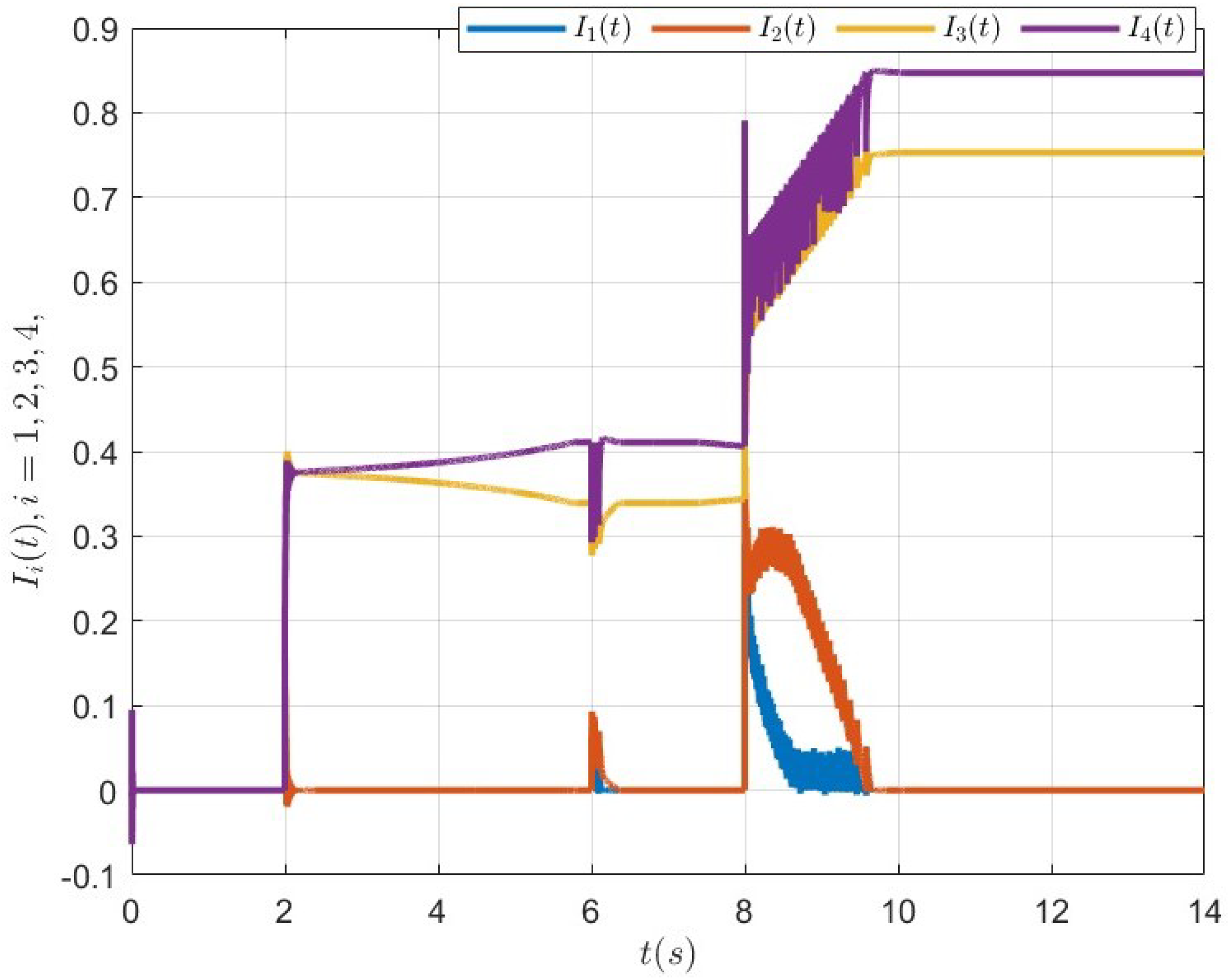
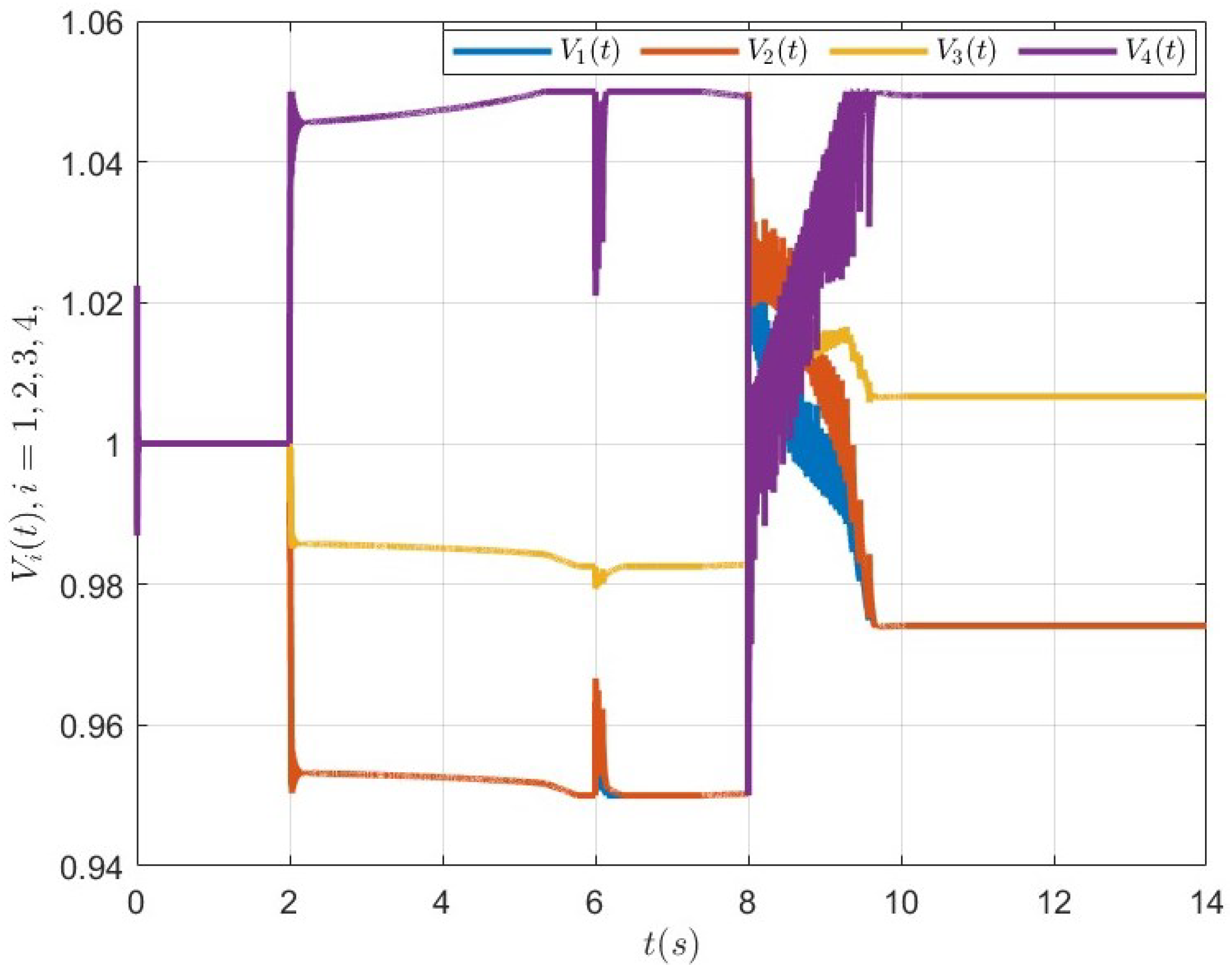
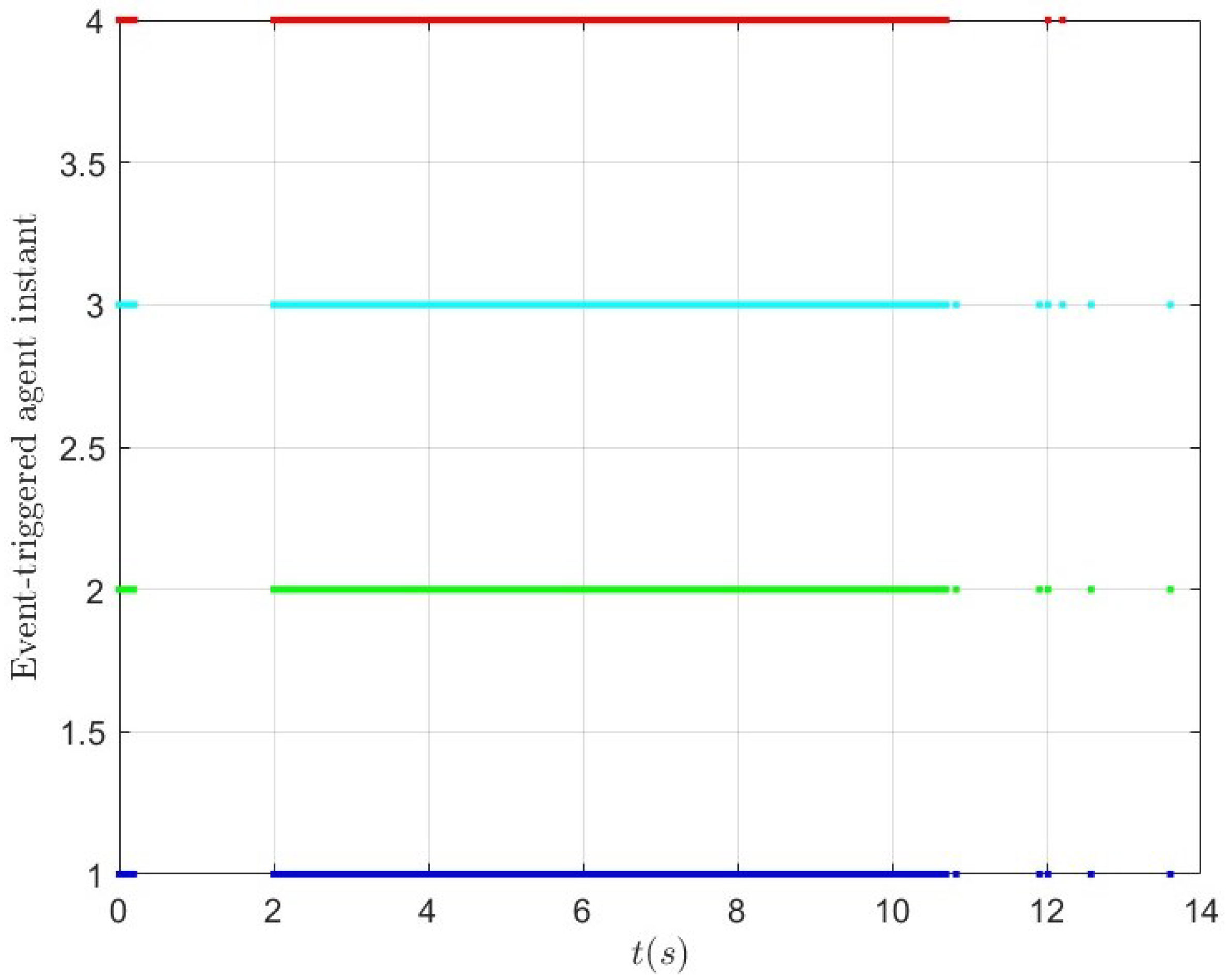
5.3. Case 2: Dynamic RG
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pires, V.F.; Pires, A.; Cordeiro, A. DC Microgrids: Benefits, Architectures, Perspectives and Challenges. Energies 2023, 16, 1217. [Google Scholar] [CrossRef]
- Rangarajan, S.S.; Raman, R.; Singh, A.; Shiva, C.K.; Kumar, R.; Sadhu, P.K.; Collins, E.R.; Senjyu, T. DC Microgrids: A Propitious Smart Grid Paradigm for Smart Cities. Smart Cities 2023, 6, 1690–1718. [Google Scholar] [CrossRef]
- Liu, X.-K.; Wang, S.-Q.; Chi, M.; Liu, Z.-W.; Wang, Y.-W. Resilient Secondary Control and Stability Analysis for DC Microgrids Under Mixed Cyber Attacks. IEEE Trans. Ind. Electron. 2024, 71, 1938–1947. [Google Scholar] [CrossRef]
- Veerasamy, V.; Sampath, L.P.; Singh, S.; Nguyen, H.D.; Gooi, H.B. Blockchain-Based Decentralized Frequency Control of Microgrids Using Federated Learning Fractional-Order Recurrent Neural Network. IEEE Trans. Smart Grid 2024, 15, 1089–1102. [Google Scholar] [CrossRef]
- Shafiqurrahman, A.; Yahyaee, S.A.; Sreekumar, P.; Khadkikar, V. A Novel Decentralized Unbalance Load Sharing Approach For Islanded Microgrids. IEEE Trans. Ind. Appl. 2024, 60, 5714–5725. [Google Scholar] [CrossRef]
- Li, S.; Hu, W.; Cao, D.; Hu, J.; Huang, Q.; Chen, Z.; Blaabjerg, F. A Novel MADRL with Spatial-Temporal Pattern Capturing Ability for Robust Decentralized Control of Multiple Microgrids under Anomalous Measurements. IEEE Trans. Sustain. Energy 2024, 15, 1872–1884. [Google Scholar] [CrossRef]
- Mirzaeva, G.; Miller, D. DC and AC Microgrids for Standalone Applications. IEEE Trans. Ind. Appl. 2023, 59, 7908–7918. [Google Scholar] [CrossRef]
- Fan, B.; Peng, J.; Yang, Q.; Liu, W. Distributed Periodic Event-Triggered Algorithm for Current Sharing and Voltage Regulation in DC Microgrids. IEEE Trans. Smart Grid 2020, 11, 577–589. [Google Scholar] [CrossRef]
- Ali, S.; Zheng, Z.; Aillerie, M.; Sawicki, J.-P.; Péra, M.-C.; Hissel, D. A Review of DC Microgrid Energy Management Systems Dedicated to Residential Applications. Energies 2021, 14, 4308. [Google Scholar] [CrossRef]
- Mosayebi, M.; Sadeghzadeh, S.M.; Gheisarnejad, M.; Khooban, M.H. Intelligent and Fast Model-Free Sliding Mode Control for Shipboard DC Microgrids. IEEE Trans. Transp. Electrif. 2021, 7, 1662–1671. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Y.; Liu, W.; Ferrese, F.; Liu, L. Fully Distributed Coordination of Multiple DFIGs in a Microgrid for Load Sharing. IEEE Trans. Smart Grid 2013, 4, 806–815. [Google Scholar] [CrossRef]
- Wang, S.; Du, M.; Lu, L.; Xing, W.; Sun, K.; Ouyang, M. Multilevel Energy Management of a DC Microgrid Based on Virtual-Battery Model Considering Voltage Regulation and Economic Optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2881–2895. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Liu, Z.; Zhang, P.; Ding, Q.; Liu, X.; Wang, W. Robust N–k CCUC model considering the fault outage probability of units and transmission lines. IET Gener. Transm. Distrib. 2019, 13, 3782–3791. [Google Scholar] [CrossRef]
- Lasabi, O.; Swanson, A.; Jarvis, L.; Aluko, A. Dynamic Distributed Collaborative Control for Equitable Current Distribution and Voltage Recovery in DC Microgrids. Energies 2023, 16, 6657. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Y.; Liu, W.; Zang, C.; Yu, H. Distributed Online Optimal Energy Management for Smart Grids. IEEE Trans. Ind. Inform. 2015, 11, 717–727. [Google Scholar] [CrossRef]
- Rahbari-Asr, N.; Zhang, Y.; Chow, M. Consensus-based distributed scheduling for cooperative operation of distributed energy resources and storage devices in smart grids. IET Gener. Transm. Distrib. 2016, 10, 1268–1277. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Fault-Tolerant Supervisory Controller for a Hybrid AC/DC Micro-Grid. IEEE Trans. Smart Grid 2018, 9, 2809–2823. [Google Scholar] [CrossRef]
- Sun, J.; Palade, V.; Wu, X.-J.; Fang, W.; Wang, Z. Solving the Power Economic Dispatch Problem with Generator Constraints by Random Drift Particle Swarm Optimization. IEEE Trans. Ind. Inform. 2014, 10, 222–232. [Google Scholar] [CrossRef]
- Garcés, A. Convex optimization for the optimal power flow on DC distribution systems. Handb. Optim. Electr. Power Distrib. Syst. 2020, 10, 121–137. [Google Scholar]
- Yang, Z.; Xiang, J.; Li, Y. Distributed Consensus Based Supply–Demand Balance Algorithm for Economic Dispatch Problem in a Smart Grid with Switching Graph. IEEE Trans. Ind. Electron. 2017, 64, 1600–1610. [Google Scholar] [CrossRef]
- Chen, G.; Yang, Q. An ADMM-Based Distributed Algorithm for Economic Dispatch in Islanded Microgrids. IEEE Trans. Ind. Inform. 2018, 14, 3892–3903. [Google Scholar] [CrossRef]
- Peng, J.; Fan, B.; Liu, W. Voltage-based distributed optimal control for generation cost minimization and bounded bus voltage regulation in DC microgrids. IEEE Trans. Smart Grid 2021, 12, 106–116. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, W.; Zhang, B. A Distributed Control Method with Minimum Generation Cost for DC Microgrids. IEEE Trans. Energy Convers. 2016, 31, 1462–1470. [Google Scholar] [CrossRef]
- Zhang, Z.; Dou, C.; Yue, D.; Zhang, B.; Xu, S.; Hayat, T.; Alsaedi, A. An Event-Triggered Secondary Control Strategy with Network Delay in Islanded Microgrids. IEEE Syst. J. 2019, 13, 1851–1860. [Google Scholar] [CrossRef]
- Lai, J.; Lu, X.; Monti, A.; De Doncker, R.W. Event-Driven Distributed Active and Reactive Power Dispatch for CCVSI-Based Distributed Generators in AC Microgrids. IEEE Trans. Ind. Appl. 2020, 56, 3125–3136. [Google Scholar] [CrossRef]
- Najafirad, M.J.; Dehkordi, N.M. Distributed event-triggered control of DC microgrids with output saturation constraint. Int. J. Electr. Power Energy Syst. 2023, 148, 936–947. [Google Scholar] [CrossRef]
- Qian, Y.-Y.; Premakumar AV, P.; Wan, Y.; Lin, Z.; Shamash, Y.A.; Davoudi, A. Dynamic Event-Triggered Distributed Secondary Control of DC Microgrids. IEEE Trans. Power Electron. 2022, 37, 10226–10238. [Google Scholar] [CrossRef]
- Shi, M.; Shahidehpour, M.; Zhou, Q.; Chen, X.; Wen, J. Optimal Consensus-Based Event-Triggered Control Strategy for Resilient DC Microgrids. IEEE Trans. Power Syst. 2021, 36, 1807–1818. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, S.; Hong, Y. Constrained Consensus Algorithms with Fixed Step Size for Distributed Convex Optimization Over Multiagent Networks. IEEE Trans. Autom. Control. 2017, 62, 4259–4265. [Google Scholar] [CrossRef]
- Kinderlehrer, D.; Stampacchia, G. An Introduction to Variational Inequalities and Their Applications; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Fan, Z.; Fan, B.; Liu, W. Distributed Control of DC Microgrids for Optimal Coordination of Conventional and Renewable Generators. IEEE Trans. Smart Grid 2021, 12, 4607–4615. [Google Scholar] [CrossRef]


| Parameters of System | Value |
|---|---|
| Nominal bus voltage (V, 1 p.u.) | 48 |
| Nominal bus Current (I, 1 p.u.) | 12 |
| Current upper bounds of CGs (p.u.) | 1.0 |
| Current lower bounds of CGs (p.u.) | 0 |
| Voltage upper bounds (p.u.) | 1.05 |
| Voltage lower bounds (p.u.) | 0.95 |
| (p.u.) | 0.0185, 0.0832, 0.008 |
| (p.u.) | 0.0185, 0.0260, 0.006 |
| Parameter | |||
|---|---|---|---|
| Value | 0.001 | 0.99 | 0.1 |
| Bus | 0–2 s | 2–6 s | 6–10 s | 10–14 s | 14–18 s |
|---|---|---|---|---|---|
| 1 | 0.0 (p.u.) | 0.20 (p.u.) | 0.15 (p.u.) | 0.0 (p.u.) | 0.0 (p.u.) |
| 2 | 0.0 (p.u.) | 0.25 (p.u.) | 0.05 (p.u.) | 0.0 (p.u.) | 0.0 (p.u.) |
| 3 | 0.0 (p.u.) | 0.40 (p.u.) | 0.80 (p.u.) | 0.90 (p.u.) | 1.20 (p.u.) |
| 4 | 0.0 (p.u.) | 0.20 (p.u.) | 0.70 (p.u.) | 1.00 (p.u.) | 1.10 (p.u.) |
| Bus | 0–2 s | 2–8 s | 8–14 s |
|---|---|---|---|
| 1 | 0.0 | 0.15 (p.u.) | 0.15 (p.u.) |
| 2 | 0.0 | 0.15 (p.u.) | 0.15 (p.u.) |
| 3 | 0.0 | 0.35 (p.u.) | 0.65 (p.u.) |
| 4 | 0.0 | 0.1 (p.u.) | 0.65 (p.u.) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Lv, X.; He, Y. Distributed Event-Triggered Optimal Algorithm Designs for Economic Dispatching of DC Microgrid with Conventional and Renewable Generators: Actuator-Based Control and Optimization. Actuators 2024, 13, 290. https://doi.org/10.3390/act13080290
Shi W, Lv X, He Y. Distributed Event-Triggered Optimal Algorithm Designs for Economic Dispatching of DC Microgrid with Conventional and Renewable Generators: Actuator-Based Control and Optimization. Actuators. 2024; 13(8):290. https://doi.org/10.3390/act13080290
Chicago/Turabian StyleShi, Wenming, Xianglian Lv, and Yang He. 2024. "Distributed Event-Triggered Optimal Algorithm Designs for Economic Dispatching of DC Microgrid with Conventional and Renewable Generators: Actuator-Based Control and Optimization" Actuators 13, no. 8: 290. https://doi.org/10.3390/act13080290
APA StyleShi, W., Lv, X., & He, Y. (2024). Distributed Event-Triggered Optimal Algorithm Designs for Economic Dispatching of DC Microgrid with Conventional and Renewable Generators: Actuator-Based Control and Optimization. Actuators, 13(8), 290. https://doi.org/10.3390/act13080290





