Abstract
As network technology continues to advance, network congestion has become an inevitable aspect of network communication. Considering the external interference, unmodeled uncertainty and the interaction between nodes, a multi-bottleneck TCP/AWM network model is established in this paper. A new fixed-time congestion controller was designed by combining a neural network and the backstepping technique. The neural network approximation property is used to eliminate the interference of unmodeled uncertainty and UDP flow in the system. The controller designed in this paper can ensure the stability of the TCP/AWM closed-loop system in a fixed time. Finally, the simulation results demonstrate the effectiveness of the proposed TCP/AWM controller.
1. Introduction
With the wide application of Internet technology, the network has become an essential component of daily life and work. However, with the surge in the number of users and the sharp increase in the amount of data transmission, the problem of network congestion is becoming increasingly severe, significantly impacting both user experience and network performance. In order to effectively alleviate this problem, Active Queue Management (AQM), as the main method of TCP network congestion control, has been paid attention by researchers [1,2]. In 1998, Braden et al. proposed the concept of AQM, expecting to ensure high throughput while reducing the queuing delay [1]. AQM notifies the sender by actively predicting and discarding partial packets to reduce the transmission rate in advance, thus effectively avoiding network congestion. The earliest AQM algorithm is Random Early Detection (RED): by proactively managing the queue length within routers, RED effectively mitigates the potential for congestion by dropping packets before they can cause significant delays or loss, thereby enhancing the overall user experience and network performance [3]. Subsequently, to mitigate the RED algorithm’s heightened sensitivity to design parameters and enhance its robustness, some researchers have proposed some improved RED algorithms [4,5,6]. However, most of these results are heuristic algorithms, and design parameters remain among the problems that congestion control algorithms need to address.
Building on TCP/AQM network modeling, Misra et al. introduced a nonlinear dynamics model, rooted in fluid flow modeling principles, which laid the foundation for solving the network congestion problem by control theory [7]. Since then, based on modern control theory, many researchers have designed congestion solutions with good results [8,9,10,11,12,13]. Ref. [10] proposed a new AQM algorithm grounded in a backstepping technique and minimum method, which shortened the signal convergence time to a certain extent. In [11], Zheng et al. considered the influence of external disturbance and unknown hysteresis, and designed an adaptive finite-time AQM network congestion controller, ensuring that the queue length efficiently aligns with the required queue within a specified finite time. By combining the prescribed performance technology, Chen et al. designed a multi-bottleneck congestion controller that can improve robustness under different numbers of sessions [12]. On this basis, Li et al. viewed the TCP/AQM network as a whole and were the first to consider the influence of dead zones on the establishment of dynamic models. The congestion control algorithm of multi-bottleneck network can optimize the utilization of link resources to their fullest potential between nodes and alleviate network congestion [13].
However, since the network has a transmission time lag, the congestion information such as the sampled queue length reflects the network condition of a previous time. When the congestion information is fed back to the sender, additional delay time is added, so the response of AQM is relatively lagging behind the actual network condition, and because of this lag, the congestion control effect may not meet expectations. In order to solve this problem, Barbera et al. introduced a novel strategy known as “Active Window Management” (AWM) [14] and analyzed the stability of the AWM algorithm [15]. The algorithm focuses more on the behavior control of the sender, and dynamically adjusts the congestion window size according to the real-time condition of the network, which can more directly cause the sending rate of the sender to respond quickly to network congestion. Based on the performance analysis of AWM, Barbera further studied the impact of parameter design on AWM networks and proposed to improve TCP performance by using network bandwidth to regulate TCP transmission rates [16]. Subsequently, Yuan et al. developed an enhanced AWM algorithm, marking its first application to routers. They controlled the sending rate by directly controlling the size of the sender window, so as to more directly control the queue length in the router [17]. Xie et al. presented an improved network model of network congestion control system, and proposed a new AWM congestion control algorithm with the help of specified performance control and an event-triggered mechanism [18]. This study focuses on single-bottleneck networks, while multi-bottleneck networks are more common in practical applications. Currently, congestion control in AWM networks remains an understudied yet challenging area of research.
Stability time is an important performance measure in control algorithms, and finite time stability with good robustness has received much attention [19,20,21,22]. In finite time control, settling time is influenced by the system’s initial value, yet in practical applications, these initial conditions are often unknown. For the first time, Polyakov formulated a sufficient criterion for achieving stability within a fixed time frame, effectively addressing the limitation where settlement time was previously influenced by the initial state. This innovation rendered the settlement time independent of initial conditions, solely determined by the designated design parameters [23]. For the parameter uncertain system, Wang et al. proposed a novel adaptive fixed time control approach in which the settlement time is exclusively governed by the control design parameters, eliminating any dependence on other factors [24]. A new adaptive fixed-time stability analysis criterion was developed to avoid the singularity problem in the controller design [25]. Meng et al.’s research delves into systems encompassing nonlinear functions with unspecified boundaries. They have devised a fixed-time controller, ensuring that all system states can be adjusted to zero [26]. Combining fixed time control and specified performance control, Shen et al. designed a AQM controller to ensure that the closed-loop system responds within a fixed time [27].
Based on the above discussion, we aimed to design a new multi-bottleneck AWM network congestion control algorithm in this paper. The key contributions can be encapsulated as follows:
- (1)
- We studied the multi-bottleneck TCP/AWM network, regarded it as a whole, considered the influence of unknown factors such as the mutual influence between the network nodes and the unmodeled uncertainties, and established a multi-bottleneck TCP/AWM model which is closer to the real network.
- (2)
- We applied fixed-time stability to multi-bottleneck TCP/AWM network congestion control for the first time. The stability duration of the system is solely determined by the design parameters, divorcing it from any reliance on the initial value state of the network system, which is more suitable for practical applications. In the design of the congestion controller, a new parameter adaptive rate and inequality is designed, which is crucial for analyzing the fixed-time stability of the closed-loop system.
The subsequent sections of this paper are structured as follows: Section 2 introduces the TCP/AWM network model and preliminaries. The adaptive neural controller design and its stability analysis are show in Section 3. In Section 4, the effectiveness of the algorithm is verified by simulation experiments. Finally, Section 5 summarizes the conclusion.
2. Model and Preliminaries
Consider the following TCP/AWM model proposed in [14]:
where W is the congestion window, q is the length of the queue for the bottleneck node, C is the link bandwidth, N is the number of sessions, is the round-trip time, and is the propagation delay. In order to make the model of this article more generic, Model (1) will be written as the form of the switching system, namely, , where is the switching signal. We regard as the size of the total congestion window. Based on this, given the external unknown disturbance, Equation (1) can be rewritten:
where is uncertain UDP flows.
The intermediate routing nodes in the network are a two-way transmission. Consider the interaction between upstream and downstream the nodes in the transmission process. The representation of the model pertaining to the i-th node can be formulated as follows.
Let , Equation(3) can rewritten as
where is the unmodeled uncertainty. To streamline the design process of the TCP/AWM controller, the subsequent definitions and lemmas are presented herein.
Remark 1.
Due to the wide existence of model inaccuracy and measurement errors, the modeling of TCP/AWM network is often accompanied by unmodeled dynamic uncertainty. In many studies, the influence of unmodeled dynamic uncertainty is ignored, but the unmodeled uncertainty should be substituted back to the closed-loop system for analysis in stability analysis; otherwise, it may lead to the instability of the system. In this paper, the adaptive fuzzy method is used to approximate the uncertain factors in the system, and the control effect is good.
Definition 1.
For any initial condition , the system described in (4) is considered practically fixed-time stable if it is practically finite-time stable and the convergence time function is bounded, i.e., there is a such that .
Lemma 1
([28]). For the system (4), if there is a Lyapunov function as follows:
for , then it is globally fixed-time stable if the following holds:
- (1)
- The system (4) is globally finite-time stable.
- (2)
- There is a global upper bound stability time function , and for all , the following inequality holds:
Lemma 2
([29]). For any real m and n, there is an inequality as follows:
where and ψ are any given positive constants.
Lemma 3
([24]). For and , the following inequality holds:
Lemma 4
([24]). Consider a differential equation as follows:
where and . Given the initial condition , is satisfied for .
In this paper, RBFNNs are applied to estimate the unknown nonlinear functions. The RBFNNs can be written as
where is the input vector, is the weight vector, represents the number of RBFNN nodes, and denotes the basis function vector. Select the Gaussian basis function as follows:
where is the center of the receptive field, and denotes the width of the Gaussian function.
Lemma 5
([30]). Let be a continuous function defined on a compact set Ω. Then, for , the following holds:
where is the ideal constant weight vector defined as
3. Adaptive Controller Design and Stability Analysis
First, based on the backstepping method design, the transfer error of the network nodes is expressed as follows:
where is the virtual control law, and is the tracking objective function.
According to (14), one has
Step 1. Consider the following Lyapunov function:
where , where represents the estimation of , with the estimation error denoted as . Then, the derivative of 1 is obtained:
Let . Then (17) can be expressed as
The RBFNNs effectively approximates the subsequent nonlinear functions, and based on Lemma 5, there is a neural network that meets the requirements for this approximation.
Then, Equation (18) is recalculated as
From Young’s inequality, the following inequality holds:
The virtual control law and adaptive law can be chosen as follows:
where is a design constant.
Step 2. Consider the following Lyapunov function:
From (14), we have
The derivative of is formulated as follows:
As in Step 1, the RBFNN is used to approximate the following unknown function in the controller:
Then (27) can be rewritten:
From Young’s inequality, the following inequality holds:
Define the following TCP/AWM congestion control law and the adaptive law as follows:
where are design constants, and .
Noting , we can derive
To ensure fixed-time stability of the system, we will apply Lemma 3 to address the relevant terms . When solving terms , Lemma 3 states that, under (31), for , must be satisfied. Furthermore, by Lemma 3, the following is obtained:
By applying Young’s inequality, we have
According to Lemma 2, let and , the following inequality can be obtained:
The block diagram shows the design procedure of the controller in Figure 1. Next, we give the main results and proofs in Theorem 1.
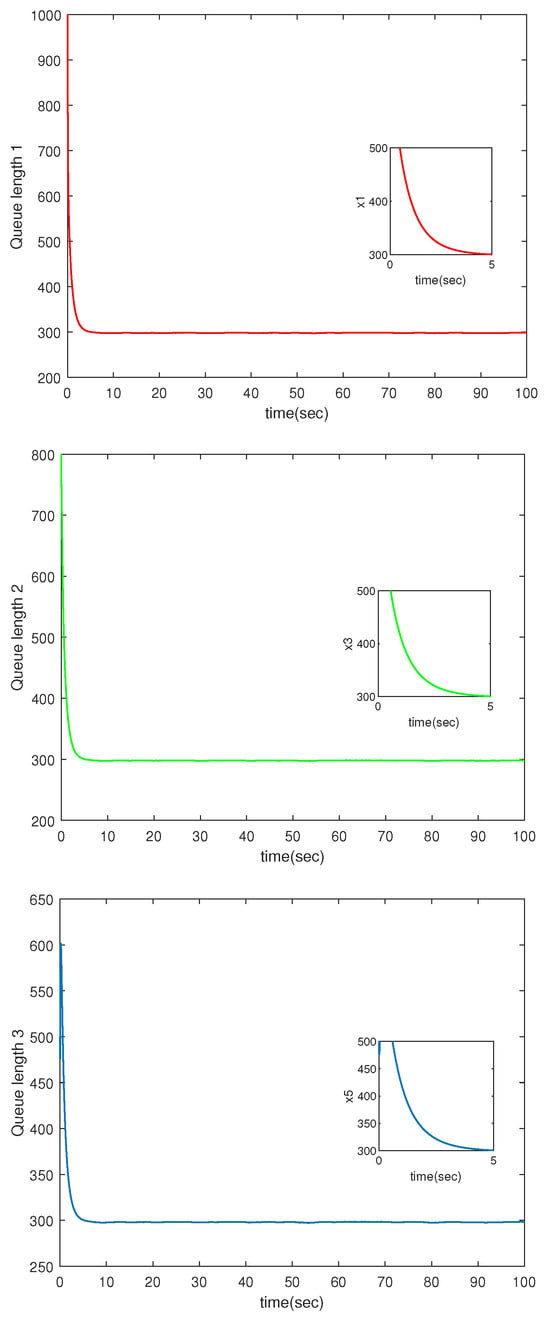
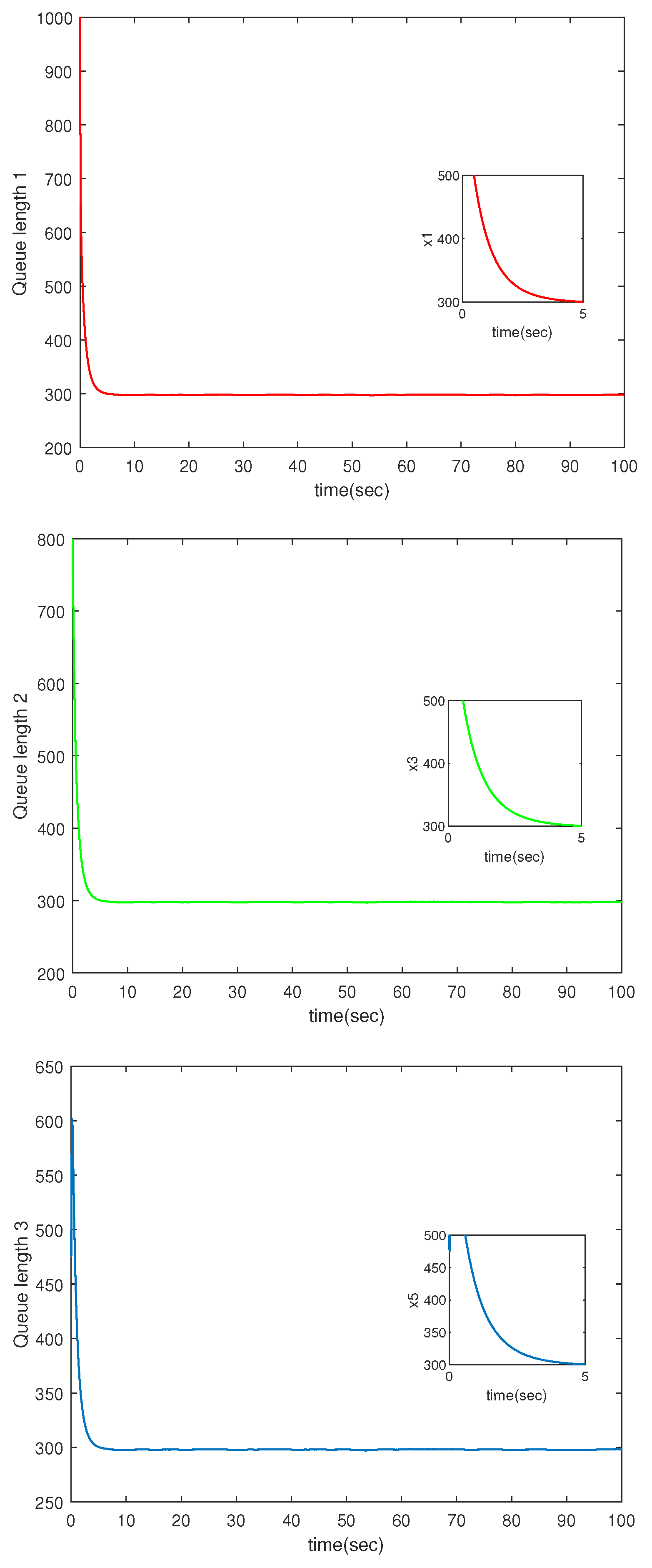
Figure 1.
The queue length of three nodes.
Theorem 1. 
For the TCP/AWM system (4), considering the virtual control law (22), the actual control input (31), and the adaptive laws (23) and (32), all signals in the TCP/AWM closed-loop system remain bounded, and the tracking error can achieve stability within a fixed time.

Proof.
Obviously, from , the following is obtained:
where . □
It is evident from Equation (39) that V is bounded. Thus, the proof of Theorem 1 is completed.
4. Simulation Result
Based on the controller design, this section examines a TCP network with three bottlenecks and evaluates the effectiveness of the congestion control algorithm using Matlab R2021b.
The initial system parameters and the controller design parameters can be selected as follows:
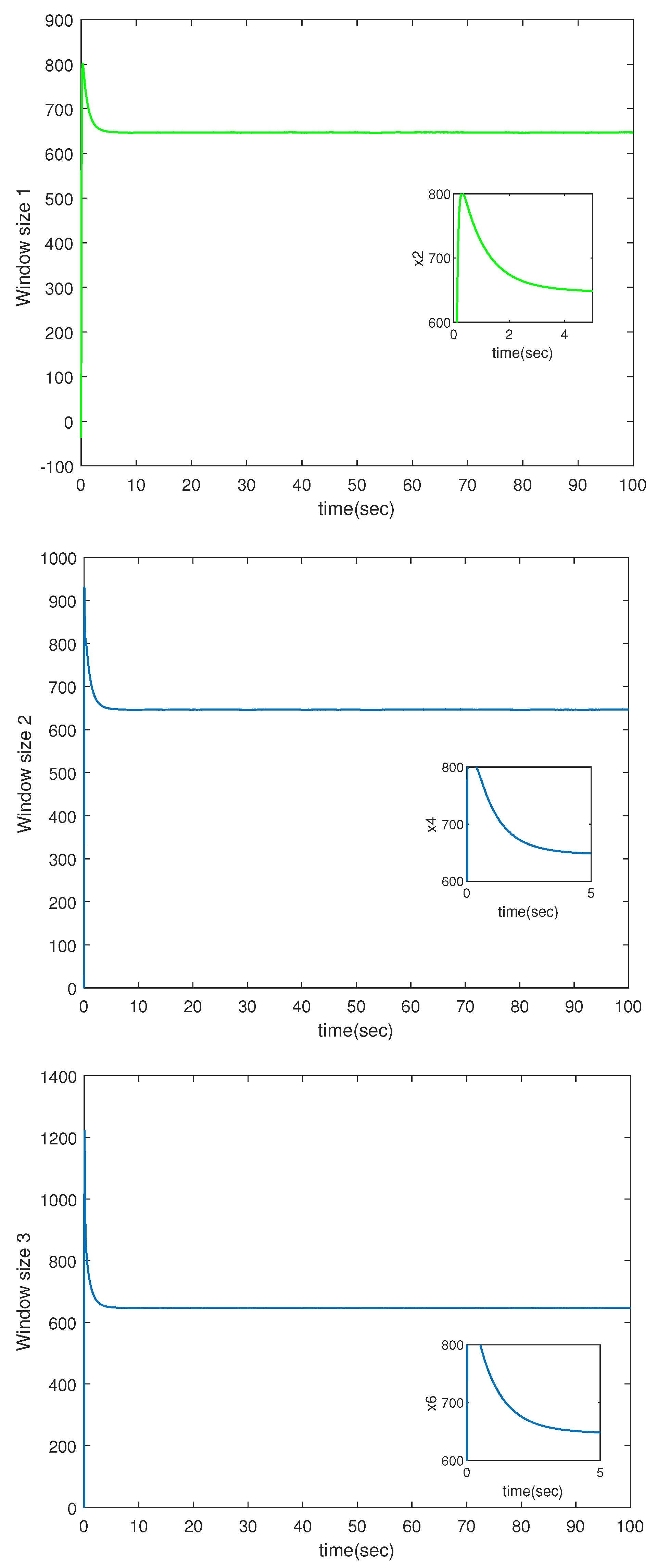
The detailed simulation results are presented in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. Figure 1 displays the queue length of the three bottleneck nodes, which tends to be stable despite the uncertainties and external disturbances. Figure 2 shows the window size at the three bottleneck nodes. Obviously, the congestion controller stabilizes the window at a certain value, thus maintaining the transmission rate at the TCP source at a stable value and reducing the generation of network congestion.
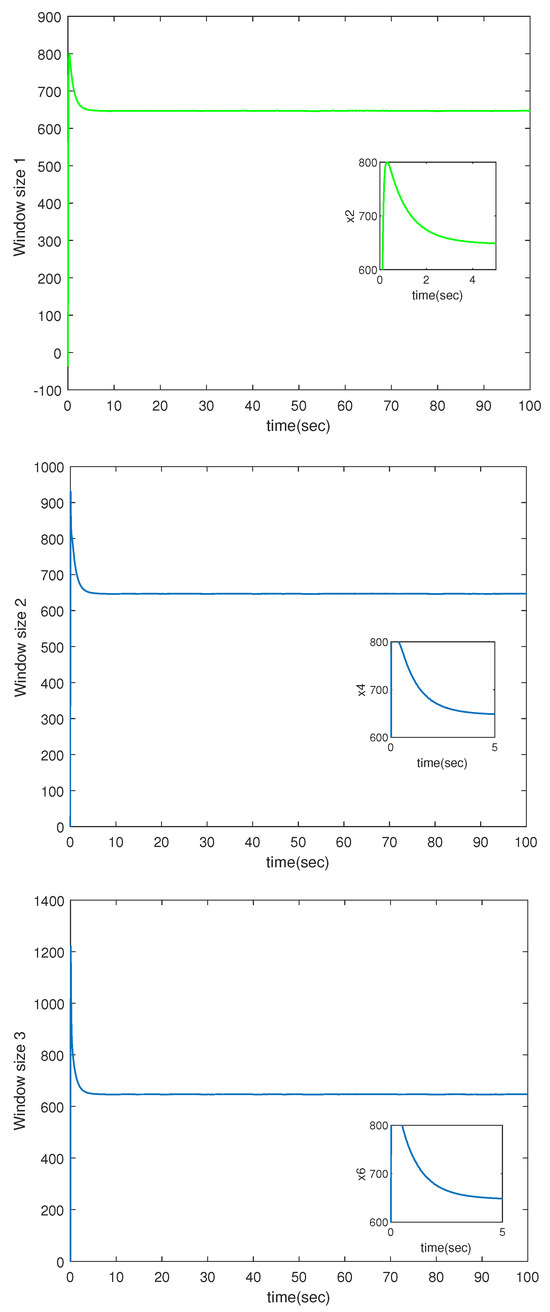
Figure 2.
The window size of three nodes.
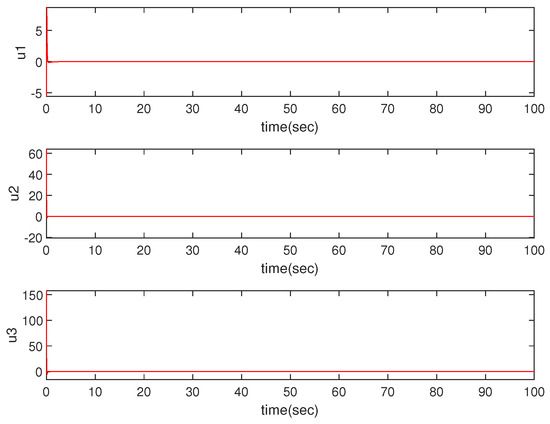
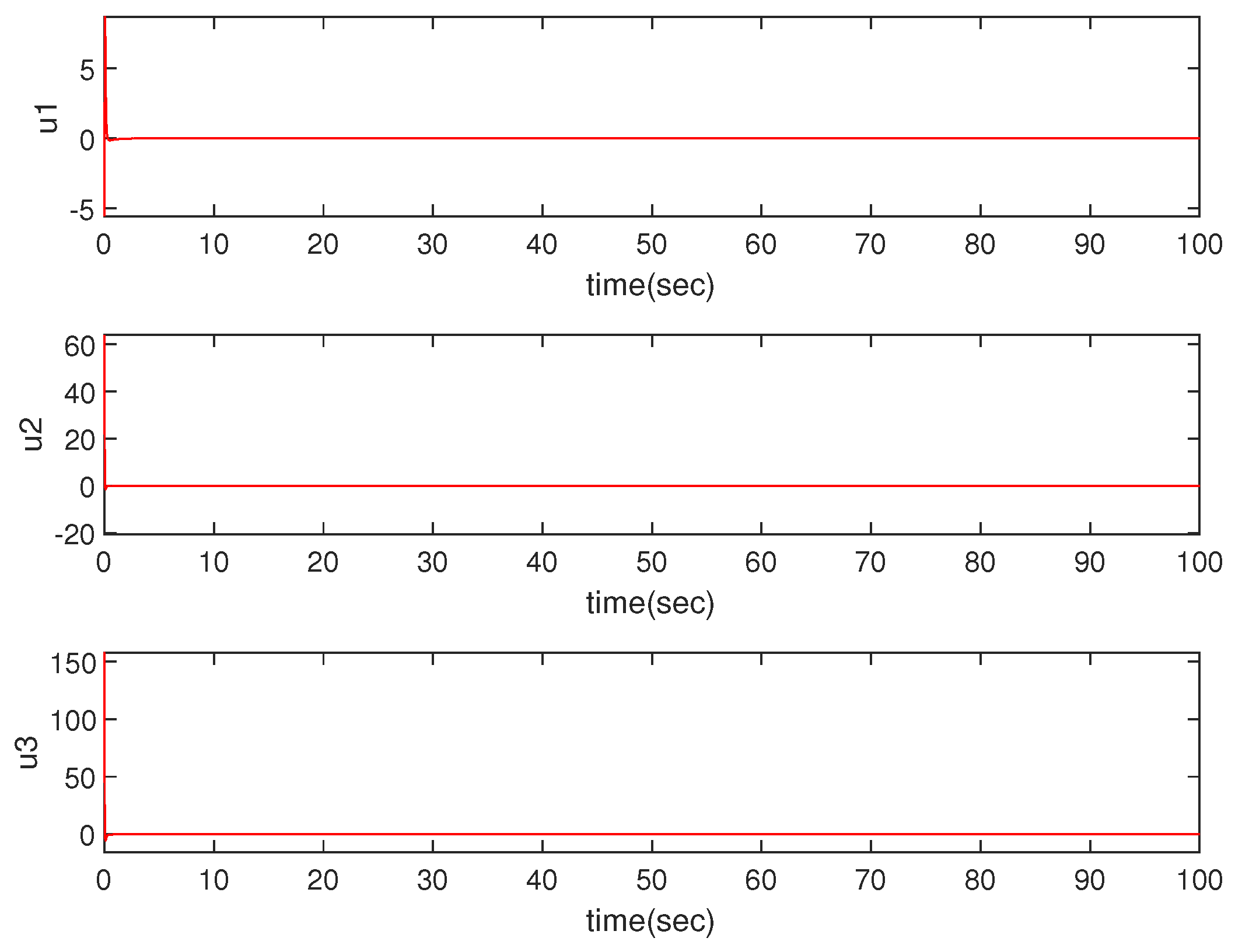
Figure 3.
Control input.
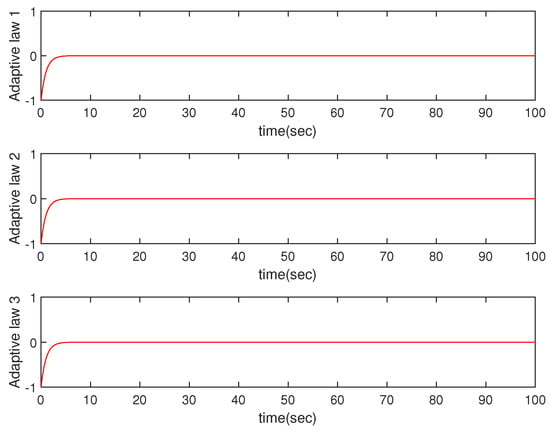
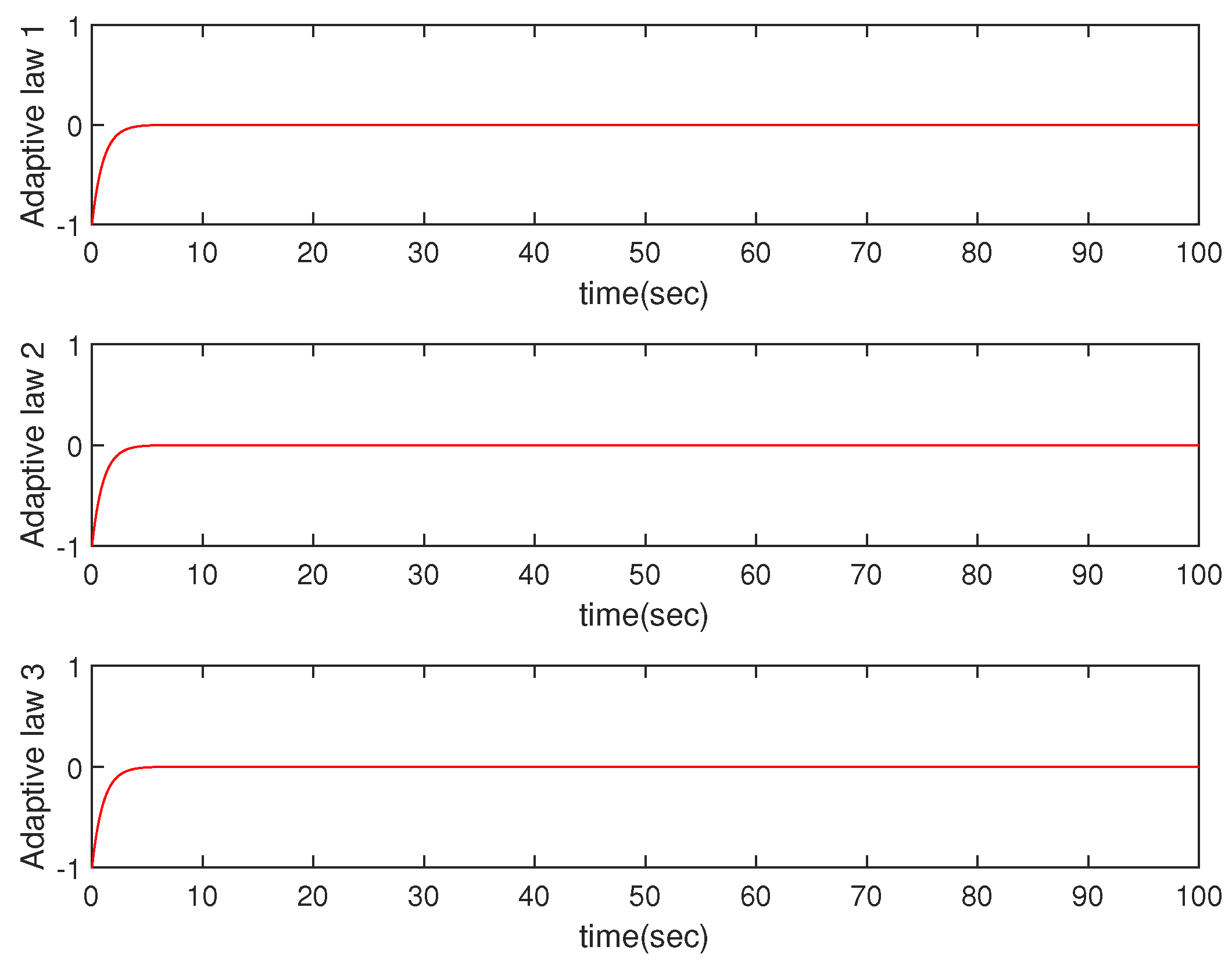
Figure 4.
Adaptive law.
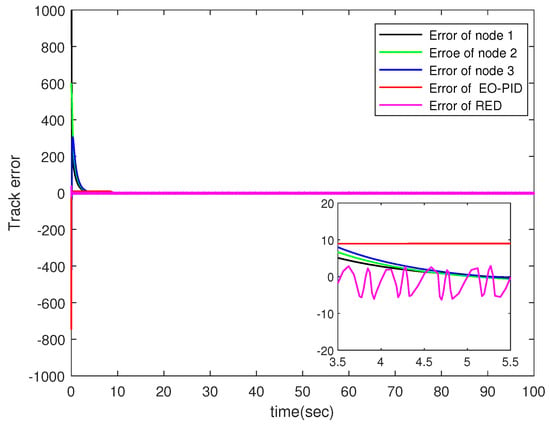
Figure 5.
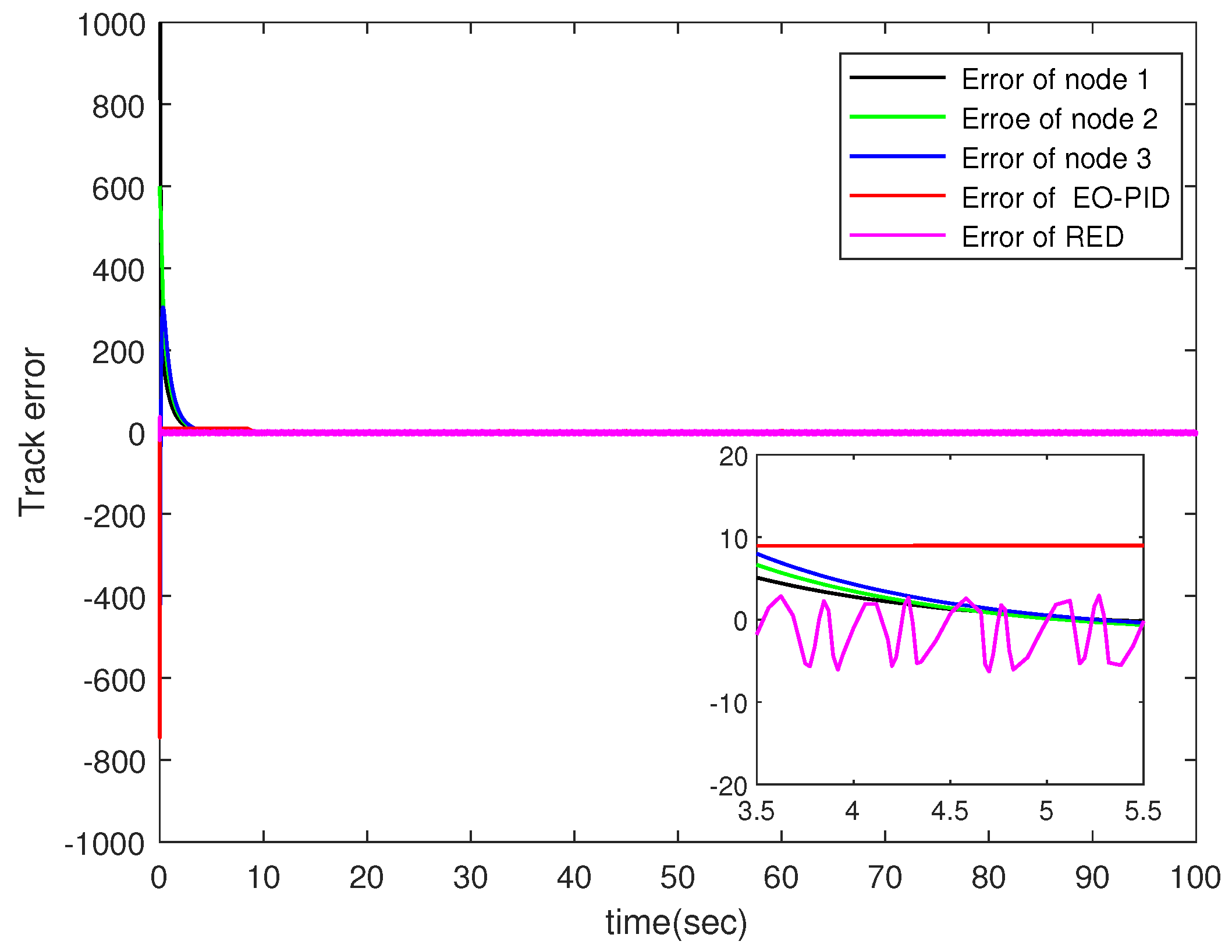
Comparison of the tracking error.
The control input signal is shown in Figure 3. As evident from the figure, u asymptotically converges to zero at 0.37 s, 0.28 s, and 0.43 s, respectively, signifying the commendable convergence performance of the congestion controller devised in this paper.
Figure 4 vividly illustrates the role of the adaptive law, showing that the significant approximation characteristics of RBFNNs play a good compensation effect, effectively reducing the influence of unknown uncertainties in the system.
Figure 5 shows the queue tracking error of three nodes and the comparison with the EO-PID [31] control algorithm and the RED [32] algorithm. The equilibrium optimization algorithm (EO) algorithm is an optimization algorithm inspired by the physics of controlled volume mass balance proposed by Faramarzi et al. in 2020 [33]. The optimization characteristic of the intelligent algorithm can more effectively realize the control scheme. Although the compared algorithms can remain within the prescribed range, the congestion control algorithm proposed in this paper shows improved steady-state performance and robustness.
5. Conclusions
A fixed time congestion control of the TCP/AWM network system was deeply studied. A new adaptive fixed-time TCP/AWM congestion controller was constructed for the TCP/AWM network model with UDP flow and unmodeled uncertainty under multiple bottlenecks, taking into account the interaction of intermediate nodes within the multi-bottleneck network. Neural network approximation was utilized to handle unmodeled uncertainties and external disturbances in the system. The designed TCP/AWM congestion controller ensures tracking performance and closed-loop system stability within a fixed time frame. Comparative analysis and simulation results demonstrate the feasibility of the proposed controller.
The model used in the design of the congestion controller described in this paper is a continuous network nonlinear model, and the network system is discretized in actual operation, and the designed controller should also be discretized before it can be configured and implemented in the router. The discretization of the continuous controller will inevitably have a certain impact on the effectiveness of the controller. Therefore, in follow-up work, it is necessary to develop the network congestion controller according to the discrete network model. In multi-bottleneck networks, different bottleneck nodes are affected by different degrees of impact. Different operating conditions, mixed wired transmission nodes and wireless transmission nodes, and other problems encountered in congestion controller design need more in-depth discussion and further research.
Author Contributions
Writing, Y.L.; methodology, J.C.; validation, S.L.; supervision, W.Z.; project administration, R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Braden, B.; Clark, D.; Crowcroft, J.; Davie, B.; Deering, S.; Estrin, D. Recommendations on queue management and congestion avoidance in the internet. RFC 2309 Inform. 1998, 10, 142–149. [Google Scholar]
- Adams, R. Active queue management: A survey. IEEE Commun. Surv. Tutorials 2013, 15, 1425–1476. [Google Scholar] [CrossRef]
- Floyd, S.; Jacobson, V. Random early detection gateways for congestion avoidance. IEEE/ACM Trans. Netw. 1993, 1, 397–413. [Google Scholar] [CrossRef]
- Ott, T.J.; Lakshman, T.V.; Wong, L.H. SRED: Stabilized RED. In Proceedings of the 18th International Conference on Computer Communications, New York, NY, USA, 21–25 March 1999; pp. 1346–1355. [Google Scholar]
- Feng, W.C.; Shin, K.G.; Kandlur, D.D.; Saha, D. The BLUE active queue management algorithms. IEEE/ACM Trans. Netw. 2002, 10, 513–528. [Google Scholar] [CrossRef]
- Liu, S.; Basar, T.; Srikant, R. Exponential-RED: A stabilizing AQM scheme for low- and high-speed TCP protocols. IEEE/ACM Trans. Netw. 2005, 13, 1068–1081. [Google Scholar]
- Misra, V.; Gong, W.B.; Towsley, D.F. Fluid-based analysis of a network of AQM routers supporting TCP flows with an application to RED. In Proceedings of the 19th IEEE Internationl Conference on SIGCOMM, Stockholm, Sweden, 28 August–1 September 2000; Volume 30, pp. 151–160. [Google Scholar]
- Unal, H.U.; Melchoraguilar, D.; Ustebay, D.; Niculescu, S.; Ozbay, H. Comparison of PI controllers designed for the delay model of TCP/AQM networks. Comput. Commun. 2013, 36, 1225–1234. [Google Scholar] [CrossRef]
- Zou, M.; Zeng, Q.; Zhang, X. Weakly-supervised Action Learning in Procedural Task Videos via Process Knowledge Decomposition. IEEE Trans. Circuits Syst. Video Technol. 2024, 20, 116–132. [Google Scholar] [CrossRef]
- Li, Z.H.; Liu, Y.; Jing, Y.W. Active queue management algorithm for TCP networks with integral backstepping and minimax. Int. J. Control Autom. Syst. 2019, 17, 1059–1066. [Google Scholar] [CrossRef]
- Zheng, W.M.; Li, Y.X.; Jing, X.W.; Liu, S.K. Adaptive finite-time congestion control for uncertain TCP/AQM network with unknown hysteresis. Complexity 2020, 2020, 4138390. [Google Scholar] [CrossRef]
- Chen, J.Q.; Jing, Y.W. Multiple bottleneck topology TCP/AQM switching network congestion control with input saturation and prescribed performance. ISA Trans. 2023, 135, 369–379. [Google Scholar] [CrossRef]
- Li, Y.X.; Liu, S.K.; Li, J.; Zheng, W.M. Congestion tracking control of multi-bottleneck TCP networks with input-saturation and dead-zone. Aims Math. 2024, 9, 10935–10954. [Google Scholar] [CrossRef]
- Barbera, M.; Lombardo, A.; Panarello, C.; Schembra, G. Active window management: An efficient gateway mechanism for TCP traffic control. In Proceedings of the 2007 IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 6141–6148. [Google Scholar]
- Barbera, M.; Lombardo, A.; Panarello, C.; Schembra, G. Active window management: Performance assessment through an extensive comparison with XCP. In Proceedings of the International Conference on Research in Networking, Singapore, 5–9 May 2008; Springer: Berlin/Heidelberg, Germany, 2008; p. 4982. [Google Scholar]
- Bruschi, R.; Lombardo, A.; Panarello, C.; Podda, E.; Santagati, E.; Schembra, G. Active window management: Reducing energy consumption of TCP congestion control. In Proceedings of the IEEE International Conference on Communications, Budapest, Hungary, 9–13 June 2013; pp. 4154–4158. [Google Scholar]
- Yuan, X.D.; Jing, Y.W.; Jiang, N. Research of control scheme of AWM based on PID. In Proceedings of the 28th IEEE Chinese Control and Decision Conference, Yinchuan, China, 28–30 May 2016; pp. 1512–1516. [Google Scholar]
- Xie, H.X.; Jing, Y.W. Event-triggered preset performance congestion control for TCP/AWM network systems. Control. Theory Appl. 2023, 40, 450. [Google Scholar]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Liang, Y.J.; Ma, R.; Wang, M.; Fu, J. Global finite-time stabilisation of a class of switched nonlinear systems. Int. J. Syst. Sci. 2015, 46, 2897–2904. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhao, S.Y.; He, W. Adaptive finite-time tracking control of full state constrained nonlinear systems with dead-zone. Automatica 2019, 100, 99–107. [Google Scholar] [CrossRef]
- Guo, R.N.; Xu, S.Y. Observer-based sliding mode synchronization control of complex-valued neural net-works with inertial term and mixed time-varying delays. Appl. Math. Comput. 2023, 442, 127761. [Google Scholar]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Automat. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Wang, F.; Lai, G.Y. Fixed-time control design for nonlinear uncertain systems via adaptive method. Syst. Control Lett. 2020, 140, 104704. [Google Scholar] [CrossRef]
- Lu, K.; Liu, Z.; Wang, Y.; Chen, C.L.P. Fixed-Time Adaptive Fuzzy Control for Uncertain Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2021, 29, 3769–3781. [Google Scholar] [CrossRef]
- Meng, Q.; Ma, Q.; Shi, Y. AAdaptive Fixed-Time Stabilization for a Class of Uncertain Nonlinear Systems. IEEE Trans. Autom. Control 2023, 68, 6929–6936. [Google Scholar] [CrossRef]
- Shen, J.D.; Jing, Y.W.; Dimirovski, G.M. Fixed-time Congestion Tracking Control for a Class of Uncertain TCP/AQM Computer and Communication Networks. Int. J. Control Autom. Syst. 2022, 20, 758–768. [Google Scholar] [CrossRef]
- Ba, D.S.; Li, Y.X.; Tong, S.T. Fixed-time adaptive neural tracking control for a class of uncertain nonstrict nonlinear systems. Neurocomputing 2019, 363, 273–280. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Chen, B.; Lin, C.; Wang, H. Finite-time adaptive control for a class of nonlinear systems with nonstrict feedback structure. IEEE Trans. Cybern. 2018, 48, 2774–2782. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Bai, W. Adaptive neural tracking control for non-affine nonlinear systems with finite-time output constraint. Neurocomputing 2020, 397, 60–69. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Oliva, D. Design and robustness analysis of an Automatic Voltage Regulator system controller by using Equilibrium Optimizer algorithm. Comput. Electr. Eng. 2021, 89, 106930. [Google Scholar] [CrossRef]
- Tan, L.; Zhang, W.; Peng, G.; Chen, G. Stability of TCP/RED systems in AQM routers. IEEE Trans. Autom. Control. 2006, 51, 1393–1398. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).