Optimal Control-Based Algorithm Design and Application for Trajectory Tracking of a Mobile Robot with Four Independently Steered and Four Independently Actuated Wheels
Abstract
1. Introduction
- The Euler method for discretization, the conjugate gradient method and the line search method with Wolfe’s conditions for minimizing the objective function have been integrated into one numerically efficient algorithm for the direct calculation of the state controller of LTV systems. This algorithm explicitly obtains the desired time-variant control law.
- The most effective version of the algorithm is subjected to both numerical simulations and experimental verification on a laboratory model of a 4ISW4IAW mobile robot system. Based on the authors’ current knowledge, the application and experimental verification of a time-varying controller designed in this way, which additionally includes the transformation into a three-input, two-chain, single-generator chained form, for a robot with four wheels that have independent drive and steer, has not been investigated yet.
2. System Description
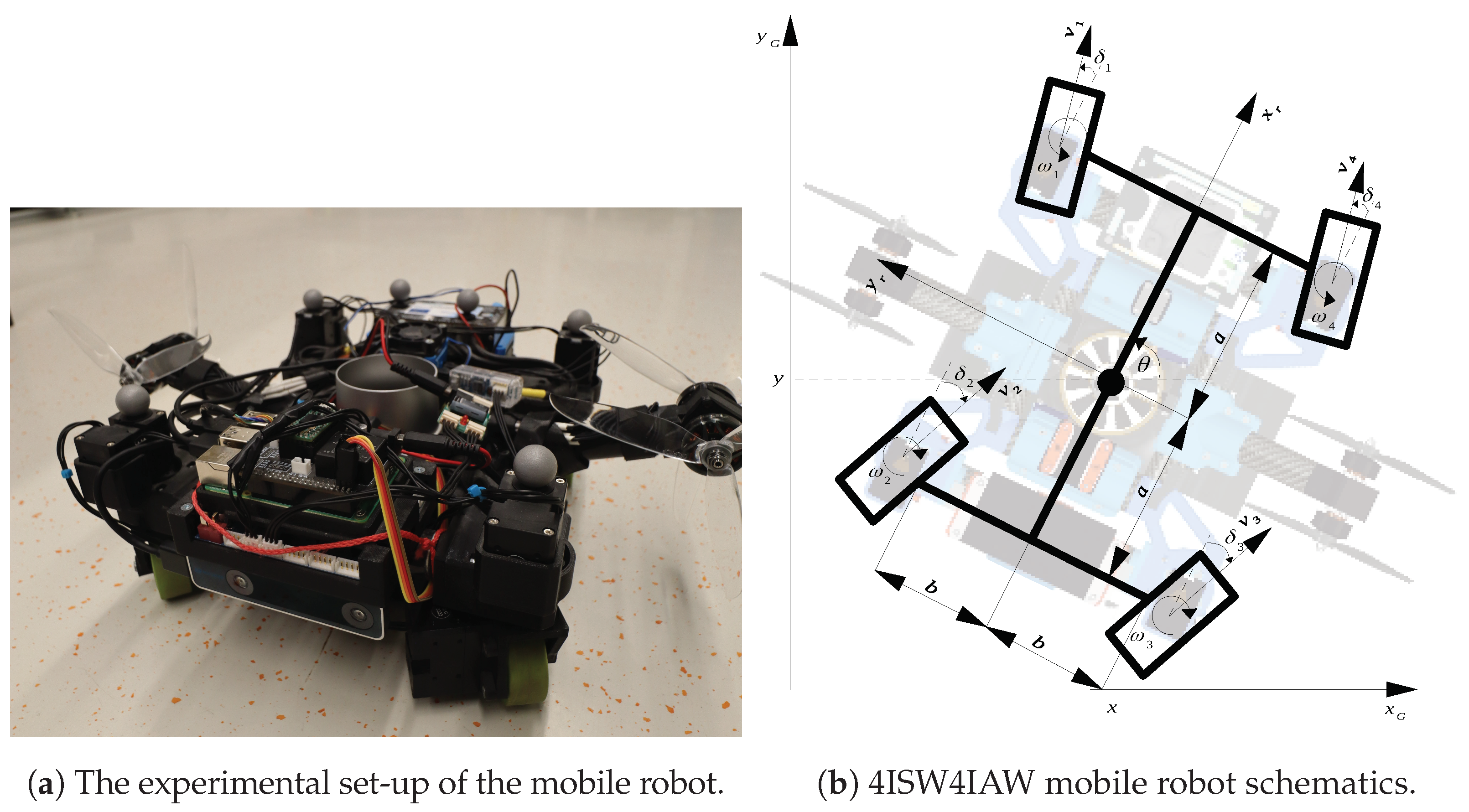
2.1. Robot Description
2.2. Mathematical Model
3. Algorithm for the Synthesis of a Time-Varying State Controller
3.1. Control Problem Formulation
3.2. Optimal Control-Based Algorithm Derivation
- For the Euler approximation (37); set the initial state vector ; set final time ; set number of time intervals N; calculate time step length .
- Choose the weight matrices , and an arbitrary initial values of for the objective function (40).
- Calculate the new using (42).
- Calculate the state vector using the Euler method (41).
4. Simulation and Experimental Validation
4.1. Simulation Results
4.1.1. Straight Line Trajectory Tracking
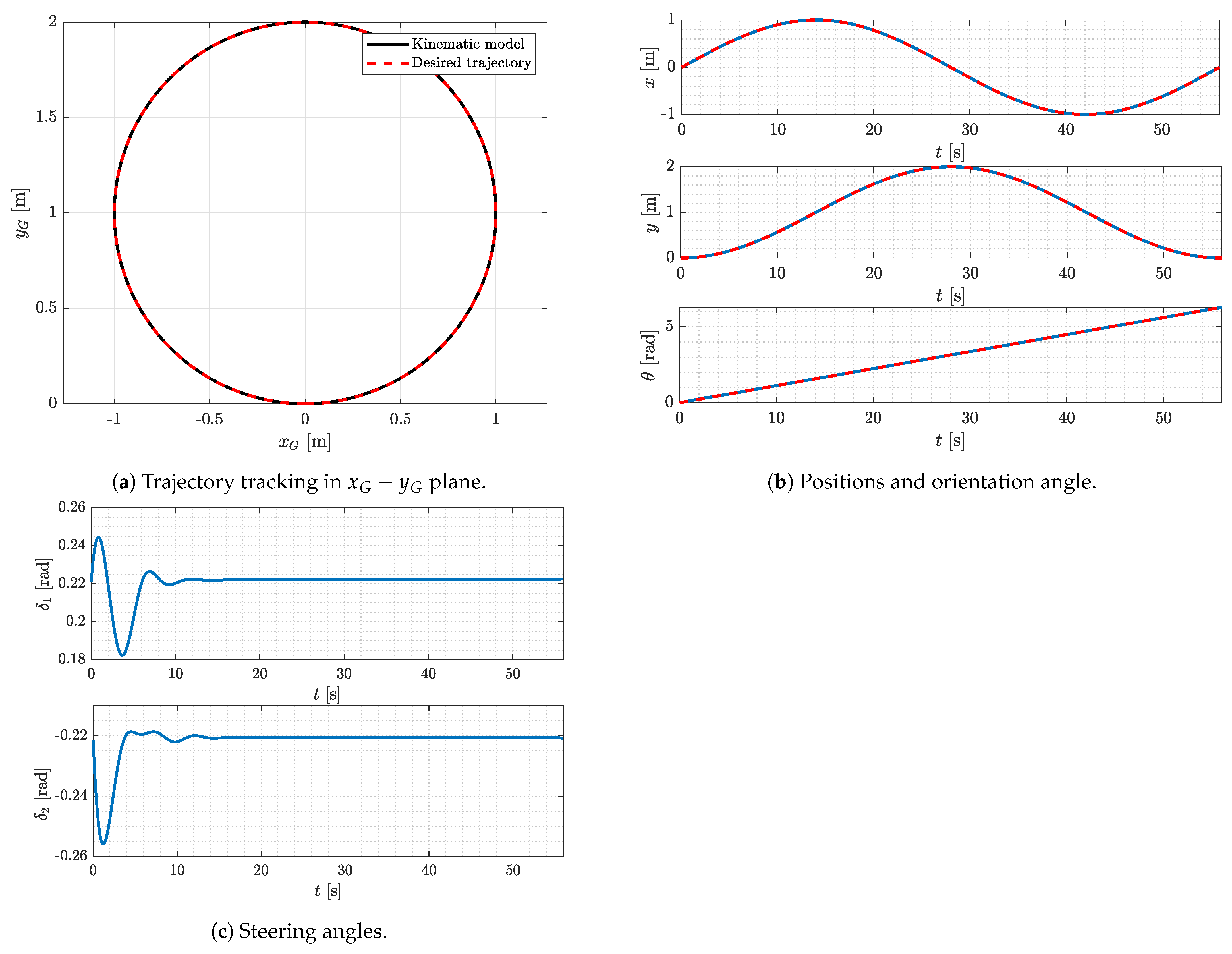
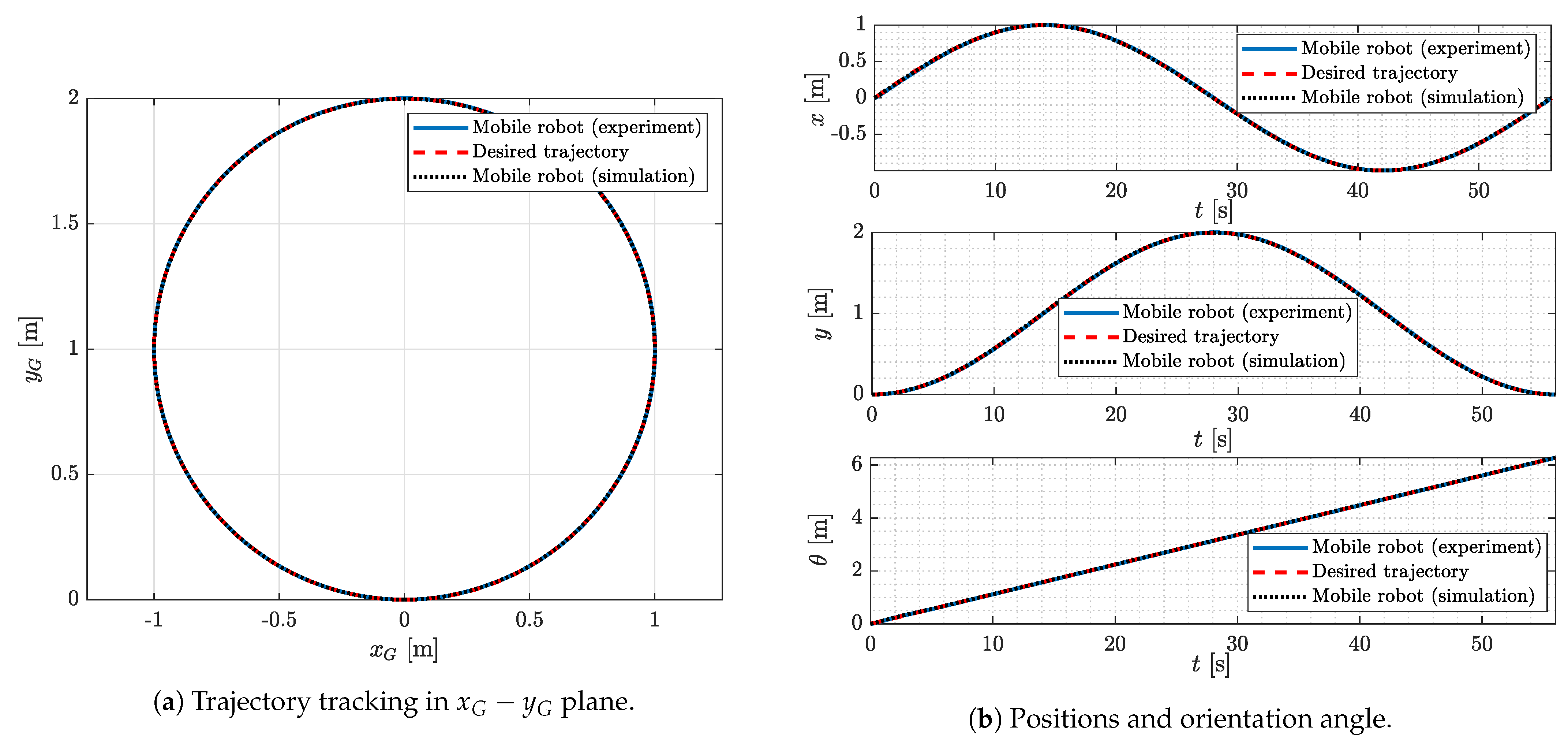
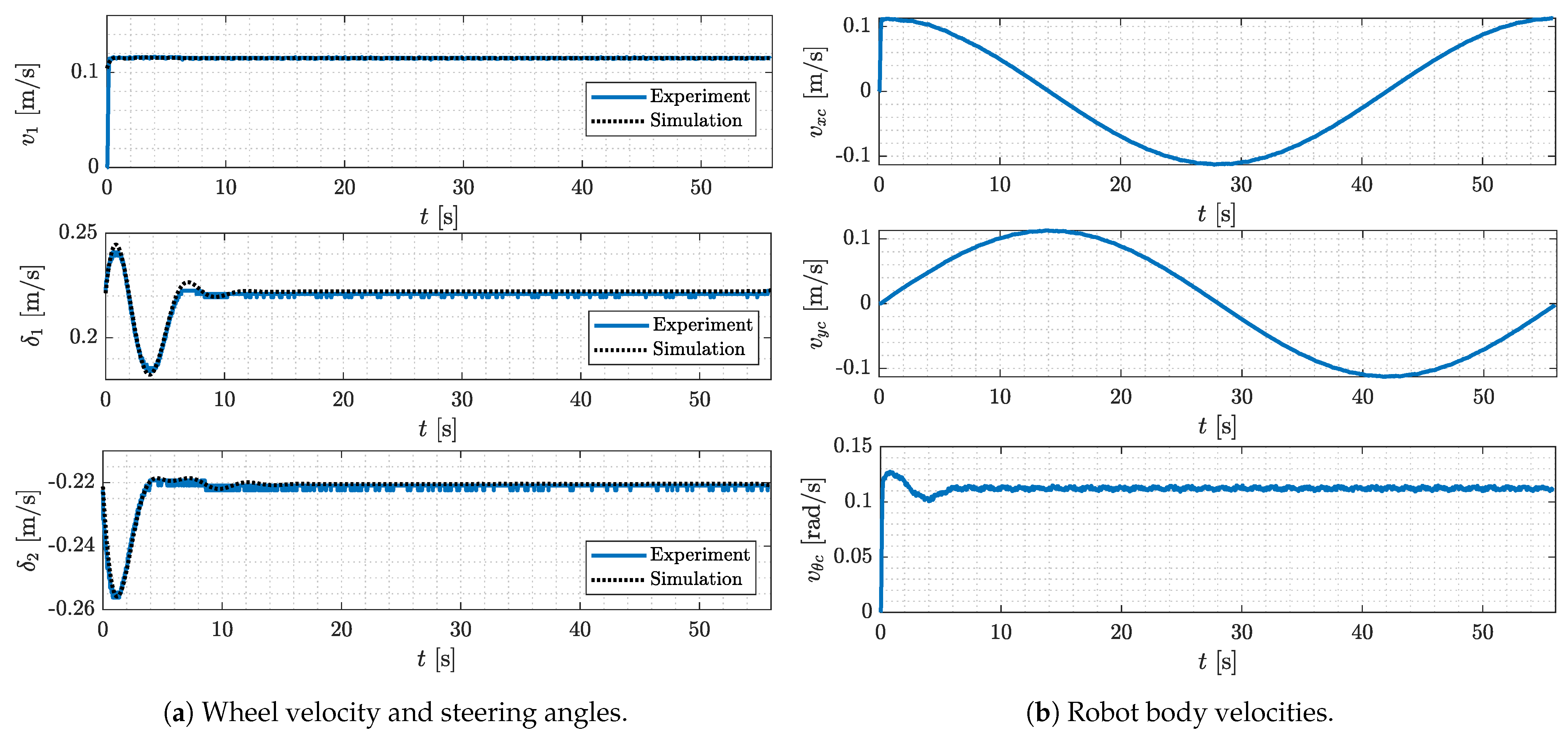
4.1.2. Circular Trajectory Tracking
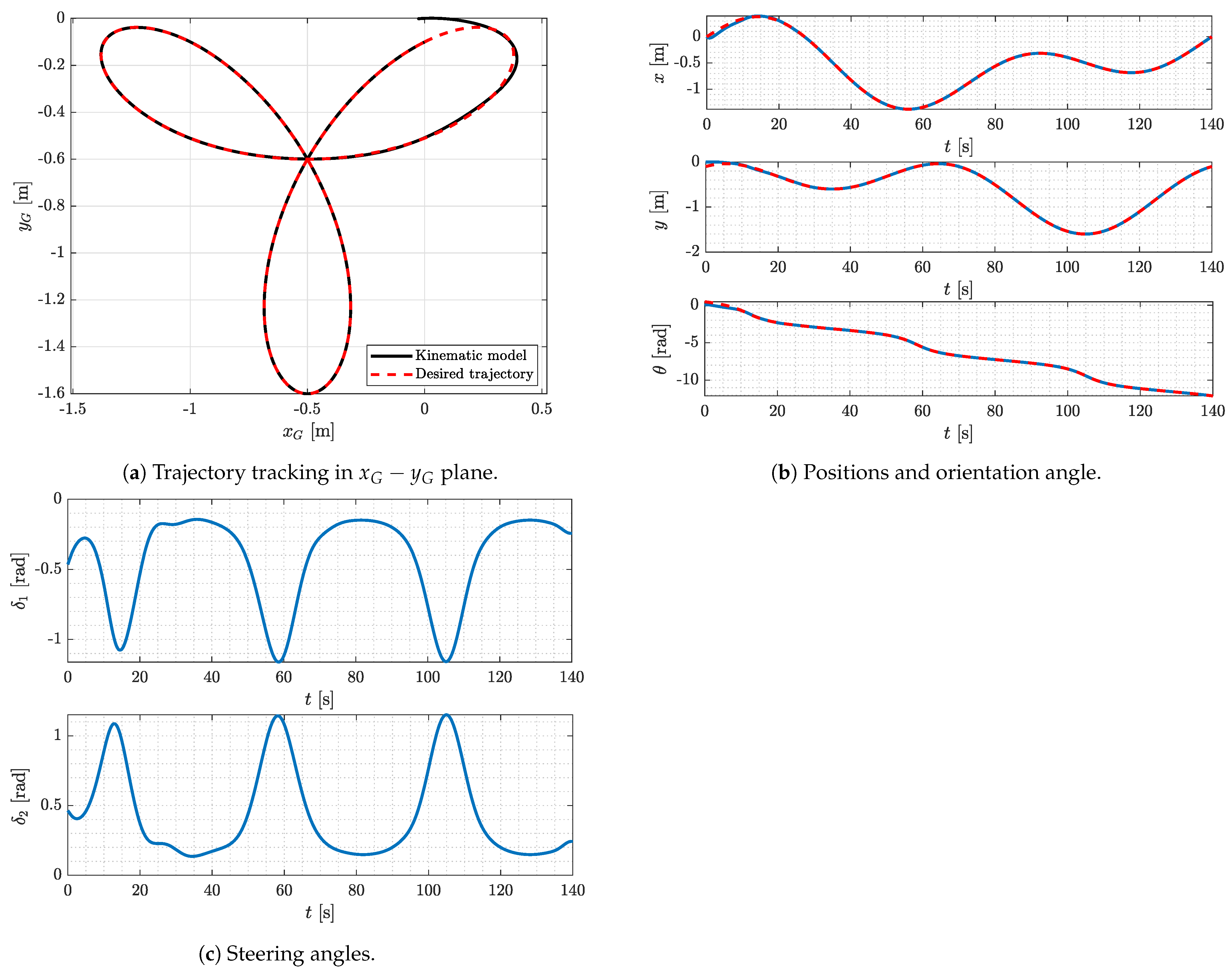
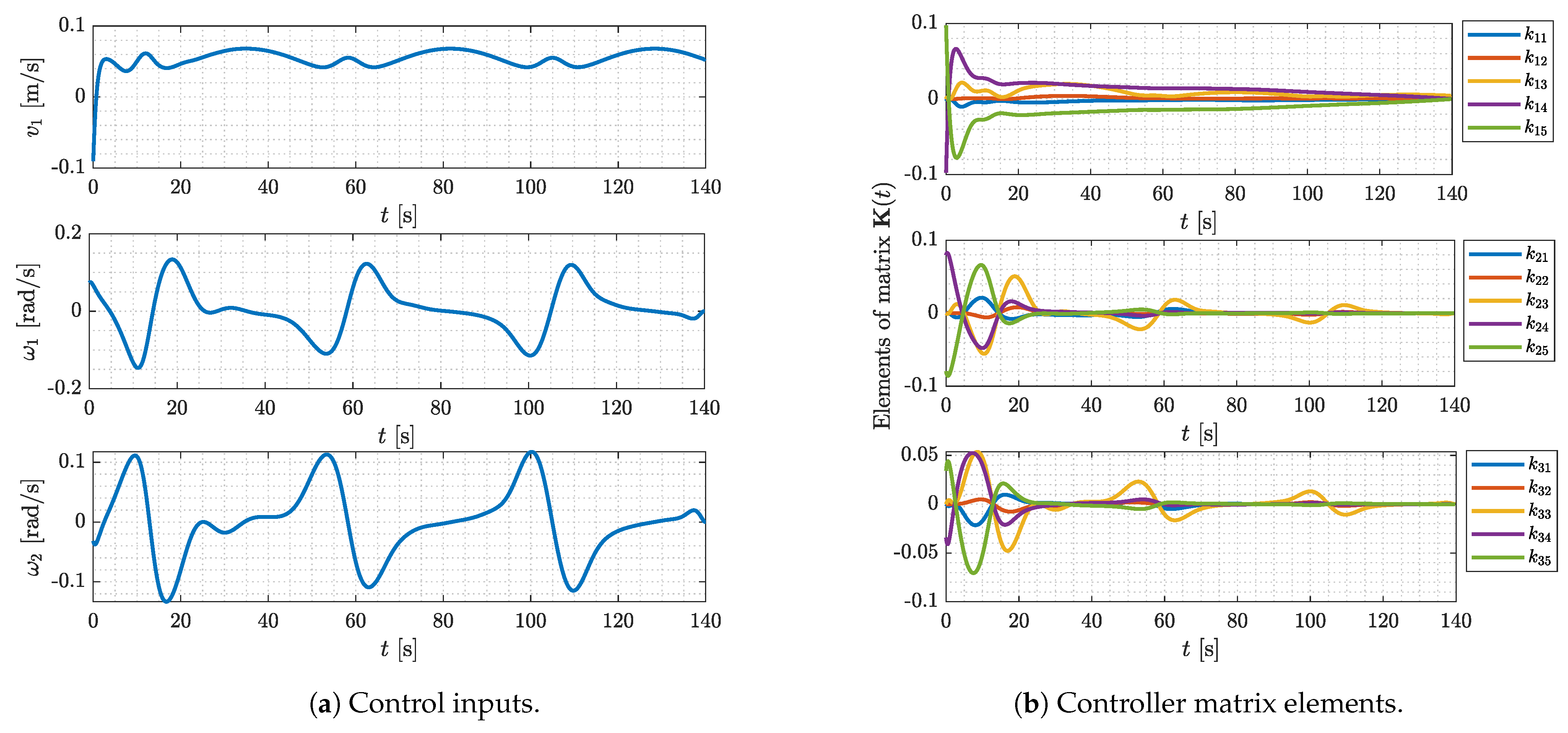
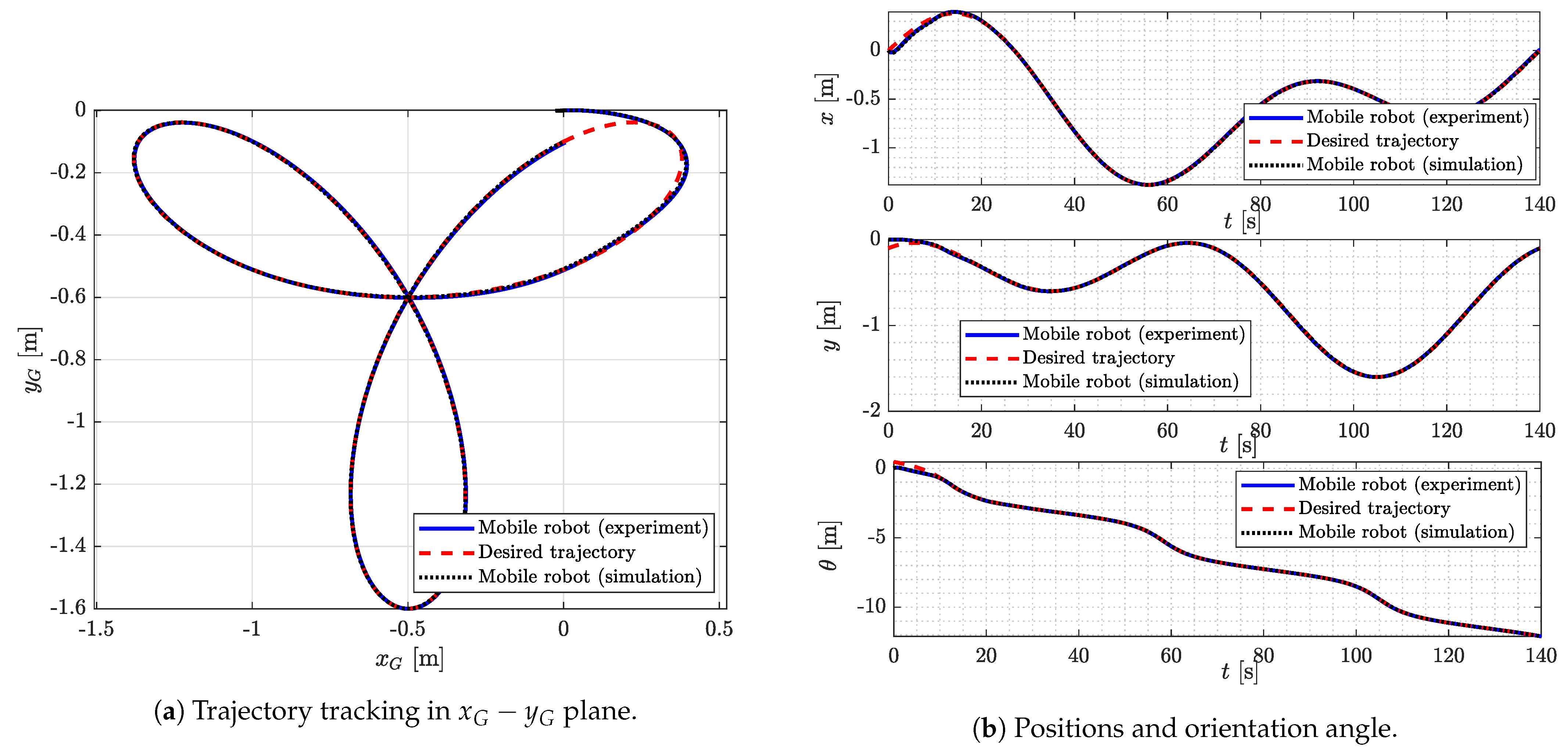
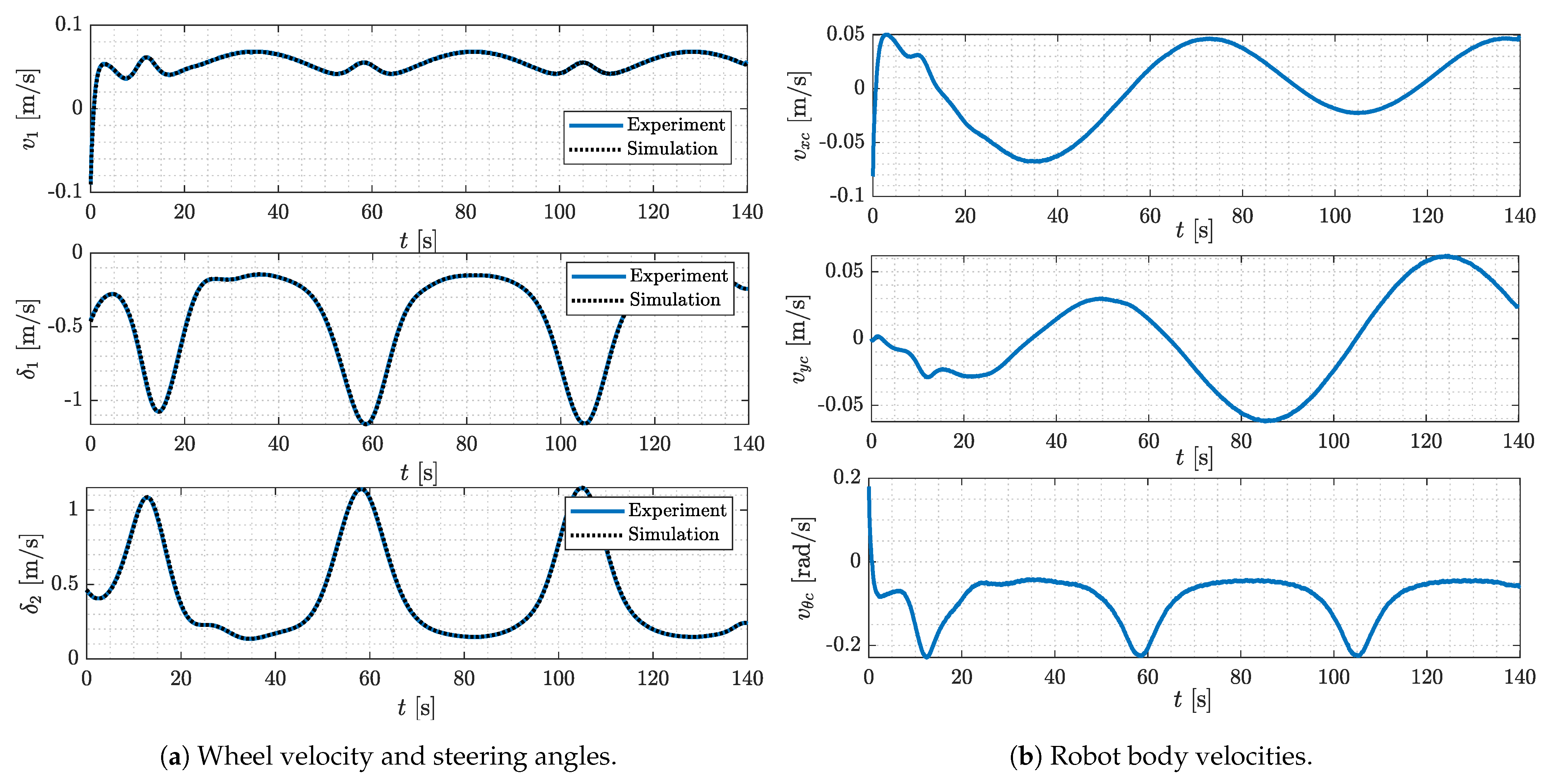
4.1.3. Curvilinear Trajectory Tracking
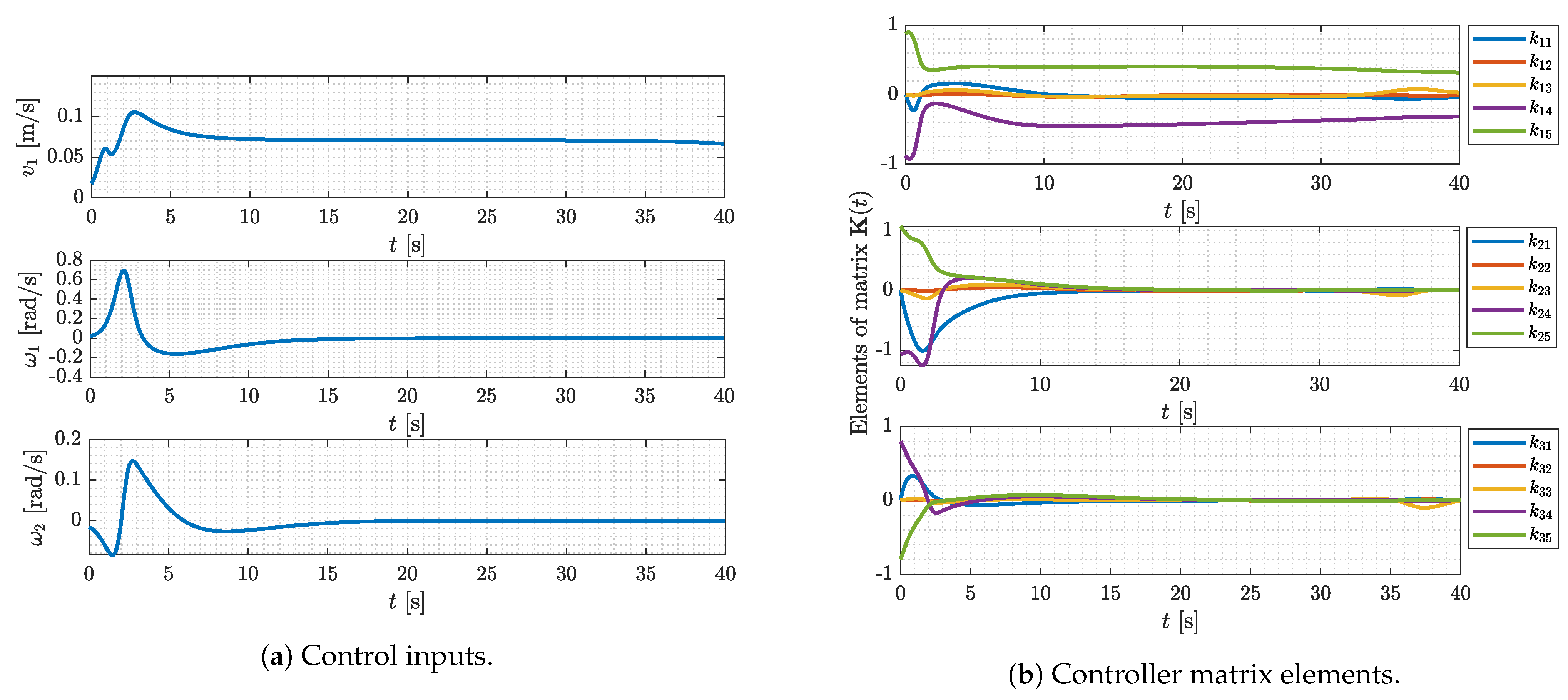
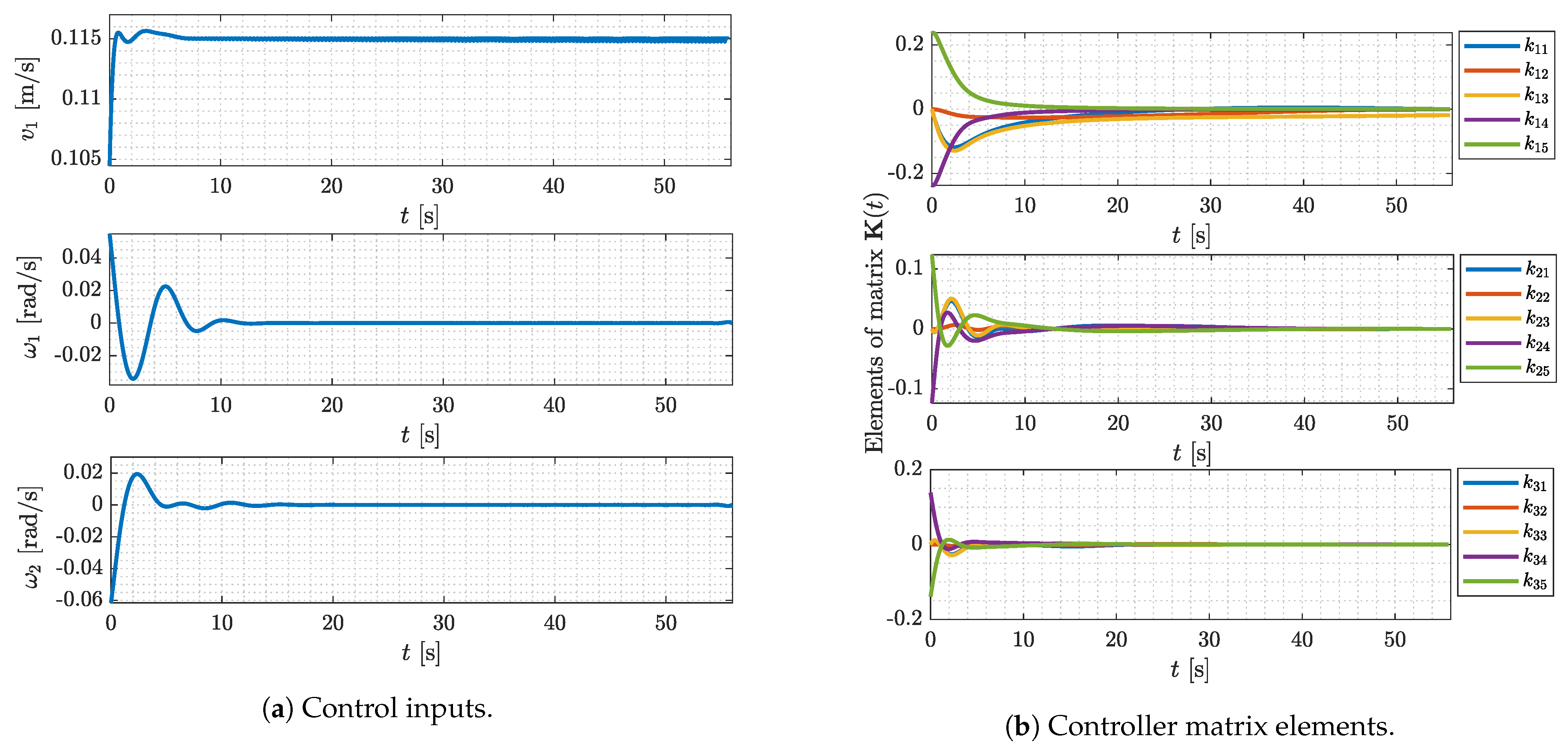
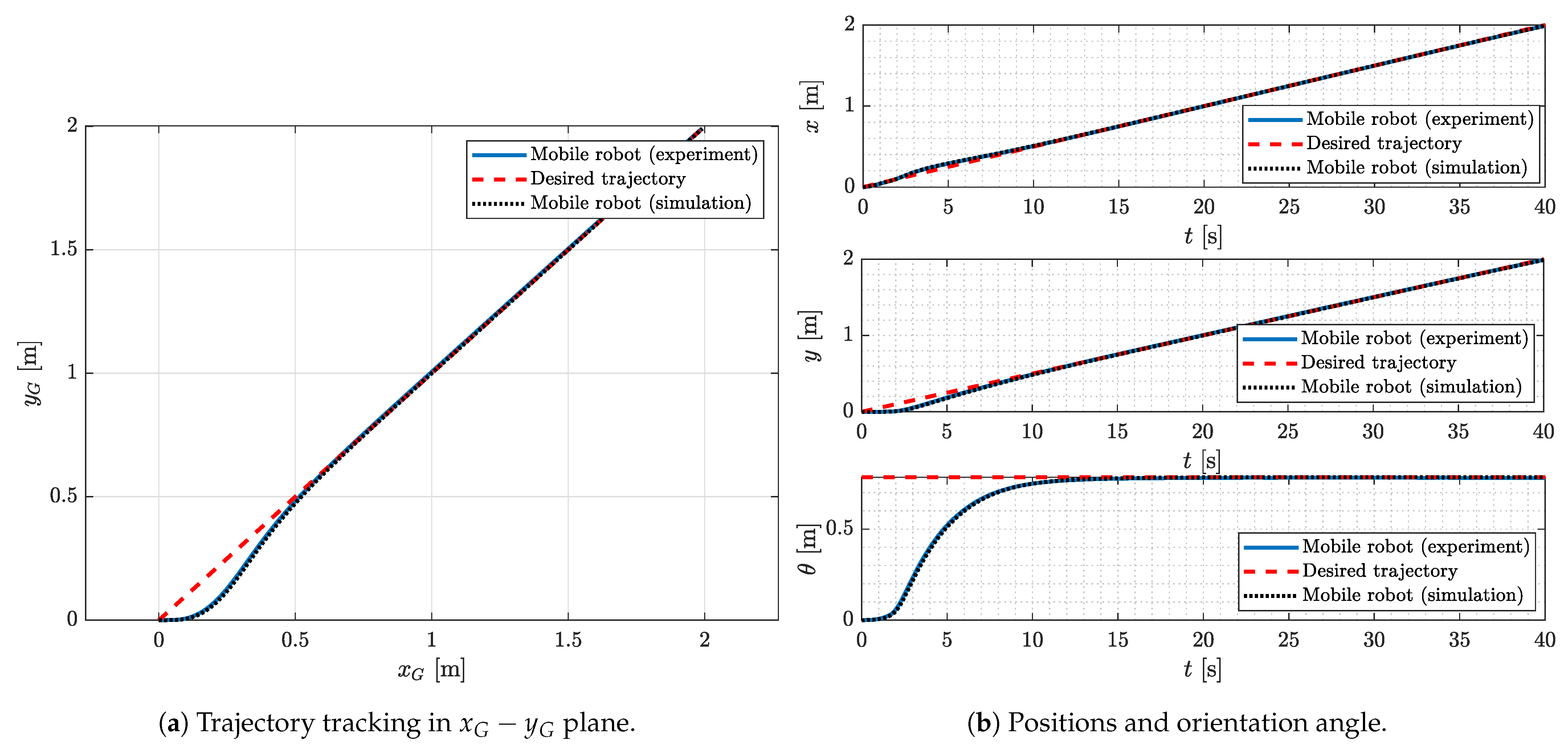
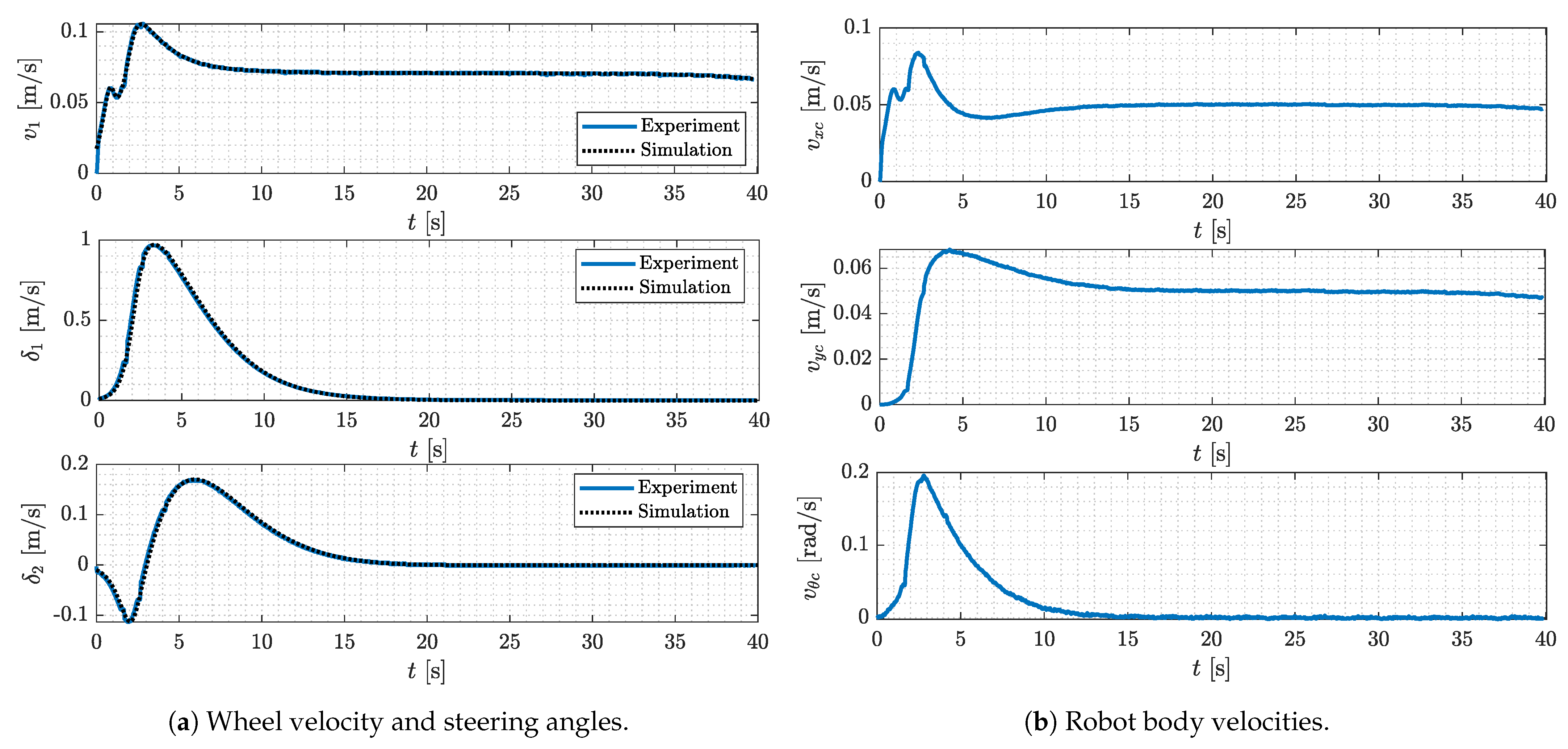
4.2. Experimental Results
4.3. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 4ISW4IAW | Four Independently Steered Wheels and Four Independently Actuated Wheels |
| ASA | Acrylonitrile Styrene Acrylate |
| DC | Direct Current |
| LMI | Linear Matrix Inequality |
| LQR | Linear Quadratic Regulator |
| LTV | Linear Time Varying |
| PID | Proportional–Integral–Derivative |
| PWM | Pulse-Width Modulation |
| ROS | Robot Operating System |
| TVLQ | Time-Varying Linear Quadratic |
References
- Tzafestas, S.G. Mobile Robot Control and Navigation: A Global Overview. J. Intell. Robot. Syst. 2018, 91, 35–58. [Google Scholar] [CrossRef]
- Rubio, F.; Valero, F.; Llopis-Albert, C. A review of mobile robots: Concepts, methods, theoretical framework, and applications. Int. J. Adv. Robot. Syst. 2019, 16, 1–22. [Google Scholar] [CrossRef]
- Alatise, M.B.; Hancke, G.P. A Review on Challenges of Autonomous Mobile Robot and Sensor Fusion Methods. IEEE Access 2020, 8, 39830–39846. [Google Scholar] [CrossRef]
- Fragapane, G.; de Koster, R.; Sgarbossa, F.; Strandhagen, J.O. Planning and control of autonomous mobile robots for intralogistics: Literature review and research agenda. Eur. J. Oper. Res. 2021, 294, 405–426. [Google Scholar] [CrossRef]
- Loganathan, A.; Ahmad, N.S. A systematic review on recent advances in autonomous mobile robot navigation. Eng. Sci. Technol. Int. J. 2023, 40, 101343. [Google Scholar] [CrossRef]
- Medina, L.; Guerra, G.; Herrera, M.; Guevara, L.; Camacho, O. Trajectory tracking for non-holonomic mobile robots: A comparison of sliding mode control approaches. Results Eng. 2024, 22, 102105. [Google Scholar] [CrossRef]
- Arab, A.; Hadžić, I.; Yi, J. Safe Predictive Control of Four-Wheel Mobile Robot with Independent Steering and Drive. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 2962–2967. [Google Scholar]
- Liu, X.; Wang, W.; Li, X.; Liu, F.; He, Z.; Yao, Y.; Ruan, H.; Zhang, T. MPC-based high-speed trajectory tracking for 4WIS robot. ISA Trans. 2022, 123, 413–424. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, X.; Meng, W.; Zheng, S.; Jiang, L.; Meng, J.; Wang, S. Coupled fractional-order sliding mode control and obstacle avoidance of a four-wheeled steerable mobile robot. ISA Trans. 2021, 108, 282–294. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Wang, S.; Xie, Y.; Meng, J.; Zheng, S.; Zhang, X.; Wu, H. Anti-Disturbance Direct Yaw Moment Control of a Four-Wheeled Autonomous Mobile Robot. IEEE Access 2020, 8, 174654–174666. [Google Scholar] [CrossRef]
- Qiao, Y.; Chen, X.; Yin, D. Coordinated Control for the Trajectory Tracking of Four-Wheel Independent Drive–Four-Wheel Independent Steering Electric Vehicles Based on the Extension Dynamic Stability Domain. Actuators 2024, 13, 77. [Google Scholar] [CrossRef]
- Tan, X.; Liu, D.; Xiong, H. Optimal Control Method of Path Tracking for Four-Wheel Steering Vehicles. Actuators 2022, 11, 61. [Google Scholar] [CrossRef]
- Xu, Q.; Li, H.; Wang, Q.; Wang, C. Wheel Deflection Control of Agricultural Vehicles with Four-Wheel Independent Omnidirectional Steering. Actuators 2021, 10, 334. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z.; Si, Z. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control and sliding mode control. Adv. Mech. Eng. 2021, 13, 1–17. [Google Scholar] [CrossRef]
- Dai, P.; Taghia, J.; Lam, S.; Katupitiya, J. Integration of sliding mode based steering control and PSO based drive force control for a 4WS4WD vehicle. Auton. Robot. 2018, 42, 553–568. [Google Scholar] [CrossRef]
- Dai, P.; Katupitiya, J. Force control for path following of a 4WS4WD vehicle by the integration of PSO and SMC. Veh. Syst. Dyn. 2018, 56, 1682–1716. [Google Scholar] [CrossRef]
- Božić, M.; Jerbić, B.; Švaco, M. Development of a Mobile Wall-Climbing Robot with a Hybrid Adhesion System. In Proceedings of the 2021 44th International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 27 September–1 October 2021; pp. 1136–1142. [Google Scholar]
- Božić, M.; Ćaran, B.; Švaco, M.; Jerbić, B.; Serdar, M. Mobile Wall-Climbing Robot for NDT inspection of vertical concrete structures. In Proceedings of the International Symposium on Non-Destructive Testing in Civil Engineering (NDT-CE 2022), Zurich, Switzerland, 16–18 August 2022; pp. 1–14. [Google Scholar]
- Bryson, A.E. Time-Varying Linear-Quadratic Control. J. Optim. Theory Appl. 1999, 100, 515–525. [Google Scholar] [CrossRef]
- Tedrake, R. Underactuated Robotics; MIT: Cambridge, MA, USA, 2023. [Google Scholar]
- Javadi, M.; Harnack, D.; Stocco, P.; Kumar, S.; Vyas, S.; Pizzutilo, D.; Kirchner, F. AcroMonk: A Minimalist Underactuated Brachiating Robot. IEEE Robot. Autom. Lett. 2023, 8, 3637–3644. [Google Scholar] [CrossRef]
- Vyas, S.; Maywald, L.; Kumar, S.; Jankovic, M.; Mueller, A.; Kirchner, F. Post-capture detumble trajectory stabilization for robotic active debris removal. Adv. Space Res. 2023, 72, 2845–2859. [Google Scholar] [CrossRef]
- Nortmann, B.; Mylvaganam, T. Direct Data-Driven Control of Linear Time-Varying Systems. IEEE Trans. Autom. Control 2023, 68, 4888–4895. [Google Scholar] [CrossRef]
- Ling, Y.; Wu, J.; Zhou, W.; Wang, Y.; Wu, C. Linear Quadratic Regulator Method in Vision-Based Laser Beam Tracking for a Mobile Target Robot. Robotica 2021, 39, 524–534. [Google Scholar] [CrossRef]
- Milić, V.; Di Cairano, S.; Kasać, J.; Bemporad, A.; Šitum, Z. A numerical algorithm for nonlinear L2-gain optimal control with application to vehicle yaw stability control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 5040–5045. [Google Scholar]
- Milić, V.; Kasać, J.; Lukas, M. An Algorithm for Solving Zero-Sum Differential Game Related to the Nonlinear H∞ Control Problem. Algorithms 2023, 16, 48. [Google Scholar] [CrossRef]
- Ćaran, B.; Švaco, M.; Šuligoj, F.; Jerbić, B. Modeling, Parameter Estimation and Control Design of 4WIS4WID Mobile Robot: Simulation and Experimental Validation. In Proceedings of the International Conference on Robotics in Alpe-Adria Danube Region, Cluj-Napoca, Romania, 12–14 June 2024; pp. 607–618. [Google Scholar]
- Lee, M.H.; Li, T.H.S. Kinematics, dynamics and control design of 4WIS4WID mobile robots. J. Eng. 2015, 2015, 6–16. [Google Scholar] [CrossRef]
- Ćaran, B.; Škifić, N.; Milić, V.; Švaco, M. Application of a Time-Varying Linear Quadratic Controller for Trajectory Tracking of a Four-Wheel Mobile Robot with Independent Steering and Drive. In Proceedings of the 2024 47th International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 20–24 May 2024; pp. 1–8. [Google Scholar]
- Tilbury, D.; Sordalen, O.; Bushnell, L.; Sastry, S. A multisteering trailer system: Conversion into chained form using dynamic feedback. IEEE Trans. Robot. Autom. 1995, 11, 807–818. [Google Scholar] [CrossRef]
- Walsh, G.; Bushnell, L. Stabilization of multiple input chained form control systems. Syst. Control Lett. 1995, 25, 227–234. [Google Scholar] [CrossRef]
- De Luca, A.; Oriolo, G.; Samson, C. Feedback control of a nonholonomic car-like robot. In Robot Motion Planning and Control; Springer: Berlin/Heidelberg, Germany, 1998; pp. 171–253. [Google Scholar]
- Fletcher, R.; Reeves, C.M. Function minimization by conjugate gradients. Comput. J. 1964, 7, 149–154. [Google Scholar] [CrossRef]
- Polak, E.; Ribiere, G. Note sur la convergence de mthodes de directions conjugues. Rev. Franaise D’inform. Et De Rech. Oprationnelle Srie Rouge 1969, 3, 35–43. [Google Scholar]
- Hestenes, M.R.; Stiefel, E. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Dai, Y.H.; Yuan, Y. A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property. SIAM J. Optim. 1999, 10, 177–182. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Science + Business Media, LLC: New York, NY, USA, 2006. [Google Scholar]
- Quigley, M.; Gerkey, B.; Smar, W.D. Programming Robots with ROS; O’Reilly Media: Boston, MA, USA, 2015. [Google Scholar]




| 3 × | 3.6 × | 5.5 × | 5 × | 6 × |
| 1.5 | 51 | 14 | 0 | 0 | 32.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ćaran, B.; Milić, V.; Švaco, M.; Jerbić, B. Optimal Control-Based Algorithm Design and Application for Trajectory Tracking of a Mobile Robot with Four Independently Steered and Four Independently Actuated Wheels. Actuators 2024, 13, 279. https://doi.org/10.3390/act13080279
Ćaran B, Milić V, Švaco M, Jerbić B. Optimal Control-Based Algorithm Design and Application for Trajectory Tracking of a Mobile Robot with Four Independently Steered and Four Independently Actuated Wheels. Actuators. 2024; 13(8):279. https://doi.org/10.3390/act13080279
Chicago/Turabian StyleĆaran, Branimir, Vladimir Milić, Marko Švaco, and Bojan Jerbić. 2024. "Optimal Control-Based Algorithm Design and Application for Trajectory Tracking of a Mobile Robot with Four Independently Steered and Four Independently Actuated Wheels" Actuators 13, no. 8: 279. https://doi.org/10.3390/act13080279
APA StyleĆaran, B., Milić, V., Švaco, M., & Jerbić, B. (2024). Optimal Control-Based Algorithm Design and Application for Trajectory Tracking of a Mobile Robot with Four Independently Steered and Four Independently Actuated Wheels. Actuators, 13(8), 279. https://doi.org/10.3390/act13080279







