Simulation Training System for Parafoil Motion Controller Based on Actor–Critic RL Approach
Abstract
1. Introduction
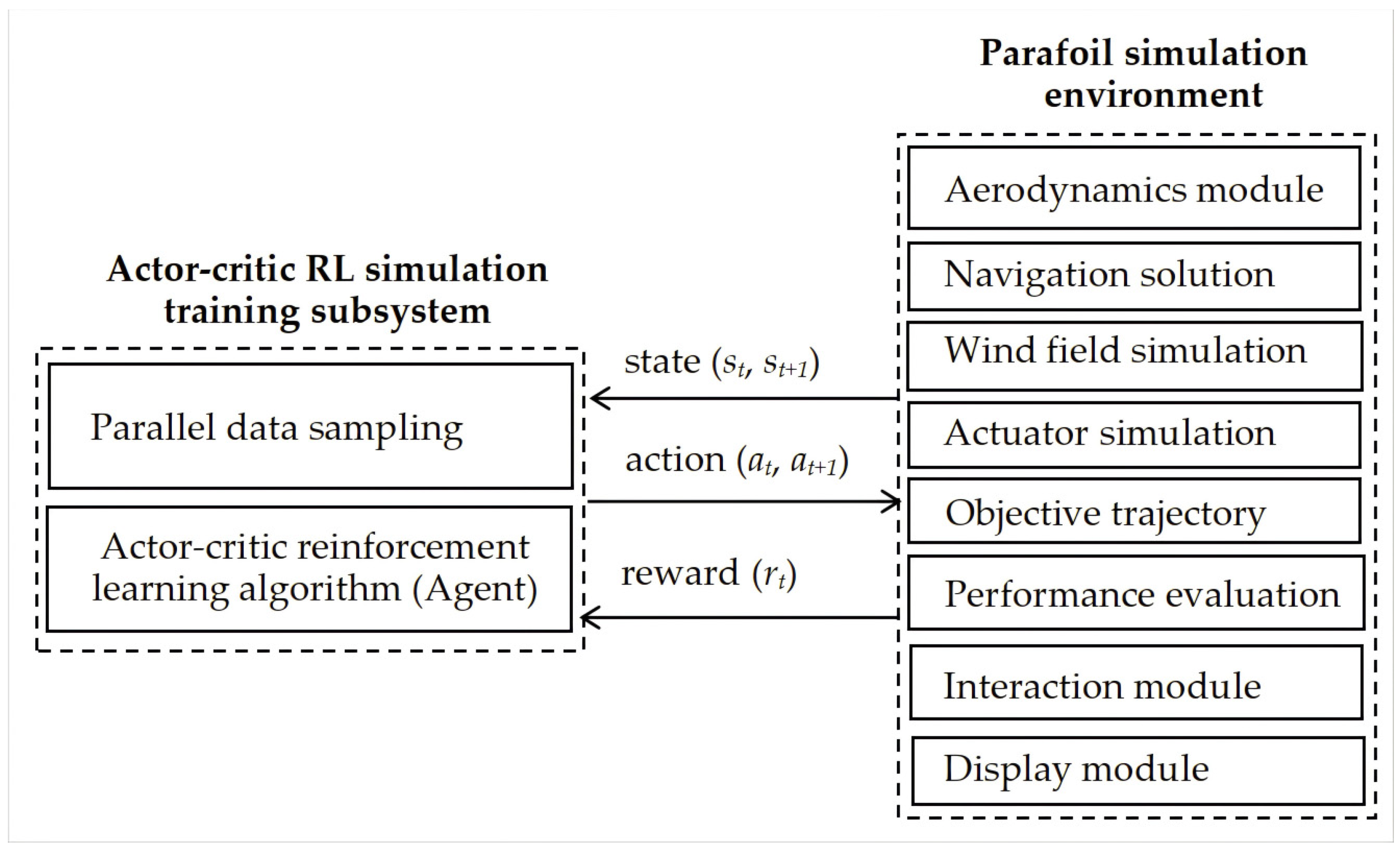
2. Principle of the Parafoil Motion-Control-Simulation Training System
- (1)
- Environmental factors, composed of an aerodynamics module, navigation solution, wind field simulation, actuator simulation, and objective trajectory;
- (2)
- The performance-evaluation module, used to evaluate the trajectory-tracking performance and provide feedback on the performance evaluation information as a reward to the agent of the actor–critic RL simulation training subsystem;
- (3)
- The interaction module, employed to exchange information between the agent and the simulation environment;
- (4)
- The display module, used to display the objective trajectory and actual flight process of the parafoil.
- (1)
- Parallel data sampling, utilizing one single GUP and multiple CPUs to speed up the parafoil motion-control-simulation training process;
- (2)
- Actor–critic reinforcement learning algorithm (Agent), using the data of the parallel data sampling to train the parafoil controller.
3. Parafoil Simulation Environment
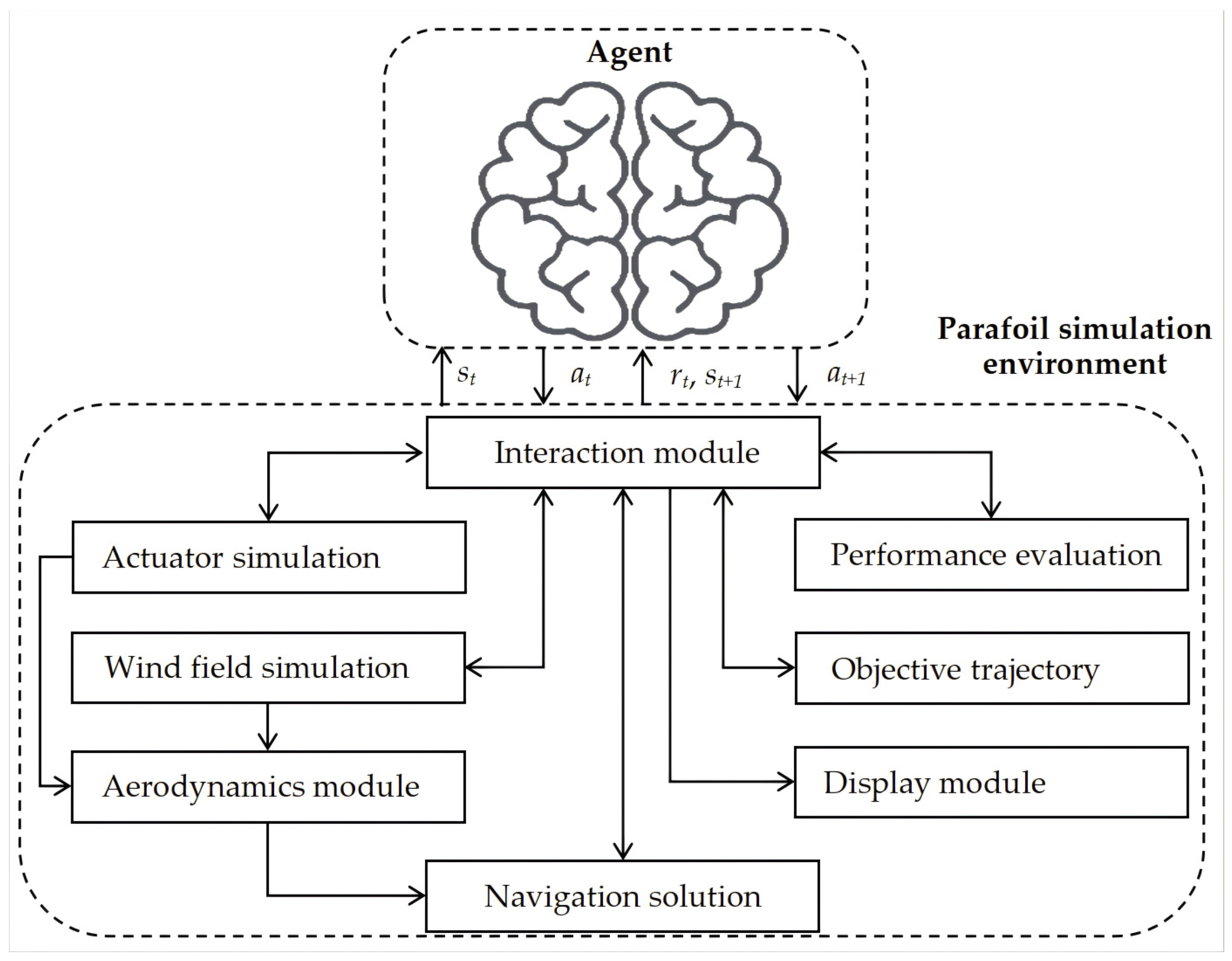
3.1. Interaction Module
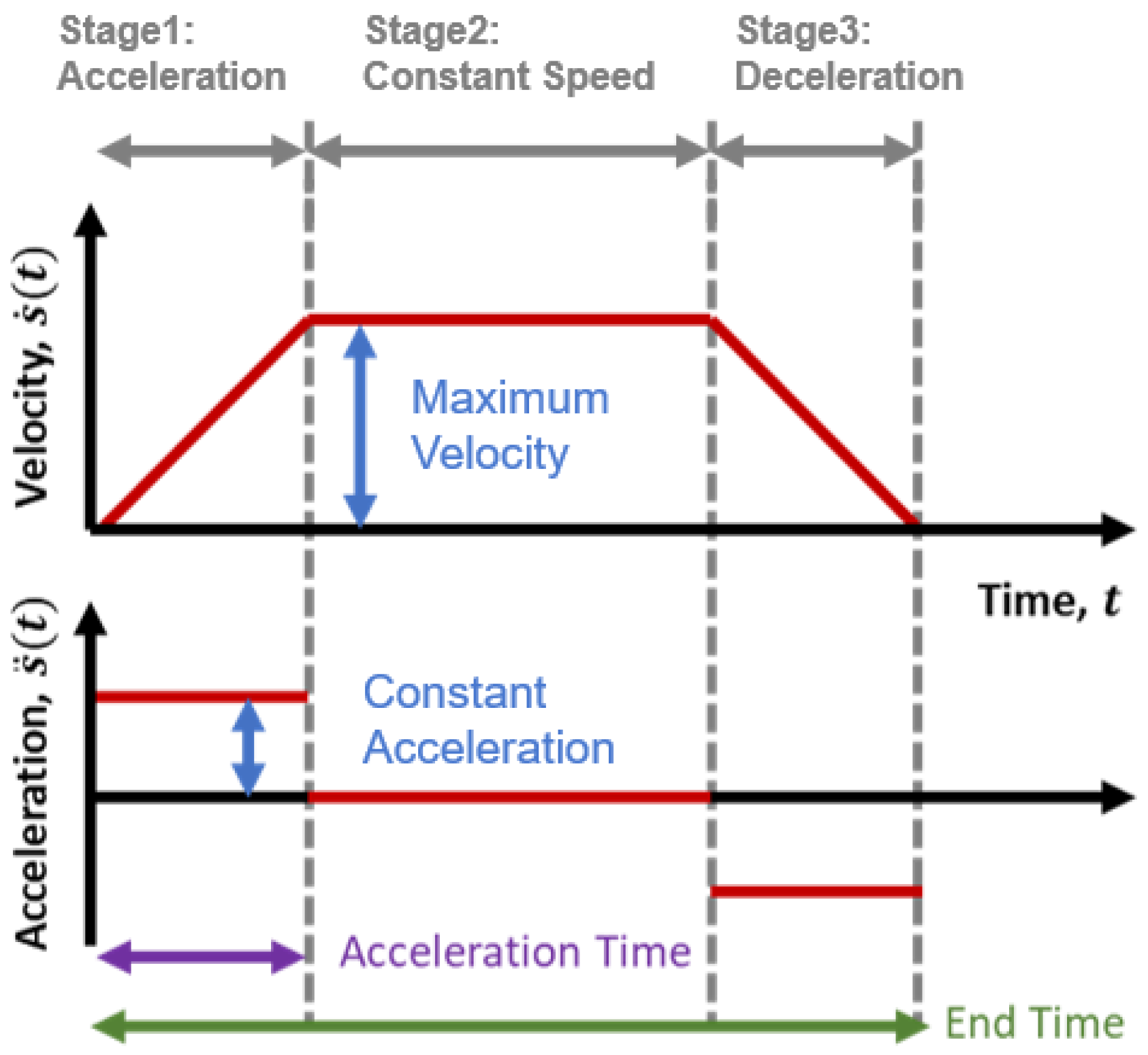
3.2. Actuator Simulation
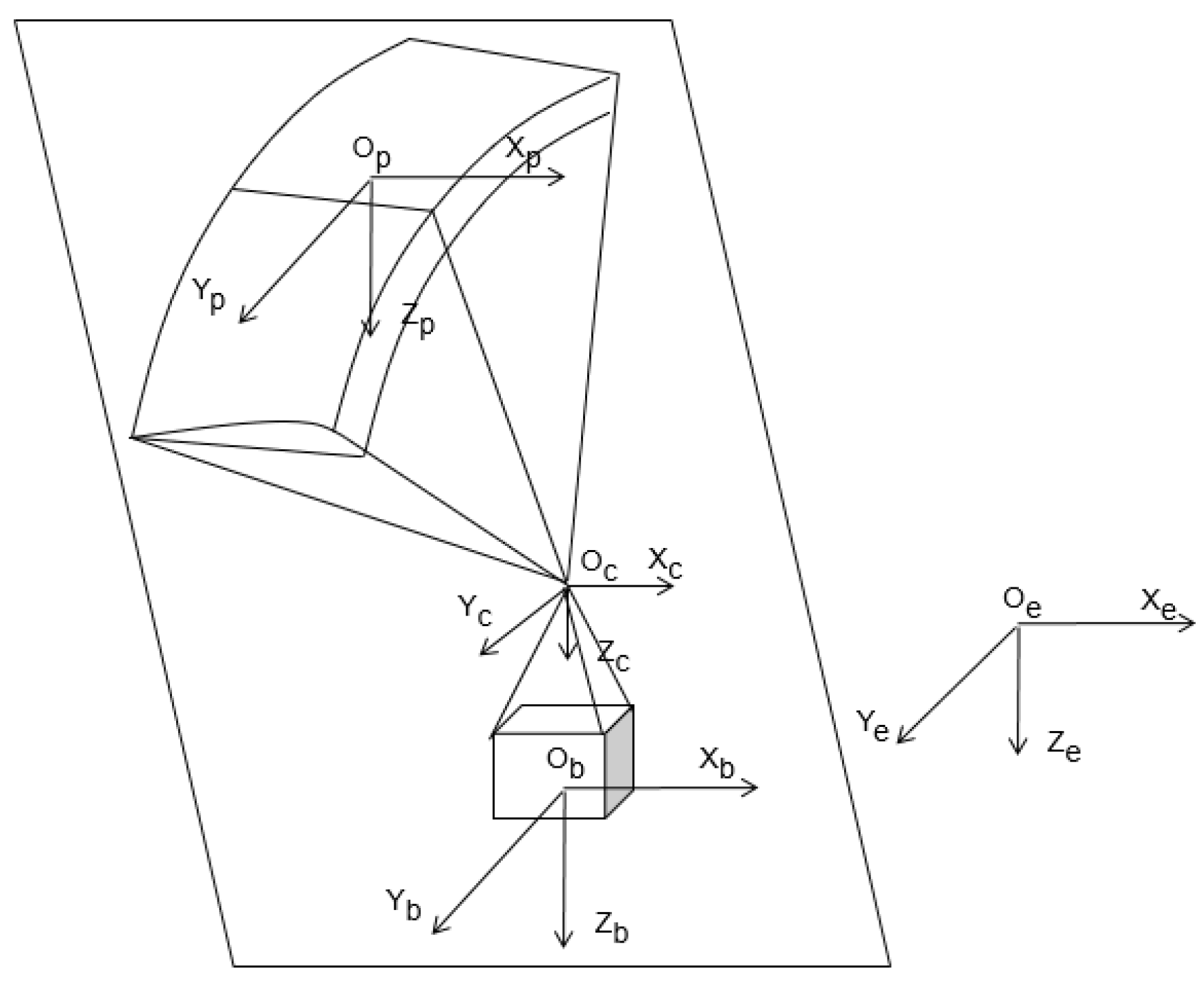
3.3. Aerodynamics Module
3.4. Wind Field Simulation
- (1)
- First, in the application of the parafoil motion control, the mean wind is the main component of the wind field [30]. The mean wind means an average wind speed along the height over a period of time.
- (2)
- Next, the random wind can be seen as a kind of continuous stochastic pulses superposed on the mean wind. Both of its speed and direction vary randomly with time and location [19]. The magnitude of the random wind applied in this study is generated using a standard Gaussian distribution (with variance adjustable as needed), and the direction is generated using a uniform distribution in three-dimensional space.
- (3)
- Finally, the gust wind, caused by air disturbance, is a kind of special instantaneous wind with a speed of at least 5 m/s faster than the mean wind [31]. The proposed wind field in this study only discusses five basic gust winds: triangle gust wind, rectangular gust wind, half-wavelength gust wind, full-wavelength gust wind, and NASA gust wind [19,30]. In subsequent simulation experiments, only the widely used NASA gusts were employed. The mathematical model of the NASA gusts can be expressed as
3.5. Navigation Solution
3.6. Objective Trajectory
3.7. Performance Evaluation
3.8. Display Module
4. Actor–Critic RL Simulation Training Subsystem
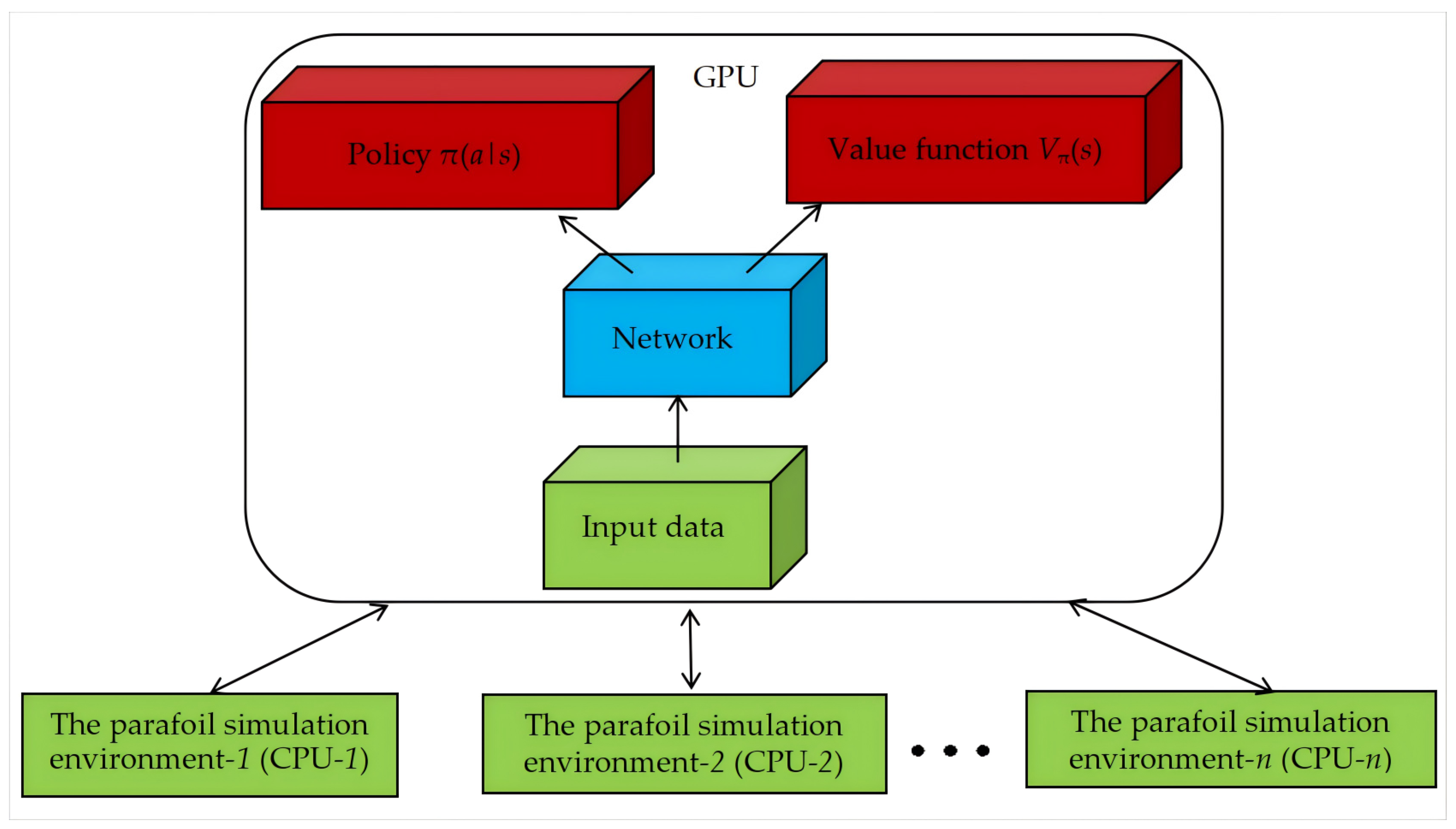
4.1. Parallel Data Sampling
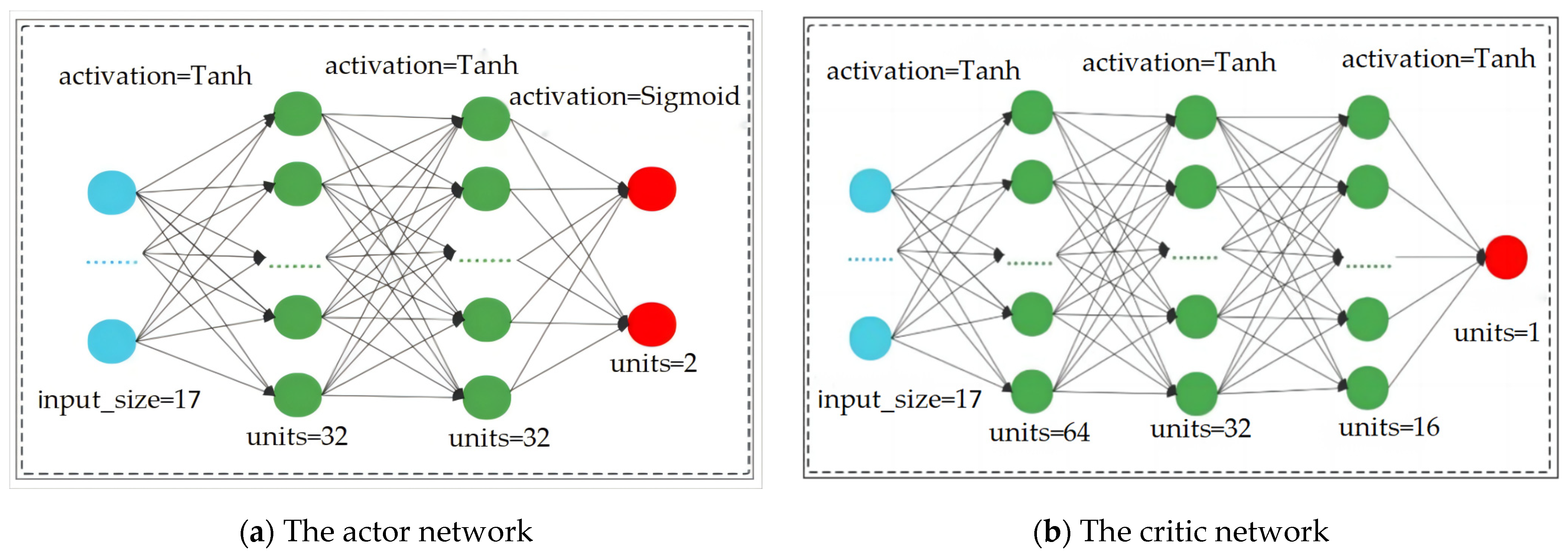
4.2. Actor–Critic Reinforcement Learning Algorithm
5. Simulation Verification
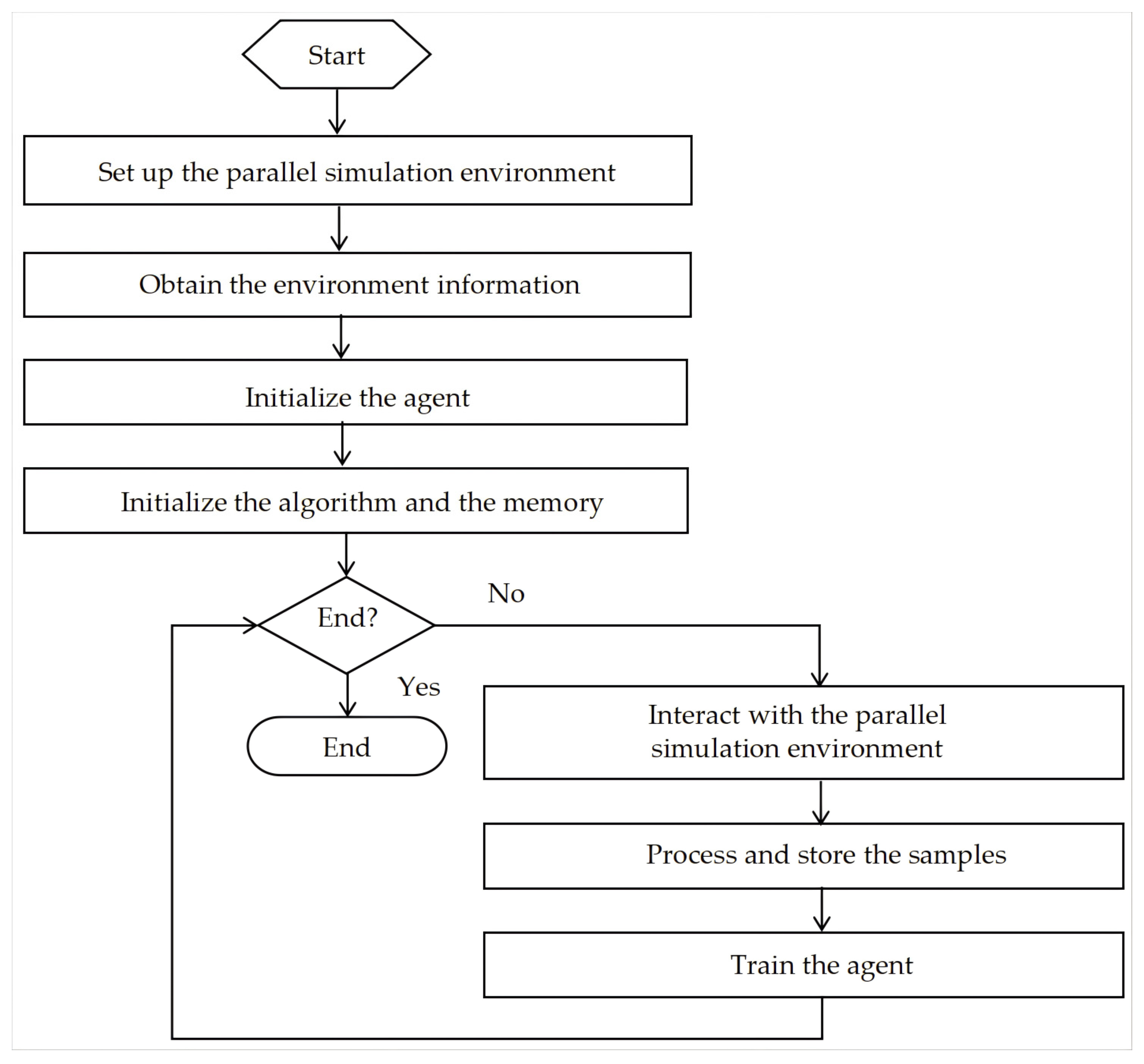
5.1. Parafoil Motion-Control-Simulation Training Procedure
5.2. Performance Index
5.3. Analysis of the Parafoil Motion-Control-Simulation Training Results
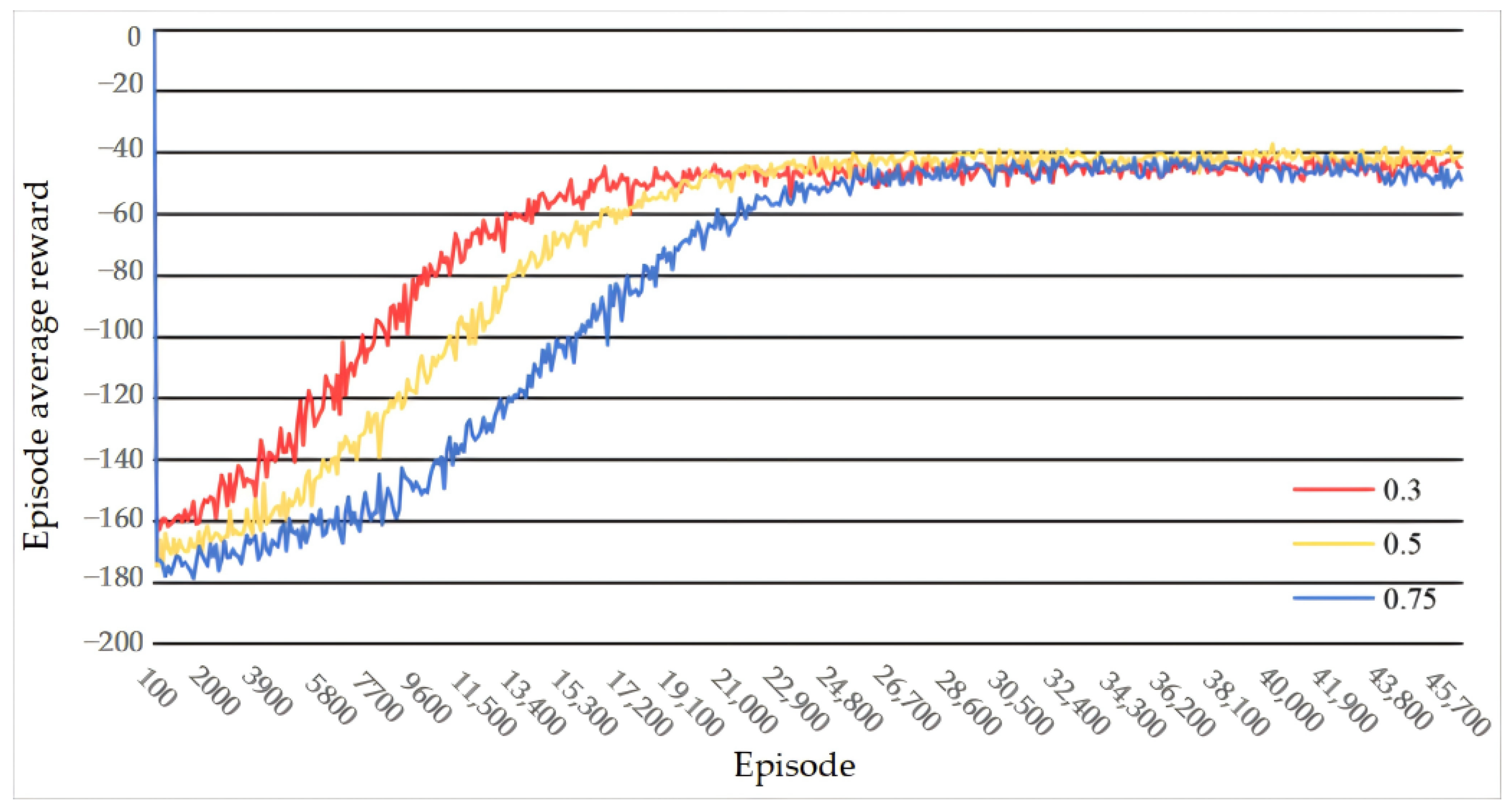
5.3.1. Influence of Hyper-Parameter Settings on Reinforcement Learning Training
5.3.2. Control Effect Comparison between PID and PPO Parafoil Motion Controllers
- (1)
- Single Flight
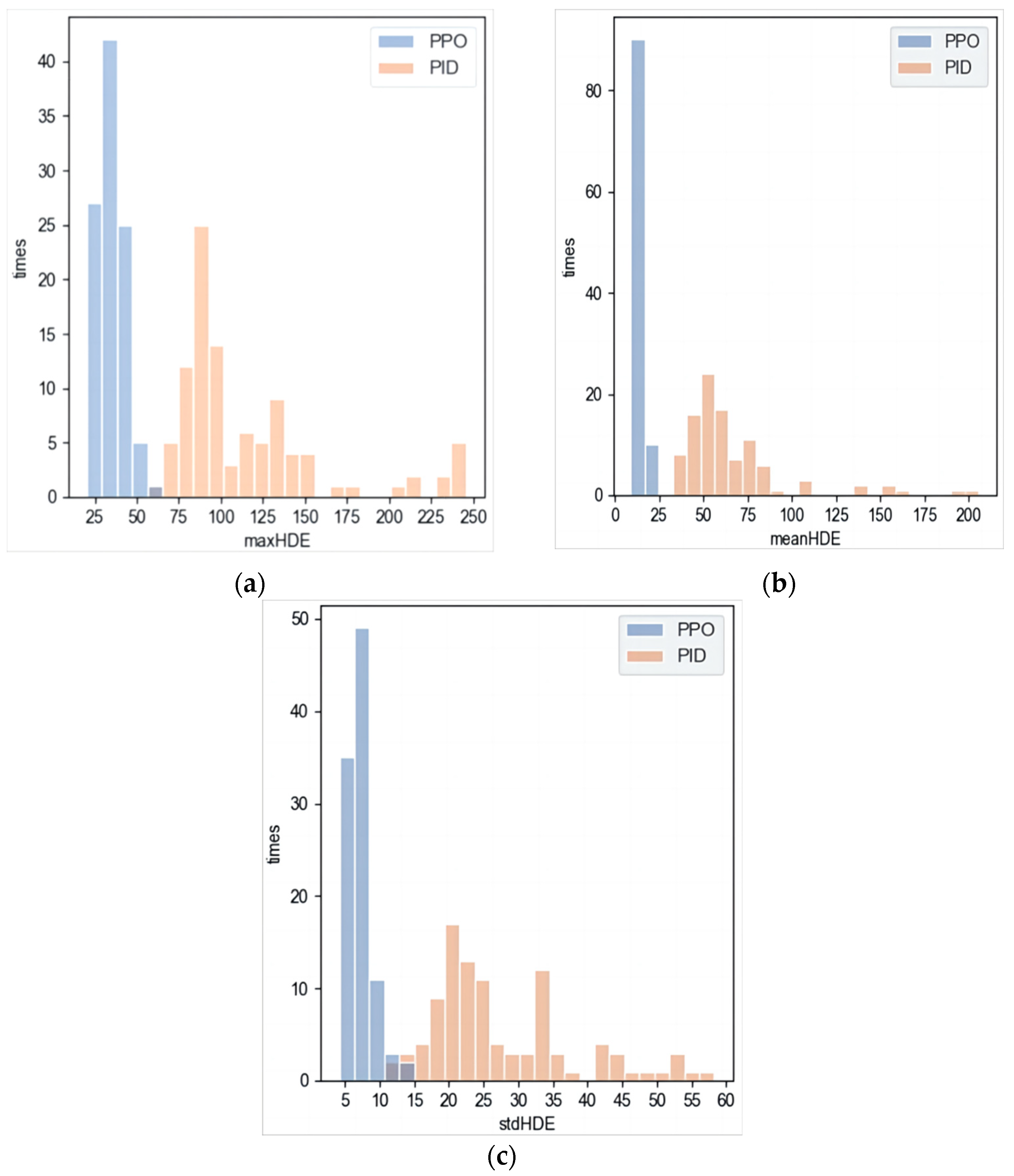
- (2)
- Multiple Flights
5.3.3. Influence of Environmental Conditions on the Parafoil Motion Controller
- (1)
- Influence of Payload Weight on the Parafoil Motion Controller
- (2)
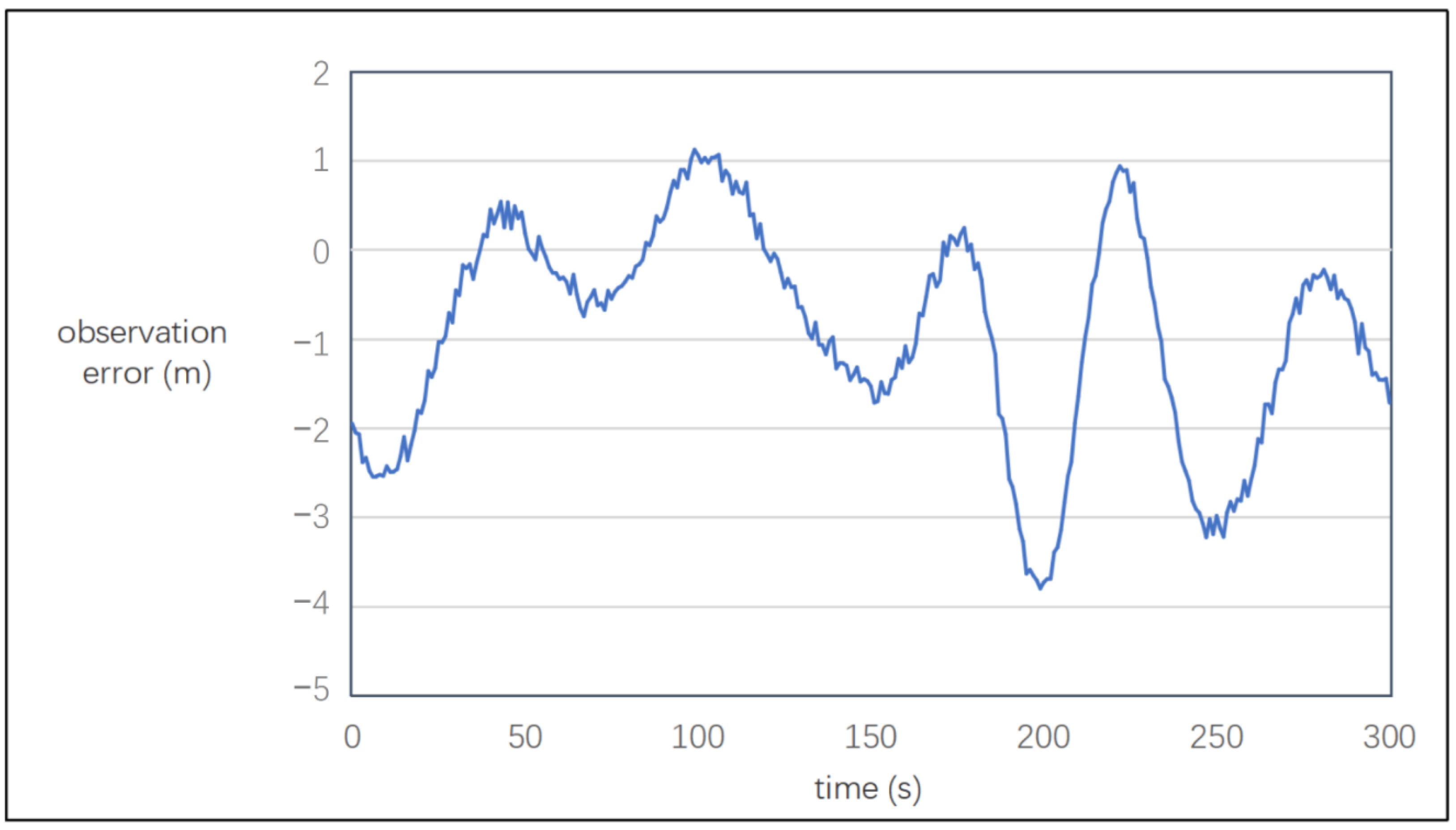
- Influence of Observation Noise on the Parafoil Motion Controller
- (3)
- Influence of Wind Speed on the Parafoil Motion Controller
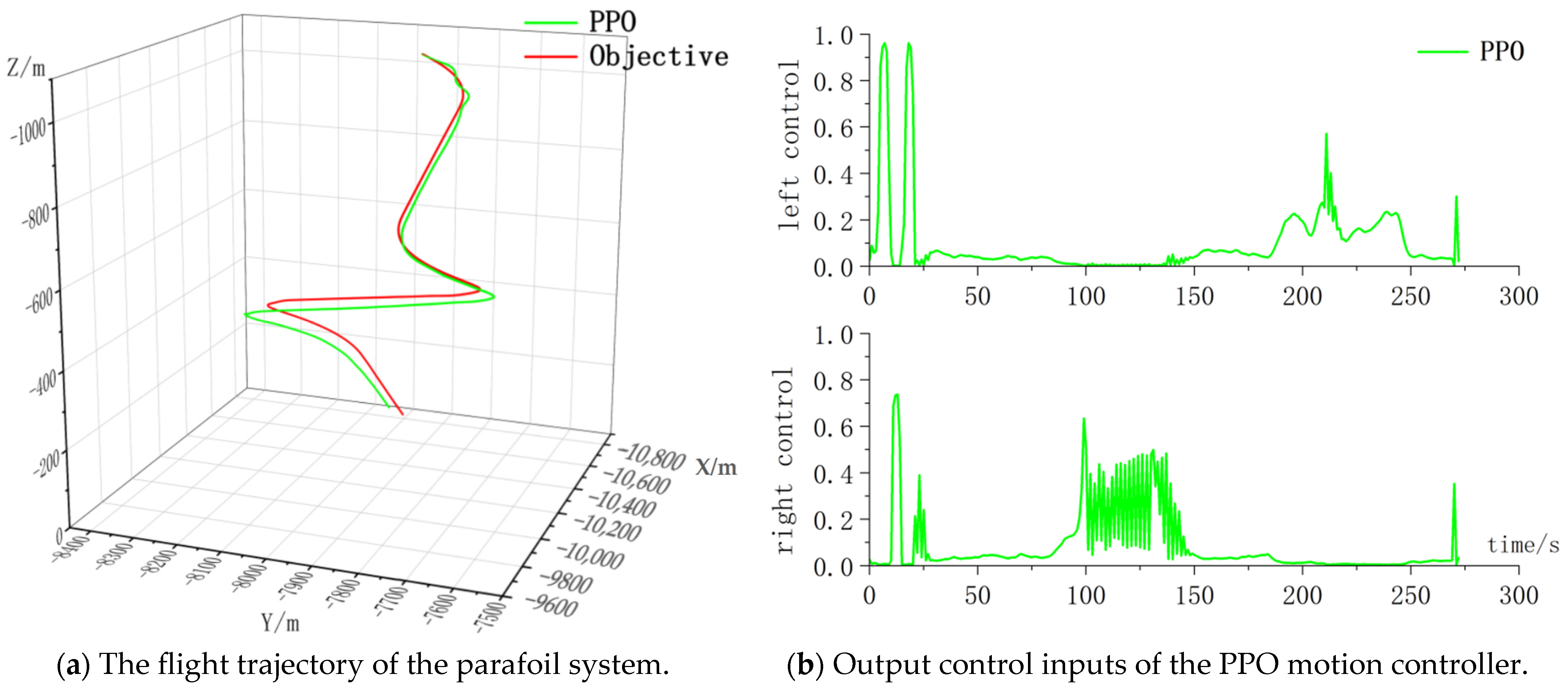
6. Real Flight Evaluation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| State Symbol | State Name | Minimum Value | Maximum Value |
|---|---|---|---|
| EAS | Velocity angle deviation | −180° | 180° |
| EFR | Descent rate deviation | −2 | 2 |
| At | Prospective angle (8-dimensional) | −90° | 90° |
| Dp2t | Target point distance | 0.0 (m) | 200.0 (m) |
| Ap2t | Target point angle | −180° | 180° |
| Cl | Actual left control quantity | 0 | 1 |
| Cr | Actual right control quantity | 0 | 1 |
| Awp | Angle between wind and target trajectory direction | −180° | 180° |
| ωh | Horizontal modulus of the wind | 0 m/s | 10 m/s |
| ωv | Vertical component of a wind | −1 m/s | 1 m/s |
Appendix B
Appendix C
Appendix D
Appendix E
References
- Tan, P.L.; Luo, S.Z.; Sun, Q.L. Control strategy of power parafoil system based on coupling compensation. Trans. Beijing Inst. Technol. 2019, 39, 378–383. [Google Scholar]
- Zhu, H.; Sun, Q.; Wu, W.N.; Sun, M.; Chen, Z. Accurate modeling and control for parawing unmanned aerial vehicle. Acta Aeronaut. Astronaut. Sin. 2019, 40, 79–91. [Google Scholar]
- Li, Y.; Zhao, M.; Yao, M.; Chen, Q.; Guo, R.P.; Sun, T.; Jiang, T.; Zhao, Z.H. 6-DOF modeling and 3D trajectory tracking control of a powered parafoil system. IEEE Access. 2020, 8, 151087–151105. [Google Scholar] [CrossRef]
- Zhao, L.G.; He, W.L.; Lv, F.K. Model-free adaptive control for parafoil systems based on the iterative feedback tuning method. IEEE Access. 2021, 9, 35900–35914. [Google Scholar] [CrossRef]
- Zhao, L.G.; He, W.L.; Lv, F.K.; Wang, X.G. Trajectory tracking control for parafoil systems based on the model-free adaptive control. IEEE Access. 2020, 8, 152620–152636. [Google Scholar] [CrossRef]
- Tao, J. Research on Modeling and Homing Control of Parafoil Systems in Complex Environments. Ph.D. Thesis, Nankai University, Tianjin, China, 2017. [Google Scholar]
- Tao, J.; Sun, Q.L.; Chen, Z.Q.; He, Y.P. LADAR-based trajectory tracking control for a parafoil system. J. Harbin Eng. Univ. 2018, 39, 510–516. [Google Scholar]
- Sun, Q.L.; Chen, S.; Sun, H.; Chen, Z.Q.; Sun, M.W.; Tan, P.L. Trajectory tracking control of powered parafoil under complex disturbances. J. Harbin Eng. Univiron. 2019, 40, 1319–1326. [Google Scholar]
- Jia, H.C.; Sun, Q.L.; Chen, Z.Q. Application of Single Neuron LADRC in Trajectory Tracking Control of Parafoil System. In Proceedings of the 2018 Chinese Intelligent Systems Conference, Wenzhou, China, 6 October 2018; pp. 33–42. [Google Scholar]
- Jagannath, J.; Jagannath, A.; Furman, S.; Gwin, T. Deep Learning and Reinforcement Learning for Autonomous Unmanned Aerial Systems: Roadmap for Theory to Deployment, 1st ed.; Springer: Berlin, Germany, 2020. [Google Scholar]
- Polosky, N.; Jagannath, J.; Connor, D.O.; Saarinen, H.; Foulke, S. Artificial neural network with electroencephalogram sensors for brainwave interpretation: Brain-observer-indicator development challenges. In Proceedings of the 13th International Conference and Expo on Emerging Technologies for a Smart World, Location of Conference, Stony Brook, NY, USA, 7–8 November 2017; Saarinen, H., Ed.; 8 November 2017. [Google Scholar]
- Jagannath, A.; Jagannath, J.; Drozd, A. Artificial intelligence-based cognitive cross-layer decision engine for next-generation space mission. In Proceedings of the 2019 IEEE Cognitive Communications for Aerospace Applications Workshop, Cleveland, OH, USA, 25–26 June 2019. [Google Scholar]
- Jagannath, A.; Jagannath, J.; Drozd, A. Neural network for signal intelligence: Theory and practice. In Machine Learning for Future Wireless Communications, 1st ed.; Luo, F., Ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2020; pp. 243–264. [Google Scholar]
- Chen, Y.; Dong, Q.; Shang, X.Z.; Wu, Z.Y.; Wang, J.Y. Multi-UAV autonomous path planning in reconnaissance missions considering incomplete information: A reinforcement learning method. Drones 2023, 7, 10. [Google Scholar] [CrossRef]
- Jiang, N.; Jin, S.; Zhang, C.S. Hierarchical automatic curriculum learning: Converting a sparse reward navigation task into dense reward. Neurocomputing 2019, 360, 265–278. [Google Scholar] [CrossRef]
- Yang, W.Y.; Bai, C.J.; Cai, C.; Zhao, Y.N.; Liu, P. Survey on sparse reward in deep reinforcement learning. Comput. Sci. 2019, 47, 182–191. [Google Scholar]
- Zhao, X.R.; Yang, R.N.; Zhong, L.S.; Hou, Z.W. Multi-UAV path planning and following based on multi-agent reinforcement learning. Drones 2024, 8, 18. [Google Scholar] [CrossRef]
- Guo, Y.M.; Yan, J.G.; Xing, X.J.; Wu, C.H.; Chen, X.R. Modeling and analysis of deformed parafoil recovery system. J. Northwest. Polytech. Univ. 2020, 38, 952–958. [Google Scholar] [CrossRef]
- Gao, F. Study on Homing Strategy for Parafoil System under Wind Field. Master Thesis, University of Defense Technology, Changsha, China, 2019. [Google Scholar]
- Liu, S.Q.; Bai, J.Q. Analysis of flight energy variation of small solar UAVs using dynamic soaring technology. J. Northwest. Polytech. Univ. 2020, 38, 48–57. [Google Scholar] [CrossRef]
- Yu, J.; Sun, H.; Sun, J.Q. Improved twin delayed deep deterministic policy gradient algorithm based real-time trajectory planning for parafoil under complicated constrains. Appl. Sci. Basel. 2022, 12, 8189. [Google Scholar] [CrossRef]
- Xing, X.J.; Gong, Q.C.; Guan, X.Q.; Han, Y.C.; Feng, L.; Guo, Y.M. Online trajectory planning for parafoil first-stage booster system in complex wind field. J. Aerosp. Eng. 2023, 36, 04023027. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018; pp. 1–398. [Google Scholar]
- Schulman, J. Research on Modeling and Homing Control of Parafoil Systems in Complex Environments Proximal Policy Optimization Algorithms. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2017. [Google Scholar]
- Lynch, K.M.; Park, F.G. Modern Robotics-Mechanics, Planning, and Control, 1st ed.; Cambridge University Press: New York, NY, USA, 2017; pp. 1–642. [Google Scholar]
- Prakash, O.; Ananthkrishnan, N. Modeling and simulation of 9-DOF parafoil-payload system flight dynamics. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Ochi, Y. Modeling and simulation of flight dynamics of a relative-roll-type parafoil. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Prakash, O.; Kumar, A. NDI based heading tracking of hybrid-airship for payload delivery. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Prakash, O. Modeling and simulation of turning flight maneuver of winged airship-payload system using 9-DOF multibody model. In Proceedings of the AIAA Scitech 2023 Forum, National Harbor, MD & Online, USA, 23–27 January 2023. [Google Scholar]
- Bian, K. Trajectory. Master Thesis, University of Defense Technology, Changsha, China, 2020. [Google Scholar]
- Hao, R.; Meng, B. Research on gust direction and suggestion for flight operation. J. Civ. Aviat. Inst. China 2021, 5, 89–92. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]




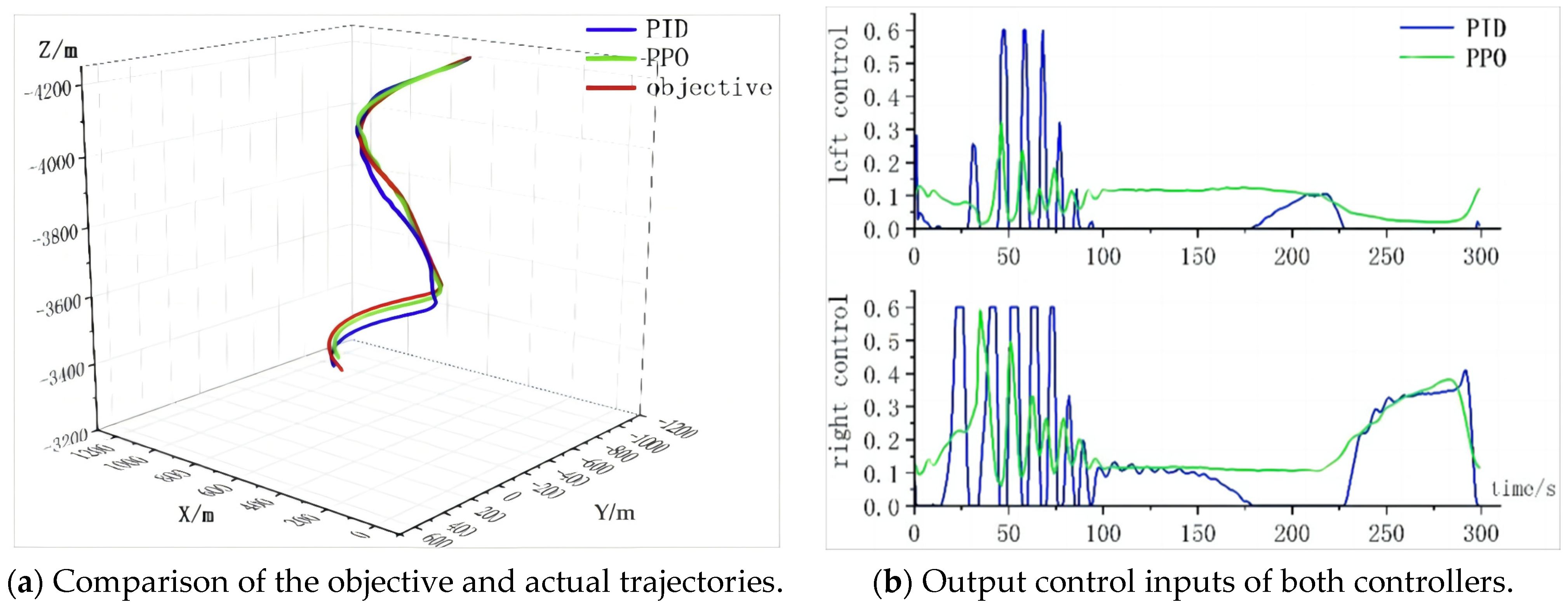

| Parafoil Motion Controller | maxHDE (m) | meanHDE (m) | stdHDE (m) |
|---|---|---|---|
| PID | 236.57 | 67.58 | 25.41 |
| PPO | 49.15 | 16.23 | 6.59 |
| Parafoil Motion Controller | max_maxHDE (m) | mean_meanHDE (m) | mean_stdHDE (m) |
|---|---|---|---|
| PID | 245.78 | 66.91 | 29.04 |
| PPO | 57.08 | 13.88 | 7.48 |
| max_maxHDE (m) | mean_meanHDE (m) | mean_stdHDE (m) | |
|---|---|---|---|
| 0.5 × Standard payload weight | |||
| PID | 234.67 | 64.72 | 25.46 |
| PPO | 77.64 | 12.54 | 7.79 |
| Standard payload weight | |||
| PID | 245.78 | 66.91 | 29.04 |
| PPO | 57.08 | 13.88 | 7.48 |
| 2 × Standard payload weight | |||
| PID | 224.85 | 84.02 | 32.55 |
| PPO | 73.35 | 21.46 | 10.85 |
| max_maxHDE (m) | mean_meanHDE (m) | mean_stdHDE (m) | |
|---|---|---|---|
| Without observation noise | |||
| PID | 245.78 | 66.91 | 29.04 |
| PPO | 57.08 | 13.88 | 7.48 |
| The first type of noise (SD = 1) | |||
| PID | 422.54 | 147.64 | 73.32 |
| PPO | 108.08 | 27.21 | 13.53 |
| The first type of noise (SD = 2) | |||
| PID | 1027.10 | 240.71 | 125.75 |
| PPO | 188.61 | 57.50 | 29.45 |
| The second type of noise (SD = 1) | |||
| PID | 326.74 | 93.67 | 45.60 |
| PPO | 154.71 | 32.13 | 17.79 |
| The second type of noise (SD = 2) | |||
| PID | 330.99 | 95.38 | 45.05 |
| PPO | 388.21 | 78.94 | 45.73 |
| max_maxHDE (m) | mean_meanHDE (m) | mean_stdHDE (m) | |
|---|---|---|---|
| Without wind | |||
| PID | 245.78 | 66.91 | 29.04 |
| PPO | 57.08 | 13.88 | 7.48 |
| 0–2 m/s | |||
| PID | 333.55 | 94.64 | 46.07 |
| PPO | 257.08 | 31.21 | 22.38 |
| 2–4 m/s | |||
| PID | 461.10 | 107.71 | 55.04 |
| PPO | 310.62 | 31.52 | 21.59 |
| 4–7 m/s | |||
| PID | 909.99 | 176.39 | 109.23 |
| PPO | 412.22 | 50.94 | 39.61 |
| Parameters | Values |
|---|---|
| Wing span and wing chord/m | 7.5, 3.75 |
| Maximum takeoff weight/kg | 200 |
| Empty weight/kg | 25 |
| Payload/kg | 135 |
| Flight time/sec | 272 |
| Wind direction | Southeast |
| Wind speed/(m/s) | 1.98–3.89 |
| Weather | Cloudless |
| Temperature/°C | 20 |
| maxHDE (m) | meanHDE (m) | stdHDE (m) | |
|---|---|---|---|
| PPO | 111.61 | 52.05 | 36.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Liu, J.; Zhao, J.; Xu, R.; Liu, Q.; Wan, J.; Yu, G. Simulation Training System for Parafoil Motion Controller Based on Actor–Critic RL Approach. Actuators 2024, 13, 280. https://doi.org/10.3390/act13080280
He X, Liu J, Zhao J, Xu R, Liu Q, Wan J, Yu G. Simulation Training System for Parafoil Motion Controller Based on Actor–Critic RL Approach. Actuators. 2024; 13(8):280. https://doi.org/10.3390/act13080280
Chicago/Turabian StyleHe, Xi, Jingnan Liu, Jing Zhao, Ronghua Xu, Qi Liu, Jincheng Wan, and Gang Yu. 2024. "Simulation Training System for Parafoil Motion Controller Based on Actor–Critic RL Approach" Actuators 13, no. 8: 280. https://doi.org/10.3390/act13080280
APA StyleHe, X., Liu, J., Zhao, J., Xu, R., Liu, Q., Wan, J., & Yu, G. (2024). Simulation Training System for Parafoil Motion Controller Based on Actor–Critic RL Approach. Actuators, 13(8), 280. https://doi.org/10.3390/act13080280





