Two-Stage Control Strategy Based on Motion Planning for Planar Prismatic–Rotational Underactuated Robot
Abstract
1. Introduction
2. Preparations
2.1. Dynamic Model
2.2. Underactuated Constraints
2.3. Control Strategy
3. Motion Planning
- ①
- Randomly generating an initialized population, while the initial parameters are expressed as , , and .
- ②
- ③
- If , , , and , where is small enough. Otherwise, the program is to ④.
- ④
- The parameters are mutated, crossed and selected, then update , , and . Back to②.
4. Controller Design
4.1. The First Controller Design
4.2. The Second Controller Design
5. Simulation
- ①
- Use the first stage controller to drive the first joint to the target position, and record the angle and angular velocity of the second joint at this time as and .
- ②
- Taking and as the initial states of the second passive joint and combining with the target state, trajectory planning is carried out. The second stage controller is used to drive the first joint to move along the planned trajectory.
5.1. Case 1
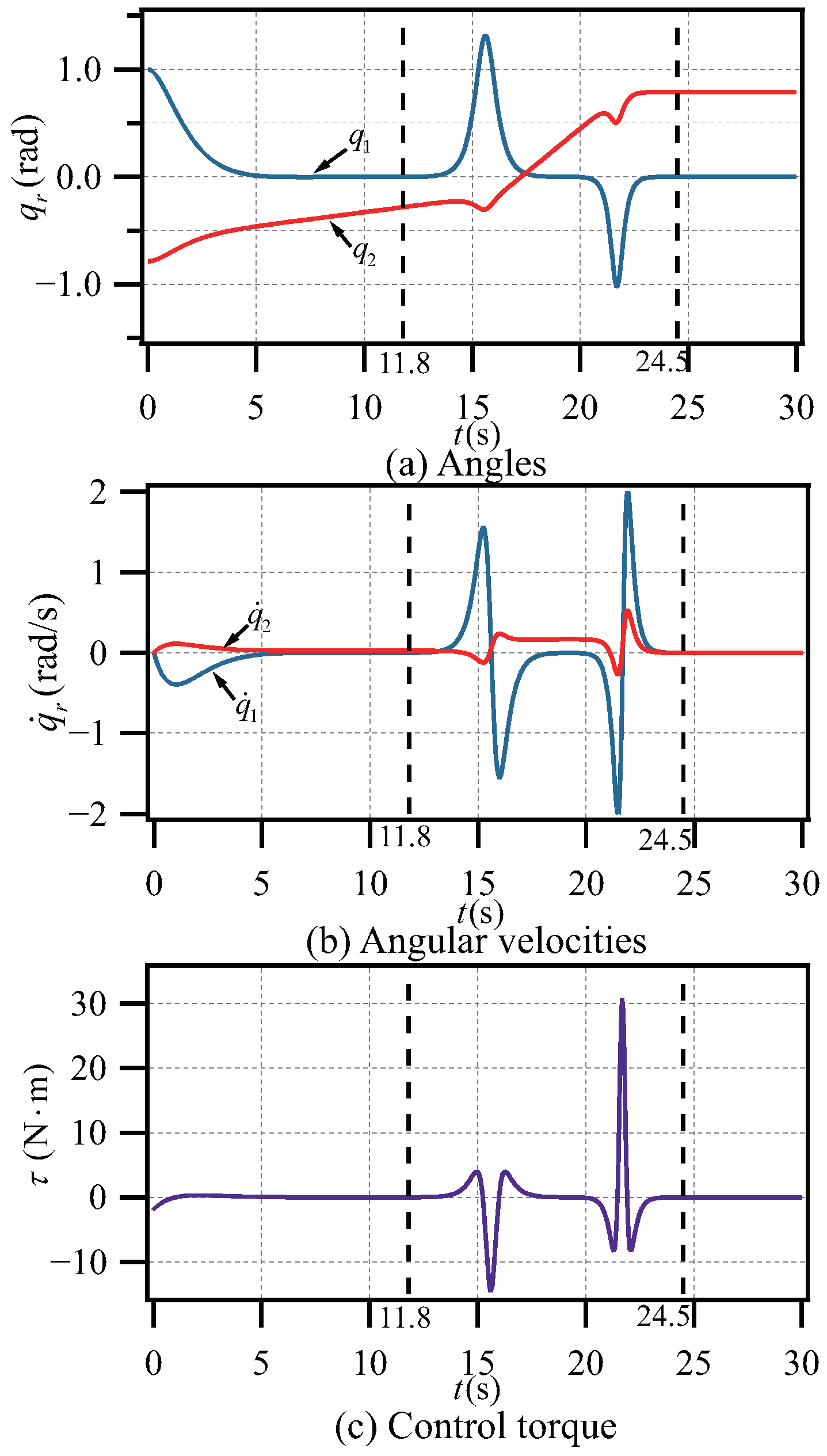
5.2. Case 2
- (1)
- Our method does not require the underactuated rotational link to meet any conditions before the start of stage 2, which greatly simplifies the control difficulty.
- (2)
- Our method can control the system to the target position in 15 s, but the method in [39] needs 38 s. This means that our method can achieve the control goal more quickly.
- (3)
- Our control process is smoother and more feasible. It can be seen from Figure 3c that the control force of the first joint will not change frequently when using our control method. But in the simulation result of [39], this torque changes sharply frequently, which is very unfavorable to the controller.
- (4)
- It is worth mentioning that we fully utilize the underactuated coupling constraint relationship, instead of complex coordinate transformation calculations.
5.3. Case 3
6. Conclusions
- (1)
- The dynamic model of the planar PR underactuated robot is established and the underactuated coupling relationships are derived.
- (2)
- In stage 1, the active prismatic link is intended to be driven by the PD controller in order to attain the desired position. In stage 2, the active prismatic link tracks the designed oscillation trajectory to the target position under the action of the designed tracking controller, and the underactuated rotational link indirectly converges to the target state during this process.
- (3)
- The simulation results demonstrate this control strategy’s viability and superiority for planar PR underactuated robots.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korteling, J.E.; van de Boer-Visschedijk, G.C.; Blankendaal, R.A.M.; Boonekamp, R.C.; Eikelboom, A.R. Human-versus artificial intelligence. Front. Artif. Intell. 2021, 4, 622364. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.M.; Yoo, J.; Kim, S.W.; Lee, J.H.; Hong, J. Autonomic machine learning platform. Int. J. Inf. Manag. 2019, 49, 491–501. [Google Scholar] [CrossRef]
- Rashid, R.; Zhang, E.; Abdi, A. On the Performance of a New Wireless Communication Compact Multichannel Underwater Receiver Using a Sphere Vector Sensor. IEEE Trans. Veh. Technol. 2023, 73, 1458–1461. [Google Scholar] [CrossRef]
- Hu, B.; Wang, Y.; Orlik, P.V.; Koike-Akino, T.; Guo, J. Co-design of safe and efficient networked control systems in factory automation with state-dependent wireless fading channels. Automatica 2019, 105, 334–346. [Google Scholar] [CrossRef]
- Mukherjee, D.; Gupta, K.; Chang, L.H.; Najjaran, H. A survey of robot learning strategies for human-robot collaboration in industrial settings. Robot. Comput. Manuf. 2022, 73, 102231. [Google Scholar] [CrossRef]
- Frennert, S.; Aminoff, H.; Östlund, B. Technological frames and care robots in eldercare. Int. J. Soc. Robot. 2021, 13, 311–325. [Google Scholar] [CrossRef]
- Gonzalez-Aguirre, J.A.; Osorio-Oliveros, R.; Rodríguez-Hernández, K.L.; Lizárraga-Iturralde, J.; Menendez, R.M.; Ramírez-Mendoza, R.A.; Ramírez-Moreno, M.A.; Lozoya-Santos, J.d.J. Service robots: Trends and technology. Appl. Sci. 2021, 11, 10702. [Google Scholar] [CrossRef]
- Chakraborty, S.; Elangovan, D.; Govindarajan, P.L.; Elnaggar, M.F.; Alrashed, M.M.; Kamel, S. A comprehensive review of path planning for agricultural ground robots. Sustainability 2022, 14, 9156. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, L.; Zhao, J.; Wang, F.; Yang, J.; Liang, K.; Li, Z. Deep-learning-based accurate identification of warehouse goods for robot picking operations. Sustainability 2022, 14, 7781. [Google Scholar] [CrossRef]
- Khanmirza, E.; Daneshjou, K.; Ravandi, A.K. Underactuated flexible aerial manipulators: A new framework for optimal trajectory planning under constraints induced by complex dynamics. J. Intell. Robot. Syst. 2018, 92, 599–613. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhao, H.; Sun, H.; Zhen, S.C.; Mamun, A.A. Optimal adaptive robust control based on cooperative game theory for a class of fuzzy underactuated mechanical systems. IEEE Trans. Cybern. 2022, 52, 3632–3644. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Giles, A.; Ruggiero, F.; Lippiello, V.; Siciliano, B. Nonprehensile manipulation of an underactuated mechanical system with second-order nonholonomic constraints: The robotic hula-hoop. IEEE Robot. Autom. Lett. 2018, 3, 1136–1143. [Google Scholar] [CrossRef]
- Lai, X.Z.; Wang, Y.W.; Wu, M.; Cao, W.H. Stable control strategy for planar three-link underactuated mechanical system. IEEE ASME Trans. Mechatron. 2016, 21, 1345–1356. [Google Scholar] [CrossRef]
- Wang, L.J.; Lai, X.Z.; Meng, Q.X.; Wu, M. Effective control method based on trajectory optimization for three-link vertical underactuated manipulators with only one active joint. IEEE Trans. Cybern. 2023, 53, 3782–3793. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Gao, H.M.; Wang, K.; Zhou, C.; Zong, Q.; Hua, C.C. Disturbance observer-based finite-time control design for a quadrotor UAV with external disturbance. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 834–847. [Google Scholar] [CrossRef]
- Huang, Z.X.; Li, X.P.; Wang, J.R.; Zhang, Y.; Mei, J.F. Human pulse detection by a soft tactile actuator. Sensors 2022, 22, 5047. [Google Scholar] [CrossRef] [PubMed]
- Massaro, M.; Lovato, S.; Limebeer, D.J.N. The optimal erection of the inverted pendulum. Appl. Sci. 2022, 12, 8112. [Google Scholar] [CrossRef]
- Du, D.J.; Zhang, C.D.; Song, Y.H.; Zhou, H.Y.; Fei, M.R.; Li, W.P. Real-time H control of networked inverted pendulum visual servo systems. IEEE Trans. Cybern. 2020, 50, 5113–5126. [Google Scholar] [CrossRef]
- Gritli, H.; Belghith, S. LMI-based synthesis of a robust saturated controller for an underactuated mechanical system subject to motion constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7663–7674. [Google Scholar] [CrossRef]
- Sun, H.; Yang, L.W.; Chen, Y.H.; Zhao, H. Constraint-based control design for uncertain underactuated mechanical system: Leakage-type adaptation mechanism. Eur. J. Control 2021, 57, 179–193. [Google Scholar] [CrossRef]
- Emran, B.J.; Najjaran, H. A review of quadrotor: An underactuated mechanical system. Annu. Rev. Control 2018, 46, 165–180. [Google Scholar] [CrossRef]
- Hu, J.Y.; Niu, H.L.; Carrasco, J.; Lennox, B.; Arvin, F. Voronoi-based multi-robot autonomous exploration in unknown environments via deep reinforcement learning. IEEE Veh. Technol. Mag. 2020, 69, 14413–14423. [Google Scholar] [CrossRef]
- Wang, L.; Lai, X.; Zhang, P.; Wu, M. A control strategy based on trajectory planning and optimization for two-link underactuated manipulators in vertical plane. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 52, 3466–3475. [Google Scholar] [CrossRef]
- Liu, D.; Lai, X.Z.; Wang, Y.W.; Wan, X.B.; Wu, M. Position control for planar four-link underactuated manipulator with a passive third joint. ISA Trans. 2019, 87, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.Y.; Wang, Y.W.; Zhang, P.; Su, C.Y. Continuous control strategy of planar 3-Linkage underactuated manipulator based on broad neural network. Actuators 2021, 10, 249. [Google Scholar] [CrossRef]
- Wang, Y.W.; Yang, H.Q.; Zhang, P. Iterative convergence control method for planar underactuated manipulator based on support vector regression model. Nonlinear Dyn. 2020, 102, 2711–2724. [Google Scholar] [CrossRef]
- Huang, Z.X.; Wang, L.J. Review of control method of planar underactuated mechanical system. J. Wuhan Inst. Technol. 2021, 43, 448–454. [Google Scholar]
- Huang, Z.X.; Wei, S.Q.; Hou, M.Y.; Wang, L.J. Finite-time control strategy for swarm planar underactuated robots via motion planning and intelligent algorithm. Mears. Control 2022, 56, 813–819. [Google Scholar] [CrossRef]
- Xiong, P.Y.; Lai, X.Z.; Wu, M. A stable control for second-order nonholonomic planar underactuated mechanical system: Energy attenuation approach. Int. J. Control 2018, 91, 1630–1639. [Google Scholar] [CrossRef]
- Tonan, M.; Doria, A.; Bottin, M.; Rosati, G. Oscillation-free point-to-point motions of planar differentially flat under-actuated robots: A Laplace transform method. Robotica 2024, 42, 1262–1280. [Google Scholar] [CrossRef]
- Agrawal, S.K.; Sangwan, V. Design of under-actuated open-chain planar robots for repetitive cyclic motions. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Philadelphia, PA, USA, 10–13 September 2006; Volume 42568, pp. 1057–1066. [Google Scholar]
- Tonan, M.; Bottin, M.; Doria, A.; Rosati, G. Motion planning of differentially flat planar underactuated robots. Robotics 2024, 13, 57. [Google Scholar] [CrossRef]
- Luca, A.D.; Oriolo, G. Trajectory planning and control for planar robots with passive last joint. Int. J. Robot. Res. 2002, 21, 575–590. [Google Scholar] [CrossRef]
- Urrea, C.; Kern, J.; Alvarez, E. Design of a generalized dynamic model and a trajectory control and position strategy for n-link underactuated revolute planar robots. Control Eng. Pract. 2022, 128, 105316. [Google Scholar] [CrossRef]
- Wu, J.D.; She, J.H.; Wang, Y.W.; Chun, C.Y. Position and posture control of planar four-Link underactuated manipulator based on neural network model. IEEE Trans. Ind. Electron. 2020, 67, 4721–4728. [Google Scholar] [CrossRef]
- Huang, Z.X.; Hou, M.Y.; Wei, S.Q.; Wang, L.J. The unified control strategy for planar Acrobot and Pendubot. J. Shenzhen Univ. Sci. Eng. 2023, 40, 275–283. [Google Scholar] [CrossRef]
- Alaci, S.; Ciornei, F.C.; Suciu, C.C.; Romanu, I.C. The effect of structural aspect for planar systems with 2DOF upon the stability of motion. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; p. 012003. [Google Scholar]
- Wu, L.C.; Xinkai, K.; Yang, G.S. Nonholonomic control of a planar Prismatic-Revolute under-actuated manipulator. In Proceedings of the 2013 Science and Information Conference, London, UK, 7–9 October 2013; pp. 144–147. [Google Scholar]
- Huang, Z.X.; Wei, S.Q.; Chen, Z.; Wang, L.J. Iterative contraction stability control strategy for planar prismatic-rotational underactuated robot. IEEE Access 2023, 11, 55947–55953. [Google Scholar] [CrossRef]
- Ichida, K.; Watanabe, K.; Izumi, K. Control of three-link underactuated manipulators by a logic-based switching method. In Proceedings of the International Conference on Networking, Sensing and Control, Okayama, Japan, 26–29 March 2009; pp. 108–112. [Google Scholar]
- Luca, A.D.; Iannitti, S. Smooth trajectory planning for XYnR planar underactuated robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; pp. 1651–1656. [Google Scholar]
- Li, J.; Wang, L.J.; Chen, Z.; Huang, Z.X. Drift suppression control based on online intelligent optimization for planar underactuated manipulator with passive middle joint. IEEE Access 2021, 9, 38611–38619. [Google Scholar] [CrossRef]
- Huang, Z.X.; Lai, X.Z.; Zhang, P.; Wang, Y.W.; Wu, M. Virtual model reduction based control strategy of planar three-link underactuated manipulator with middle passive joint. Int. J. Control Autom. Syst. 2020, 19, 29–39. [Google Scholar] [CrossRef]
- LaSalle, J.P. Stability theory for ordinary differential equations. J. Differ. Equ. 1968, 4, 57–65. [Google Scholar] [CrossRef]
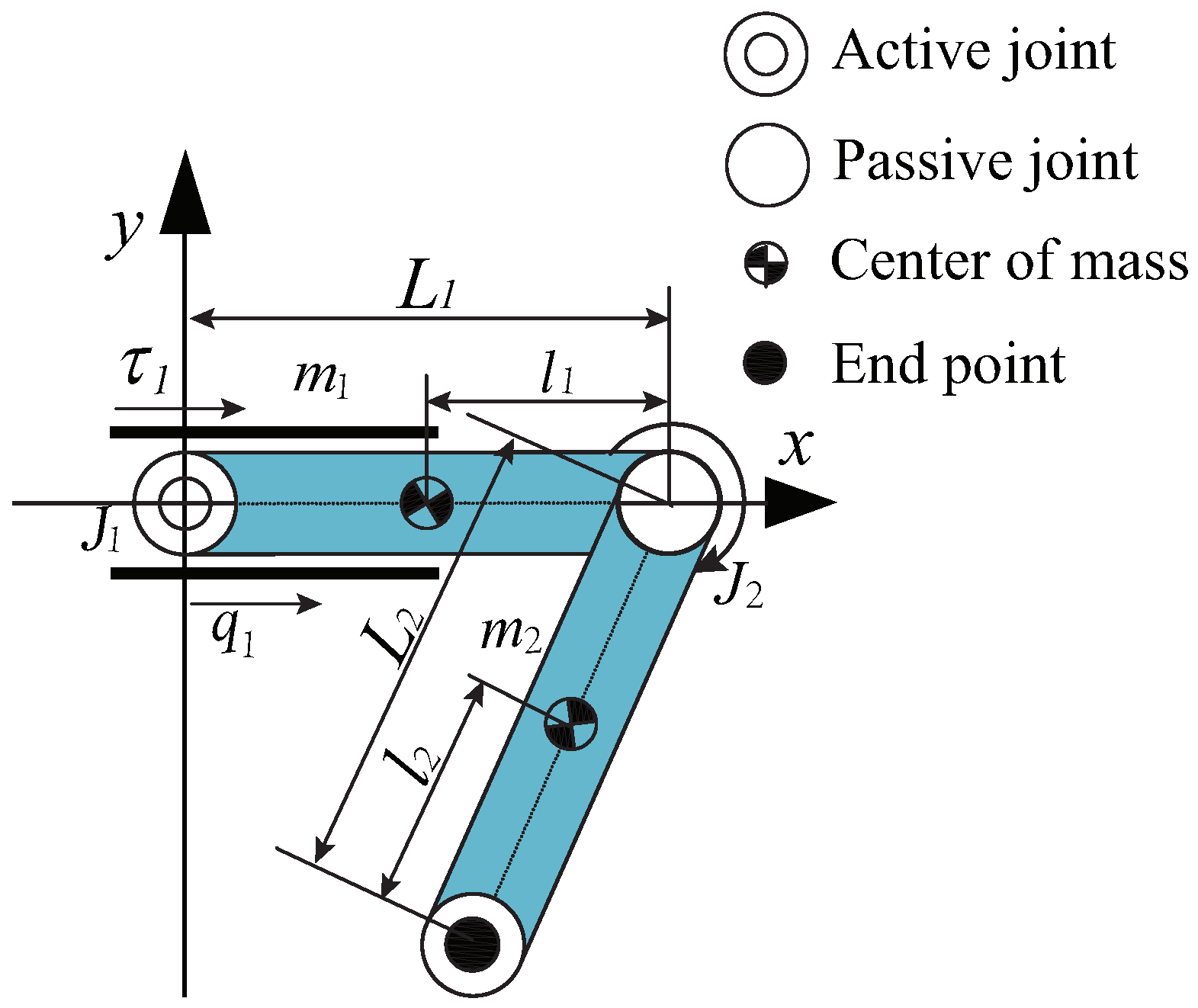


| Parameters | Meaning |
|---|---|
| length of the pth link | |
| distance from pth joint to its center of mass | |
| distance the first joint moves | |
| rotation angle of the second joint | |
| mass of the pth link | |
| inertia of the pth link |
| Link p | (kg) | (m) | (m) | (kg·m2) |
|---|---|---|---|---|
| 1 | 1.0000 | 1.0000 | 0.5000 | 0.0000 |
| 2 | 1.0000 | 1.0000 | 0.5000 | 0.0833 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Wei, Z.; Huang, Z. Two-Stage Control Strategy Based on Motion Planning for Planar Prismatic–Rotational Underactuated Robot. Actuators 2024, 13, 278. https://doi.org/10.3390/act13080278
Li D, Wei Z, Huang Z. Two-Stage Control Strategy Based on Motion Planning for Planar Prismatic–Rotational Underactuated Robot. Actuators. 2024; 13(8):278. https://doi.org/10.3390/act13080278
Chicago/Turabian StyleLi, Dawei, Ziang Wei, and Zixin Huang. 2024. "Two-Stage Control Strategy Based on Motion Planning for Planar Prismatic–Rotational Underactuated Robot" Actuators 13, no. 8: 278. https://doi.org/10.3390/act13080278
APA StyleLi, D., Wei, Z., & Huang, Z. (2024). Two-Stage Control Strategy Based on Motion Planning for Planar Prismatic–Rotational Underactuated Robot. Actuators, 13(8), 278. https://doi.org/10.3390/act13080278






