Active Disturbance Rejection Control for the Trajectory Tracking of a Quadrotor

Abstract

In the last decade, quadrotors have gained popularity among industry and academia due to their capabilities and the various applications in which they can be found. In addition to the above, because this is an underactuated system, researchers have found it a great challenge to control. Despite this, there is a wide variety of methodologies in the literature to control this type of system. Based on the above, this work proposed an alternative to trajectory tracking control for quadrotor unmanned aerial vehicles (UAV). The problem was divided into two main control loops: an outer control loop for the position coordinates, tackled through linear active disturbance rejection controllers (ADRC), and an inner control loop related to the orientation variables, addressed via robust proportional-integral-differential (PID) controllers. Furthermore, a generalized proportional integral observer (GPIO) was implemented to estimate the velocity and internal and external disturbances; therefore, the control strategy only depended on the attitude (position and orientation) quadrotor measurements. Then, the control performance was tested through numerical simulations and experimental tests, including wind disturbance inputs.

1. Introduction

An unmanned aerial vehicle (UAV) is a mobile robot that moves through the air autonomously; it can fly with little or no human intervention. They have emerged as a technological tool that has allowed the development of diverse applications that are dangerous or difficult for humans to realize [1,2,3].

Among the diverse range of UAVs, quadrotor drones, also known as quadcopters, have gained immense popularity in the past decade. Their unique ability to take off and land vertically, with their maneuverability and hovering capability, has made them a favorite for various applications and services in industrial sectors such as logistics, agriculture, environmental monitoring, and sanitization, among others [4,5,6,7,8,9,10]. However, the underactuated nature of these systems and the intricate relationship between translational and rotational dynamics present a formidable challenge for researchers in controlling their position along a desired trajectory. For example, in [11], the authors reviewed different methodologies for controlling multi-rotor aerial robot systems and pointed out that most research has focused on proving the theory rather than the feasibility of the controller itself, since experiments with real robots raise several problems that directly affect the controllers. This complexity underscores the need for innovative and robust control strategies, such as the one proposed in this work.

The vast literature on drone trajectory control is a testament to the complexity of this challenge. For example, in [12,13], the authors proposed the basic proportional-integral-derivative (PID) technique to control quadrotor motion. In a similar context, the authors in [14] implemented a PID approach with a backstepping methodology, and in [15], the authors used a nested saturation algorithm. Nevertheless, quadrotor drones are susceptible to environmental disturbances impacting their performance in practical applications. These disturbances, which can arise from Coriolis forces, friction, aerodynamic coefficients, inertia moments, or unmodeled dynamics, underscore the need for a robust control strategy to handle them effectively. To overcome this problem, a diversity of robust control strategies have been designed, developed, and studied, such as sliding mode control (SMC) [16,17,18,19,20], ${\mathcal{H}}_{\infty }$ [21,22] and backstepping with SMC [23,24,25,26], among other methodologies [27].

One concept that has stood out and gained popularity among researchers and academia in recent years is active disturbance rejection control (ADRC) [28,29], which is based on representing the system as a disturbed chain of integrators, where the total disturbance represents all the internal and external disturbing effects. Such perturbations are estimated using an extended state observer (ESO) and further canceled out in the control law.

Despite being a widely studied topic, research areas continue to emerge as technology advances, for example, fault estimation diagnosis [30,31,32], estimation of unknown states or disturbances [33,34], and collision avoidance [35,36], among others. Nevertheless, this introduction is focused on those related to the purpose of this work, i.e., robust tracking control by employing ADRC. Related work can be found in [37,38,39,40,41,42,43,44,45]. For instance, in [37], a cascade ADRC scheme for the attitude subsystem was presented, while a backstepping SMC scheme was developed for the position subsystem; in [38], the authors improved the ADRC by structurally designing an extended state observer, concluding that the improved ADRC can estimate disturbances faster and more accurately than the conventional ADRC. A robust nonlinear ADRC was designed in [39] to track a desired trajectory and solve the attitude control problem of a quadrotor; similarly, in [40], a robust control strategy for controlling the flight of a UAV with a passively (fixed) tilted hexacopter was presented, which is based on a robust extended-state observer to estimate and reject internal dynamics and external disturbances; a control law, based on a tracking differentiator, extended state observers, and state error feedback approaches, was designed in [41] to control the attitude and altitude of a quadrotor. In [42], an adaptive sliding-mode-based ADRC strategy was proposed for the altitude and attitude control of a quadrotor subjected to external disturbances. An ADRC application for quadrotor system stabilization and obstacle avoidance under external disturbances was proposed in [43]. A modified ADRC was designed in [44] to obtain high-performance quadrotor flight with the presence of external disturbances and input delays. The experimental results, with artificial external wind gusts as the disturbances, illustrated the approach’s effectiveness. Finally, in [45], the authors presented theoretical, simulation, and experimental results by applying ADRC for controlling the altitude of a quadrotor using an in-ground-effect model. Even though the ADRC methodology has been successfully implemented to control quadrotors, some of the cited works still need improvement. For example, in [43,44], the dynamic model only considered disturbances in the orientation dynamics; the control strategies depended on positions and velocity measurements in [43]; the control strategy was developed considering the linearization of the dynamic model in [44], and only the altitude of the quadrotor was considered in [45].

When ADRC is carried out for systems in trajectory tracking tasks, it is helpful to combine it with differential flatness-based controllers [46,47], in which a set of variables, denoted as flat outputs, can parametrize all the system variables in terms of flat outputs and their finite-order time derivatives. The last aspect allows us to derive a reference trajectory from the system’s natural tracking. Even when this approach was tackled in some contributions (see [48,49]), the reported flat output construction was too complex for real-time implementations. Since the flat outputs of a system are not unique, the flatness-based problem is still open, with practical alternatives (in the sense of their easiness of implementation) becoming essential.

Building on the existing body of knowledge and motivated by previous works, the highlights of this article are summarized as follows:

• The proposed approach is based on two sets of ADRC control loops, one for tracking a reference in the z axis (denoted as a direct loop) and an additional loop to control the reference trajectories in the $x,y$ plane. This action is indirectly performed, since it depends on the orientation control (indirect loop).
• The orientation control design, a crucial aspect of our research, involves a comprehensive algebraic procedure. This procedure provides the dynamic relation between the $x,y$ dynamics, the orientation control inputs, and the ADRC design, ensuring a robust and reliable system.
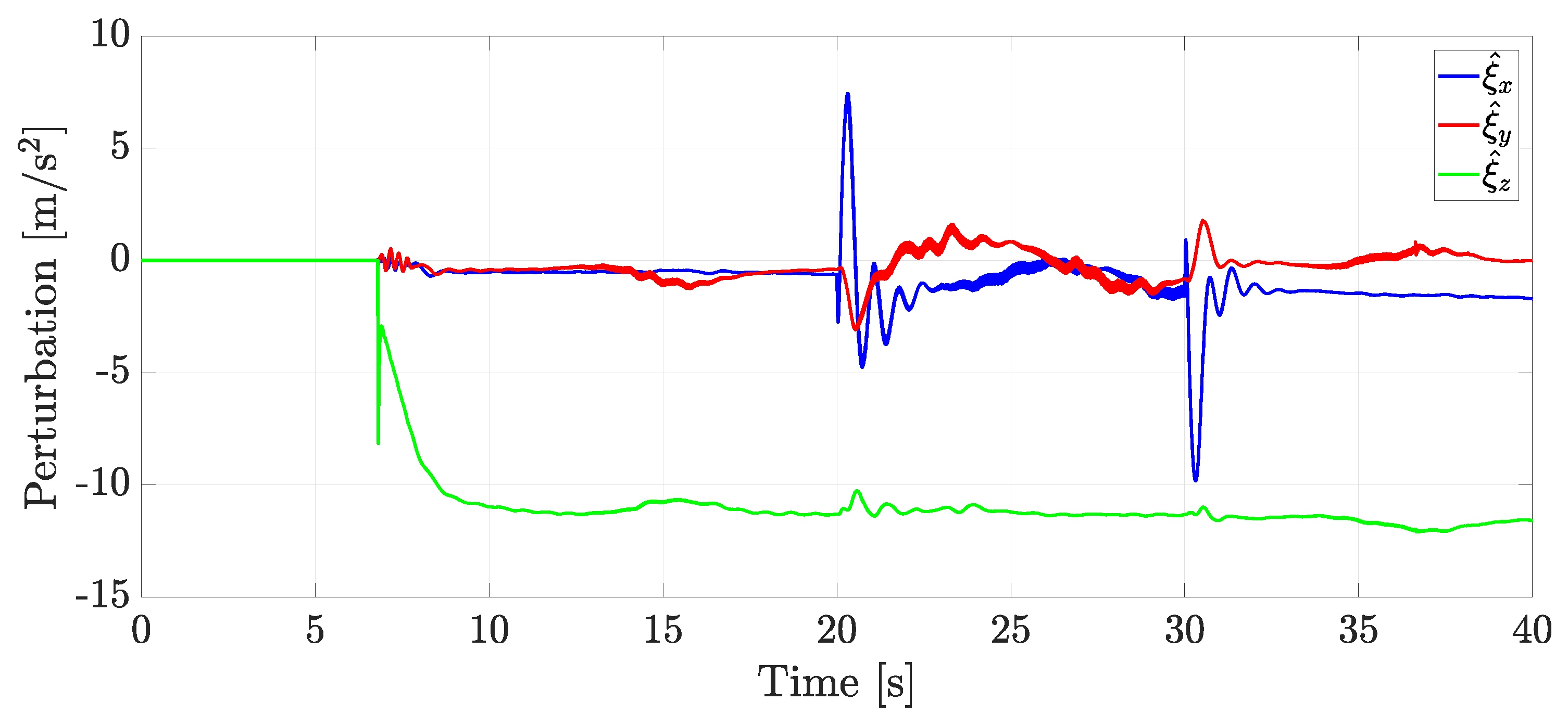
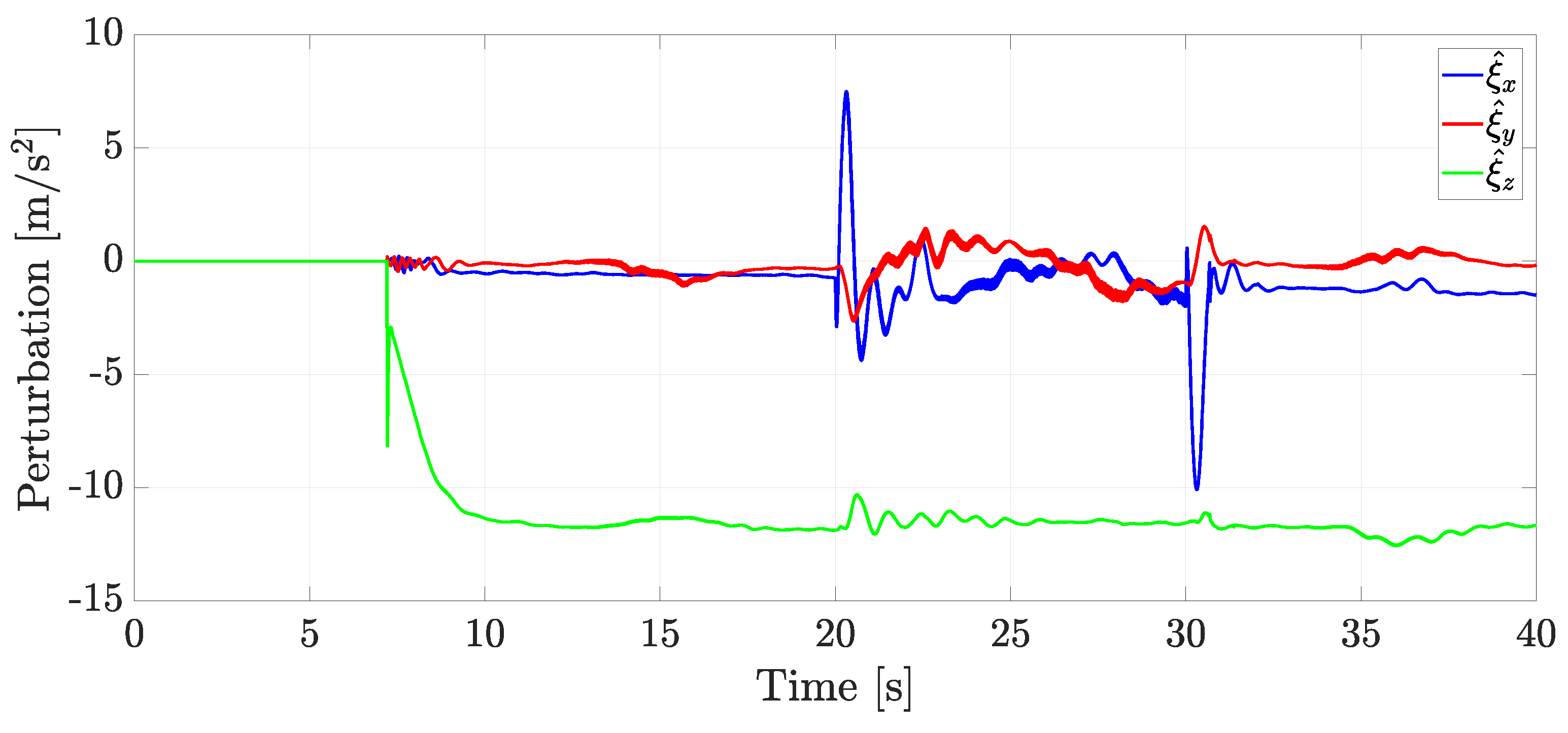
• The scheme also considers the estimation and cancellation of external disturbances and internal perturbations, such as non-modeled dynamics of possible coupling effects through the ESO.
• The proposal is not just theoretical. It was experimentally assessed in trajectory-tracking tasks, considering a fan that provided external perturbations. This practical assessment reaffirmed the applicability of our approach in real-world scenarios.

The outline of this work is as follows: Section 2 describes the problem statement and the dynamic model. Section 3 presents the design of the control strategy, together with the GPIO. Section 4 describes the numerical simulations and real-time experiments, while Section 5 discusses the results. Finally, Section 6 presents some concluding remarks and offers insights for future work.

2. Problem Statement

Consider the mathematical model of a quadrotor [50], described in Figure 1, where the vector $\mathbf{\zeta }={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^{\top }\in {\mathbb{R}}^3$ represents the position coordinates and the vector $\mathit{\eta }={\left[\begin{array}{ccc}\psi & \theta & \varphi \end{array}\right]}^{\top }\in {\mathbb{R}}^3$ stands for the orientation coordinates yaw, pitch, and roll, respectively, from the body frame $\mathcal{B}=\{X_b,Y_b,Z_b\}$ with respect to an inertial frame $\mathcal{I}=\{X_{\mathcal{I}},Y_{\mathcal{I}},Z_{\mathcal{I}}\}$. In this work, a cross-shaped configuration is considered; therefore, its dynamics are given as

$$\begin{array}{ccc}\hfill \ddot{x}& =& {\displaystyle \frac{F}{m}}\left(sin\varphi sin\psi +cos\varphi cos\psi sin\theta \right)+{\xi }_x\left(t\right),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \ddot{y}& =& {\displaystyle \frac{F}{m}}\left(cos\varphi sin\psi sin\theta -sin\varphi cos\psi \right)+{\xi }_y\left(t\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \ddot{z}& =& {\displaystyle \frac{F}{m}}cos\varphi cos\theta +{\xi }_z\left(t\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \ddot{\mathit{\eta }}& =& \mathit{\tau }+{\mathit{\xi }}_{\eta }\left(t\right),\hfill \end{array}$$

(4)

where $m\in \mathbb{R}$ is the mass of the quadrotor, $F\in \mathbb{R}$ is the thrust force, and $\mathit{\tau }={\left[\begin{array}{ccc}{\tau }_{\psi }& {\tau }_{\theta }& {\tau }_{\varphi }\end{array}\right]}^{\top }\in {\mathbb{R}}^3$ is a vector of the control inputs. The terms ${\xi }_x$, ${\xi }_y$, ${\xi }_z$, and ${\mathit{\xi }}_{\eta }={\left[\begin{array}{ccc}{\xi }_{\psi }& {\xi }_{\theta }& {\xi }_{\varphi }\end{array}\right]}^{\top }\in {\mathbb{R}}^3$ represent perturbations such as Coriolis forces, friction, aerodynamic coefficients, inertia moments, or unmodeled dynamics. It is worth mentioning that the term ${\xi }_z$ includes the gravity term $g\in \mathbb{R}$.

Assumption 1.

The perturbations ${\xi }_j$, for $j=x,y,z,\psi ,\theta ,\varphi$, are smooth bounded signals. Therefore, real positive numbers exist $K_j$ such that ${\sup }_t\left|{\xi }_j\right|\le K_j$.

Assumption 2.

The disturbances ${\xi }_j$ can be modeled as a family of fixed-degree Taylor series polynomials of order $h-1$, which satisfies ${\displaystyle \frac{d^h}{d{t}^h}}{\xi }_j={\displaystyle \frac{d^h}{d{t}^h}}{r}_j\left(t\right)\approx 0$, where $r_j\left(t\right)$ is a residual term (see [51]).

The problem consists of designing a robust control strategy that drives the quadrotor to follow a desired time-varying trajectory, even with the presence of unknown disturbances, such that

$$\underset{t\to \infty }{lim}\left[\begin{array}{c}\mathit{\zeta }-{\mathit{\zeta }}^{*}\\ \mathit{\eta }-{\mathit{\eta }}^{*}\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right],$$

where ${\mathit{\zeta }}^{*}={\left[\begin{array}{ccc}{x}^{*}& y^{*}& z^{*}\end{array}\right]}^{\top }\in {\mathbb{R}}^3$ is the vector of the desired positions, while ${\mathit{\eta }}^{*}={\left[\begin{array}{ccc}{\psi }^{*}& {\theta }^{*}& {\varphi }^{*}\end{array}\right]}^{\top }$$\in {\mathbb{R}}^3$ is the vector of the desired angles. For this purpose, a hierarchical strategy is proposed, where it is assumed that the rotation angles converge faster than the position coordinates. In this sense, the inner control loop, related to the orientation angles, can be directly solved through classic control schemes such as PID [52]. On the other hand, the outer control loop is tackled through algebraic manipulations and the ADRC approach.

3. Control Strategy

This section describes how the control inputs are obtained. In the first step, the control for the coordinate z is presented. Then, the control for the coordinates x and y is detailed. Finally, the control for the orientation angles is given.

3.1. Trajectory Tracking Control of z: A Direct ADRC Scheme

Using the ultra-local model approximation described in [53,54], one can consider that ${\dot{\xi }}_z\approx 0$. Then, defining $z_1=z$ and $z_2=\dot{z}$, system (3) can be rewritten in state-space as

$$\begin{array}{cc}\hfill {\dot{z}}_1& =z_2,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\dot{z}}_2& ={\displaystyle \frac{F}{m}}cos\varphi cos\theta +{\xi }_z.\hfill \end{array}$$

(6)

Remark 1.

Notice that in system (6), it has been assumed that a piece-wise function approximates the generalized disturbance input. However, the complexity of the disturbance may imply the use of a more significant order approximation, as stated in Assumption 2.

Based on (5) and (6), the following GPIO [55] is proposed as

$$\begin{array}{cc}\hfill {\dot{\widehat{z}}}_1& ={\widehat{z}}_2+{\lambda }_{2_z}(z_1-{\widehat{z}}_1),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\dot{\widehat{z}}}_2& ={\displaystyle \frac{F}{m}}cos\varphi cos\theta +{\widehat{\xi }}_z+{\lambda }_{1_z}(z_1-{\widehat{z}}_1),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\dot{\widehat{\xi }}}_z& ={\lambda }_{0_z}(z_1-{\widehat{z}}_1),\hfill \end{array}$$

(9)

where ${\lambda }_{i_z}>0$ is the gain observer, for $i=0,1,2$. The observer injection error is defined as ${\tilde{e}}_z:=z_1-{\widehat{z}}_1$, thus, from (5) and (6) and (7)–(9), it is easy to see that the injection error satisfies the following linear dominant dynamics:

$$\begin{array}{c}\hfill {\stackrel{⃛}{\tilde{e}}}_z+{\lambda }_{2_z}{\ddot{\tilde{e}}}_z+{\lambda }_{1_z}{\dot{\tilde{e}}}_z+{\lambda }_{0_z}{\tilde{e}}_z=0.\end{array}$$

For tuning the observer gains, the characteristic polynomial of the observer error is matched with Hurwitz polynomials as [56]

$$s^3+{\lambda }_{2_z}{s}^2+{\lambda }_{1_z}s+{\lambda }_{0_z}=(s^2+2{\zeta }_z{w}_{n_z}+w_{n_z}^2)(s+w_{n_z}),$$

(10)

where ${\zeta }_z$ is the desired damping coefficient and $w_{n_z}$ is the desired natural frequency. Therefore, the injection gains are selected as ${\lambda }_2=2{\zeta }_z{w}_{n_z}+w_{n_z}$, ${\lambda }_1=2{\zeta }_z{w}_{n_z}^2+w_{n_z}^2$, and ${\lambda }_0=w_{n_z}^3$. By properly choosing the gain observers, ${\lambda }_i$ can guarantee the convergence to the estimated values, that is, ${\widehat{z}}_1\to z$, ${\widehat{z}}_2\to \dot{z}$, and ${\widehat{\xi }}_z\to {\xi }_z$ [51].

Remark 2.

Another manner of tuning the gain observers was developed in [57], where all-pole systems can be constructed by adjusting a simple parameter.

The position error is $e_z=z-z^{*}$, where $z^{*}$ is the desired altitude. Then, the error dynamics of $e_z$ are given by

$${\ddot{e}}_z={\displaystyle \frac{F}{m}}cos\varphi cos\theta +{\xi }_z-{\ddot{z}}^{*},$$

(11)

therefore, based on (7)–(9) and (11), the control input F is designed as

$$\begin{array}{cc}\hfill F& ={\displaystyle \frac{m}{cos\varphi cos\theta }}\left[{\ddot{z}}^{*}-k_{z_1}{e}_z-k_{z_2}{\widehat{e}}_z-{\widehat{\xi }}_z\right],\hfill \end{array}$$

(12)

where ${\widehat{e}}_z={\widehat{z}}_2-{\dot{z}}^{*}$.

Theorem 1.

Let the control (12), along with the GPIO given in (7)–(9) be applied in system (11). Then, the position error $e_z$ will converge to a vicinity near the origin as $t\to \infty$.

Proof. 

Let us define ${\mathit{ϵ}}_z={\left[\begin{array}{cc}{e}_z& {\dot{e}}_z\end{array}\right]}^{\top }$, then, substituting (12) into (11) yields the following state-space system

$${\dot{\mathit{ϵ}}}_z=A_z{\mathit{ϵ}}_z+\mathit{Z}({\tilde{z}}_2,{\tilde{\xi }}_z),$$

where $A_z=\left[\begin{array}{cc}0& 1\\ -k_{z_1}& -k_{z_2}\end{array}\right]$, $\mathit{Z}({\tilde{z}}_2,{\tilde{\xi }}_z)={\left[\begin{array}{cc}0& k_{z_2}{\tilde{z}}_2+{\tilde{\xi }}_z\end{array}\right]}^{\top }$ is the perturbation term, with ${\tilde{z}}_2=z_2-{\widehat{z}}_2$ and ${\tilde{\xi }}_z={\xi }_z-{\widehat{\xi }}_z$. Note that if the gains $k_{z_1}$ and $k_{z_2}>0$, matrix $A_z$ is Hurwitz. Furthermore, if the perturbation term $\mathit{Z}({\tilde{z}}_2,{\tilde{\xi }}_z)=0$, the equilibrium point ${\mathit{ϵ}}_z=0$ is globally asymptotically stable. On the other, considering the perturbation term $\mathit{Z}({\tilde{z}}_2,{\tilde{\xi }}_z)$, from [51] one knows that ${\widehat{z}}_2\to \dot{z}$ and ${\widehat{\xi }}_z\to {\xi }_z$, which implies that ${\tilde{z}}_2$ and ${\tilde{\xi }}_z$ converge asymptotically to an arbitrary small vicinity near the origin. Moreover, from the result given in [58], one can conclude that the state z practically tracks the reference signal $z^{*}$, in the sense that, for any $\sigma >0$, there exists a constant ${\epsilon }^{*}$ such that for any $\epsilon \in (0,{\epsilon }^{*})$

$$\left|z-z^{*}\right|\le \sigma \mathrm{uniformly}\mathrm{in}t\in \left[t_{\epsilon },\infty \right],$$

where $t_{\epsilon }$ is an $\epsilon$-dependent constant. In particular,

$$\underset{t\to \infty }{lim}\sup \left|z-z^{*}\right|\le \sigma . \square$$

Remark 3.

Note that control (12) presents a singularity when $cos\varphi cos\theta =0$. This happens when ϕ or $\theta =\pm {\displaystyle \frac{\pi }{2}}$. Since, in this work, aggressive maneuvers are not considered, the orientation angles ϕ, $\theta \in \left(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right)$ which imply that $cos\varphi cos\theta \ne 0$ and singularity are avoided.

3.2. Trajectory Tracking Control of $x,y$: An Indirect ADRC Scheme

The latter analysis only involved the dynamics of z, which can be carried out through a direct control loop. The control design for the tracking task in the variables $x,y$ involves a recursive design regarding the orientation control. In that sense, in the following procedure, a relation between the orientation angles and the $x,y$ coordinates, which will be used for the design of a set of auxiliary control inputs, is denoted as $u_x,u_y$, which will provide reference signals for the orientation angles to then be controlled in an internal control loop. In this sense, substituting (12) into (1) and into (2), one has

$$\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\end{array}\right]=u_{z}R\left(\psi \right)\left[\begin{array}{c}{\displaystyle \frac{tan\varphi }{cos\theta }}\\ tan\theta \end{array}\right]+\left[\begin{array}{c}{\xi }_x\left(t\right)\\ {\xi }_y\left(t\right)\end{array}\right],$$

(13)

where $u_z={\ddot{z}}^{*}-k_{z_1}{e}_z-k_{z_2}{\dot{\widehat{e}}}_z-{\widehat{\xi }}_z$, and

$$\begin{array}{cc}\hfill R\left(\psi \right)& :=\left[\begin{array}{cc}sin\psi & cos\psi \\ -cos\psi & sin\psi \end{array}\right].\hfill \end{array}$$

The system (13) can be related to a control system in which the term $u_{z}R\left(\psi \right)$ can be stated as a nonlinear matrix control gain and the control vector is defined by ${\left[\begin{array}{cc}{\displaystyle \frac{tan\varphi }{cos\theta }}& tan\theta \end{array}\right]}^{\top }$. This relation is used to define a hierarchical control scheme consisting of the following loops:

• An external control loop of ADRC nature involved in the trajectory tracking control of $x,y$, whose control input is $\theta$ and $\varphi$.
• An internal control loop taking the control inputs obtained from the external control loop as reference states to be further controlled in the dynamics of (4).
• Notice that the internal control loop is assumed to be fast enough to respect the time scale separation principle (see [59]).

3.2.1. External Control Loop Design

The following relation can be obtained from (13)

$$\left[\begin{array}{c}{\displaystyle \frac{tan{\varphi }^{*}}{cos{\theta }^{*}}}\\ tan{\theta }^{*}\end{array}\right]={\displaystyle \frac{R^{\top }\left(\psi \right)}{u_z}}\left[\begin{array}{c}{u}_x\\ u_y\end{array}\right],$$

(14)

where $u_x$ and $u_y$ are auxiliary control inputs.

Remark 4.

Note that if $u_z=0$, (14) is singular. Nevertheless, $\underset{t\to \infty }{lim}{u}_z={\ddot{z}}^{*}-{\widehat{\xi }}_z$. Since $z^{*}$ and its time-derivatives are known, $z^{*}$ can be designed so that $u_z\ne 0$.

Assuming that ${\displaystyle \frac{tan{\varphi }^{*}}{cos{\theta }^{*}}}\to {\displaystyle \frac{tan\varphi }{cos\theta }}$ and $tan{\theta }^{*}\to tan\theta$, then, substituting (14) into (13) one obtains the following system:

$$\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\end{array}\right]=\left[\begin{array}{c}{u}_x\\ u_y\end{array}\right]+\left[\begin{array}{c}{\xi }_x\left(t\right)\\ {\xi }_y\left(t\right)\end{array}\right].$$

(15)

System (15) allows us to propose a flatness-based linear ADRC synthesis. Then, defining ${\mathit{\chi }}_1={\left[\begin{array}{cc}x& y\end{array}\right]}^{\top }$, ${\mathit{\chi }}_2={\left[\begin{array}{cc}\dot{x}& \dot{y}\end{array}\right]}^{\top }$, and considering the ultra-local model approximation for (15), again using one extended state for each disturbance input (as presented by the ADRC design to control the variable z and Assumption 2), that is ${\dot{\mathit{\chi }}}_3={\left[\begin{array}{cc}{\dot{\xi }}_x& {\dot{\xi }}_y\end{array}\right]}^{\top }\approx 0$, then, system (15) can be rewritten as

$$\begin{array}{cc}\hfill {\dot{\mathit{\chi }}}_1& ={\mathit{\chi }}_2,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\dot{\mathit{\chi }}}_2& ={\mathbf{u}}_{xy}+{\mathit{\chi }}_3,\hfill \end{array}$$

(17)

where ${\mathbf{u}}_{xy}={\left[\begin{array}{cc}{u}_x& u_y\end{array}\right]}^{\top }$. Proposing the GPIO for (16) and (17), one has

$$\begin{array}{cc}\hfill {\dot{\widehat{\mathit{\chi }}}}_1& ={\widehat{\mathit{\chi }}}_2+{\lambda }_{2_{xy}}({\mathit{\chi }}_1-{\widehat{\mathit{\chi }}}_1),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\dot{\widehat{\mathit{\chi }}}}_2& ={\mathbf{u}}_{xy}+{\widehat{\mathit{\chi }}}_3+{\lambda }_{1_{xy}}({\mathit{\chi }}_1-{\widehat{\mathit{\chi }}}_1),\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\dot{\widehat{\mathit{\chi }}}}_3& ={\lambda }_{0_{xy}}({\mathit{\chi }}_1-{\widehat{\mathit{\chi }}}_1),\hfill \end{array}$$

(20)

where ${\lambda }_{i_{xy}}\in {\mathbb{R}}^{2\times 2}$ is the matrix observer gain. The linear dominant dynamics of the injection errors, say ${\tilde{\mathbf{e}}}_{\chi }:={\mathit{\chi }}_1-{\widehat{\mathit{\chi }}}_1$, are given by

$$\begin{array}{c}\hfill {\stackrel{⃛}{\tilde{\mathbf{e}}}}_{\chi }+{\lambda }_{2_{xy}}{\ddot{\tilde{\mathbf{e}}}}_{\chi }+{\lambda }_{1_{xy}}{\dot{\tilde{\mathbf{e}}}}_{\chi }+{\lambda }_{0_{xy}}{\tilde{\mathbf{e}}}_{\chi }=0.\end{array}$$

(21)

System (21) can be matched with Hurwitz polynomials with the same structure as those presented in (10), then, the injection errors are forced to be ultimately bounded, ensuring sufficiently accurate estimations to carry out the ADRC loops. By properly choosing the gain observers, ${\lambda }_{i_{xy}}$ can guarantee the convergence of the estimated values, that is, ${\widehat{\mathit{\chi }}}_1\to {\mathit{\chi }}_1$, ${\widehat{\mathit{\chi }}}_2\to {\mathit{\chi }}_2$, and ${\widehat{\mathit{\chi }}}_3\to {\mathit{\chi }}_3$. Let us define the position error as ${\mathbf{e}}_{\chi }={\mathit{\chi }}_1-{\mathit{\chi }}^{*}$, where ${\mathit{\chi }}^{*}={\left[\begin{array}{cc}{x}^{*}& y^{*}\end{array}\right]}^{\top }$ is the desired position, which is at least twice differentiable, then, the error dynamics are given as

$${\ddot{\mathbf{e}}}_{\chi }={\mathbf{u}}_{xy}+{\mathit{\chi }}_3-{\ddot{\mathit{\chi }}}^{*}.$$

(22)

Based on (18)–(20) and (22), the auxiliary control inputs are proposed as

$${\mathbf{u}}_{xy}={\ddot{\mathit{\chi }}}^{*}-\left[\begin{array}{cc}{k}_{x_1}& 0\\ 0& k_{y_1}\end{array}\right]{\mathbf{e}}_{\chi }-\left[\begin{array}{cc}{k}_{x_2}& 0\\ 0& k_{y_2}\end{array}\right]{\widehat{\mathbf{e}}}_{\chi }-{\widehat{\mathit{\chi }}}_3,$$

(23)

where ${\dot{\widehat{\mathbf{e}}}}_{\chi }={\widehat{\mathit{\chi }}}_2-{\dot{\mathit{\chi }}}^{*}$, and the gains $k_{x_1},k_{x_2}$, $k_{y_1}$, and $k_{y_2}$ are positive.

Theorem 2.

Let the control (23), along with the GPIO given in (18)–(20), be applied in system (22). Then, the trajectory tracking error ${\mathbf{e}}_{\chi }$ is restricted to an ultimately bounded vicinity of the origin of the phase plane.

3.2.2. Internal Control Loop

From the external control loop (23) and the definition of the auxiliary control inputs $u_x$, and $u_y$, the reference values of the orientation variables $\theta$, and $\varphi$, denoted by ${\theta }^{*}$ and ${\varphi }^{*}$, can be obtained from (14) as follows:

$$\begin{array}{cc}\hfill {\theta }^{*}& =arctan\left({\displaystyle \frac{u_{x}cos\psi +u_{y}sin\psi }{u_z}}\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\varphi }^{*}& =arctan\left[\left({\displaystyle \frac{cos{\theta }^{*}}{u_z}}\right)\left(u_{x}sin\psi -u_{y}cos\psi \right)\right].\hfill \end{array}$$

(25)

3.3. Orientation Control

The orientation error is defined as ${\mathbf{e}}_{\eta }=\mathit{\eta }-{\mathit{\eta }}^{*}$, whose dynamics are given as ${\ddot{\mathbf{e}}}_{\eta }=\mathit{\tau }+{\mathbf{p}}_{\eta }$, where ${\mathbf{p}}_{\eta }={\mathit{\xi }}_{\eta }-{\ddot{\mathit{\eta }}}^{*}$ is the total perturbation. Let us define ${\mathbf{e}}_{{\eta }_1}={\mathbf{e}}_{\eta }$, ${\mathbf{e}}_{{\eta }_2}={\dot{\mathbf{e}}}_{\eta }$ and considering Assumption 2, that is, ${\dot{\mathbf{p}}}_{\eta }\approx 0$, then, one can obtain the following state-space system:

$$\begin{array}{ccc}\hfill {\dot{\mathbf{e}}}_{{\eta }_1}& =& {\mathbf{e}}_{{\eta }_2},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill {\dot{\mathbf{e}}}_{{\eta }_2}& =& \mathit{\tau }+{\mathbf{p}}_{\eta }.\hfill \end{array}$$

(27)

A GPIO is proposed for system (26) and (27) as

$$\begin{array}{ccc}\hfill {\dot{\widehat{\mathbf{e}}}}_{{\eta }_1}& =& {\widehat{\mathbf{e}}}_{{\eta }_2}+{\lambda }_{2_{\eta }}({\mathbf{e}}_{{\eta }_1}-{\widehat{\mathbf{e}}}_{{\eta }_1}),\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill {\widehat{\dot{\mathbf{e}}}}_{{\eta }_2}& =& \mathit{\tau }+{\widehat{\mathbf{p}}}_{\eta }+{\lambda }_{1_{\eta }}({\mathbf{e}}_{{\eta }_1}-{\widehat{\mathbf{e}}}_{{\eta }_1}),\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill {\dot{\widehat{\mathit{\xi }}}}_{\eta }& =& {\lambda }_{0_{\eta }}({\mathbf{e}}_{{\eta }_1}-{\widehat{\mathbf{e}}}_{{\eta }_1}),\hfill \end{array}$$

(30)

where ${\lambda }_{i_{\eta }}\in {\mathbb{R}}^{3\times 3}$ is the matrix observer gain. The linear dominant dynamics of the injection errors, defined as ${\tilde{\mathbf{e}}}_{\eta }:={\mathbf{e}}_{{\eta }_1}-{\widehat{\mathbf{e}}}_{{\eta }_1}$, are given by

$$\begin{array}{c}\hfill {\stackrel{⃛}{\tilde{\mathbf{e}}}}_{\eta }+{\lambda }_{2_{\eta }}{\ddot{\tilde{\mathbf{e}}}}_{\eta }+{\lambda }_{1_{\eta }}{\dot{\tilde{\mathbf{e}}}}_{\eta }+{\lambda }_{0_{\eta }}{\tilde{\mathbf{e}}}_{\eta }=0.\end{array}$$

(31)

System (31) can be matched with Hurwitz polynomials with the same structure as those presented in (10), then, the injection errors are forced to be ultimately bounded, ensuring sufficiently accurate estimations to carry out the ADRC loops. By properly choosing the gain observers, ${\lambda }_{i_{\eta }}$ can guarantee the convergence of the estimated values, that is, ${\widehat{\mathbf{e}}}_{{\eta }_1}\to {\mathbf{e}}_{\eta }$, ${\widehat{\mathbf{e}}}_{{\eta }_2}\to {\dot{\mathbf{e}}}_{\eta }$, and ${\widehat{\mathit{\xi }}}_{\eta }\to {\mathit{\xi }}_{\eta }$. Based on the above, the control law for the orientation angles is given as

$$\mathit{\tau }=-{\kappa }_0{\int }_0^t{\mathbf{e}}_{\eta }d\overline{\tau }-{\kappa }_1{\mathbf{e}}_{\eta }-{\kappa }_2{\widehat{\mathbf{e}}}_{{\eta }_2}-{\widehat{\mathbf{p}}}_{\eta },$$

(32)

where ${\kappa }_0=\mathrm{diag}\{{\kappa }_{{\psi }_0},{\kappa }_{{\theta }_0},{\kappa }_{{\varphi }_0}\}$, ${\kappa }_1=\mathrm{diag}\{{\kappa }_{{\psi }_1},{\kappa }_{{\theta }_1},{\kappa }_{{\varphi }_1}\}$ and ${\kappa }_2=\mathrm{diag}\{{\kappa }_{{\psi }_2},{\kappa }_{{\theta }_2},{\kappa }_{{\varphi }_2}\}$ are definite positive matrices that correspond to the control gains.

Theorem 3.

Let the control (32), along with the GPIO given in (28)–(30), be applied in system (26) and (27). Then, the orientation error ${\mathbf{e}}_{\eta }$ is restricted to an ultimately bounded vicinity of the origin of the phase plane.

Proof. 

The proofs of Theorems 2 and 3 are similar to the one presented for Theorem 1.  □

Remark 5.

It is worth mentioning that the controls (12), (23), (24), (25) and (32) only depend on the measurement of a quadrotor’s positions and orientations, since its velocities and disturbances are estimated through the GPIO.

Remark 6.

It must be clarified that the control law (32) only serves to make a numerical simulation comparison with another control strategy and determine its performance, because, practically, the control that is being sent to the quadrotor is the one obtained in (24) and (25).

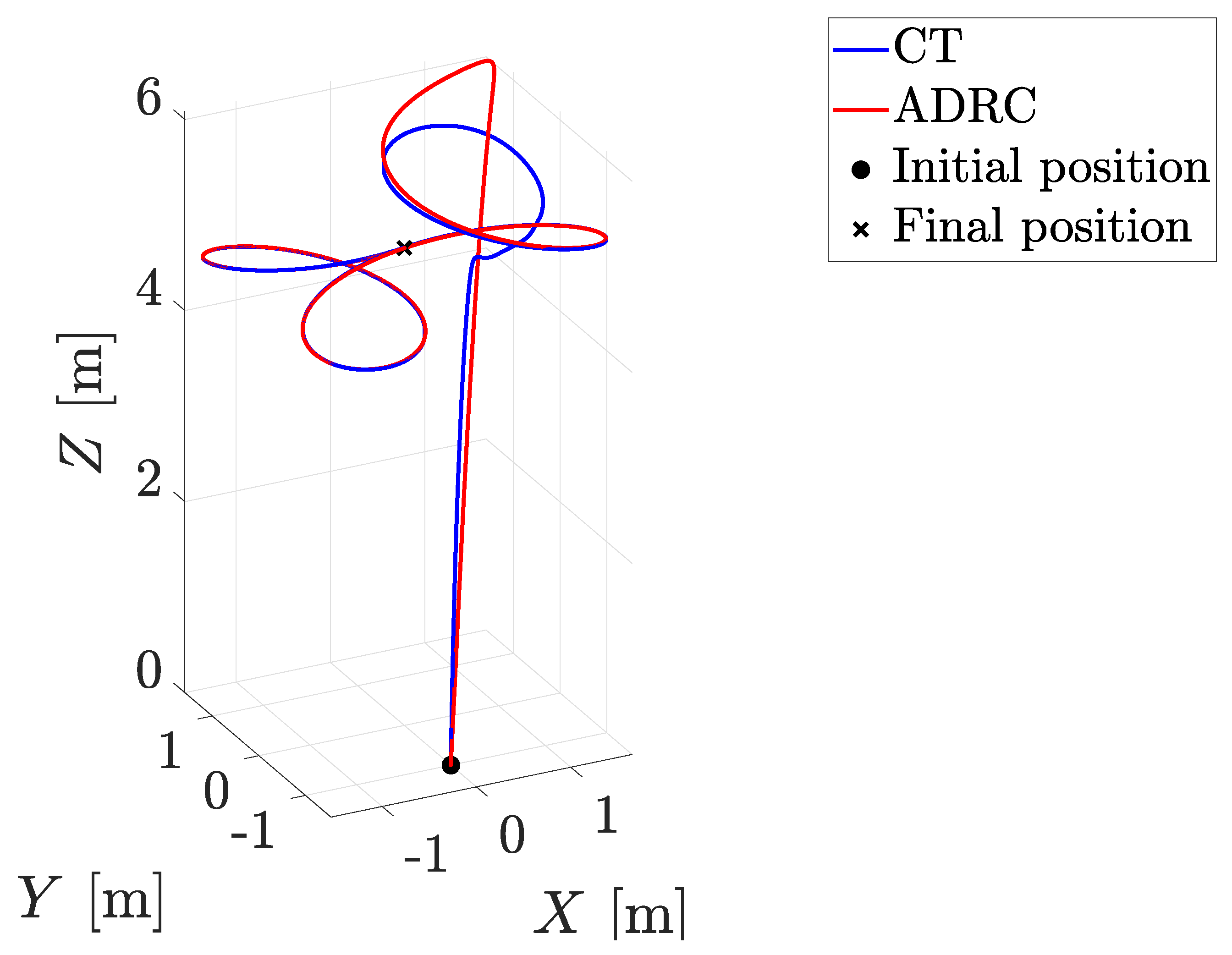
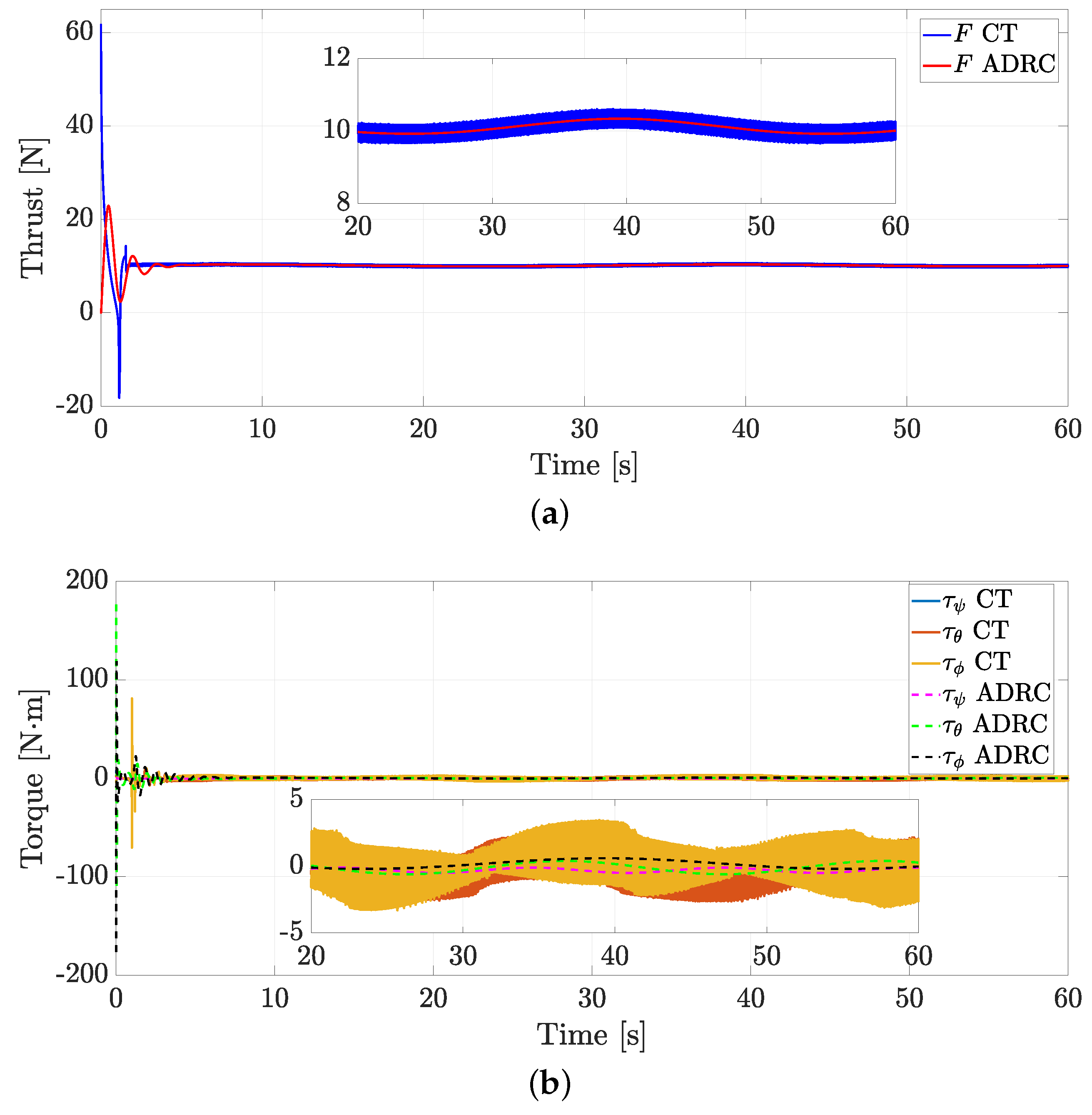
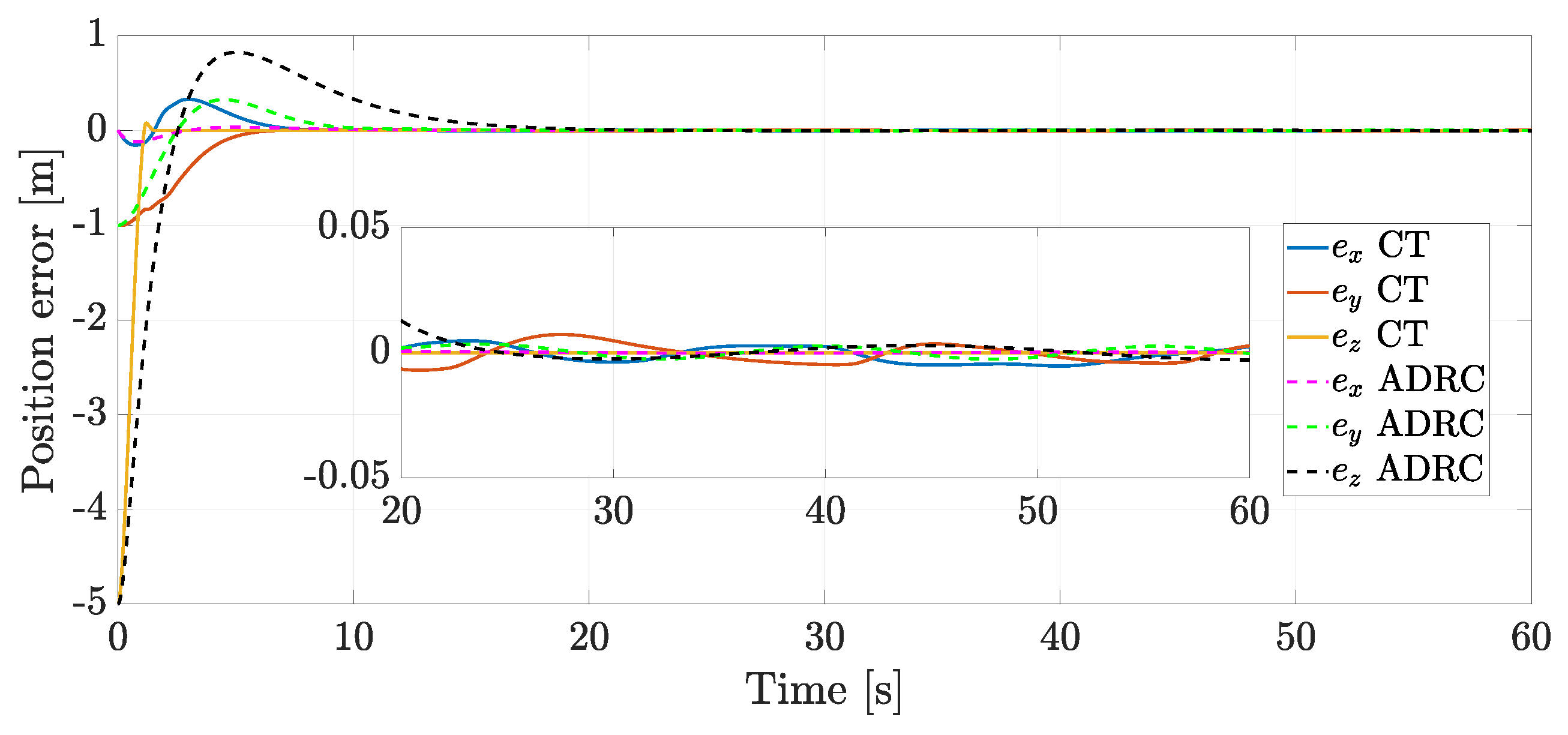
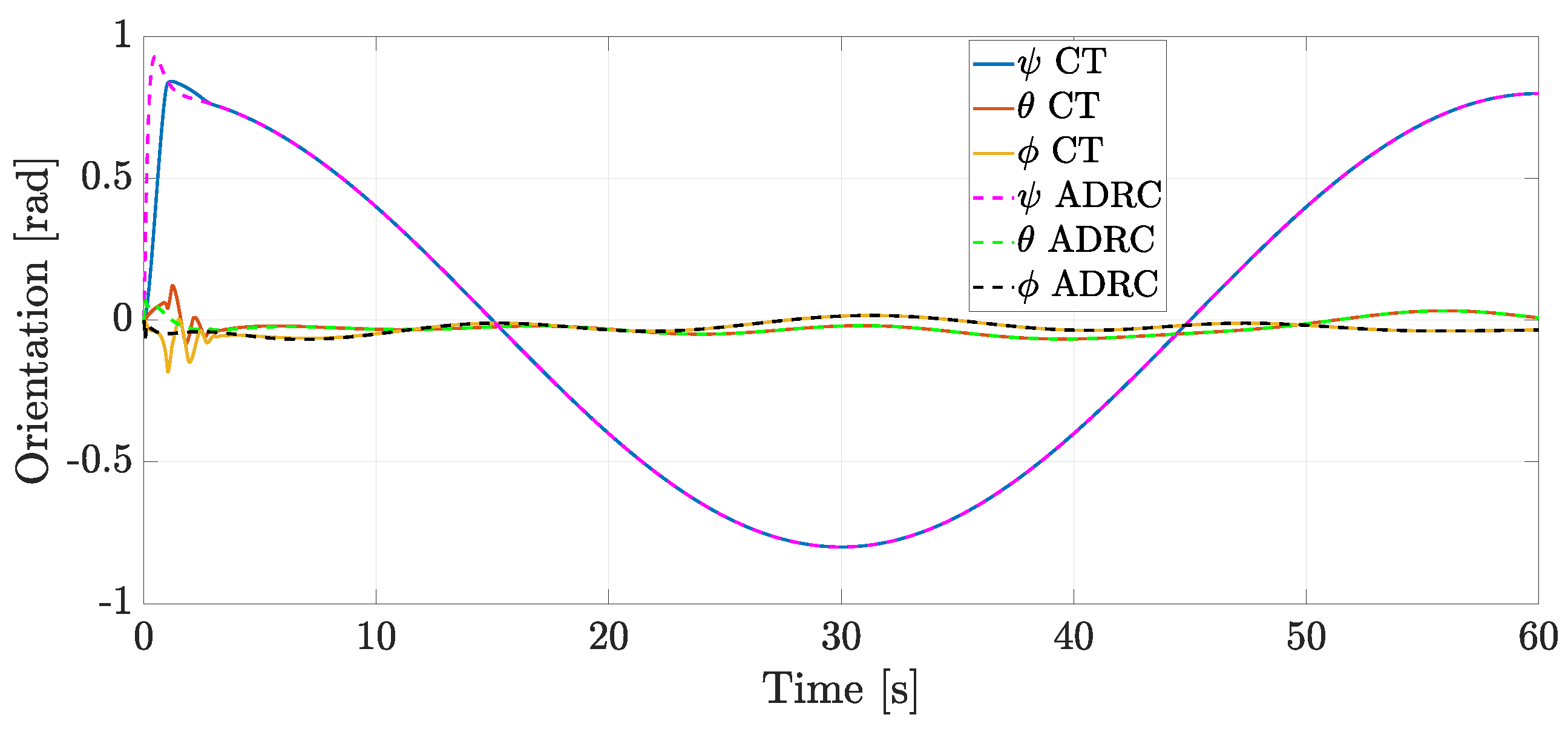
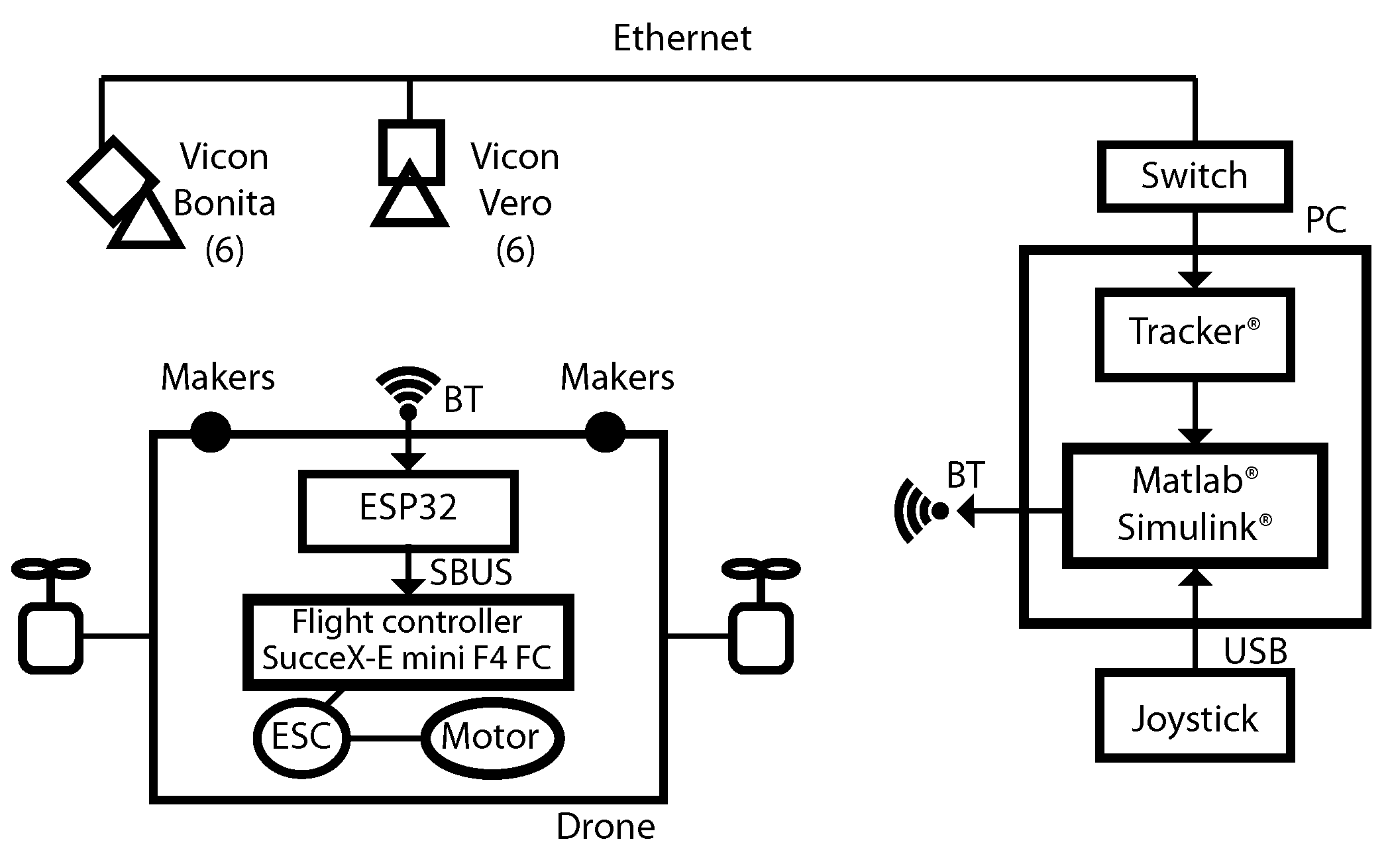
4. Numerical Simulations and Real-Time Experiments

The first part of this section is dedicated to presenting the results of numerical simulations obtained by comparing the control strategy developed in this work and a technique based on sliding modes. Subsequently, the results practically obtained using a commercial quadrotor are described.

4.1. Numerical Simulations

The proposed control strategy’s performance was evaluated and compared with the continuous twisting (CT) robust control law defined in [60]. The simulations were implemented in MATLAB^®-Simulink^® R2017b (The MathWorks Inc., Natick, MA, USA) with a sampling time of $0.001$ s using Euler’s integration method with $m=1$ kg. The quadrotor’s initial condition was ${\left[\begin{array}{cc}{\mathit{\zeta }}^{\top }\left(0\right)& {\mathit{\eta }}^{\top }\left(0\right)\end{array}\right]}^{\top }={\left[\begin{array}{cccccc}0& -1& 0& 0& 0& 0\end{array}\right]}^{\top }$, while the desired trajectory was a Lissajous curve defined with the following parametric functions

$$\begin{array}{cccc}\hfill x^{*}& =2sin\left(2wt\right)cos\left(wt\right),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & \hfill y^{*}& =2sin\left(2wt\right)sin\left(wt\right),\hfill \\ \hfill z^{*}& =0.5sin\left(wt\right)+5,\hfill & \hfill {\psi }^{*}& =0.8cos\left(wt\right),\hfill \end{array}$$

with $w={\displaystyle \frac{\pi }{30}}$. The perturbations were defined as

$$\begin{array}{cccc}\hfill {\xi }_x& =-{\displaystyle \frac{a_x}{m}}\dot{x}+0.2sin\left(0.2t\right)+0.3,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & \hfill {\xi }_y& =-{\displaystyle \frac{a_y}{m}}\dot{y}+0.2cos\left(0.4t\right)-0.3,\hfill \\ \hfill {\xi }_z& =-{\displaystyle \frac{a_z}{m}}\dot{z}-0.2sin\left(0.2t\right)-0.3,\hfill & \hfill {\xi }_{\psi }& =a_{\psi }\dot{\psi }\dot{\varphi }+0.2sin\left(0.5t\right)+0.3,\hfill \\ \hfill {\xi }_{\theta }& =a_{\theta }\dot{\theta }\dot{\varphi }+0.5sin\left(0.3t\right)+0.1,\hfill & \hfill {\xi }_{\varphi }& =a_{\varphi }\dot{\theta }\dot{\psi }-0.4sin\left(0.2t\right)-0.4,\hfill \end{array}$$

where $a_x=a_y=a_z=0.01$, $a_{\psi }={\displaystyle \frac{I_x-I_y}{I_z}}$, $a_{\theta }={\displaystyle \frac{I_z-I_x}{I_y}}$, $a_{\varphi }={\displaystyle \frac{I_y-I_z}{I_x}}$, with $I_x=I_y=0.015$ kg·m², and $I_z=0.03$ kg·m² as the inertia moments. The control gains were set as $k_{z_1}=5$, $k_{z_2}=4$, $k_{x_1}=k_{y_1}=5$, $k_{x_2}=k_{y_2}=3$, ${\kappa }_0=\mathrm{diag}\left\{652.99\right\}$, ${\kappa }_1=\mathrm{diag}\left\{336.32\right\}$, and ${\kappa }_2=\mathrm{diag}\left\{48\right\}$, while the observer parameters were set as ${\zeta }_z=4$, $w_{n_z}=35$, which yielded ${\lambda }_{2_z}=315$, ${\lambda }_{1_z}=\mathrm{11,025}$, ${\lambda }_{0_z}=\mathrm{42,875}$, ${\lambda }_{0_{xy}}=\mathrm{diag}\left\{{\lambda }_{0_z}\right\}$, ${\lambda }_{1_{xy}}=\mathrm{diag}\left\{{\lambda }_{1_z}\right\}$, ${\lambda }_{2_{xy}}=\mathrm{diag}\left\{{\lambda }_{2_z}\right\}$, ${\lambda }_{0_{\eta }}=\mathrm{diag}\left\{{\lambda }_{0_z}\right\}$, ${\lambda }_{1_{\eta }}=\mathrm{diag}\left\{{\lambda }_{1_z}\right\}$, and ${\lambda }_{2_{\eta }}=\mathrm{diag}\left\{{\lambda }_{2_z}\right\}$.

Figure 2 shows a motion comparison of the quadrotor in a $3—$dimensional space, while Figure 3a,b present the thrust and the torques, respectively. One can note that the thrust and torques with the CT approach had high-frequency oscillations, which could lead to motor failure.

The position tracking error comparison is depicted in Figure 4, where it is evident that both strategies led the error to converge to zero. On the other hand, Figure 5 illustrates the orientation angle comparison.

To assess the overall performance, the following average RMS over a suitable receding-horizon time interval of finite length was calculated as

$$\begin{array}{cccc}\hfill F_{RMS}& ={\left({\displaystyle \frac{1}{\Delta t}}{\int }_{t-\Delta t}^t{F}^2\left(\overline{\tau }\right)d\overline{\tau }\right)}^{{\displaystyle \frac{1}{2}}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & \hfill {\mathit{\tau }}_{RMS}& ={\left({\displaystyle \frac{1}{\Delta t}}{\int }_{t-\Delta t}^t{∥\mathit{\tau }\left(\overline{\tau }\right)∥}^{2}d\overline{\tau }\right)}^{{\displaystyle \frac{1}{2}}},\hfill \end{array}$$

(33)

$$\begin{array}{cccc}\hfill {\mathbf{e}}_{{\zeta }_{RMS}}& ={\left({\displaystyle \frac{1}{\Delta t}}{\int }_{t-\Delta t}^t{∥{\mathbf{e}}_{\zeta }\left(\overline{\tau }\right)∥}^{2}d\overline{\tau }\right)}^{{\displaystyle \frac{1}{2}}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & \hfill {\mathbf{e}}_{{\eta }_{RMS}}& ={\left({\displaystyle \frac{1}{\Delta t}}{\int }_{t-\Delta t}^t{∥{\mathbf{e}}_{\eta }\left(\overline{\tau }\right)∥}^{2}d\overline{\tau }\right)}^{{\displaystyle \frac{1}{2}}},\hfill \end{array}$$

(34)

where ${\mathbf{e}}_{\zeta }=\mathit{\zeta }-{\mathit{\zeta }}^{*}$, $\Delta t=2$ s is the time window width in which the corresponding signal is evaluated. From Figure 6a, one can note that the signals are similar; however, high-frequency oscillations still appeared in the CT approach. Furthermore, from Figure 6b, the ADRC methodology needed more energy to carry out the quadrotor motion.

Figure 7a depicts the position error index, where it is evident that the CT algorithm decreased to zero faster than the ADRC, while for Figure 7b, the transient response had a better performance using the ADRC methodology and converged faster to zero than the CT control.

Based on the results presented above, both strategies solved the trajectory-tracking problem of a quadrotor with external perturbations. However, it is essential to note that when using the CT, the control signals presented high-frequency oscillations, which can cause the motors to fail. In addition, the CT of [60] presented another restriction, that is, the angle $\psi \in (-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}})$, unlike the strategy presented in this work, where there is no restriction for this angle.

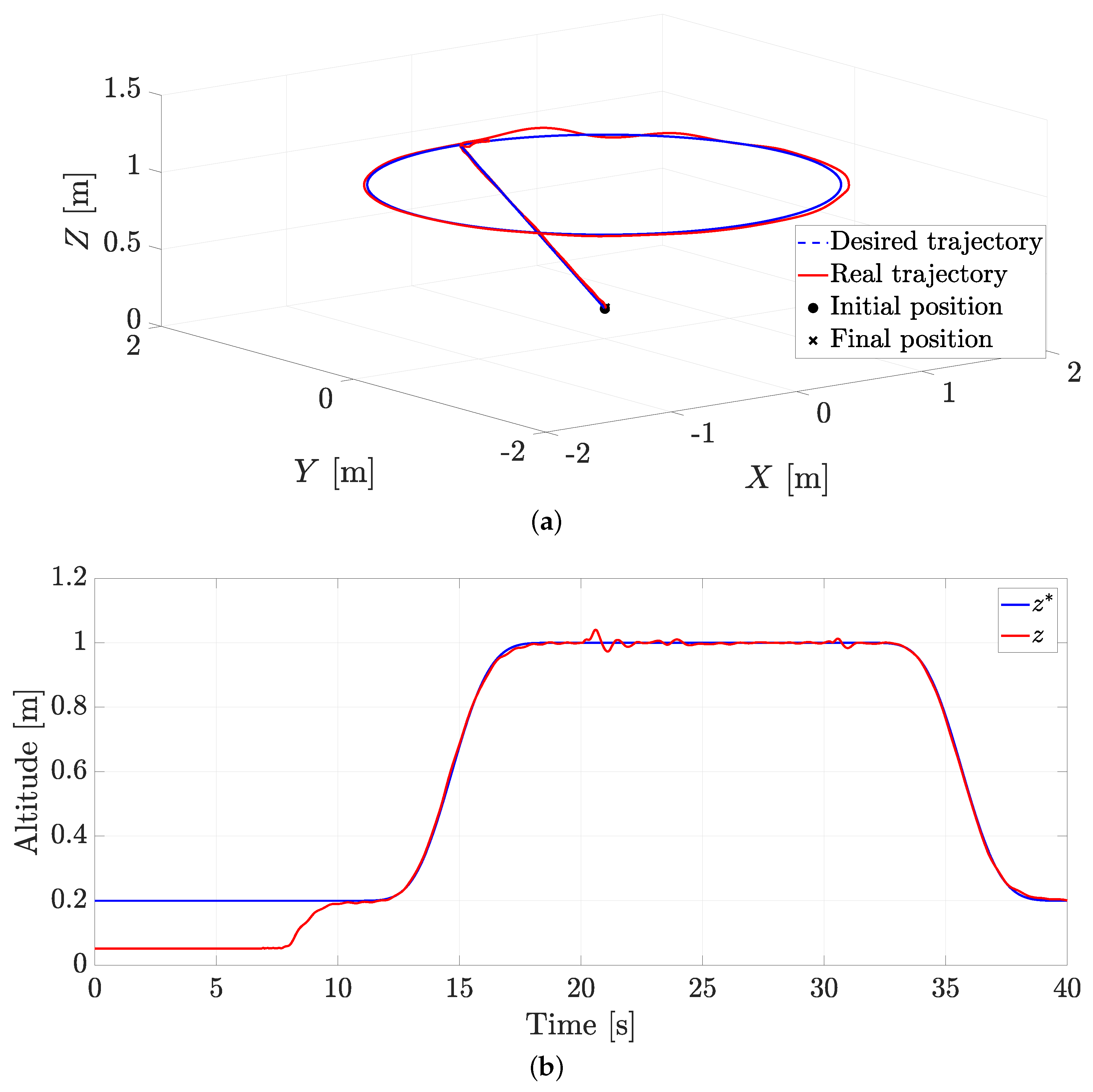
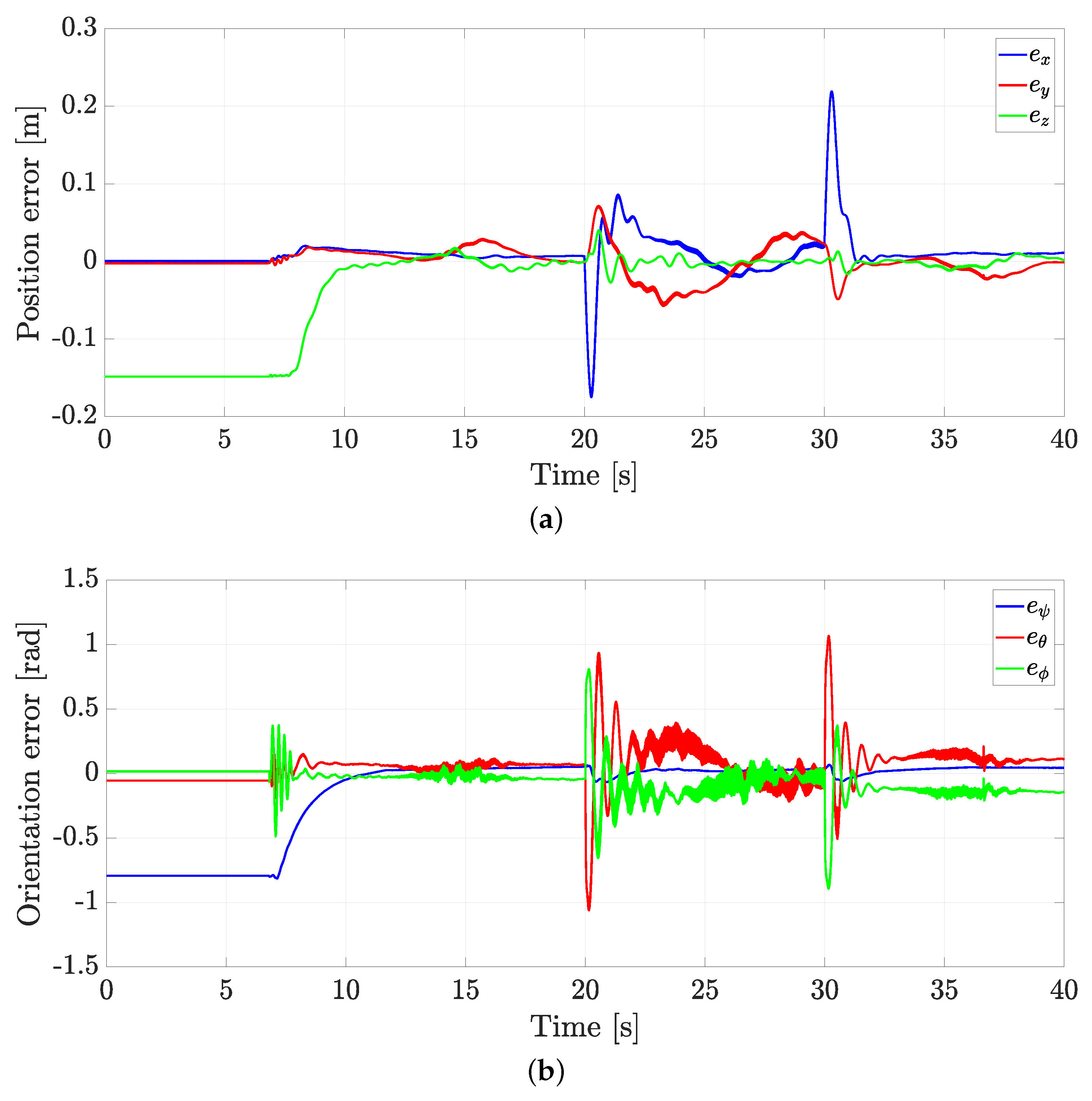
4.2. Real-Time Experiments

The control was implemented using an Iflight Quad^© green hornet v2 (F6, Building B2, Galaxy IMC, Beixin Road,No.6, Zhongkai Avenue, Huizhou, China) shown in Figure 8. This system has 6 mm spherical reflective markers placed along the drone’s body and has 4 outrunner motors model XING-1408 3600 KV with 4 ESCs. Each motor has a three-blade propeller 5 cm in width. The flight controller is a SucceX-E mini F4 FC with serial communication to other electronic devices. The drone is powered by a 4 cells LiPO Lumenier^© 1550 mAh. Figure 8 depicts the propellers protected by the frame with plastic materials and a smooth foam case.

The control implementation is described in Figure 9. The flight controller was connected by wired serial communication to an ESP32 microcontroller. This was a wireless packet receiver that received the desired angular setpoints from the computer through a Bluetooth communication via a Wi-Fi Bluetooth 5.2 PCIe adapter. Thus, the inner loop ran in the flight controller using manufacturer default orientation PID controllers, and the PID gains were adjusted through Betaflight Configurator v10.8 software. On the other hand, the outer loop for the position control used a VICON^® Motion Capture System v3.10 (14 Minns Business Park, West Way OX2 0JB OXFORD, GBR) composed of 6 infrared cameras model Bonita and 6 cameras model Vero. The 12 cameras covered a volumetric workspace with dimensions of 6 m in length, 6 m in width, and 2 m in height. The resolution of the cameras was around $0.5$ mm and $0.1$ rad. The sample time for measurements was about 200 samples per second. All the cameras were connected to a switch by Ethernet and TCP/IP. The switch sent the camera’s data to a computer with an Intel i9 processor with 64 GB of RAM. The VICON^® Tracker software v3.10 captured the position and rotation angles. The tracker sent the data to an application programmed in MATLAB^®-Simulink^® R2021 (The MathWorks Inc., Natick, MA, USA) [61]. MATLAB^® software R2021 ran in real time with a sample time of 5 ms, the outer loop controller and observer were implemented in continuous time using the Simulink Desktop Real-Time^TM Toolbox, a fixed-step sample time was configured, and the ode4 Runge-Kutta solver algorithm was used. The computer executed the outer loop controller by sending the setpoints for the inner loop through Bluetooth.

The desired trajectory $z^{*}$ was defined by implementing smooth interpolation polynomials. In that sense, in the first instance, the drone was at a height of $0.2$ m and rose smoothly to a height of 1 m in 10 s. Subsequently, it remained at that height for 15 s and began its descent using another smooth interpolation polynomial. When the drone had reached the height of 1 m, a circular path in the $X-Y$ plane was defined, with the following parametric functions $x^{*}(t-15)=sin\left({\displaystyle \frac{2\pi }{10}}(t-15)\right)$, $y^{*}(t-15)=cos\left({\displaystyle \frac{2\pi }{10}}(t-15)\right)$. The desired yaw angle was established as a constant given by ${\psi }^{*}={\displaystyle \frac{\pi }{4}}$. The model parameter for the dynamical system was $m=0.6$ kg.

For the rotation inner-loop running in the flight controller, the control gains for the PID were set as ${\kappa }_0=\mathrm{diag}\{90,90,85\}$, ${\kappa }_1=\mathrm{diag}\{30,46,42\}$, and ${\kappa }_2=\mathrm{diag}\{30,38,35\}$. For the position outer-loop, the observer gains were set as ${\zeta }_z=4$, $w_{n_z}=35$, ${\lambda }_{0_z}$ = 42,875, ${\lambda }_{1_z}$ = 11,025, ${\lambda }_{2_z}=315$, ${\lambda }_{0_{xy}}=\mathrm{diag}\{{\lambda }_{0_z},{\lambda }_{0_z}\}$, ${\lambda }_{1_{xy}}=\mathrm{diag}\{{\lambda }_{1_z},{\lambda }_{1_z}\}$, ${\lambda }_{2_{xy}}=\mathrm{diag}\{{\lambda }_{2_z},{\lambda }_{2_z}\}$, ${\lambda }_{0_{\eta }}=\mathrm{diag}\{{\lambda }_{0_z},{\lambda }_{0_z}.{\lambda }_{0_z}\}$, ${\lambda }_{1_{\eta }}=\mathrm{diag}\{{\lambda }_{1_z},{\lambda }_{1_z},{\lambda }_{1_z}\}$, and ${\lambda }_{2_{\eta }}=\mathrm{diag}\{{\lambda }_{2_z},{\lambda }_{2_z},{\lambda }_{2_z}\}$; while the control gains were set as $k_{z_1}=25$, $k_{z_2}=8$, $k_{x_1}=k_{y_1}=25$, and $k_{x_2}=k_{y_2}=9$.

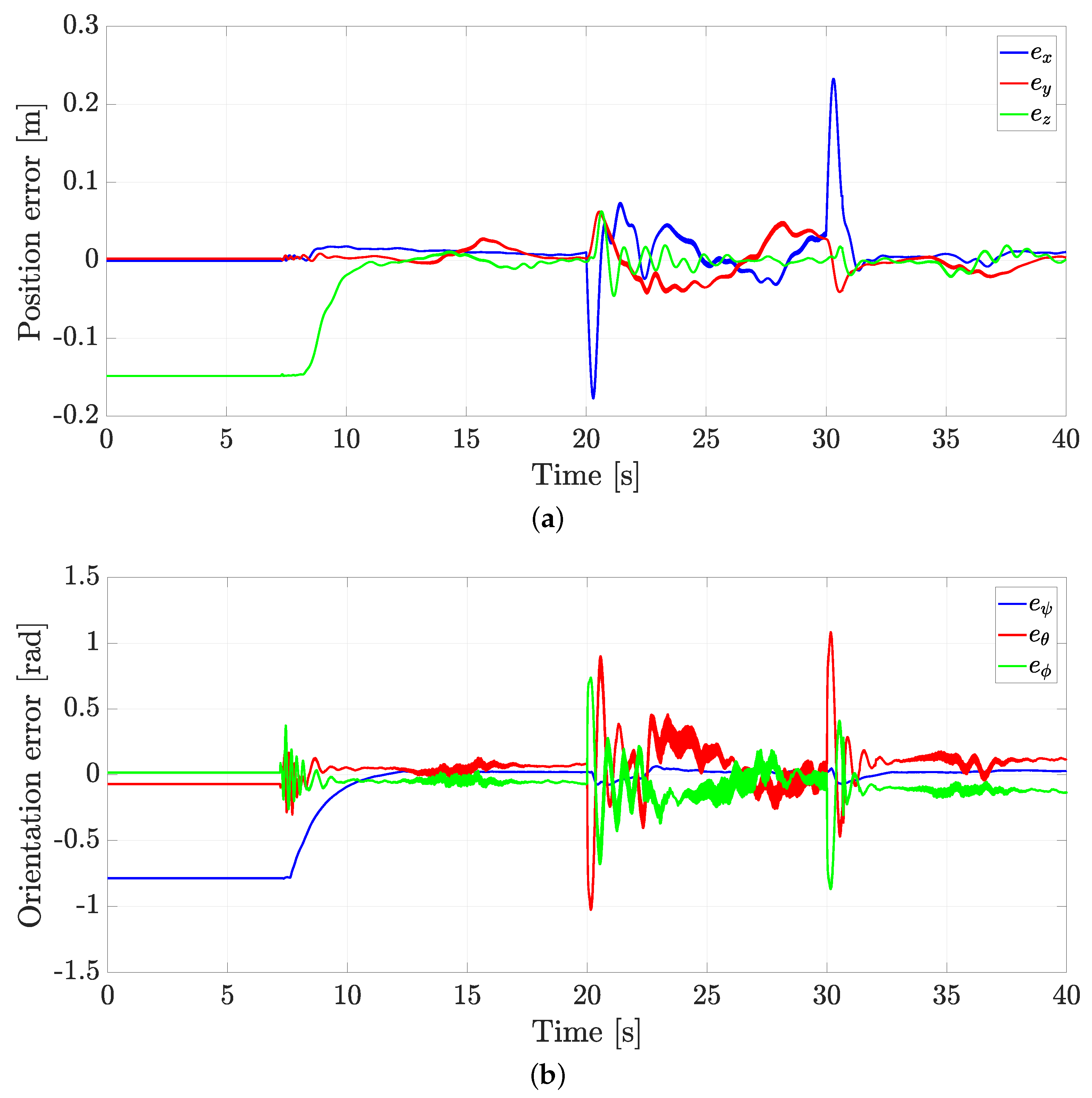
4.3. Experiment without External Disturbances

Figure 10a compares the desired trajectory and that performed by the quadcopter, while Figure 10b illustrates the trajectory tracking in the Z coordinate. It is worth pointing out that the quadrotor could achieve trajectory tracking. This is displayed in Figure 11, where both the position and orientation errors oscillate around zero.

From Figure 11, one can note that there were peaks of great amplitude at 20 s and 30 s. At $t=20$ s, the controller gains caused the quadrotor to move abruptly to follow the desired trajectory. Similarly, at $t=30$ s, the quadrotor had a certain inertia that was reflected when it finished following the trajectory in the plane.

The internal online disturbance estimation is depicted in Figure 12, where it can be noticed that the internal estimated disturbance ${\widehat{\xi }}_z$ had a magnitude closer to the gravity term g. Furthermore, unmodeled dynamics are also lumped in this estimation.

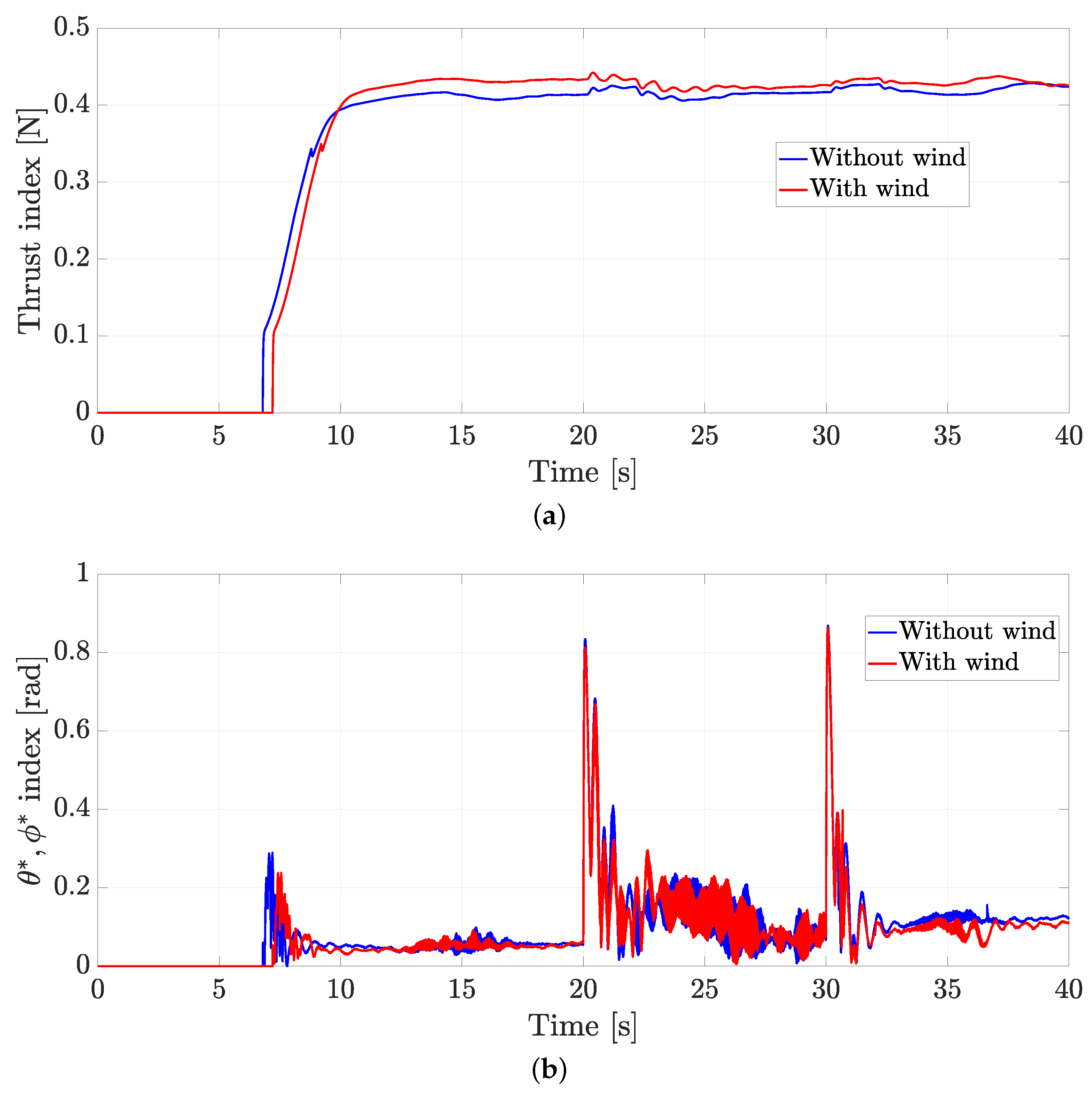
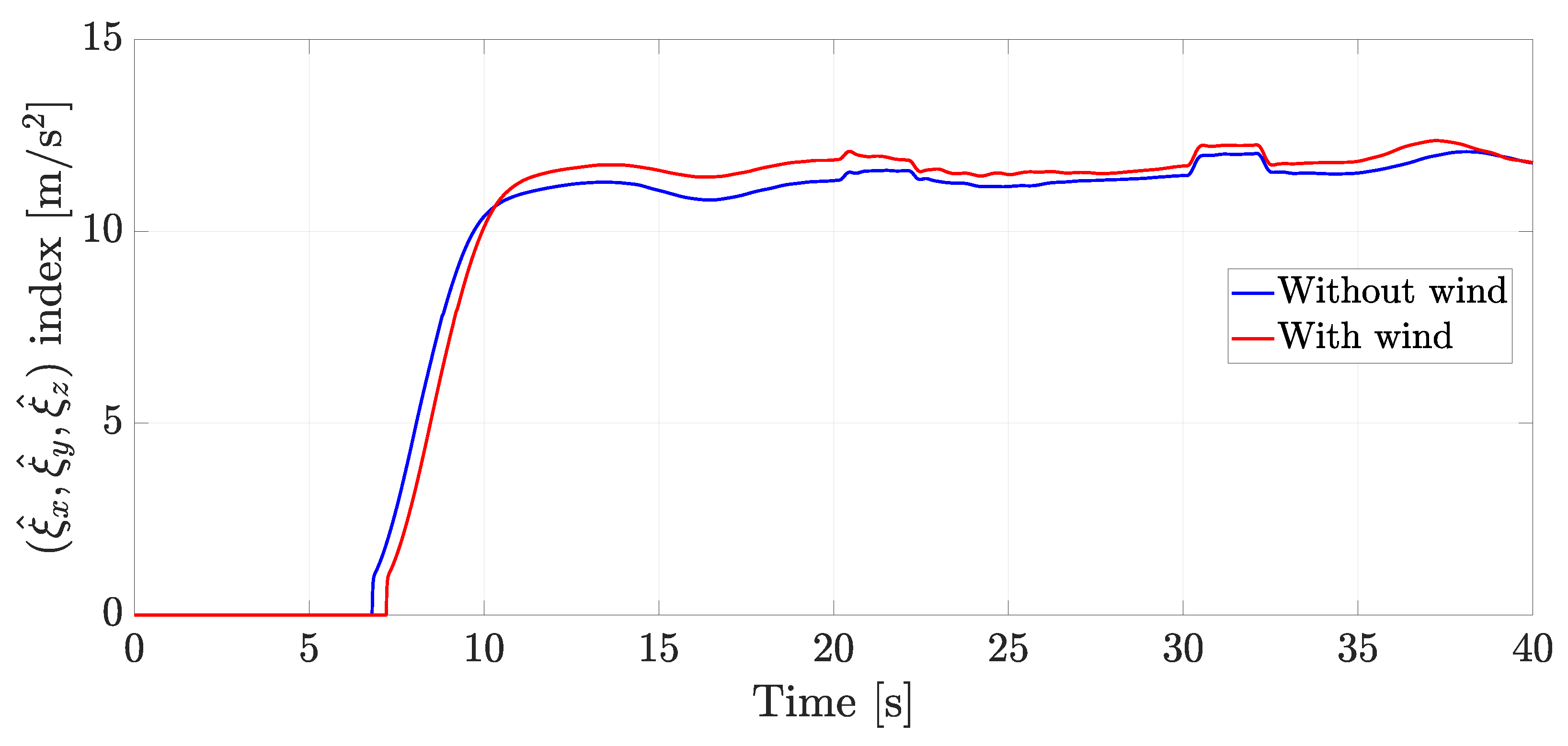
4.4. Experiment with Wind Applied as an External Disturbance

A second experiment with external disturbance was proposed, using the wind produced by a fan in the direction of the X axis and located at ${\left[\begin{array}{ccc}2.5& 0& 1\end{array}\right]}^{\top }$ m.

Table 1. The fan’s velocity concerning the distance to the fan.

Distance [m]	Velocity [m/s]
1	$4.2$
$1.5$	$2.9$
$2.5$	$2.6$
$3.5$	$1.9$
5	$1.4$

presents fan’s velocity concerning the distance in the X direction.

Figure 13 depicts the quadrotor’s motion, which achieved the trajectory tracking. Note that when the quadrotor was closest to the fan, it was subject to a more significant external disturbance, causing it to momentarily not follow the desired trajectory. However, the control could return the system to the desired trajectory through the disturbance estimation.

Figure 14 shows that the position and orientation errors were close to zero, even in the presence of external perturbations.

Figure 15 shows the estimation of internal and external online disturbances. When comparing Figure 12 with Figure 15, one can notice that the estimated disturbances had a similar structure but different magnitudes.

A video of the experimental results can be watched at https://www.dropbox.com/scl/fi/b4dqnlwryrxhb1l8erfwz/Experiment.mp4?rlkey=c3x903t2gzyrz89fa49ekg9la&st=584hz96g&dl=0 (accessed on 2 September 2024).

5. Discussion

The same average RMS equations given in (33) were used to compare the control’s performance when internal and external perturbations were present, to assess the overall performance.

As Figure 16a shows, more energy was needed when external disturbances affected the motion of the quadrotor. At the same time, in Figure 16b, one can conclude that the desired angles ${\theta }^{*}$ and ${\varphi }^{*}$ had a similar behavior. Therefore, the proposed ADRC could deal with both internal and external disturbances.

On the other hand, Figure 17 illustrates the average RMS online disturbance estimation index. Note that these disturbances had the same structure; however, when the quadrotor approached the fan, the disturbances increased their amplitude. Based on those mentioned earlier, one can conclude that, even though the estimated perturbations were different, the control strategy could deal with them.

6. Conclusions

This work contributes to the design of a control strategy based on the ADRC approach to control the trajectory tracking of a quadrotor. To achieve this purpose, it was assumed that the internal loop, given by the orientation control, indirectly controls the position (outer loop). Because a GPIO was implemented, which allowed system disturbances to be estimated, the control law only depended on the drone pose measurements. The experimental results allowed us to validate the proposed control scheme. Furthermore, the controller’s performance was tested by estimating internal and external disturbances, where it was evident that it could deal with this type of perturbation.

Further investigations could be related to the problem of multi-agent systems involving robust trajectory tracking, formation, communication delays, and fault estimation diagnosis.