A Steady-Pressure Control Method for Emulsion Pump Station Based on Online Updating of Optimal Flow Rate
Abstract
1. Introduction
2. Establishment of a Simulation Platform and Its Verification
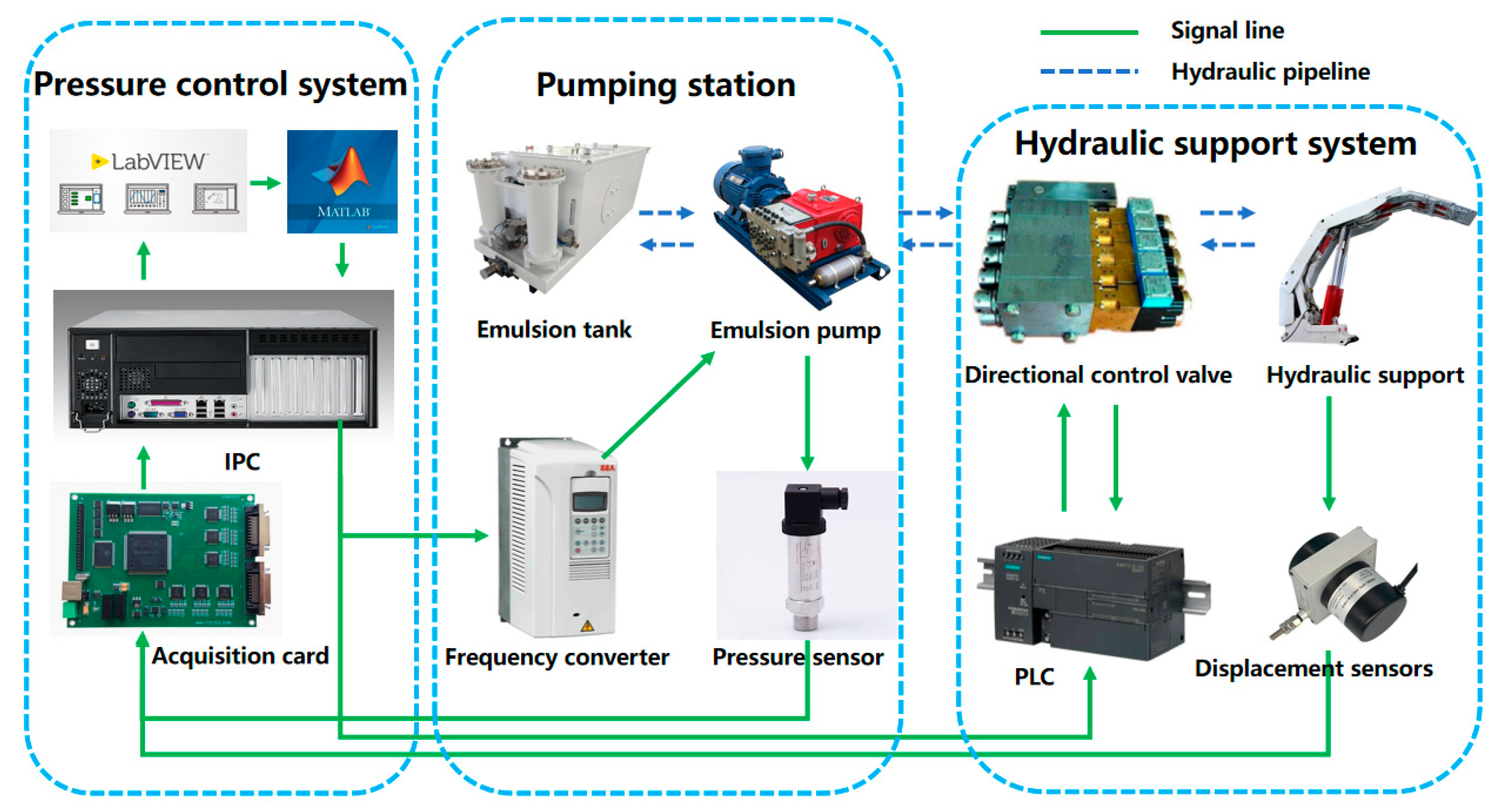
2.1. Experiment System
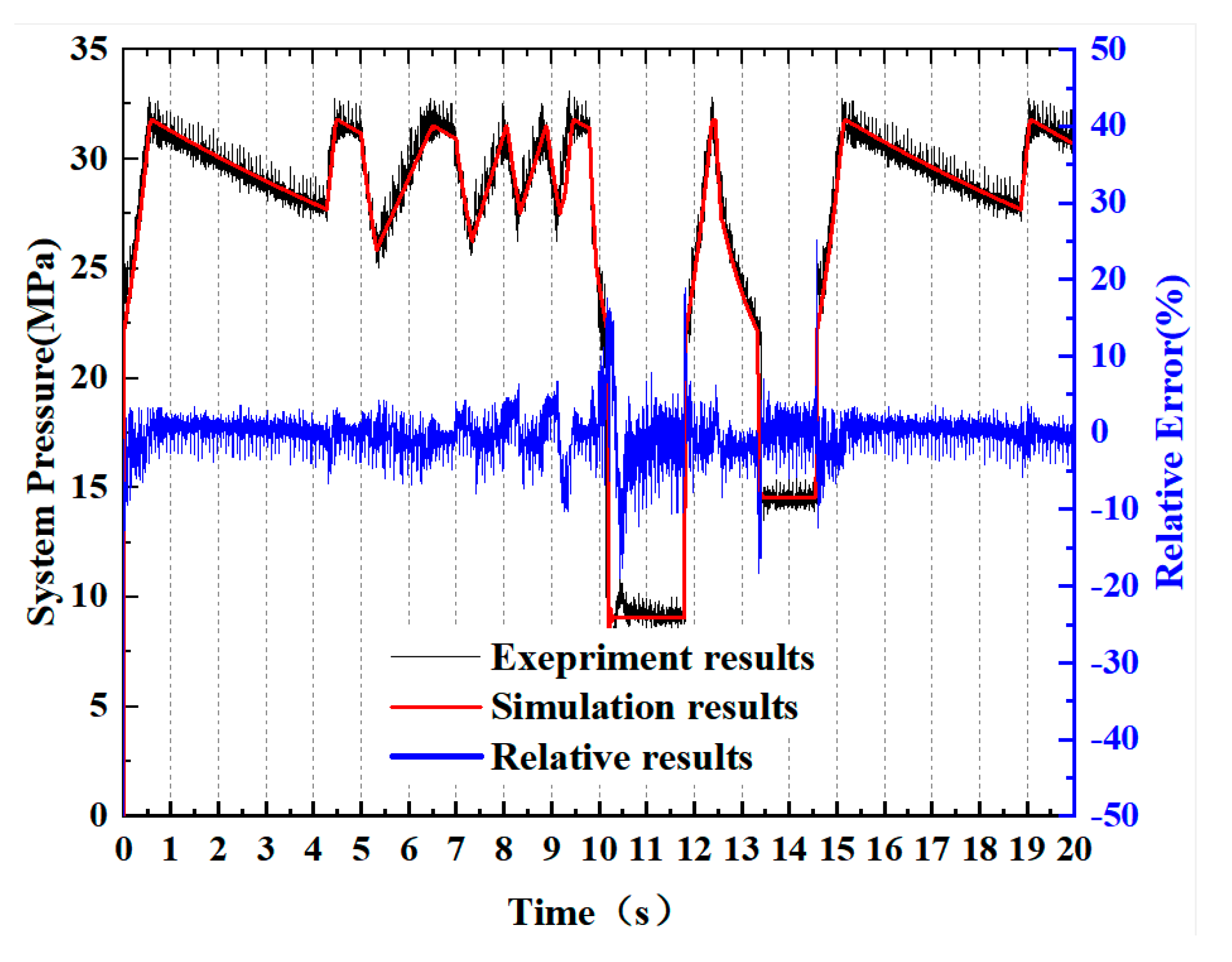
2.2. Establishment and Verification of the Simulation Platform
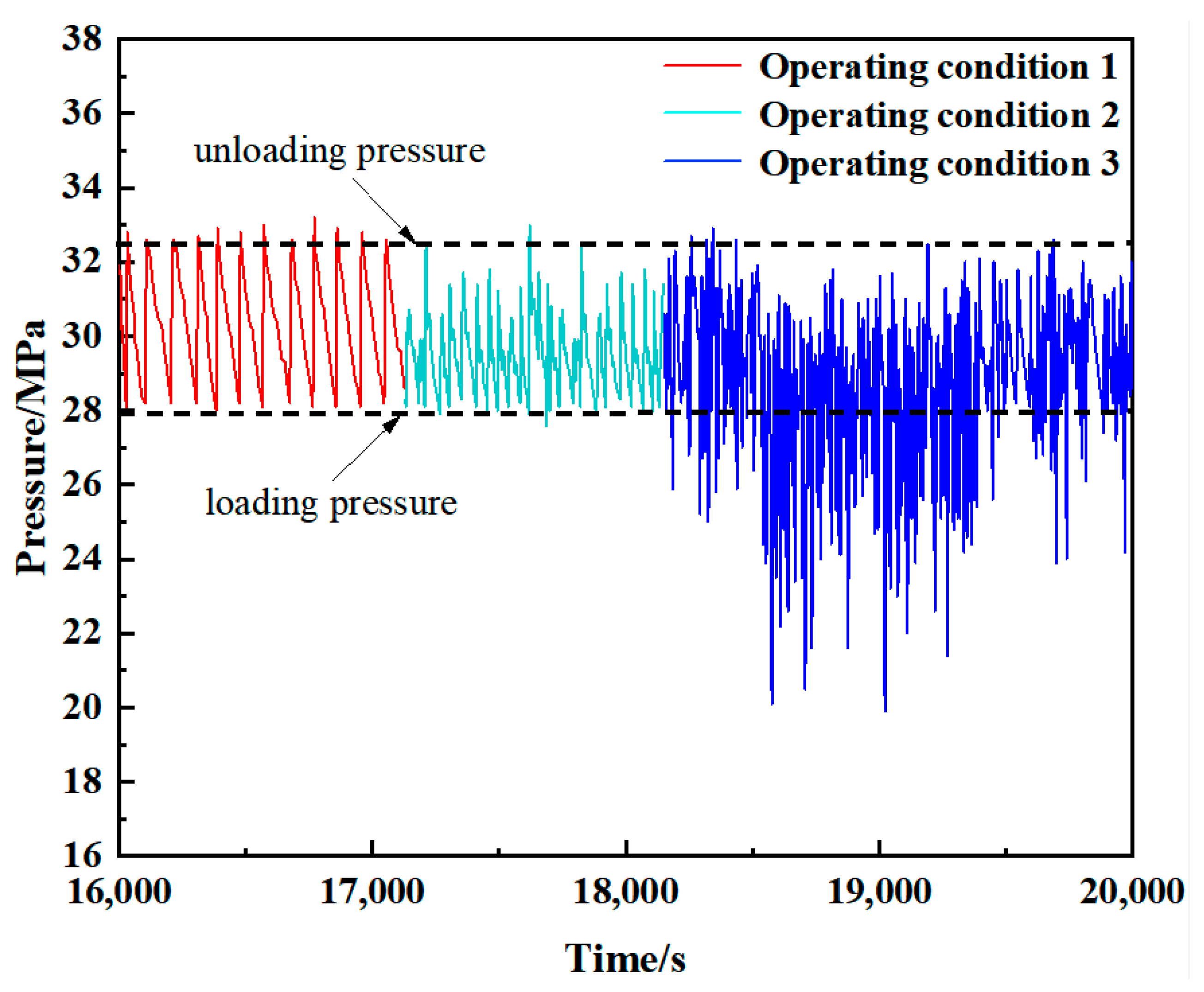
2.3. Establishment of Optimal Flow Datasets under Different Operating Conditions
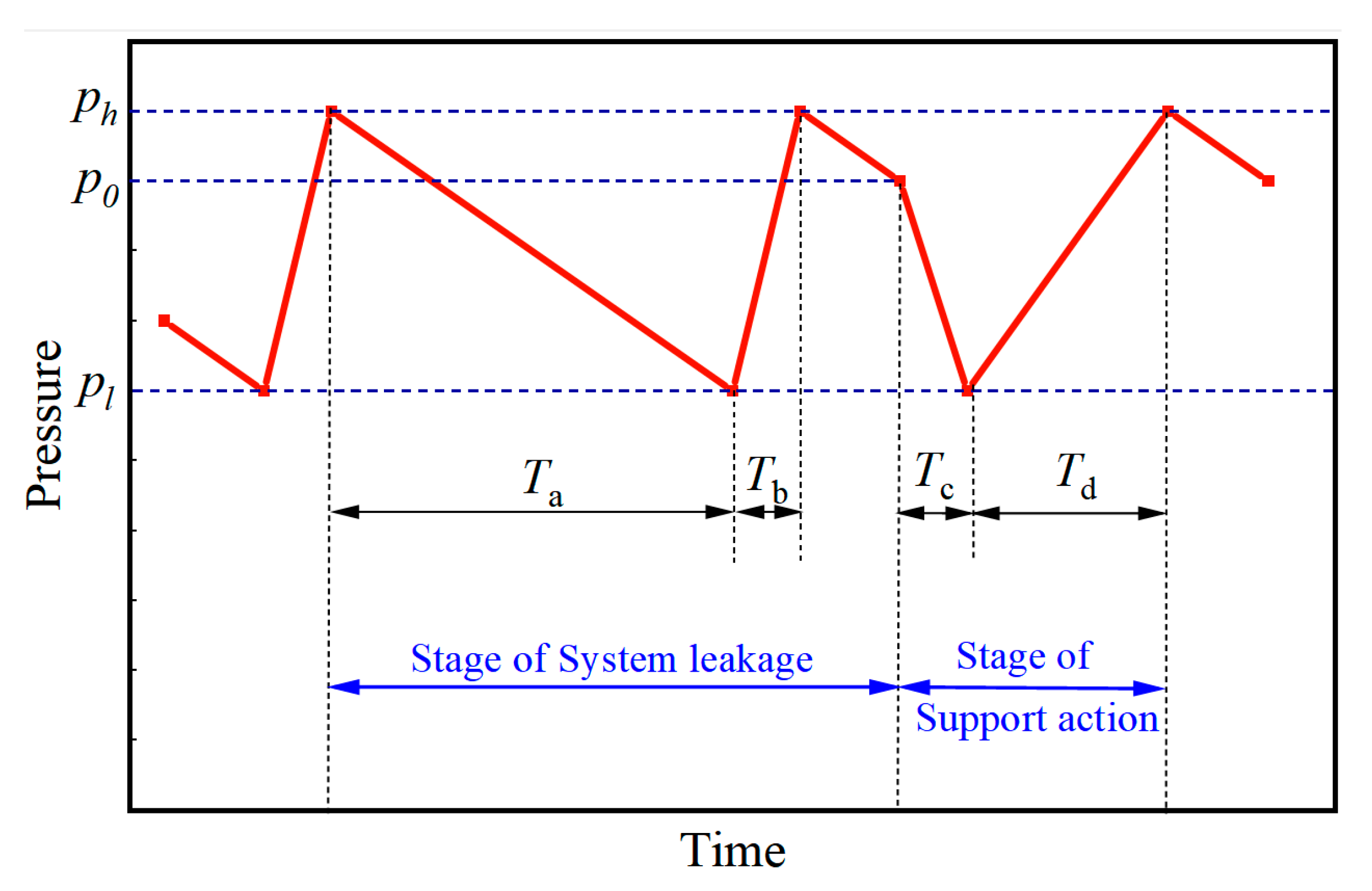
2.3.1. Steady-Pressure Fluid Supply Process
2.3.2. The Concept of Optimal Flow Rate
2.3.3. Optimal Flow Dataset under Different Working Conditions
3. Establishment of a GRNN Model for Predicting the Optimal Dataset of Flow Rates
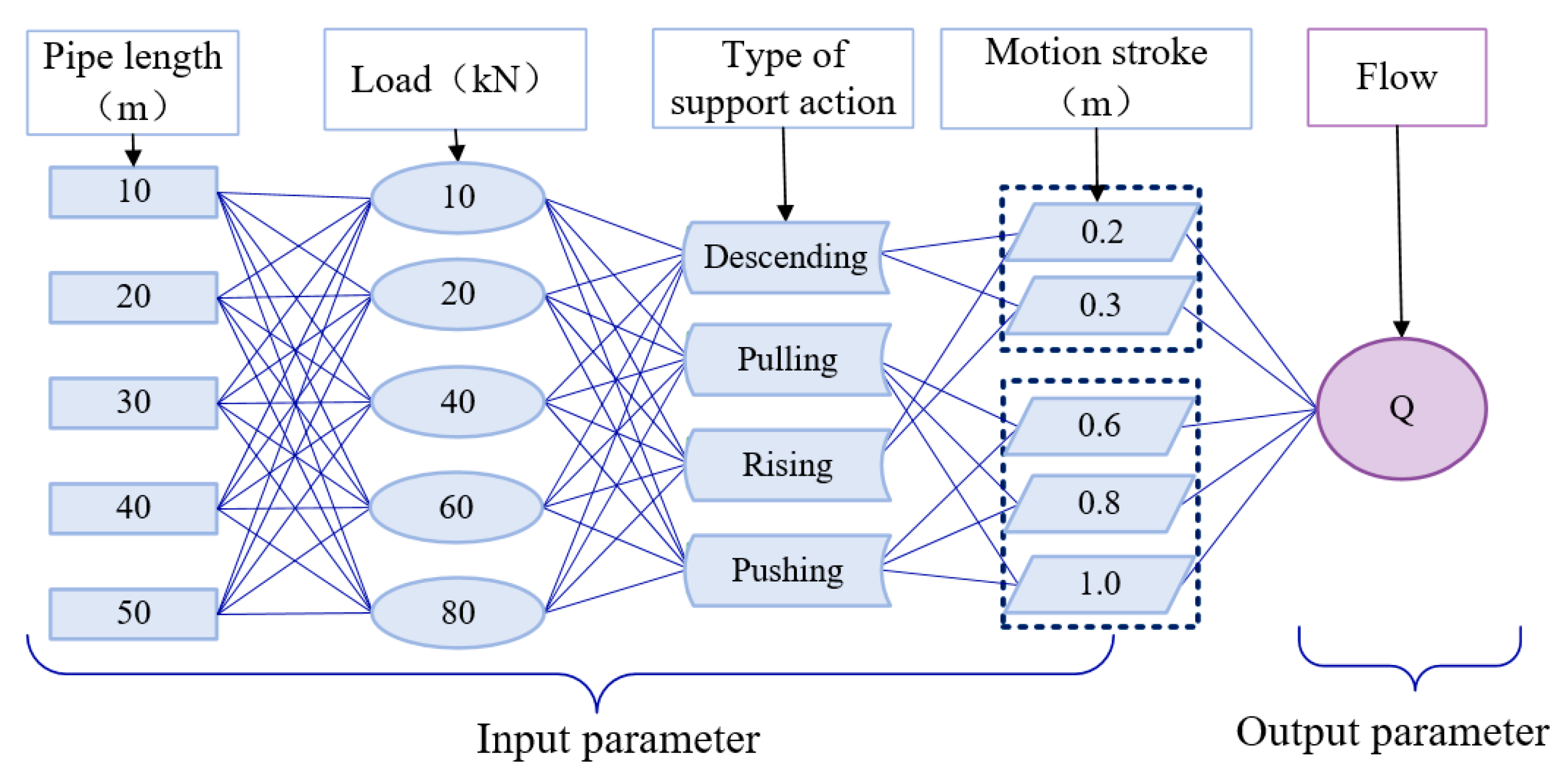
3.1. Input and Output Parameters of the GRNN Model
3.2. Training and Testing of GRNN Models
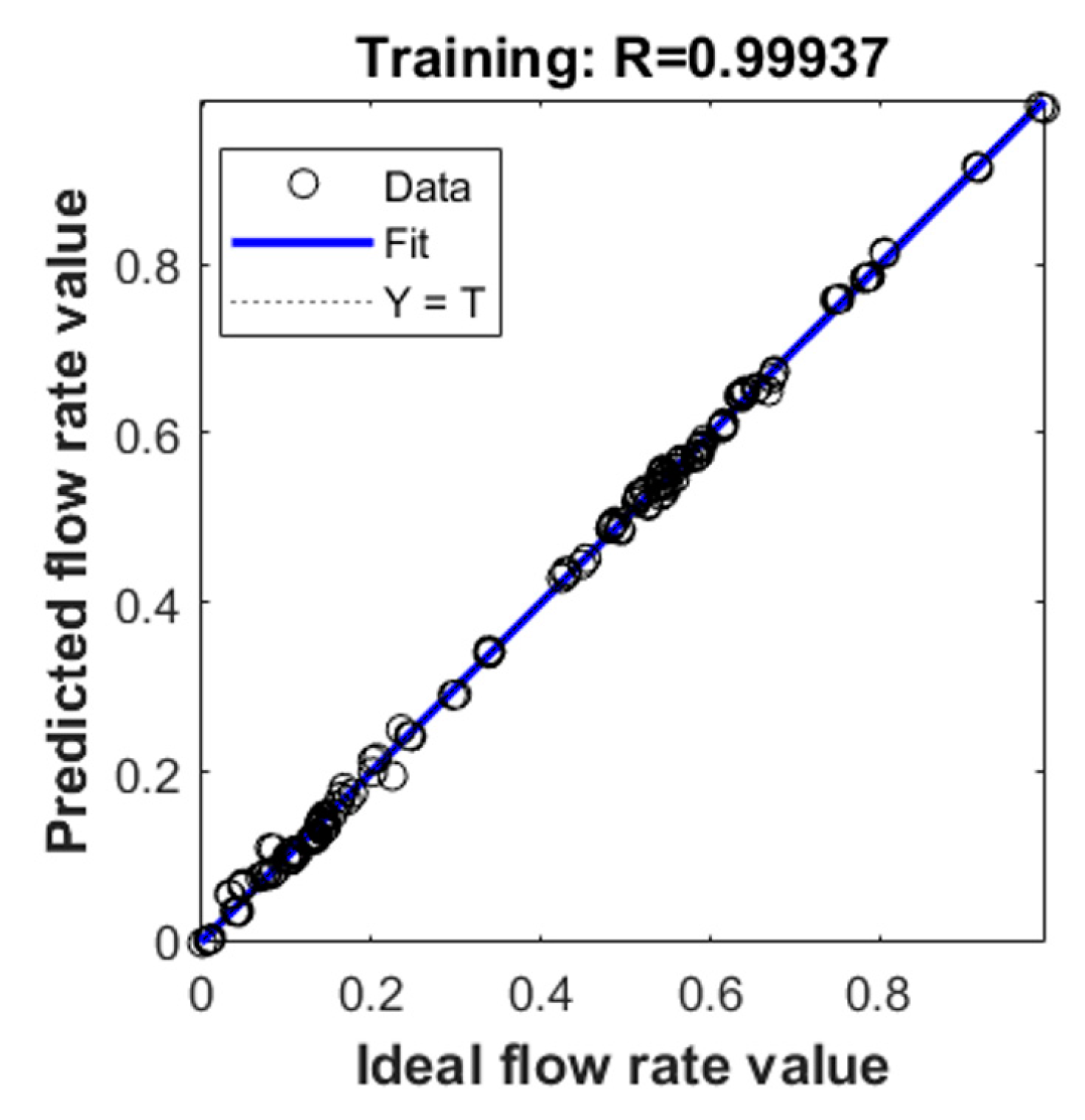
3.2.1. Training of the GRNN Model
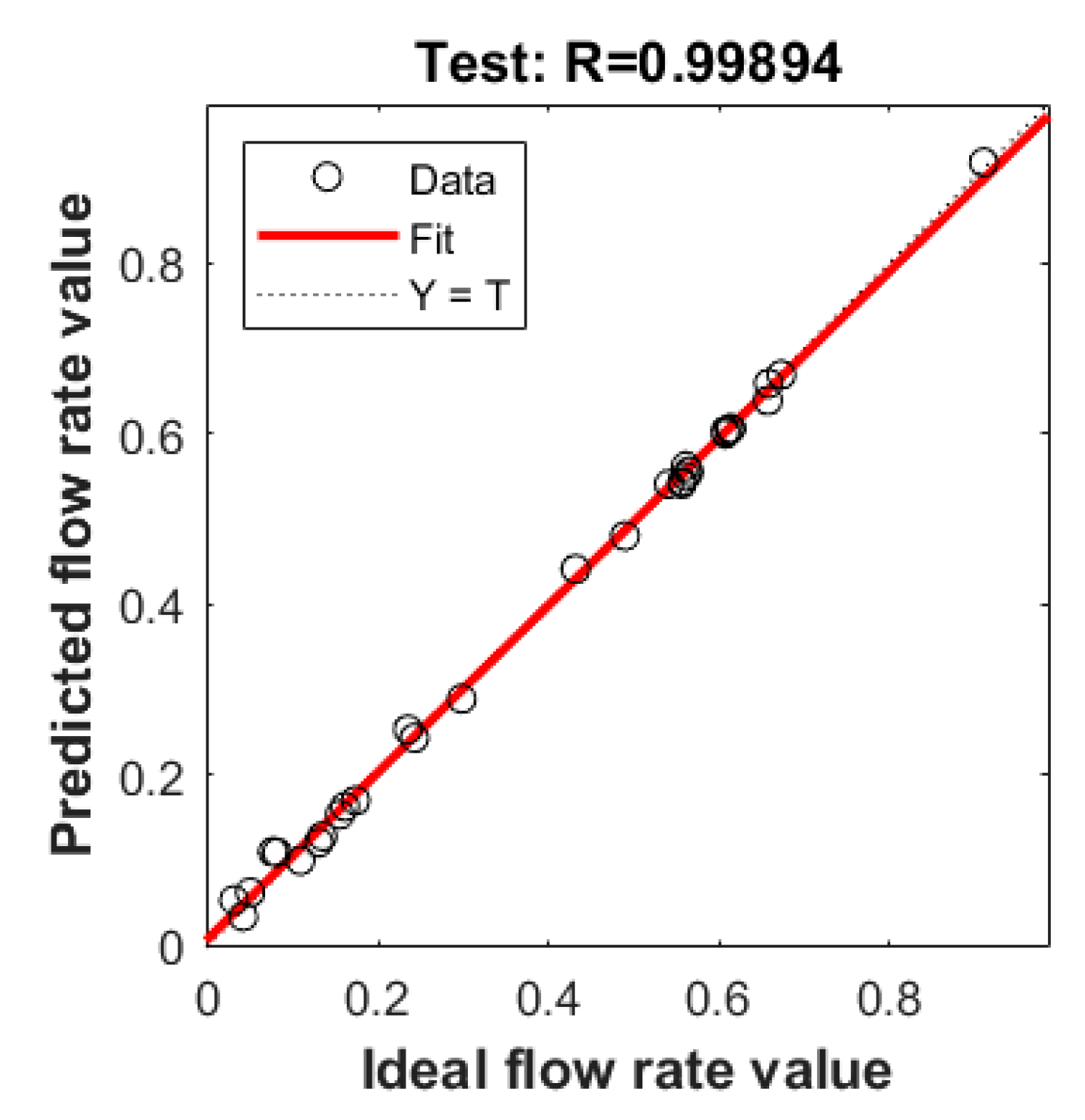
3.2.2. Testing of GRNN Model
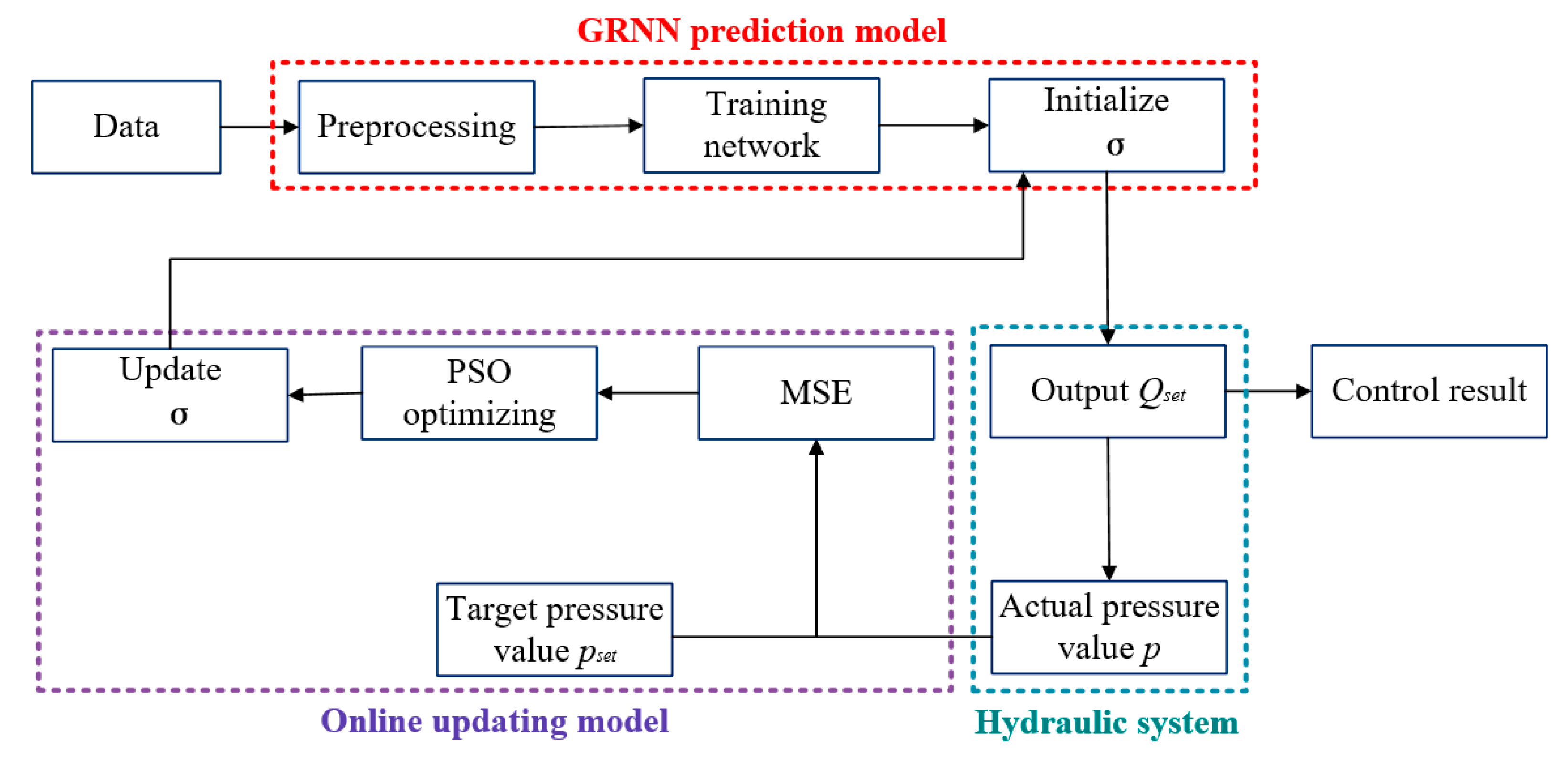
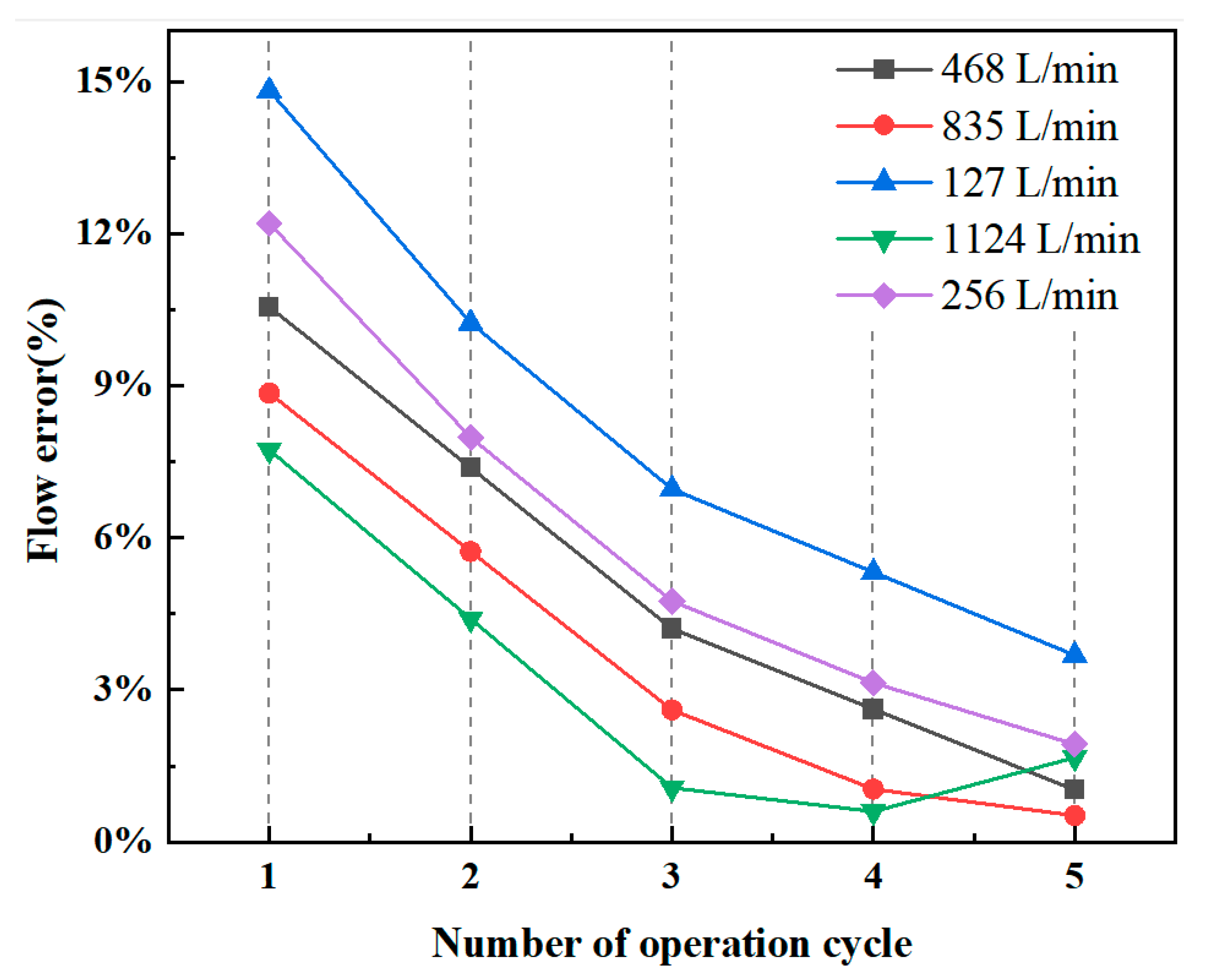
3.3. Online Updating of GRNN Model
4. A Numerical Study on the Development of Steady-Pressure Fluid Supply Method and Its Numerical Implementation
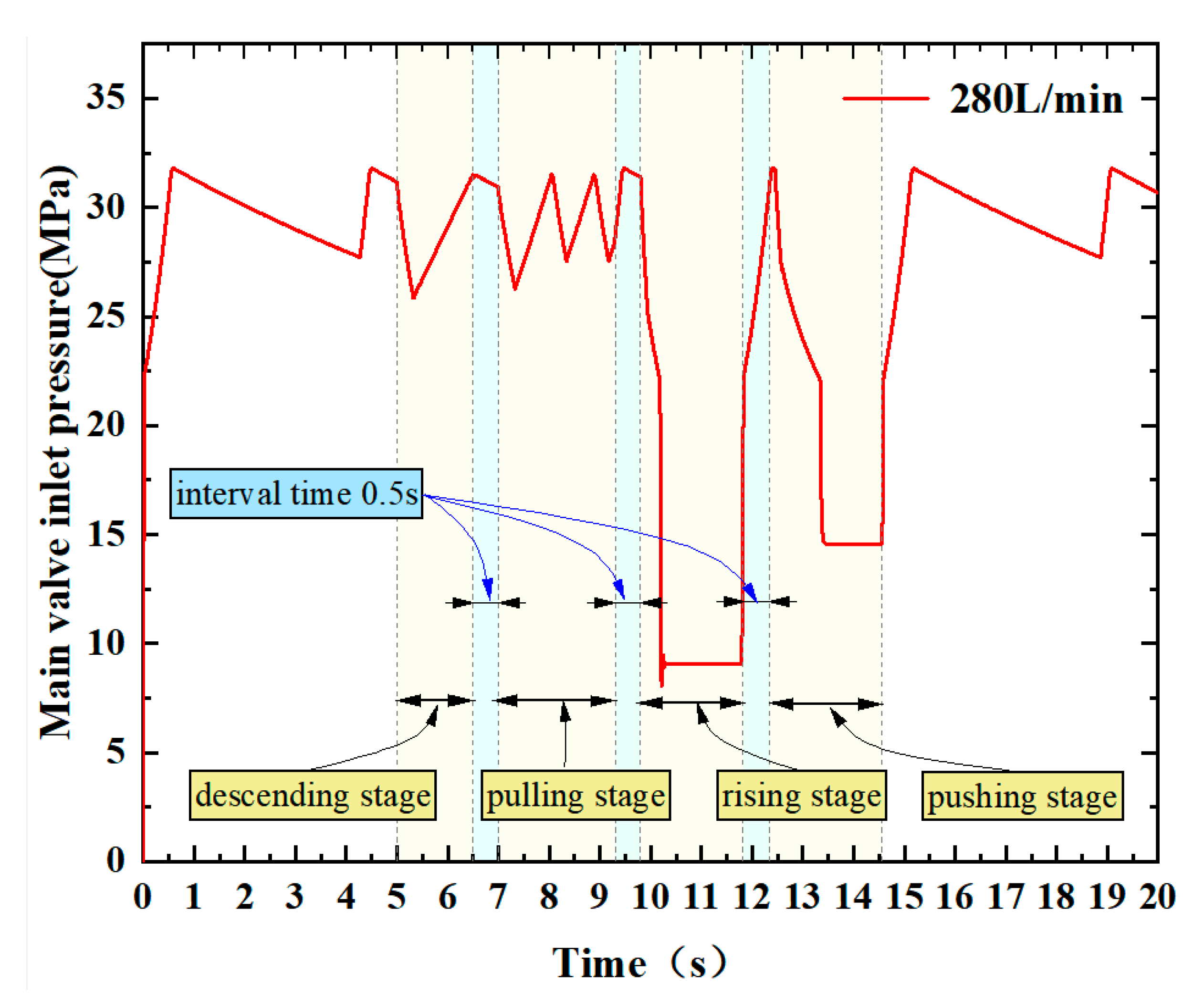
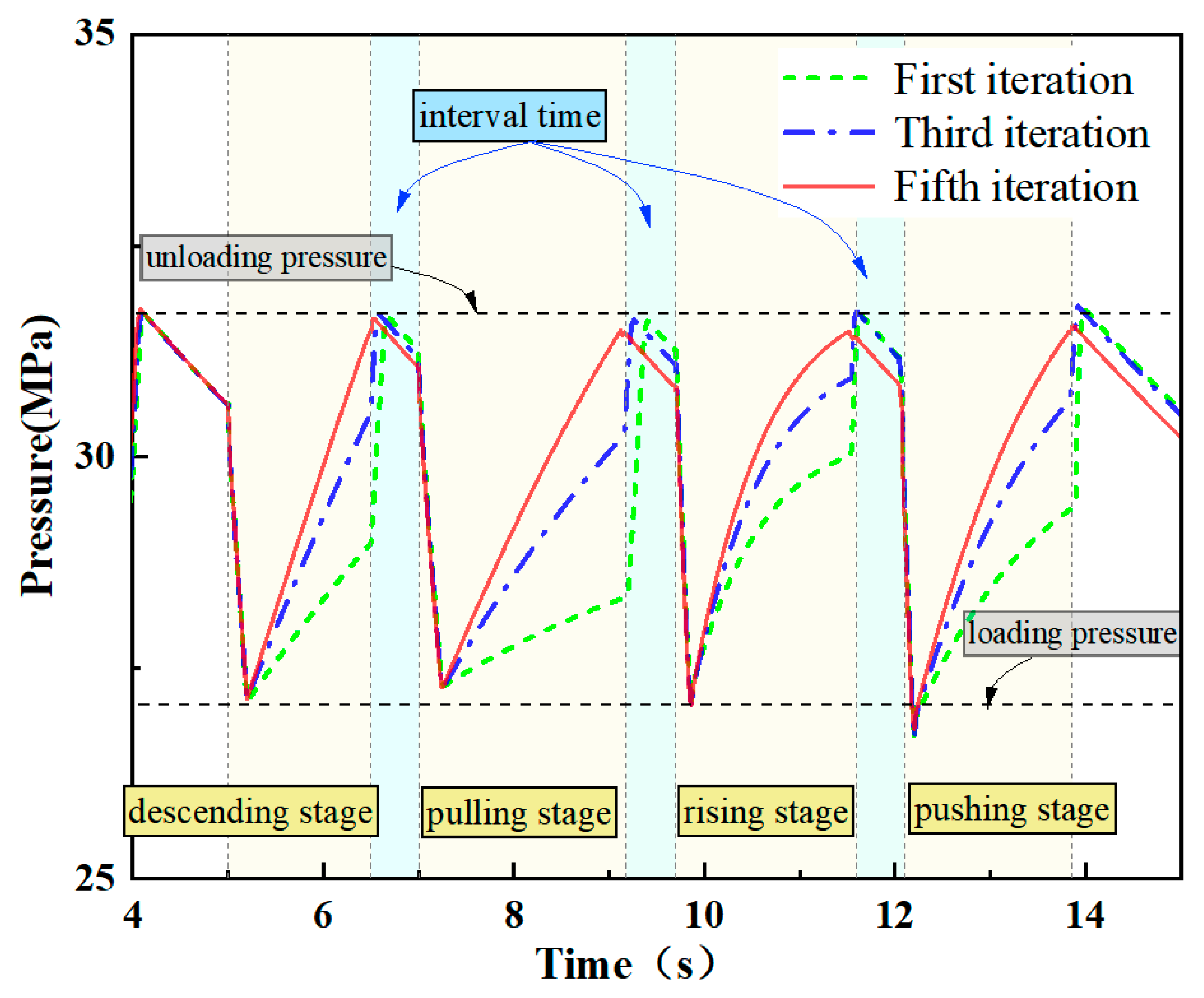
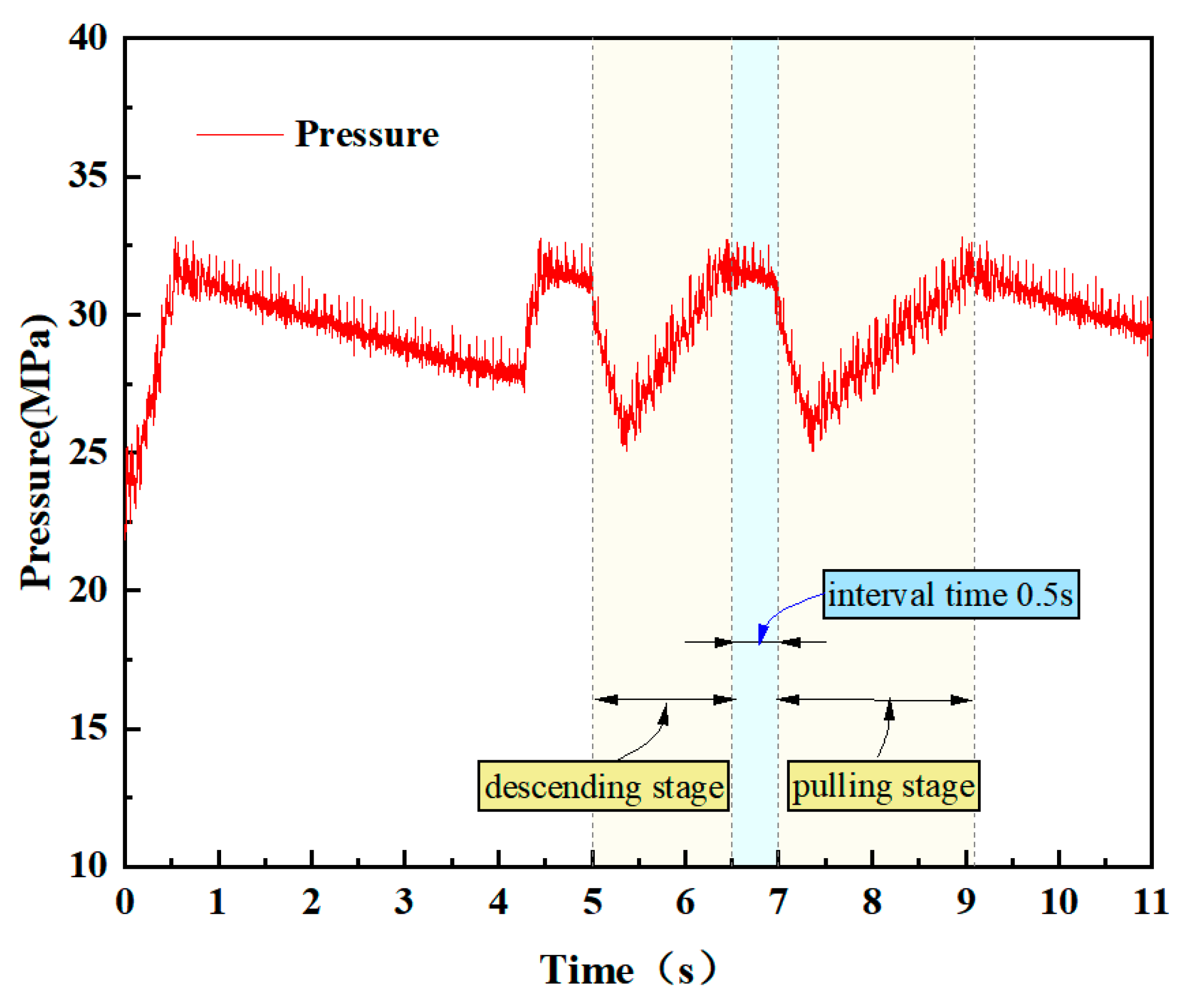
4.1. Single-Cycle Constant Load Steady-Pressure Fluid Supply Control
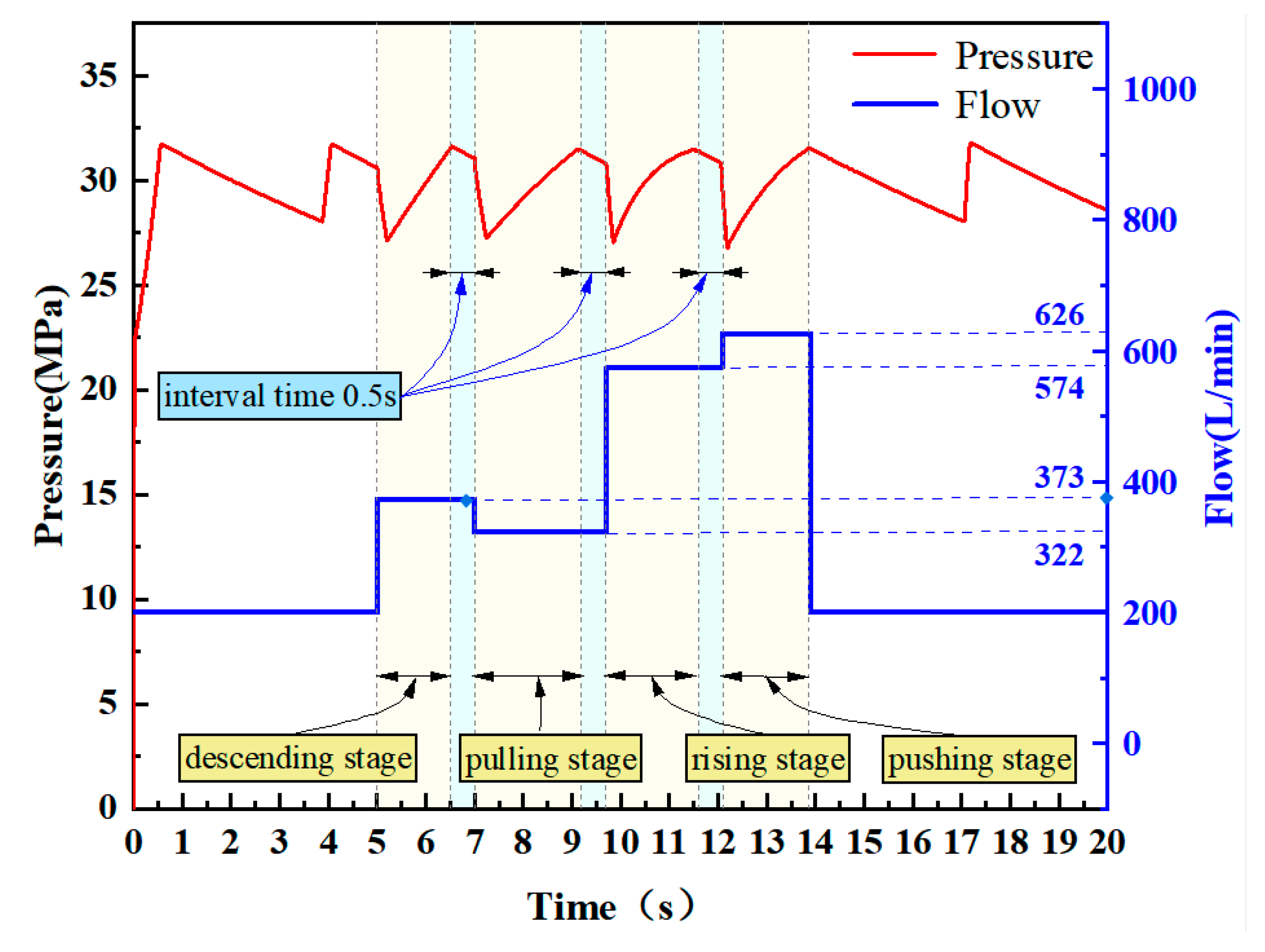
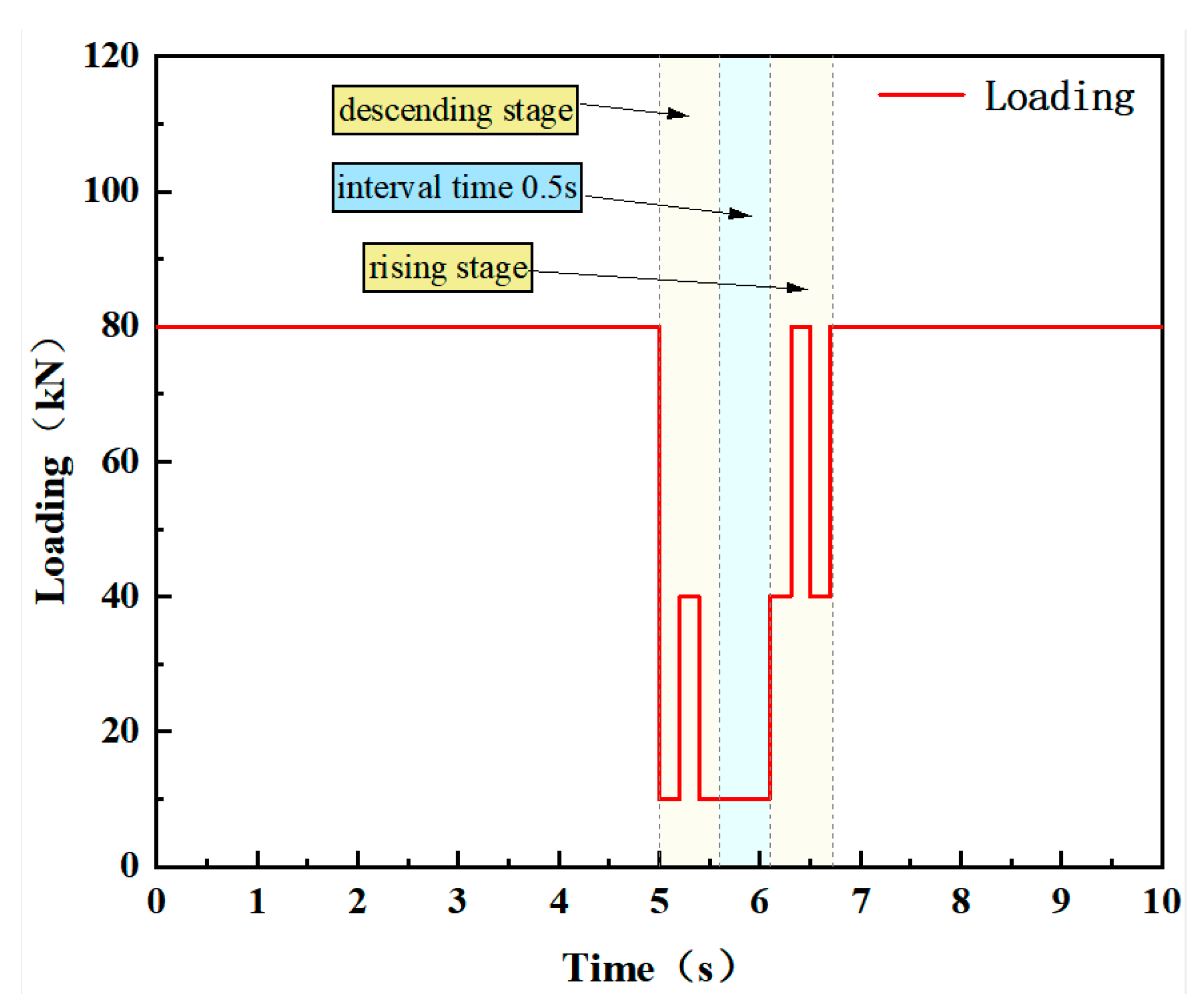
4.2. Online Updating of Steady-Pressure Fluid Supply Control for Variable Load Conditions
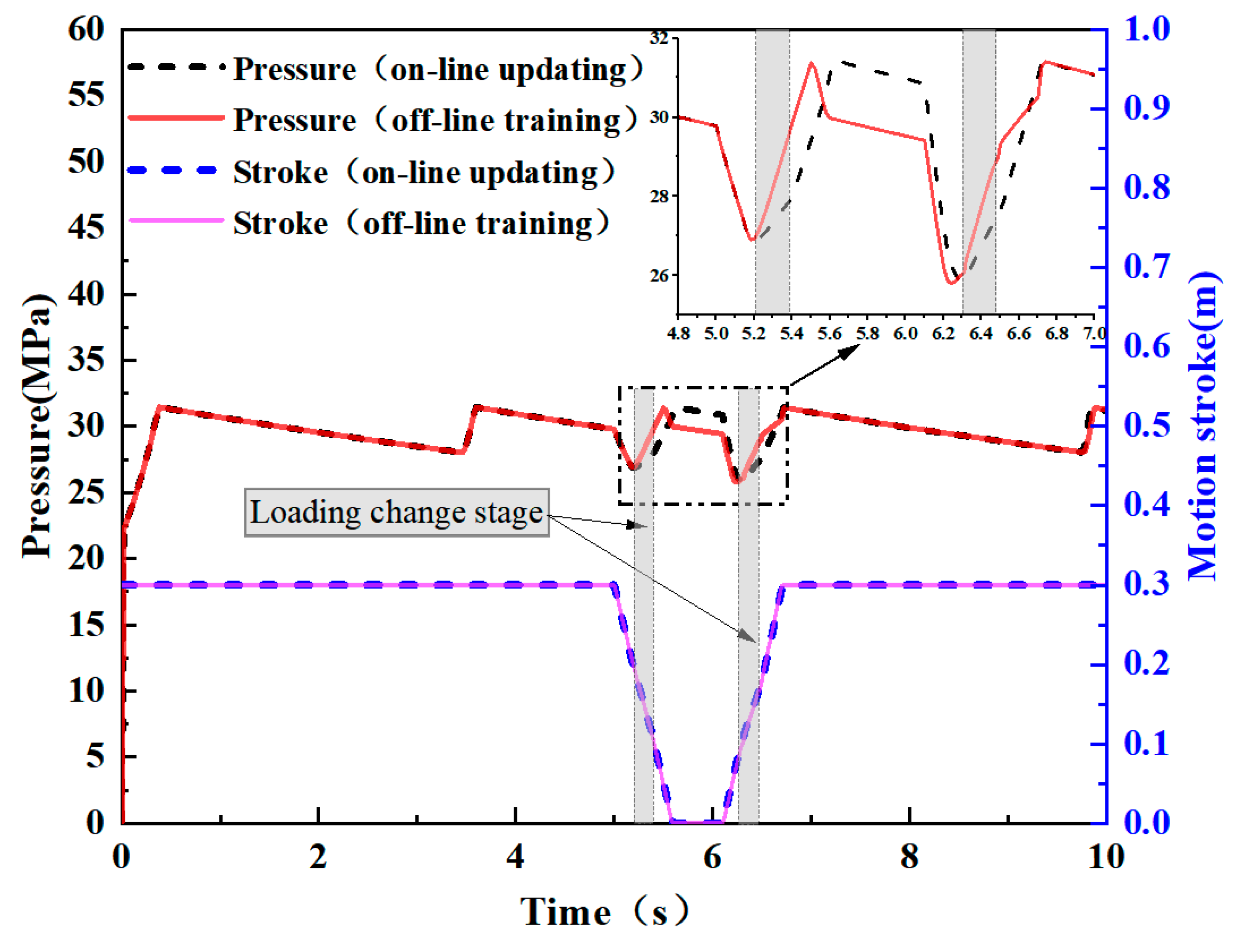
4.3. Online Updating of Steady-Pressure Fluid Supply Control
5. Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, R.; Liu, B.; Wang, D.; Chen, J.; Wang, T.; Zhou, R.; Wang, J.; Zhao, K.; Yu, Y.; Qin, H.; et al. Progress and application of intelligent fluid supply technology in working face. Coal Sci. Technol. 2022, 50, 247–253. [Google Scholar]
- Ran, L. Intelligent fluid supply technology in fully-mechanized coal mining face and its development trend. Coal. Sci. Technol. 2019, 47, 203–207. [Google Scholar]
- Su, J. Research on Constant Pressure Controlsystem in the Emulsion Pump Station; Taiyuan University of Technology: Taiyuan, China, 2012. [Google Scholar]
- Wang, G.; Xu, Y.; Ren, H. Intelligent and ecological coal mining as well as clean utilization technology in China: Review and prospects. Int. J. Min. Sci. Technol. 2019, 29, 161–169. [Google Scholar] [CrossRef]
- Zhou, R.; Li, S.; Wei, W.; Zhang, L.; Wang, W. Study on coupling mechanism of pressure and flow in following hydraulic system of mining face. Coal. Sci. Technol. 2020, 48, 129–136. [Google Scholar]
- Mamcic, S.; Bogdevicius, M. Simulation of dynamic processes in hydraulic accumulators. Transport 2010, 25, 215–221. [Google Scholar] [CrossRef]
- Van de Ven, J.D. Constant pressure hydraulic energy storage through a variable area piston hydraulic accumulator. Appl. Energy 2013, 105, 262–270. [Google Scholar] [CrossRef]
- Li, Z.; Guo, Y.; Lian, Z. Analysis of frequency characteristics of hydraulic support’s liquid pipeline. J. Taiyuan Univ. Technol. 2012, 43, 203–206. [Google Scholar]
- Li, Z. Research and analysis on main supply and return system of hydraulic support for large mining height. Mech. Manag. Dev. 2018, 46–48. [Google Scholar]
- Shu, F.; Wang, Y.; Li, J. Simulate calcultion about pressure loss in hydraulic pipe system of roof supports. Coal. Technol. 2009, 28, 26–28. [Google Scholar]
- Zhao, X. Pressure Loss and Dynamic Characteristics of Emulsion Supply and Return Pipeline for Hydraulic Support; Taiyuan University of Science and Technology: Taiyuan, China, 2018. [Google Scholar]
- Yang, S. Simulation of the unloading pressure and recovery pressure of internal unloading valve for emulsion pump station, Appl. Mech. Mater. 2011, 48–49, 531–536. [Google Scholar]
- Tian, C.; Su, C.; Zhao, W. Application of plc in variable frequency constant pressure control system for mine emulsion pump station. J. Phys. Conf. Ser. 2021, 1982, 012187. [Google Scholar] [CrossRef]
- Qiao, T.; Yan, L. Fuzzy-PID control and application in constant fluid feeding system. Coal. Eng. 2011, 10, 95–97. [Google Scholar]
- Chao, T.; Nan, Q. A pressure control method for emulsion pump station based on elman neural network. Comput. Intell. Neurosci. 2015, 5, 1–8. [Google Scholar] [CrossRef]
- Wang, G.; Li, Z. Optimization design of emulsion pump station using variable frequency driving method in working face with high mining height. Coal Sci. Technol. 2014, 42, 66–69. [Google Scholar]
- Li, R.; Wei, W.S.; Lai, Y.H. Long-distance intelligent liquid supply for coal mining faces based on liquid demand prediction. J. Phys. Conf. Ser. 2023, 2561, 012018. [Google Scholar] [CrossRef]
- Ma, C.; Xu, B.; Liu, H. The Optimization of the Constant Flow Parallel Micropump Using RBF Neural Network. In Proceedings of the 2021 6th International Conference on Robotics and Automation Engineering (ICRAE), Guangzhou, China, 19–22 November 2021; pp. 185–195. [Google Scholar]
- Umrao, R.; Chaturvedi, D.K. A novel fuzzy control approach for load frequency control. In Recent Advancements in System Modelling Applications, Proceedings of National Systems Conference 2012; Springer: New Delhi, India, 2013; pp. 239–247. [Google Scholar]
- Tian, C.; Wei, X.W.; Zheng, Y. The intelligent control of emulsion pump station. J. Phys. Conf. Ser. 2021, 1881, 022044. [Google Scholar] [CrossRef]
- Tian, C.; Wei, X.W.; Yang, C.; Su, C. Optimization Technology of frequency conversion constant pressure control system of mine emulsion pump station in electrical engineering and automation Specialty. Adv. Civ. Eng. 2021, 2021, 5569994. [Google Scholar] [CrossRef]
- Si, M.; Wu, B.; Wang, Z. Research on large flow intelligent liquid supply system in fully mechanized working face. J. Mine Autom. 2022, 48, 66–72. [Google Scholar]
- Peng, Y.; Kou, Z.; Wu, J.; Luo, J.; Liu, H.; Zhang, B. Research on a Pressure Control Method for a Liquid Supply System Based on Online Updating of a Radial Basis Function Neural Network. Processes 2023, 12, 57. [Google Scholar] [CrossRef]
- Fu, X. Research on Intelligent Hydraulic Fluid Supply Theory and Technology for Adapting Supports Operation; Taiyuan University of Technology: Taiyuan, China, 2017. [Google Scholar]
- Sun, Y.; Xue, H.; Wang, W.; Wu, S.; Wu, Y.; Hong, Y.; Deng, S. Development of an optimal control method of chilled water temperature for constant-speed air-cooled water chiller air conditioning systems. Appl. Therm. Eng. 2020, 180, 115802. [Google Scholar] [CrossRef]
- Pławiak, P. An estimation of the state of consumption of a positive displacement pump based on dynamic pressure or vibrations using neural networks. Neurocomputing 2014, 144, 471–483. [Google Scholar] [CrossRef]
- Bukhari, A.H.; Raja, M.A.Z.; Alquhayz, H.; Abdalla, M.Z.; Alhagyan, M.; Gargouri, A.; Shoaib, M. Design of intelligent hybrid NAR-GRNN paradigm for fractional order VDP chaotic system in cardiac pacemaker with relaxation oscillator. Chaos Solitons Fractals 2023, 175, 114047. [Google Scholar] [CrossRef]
- Lopez-Sanchez, I.; Rossomando, F.; Pérez-Alcocer, R.; Soria, C.; Carelli, R.; Moreno-Valenzuela, J. Adaptive trajectory tracking control for quadrotors with disturbances by using generalized regression neural networks. Neurocomputing 2021, 460, 243–255. [Google Scholar] [CrossRef]
- Li, C.; Bovik, A.C.; Wu, X. Blind image quality assessment using a general regression neural network. IEEE Trans. Neural. Netw. 2011, 22, 793–799. [Google Scholar] [PubMed]
- Aengchuan, P.; Wiangkham, A.; Klinkaew, N.; Theinnoi, K.; Sukjit, E. Prediction of the influence of castor oil–ethanol–diesel blends on single-cylinder diesel engine characteristics using generalized regression neural networks (GRNNs). Energy Rep. 2022, 8, 38–47. [Google Scholar] [CrossRef]
- Iban, M.C.; Şentürk, E. Machine learning regression models for prediction of multiple ionospheric parameters. Adv. Space Res. 2022, 69, 1319–1334. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef]
- Xia, C.; Lei, B.; Wang, H.; Li, J. GRNN short-term load forecasting model and virtual instrument design. Energy Procedia 2011, 13, 9150–9158. [Google Scholar]

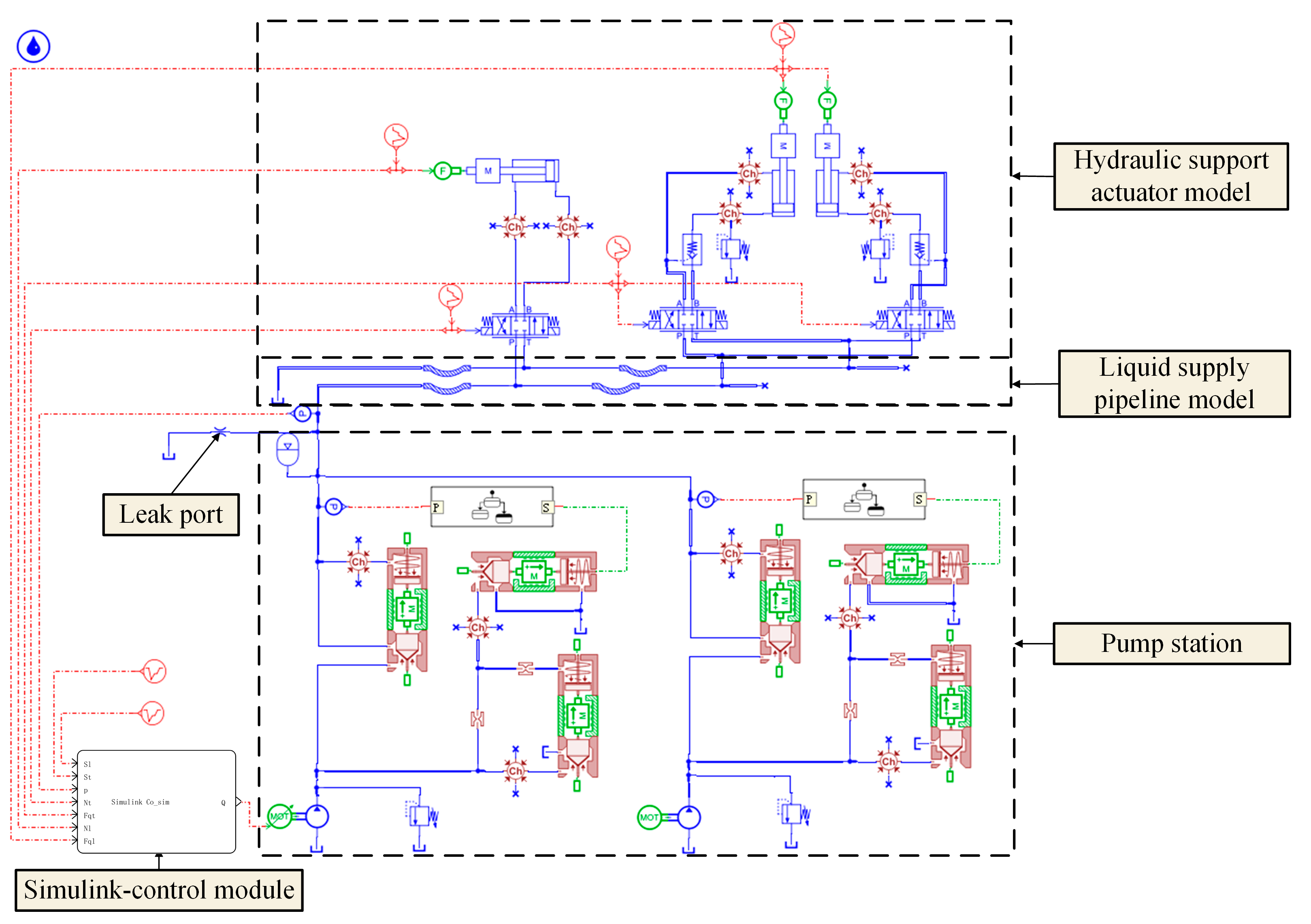

| Name | Parameter | Value | Units |
|---|---|---|---|
| Emulsion | Density | 998 | kg/m3 |
| Emulsion pump | Flow | 200/80 | L/min |
| Energy accumulator | Capacity | 20 | L |
| Loading cylinder | amount | 3 | / |
| Cylinder/rod diameter | 160/105 | mm | |
| Column cylinder | amount | 2 | / |
| Cylinder/rod diameter | 110/80 | mm | |
| Pushing cylinder | amount | 1 | / |
| Cylinder/rod diameter | 110/80 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Kou, Z.; Wu, J.; Hou, T.; Peng, Y.; Zhang, B. A Steady-Pressure Control Method for Emulsion Pump Station Based on Online Updating of Optimal Flow Rate. Actuators 2024, 13, 247. https://doi.org/10.3390/act13070247
Xu P, Kou Z, Wu J, Hou T, Peng Y, Zhang B. A Steady-Pressure Control Method for Emulsion Pump Station Based on Online Updating of Optimal Flow Rate. Actuators. 2024; 13(7):247. https://doi.org/10.3390/act13070247
Chicago/Turabian StyleXu, Peng, Ziming Kou, Juan Wu, Tengyan Hou, Yanwei Peng, and Buwen Zhang. 2024. "A Steady-Pressure Control Method for Emulsion Pump Station Based on Online Updating of Optimal Flow Rate" Actuators 13, no. 7: 247. https://doi.org/10.3390/act13070247
APA StyleXu, P., Kou, Z., Wu, J., Hou, T., Peng, Y., & Zhang, B. (2024). A Steady-Pressure Control Method for Emulsion Pump Station Based on Online Updating of Optimal Flow Rate. Actuators, 13(7), 247. https://doi.org/10.3390/act13070247








