Abstract
Aiming to solve the problem that the significant error between the actual joint torque and the calculated joint torque of a welding robot leads to the vibration of the end-effector, which in turn affects the stability of the end-effector, this paper proposes a identification algorithm based on the Weighted Least Squares Genetic Algorithm (WLS-GA) to construct and solve the dynamical model to obtain the accurate dynamical parameters. Firstly, a linear model of welding robot dynamics is derived. The fifth-order optimal Fourier series excitation trajectory is designed to collect experimental data such as joint torque. Then, a rough solution of the parameters to be recognized is obtained by solving the dynamics model through the Weighted Least Squares (WLS) method, the search space is determined based on the rough solution, and the optimal solution is obtained by using the Genetic Algorithm (GA) to perform a quadratic search in the search space. Finally, the identification data obtained from the algorithm is analyzed and compared with the experimental data. The results show that the error between the identification data obtained using the WLS-GA identification algorithm and the experimental data is relatively small. The results show that the identification data obtained using the WLS-GA identification algorithm have less error than the experimental data, taking the Root Mean Square (RMS) value of the joint torque error obtained using the weighted least squares algorithm as a criterion. The accuracy of the WLS-GA identification algorithm can be improved by up to 66.85% compared with that of the weighted least squares algorithm and by up to 78.0% compared with that of the Ordinary Least Squares (OLS) algorithm. In summary, the WLS-GA identification algorithm can accurately identify the dynamic parameters of the welding robot and more accurately construct a dynamic model to solve the effect of joint torque error on the control characteristics of the welding robot. It can improve the stability of the end-effector of the welding robot to ensure the quality of the automobile body and beam welding and welding speed.
1. Introduction
A welding robot is a multi-joint robotic arm for industrial applications, widely used in automotive manufacturing, the electronics industry, home appliance manufacturing, and other fields. In automobile manufacturing, the welding quality of the car body and beam directly affects the car’s service life, and it is increasingly important to improve the stability of the end-effector of the welding robot through more accurate parameter identification.
Perrusquía et al. disclosed a Closed-loop Input Error (CLIE) algorithm for the online identification of robot manipulators with another parameter identification algorithm based on the composite updating method, and both algorithms improved the parameter convergence of the updating rules, the robustness and the stability of the estimation of the model related to the closed-loop dynamics [1]. Ren et al. proposed an improved strategy based on an improved fuzzy adaptive algorithm, and the research results show that the control strategy of the improved fuzzy algorithm has significant advantages in energy control. Combining it with a wrist rehabilitation robot can save energy and consume less [2]. Zhao et al. proposed a dynamic identification and optimization algorithm for composite constraints weight sequences, with significant improvement in kinematic performance and machining accuracy, which improves the machining quality of the robot and lays the foundation of optimization in robotics manufacturing [3]. Li et al. proposed a Virtual Repulsive Potential Field (VRPF) algorithm considering mechanical and kinematic constraints, and the proposed continuous-domain VRPF algorithm has advantages in terms of milling quality and computational cost [4]. Urrea et al. studied and discussed the design of different parameter identification methods applied to robotic systems and demonstrated that it is possible to adequately select different identification methods for obtaining parameters characterizing the dynamics of an industrial robot. At the same time, these values of the parameters underlying the robot promote the design of new control methods [5]. Tang et al. proposed an identification algorithm based on weighted least squares and random weighted particle swarm optimization (WLS-RWPSO), which helps to improve the accuracy and stability of trajectory control of collaborative robots [6]. Dong et al. proposed an online parametric estimation algorithm under the framework of the least squares algorithm and analyzed the convergence of the algorithm. Numerical simulation and experimental test results verify the superiority and advantages of the algorithm and fault-tolerant control strategy, which can provide good references and guidance for other complex systems in theoretical research and engineering applications [7]. Zhang et al. used a hybrid whale optimization algorithm and genetic algorithm (WOA-GA) to identify the dynamic parameters of six robotic joints. The results showed that the average matching degree of the estimated torque based on WOA-GA could reach 93.86%, 0.4–2% higher than the other optimization algorithms (WOA, GA, and PSO-GA) [8]. Al-Dabbagh et al. estimated the center of gravity parameters of the single-jointed CRS A465 robot arm dynamics using the fuzzy adaptive differential evolution algorithm (FADE). Experimental results show that the fuzzy adaptive DE performs better than ordinary least squares and standard DE with fixed parameters [9]. Zutven et al. propose an algorithm that automatically converts a system model into least-order regression form. The algorithm can be applied to general Euler–Lagrange systems and not only to specific kinematic configurations in existing methods [10]. West et al. developed a genetic algorithm to solve the problem of systematically identifying output errors for a specific joint so that the joint parameters converge to the desired set of parameters with acceptable accuracy. The developed GA algorithm can estimate the parameters of the dynamic model with reasonable accuracy, and the model’s output is very close to the simulated output [11]. Ali et al. proposed a novel moment of inertia estimation algorithm that is capable of estimating the moment of inertia of the AFC-controlled robots and also developed a new proportional-differential active force controller, where the combination of the algorithm and the controller can enable the Wheeled Mobile Robot (WMR) robot to be operated with a high level of accuracy. Combining the algorithm and controller enables the WMR robot to move robustly in constrained environments [12]. Joseph et al. comprehensively reviewed the state-of-the-art and classical methods for tuning Proportional Integral Derivative (PID) control parameters. They detailed the PID parameter tuning process, applications, formulations, and challenges encountered in meta-heuristic optimization methods [13]. Son et al. proposed a novel control system combining an adaptive feed-forward neural controller and a PID controller, identifying all nonlinear features and optimizing them to improve accuracy and eliminate steady-state errors in joint position control [14]. Yusof et al., a recurrent neural network combined with a Kalman filter capable of recognizing nonlinear terms can be used to identify the dynamic conditions of a robotic manipulator. Experimental validation on a dual-rotor helicopter evaluated the steady-state performance of the method for control applications [15] West. et al. proposed a new method for representing the state-dependent gains that integrates input signal calibration, system identification, and nonlinear control system design steps, allowing for state-dependent parameter (SDP) model identification for joint angle control [16]. Mendes et al. identify T-S fuzzy models from input–output data to approximate unknown nonlinear processes, a co-evolutionary Hierarchical Genetic Algorithm (HGA) approach to determine the structure and parameters of the model; it is shown that the proposed approach has a faster response and better results compared to the identification results obtained using the hierarchical genetic algorithm [17].
Alves et al. introduced a method to linearly parameterize the model, enabling the recursive least square (RLS) algorithm to determine the system parameters. The results show that the model response conforms to the dynamics of the WMR even under non-ideal mechanical conditions [18]. Agand et al. proposed a fuzzy modeling approach for modeling nonlinear control processes based on the Takagi–Sugeno (T-S) fuzzy model, combined with a genetic algorithm and recursive least square fuzzy modeling approach for nonlinear control process modeling; experimental results show that the proposed approach provides better modeling results compared to the Takagi–Sugeno fuzzy modeling technique and linear modeling approach [19]. Adánez. et al. proposed a new approach for the Takagi–Sugeno (T-S) fuzzy modeling based on multidimensional dependency functions (MDMFs); a nonlinear multivariate system was selected for validation, and the results showed that the method has a minor identification error compared to the one-dimensional dependency function fuzzy inference approach [20]. Marie et al. proposed the two modeling approaches based on analytical parametric modeling and the Takagi–Sugeno fuzzy inference system, respectively, for improving the static attitude accuracy of industrial robots involved in machining, molding or assembly applications [21].
In the welding process of the body and beam, the welding robot end-effector must maintain a stable state to ensure the welding quality and efficiency. However, because of the welding robot’s actual joint torque and the calculation of the joint torque, there is a significant error between the joint torque, resulting in an unstable end-joint attitude control and vibration, thus affecting the stability of the welding robot end-effector. Therefore, this paper proposes a WLS-GA identification algorithm to construct and solve the dynamics model to obtain accurate dynamics parameters. The WLS-GA identification algorithm combines a genetic algorithm and weighted least squares, which can improve the algorithm’s robustness and the global search ability, and it can be well suited for complex data fitting and parameter optimization problems. Firstly, the linear model of welding robot dynamics is derived. The fifth-order optimal Fourier series excitation trajectory is designed to collect experimental data such as joint torque. Then, the rough solution of the parameters to be recognized is obtained by solving the dynamics model using the weighted least squares method. Then, the search space is determined based on the rough solution. The optimal solution is obtained using the genetic algorithm to perform a quadratic search in the search space and solve the optimal solution. Then, finally, the recognized data obtained from the algorithm are analyzed and compared with the experimental data; the identification process is shown in Figure 1. The results show that the identification data of the WLS-GA algorithm matches the experimental data well. The WLS-GA algorithm can accurately recognize the dynamical parameters of the welding robot, construct the dynamical model more accurately to solve the influence of the joint torque error on the control characteristics of the welding robot and ensure that the welding robot is capable of adapting to the force and torque requirements of a specific task, to ensure the stability and accuracy of the welding.
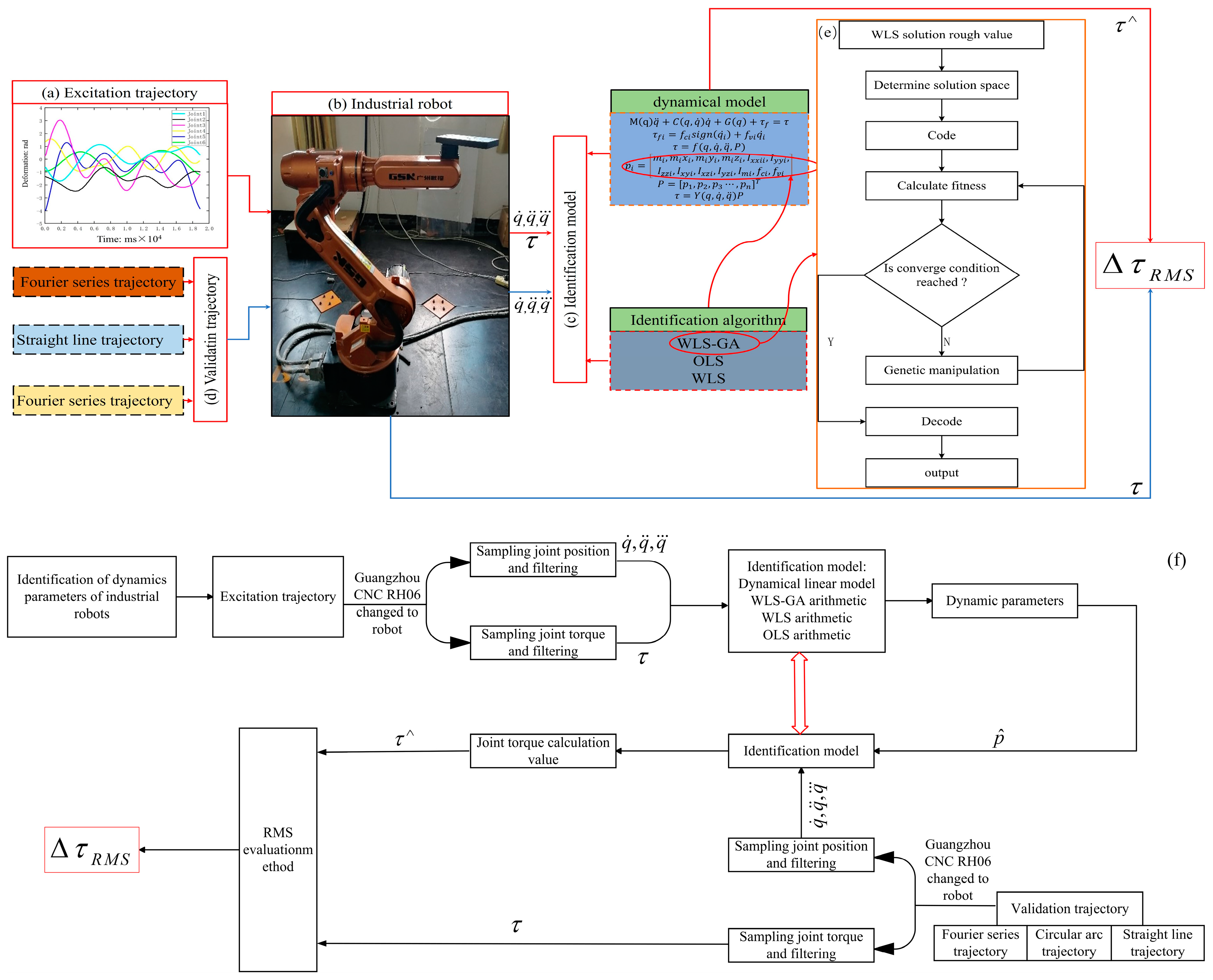
Figure 1.
Identification process: (a) excitation trajectory; (b) welding robot; (c) identification model; (d) validation trajectory; (e) WLS-GA identification algorithm; (f) specific identification process.
2. Constructing Dynamical Models
Using Lagrange’s equations, the dynamics equations of an n-degree-of-freedom jointed tandem robot can be established as shown in Equation (1):
where is a positive definite inertia matrix, is the centrifugal force and Coriolis force matrix, is the gravity vector, is the joint friction torque vector, is the joint driving torque vector, is the joint angle vector, is the joint angular velocity vector, and is the joint angular acceleration vector.
The joint friction model is a complex nonlinear function, which is challenging to model accurately. Considering the cost, efficiency, accuracy, and other factors, only Coulomb and viscous friction are considered in the identification. The dynamical equation for the friction moment of joint i is:
where is the frictional moment at joint i, i.e., the ith element of ; is the coulomb friction coefficient at joint i; and is the coefficient of viscous friction at joint i. Equation (2) can be rewritten as Equation (3)
The joint moment in Equation (3) is a function of the joint angle, joint angular velocity, joint angular acceleration, and the dynamical parameters, where the dynamics parameter of the ith rod is:
Among them, is the mass of the connecting rod i; , , are the connecting rods, i is the coordinate of the centroid of i in the coordinate system i; , , is a connecting rod i inertia moment in the ith coordinate system; , , is the inertia product of the connecting rod i to x and y axes in the ith coordinate system, , is the same; is the equivalent moment of inertia of the motor i.
The dynamical parameter P is the vector for:
Extracting the dynamical parameter P in Equation (3), there is a linear relationship between the joint moments and the dynamical parameters as shown in Equation (6):
3. WLS-GA Identification Algorithm
3.1. Algorithm Flow
This paper used the weighted least squares genetic algorithm to identify the unknown parameters in Equation (4); firstly, it used the weighted least squares method to generate a rough solution to obtain the range of the solution space, and then it used the genetic algorithm to find the exact solution. The flow of the algorithm is shown in Figure 1e.
3.2. Algorithmic Components
The weighted least squares algorithm is a statistical method used to fit data by assigning weights to each data point to make the fit more realistic. In weighted least squares, the weighted residual sum of squares is usually minimized to determine the model parameters. Suppose there are n data points (xi, yi), where xi is the independent variable and yi is the dependent variable. We can define the weights wi for each data point for weighted least squares and then solve for the model parameters by minimizing the sum of squares of the weighted residuals. The goal of the weighted least squares is to find a set of model parameters β such that the weighted residual sum of squares is minimized:
where f(xi, β) is the model’s predicted value for xi.
Standard weighted least squares methods include weighted linear regression and weighted nonlinear regression. In practical applications, the appropriate weighting function and weight-setting method can be selected according to the characteristics and needs of the data.
However, weighted least squares is usually a local optimization method, which is easy to fall into the local optimal solution. By introducing the global search capability of the genetic algorithm, the solution space can be better explored, which helps to find the global optimal solution. The weighted least squares method may be limited by the initial value selection or local search capability when dealing with complex multimodal problems. Genetic algorithms can effectively deal with such issues and help to jump out of the local optimal solution and find a better solution through the diversity and randomness of the population. In some complex models, the optimization of parameters may require the consideration of multiple constraints or objective functions, and weighted least squares may need help to deal with this complexity directly. By introducing a genetic algorithm, the parameter optimization problem can be handled more flexibly using simultaneously considering multiple objectives and constraints. The genetic algorithm’s fitness function is more flexible, and the fitness function can be designed according to the specific problem’s characteristics to better reflect the problem’s optimization objective. Therefore, combining genetic algorithms with weighted least squares can make up for some of the shortcomings of weighted least squares in global search, complex multimodal problems, parameter optimization, and fitness function design and improve the effectiveness and efficiency of optimization. This combination can be better applied to complex data fitting and parameter optimization problems to improve the algorithm’s robustness and global search ability.
The WLS-GA algorithm treats each to-be-identified dynamical parameter of the welding robot as a base pair, and all to-be-identified parameters form a segment of a gene, representing a possible solution. According to the coding principle, all the parameters to be recognized are composed of individuals. The optimization calculation of parameter identification is carried out by collecting each robot joint’s torque and angular position data as training samples. When the constraints are satisfied, the accurate dynamics parameters are obtained. The algorithm consists of the following parts.
3.2.1. Use Least Squares to Obtain the Range of the Solution Space
This paper used the weighted least squares method to solve Equation (6) to obtain a rough solution for the dynamical parameters to be identified, and the extent of the solution space is determined based on the rough solution to prepare for further identification.
3.2.2. Composition of the Initial Antibody
The weighted least squares solution’s range was used as the initial population’s generating region to improve the identification effect. Several initial individuals are randomly generated in the generating region, and all the initial individuals are combined to form the initial population. Using this way to create the population enables the generated individuals to be evenly distributed in the region to be solved to ensure the diversity of individuals.
3.2.3. Coding
Coding represents the problem’s variables as ordered strings of numbers from 0 to 1 because population genetics and evolution are all about “chromosomes”. The solution vector of the problem is a “chromosome”, in which an element of the problem’s solution is called a gene. Coding is critical in linking a practical problem’s solution to a biological evolution model.
3.2.4. Adaptation Evaluation
In the process of evolution, nature severely tests organisms by climate, food, sunlight, and water, to name a few, which are all-natural selections. In short, the organism needs to be evaluated to show the direction of biological evolution. According to the optimization objective of the actual problem, such genetic algorithms also needed an evaluation function called the fitness function, which determined the choice of the fitness function. The fitness function is generally transformed from the objective function, and Equation (7) shows the fitness function.
where F is the fitness function and is the matrix paradigm.
By reasonably designing the fitness function, the genetic algorithm can be guided to search effectively in the parameter identification problem to find the optimal parameter combinations to realize the goal of system parameter identification.
3.2.5. Selection
Selection refers to eliminating individuals from a population that is not adapted to their “environment” according to a fitness function during the evolution of the population. The more adapted an individual is to their “environment”, the more likely he is to be selected to remain. The more adapted individuals are, the more likely they are to be retained by selection, and the greater the number of offspring of well-adapted individuals will be in the next generation. Selection is the driving force behind the evolution of a population towards adaptation to its environment.
3.2.6. Crossover
Crossover is an operation in which specific exchanged segments of the “chromosomes” of two selected individuals create new individuals. Crossover allows for the preservation of the parent’s superior “chromosomes”. In contrast, the offspring’s “chromosomes” may concentrate the best parts of both parents, resulting in individuals better adapted to the environment than the parent, i.e., the blue is better than the blue. In the crossover operation, individuals are randomly selected from the population, the crossover position is also randomized, and the crossover probability is usually very high, around 0.6–0.9.
3.2.7. Mutation
Mutation operation refers to the probability that the individual “chromosome” segments in the population will be mutated, i.e., from 0 to 1 or from 1 to 0. Mutation operation is essential to ensure the population’s genetic diversity and, to a certain extent, prevent the loss of some excellent genes. At the same time, the mutation operation can improve the genetic algorithm’s local search ability and prevent premature population maturation. The mutation probability is relatively small, generally set to about 0.001–0.1.
3.2.8. Decoding
The “chromosome” becomes more stable when the population has evolved to an optimally adapted state. Currently, the “chromosome” corresponds to the optimal solution to the problem. The decoding operation changes the “chromosome” string into the numerical solution to the problem. The decoding formula is shown in Equation (8):
where denotes the genes of an individual. The length of the gene is l. The larger the gene size, the higher the accuracy of the problem, but at the same time, the longer the program’s running time. Moreover, and are the two boundaries of the definition domain of the ith variable of the solution vector.
4. Experimental Validation
4.1. Experimental Equipment
In this paper, the RH06 modified six-degree-of-freedom welding robot of Guangzhou CNC Equipment Co. (Guangzhou, China) is taken as the research object, as shown in Figure 1b. The range of motion of each joint is shown in Table 1.

Table 1.
Joint range of motion.
4.2. Parameter Identification
Making the welding robot run the designed excitation trajectory through the encoder can collect the joint angle of the welding robot in the process of movement; through the feedback current of the servo motor the motor torque can be calculated, and through the speed reducer it can be expanded to obtain the joint torque data in the process of the welding robot movement, the use of a low-pass filter on the joint angle and the joint torque data filtering process. The filtered data are brought into the identification model, and different identification algorithms are used to identify the dynamical parameters. The welding robot runs any verification trajectory to collect data to evaluate the identification results; Figure 1f shows the specific process.
The excitation trajectory is designed like Chao [22], a fifth-order Fourier series trajectory with a base angular frequency of 0.05 rad/s, and uses an interval angular frequency of 0.3 rad/s. The trajectory parameters are optimized to minimize the observation matrix condition number, and the optimized trajectory is shown in Figure 1a.
In order to verify the accuracy of the identified results, three arbitrary trajectories are used for the experiment so that the welding robot runs according to a random trajectory. The joint angle during the movement of the welding robot is collected through the encoder, the motor torque can be calculated through the feedback current of the servomotor, and the joint torque data during the movement of the welding robot is obtained after expanding through the speed reducer; the joint angle and the joint torque data during the movement of the welding robot are filtered using the low-pass filter, and then the joint angle data and the recognized dynamical parameters are brought into the dynamical model to calculate the joint torque value. Finally, the joint torque acquisition value is compared with the estimated value and the RMS method is used to calculate the root-mean-square (RMS) of the difference between the two, so as to make an evaluation of their difference; the smaller the RMS value is, the better the identification effect is represented. To have universal applicability, the three validation trajectories are selected as Fourier series trajectory, end straight line trajectory, and end circular arc trajectory. Figure 2a–c show the motion curves of the three validation trajectories in joint space, respectively.
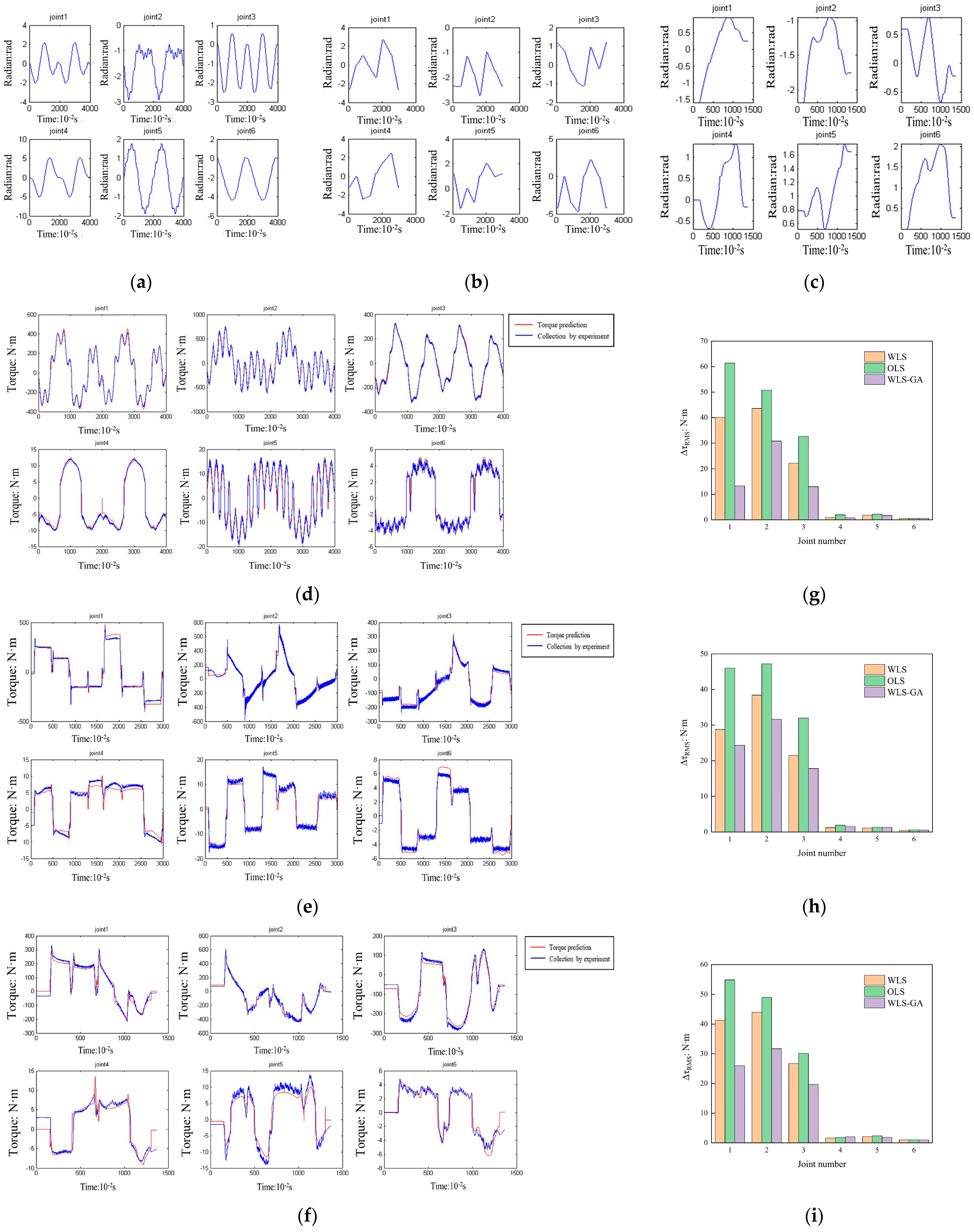
Figure 2.
Images of trajectories and validation results: (a) Fourier series trajectory; (b) straight line trajectory; (c) circular arc trajectory; (d) validation results of the WLS-GA method for Fourier trajectory; (e) linear trajectories; (f) circular trajectory; (g) comparison of verification results for Fourier series trajectory; (h) linear trajectory; (i) circular trajectory.
4.3. Parameter Verification
The weighted least squares genetic algorithm (WLS-GA) was used to identify the dynamical parameters of the welding robot. The initial population size set is 60, the gene length is 17, the crossover probability is 0.6, the variance probability is 0.02, and the maximum number of iterations is 120; Matlab(R2020b) software calculated the identification results. The results of calculated and experimentally measured torques are shown in Figure 2d–f.
As can be seen from Figure 2d–f, the Fourier trajectory verification validation using the WLS-GA algorithm is closest to the computed torque and the collected torque from joint 1 to joint 6; the straight line trajectory validation using the WLS-GA algorithm is also better, and only the computed torque of joint 4 has a particular gap with the acquisition torque. The circular trajectory validation using the WLS-GA algorithm has the worst effect, while the computed torque of joints 1 to joint 6 have some errors between the calculated torque and the acquired torque, but the errors are not significant. Overall, the three trajectories’ calculated torques are closer to the collected torque, indicating that the parameter identification is accurate. This paper adopts the Guangzhou CNC Equipment Co., Ltd. (Guangzhou, China) RH06 modified six-degree-of-freedom welding robot, and joints 1 and 2 using 150SJTRG-MZ100C servo motors (Guangzhou CNC Co., Ltd., Guangzhou, China) (rated torque 10 N·m) + a GSK-BJN-40E-121 reducer (reduction ratio of 12:1) control system, which can fully meet the joints’ torque requirements.
This paper adopted the WLS-GA algorithm to verify the three verification trajectories with the traditional method of least squares (OLS) and weighted least squares (WLS), and then the actual joint torque data obtained from the welding robot was recorded with the computed joint torque and the RMS value of the joint torque error was calculated. Table 2 shows the RMS value, and finally, the RMS value of the computed joint torque error was compared with the computed joint torque error. Figure 2g–i show the comparative results. The root mean square (RMS) value of the joint torque error obtained using the weighted least squares (WLS) algorithm is taken as the standard, and Table 3 shows the accuracy values improved using the WLS-GA algorithm and the OLS algorithm.

Table 2.
RMS of joint torques from different identification algorithms.

Table 3.
Accuracy of different identification algorithms.
Figure 2g–i, and Table 2 show that the RMS values of the ordinary least squares algorithm for the torque errors at the end joints are small, at only 0.57–1.02. However, the RMS values of the torque errors at joints 1, 2, and 3 are more significant. The RMS value of the torque error of the ordinary least squares algorithm under the validation results of the Fourier series trajectory is 61.4, which is three times the RMS value of the torque errors at the same joints under the WLS-GA method.
The RMS values of the weighted least squares torque error remain at the middle level of the three methods. Although the RMS values of the torque errors of some joints are more significant than those of the other two methods, the difference is not generally very large, especially since the RMS values of the torque errors of joints 4, 5, and 6 are relatively small, and the RMS values of the torque errors of joints 1, 2, and 3 are smaller than that of the ordinary least squares algorithm but not as significant as that of the WLS-GA algorithm.
The torque error RMS values obtained using the WLS-GA algorithm are relatively small. In some cases, the torque error RMS values of joints 4, 5, and 6 are slightly larger than the corresponding joint RMS values of the weighted least squares method. The torque error RMS values of the end joints are somewhat more significant than the corresponding joint RMS values of the least squares method. However, its RMS values at joints 1, 2, and 3 have a considerable advantage over other methods. Table 3 shows that the accuracy of the WLS-GA algorithm can be improved by up to 66.85% over the weighted least squares algorithm and by up to 78.0% over the ordinary least squares.
5. Conclusions
Aiming to solve the problem concerning the significant error between the actual joint torque and the calculated joint torque of the welding robot that leads to the vibration of the end-effector, which consequently affects the stability of the end-effector, this paper proposes a WLS-GA identification algorithm to construct and solve the dynamics model to obtain the accurate dynamics parameters. Furthermore, this paper designs the fifth-order optimal Fourier series excitation trajectory to collect the experimental data such as joint torque, and then analyze and compare the identified data with the experimental data using the validation trajectory through the WLS-GA identification algorithm. The WLS-GA identification algorithm obtains the optimal solution, and the identification data obtained using the identification algorithm are analyzed and compared with the experimental data using the validation trajectory to conclude:
The WLS-GA identification algorithm has high accuracy, which combines the simple and reliable characteristics of the weighted least squares method and the excellent characteristics of the genetic algorithm in optimization search. However, the difference between its identification effect on joints 4, 5, and 6 and the other two methods must be apparent. However, this algorithm has the best accuracy for the joint torque identification of joints 1, 2, and 3, which is 66.85% higher than the weighted least-squares algorithm and 78.0% higher than the ordinary least-squares algorithm, and it achieves a better identification effect in the experiments. The WLS-GA identification algorithm accurately constructs the dynamics model. It has been applied to the control system of the RH06 modified six-degree-of-freedom welding robot of Guangzhou Numerical Control Equipment Co. The control error of the end-effector will be reduced accordingly, which can reduce the jitter and fluctuation of the robot in the process of movement, maintain the stability of the end-effector, ensure the smooth movement of the welding process, avoid welding quality problems, and at the same time, improve the dynamic response of the robot to make it easier to adapt to the requirements of different welded workpieces, while maintaining a high degree of accuracy in the welding of the automobile body and beam welding operation.
WLS-GA identification algorithms can be used to identify and model the dynamic characteristics of various systems, including control systems, mechanical systems, and electrical systems; WLS-GA identification algorithms can be used to improve the effect and performance of signal processing algorithms by optimizing the parameters, and are used in the field of signal processing, for example, filter design, signal denoising, and signal analysis. WLS-GA identification algorithms can also be used to improve the accuracy and generalization ability of the data model by optimizing the parameters, and are used in data modeling and prediction.
Of course, the method also has some things that could be improved, such as the method needing to constantly carry out the evolution of the population, which takes more time. In addition, since the method is an intelligent optimization algorithm that mimics the evolution of biological populations, the selection of the model’s parameters, such as the number of populations, the mutation rate, the length of genes, the number of generations, etc., depends on experience. The discriminative effect of the WLS-GA will be more significant if these parameters are optimally selected with the combination of big data.
Author Contributions
L.L. and Y.Z. conceived and designed the experiment; Y.Z. and B.W. experimented; L.L., Y.Z., B.W. and G.Y. analyzed the data and prepared the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Youth Fund Project of the Science and Technology Research Project of Colleges and universities in Hebei Province (QN2024222) and the Natural Science Foundation of Hebei Province, Beijing-Tianjin-Hebei Basic Research Cooperation Project (H2022208073) and the Hebei Provincial Department of Human Resources and Social Security, Hebei Province Three Talent Project Funding Project (B20221004).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| WLS-GA | Weighted Least Squares Genetic Algorithm |
| WLS | Weighted Least Squares |
| GA | Genetic Algorithm |
| RMS | Root Mean Square |
| OLS | Ordinary Least Squares |
| CLIE | Closed-loop Input Error |
| VRPF | Virtual Repulsive Potential Field |
| WLS-RWPSO | Weighted Least Squares and Random Weighted Particle Swarm Optimization |
| WOA-GA | Whale Optimization Algorithm and Genetic Algorithm |
| FADE | Fuzzy Adaptive Differential Evolution |
| WMR | Wheeled Mobile Robot |
| PID | Proportional Integral Derivative |
| SDP | State-dependent Parameter |
| RLS | Recursive Least Square |
| T-S | Takagi–Sugeno |
| MDMFs | Multidimensional Membership Functions |
| HGA | Hierarchical Genetic Algorithm |
References
- Perrusquía, A.; Garrido, R.; Yu, W. Stable robot manipulator parameter identification: A closed-loop input error approach. Automatica 2022, 141, 110294. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, H. Control strategy based on improved fuzzy algorithm for energy control of wrist rehabilitation robot. Alex. Eng. J. 2023, 77, 634–644. [Google Scholar] [CrossRef]
- Zhao, S.; Peng, F.; Sun, H.; Yan, R.; Tang, X.; Zhang, H. Robotic milling posture adjustment under composite constraints: A weight-sequence identification and optimization strategy. Rob. Comput. Integr. Manuf. 2024, 85, 102635. [Google Scholar] [CrossRef]
- Li, Z.; Peng, F.; Yan, R.; Tang, X.; Xin, S.; Wu, J. A virtual repulsive potential field algorithm of posture trajectory planning for accuracy improvement in robotic multi-axis milling. Robot. Comput.-Integr. Manuf. 2022, 74, 102288. [Google Scholar] [CrossRef]
- Urrea, C.; Pascal, J. Design, simulation, comparison and evaluation of parameter identification methods for an industrial robot. Comput. Electr. Eng. 2018, 67, 791–806. [Google Scholar] [CrossRef]
- Tang, M.; Yan, Y.; An, B.; Wang, W.; Zhang, Y. Dynamic Parameter Identification of Collaborative Robot Based on WLS-RWPSO Algorithm. Machines 2023, 11, 316. [Google Scholar] [CrossRef]
- Dong, S.; Zhang, Y. Identification Modelling and fault-tolerant predictive control for industrial input nonlinear actuator system. Machines 2023, 11, 240. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Chen, J.; Chen, K.; Lin, B.; Xu, F. Dynamic modeling for a 6-DOF robot manipulator based on a centrosymmetric static friction model and whale genetic optimization algorithm. Adv. Eng. Softw. 2019, 135, 102684. [Google Scholar] [CrossRef]
- Al-Dabbagh, R.D.; Kinsheel, A.; Mekhilef, S.; Baba, M.S.; Shamshirband, S. System identification and control of robot manipulator based on fuzzy adaptive differential evolution algorithm. Adv. Eng. Softw. 2014, 78, 60–66. [Google Scholar] [CrossRef]
- van Zutven, P.; Kostić, D.; Nijmeijer, H. Parameter identification of robotic systems with series elastic actuators. IFAC Proc. Vol. 2010, 43, 350–355. [Google Scholar] [CrossRef]
- West, C.; Montazeri, A.; Monk, S.D.; Taylor, C.J. A genetic algorithm approach for parameter optimization of a 7DOF robotic manipulator. IFAC-PapersOnLine 2016, 49, 1261–1266. [Google Scholar] [CrossRef]
- Ali, M.A.; Radzak, M.S.; Mailah, M.; Yusoff, N.; Abd Razak, B.; Karim, M.S.A.; Ameen, W.; Jabbar, W.A.; Alsewari, A.A.; Rassem, T.H.; et al. A novel inertia moment estimation algorithm collaborated with Active Force Control scheme for wheeled mobile robot control in constrained environments. Expert Syst. Appl. 2021, 183, 115454. [Google Scholar] [CrossRef]
- Joseph, S.B.; Dada, E.G.; Abidemi, A.; Oyewola, D.O.; Khammas, B.M. Metaheuristic algorithms for PID controller parameters tuning: Review, approaches and open problems. Heliyon 2022, 8, e09399. [Google Scholar] [CrossRef]
- Son, N.N.; Kien, C.V.; Anh, H.P.H. A novel adaptive feed-forward-PID controller of a SCARA parallel robot using pneumatic artificial muscle actuator based on neural network and modified differential evolution algorithm. Robot. Auton. Syst. 2017, 96, 65–80. [Google Scholar] [CrossRef]
- Yusof, R.; Abdul Rahman, R.Z.; Khalid, M.; Ibrahim, M.F. Optimization of fuzzy model using genetic algorithm for process control application. J. Franklin Inst. 2011, 348, 1717–1737. [Google Scholar] [CrossRef]
- West, C.; Wilson, E.D.; Clairon, Q.; Monk, S.; Montazeri, A.; Taylor, C.J. State-dependent parameter model identification for inverse dead-zone control of a hydraulic manipulator. IFAC-PapersOnLine 2018, 51, 126–131. [Google Scholar] [CrossRef]
- Mendes, J.; Araújo, R.; Souza, F. Adaptive fuzzy identification and predictive control for industrial processes. Expert Syst. Appl. 2013, 40, 6964–6975. [Google Scholar] [CrossRef]
- Alves, T.G.; Lages, W.F.; Henriques, R.V.B. Parametric Identification and Controller Design for a Differential-Drive Mobile Robot. IFAC-PapersOnLine 2018, 51, 437–442. [Google Scholar] [CrossRef]
- Agand, P.; Shoorehdeli, M.A.; Khaki-Sedigh, A. Adaptive recurrent neural network with Lyapunov stability learning rules for robot dynamic terms identification. Eng. Appl. Artif. Intell. 2017, 65, 1–11. [Google Scholar] [CrossRef]
- Adánez, J.M.; Al-Hadithi, B.M.; Jiménez, A. Multidimensional membership functions in T–S fuzzy models for modelling and identification of nonlinear multivariable systems using genetic algorithms. Appl. Soft Comput. 2019, 75, 607–615. [Google Scholar] [CrossRef]
- Marie, S.; Courteille, E.; Maurine, P. Elasto-geometrical modeling and calibration of robot manipulators: Application to machining and forming applications. Mech. Mach. Theory 2013, 69, 13–43. [Google Scholar] [CrossRef]
- Xu, C. Research on Dynamic Parameter Identification and Feedforward Control of Articulated Robot. Master’s Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).