Abstract
This paper presents a unified Lyapunov-based predefined-time stability theorem that includes three sufficient conditions. The standard theoretical analysis method for achieving predefined-time stability of non-linear systems using this theorem is provided within the framework of Lyapunov theory. The developed Lyapunov-based theorem facilitates the establishment of equivalence between the existing Lyapunov theorems concerning predefined-time stability. Furthermore, when the presented sufficient conditions are relaxed, the predefined-time stability conclusion for non-linear systems degenerates into a finite-time one. Consequently, a standard non-singular sliding mode control framework based on the unified Lyapunov-based theorem is developed for a Lagrangian system to ensure its predefined-time stability. Exemplary numerical simulation results are subsequently given, in order to illustrate the convergence behavior of the system states and confirm that the controlled systems are predefined-time stable.
1. Introduction
The convergence rate is an important index for evaluating the control performance of a controlled system. The finite-time control method was introduced to attain rapid stability [1], thereby addressing limitations inherent in asymptotically stable control systems characterized by infinite convergence time. The convergence time is contingent upon the system’s initial states, resulting in a variable settling time corresponding to different initial states that becomes indeterminate. The fixed-time control method was defined to make the upper bound on the convergence time less conservative [2,3], and severs the dependence of settling time on the system’s initial states. However, it involves a complex function with multiple control gains to characterize the upper bound of the convergence time, making it challenging to arbitrarily select a convergence time through the tuning of multiple control gains. To this end, the predefined-time control technique, with the settling time as an explicit parameter that can be determined in advance, was discussed in [4,5,6,7,8]. This approach has greater flexibility in determining the settling time than finite- and fixed-time control methodologies, thus facilitating the design of observers and controllers that are suitable for addressing challenges necessitating adherence to rigorous time constraints.
Lyapunov theory—an effective instrument for analyzing the stability of control systems—is often combined with sliding mode control, backstepping control, and adding power integrator techniques to design controllers to ensure asymptotic [9], finite-time [10,11,12], fixed-time [13,14,15], and predefined-time [16,17] stability of the controlled system. In particular, the sliding mode control technique is usually used to design a controller to guarantee the controlled system’s finite-time stability [17,18,19,20,21,22]. As detailed in [4,23,24], some paradigms of the predefined-time controller were formulated to achieve the control requirements of second-order non-linear systems featuring uncertainties, but challenges related to the singularity of sliding mode control were encountered. To overcome this drawback, alternative non-singular predefined-time sliding mode controllers were presented in [17,20,25]. The aforementioned predefined-time controllers, designed using different Lyapunov-based predefined-time stability theorems, can be applied to many systems and exhibit predefined-time stability properties. In fact, through analyzing these theorems, one can derive a unified Lyapunov theorem that covers the existing Lyapunov theorems presented in [6,19,23,26], equally ensuring the predefined-time stability of non-linear systems.
On the basis of Lyapunov theory, this study develops a unified Lyapunov-based theorem guaranteeing the predefined-time/finite-time stability of non-linear systems. The main contributions are stated as follows:
- (1)
- A unified Lyapunov theorem with three sufficient conditions is proposed, which guarantees that non-linear systems achieve predefined-time stability. This differs from that reported in [6], which stated that a strictly increasing regulator function is required for the Lyapunov-based predefined-time stability theorem to hold true, thus restricting the Lyapunov-based predefined-time theorem’s selection. The results presented in this paper relax this constraint. The new Lyapunov-based predefined-time stability theorem allows for the use of an arbitrary, strictly monotonically bounded increasing or decreasing regulator function. Moreover, it serves to unify the Lyapunov-based predefined-time stability theorems for non-linear systems previously published in the literature [6,19,25,26,27].
- (2)
- A unified finite-time stability solution for non-linear systems using Lyapunov theory is derived. Despite the widespread application of the Lyapunov-based finite-time stability theorem, this study’s results not only uncover additional potential Lyapunov-based finite-time stability theorems through the selection of different strictly monotonically unbounded increasing or decreasing regulator functions but also cover the existing Lyapunov-based finite-time stability theorems in [28,29,30].
- (3)
- Using the sliding mode control technique and the proposed unified Lyapunov-based predefined-time stability theorem, a class of non-singular predefined-time sliding mode control frameworks is developed for a second-order Lagrangian system, ensuring its predefined-time stability. Simulation examples further substantiate the effectiveness of the aforementioned control method, and the simulation results provide a comprehensive exposition of the proposed controller’s behavior, including its control accuracy and settling time.
The subsequent sections of this work are organized as follows: The preliminaries and motivation are given in Section 2. Section 3 presents the unified predefined-/finite-time stability conclusions. A standard predefined-time controller design method is developed in Section 4. The numerical simulation examples carried out to validate the effectiveness of the proposed control method are detailed in Section 5. Finally, Section 6 concludes this paper.
2. Preliminaries and Motivation
2.1. Notation
For the convenience of reading, the following notation is used: is a set of real numbers. Let be the m-dimensional Euclidean space. For , denotes its transpose, and denotes the time derivative of . For a scalar function , represents a standard exponential function with a natural constant e as the base, and denotes the absolute value of . A function is said to be a class function if it is strictly increasing with .
2.2. Definitions
Consider the following non-linear system:
where is the system state, stands for the control input, and is the system’s initial state. The origin is the unique equilibrium of the system (1). The smooth function such that the solutions of system (1) exist and are unique in the sense of Filippov.
Definition 1
([6]). The origin of system (1) is said to be Lyapunov stable if, for any initial state , the solution is well defined for all . Additionally, for any arbitrarily chosen , there exists a corresponding such that, for any satisfying , it follows that for all .
Definition 2
([3]). The origin of system (1) is regarded as having asymptotic stability when it exhibits Lyapunov stability and satisfies the condition that as for any initial state vector .
Definition 3
([3]). The origin of system (1) is deemed finite-time stable if it satisfies Lyapunov stability and, for any , there exists a settling time function such that for all .
Definition 4
([3]). The origin of system (1) is considered to be fixed-time stable if it satisfies finite-time stability and if its settling time, denoted by , is constrained by a bound; that is, there exists such that .
2.3. Motivating Example
Consider the common finite-time stable first-order scalar system [31].
with and , where x represents the system state. Let be the initial value of the system state. Its state trajectory is finite-time stable by Lyapunov analysis with a positive function selected. The upper bound of the convergence time can be determined as with . When , one obtains . As the initial value increases, the convergence time will also synchronously increase. Hence, we will give a solution that the system’s settling time is independent of the initial condition and can be assigned arbitrarily. Hence, for the dynamics system (2), we can rewrite its right-hand control input to make it a predefined-time stable system as follows:
with and being the predefined time constant. Taking the time derivative of V yields
Intuitively, the scalar system (3) is asymptotically stable due to the fact that always holds. Simultaneously, we can compute its convergence time. Rewriting (4) yields
where is an increasing function with . Therefore, will decrease to the minimum from any initial value . Integrating (5) yields
3. Unified Predefined-/Finite-Time Stability Theorem
This section explores the sufficient conditions for ensuring that non-linear systems exhibit predefined-/finite-time stability within the framework of Lyapunov theory. We endeavor to establish a unified Lyapunov-based predefined-/finite-time stability theorem that not only can yield more potential Lyapunov-based predefined-/finite-time stability theorems but also covers the existing Lyapunov predefined-/finite-time stability theorems through the selection of different regulator functions.
Theorem 1.
For system (1), if there exists a regulator function , with V being a positive, radically unbounded function, and the following three sufficient conditions are satisfied:
- (i)
- , , with and ;
- (ii)
- , with ;
- (iii)
- , with ,
then system (1) is predefined-time stable, and the upper bound of the settling time is .
Proof.
Remember the system (1) and the candidate Lyapunov chosen as . If the planned control input can make the Lyapunov function V meet sufficient condition (iii) in Theorem 1, then it is easy to observe that the system’s origin is Lyapunov asymptotic stable. Next, taking the time derivative of and invoking sufficient condition (iii) in Theorem 1 yields
From (7), the function will stabilize at its minimum from any initial value . Therefore, the selected V also decreases to zero simultaneously. Then, we calculate the convergence time of from the initial state to the minimum . Integrating both sides with respect to time, we have
As a consequence, the following inequality holds:
Hence, decreases from an arbitrary initial value to the minimum , whose convergence time satisfies . Through the introduction of the function , as it undergoes a decrease from its initial value to the minimum within the predefined time , its independent variable V simultaneously converges to the origin. Consequently, the state of system (1), starting from any arbitrary initial state , exhibits convergence toward the equilibrium state when . □
Through the above analysis, a unified predefined-time stability theorem using the Lyapunov theory has been presented. The choice of function is critical to obtaining the Lyapunov theorem and predefined-time stability. Moreover, the existing Lyapunov predefined-time stability theorems documented in the literature [19,23,26] can be regarded as special cases of Theorem 1. Several examples are given in the following:
Example 1.
A specified regulator function is selected, with , , and . The fact that always holds implies that . Differentiating with respect to , one has . Thus, sufficient condition (iii) in Theorem 1 becomes
Using Theorem 1, the system (1) is predefined-time stable with convergence time such that . When selecting , formula (10) reduces to , . Hence, this specific case covers the results in [23].
Example 2.
A particular selection of the regulator function is given, with . Using simple mathematical operations, one has . Therefore, . Differentiating with respect to , it can be deduced that . The sufficient condition (iii) in Theorem 1 is given as follows:
On the basis of Theorem 1, system (1) is stable within predefined time . Further, Formula (11) can be rewritten as , . This is identical to the result provided in [26].
Example 3.
Choosing a regulator function with , , and , one can conclude that ; that is, . Differentiating with respect to , it can be derived as . Thus, the sufficient condition (iii) in Theorem 1 becomes
Using Theorem 1, the state of system (1) converges to the origin when . If and are selected, the inequality (12) reduces to , which is equivalent to Theorem 1 of [19] with the special selection.
Example 4.
To achieve predefined-time stability of system (1), a generalized Lyapunov-like theorem has been provided in [6]. As the inequality needs to be satisfied and the derived settling time function should be met, it requires a strict constraint that the function is a function. In contrast, the theorem reported in this study breaks this constraint. Only an arbitrary increasing function is needed, increasing the flexibility in selecting . As such, the unified Lyapunov-based predefined-time stability Theorem 1 was derived, which can ensure the predefined-time stability of the controlled system. Due to the fact that the interval can be included in the interval , the results in [6] are covered by Theorem 1.
Therefore, the aforementioned Lyapunov-based predefined-time stability examples are covered by Theorem 1 with a specific regulator function .
Corollary 1.
For system (1), if there is a regulator function , with V being a positive and radically unbounded function, and the following three sufficient conditions are satisfied:
- (i)
- , , with and ;
- (ii)
- , with ;
- (iii)
- , with ,
then system (1) is predefined-time stable, and the upper bound of the settling time is .
Proof.
Consider the system (1) and the regulator function with . Develop a control input to make the Lyapunov function V satisfy the sufficient condition (iii) in Corollary 1. The straightforward derivation of the result regarding the system’s origin is asymptotically stable.
Then, taking the time derivative of and invoking sufficient condition (iii) in Corollary 1 yields , which means that the function will stabilize at its maximum from any initial value . Therefore, the selected V also decreases to zero simultaneously. Then, we calculate the convergence time of from the initial state to the maximum . Integrating both sides , one obtains . As a consequence, the following holds:
Hence, from arbitrary initial value to the maximum has convergence time such that . When the function increases from the initial value to the maximum value within the predefined time , its independent variable V also converges synchronously to the origin. Therefore, the system state in (1) from the arbitrary initial state converges to the equilibrium when . □
Summarizing the analysis of Theorem 1 and Corollary 1, the predefined-time stability of system (1) can be guaranteed. On this basis, we can obtain a series of predefined-time stable dynamic systems. We give the standard predefined-time controller design process as follows:
- S1.
- Choose a strictly monotonically increasing function or decreasing function ;
- S2.
- Choose a positive Lyapunov candidate to obtain the functions and , with . The two functions satisfy with and , where ;
- S3.
- Take the derivatives of and with respect to ;
- S4.
- Construct a Lyapunov inequality form of to meet the following inequalities: and ;
- S5.
- Design a control input u to meet the Lyapunov form of in step S4 and guarantee the predefined-time stability of the system (1).
Summarizing the above analysis, let the Lyapunov function V be the independent variable of the strictly monotonically increasing/decreasing bounded function or . Utilizing the characteristics of the monotonic regulator function or forces V to decay to zero with the regulator function decreasing/increasing to its minimum/maximum. Therefore, we establish an equivalent relationship between the system’s convergence and the decreasing/increasing characteristics of the regulator function, further reflecting the system’s settling time. The selection of the regulator functions and is key to achieving predefined-time stability. Some examples of regulator functions are listed in Table 1.

Table 1.
Candidate examples for Theorem 1 and Corollary 1.
Moreover, if the regulator function in Theorem 1 does not meet the sufficient condition (i), and is a strictly monotonically increasing unbounded function, the conclusion of Theorem 1 degenerates into a finite-time one. The following unified finite-time stability corollaries based on Theorem 1 are presented.
Corollary 2.
For the system (1), if there is a regulator function , with V being a positive and radically unbounded function, and the following three sufficient conditions are satisfied:
- (i)
- , , with ;
- (ii)
- , with ;
- (iii)
- , with ,
then system (1) is finite-time stable, and the upper bound of the settling time is .
Proof.
The upper bound of the settling time can also be computed using a similar method as in Theorem 1. Now, differentiating and invoking condition (iii) in Corollary 2, one obtains . Therefore, will decrease to the minimum from the initial value . Integrating it on both sides yields . Then, we have . Thus, it is proved that any decreases to the minimum of when . The Lyapunov candidate V also converges to zero simultaneously. The selected V is radially unbounded. For any initial system state , it can converge to the equilibrium when . Therefore, we can further summarize the following Lyapunov-based finite-time stability corollary on the basis of Corollary 1. □
Corollary 3.
For system (1), if there is a regulator function , with V being a positive and radically unbounded function, and the following three sufficient conditions are satisfied:
- (i)
- , , with ;
- (ii)
- , with ;
- (iii)
- , with ,
then system (1) is finite-time stable, and the upper bound of the settling time is .
Proof.
The analysis process is similar to Corollary 1 and, thus, is omitted here. □
Selection of the regulator function is important in deriving the Lyapunov-based finite-time stability theorem and ensuring the finite-time stability of the controlled system. Moreover, the existing Lyapunov-based finite-time stability theorems documented in the literature [28,29,30] can be regarded as special cases of Corollary 2. Several examples are given in the following:
Example 5.
A specified regulator function is selected with and , such that always holds. Differentiating with respect to , one has . Thus, sufficient condition (iii) in Corollary 2 becomes
Using Corollary 2, system (1) is finite-time stable when , where is a time constant. When selecting , formula (14) reduces to , . Hence, this special case covers the results in [28,29].
Example 6.
A special selection of is chosen, with . Using simple mathematical operations, one has . Differentiating with respect to , it can be derived as . The sufficient condition (iii) in Corollary 2 is given as follows:
On the basis of Corollary 2, the system (1) is stable within finite time , where is a time constant. This is identical to the result of [30].
Summarizing the above analysis for Corollaries 2 and 3, the finite-time stability of system (1) can be guaranteed. On this basis, we can obtain a series of finite-time stable dynamic systems. Let the candidate Lyapunov function V be the independent variable of the strictly monotonically increasing/decreasing unbounded function or . Utilizing the characteristics of the monotonic regulator function or forces V to decay to zero with the regulator function decreasing/increasing to its minimum/maximum. Therefore, we establish an equivalent relationship between the system’s convergence and the decreasing/increasing characteristics of the regulator function, which further reflects the system’s settling time. Therefore, the selection of a decreasing/increasing regulator function is important in the derivation of Corollaries 2 and 3. Some possible regulator functions are listed in Table 2.

Table 2.
Candidate examples for Corollaries 2 and 3.
4. Standard Predefined-Time Controller Design
Due to the fact that many actual mechanical systems, including robot manipulator systems [32], unmanned aerial vehicles [33,34], and spacecraft attitude control systems [35,36], are typically described by the Lagrangian dynamic equations of motion, the study objective of this section is to develop a standard predefined-time controller design method for the Lagrangian system considering external disturbances. The associated mathematical model is given as follows:
where , ; denote the generalized position, velocity, and acceleration vectors, respectively; is a positive definite moment of inertia matrix; is the centripetal Coriolis matrix; is the gravity vector; represents the uncertainty vector; and denotes the control input. For the convenience of controller design, let and . Therefore, the Lagrangian system (16) with can be rewritten as follows:
where is the available state vector; and are known non-linear functions; denotes the disturbances and system uncertainties, which satisfies where b is a positive scalar; and is the control input.
Through the application of Theorem 1, a standard predefined-time controller design method is presented here based on the sliding mode control technique for system (17). In the control framework, a new predefined-time sliding mode surface is first designed using piecewise function methods, in order to avoid potential singularities. A non-singular sliding mode controller is then designed, which ensures that the system (17) is predefined-time stable.
Choose a regulator function which satisfies the sufficient conditions (i) and (ii) in Theorem 1, and define . For the system (17), a novel non-singular sliding mode surface is designed as follows:
where , , , and with ; is a predefined-time constant; and and are selected to meet the continuity of . Differentiating s yields
The terms and are non-singular. Then, can be computed from (18), as follows:
where . Specifically, it can be observed that, when , will not exhibit singularity. When , it is possible for the term to have a negative power term of . Then, according to the definition of , assuming the term with and is reasonable, denotes a smooth function. Hence, the limit of the term exists when . Therefore, there is no singularity for the term when an appropriate q is selected. For system (17), the control input u is designed as
where and . is the predefined convergence time, and is a Lyapunov function. Summarizing the above analysis, the presented predefined-time sliding mode controller (21) has no singularity.
Theorem 2.
Proof.
From (22), will converge to zero within the predefined time on the basis of Theorem 1. The ideal sliding mode motion is established simultaneously. Once s reaches zero, the designed sliding surface (18) satisfies . Then, one has when . Taking the time derivative of , one can obtain . Using Theorem 1, and will converge to the origin along the sliding manifold within the predefined time . When approaches zero along the general sliding manifold, one has . The second phase of s in (18) is asymptotically stable. Hence, the predefined-time convergence of system state —that is, —is achieved, and the singularity problem of predefined-time sliding control can be circumvented.
Moreover, the presented Theorem 1 can also be applied for the stability analysis of high-order non-linear systems. In this case, the recursive sliding mode control scheme [37,38,39] or integral high-order sliding controller [40,41,42] can be designed to stabilize the high-order systems. In the sliding mode control method, the proposed Theorem 1 can be used for the controller design of the reaching phase. One can construct a controller to satisfy the condition (iii) of Theorem 1, ensuring that the system states reach the sliding mode surface within a predefined time. Once the ideal sliding mode is established, the system states will converge to the origin along the sliding mode surface. Therefore, the stability of high-order non-linear systems can be achieved. □
5. Simulation Examples
To validate the previous theoretical results, the proposed predefined-time control framework (21) was applied to a second-order Lagrangian system and an actual attitude control system, and the effectiveness of the designed control scheme was verified through numerical simulation.
5.1. Predefined-Time Controller for a Second-Order Lagrangian System
Consider system (17) with , , and . The control input is given by (21). In order to verify that, under different initial conditions, the designed predefined-time controllers can ensure that the state converges to the vicinity of the origin within a predefined time, Monte Carlo simulations with 500 dispersed scenarios were conducted. In the simulation, the initial conditions of and satisfied and , respectively.
On the one hand, for the sliding surface (18), we selected a monotonically increasing regulator function with , , , and . One can obtain that . Therefore, one has and . Thus, the sufficient conditions (i) and (ii) for the regulator function in Theorem 1 have been satisfied. On this basis, the specific controller of (21), guaranteeing controlled system predefined-time stability, can be obtained using the regulator function . In the Monte Carlo simulations, the control parameters were chosen as , , , and . The predefined-time constants were set as and . Figure 1a,c display the convergence performance of the system state and sliding surface s driven by the controller (21). The convergence accuracy of system state was superior to for any initial state, which can be verified from the depiction of the steady behavior of state in Figure 1b. To achieve predefined-time stability of the second-order non-linear system, the required control input is also illustrated in Figure 1d. The simulation results show that the system state converged to the origin within the predefined time second.
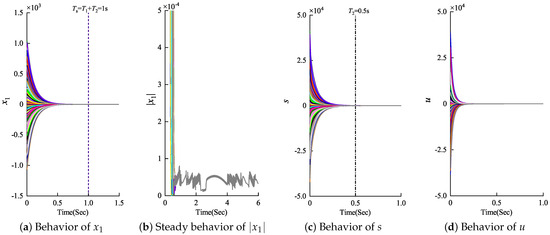
Figure 1.
Convergence behavior of system state , sliding surface s, and control input u in the Monte Carlo simulations with an increasing function .
On the other hand, for the sliding surface (18), we selected a monotonically decreasing regulator function with , , and . One can obtain that . Therefore, one has and . The sufficient conditions (i) and (ii) for the regulator function in Corollary 1 were satisfied. Hence, the unique control input (21) with the decreasing regulator function being used could be obtained to ensure the predefined-time stability of the controlled system. In the Monte Carlo simulations, the control gains were selected as and , and the given time constants were and . Figure 2a,c plot the convergence performance of the system state and sliding surface s, respectively. From Figure 2b, it can observed that, for any initial state value, the system state converged to a small region around zero (i.e., ). The time response curve of the control input (21) is shown in Figure 2d. One can see that the system state converged to the small region around within the predefined time second. Summarizing the analysis of the above simulation results, the theoretical results in Theorem 2 were numerically validated through Monte Carlo simulations.
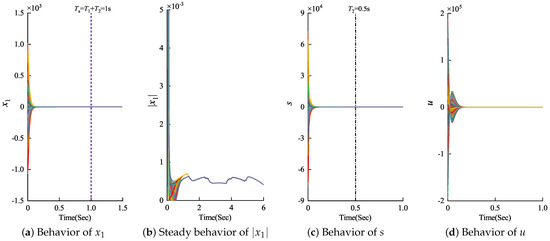
Figure 2.
Convergence behavior of system state , sliding surface s, and control input u in the Monte Carlo simulations with a decreasing function .
5.2. Predefined-Time Controller for a Spacecraft Attitude Control System
To verify the applicability and effectiveness of Theorem 2 in the context of actual control systems, a spacecraft attitude stabilization control system was taken as an example for verification. The MRPs were chosen to represent the attitude information. The attitude control model of a rigid spacecraft is given as follows [43]:
with being the angular velocity and ; is the inertia matrix of the spacecraft; denotes the control input; represents the external disturbance torque; is given as with ; and is an identity matrix. The system (23) can be transformed into
with , , and . Defining and , the system (24) can be rewritten as follows:
with and , and denotes the synthetic external disturbance. Assume , with being a positive real number.
To stabilize the attitude control system within a predefined time, the corresponding sliding mode surface and attitude controller were designed according to Theorem 2. Hence, the regulator function was designed as with , , , and . Referring to (18) and using the regulator function , a non-singular sliding mode surface for system (25) was developed as follows:
with . with . Using (26) and recalling (21), a non-singular predefined-time sliding mode controller for system (23) was designed, as follows:
with . with .
Then, a simulation study was conducted to test the control performance of the designed attitude controller (27). In the simulation, the inertia matrix of the spacecraft was set as . The external disturbance was assumed as . The initial settings of the attitude control system were set as and . The main control gains in (26) and (27) were selected as , , , , , , , and . According to the simulation results, the convergence performance of spacecraft attitude MRPs and sliding mode surface are shown in Figure 3a and Figure 3b, respectively. The attitude MRPs converged to a small region around the origin rapidly within the predefined time of s. To achieve attitude stabilization, the time response curve of the control input is plotted in Figure 3c. It can be observed that attitude stabilization was completed when s, and the control input remained around zero. Hence, the conclusions in Theorem 2 were numerically validated.
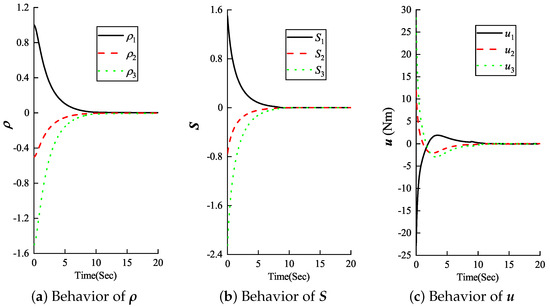
Figure 3.
Time response curve of MRPs , sliding surface , and control input in attitude stabilization simulation example.
6. Conclusions
This study investigated sufficient conditions within the framework of Lyapunov theory for guaranteeing the predefined-/finite-time stability of non-linear systems. The developed Lyapunov-based theorem allowed us to establish equivalence with existing Lyapunov-based theorems for predefined-/finite-time stability in non-linear systems. The proposed theorem not only allows for the establishment of more possible Lyapunov-based predefined-/finite-time stability theorems through the choice of different regulator functions but also covers existing Lyapunov predefined-/finite-time stability theorems [6,19,23,26,28,29]. On this basis, a standard non-singular sliding mode control framework guaranteeing the predefined-time stability of second-order Lagrangian systems was provided. Furthermore, numerical simulation results verified the effectiveness of the proposed control approaches.
Author Contributions
Conceptualization, B.X. and S.Z.; methodology, B.X. and H.Z.; software, H.Z. and S.Z.; validation, L.C. and Z.C.; investigation, H.Z. and S.Z.; resources, B.X. and Z.C.; writing—original draft preparation, B.X.; writing—review and editing, B.X. and H.Z.; supervision, B.X. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Major Science and Technology Projects of China under Grant J2019-I-0021-0020.
Data Availability Statement
Data sharing is not applicable to this article, as no datasets were generated or analyzed during the current study.
Acknowledgments
The authors sincerely appreciate the editors’ and reviewers’ kind attention and valuable comments dedicated to this paper.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Bhat, S.P.; Bernstein, D.S. Geometric homogeneity with applications to finite-time stability. Math. Control Signals Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef]
- Andrieu, V.; Praly, L.; Astolfi, A. Homogeneous approximation, recursive observer design, and output feedback. Siam J. Control Optim. 2008, 47, 1814–1850. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Wu, C.; Yan, J.; Shen, J.; Wu, X.; Xiao, B. Predefined-time attitude stabilization of receiver aircraft in aerial refueling. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3321–3325. [Google Scholar] [CrossRef]
- Cui, B.; Wang, Y.; Liu, K.; Xia, Y. Sliding mode based prescribed-time consensus tracking control of second-order multi-agent systems. Automatica 2023, 158, 111296. [Google Scholar] [CrossRef]
- Jiménez-Rodríguez, E.; Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Defoort, M.; Loukianov, A.G. A Lyapunov-like characterization of predefined-time stability. IEEE Trans. Autom. Control 2020, 65, 4922–4927. [Google Scholar] [CrossRef]
- Xiao, B.; Wu, X.; Cao, L.; Hu, X. Prescribed time attitude tracking control of spacecraft with arbitrary disturbance. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2531–2540. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.; Yang, Y.; Xiao, B.; Ran, D. Appointed fixed time observer-based sliding mode control for a quadrotor UAV under external disturbances. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 290–303. [Google Scholar] [CrossRef]
- Chen, L.; Shi, P.; Liu, M. Fault reconstruction for Markovian jump systems with iterative adaptive observer. Automatica 2019, 105, 254–263. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, L.; Shi, P.; Zhao, Y. Fault estimation sliding-mode observer with digital communication constraints. IEEE Trans. Autom. Control 2018, 63, 3434–3441. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Wei, C.; Li, Y.; Yin, Z.; Zhou, L.; Feng, J. On finite-time anti-saturated proximity control with a tumbling non-cooperative space target. Space Sci. Technol. 2023, 3, 45. [Google Scholar] [CrossRef]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Zou, A.M.; Kumar, K.D.; de Ruiter, A.H. Fixed-time attitude tracking control for rigid spacecraft. Automatica 2020, 113, 108792. [Google Scholar] [CrossRef]
- Ahmed, S.; Azar, A.T.; Tounsi, M.; Anjum, Z. Trajectory tracking control of euler–lagrange systems using a fractional fixed-time method. Fractal Fract. 2023, 7, 355. [Google Scholar] [CrossRef]
- Jang, S.G.; Yoo, S.J. Predefined-time-synchronized backstepping control of strict-feedback nonlinear systems. Int. J. Robust Nonlinear Control 2023, 33, 7563–7582. [Google Scholar] [CrossRef]
- Xiao, B.; Zhao, S.; Chen, Z.; Cao, L. Prescribed convergence time control of spacecraft attitude dynamics with parametric uncertainty. Nonlinear Dyn. 2023, 111, 16175–16186. [Google Scholar] [CrossRef]
- Lian, X.; Zhang, J.; Song, X.; Hong, Z.; Zhou, S.; Lin, M. Mode switching control for drag-free satellite based on region of attraction. Space Sci. Technol. 2023, 3, 20. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Jiménez-Rodríguez, E.; Loukianov, A.G. Predefined-time robust stabilization of robotic manipulators. IEEE/ASME Trans. Mechatron. 2019, 24, 1033–1040. [Google Scholar] [CrossRef]
- Ye, D.; Zou, A.M.; Sun, Z. Predefined-time predefined-bounded attitude tracking control for rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 464–472. [Google Scholar] [CrossRef]
- Huang, Z.; Tang, C.; Yu, Q.; Khaliel, M.S.S.; Wei, C. Dynamics and FNTSM control of spacecraft with a film capture pocket system. Space Sci. Technol. 2023, 3, 79. [Google Scholar] [CrossRef]
- Xue, H.; Liu, X. A novel fast terminal sliding mode with predefined-time synchronization. Chaos Solitons Fractals 2023, 175, 114049. [Google Scholar] [CrossRef]
- Wang, F.; Miao, Y.; Li, C.; Hwang, I. Attitude control of rigid spacecraft with predefined-time stability. J. Frankl. Inst. 2020, 357, 4212–4221. [Google Scholar] [CrossRef]
- Xu, C.; Wu, B.; Zhang, Y. Distributed prescribed-time attitude cooperative control for multiple spacecraft. Aerosp. Sci. Technol. 2021, 113, 106699. [Google Scholar] [CrossRef]
- Liang, C.D.; Ge, M.F.; Liu, Z.W.; Ling, G.; Zhao, X.W. A novel sliding surface design for predefined-time stabilization of Euler–Lagrange systems. Nonlinear Dyn. 2021, 106, 445–458. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Tang, Y.; Liu, C. Predefined-time consensus tracking of second-order multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2550–2560. [Google Scholar] [CrossRef]
- Li, K.; Li, Y. Adaptive predefined-time optimal tracking control for underactuated autonomous underwater vehicles. IEEE/CAA J. Autom. Sin. 2023, 10, 1083–1085. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Chen, W.; Jiao, L.C. Finite-time stability theorem of stochastic nonlinear systems. Automatica 2010, 46, 2105–2108. [Google Scholar] [CrossRef]
- Shen, Y.; Huang, Y. Uniformly observable and globally lipschitzian nonlinear systems admit global finite-time observers. IEEE Trans. Autom. Control 2009, 54, 2621–2625. [Google Scholar] [CrossRef]
- Hong, Y.; Huang, J.; Xu, Y. On an output feedback finite-time stabilization problem. IEEE Trans. Autom. Control 2001, 46, 305–309. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Liu, Z.; Jing, X.; Hu, C. A new recursive composite adaptive controller for robot manipulators. Space Sci. Technol. 2021, 2021, 9801421. [Google Scholar] [CrossRef]
- Li, B.; Liu, H.; Ahn, C.K.; Gong, W. Optimized intelligent tracking control for a quadrotor unmanned aerial vehicle with actuator failures. Aerosp. Sci. Technol. 2024, 144, 108803. [Google Scholar] [CrossRef]
- Liu, H.; Li, B.; Xiao, B.; Ran, D.; Zhang, C. Reinforcement learning-based tracking control for a quadrotor unmanned aerial vehicle under external disturbances. Int. J. Robust Nonlinear Control 2023, 33, 10360–10377. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Z.; Xiao, B.; Li, B. Fast fixed-time attitude tracking control of spacecraft with prescribed performance. Int. J. Robust Nonlinear Control 2023, 33, 5229–5245. [Google Scholar] [CrossRef]
- Tayebi, J.; Chen, T.; Wang, H. Dynamics and control of flexible satellite using reaction sphere actuators. Space Sci. Technol. 2023, 3, 77. [Google Scholar] [CrossRef]
- Zhang, H.; Li, B.; Xiao, B.; Yang, Y.; Ling, J. Nonsingular recursive-structure sliding mode control for high-order nonlinear systems and an application in a wheeled mobile robot. ISA Trans. 2022, 130, 553–564. [Google Scholar] [CrossRef] [PubMed]
- Mobayen, S. Finite-time tracking control of chained-form nonholonomic systems with external disturbances based on recursive terminal sliding mode method. Nonlinear Dyn. 2015, 80, 669–683. [Google Scholar] [CrossRef]
- Mishra, J.; Patel, R.; Yu, X.; Jalili, M. Recursive surface structure for fixed-time convergence with applications to power systems. IET Control Theory Appl. 2018, 12, 2595–2604. [Google Scholar] [CrossRef]
- Zong, Q.; Zhao, Z.S.; Zhang, J. Higher order sliding mode control with self-tuning law based on integral sliding mode. IET Control Theory Appl. 2010, 4, 1282–1289. [Google Scholar] [CrossRef]
- Li, B.; Zhang, H.; Xiao, B.; Wang, C.; Yang, Y. Fixed-time integral sliding mode control of a high-order nonlinear system. Nonlinear Dyn. 2022, 107, 909–920. [Google Scholar] [CrossRef]
- Mondal, S.; Mahanta, C. Adaptive integral higher order sliding mode controller for uncertain systems. J. Control Theory Appl. 2013, 11, 61–68. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, H.; Chen, Z.; Cao, L. Fixed-time fault-tolerant optimal attitude control of spacecraft with performance constraint via reinforcement learning. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7715–7724. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).