Abstract
This study presents a machine learning model for predicting lumbar spine moments using data from low-cost sensors, with the ultimate aim of developing a control strategy for waist-active exoskeleton devices. The limitation of sparse features in low-cost insoles was addressed by leveraging a source model constructed based on data acquired from the high-precision Pedar-X device, employing a transfer learning technique. The model’s performance saw significant improvement through a training approach that incorporated high-precision commercial insole data and fine-tuning with low-cost insole data. In comparison to the conventional model, this method resulted in a noteworthy 7% enhancement in performance, achieving an rRMSE of approximately 12% and a correlation coefficient of 0.9 in lumbar joint moment prediction. If the model can demonstrate real-time efficacy and effectiveness across various operations in future applications, it holds substantial potential for deployment as an active exoskeleton device for the waist.
1. Introduction
Low back pain (LBP) is a highly prevalent symptom that approximately 84% of adults are expected to experience at least once in their lifetime [1]. Lumbar pain, or lower back pain, occurs because of repetitive mechanical stress on the vertebral bones, which leads to the accumulation of tissue damage in structures such as bones, muscles, and ligaments [2]. It accounts for 62% of work-related musculoskeletal disorders associated with lifting tasks [3] and lifting motions have been identified as a significant risk factor for low back pain [4]. To mitigate the high mechanical load experienced by the waist during lifting tasks, researchers have developed wearable exoskeleton devices [5]. These wearable exoskeleton devices aim to prevent injury by reducing the load on the wearer while preserving the degree of freedom of movement needed for whatever task(s) the wearer intends to perform [6]. Exoskeleton devices can be categorized into passive types, which utilize springs or similar mechanisms to aid force or torque, and active types, which directly employ actuators like electric motors [7]. Both devices have shown the potential to reduce low back muscle activity by up to 40% during lifting tasks [8]. Active systems also have the advantage of being adaptable to various lifting operations [6].
An active exoskeleton device must efficiently control the actuator based on the user’s intentions during operation, thus requiring the collection of wearer intentions to establish appropriate control strategies [8]. An appropriate control strategy specifically means one that correctly grasps the intention of the user and thereby provides the appropriate signal to the actuator; accurately grasping the intention of the user and simulating behavior patterns in a similar manner remains a challenge [9]. Considering that the lumbar load is highly related to the moment [10], gathering real-time measured data of the lumbar moment can help establish an optimal control strategy for an exoskeleton device [11]. In a specific example, it has been shown that rehabilitation performance and convenience can be improved when the lumbar moment generated in the waist bending and twisting operation during the lifting operation is simulated and used as a control parameter for the exoskeleton device [12]. Therefore, the lumbar moment is considered an important parameter in the control of an exoskeleton device for back assistance during lifting operations.
During lifting, the lumbar joint moment is calculated by an inverse dynamics technique using a three-dimensional motion analysis system [13]. The inverse dynamics method is a method of calculating the net force and moment of each joint by applying the three-dimensional trajectory of an optical marker attached to the human body, ground reaction force data, and anthropometric information as input information to the Newton–Euler equation [14]. However, three-dimensional motion analysis systems that include a six-axis ground reaction force system are limited by their high price and the fact that analysis is only possible under specific conditions, such as in a laboratory space [15]. In a recent study, Faber et al. (2020) attempted to calculate the lumbar moment using force shoes with 17 inertial sensors and a six-degree force sensor attached [16]. However, the complexity of that system was substantially increased due to the attachment of so many sensors, and its field applicability was limited by the unnaturalness and convenience of operation [17]. Therefore, it would be valuable to extract the lumbar moment by utilizing a low-cost insole system that does not have the spatial constraints and that is easy to apply in the field.
It is considered impractical to construct sufficient input features for an inverse dynamic method solely using pressure sensor signals extracted from an insole system. In cases where dimensional inputs are insufficient, machine learning models can serve as a viable solution [18]. Even in problems that involve intricate and nonlinear relationships between the input and output, researchers have successfully employed machine learning techniques to estimate biomechanical parameters. For example, Aghazadeh et al. (2020) took a novel approach by estimating the lumbar region’s moment along three axes through machine learning while incorporating input variables such as hand position and object weight. Although this method demonstrated the potential to estimate joint moments, it came with the caveat that the model required the inputs of hand position and object weight [19]. Another study developed a long short-term memory (LSTM) model to forecast lumbar region moments during symmetric lifting operations while employing the costly Pedar-X insole system [20]. Despite the inherent limitation of relying on an expensive insole system, the machine learning system exhibited an average relative root mean square error (rRMSE) accuracy of 10% compared to lumbar joint moments derived using the gold-standard method. Even though the results of that study substantiated the efficacy of using pressure information from an insole system for lumbar moment prediction, the limitations lie in the model’s dependence on a substantial amount of pressure information and its restricted applicability to specific lifting operations.
To accurately estimate three-axis lumbar joint moments using a limited set of pressure information, it is necessary to employ more sophisticated machine learning techniques. Recent studies have proposed that transfer learning models yield high-performance results [21,22,23]. Transfer learning involves the construction of a source model using a relatively abundant source domain along with subsequent fine-tuning in the target domain by leveraging the weights and biases of the established model [24]. By capitalizing on the knowledge acquired from the pre-trained source model, transfer learning offers the advantage of rapid learning without the need for exhaustive searches of the target model [25]. This approach has already demonstrated success in domains such as image classification, image segmentation, object recognition, and natural language processing, where it outperforms models trained on single datasets [22,23]. Therefore, it is reasoned that employing the weights and biases of pre-trained models can even enhance the performance of the model in domains with relatively limited datasets. Hence, the aim of this study is to introduce a transfer learning model that can estimate the three-axis lumbar moment during lifting tasks while leveraging a cost-effective insole system. To this end, a prototype of the insole system with a limited number of pressure sensors is manufactured. A deep learning model is developed to forecast the three-axis lumbar joint moment using foot pressure data acquired from Pedar-X. The ultimate objective is to develop a transfer learning model using a previously established deep learning model while utilizing the pressure information derived from the designed low-cost insole system.
2. Proposed Strategy Based on Deep and Transfer Learning
The study employs a transfer learning approach to enhance the model’s performance by transferring knowledge from a source domain, comprising pressure sensor data from the Pedar-X system and concurrently acquired lumbar joint moments, to a target domain. In the target domain, pressure data from the developed low-cost system and lumbar joint moments are input into the model. Thus, the proposed strategy for lumbar joint moment estimation in this study encompasses sensor signal preprocessing, the development of a deep learning model, and the transfer learning process (see Figure 1).
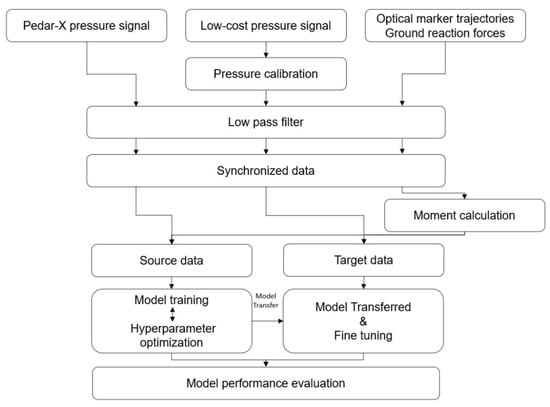
Figure 1.
The total process utilized in this study.
2.1. Preprocessing
Three types of raw data were acquired: Pedar-X pressure signals, low-cost pressure signals, and optical marker trajectories with ground reaction forces. To remove noise, a low-pass filter was applied to the raw data. This low-pass filter was tailored differently for pressure values and motion analysis data, using filtering techniques and frequencies that were selected based on previous studies. The pressure data were treated with a 3rd-order Butterworth, zero-lag low-pass filter with a frequency of 7 Hz [20], the motion analysis data were treated with a 4th-order, low-pass Butterworth filter with a cutoff frequency of 5 Hz [26]. The two systems collecting pressure data operated at a sampling rate of 100 Hz, and the motion analysis system had a sampling rate of 120 Hz, thus necessitating data synchronization. Synchronization involved the subject stomping their feet prior to the initiation of the experimental operation, with manual adjustments made based on the time when data were preprocessed [20]. The pressure data were aligned with the length-of-motion analysis system data using the spline method. Optical marker trajectory and ground reaction force data were integrated with human anthropometric information to compute the lumbar joint torque. This torque was then calculated employing the established inverse dynamics technique from previous research [14].
2.2. Deep Learning
The input data for the deep learning model were categorized into source data and target data according to whether they originated from the Pedar-X or the low-cost pressure insole, respectively. The source data consisted of a dataset obtained using 198 sensor data points acquired from the Pedar-X system as input data, targeting the 3-axis lumbar moment as the output. Meanwhile, the target data consisted of a dataset inputting 18 pressure sensor data points from a low-cost pressure insole, also targeting the 3-axis lumbar moment. For the source data, 3420 datasets were formed from 70 subjects, with input and output data structured as 198 × data length and 3 × data length, respectively. On the other hand, the target data consisted of 300 datasets obtained from 10 subjects, with input and output data structured as 18 × data length and 3 × data length, respectively. A recurrent neural network (RNN) is a specialized neural network that is capable of transmitting feedback between neurons on the same layer, thus allowing the model to capture time-series characteristics. The long short-term memory (LSTM) layer, which is a type of RNN layer, addresses the gradient vanishing problem that is inherent in traditional RNN layers; this problem occurs when the weight values of long data sequences disappear over time. The LSTM has a neuron structure with a cell state and three types of gates: forget, input, and output gates. The forget gate controls how much the past state influences the current state, the input gate determines whether new information updates the cell state, and the output gate determines the output information based on the cell state. The current study used an artificial intelligence system based on the LSTM layer to predict lumbar torque (Figure 2B). This system consists of an input layer, two blocks comprising LSTM and dropout layers, and an output layer. During the model training process, hyperparameter optimization was conducted using the Bayesian optimization method, and the optimized hyperparameters are presented in Table 1. The objective function employed for optimization was the rRMSE of the model.
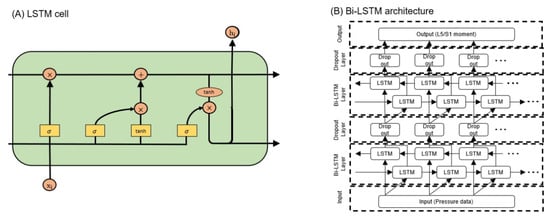
Figure 2.
Artificial intelligence architecture: (A) LSTM cell, (B) Bi-LSTM architecture.

Table 1.
Hyperparameters used in optimization and their ranges.
2.3. Transfer Learning
In this study, the weights and biases of the model for two LSTM layers were transferred from the source domain, and three different types of fine-tuning were applied. The deep learning architecture used here is detailed in Section 2.2. Figure 3 illustrates a conceptual diagram of the five models developed in this study. Figure 3A represents the source model, which was trained using data from the source domain and task. The source domain here refers to plantar pressure acquired from Pedar-X and lumbar moments obtained from a motion analysis system. Figure 3B depicts the conventional model, trained using data from the target domain and task. The target domain and task refer to plantar pressure obtained from a low-cost insole and lumbar moments acquired from a motion analysis system. Figure 3C–E show models constructed by transferring a pre-trained model from the source domain to the target domain. Here, “freeze” and “update” refer to determining whether to update the transitioned weights and biases of each layer during fine-tuning, denoted as “update” or “freeze,” respectively. Figure 3C–E vary based on the freezing and updating of LSTM layers during fine-tuning. Specifically, Figure 3C (target #1) freezes the second LSTM layer and updates the first LSTM layer. In contrast, Figure 3D (target #2) freezes the first LSTM layer and updates the second LSTM layer. Lastly, Figure 3E (target #3) updates both LSTM layers. The learning rate for fine-tuning (Figure 3C–E) was chosen by multiplying the learning rate used in the original source domain by 0.001. All models were implemented using MATLAB R2022b version (The Mathworks, Inc., Natick, MA, USA) and an RTX 2080 Ti GPU.
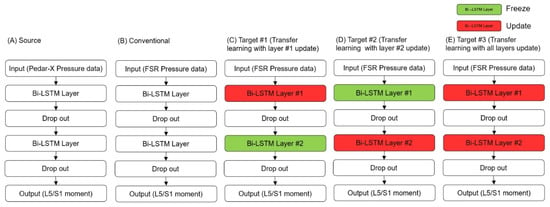
Figure 3.
Transfer learning method with fine-tuning: (A) source, (B) conventional, (C) target #1, (D) target #2, (E) target #3.
3. Experiments
3.1. Subject
In total, 80 male participants without musculoskeletal disorders (age: 26.11 ± 1.37 years; weight: 69.33 ± 6.68 kg; height: 1766.11 ± 49.60 mm) took part in the asymmetrical lifting experiment. Informed consent was obtained from all participants, and the experiment received approval from the Ethics Committee of the Institute of Biomedical Engineering, Sungkyunkwan University.
3.2. Apparatus
The equipment used in this study included a motion analysis system, Pedar-X, and a low-cost insole system. The motion analysis system comprised six MCam2 cameras (VICON, Oxford Metrics, Oxford, UK) and two OR6-6-2000 force plates (AMTI Inc., Newton, MA, USA). The cameras operated at a sampling rate of 120 Hz, capturing optical marker trajectories, while the force plates recorded ground reaction force data at a rate of 1080 Hz. The data collected from the cameras and force plates were synchronized at 120 Hz using the Vicon 460 system. The Pedar-X mobile system (Pedar Mobile, Novel Electronics Inc., GmbH, Munich, Germany) was worn for foot pressure measurement, and data were collected from this system at a sampling rate of 100 Hz (Figure 4A). The PCB and circuit diagram of the low-cost insole system are illustrated in Figure 4B. Each insole featured nine Tekscan A301 pressure sensors, all of which were mounted on a thin and flexible panel that was strategically placed based on the anatomical structure of the foot [27]. This panel was designed in three different sizes (250 mm, 260 mm, 270 mm) to accommodate various foot sizes. Both systems collected data at a sampling rate of 100 Hz. The signals from the low-cost insole were acquired using the LabVIEW software (LabVIEW version 20.0, National Instruments Corp., Austin, TX, USA). Pressure calibration was performed to convert the voltage values obtained from the low-cost pressure insole to pressure values. This calibration accounted for variations in the resistance values of each pressure sensor, and a calibration was carried out by applying vertical force to the system using a jig device with an embedded digital push–pull gauge (DTG-100, DIGITECHCO. Ltd., Osaka, Japan) [28]. The calibration results showed a correlation coefficient of 0.97 ± 0.03 and a root mean square error of 3.15 ± 1.39 N.
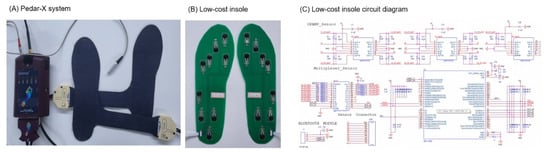
Figure 4.
Equipment used in the experiment: (A) Pedar-X system; (B) low-cost insole; (C) low-cost insole circuit diagram.
3.3. Experimental Protocols
During this experiment, participants wore either the Pedar-X or the self-developed low-cost insole, as determined by the experimenter. The chosen device was worn over friction socks [28], and participants wore body-hugging shorts to minimize marker concealment during the experiment. Sixteen anatomical landmarks spread across the lower extremities and lumbar region were marked with optical markers following the modified Helen Hayes marker set protocol [13]. The lifting box’s dimensions were 32 × 40 × 25 cm3. An additional optical marker was attached to the lifting box to identify the main phase of the experimental operation. All participants were allowed to engage in practice movements to acquaint themselves with the experimental protocol [28]. Lifting operations were conducted at four angles: 0, 30, 60, and 90 degrees [29,30]. Symmetric lifting operations included squat and stoop variations [30], while asymmetric lifting operations were performed in a free-style manner (Figure 5A). Weights of 4 and 8 kg were used for the lifting operations, and the lifting speed was set to the subject’s comfort level. Lowering operations mirrored the parameters of the lifting operations, maintaining the same weight, angle, and speed (Figure 5B). To mitigate fatigue during the experiment, participants were provided with rest opportunities between operations. The order of each experimental operation was also randomized to prevent subjects from becoming accustomed to the experiments.
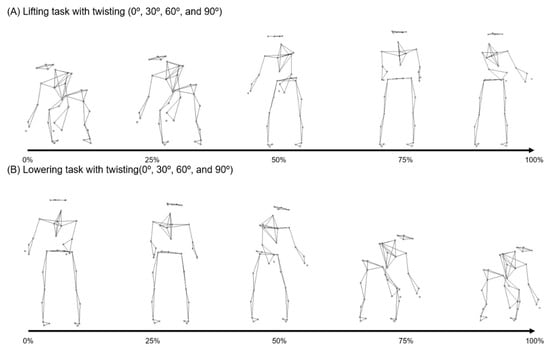
Figure 5.
Experimental descriptions: (A) lifting; (B) lowering.
4. Performance Evaluation
To evaluate the models predicting the moment of the lumbar spine along three axes during the lifting operation proposed in this study, the results were obtained through five-fold cross-validation. The dataset was divided into training and testing sets with a ratio of 8:2. The performance of the lumbar joint moment prediction model was evaluated using root mean square error (RMSE), rRMSE, and the Pearson correlation coefficient (R). The performance evaluation parameters were calculated using the following equations.
In the equations above, represents the actual value, represents the value predicted by the artificial intelligence model, and N represents the length of one trial. In Equation (2), R represents the value of the Pearson correlation coefficient. is the average of the actual values, () is the average of the values predicted by the artificial intelligence model, max() is the largest value in one trial, and min() is the smallest value in one trial. One-way ANOVA and post-test were performed to assess the statistical significance of any differences in the performance of each model. Statistical analysis was conducted using the PASW program, version 18 (SPSS Inc., Chicago, IL, USA). One-way ANOVA and post-test were performed to confirm the statistical significance of any differences in the performance of each model.
5. Result
Figure 6 illustrates the results of ground truth, source, conventional, and target #3 for asymmetric lifting operations executed at 0°, 30°, 60°, and 90°. Representative values were selected to be presented for each operation. For the asymmetric lifting operation at 0 degrees, the values are near 0 (N·M/kg) for lateral flexion and twisting moments. The peak value of the flexion/extension moment tends to decrease as the angle increases. Moreover, the twisting moment increases proportionally to the angle value. Figure 7 is like Figure 6, again representing the results for asymmetric lowering operations at 0°, 30°, 60°, and 90°. Lowering shows a similar trend to lifting, with the peak value of the flexion/extension moment decreasing as the angle increases, and where the twisting moment’s peak value tends to increase with the angle.
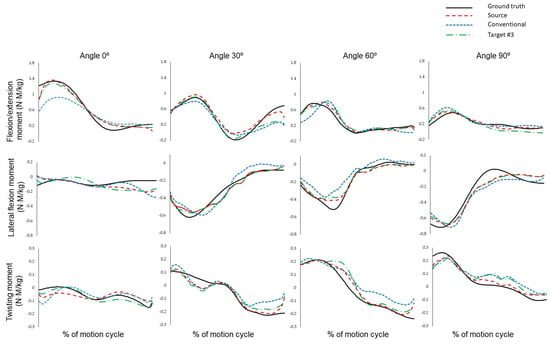
Figure 6.
Representative result of lumbar joint moment during lifting.
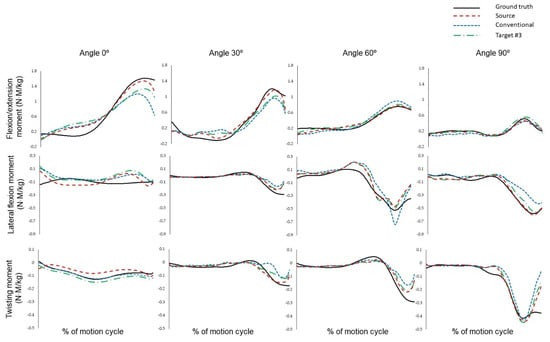
Figure 7.
Representative result of lumbar joint moment during lowering.
Figure 8 represents Bland–Altman plots of the lumbar flexion/extension moment based on the fine-tuning technique. Three methods (target #1, target #2, and target #3) were proposed for the lifting and lowering operations, and six Bland–Altman plots are presented for each operation. The upper limits for (A) to (C) in Figure 8 are, respectively, 0.150, 0.145, and 0.115, while the lower limits are −0.155, −0.219, and −0.133. On the other hand, for (D) to (F) in Figure 8, the upper limits are 0.084, 0.068, and 0.122, and the lower limits are −0.173, −0.264, and −0.121. In both the lifting and lowering tasks, the standard deviation of the target #3 model was the least.
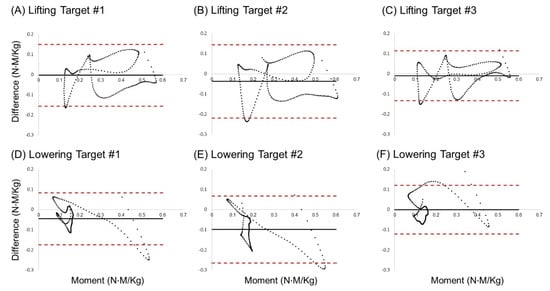
Figure 8.
Bland–Altman plot of 60° asymmetric lifting L5/S1 flexion/extension moment: (A) lifting target #1, (B) lifting target #2, (C) lifting target #3, (D) lowering target #1, (E) lowering target #2, and (F) lifting target #3.
Figure 9 is a graph showing RMSE values by model and operation, while indicating whether there is a statistically significant difference between the source model and other models. In the lifting operation, a significant difference can be seen in performance between the source model and the remaining three models, aside from the target #3 model. Regarding the lowering operation, the source model shows a statistically significant difference in performance for all models, and the target #3 model does not exhibit a difference in performance that is statistically significant at the p-value level of 0.05.
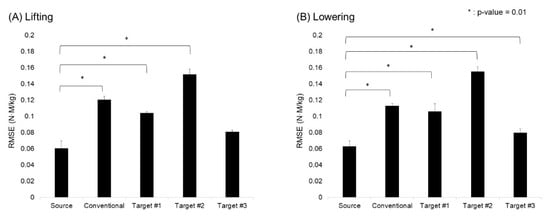
Figure 9.
Model-specific predictive performance of lumbar joint moment: (A) lifting; (B) lowering.
Table 2 presents the RMSE, rRMSE, and correlation coefficient values for each model, operation, and angle for the flexion/extension moment. Source, conventional, target #1, target #2, and target #3 show respective values of 9.60–11.74%, 15.86–18.87%, 15.15–17.07%, 19.34–21.50%, and 11.94–13.13%. From these results, no significant trend in performance change is observed based on the operation and angle.

Table 2.
Overall performance of our proposed lumbar flexion/extension joint moment prediction model.
6. Discussion
This study has proposed a machine learning model that can be used to estimate lumbar joint moment during lifting operations, with the ultimate intention of helping establish a control strategy for active exoskeleton devices designed to support the waist. The model’s performance was enhanced through pre-training with Pedar-X device data, which is known for its higher precision than data collected from low-cost insoles. The trained model’s weights were then transferred to a low-cost insole domain model. The resulting model demonstrated an rRMSE of 11.94–13.13% and a correlation coefficient (r) exceeding 0.9. This model is envisioned to be particularly useful in controlling the torque generated by actuators by enabling the prediction of lumbar spine torque during lifting operations. A. Tabasi et al. (2020) previously constructed a polynomial curve regression model for lumbar spine moment prediction utilizing kinematic data and eight EMGs from subjects and exoskeleton devices [11]. While their study achieved a coefficient of determination of 0.98 when using all data as input variables, the coefficient varied from 0.38 to 0.97 depending on the number of sEMG sensors used. Although the current study presented a lower coefficient of determination (0.85) than previous work, the present model showed higher accuracy when predicting lumbar moments without the use of sEMG sensor data (coefficient of determination: 0.38). In another study, Koopman et al. (2019) estimated torque for lumbar compression force control and obtained results like those obtained in the current study [31]. Thus, the lumbar moments predicted in this study are expected to be appropriate for use as a parameter for control strategies requiring information on the necessary net moment near joints.
To enhance lumbar moment prediction performance, a transfer learning strategy was employed wherein knowledge was transferred from a source domain (Pedar-X device data) to a target domain (low-cost insole data). The heterogeneous transfer learning technique that was used here, which involved different feature areas, demonstrated a performance difference of about 7% between the source and target domains. This performance difference is comparable to that obtained in a prior study by constructing a model (8.50–11.20%) that predicted sagittal plane lumbar moments using Pedar-X device pressure data [20]. Despite having certain limitations, such as computational considerations and the data’s limited laboratory environment, the current study emphasizes the potential for real-time model application in future working environments, thus paving the way for the model’s use in active-waist exoskeleton devices.
The transfer learning approach employed in this study is a heterogeneous technique that involves transferring knowledge across different feature areas. Specifically, the weights were transferred to a low-cost insole model, which was trained based on data obtained from the Pedar-X commercial device. Unlike homogeneous transfer learning, this method offers a broader range of applications, since the features used in the source and target domains may differ [32]. However, due to the distance between the source and target domains, which can potentially be considerably large, there is a higher likelihood of success for negative transfer learning compared to homogeneous transfer learning [33]. To investigate this, a case study was conducted to examine whether the LSTM layer weight values were updated or frozen during transfer learning. In the case of target #1, similar results were observed compared to the conventional model (which was used as the control group). Target #2 exhibited lower performance than the control group, thus indicating a negative transfer learning example, as it showed a decrease in rRMSE by about 3.6% compared to the conventional model. By contrast, target #3, the proposed model, demonstrated higher performance than the control group, specifically, achieving a 7% improvement in rRMSE compared to the conventional model. While it is common to empirically update the last layer during fine-tuning [34], the selection of a fine-tunable layer is not always a straightforward task, as evidenced by cases where selecting the last layer does not necessarily yield high performance [34,35]. Therefore, it is essential to carefully consider which layers to update and freeze during fine-tuning.
The present study has several limitations. Firstly, the model was constructed on a workstation without computational or capacity constraints, thus neglecting considerations of model capacity or computational requirements. When applying the lumbar estimation model constructed in this study to real-world working environments, the model’s capacity and computational demands should be considered in relation to accuracy to strike an appropriate trade-off. Secondly, this study only utilized an architecture based on LSTM for constructing the lumbar estimation model. Further research utilizing various models to evaluate model performance is necessary. Secondly, there are several limitations from the perspective of deep learning models. The use of only LSTM models for estimating lumbar moments is a limitation. The rapid advancements in the field of deep learning have introduced various validated architectures, such as attention modules based on CNNs [36,37]. Additionally, when configuring transfer learning, the study did not consider the biased errors of the source model due to the limited dataset. Some previous research has revealed the existence of biases in the transferred target model when utilizing a biased source model [38]. Therefore, for future research, evaluating the bias in model datasets and exploring diverse state-of-the-art architectures is deemed necessary to enhance the prediction performance of lumbar moments. Thirdly, the model was constructed based on data obtained in a controlled laboratory environment. When applied to actual working conditions, the proposed accuracy might be lower. Therefore, incorporating various operational scenarios (e.g., lifting objects from uneven ground) in future data collection efforts is essential to build a more robust model. Lastly, this study developed a model utilizing data from specific groups and specific pressure sensors. The workplace includes various groups, such as diverse genders and age groups. Additionally, there may be various types of pressure measurement settings, ranging from precise force plates to low-cost FSR sensors. Nevertheless, this study proposes a generalized process that operates with data only from areas where pressure is concentrated on the foot, estimating lumbar moments using pressure signals. In the future, to further enhance generalizability, it will be necessary to apply this process to various population groups and diverse environmental settings.
7. Conclusions
This study proposes a machine learning model that can predict lumbar spine moments using low-cost sensor data, with the aim of developing a control strategy for waist-active exoskeleton devices. To enhance the model’s performance, a training method using high-precision commercial insole data and fine-tuning with low-cost insole data was employed. Compared to the conventional model, this approach resulted in a 7% performance improvement, achieving an rRMSE of approximately 12% and a correlation coefficient of 0.9 in torque prediction. If the model can secure real-time performance and demonstrate effectiveness across various operations in future applications, it could hold substantial potential for deployment as an active exoskeleton device for the waist.
Author Contributions
Conceptualization, A.C.; methodology, S.C.; validation, S.C.; formal analysis, S.C.; resources, J.H.M.; data curation, J.K.; writing—original draft preparation, S.C., A.C. and J.K.; writing—review and editing, S.C. and A.C.; supervision, J.H.M.; project administration, J.H.M.; funding acquisition, J.H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research Foundation of Korea (NRF), Korea Government (MSIT), grant number 2021R1A2C1009951 and this work was in part supported by a grant (Project No.: 20016285) of Technology Innovation Program funded by the Ministry of Trade, Industry and Energy (MOTIE), Republic of Korea.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Balagué, F.; Mannion, A.F.; Pellisé, F.; Cedraschi, C. Non-specific low back pain. Lancet 2012, 379, 482–491. [Google Scholar] [CrossRef] [PubMed]
- Radwin, R.G.; Marras, W.S.; Lavender, S.A. Biomechanical aspects of work-related musculoskeletal disorders. Theor. Iss. Ergon. Sci. 2001, 2, 153–217. [Google Scholar] [CrossRef]
- Bernard, B.P.; Putz-Anderson, V. Musculoskeletal Disorders and Workplace Factors—A Critical Review of Epidemiologic Evidence for Work-Related Musculoskeletal Disorders of the Neck, Upper Extremity, and Low Back; The National Institute for Occupational Safety and Health (NIOSH): Washington, DC, USA, 1997.
- Kingma, I.; de Looze, M.P.; Toussaint, H.M.; Klijnsma, H.G.; Bruijnen, T.B. Validation of a full body 3-D dynamic linked segment model. Hum. Mov. Sci. 1996, 15, 833–860. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, H. A lower-back robotic exoskeleton: Industrial handling augmentation used to provide spinal support. IEEE Robot. Autom. Mag. 2018, 25, 95–106. [Google Scholar] [CrossRef]
- Lazzaroni, M.; Fanti, V.; Sposito, M.; Chini, G.; Draicchio, F.; Di Natali, C.; Ortiz, J. Improving the efficacy of an active back-support exoskeleton for manual material handling using the accelerometer signal. IEEE Robot. Autom. Lett. 2022, 7, 7716–7721. [Google Scholar] [CrossRef]
- Pesenti, M.; Antonietti, A.; Gandolla, M.; Pedrocchi, A. Towards a functional performance validation standard for industrial low-back exoskeletons: State of the art review. Sensors 2021, 21, 808. [Google Scholar] [CrossRef]
- Toxiri, S.; Näf, M.B.; Lazzaroni, M.; Fernández, J.; Sposito, M.; Poliero, T.; Ortiz, J. Back-support exoskeletons for occupational use: An overview of technological advances and trends. IISE Trans. Occup. Ergon. Hum. Factors 2019, 7, 237–249. [Google Scholar] [CrossRef]
- Moya-Esteban, A.; van der Kooij, H.; Sartori, M. Robust estimation of lumbar joint forces in symmetric and asymmetric lifting tasks via large-scale electromyography-driven musculoskeletal models. J. Biomech. 2022, 144, 111307. [Google Scholar] [CrossRef]
- Plamondon, A.; Gagnon, M.; Gravel, D. Moments at the L5/S1 joint during asymmetrical lifting: Effects of different load trajectories and initial load positions. Clin. Biomech. 1995, 10, 128–136. [Google Scholar] [CrossRef]
- Tabasi, A.; Kingma, I.; de Looze, M.P.; van Dijk, W.; Koopman, A.S.; van Dieën, J.H. Selecting the appropriate input variables in a regression approach to estimate actively generated muscle moments around L5/S1 for exoskeleton control. J. Biomech. 2020, 102, 109650. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Zhao, S.; Yuan, Y.; Kang, Y.; Chen, C.P. Adaptive neural control of a kinematically redundant exoskeleton robot using brain–machine interfaces. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3558–3571. [Google Scholar] [CrossRef]
- Gallagher, S.; Kotowski, S.; Davis, K.G.; Mark, C.; Compton, C.S.; Huston, R.L.; Connelly, J. External L5–S1 joint moments when lifting wire mesh screen used to prevent rock falls in underground mines. Int. J. Ind. Ergon. 2009, 39, 828–834. [Google Scholar] [CrossRef]
- Choi, A.R.; Yun, T.S.; Lee, K.S.; Min, K.K.; Hwang, H.; Lee, K.Y.; Mun, J.H. Asymmetric loading of erector spinae muscles during sagittally symmetric lifting. J. Mech. Sci. Technol. 2009, 23, 64–74. [Google Scholar] [CrossRef]
- Choi, A.; Lee, J.M.; Mun, J.H. Ground reaction forces predicted by using artificial neural network during asymmetric movements. Int. J. Precis. Eng. Manuf. 2013, 14, 475–483. [Google Scholar] [CrossRef]
- Faber, G.S.; Kingma, I.; Chang, C.C.; Dennerlein, J.T.; Van Dieen, J.H. Validation of a wearable system for 3D ambulatory L5/S1 moment assessment during manual lifting using instrumented shoes and an inertial sensor suit. J. Biomech. 2020, 102, 109671. [Google Scholar] [CrossRef] [PubMed]
- Hlucny, S.D.; Novak, D. Characterizing human box-lifting behavior using wearable inertial motion sensors. Sensors 2020, 20, 2323. [Google Scholar] [CrossRef]
- Kim, T.H.; Choi, A.; Heo, H.M.; Kim, H.; Mun, J.H. Acceleration magnitude at impact following loss of balance can be estimated using deep learning model. Sensors 2020, 20, 6126. [Google Scholar] [CrossRef] [PubMed]
- Aghazadeh, F.; Arjmand, N.; Nasrabadi, A.M. Coupled artificial neural networks to estimate 3D whole-body posture, lumbosacral moments, and spinal loads during load-handling activities. J. Biomech. 2020, 102, 109332. [Google Scholar] [CrossRef] [PubMed]
- Chae, S.; Choi, A.; Jung, H.; Kim, T.H.; Kim, K.; Mun, J.H. Machine learning model to estimate net joint moments during lifting task using wearable sensors: A preliminary study for design of exoskeleton control system. Appl. Sci. 2021, 11, 11735. [Google Scholar] [CrossRef]
- Houlsby, N.; Giurgiu, A.; Jastrzebski, S.; Morrone, B.; De Laroussilhe, Q.; Gesmundo, A.; Gelly, S. Parameter-efficient transfer learning for NLP. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2790–2799. [Google Scholar]
- Han, X.; Zhang, Z.; Ding, N.; Gu, Y.; Liu, X.; Huo, Y.; Zhu, J. Pre-trained models: Past, present and future. AI Open 2021, 2, 225–250. [Google Scholar] [CrossRef]
- Qiu, X.; Sun, T.; Xu, Y.; Shao, Y.; Dai, N.; Huang, X. Pre-trained models for natural language processing: A survey. Sci. China Technol. Sci. 2020, 63, 1872–1897. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Niu, S.; Liu, Y.; Wang, J.; Song, H. A decade survey of transfer learning (2010–2020). IEEE Trans. Artif. Intell. 2020, 1, 151–166. [Google Scholar] [CrossRef]
- Kuijer, P.P.F.M.; van Oostrom, S.H.; Duijzer, K.; Van Dieen, J.H. Maximum acceptable weight of lift reflects peak lumbosacral extension moments in a functional capacity evaluation test using free style, stoop and squat lifting. Ergonomics 2012, 55, 343–349. [Google Scholar] [CrossRef]
- Mei, Q.; Gu, Y.; Xiang, L.; Yu, P.; Gao, Z.; Shim, V.; Fernandez, J. Foot shape and plantar pressure relationships in shod and barefoot populations. Biomech. Model. Mechanobiol. 2009, 19, 1211–1224. [Google Scholar] [CrossRef]
- Mun, F.; Choi, A. Deep learning approach to estimate foot pressure distribution in walking with application for a cost-effective insole system. J. NeuroEng. Rehabil. 2022, 19, 4. [Google Scholar] [CrossRef]
- Alemi, M.M.; Geissinger, J.; Simon, A.A.; Chang, S.E.; Asbeck, A.T. A passive exoskeleton reduces peak and mean EMG during symmetric and asymmetric lifting. J. Electromyogr. Kinesiol. 2019, 47, 25–34. [Google Scholar] [CrossRef]
- Hwang, S.; Kim, Y.; Kim, Y. Lower extremity joint kinetics and lumbar curvature during squat and stoop lifting. BMC Musculoskelet. Disord. 2009, 10, 15. [Google Scholar] [CrossRef] [PubMed]
- Koopman, A.S.; Toxiri, S.; Power, V.; Kingma, I.; van Dieën, J.H.; Ortiz, J.; de Looze, M.P. The effect of control strategies for an active back-support exoskeleton on spine loading and kinematics during lifting. J. Biomech. 2019, 91, 14–22. [Google Scholar] [CrossRef] [PubMed]
- Day, O.; Khoshgoftaar, T.M. A survey on heterogeneous transfer learning. J. Big Data 2017, 4, 29. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, L.; Zhang, L.; Wu, D. A survey on negative transfer. IEEE/CAA J. Autom. 2022, 10, 305–329. [Google Scholar] [CrossRef]
- Vrbančič, G.; Podgorelec, V. Transfer learning with adaptive fine-tuning. IEEE Access 2020, 8, 196197–196211. [Google Scholar] [CrossRef]
- Guo, Y.; Shi, H.; Kumar, A.; Grauman, K.; Rosing, T.; Feris, R. Spottune: Transfer learning through adaptive fine-tuning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4805–4814. [Google Scholar]
- Wang, F.; Jiang, M.; Qian, C.; Yang, S.; Li, C.; Zhang, H.; Tang, X. Residual attention network for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR 2017, Honolulu, HI, USA, 21–26 June 2017; pp. 3156–3164. [Google Scholar]
- Chen, L.; Hu, D. An effective swimming stroke recognition system utilizing deep learning based on inertial measurement units. Adv. Robot. 2023, 37, 467–479. [Google Scholar] [CrossRef]
- Salman, H.; Jain, S.; Ilyas, A.; Engstrom, L.; Wong, E.; Madry, A. When does Bias Transfer in Transfer Learning? arXiv 2022, arXiv:2207.02842. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).