Abstract
Needle manipulation with the guidance of magnetic resonance imaging (MRI) plays a key role in minimally invasive procedures such as biopsy and ablation. However, the confined bore and strong magnetic field of the MR environment pose great challenges in developing a robotic system that fulfills the needle manipulation function. This paper presents the design and analysis of a soft needle manipulator (SoNIM) that can achieve needle manipulation in the MR environment. This pneumatically actuated manipulator consists of two bending actuators and one elongation actuator that are completely made of non-magnetic materials. These soft pneumatic actuators can generate flexible movements while maintaining a compact design, ensuring that the SoNIM is accommodated within the MRI bore. The kinematic modeling and closed-loop control of the SoNIM are investigated to achieve the position control of the needle tip. Experiments showed that the SoNIM was capable of directing the needle tip to reach the targets with a satisfactory accuracy of 2.9 ± 0.98 mm. Furthermore, the functionality and MRI compatibility of the SoNIM were validated in the clinical setting, demonstrating the capability of the SoNIM to perform needle manipulation in the MRI bore with negligible degradation to the image quality. With excellent MRI compatibility, compact design, and flexible movements, the SoNIM provides a promising solution for manipulating surgical needles in MRI-guided minimally invasive surgeries.
1. Introduction
Needle manipulation is a key procedure in minimally invasive surgeries, such as the biopsy and ablation of tumors []. During the procedure, surgeons need to spend a lot of effort adjusting the needle to reach the target tumors with the guidance of magnetic resonance imaging (MRI) []. Surgical robots offer an alternative way to assist with this procedure []. However, there is still a lack of a surgical robot that fulfills this needle manipulation function in the MR environment.
The development of surgical robots that operate within the MRI bore during a surgical procedure remains a great challenge due to the strong magnetic field and the confined space of the MRI scanner. Some criteria have been established to guide the design of MRI-compatible surgical robots []. First of all, these robots should be constructed from non-magnetic and non-metallic materials to avoid interference with the magnetic field of the MRI scanner. Additionally, the actuation of these surgical robots should be MRI-compatible to prevent electromagnetic interference and MR image artifacts. The common actuation methods that meet these design criteria include piezoelectric motors, hydraulic actuators, and pneumatic actuators []. New actuation technologies for MRI-compatible surgical robots have also attracted much attention. For example, a new electromagnetic servomotor (EMSM) constructed from non-magnetic components was reported []. This motor generated high-torque and rotary actuation via the interaction between the electrical current in the servomotor armature and the magnetic field of the MRI scanner itself. Another notable advancement is a pneumatic actuator (PM) designed based on the operation principle of step motors, which provides high-resolution and fast rotational motion []. The above actuation technologies represent a new generation of actuators, which can simplify the design of MRI-compatible surgical robots.
Based on the above design criteria, several representative MRI-compatible surgical robots have been developed. The earliest work can be traced back to a needle insertion manipulator (NIM) with the purpose of MRI-guided intracranial biopsies []. The NIM was actuated by commercial piezoelectric motors with satisfactory control accuracy and actuation speed. However, the operation of the motor drivers caused excessive artifacts in the images, limiting the application of the NIM in the MR environment. Another example is a fully actuated robotic system (FARS) driven by piezoelectric motors for needle manipulation in percutaneous prostate brachytherapy []. This compact robotic system demonstrated that the customized motor drivers had the potential to minimize image artifacts. However, these motor drivers were expensive and the operation of the motor drivers still impaired the image quality. Besides piezoelectrically actuated robots, an electrophysiology catheter robot (EPCR) actuated via hydraulic motors was developed for ultrasound thermal therapy under MRI. This robot was completely made of non-magnetic materials, thereby ensuring no interference with MR imaging. But, hydraulic motors still face challenges like potential fluid leakage []. Furthermore, a needle-guiding robot (NGR) was developed using pneumatic cylinders []. These pneumatic cylinders offer a simple and low-cost actuation method to deal with the leakage issue of hydraulic actuation. However, the bulky size and sophisticated arrangement of the pneumatic cylinders make it difficult to generate both rotational and linear motion, restricting the capacity of the robot to manipulate the ablation needle.
Soft robots present another potential solution to overcome the drawbacks of traditional robots due to their intrinsic compliance and MRI compatibility []. For example, a continuum neurosurgical robot, MINIR, actuated by shape memory alloy (SMA), was proposed for the ablation of brain tumors [,]. With the inherent compliance and small size, MINIR enabled flexible movements of an electrocautery needle in a gelatin slab. But the low actuation speed and nonlinear properties of the SMA hindered the practical application of the MINIR. Fang et al. proposed an MRI-compatible soft endoscopic manipulator (SEM) to achieve the transoral laser ablation of tumors using soft actuators [,]. This work demonstrated the feasibility of soft robots for ablation surgery in an MR environment. However, the SEM was dedicated to noncontact ablations and the needle manipulation function was not considered. The aforementioned prototypes are also summarized in Table 1. It is evident that the design, material, and actuation method are still challenging for surgical robots that manipulate a needle in an MR environment. Therefore, there remains a gap in the knowledge about the effective solution to achieve needle manipulation in the MRI bore while preserving the quality of the MRI.

Table 1.
Comparison of several typical MRI-compatible actuators and surgical robots.
In this paper, we report an MRI-compatible soft needle manipulator (SoNIM) that can direct the needle tip toward the target with acceptable accuracy. This pneumatically actuated manipulator consists of three silicon segments that are the proximal bending, middle bending, and distal elongation actuator. The SoNIM harnesses the collective deformation of the actuators, fulfilling the needle manipulation function. The performance of the bending and elongation actuators is characterized, showing the capability to manipulate and insert the needle. Then, the analytical model of the SoNIM is derived and an online Jacobian estimation method is further proposed to improve the modeling accuracy. Consequently, a closed-loop control scheme is formulated based on the Jacobian estimation to achieve the position control of the needle tip. Set-point tracking experiments illustrate that the SoNIM was capable of directing the needle tip to reach the target points with an accuracy of 2.9 ± 0.98 mm. In addition, the SoNIM was able to insert the needle tip into a tumor-like gelatin phantom using the developed control scheme, demonstrating its potential application for the biopsy of tumors. Finally, the functionality and MRI compatibility of the SoNIM were examined in an MR environment, which showed that the SoNIM had the capability to perform needle manipulation in the MRI scanner with negligible degradation to the image quality.
To the best of our knowledge, the SoNIM presents the first attempt to advance soft robotics in needle-based minimally invasive surgeries. Unlike traditional soft manipulators, the SoNIM is dedicated to performing needle manipulation in minimally invasive surgeries. The unique design of the bending and elongation actuators endows the SoNIM with the needle manipulation function. The experimental validation of the SoNIM in the MR environment also demonstrates the potential of soft robots to perform needle manipulation in the MRI bore, laying a foundation for their applications in MRI-guided minimally invasive surgeries.
The rest of the paper is organized as follows. Section 2 presents the design and working principle of the SoNIM. Then, the kinematic modeling and closed-loop control of the SoNIM are introduced in Section 3. Section 4 elaborates on experiments to examine the proposed soft actuators, kinematics, control method, and MRI compatibility of the SoNIM. The corresponding experimental results are analyzed in Section 5. Section 6 concludes our current work and future plan for the SoNIM.
2. Design and Working Principle
MRI-compatible surgical robots hold great potential to facilitate needle manipulation in minimally invasive procedures. However, the confined bore, strong magnetic field, and needle-manipulating function impose strict requirements on the design, material selection, and actuation method of the surgical robot. First, the design of the surgical robot should be compact enough to be accommodated inside the MRI bore, which commonly has a diameter ranging from 500 to 700 mm. The design should also take the needle-manipulating function into consideration, particularly the function of needle insertion, which is the key step in biopsy, ablation, and brachytherapy. Second, the material selection for the MRI environment should be non-magnetic and non-metallic, which share the key features of the soft robotic techniques. Third, the actuation method should be not only MRI-compatible to prevent image artifacts but also reliable and efficient in driving the needle.
To fulfill the above requirements, the design of the SoNIM is proposed as shown in Figure 1a. The SoNIM is a compact soft pneumatic manipulator that is made of silicone material. The SoNIM consists of three soft actuators, including the proximal bending, middle bending, and distal elongation actuators. These actuators are sequentially linked, forming the prototype of the SoNIM. The SoNIM exploits the collective deformation of these actuators to guide the motion of the mock needle that is affixed to the end of the manipulator.
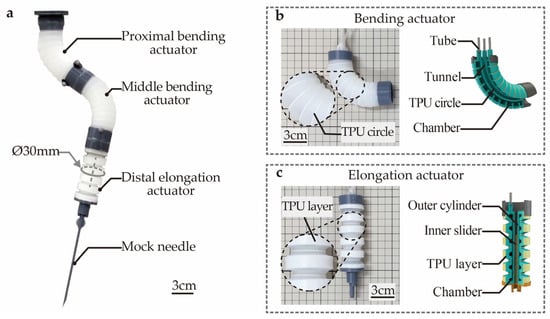
Figure 1.
Design of the soft needle manipulator (SoNIM). (a) The prototype of the SoNIM. The prototype (left) and the cross-sectional image (right) of (b) the bending actuator and (c) the elongation actuator.
Figure 1b depicts the prototype and the cross-sectional image of the bending actuator. The bending actuator is embedded with three air chambers that are uniformly distributed along its circumference. This actuator can achieve omnidirectional bending movements by regulating the inflation pressures of its chambers. The current bending actuator is an enhanced version of our earlier design []. Distinct from the previous design, an array of thermoplastic polyurethane (TPU) circles is attached to the surface of the bending actuator. These TPU circles play a key role in limiting the radial expansion of the actuator, thereby enhancing the repeatability of the bending deformation. Figure 1c illustrates the elongation actuator that is embedded with a bellows-like air chamber. Similar to the bending actuator, TPU layers are attached to the surface of the elongation actuator to restrict the radial expansion. The elongation actuator enables linear movement when pressurized, thereby fulfilling the function of needle insertion.
Figure 2 illustrates the deployment of the SoNIM within an MRI setting. The SoNIM is mounted on a non-metallic frame and positioned inside the bore of the MRI scanner. To avoid interference with the magnetic field of the MRI scanner, the actuation system of the manipulator is situated in the adjacent control room. Ten-meter pneumatics tubes are used to connect the SoNIM to its actuation system. This system, including an air source, seven pressure regulators, and a computer, is equipped to actuate the SoNIM. The SoNIM is pneumatically actuated to direct the movement of the needle inside the confined bore of the MRI scanner, ensuring effective needle manipulation in this sensitive environment.

Figure 2.
Schematic diagram of the deployment of the soft needle manipulator (SoNIM) within an MRI setting.
These soft pneumatic actuators were selected for the SoNIM system to overcome the limitations of other prevalent methods, such as piezoelectric motors and hydraulic actuators. Piezoelectric motors were commonly used in MRI-compatible systems, but these motors created artifacts in the MR images when placed near the imaging area. Hydraulic actuators are MRI-compatible due to the absence of electrical and magnetic components, but these actuators still face challenges like complex mechanical structures and potential fluid leakage. In contrast, these pneumatic actuators, despite their nonlinear behavior and lower bandwidth, offer several notable advantages, such as MRI compatibility, compact design, inherent flexibility, and cost-effectiveness. These advantages make it well suited for MRI settings.
3. Kinematics and Control
In this section, an analytical model is formulated based on the constant curvature assumption to describe the kinematics of the SoNIM. An online Jacobian estimation approach is further proposed to capture modeling errors due to the unmodeled factors. Finally, a closed-loop control strategy is developed based on the Jacobian estimation to achieve the position control of the SoNIM.
3.1. Analytical Model of the SoNIM
The analytical model of the SoNIM is established under the constant curvature assumption to describe the needle tip position. Within this model, the configuration of each bending actuator is regarded as an arc characterized by three parameters, including the arc length s1, bending angle θ1, and deflection angle φ1, as labeled in the inset of Figure 3a. Additionally, the elongation actuator is regarded as a prismatic joint that describes linear movement. The key variables involved in the analytical model are demonstrated in Figure 3a. The chamber lengths of the three actuators are denoted as [l11, l12, l13, l21, l22, l23, le] as labeled in the figure. The inflation pressures corresponding to the seven chambers are represented by [p11, p12, p13, p21, p22, p23, pe]. Furthermore, four coordinate systems are added to the top surface, two connection parts, and the needle tip of the SoNIM, which facilitates the following derivation of the analytical model.
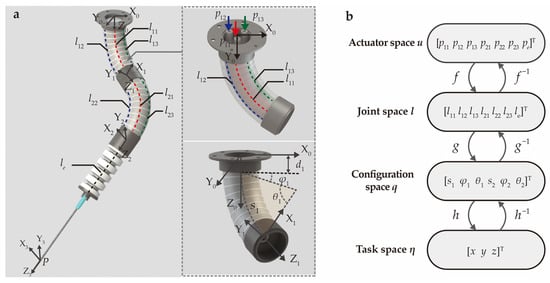
Figure 3.
The schematic illustration of the kinematic modeling for the SoNIM. (a) Schematics of the manipulator annotated with coordinate systems and key variables. Dotted lines represent the chambers labeled with the corresponding length. The inset displays the proximal bending actuator marked with the input pressures p11, p12, p13 and the arc parameters s1, φ1, θ1. (b) The kinematics of the manipulator that contains three mappings connecting four spaces.
The analytical model of the SoNIM consists of three mappings f, g, and h as shown in Figure 3b. These three mappings describe the relationships among the actuator space u, the joint space l, the configuration space q, and the task space η. Specifically, the actuator space u = [p11, p12, p13, p21, p22, p23, pe]T is composed of the input pressure in the air chambers, and the joint space l = [l11, l12, l13, l21, l22, l23, le]T refers to the corresponding chamber length. The configuration space q = [s1, φ1, θ1, s2, φ2, θ2]T represents the arc parameters of two bending actuators. The task space η = [x, y, z]T represents the position of the needle tip with respect to the global coordinate system {X0 Y0 Z0}.
The first mapping l = f(u) describes the relationship between the input pressure u and the length of each chamber l. This mapping is established via a series of characterization experiments conducted on the bending and elongation actuators. The second mapping q = g(l) explicates the connection between the chamber length l and the arc parameters q of the two bending actuators. According to the constant curvature assumption, the arc parameters {si, φi, θi|i = 1, 2} are derived from the chamber length {li1, li2, li3|i = 1, 2} as shown below.
where i = 1, 2 refer to the proximal and middle bending actuators, respectively. d denotes the radius of the bending actuator.
The third mapping η = h(q) establishes the connection between the configuration space q and the task space η. This mapping h is derived from a parameterized homogenous transformation using the Denavit-Hartenberg (D-H) approach as shown below. The D-H method is a basic method to derive the homogeneous transformation for the bending actuator within the constant curvature model. The specific D-H definition of the bending actuator has been well established in existing literature [].
η = [(1,4) (2,4) (3,4)]T denotes the position of the needle tip in the global coordinate system, where (m,n) denotes the element in the mth row and nth column of the matrix . is a 3 × 3 rotation matrix representing the orientation of the needle.
Specifically, the transformation matrix is obtained by multiplying the transformation matrices of the three actuators as shown below.
and denote the transformation matrices corresponding to the proximal and middle bending actuators. The two transformation matrices are calculated based on the arc parameters {si, φi, θi|i = 1, 2} as shown in Equation (4). It is noted that a constant di is incorporated into the two transformation matrices to accommodate the length of the rigid connectors. is the translation transformation corresponding to the elongation actuator, where le and ln denote the lengths of the elongation actuator and needle, respectively.
Once the mappings g and h are established, the analytical model of the SoNIM is presented as follows.
The derived analytical model (5) offers a mapping from the joint space l to the task space η, enabling the prediction of the needle tip position. This analytical model offers a straightforward expression for the kinematics of the SoNIM, which facilitates the closed-loop control of the robot. However, this analytical approach suffers from modeling errors due to unmodeled factors, such as gravity and fabrication uncertainty, which degrade the control accuracy of the SoNIM.
3.2. Online Jacobian Estimation
The online estimation approaches offer a way to obtain the Jacobian of the soft manipulator and overcome the limitation of the analytical model. However, existing online Jacobian estimation methods are faced with problems of sensitivity to measurement noise and dependency on sufficient data volume. For example, Yip et al. introduced a purely data-driven approach to estimating the Jacobian of a soft manipulator []. Moreover, Li et al. proposed to estimate the Jacobian via a Kalman filter, enabling the trajectory-tracking control of a soft robot []. These methods often yield inaccurate Jacobian estimations in the initial stages due to the insufficiency of the collected data. Additionally, the measurement noise further reduced the reliability of these estimation approaches.
To overcome the above limitations, a new online Jacobian estimation method is proposed. This method combines the online estimation with the analytical model, providing a way to enhance the reliability and accuracy of the estimated Jacobian. To introduce this method, the analytical model-based Jacobian matrix of the SoNIM is first derived. The Jacobian of the SoNIM is the derivative of the analytical model (5) with respect to time. The Jacobian offers a linear transformation to describe the kinematics of the SoNIM as shown below.
where g and h represent the two nonlinear mappings of the kinematics. represents the Jacobian matrix that maps the velocities in the joint space to those in the task space .
The proposed Jacobian estimation approach combines the online estimation with the analytical model, which is formulated as shown below.
Here, and denote the actual velocities of the needle tip and the actual Jacobian of the SoNIM. The actual Jacobian is composed of two parts, which are the Jacobian J(l) based on the analytical model and the additive term ΔJ accounting for the effect of modeling errors.
Furthermore, an online optimization algorithm is proposed to estimate the actual Jacobian of the SoNIM. In this algorithm, the Jacobian estimation is formulated as an optimization problem with the cost function and constraint as shown below.
where and represent the estimation of the actual Jacobian and the estimation of the additive term, respectively. and are positive-definite matrices. minimizes the deviation between the actual velocities of the needle tip and those predicted by the Jacobian estimation , ensuring the Jacobian estimation reduces the modeling errors. minimizes the Frobenius norm of the additive term , which can prevent the system instability caused by measurement noise. The constraint illustrates that the Jacobian estimation combines the prior knowledge of the analytical model and the new information of the system from the experimental data. This combination enables the online Jacobian estimation to minimize the effect of measurement noise and improve the modeling accuracy.
3.3. Closed-Loop Control Scheme
Based on the Jacobian estimation , we propose a closed-loop control scheme to guide the needle tip of the soft manipulator to reach the desired position as shown below.
Here, is the pseudoinverse of the Jacobian. and represent the measured position and the desired position of the needle tip, respectively. The symbol denotes the feedback gain, which is a positively defined matrix. After formulating the controller (9), the input pressure u is derived according to the inverse mapping u = f−1(l). The derived input pressure u is applied to inflate the SoNIM, thereby directing the needle tip to reach the targets.
This control scheme is composed of three elements, including the feedforward component , the feedback component , and the online Jacobian estimation. The feedforward component aims to track the desired velocity . Meanwhile, the feedback component is responsible for minimizing the tracking errors between the actual position of the needle tip and the desired position . The online Jacobian estimation is exploited to update the actual Jacobian of the SoNIM, thereby improving the control accuracy. The synergy of these three components offers an approach to achieve the accurate position control of the SoNIM.
4. Experiments
Experiments were carried out to evaluate the performance of the SoNIM in four aspects. Initially, the bending and elongation actuators were examined to evaluate their deformation performance and establish the relationship between the chamber length and the inflation pressure. Subsequently, the accuracy of the proposed analytical model and online Jacobian estimation were examined by predicting the position of the needle tip under a given set of inflation pressures. Then, set-point tracking experiments were conducted to test the closed-loop control accuracy of the SoNIM in the laboratory setting. Finally, the functionality and MRI compatibility of the SoNIM were evaluated in the MR environment.
4.1. Experiments for Characterization of Soft Actuators
Characterization experiments of the bending and elongation actuators were conducted to derive the relationship between the chamber length and the inflation pressure, which is a key part of the kinematics of the SoNIM. During the experiments, a high-resolution camera (3072 × 2048 pixels, TBS060; HIKVISION, Hangzhou, China) was used to record the deformation of the two actuators under inflation and deflation at a rate of 100 Hz. A MATLAB script was employed to process the captured images and calculate the chamber length of the actuators. Specifically, the bending actuator and elongation actuator were incrementally inflated by 5 kPa, reaching a maximum pressure of 40 kPa. The inflated actuators were held for five seconds at each pressure to measure the chamber length accurately. This test setup was repeated five times to evaluate the consistency and repeatability of the actuators.
4.2. Experiments for the Kinematics
The proposed analytical model and online Jacobian estimation were examined to evaluate the modeling accuracy with the experimental setup in Figure 4. Seven proportional pressure regulators (VPPM series, 0–2 bar; Festo, Esslingen, Germany) were installed to govern the inflation pressure in the chambers of the SoNIM. During the inflation, the needle tip position of the manipulator was measured by a motion capture system (Vantage V16; Vicon Industries, Culver City, CA, USA) at a frequency of 100 Hz. A customized program was executed on a computer (MIC-7900; Advantech, Taiwan, China) to record the motion data and transmit control signals to the pressure regulators.

Figure 4.
Experimental setup used to test the proposed soft needle manipulator (SoNIM).
In the experiments, the SoNIM was inflated to generate a trajectory of the needle tip, which was used to evaluate the proposed modeling approaches. The inflation pressures of the air chambers were prescribed as periodic sinusoidal signals with different phases and amplitudes. The selection of the input pressure is suitable for the evaluation purpose because the SoNIM generated a representative trajectory in the three-dimensional space.
4.3. Experiments for Closed-Loop Control
Set-point tracking experiments were carried out to validate the control accuracy of the SoNIM. Five target points were selected within an area of 40 mm × 40 mm. This selected area is sufficient to cover an average-sized tumor in neurosurgeries, which has been reported to have a diameter of 30 mm []. In the tests, the proposed closed-loop control strategy was implemented to regulate the movement of the needle tip at a frequency of 50 Hz. The position of the needle tip was measured by the motion capture system, which provided the feedback information in the closed-loop system. For each target point, the same test was repeated five times.
Furthermore, a phantom test was carried out to simulate the biopsy procedure and assess the capability of the SoNIM for needle insertion. In this procedure, a hemispherical gelatin phantom was employed to simulate the tumor tissue. The SoNIM directed the needle tip to reach the target point using the proposed closed-loop controller. Afterward, the elongation actuator was inflated to insert the needle into the gelatin, simulating the biopsy of tumors.
4.4. Phantom Test in MRI Scanner
To validate the functionality and MRI compatibility, the SoNIM was investigated in an MR environment as shown in Figure 5. The SoNIM was mounted on a plastic frame and placed inside the MRI scanner (Ingenia 3.0T CX, Philips, Amsterdam, The Netherlands) with a bore size of seventy centimeters. The pressure regulators and other components that actuated the SoNIM were placed outside the MRI room to avoid affecting the magnetic field of the scanner. Ten-meter pneumatic tubes passed beneath the door of the MRI room to connect the SoNIM to the pressure regulators. The SoNIM was inflated inside the MRI bore to simulate a needle manipulation procedure with an interoperative MRI. The body coil was used in the MRI compatibility experiment to accommodate the soft needle manipulator. The configuration of the SoNIM during the inflation was observed through the MRI scanner as shown in the inset of Figure 5. Each pressurized state was held for ten seconds to acquire the MR images of the SoNIM.
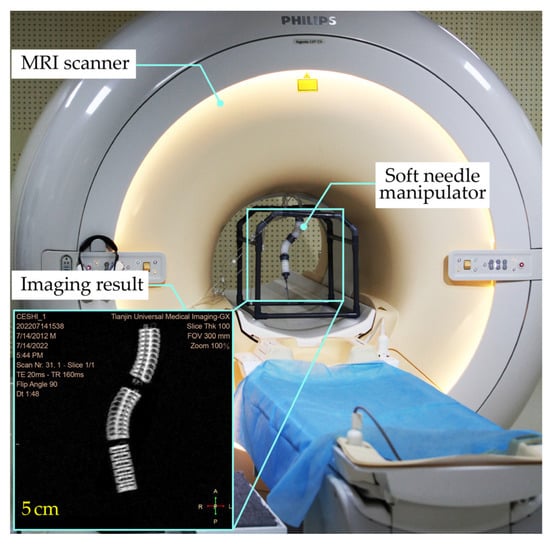
Figure 5.
Experimental setup for the phantom test in an MR environment. The soft needle manipulator (SoNIM) was mounted on a plastic frame and placed inside the MRI bore. The inset shows one frame of the image obtained by the MRI scanner.
To further evaluate the MR compatibility, the signal-to-noise ratio (SNR) analysis was adopted to quantify the image quality according to the National Electrical Manufacturers Association (NEMA) standard MS1-2008 []. The T1-weighted and T2-weighted fast-spin echo (FSE) sequences were implemented to acquire images of a cylindrical phantom. This phantom is a cylindrical bottle filled with CuSO4 solution, which is commonly used in MRI compatibility tests [,]. The MR images of the cylindrical phantom were obtained under three different conditions: (i) Baseline: Only the phantom was placed inside the MRI scanner. (ii) Static: The SoNIM was placed beside the phantom with the pneumatic control system powered off. (iii) Operating: The SoNIM was being operated and placed beside the phantom. After the image acquisition, the SNRs of the MR images in three conditions were compared to investigate the influence of the SoNIM on the image quality.
5. Results and Discussions
5.1. Characterization of Soft Actuators
Characterization experiments were conducted to examine the performance of the bending actuator and elongation actuator and derive the relationship between the chamber length and the inflation pressure (see Supplementary Movie S1). Figure 6 depicts the variations in chamber length for the bending actuator and elongation actuator across five cycles of inflation and deflation. It was observed that the deformation of these two actuators exhibited hysteresis and nonlinearity, which was mainly attributed to the inherent elastic properties of soft materials. Furthermore, the repeatability of the two actuators was evaluated via the maximum standard deviation (MSD). The calculation results illustrate that both the bending actuator and the elongation actuator achieved repeatable deformation patterns with an MSD of 1.83 mm and 1.04 mm, respectively. It was noted that the elongation actuator achieved a maximum linear extension of 38 mm at a pressure of 40 kPa. This linear extension can fulfill the requirement of some needle-based surgeries like the biopsy of breast tumors, considering the fact that the maximum depth of these tumors is commonly less than 30 mm [].

Figure 6.
The relationship between the chamber length and input pressure of (a) the bending actuator and (b) the elongation actuator across five cycles of inflation and deflation. The square points and stick bars represent mean values and standard deviations of the experimental data, respectively.
Furthermore, the polynomial regression method was adopted to describe the chamber length of the actuators under different input pressures. With the regression method, the chamber length was characterized as polynomial functions of the input pressure plotted by the blue lines in Figure 6. These polynomial functions were used as the nonlinear mapping l = f(u) in the analytical model of the SoNIM.
5.2. Evaluation of the Kinematics of the SoNIM
After the characterization of the actuators, the proposed analytical model and online Jacobian estimation method were examined to evaluate the modeling accuracy (see Supplementary Movie S2). The input pressures of the SoNIM were in the sinusoidal form with different phases and amplitudes as shown in Figure 7a, which enabled the needle tip to generate a representative trajectory in the three-dimensional space. The trajectory of the needle tip during the inflation process was measured via the motion capture system to evaluate the two modeling approaches.

Figure 7.
Evaluation of the kinematics of the SoNIM. (a) The coordinated input pressure for the SoNIM. Comparison among the measured trajectory of the needle tip, the predicted trajectories, and the estimated trajectory in (b) the three-dimensional space and (c) the time domain. The predicted trajectories and the estimated trajectory are derived from the analytical model and the online Jacobian estimation, respectively.
The measured trajectory of the needle tip was compared with the trajectories predicted by the analytical model and online Jacobian estimation in the three-dimensional space and time domain, as shown in Figure 7b,c. The result shows that the trajectory of the analytical model merely predicted the trend of the measured trajectory. The discrepancies shown by the analytical model are mainly caused by unmodeled factors, such as the gravity of the SoNIM and fabrication uncertainties. To improve the modeling accuracy, the online Jacobian estimation was used to capture these unmodeled factors based on the experimental data. The result shows that the trajectory predicted by the online Jacobian estimation matched well with the measured trajectory. It proves that online Jacobian estimation has the ability to reduce the modeling error. Furthermore, the average Euclidean distance between the predicted trajectory and the measured trajectory was used to evaluate the accuracy of the two methods. The average Euclidean distance is defined as
where and represent the positions of the ith point of the predicted trajectory and the measured trajectory, respectively. N represents the number of points. The average Euclidean distances corresponding to the analytical model and the online Jacobian estimation were calculated as 17.6 mm and 1.5 mm, respectively. This result shows that the modeling errors of the analytical model were reduced by 91.5% via the online Jacobian estimation. This demonstrates that the online Jacobian estimation offers an effective method to accurately describe the kinematics of the SoNIM.
5.3. Evaluation of the Closed-Loop Control Performance
Set-point tracking experiments were conducted to validate the accuracy of the proposed online Jacobian-based closed-loop control scheme. In the tests, the proposed control scheme was implemented to direct the needle tip to reach the target points. The actual position of the needle tip was measured via the motion capture system to evaluate the control performance.
Figure 8a compares the measured positions of the needle tip with the desired positions of target points. It can be observed that the needle tip of the SoNIM reached the target points in all the tracking tests. To quantitatively assess the tracking error, the Euclidean distance between the measured positions of the needle tip and the target points was calculated. The calculation result demonstrated that the needle tip of the SoNIM reached the target points with a mean tracking error of 2.40 ± 0.98 mm. This result suggests that the SoNIM was capable of performing accurate and repeatable needle manipulation in the set-point tracking tasks. Considering that the accuracy of the previous surgical robots was around 5 mm, the control accuracy of the SoNIM is sufficient to direct the needle to reach the tumor area.

Figure 8.
Evaluation of the control performance of the SoNIM. (a) The results of set-point tracking experiments. The measured position (red asterisk) of the needle tip was compared with the position of the target points (blue plus sign) to validate the closed-loop scheme. (b) Snapshot of the phantom test that simulates a needle insertion procedure.
With the validated closed-loop control, the phantom experiment was conducted to simulate a needle manipulation procedure. The soft manipulator showed the capability to direct the needle tip toward the target point and insert the needle into the gelatin phantom, as shown in Figure 8b. The whole procedure was demonstrated in Supplementary Movie S3. This phantom test demonstrates the potential of the SoNIM to perform needle manipulation in minimally invasive surgeries. However, the control performance was merely validated in laboratory settings. To achieve closed-loop control in an MR environment, MRI-compatible feedback methods need to be implemented. A viable approach is the use of fiber Bragg grating (FBG) sensors. These sensors are able to measure the shape deformation of the soft needle manipulator without being affected by the magnetic field []. However, the high cost of these FBG sensors is a significant consideration for their practical applications. Another promising feedback method is to use MR images. This approach eliminates the need for additional sensors, but it relies on the development of advanced three-dimensional MRI reconstruction algorithms capable of processing MRI data in real time, which is critical for providing effective feedback to the control system [].
5.4. Evaluation of the SoNIM in MR Environment
The SoNIM was used to simulate a needle manipulation procedure in the MR environment to evaluate its functionality (see Supplementary Movie S4). During the procedure, the proximal and middle bending segments were inflated to achieve the desired bending state. Then, the elongation segment was inflated to insert the needle. Figure 9a shows the MR image sequence of the SoNIM and the corresponding input pressure during the needle manipulation procedure. It can be observed that the configuration of the SoNIM at each pressurization state was clearly recorded via the MRI scanner. This result demonstrates the ability of the SoNIM to manipulate the needle in the closed MRI bore. Additionally, it implies that the MRI offers an alternative way to measure the configuration of the SoNIM and achieve closed-loop control in the MR environment.

Figure 9.
Validation of the SoNIM in MR environment. (a) Validation of the functionality in the MR environment. i–viii display the MR image sequence of the SoNIM with the coordinated input pressure. (b) Comparison among the T1-weighted and T2-weighted MR images of the cylindrical phantom in the baseline, static, and operating conditions.
To investigate the MRI compatibility of the SoNIM, MR images of the cylindrical phantom were acquired under the baseline, static, and operating conditions using the T1-weighted and T2-weighted sequences. Figure 9b displays the obtained MR images of the phantom for the aforementioned three conditions. It shows that the images of the cylindrical phantom were almost identical in all three conditions. This result indicates that the SoNIM caused no observable image artifacts in either T1-weighted or T2-weighted imaging sequences. Furthermore, the SNR of the MR images at each condition was calculated to quantitatively analyze the influence of the SoNIM on the image quality following the guidelines of the NEMA standard MS 1-2008. According to the NEMA standard, the SNR of the MR images is defined as the mean signal in the center of the phantom μ divided by the noise outside the phantom σ as shown below.
The mean signal μ is the mean of the 40 × 40 pixel region at the center of the phantom. The noise σ is the standard deviation of the 40 × 40 pixel region at the corner of the image []. The SNRs of the images corresponding to the aforementioned three conditions under the T1-weighted and T1-weighted sequences were calculated and are listed in Table 2. The calculation result shows that the SNR losses in the T1-weighted and T2-weighted images caused by the SoNIM were 1.18% and 1.78%, respectively. The SNR losses caused by the SoNIM were much less than the existing surgical robots actuated via piezoelectric motors [,] and pneumatic actuators [], indicating that the SoNIM offers a better option to meet the requirement of MRI compatibility.

Table 2.
SNRs of the MR images in three conditions.
6. Conclusions
This paper presents an MRI-compatible soft needle manipulator (SoNIM) that can achieve needle manipulation in an MR environment. The SoNIM applied soft robotic techniques to meet the strict requirement of MRI compatibility and needle manipulation function. This manipulator exploited the collective deformation of two bending actuators and one elongation actuator to manipulate the needle. The kinematic modeling and closed-loop control of this manipulator were studied, aiming to achieve the position control of the needle tip. Furthermore, a series of experiments were conducted to validate the modeling and control accuracy, needle insertion capability, and MRI compatibility of the SoNIM.
The SoNIM offers three-fold advantages, making it well suited for MRI settings. First, as the proposed soft actuators are completely made of non-magnetic materials, these actuators exhibit better MRI compatibility compared to traditional actuators, such as piezoelectric motors. This excellent MRI compatibility prevents the use of the SoNIM from affecting the imaging quality. Second, these soft pneumatic actuators can generate flexible movements while maintaining a more compact design compared to rigid actuators, such as hydraulic cylinders and pneumatic cylinders. The flexible movements and compact design of these actuators ensure that the SoNIM is accommodated within the MRI bore. Third, the production cost of these soft actuators is much lower than that of the existing MRI-compatible actuators. Thus, the SoNIM offers a more affordable option for MRI-compatible robots. Although the SoNIM still faces some limitations, such as nonlinear behavior and lower bandwidth, the set-point tracking experiment and gelatin phantom test demonstrate the potential of the SoNIM to perform needle manipulation for the biopsy and ablation.
This study represents a preliminary attempt to use soft robots for needle manipulation in MR environments. There is still room for improvement. The needle insertion capability of the manipulator was merely validated using a mock needle and a gelatin phantom. In the future, surgical devices, such as the biopsy needle and ablation probe, should be integrated into the manipulator to validate its application in surgeries. Additionally, the use of digital tools plays a crucial role in advancing the real-world application of this soft robotic system, particularly in MRI-guided interventions. For example, three-dimensional MRI reconstruction algorithms can digitize the shape deformation of the soft needle manipulator during its operation. This digital tool has the potential to enhance the modeling and control accuracy of the soft needle manipulator within MRI environments, significantly contributing to the clinical application of this robot.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/act13020059/s1, Video S1: Characterization of the bending actuator and elongation actuator; Video S2: Evaluation of the kinematics of the soft needle manipulator; Video S3: Evaluation of the needle insertion capability of the soft needle manipulator; Video S4: Evaluation of the functionality of the soft needle manipulator in MR environment.
Author Contributions
Conceptualization, J.C., Y.D. and J.H.; Methodology, J.C.; Software, J.C.; Validation, J.C., J.Z. and Y.D.; Formal analysis, J.C.; Investigation, J.C. and J.Z.; Resources, J.C. and J.Z.; Data curation, J.C.; Writing—original draft, J.C.; Writing—review and editing, J.C., T.J., Y.D. and J.H.; Supervision, Y.D. and J.H.; Project administration, T.J. and J.H.; Funding acquisition, T.J. and Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Key R&D Program of China (2022YFB4703500) and the National Natural Science Foundation of China (Grant No. 62203234).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ginalis, E.E.; Danish, S.F. Magnetic resonance-guided laser interstitial thermal therapy for brain tumors in geriatric patients. Neurosurg. Focus 2020, 49, E12. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Kruecker, J.; Amalou, H.; Kwak, J.; Wood, B. Real-time treatment iterative planning for composite ablations. In Proceedings of the Computer Assisted Radiology and Surgery 28th International Congress and Exhibition (CARS 2014), Fukuoka, Japan, 25–28 June 2014; pp. 25–28. [Google Scholar]
- Monfaredi, R.; Cleary, K.; Sharma, K. MRI robots for needle-based interventions: Systems and technology. Ann. Biomed. Eng. 2018, 46, 1479–1497. [Google Scholar] [CrossRef] [PubMed]
- Chinzei, K.; Kikinis, R.; Jolesz, F.A. MR compatibility of mechatronic devices: Design criteria. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI’99: Second International Conference, Cambridge, UK, 19–22 September 1999; pp. 1020–1030. [Google Scholar]
- Tsekos, N.V.; Khanicheh, A.; Christoforou, E.; Mavroidis, C. Magnetic resonance–compatible robotic and mechatronics systems for image-guided interventions and rehabilitation: A review study. Annu. Rev. Biomed. Eng. 2007, 9, 351–387. [Google Scholar] [CrossRef] [PubMed]
- Hofstetter, L.W.; Hadley, J.R.; Merrill, R.; Pham, H.; Fine, G.C.; Parker, D.L. MRI-compatible electromagnetic servomotor for image-guided medical robotics. Commun. Eng. 2022, 1, 4. [Google Scholar] [CrossRef]
- Chen, Y.; Godage, I.S.; Tse, Z.T.H.; Webster, R.J.; Barth, E.J. Characterization and control of a pneumatic motor for MR-conditional robotic applications. IEEE/ASME Trans. Mechatron. 2017, 22, 2780–2789. [Google Scholar] [CrossRef]
- Masamune, K.; Kobayashi, E.; Masutani, Y.; Suzuki, M.; Dohi, T.; Iseki, H.; Takakura, K. Development of an MRI-compatible needle insertion manipulator for stereotactic neurosurgery. J. Image Guid. Surg. 1995, 1, 242–248. [Google Scholar] [CrossRef]
- Li, G.; Patel, N.A.; Burdette, E.C.; Pilitsis, J.G.; Su, H.; Fischer, G.S. A fully actuated robotic assistant for MRI-guided precision conformal ablation of brain tumors. IEEE/ASME Trans. Mechatron. 2021, 26, 255–266. [Google Scholar] [CrossRef]
- Dong, Z.; Guo, Z.; Lee, K.-H.; Fang, G.; Tang, W.L.; Chang, H.-C.; Chan, D.T.M.; Kwok, K.-W. High-performance continuous hydraulic motor for MR safe robotic teleoperation. IEEE Robot. Autom. Lett. 2019, 4, 1964–1971. [Google Scholar] [CrossRef]
- Stoianovici, D.; Jun, C.; Lim, S.; Li, P.; Petrisor, D.; Fricke, S.; Sharma, K.; Cleary, K. Multi-imager compatible, MR safe, remote center of motion needle-guide robot. IEEE Trans. Biomed. Eng. 2018, 65, 165–177. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Lyu, L.X.; Xu, Y.; Liang, H.G.; Zhang, X.P.; Ding, H.; Wu, Z.G. Intelligent soft surgical robots for next-generation minimally invasive surgery. Adv. Intell. Syst. 2021, 3, 2100011. [Google Scholar] [CrossRef]
- Kim, Y.; Cheng, S.S.; Desai, J.P. Active stiffness tuning of a spring-based continuum robot for MRI-guided neurosurgery. IEEE Trans. Robot. 2018, 34, 18–28. [Google Scholar] [CrossRef]
- Shao, S.; Sun, B.; Ding, Q.; Yan, W.; Zheng, W.; Yan, K.; Hong, Y.; Cheng, S.S. Design, modeling, and control of a compact SMA-actuated MR-conditional steerable neurosurgical robot. IEEE Robot. Autom. Lett. 2020, 5, 1381–1388. [Google Scholar] [CrossRef]
- Fang, G.; Wang, X.; Ho, J.D.L.; Wang, K.; Chow, C.-K.; Lee, K.-H.; Xie, X.; Tang, W.L.; Liang, L.; Chang, H.-C.; et al. Epipolar geometry-based visual servoing of soft endoscopic manipulator for transoral laser ablation. Adv. Intell. Syst. 2022, 4, 2200197. [Google Scholar] [CrossRef]
- Fang, G.; Chow, M.C.K.; Ho, J.D.L.; He, Z.; Wang, K.; Ng, T.C.; Tsoi, J.K.H.; Chan, P.-L.; Chang, H.-C.; Chan, D.T.-M.; et al. Soft robotic manipulator for intraoperative MRI-guided transoral laser microsurgery. Sci. Rob. 2021, 6, eabg5575. [Google Scholar] [CrossRef]
- Chen, J.; Dang, Y.; Han, J. Offset-free model predictive control of a soft manipulator using the Koopman operator. Mechatronics 2022, 86, 102871. [Google Scholar] [CrossRef]
- Webster, R.J.; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Rob. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Yip, M.C.; Camarillo, D.B. Model-less feedback control of continuum manipulators in constrained environments. IEEE Trans. Robot. 2014, 30, 880–889. [Google Scholar] [CrossRef]
- Li, M.; Kang, R.; Branson, D.T.; Dai, J.S. Model-free control for continuum robots based on an adaptive Kalman filter. IEEE/ASME Trans. Mechatron. 2018, 23, 286–297. [Google Scholar] [CrossRef]
- Tonning Olsson, I.; Perrin, S.; Lundgren, J.; Hjorth, L.; Johanson, A. Long-term cognitive sequelae after pediatric brain tumor related to medical risk factors, age, and sex. Pediatr. Neurol. 2014, 51, 515–521. [Google Scholar] [CrossRef] [PubMed]
- NEMA MS 1:2008; Determination of Signal-to-Noise Ratio (SNR) in Diagnostic Magnetic Resonance Imaging. NEMA Standards Publication: Rosslyn, VA, USA, 2008.
- Su, H.; Shang, W.; Cole, G.; Li, G.; Harrington, K.; Camilo, A.; Tokuda, J.; Tempany, C.M.; Hata, N.; Fischer, G.S. Piezoelectrically actuated robotic system for MRI-guided prostate percutaneous therapy. IEEE/ASME Trans. Mechatron. 2015, 20, 1920–1932. [Google Scholar] [CrossRef] [PubMed]
- Oraevsky, A.; Clingman, B.; Zalev, J.; Stavros, A.; Yang, W.; Parikh, J. Clinical optoacoustic imaging combined with ultrasound for coregistered functional and anatomical mapping of breast tumors. Photoacoustics 2018, 12, 30–45. [Google Scholar] [CrossRef]
- Lu, Y.; Lu, B.; Li, B.; Guo, H.; Liu, Y.-H. Robust three-dimensional shape sensing for flexible endoscopic surgery using multi-core fbg sensors. IEEE Robot. Autom. Lett. 2021, 6, 4835–4842. [Google Scholar] [CrossRef]
- Nayak, K.S.; Lim, Y.; Campbell-Washburn, A.E.; Steeden, J. Real-time magnetic resonance imaging. J. Magn. Reson. Imaging 2022, 55, 81–99. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Wen, Y.; Liu, Y.-H. Developing a parallel robot for MRI-guided breast intervention. IEEE Trans. Med. Robot. Bionics 2020, 2, 17–27. [Google Scholar] [CrossRef]
- Sutherland, G.R.; Lama, S.; Gan, L.S.; Wolfsberger, S.; Zareinia, K. Merging machines with microsurgery: Clinical experience with neuroarm. J. Neurosurg. 2013, 118, 521–529. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).