Design of Soft Pneumatic Actuator with Two Oblique Chambers for Coupled Bending and Twisting Movements
Abstract
:1. Introduction
2. Materials and Methods
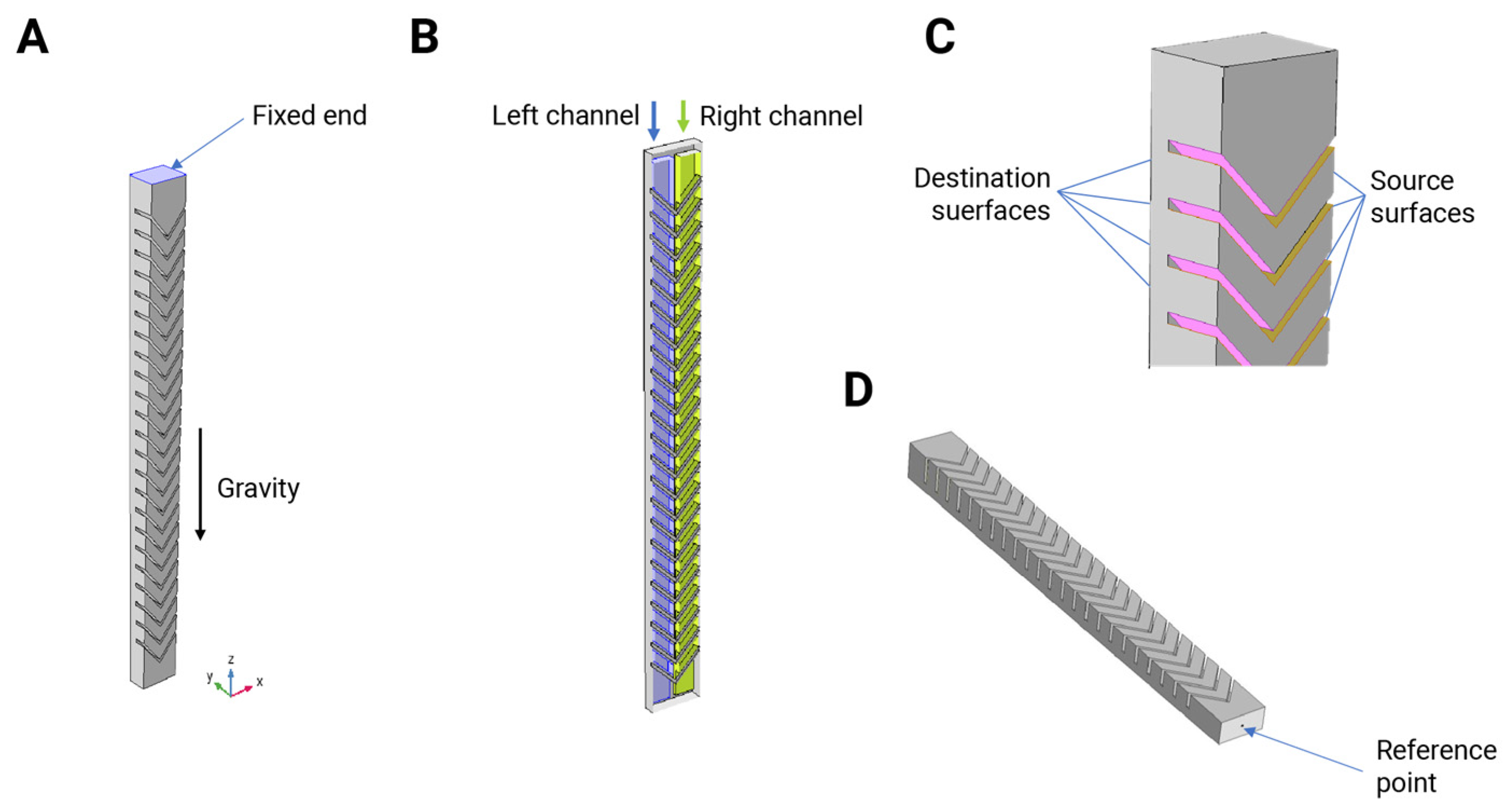
Design and Simulation
3. Results
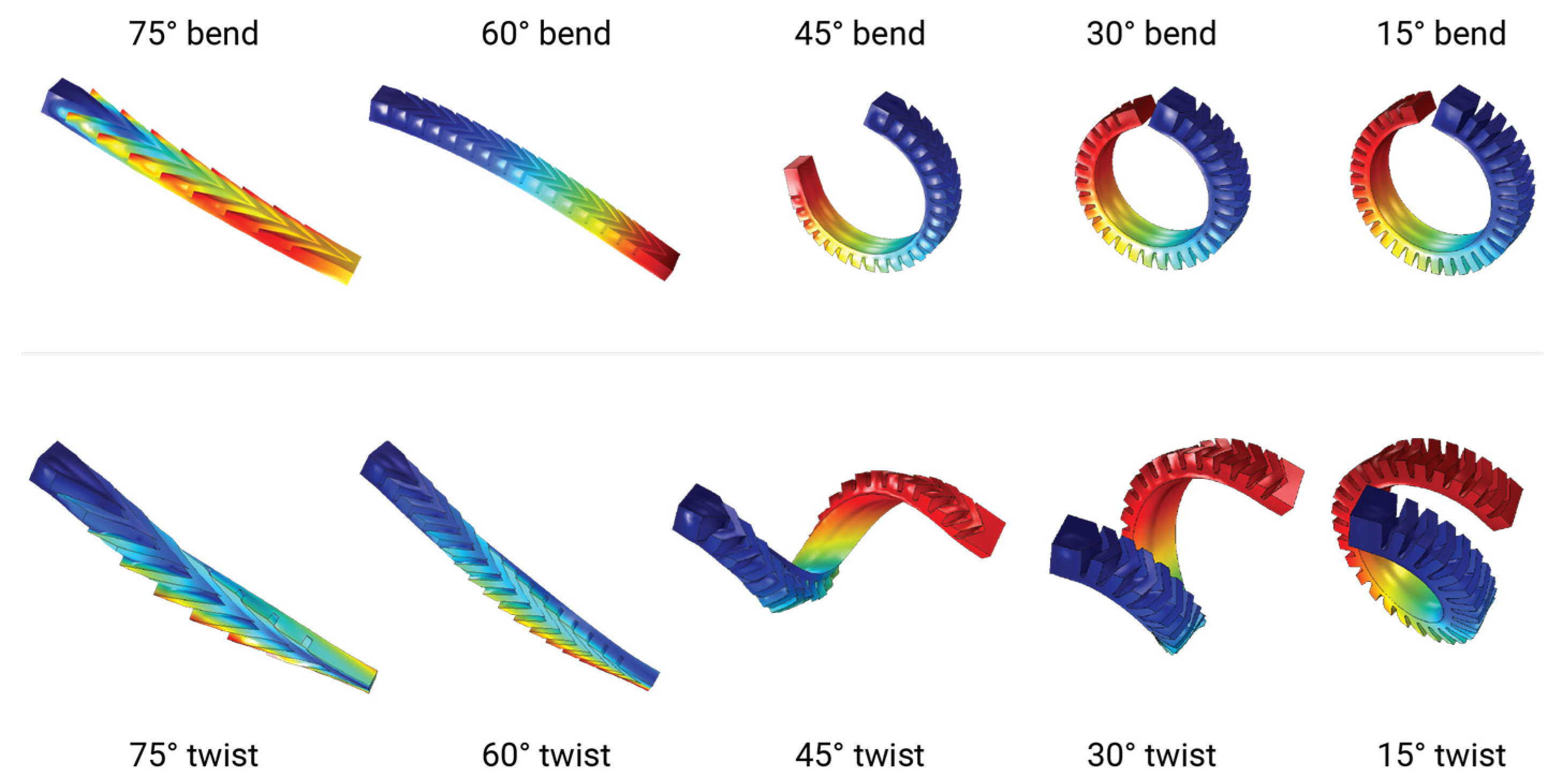
3.1. Simulations
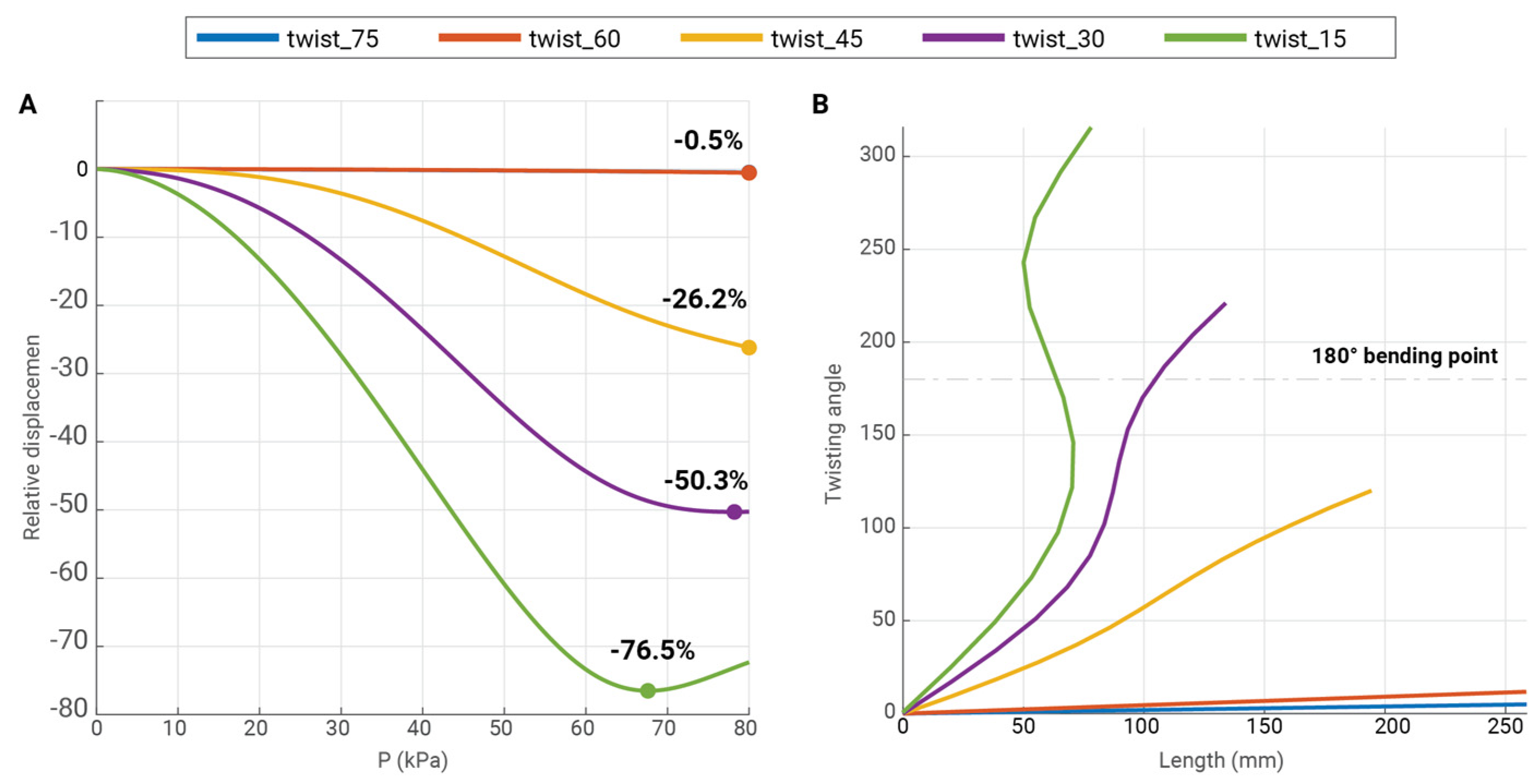
3.2. Parameter Optimization
3.3. Manufacturing
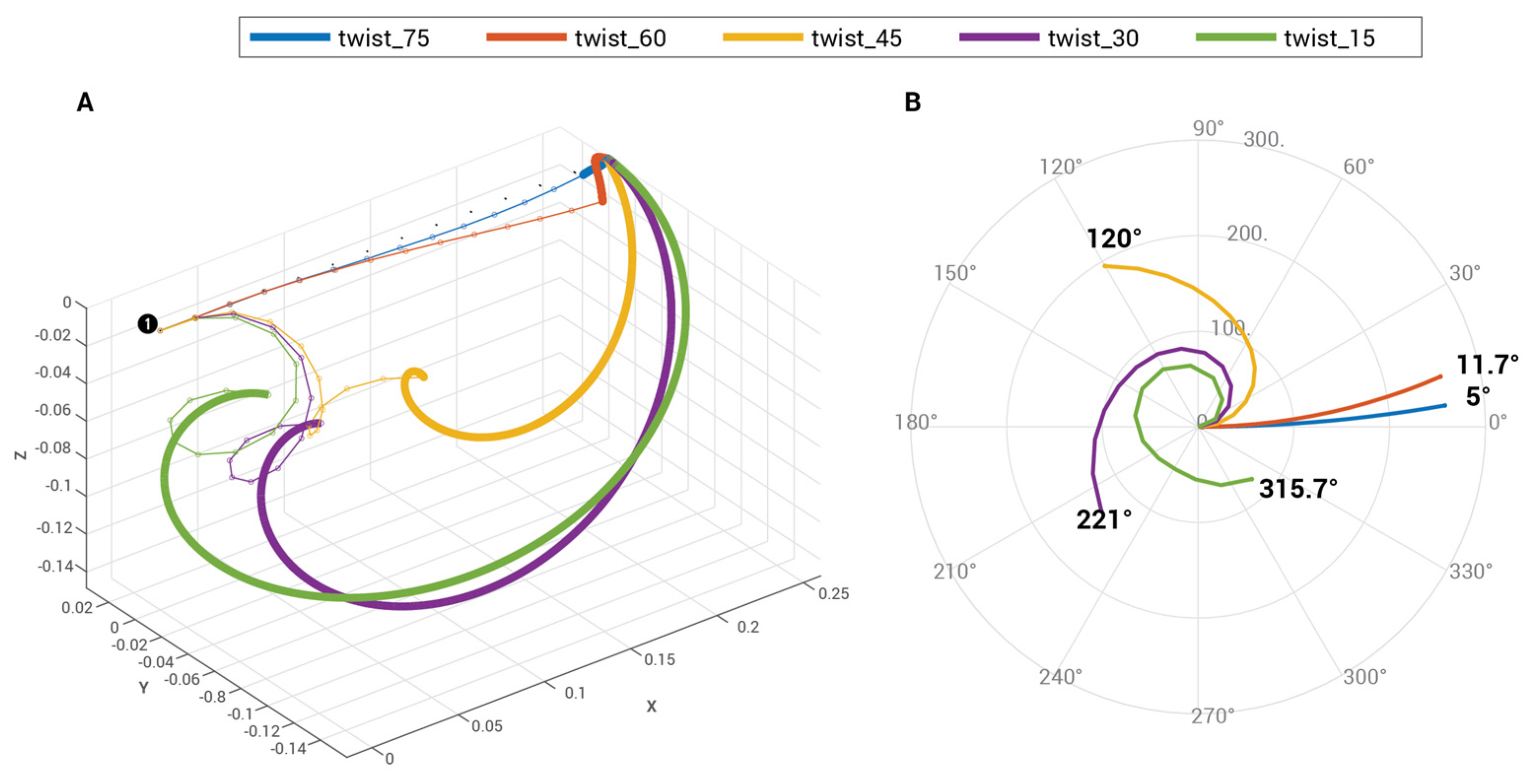
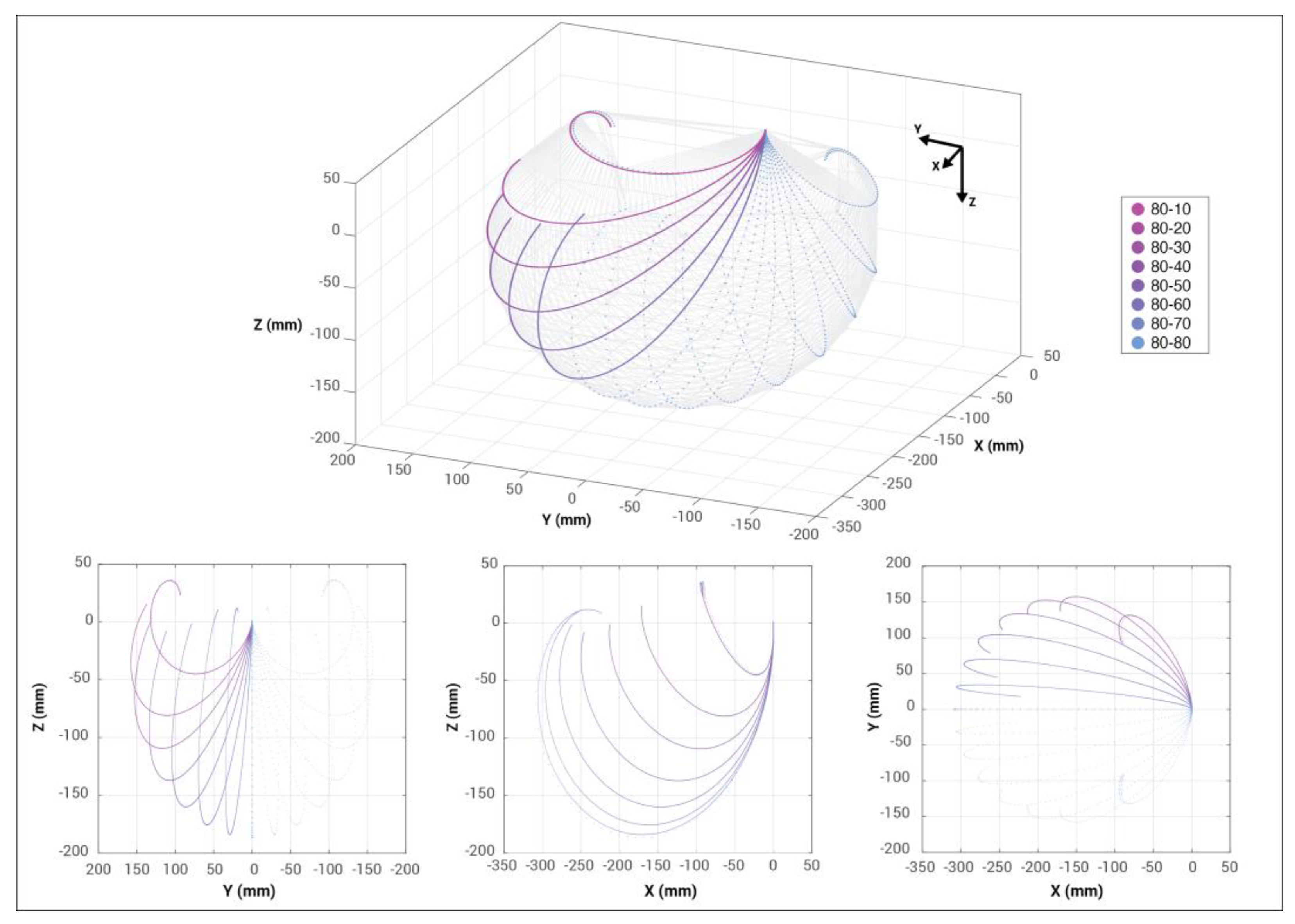
3.4. Workspace Analysis
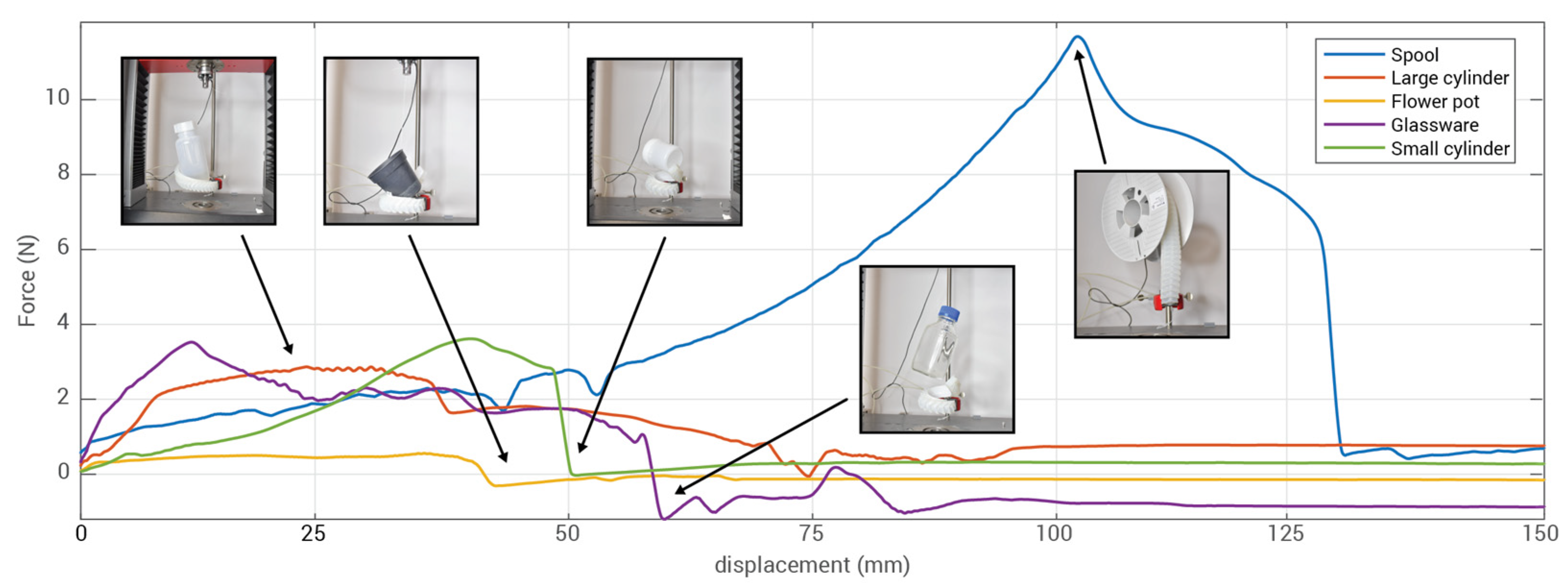
3.5. Grasping Force
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deimel, R.; Brock, O. A Novel Type of Compliant and Underactuated Robotic Hand for Dexterous Grasping. Int. J. Robot. Res. 2016, 35, 161–185. [Google Scholar] [CrossRef]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait Soft Robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, A.; Mondini, A.; Mazzolai, B. Toward Self-Growing Soft Robots Inspired by Plant Roots and Based on Additive Manufacturing Technologies. Soft Robot. 2017, 4, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.-T.; Leisk, G.G.; Trimmer, B. GoQBot: A Caterpillar-Inspired Soft-Bodied Rolling Robot. Bioinspiration Biomim. 2011, 6, 026007. [Google Scholar] [CrossRef]
- Calisti, M.; Arienti, A.; Renda, F.; Levy, G.; Hochner, B.; Mazzolai, B.; Dario, P.; Laschi, C. Design and Development of a Soft Robot with Crawling and Grasping Capabilities; IEEE: Saint Paul, MN, USA, 2012; pp. 4950–4955. [Google Scholar]
- Li, G.; Chen, X.; Zhou, F.; Liang, Y.; Xiao, Y.; Cao, X.; Zhang, Z.; Zhang, M.; Wu, B.; Yin, S. Self-Powered Soft Robot in the Mariana Trench. Nature 2021, 591, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Xia, C.; Fang, N.X. First Jump of Microgel; Actuation Speed Enhancement by Elastic Instability. Soft Matter 2010, 6, 4342–4345. [Google Scholar] [CrossRef]
- Walker, J.; Zidek, T.; Harbel, C.; Yoon, S.; Strickland, F.S.; Kumar, S.; Shin, M. Soft Robotics: A Review of Recent Developments of Pneumatic Soft Actuators; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2020; Volume 9, p. 3. [Google Scholar]
- Shen, Q.; Trabia, S.; Stalbaum, T.; Palmre, V.; Kim, K.; Oh, I.-K. A Multiple-Shape Memory Polymer-Metal Composite Actuator Capable of Programmable Control, Creating Complex 3D Motion of Bending, Twisting, and Oscillation. Sci. Rep. 2016, 6, 24462. [Google Scholar] [CrossRef]
- Rodrigue, H.; Wang, W.; Han, M.-W.; Kim, T.J.; Ahn, S.-H. An Overview of Shape Memory Alloy-Coupled Actuators and Robots. Soft Robot. 2017, 4, 3–15. [Google Scholar] [CrossRef]
- Carpi, F.; Kornbluh, R.; Sommer-Larsen, P.; Alici, G. Electroactive Polymer Actuators as Artificial Muscles: Are They Ready for Bioinspired Applications? Bioinspiration Biomim. 2011, 6, 045006. [Google Scholar] [CrossRef]
- Visentin, F.; Murali Babu, S.P.; Meder, F.; Mazzolai, B. Selective Stiffening in Soft Actuators by Triggered Phase Transition of Hydrogel-Filled Elastomers. Adv. Funct. Mater. 2021, 31, 2101121. [Google Scholar] [CrossRef]
- Kofod, G.; Wirges, W.; Paajanen, M.; Bauer, S. Energy Minimization for Self-Organized Structure Formation and Actuation. Appl. Phys. Lett. 2007, 90, 081916. [Google Scholar] [CrossRef]
- Mao, Z.; Peng, Y.; Hu, C.; Ding, R.; Yamada, Y.; Maeda, S. Soft Computing-Based Predictive Modeling of Flexible Electrohydrodynamic Pumps. Biomim. Intell. Robot. 2023, 3, 100114. [Google Scholar] [CrossRef]
- Tauber, F.; Desmulliez, M.; Piccin, O.; Stokes, A.A. Perspective for Soft Robotics: The Field’s Past and Future. Bioinspiration Biomim. 2023, 18, 035001. [Google Scholar] [CrossRef] [PubMed]
- Hirai, S.; Masui, T.; Kawamura, S. Prototyping Pneumatic Group Actuators Composed of Multiple Single-Motion Elastic Tubes. J. Robot. Soc. Jpn. 2002, 20, 299–306. [Google Scholar] [CrossRef]
- Martinez, R.V.; Branch, J.L.; Fish, C.R.; Jin, L.; Shepherd, R.F.; Nunes, R.M.; Suo, Z.; Whitesides, G.M. Robotic Tentacles with Three-dimensional Mobility Based on Flexible Elastomers. Adv. Mater. 2013, 25, 205–212. [Google Scholar] [CrossRef]
- Wang, B.; McDaid, A.; Biglari-Abhari, M.; Giffney, T.; Aw, K. A Bimorph Pneumatic Bending Actuator by Control of Fiber Braiding Angle. Sens. Actuators A Phys. 2017, 257, 173–184. [Google Scholar] [CrossRef]
- Connolly, F.; Walsh, C.J.; Bertoldi, K. Automatic Design of Fiber-Reinforced Soft Actuators for Trajectory Matching. Proc. Natl. Acad. Sci. USA 2017, 114, 51–56. [Google Scholar] [CrossRef]
- Bishop-Moser, J.; Krishnan, G.; Kim, C.; Kota, S. Design of Soft Robotic Actuators Using Fluid-Filled Fiber-Reinforced Elastomeric Enclosures in Parallel Combinations; IEEE: Vilamoura-Algarve, Portugal, 2012; pp. 4264–4269. [Google Scholar]
- Robertson, M.A.; Sadeghi, H.; Florez, J.M.; Paik, J. Soft Pneumatic Actuator Fascicles for High Force and Reliability. Soft Robot. 2017, 4, 23–32. [Google Scholar] [CrossRef]
- Bishop-Moser, J.; Kota, S. Towards Snake-like Soft Robots: Design of Fluidic Fiber-Reinforced Elastomeric Helical Manipulators; IEEE: Tokyo, Japan, 2013; pp. 5021–5026. [Google Scholar]
- de Payrebrune, K.M.; O’Reilly, O.M. On Constitutive Relations for a Rod-Based Model of a Pneu-Net Bending Actuator. Extrem. Mech. Lett. 2016, 8, 38–46. [Google Scholar] [CrossRef]
- Galloway, K.C.; Becker, K.P.; Phillips, B.; Kirby, J.; Licht, S.; Tchernov, D.; Wood, R.J.; Gruber, D.F. Soft Robotic Grippers for Biological Sampling on Deep Reefs. Soft Robot. 2016, 3, 23–33. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, T.; Ren, Z.; Gong, Z.; Wang, H.; Yang, X.; Guan, S.; Wen, L. Modeling and Experiments of a Soft Robotic Gripper in Amphibious Environments. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417707148. [Google Scholar] [CrossRef]
- Shahabi, E.; Lu, W.-H.; Lin, P.T.; Kuo, C.-H. Computer Vision-Based Object Recognition and Automatic Pneumatic Soft Gripping; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59292, p. V009T12A006. [Google Scholar]
- Peng, Y.; Sakai, Y.; Nakagawa, K.; Funabora, Y.; Aoyama, T.; Yokoe, K.; Doki, S. Funabot-Suit: A Bio-Inspired and McKibben Muscle-Actuated Suit for Natural Kinesthetic Perception. Biomim. Intell. Robot. 2023, 3, 100127. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, Y.-X.; Juang, J.-Y. Single-Actuator Soft Robot for in-Pipe Crawling. Soft Robot. 2023, 10, 174–186. [Google Scholar] [CrossRef]
- Polygerinos, P.; Lyne, S.; Wang, Z.; Nicolini, L.F.; Mosadegh, B.; Whitesides, G.M.; Walsh, C.J. Towards a Soft Pneumatic Glove for Hand Rehabilitation; IEEE: Tokyo, Japan, 2013; pp. 1512–1517. [Google Scholar]
- Liu, Z.; Wang, F.; Liu, S.; Tian, Y.; Zhang, D. Modeling and Analysis of Soft Pneumatic Network Bending Actuators. IEEE/ASME Trans. Mechatron. 2020, 26, 2195–2203. [Google Scholar] [CrossRef]
- Zhao, S.; Li, D.; Xiang, J. Design and Application of PneuNets Bending Actuator. Aircr. Eng. Aerosp. Technol. 2020, 92, 1539–1546. [Google Scholar] [CrossRef]
- Lin, P.T.; Shahabi, E.; Yang, K.-A.; Yao, Y.-T.; Kuo, C.-H. Parametrically Modeled DH Table for Soft Robot Kinematics: Case Study for a Soft Gripper; Springer: Berlin/Heidelberg, Germany, 2019; pp. 617–625. [Google Scholar]
- Sun, Y.; Song, Y.S.; Paik, J. Characterization of Silicone Rubber Based Soft Pneumatic Actuators; IEEE: Tokyo, Japan, 2013; pp. 4446–4453. [Google Scholar]
- Ilievski, F.; Mazzeo, A.D.; Shepherd, R.F.; Chen, X.; Whitesides, G.M. Soft Robotics for Chemists. Angew. Chem. 2011, 123, 1930–1935. [Google Scholar] [CrossRef]
- Gorissen, B.; Chishiro, T.; Shimomura, S.; Reynaerts, D.; De Volder, M.; Konishi, S. Flexible Pneumatic Twisting Actuators and Their Application to Tilting Micromirrors. Sens. Actuators A Phys. 2014, 216, 426–431. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, D.; Zhao, B.; Liao, Z.; Gu, G. Modeling and Inverse Design of Bio-Inspired Multi-Segment Pneu-Net Soft Manipulators for 3D Trajectory Motion. Appl. Phys. Rev. 2021, 8, 041416. [Google Scholar] [CrossRef]
- Bira, N.; Dhagat, P.; Davidson, J.R. Tuning the Grasping Strength of Soft Actuators with Magnetic Elastomer Fingertips. Smart Mater. Struct. 2022, 31, 045013. [Google Scholar] [CrossRef]
- Hu, W.; Li, W.; Alici, G. 3D Printed Helical Soft Pneumatic Actuators; IEEE: Auckland, New Zealand, 2018; pp. 950–955. [Google Scholar]
- Wang, T.; Ge, L.; Gu, G. Programmable Design of Soft Pneu-Net Actuators with Oblique Chambers Can Generate Coupled Bending and Twisting Motions. Sens. Actuators A Phys. 2018, 271, 131–138. [Google Scholar] [CrossRef]
- Gu, G.; Wang, D.; Ge, L.; Zhu, X. Analytical Modeling and Design of Generalized Pneu-Net Soft Actuators with Three-Dimensional Deformations. Soft Robot. 2021, 8, 462–477. [Google Scholar] [CrossRef] [PubMed]
- Shahabi, E.; Yao, Y.-T.; Chuang, C.-H.; Lin, P.T.; Kuo, C.-H. Design and Testing of 2-Degree-of-Freedom (DOF) Printable Pneumatic Soft Finger; Springer: Berlin/Heidelberg, Germany, 2019; pp. 298–308. [Google Scholar]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic Networks for Soft Robotics That Actuate Rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Marechal, L.; Balland, P.; Lindenroth, L.; Petrou, F.; Kontovounisios, C.; Bello, F. Toward a Common Framework and Database of Materials for Soft Robotics. Soft Robot. 2021, 8, 284–297. [Google Scholar] [CrossRef] [PubMed]
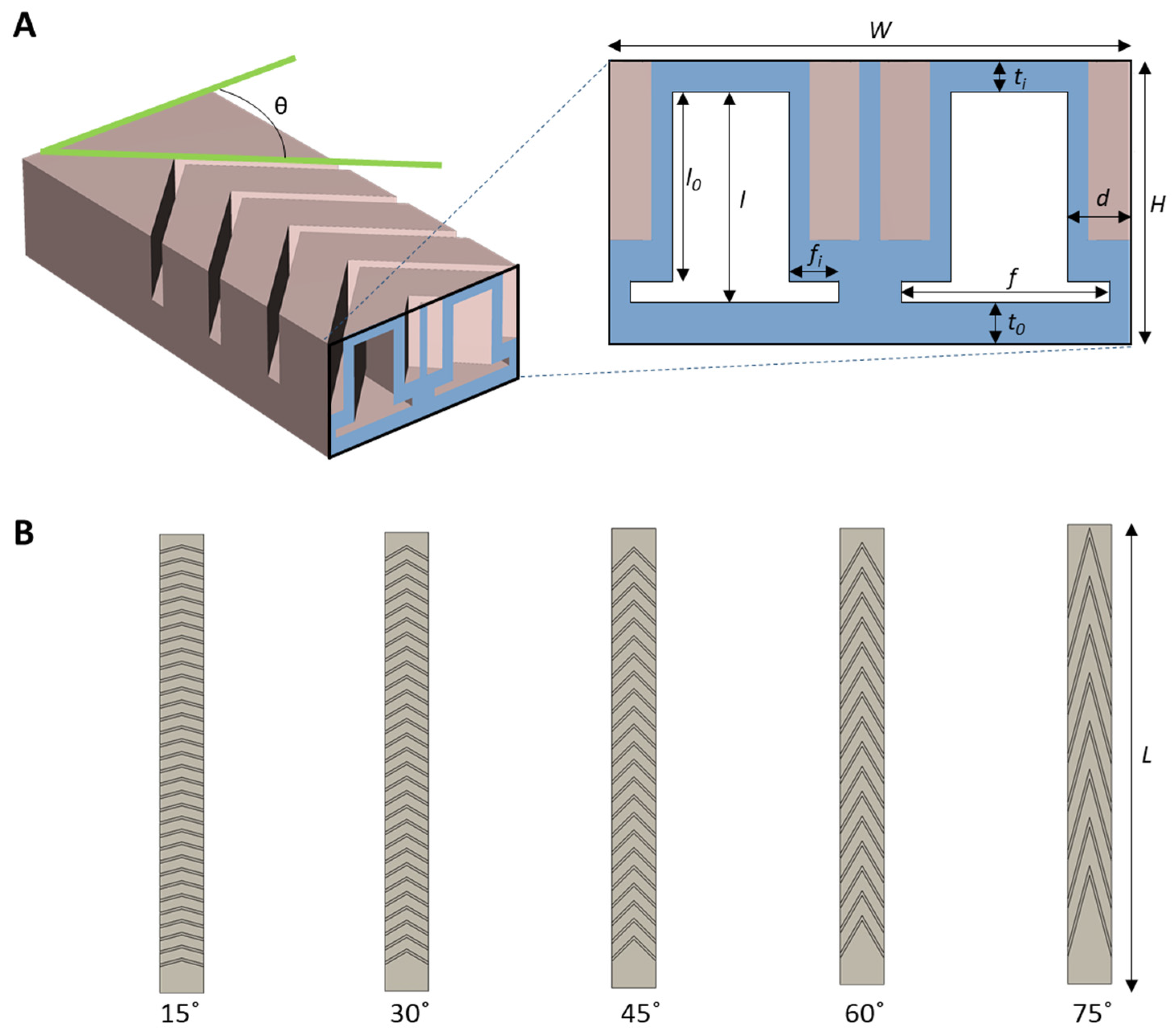



| Symbol | Value |
|---|---|
| L | 260 mm |
| H | 20 mm |
| W | 25 mm |
| f | 10 mm |
| fi | 4 mm |
| d | 1.5 mm |
| t0 | 2 mm |
| ti | 1.5 mm |
| l | 15.8 mm |
| l0 | 14.8 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahabi, E.; Kamare, B.; Visentin, F.; Mondini, A.; Mazzolai, B. Design of Soft Pneumatic Actuator with Two Oblique Chambers for Coupled Bending and Twisting Movements. Actuators 2023, 12, 446. https://doi.org/10.3390/act12120446
Shahabi E, Kamare B, Visentin F, Mondini A, Mazzolai B. Design of Soft Pneumatic Actuator with Two Oblique Chambers for Coupled Bending and Twisting Movements. Actuators. 2023; 12(12):446. https://doi.org/10.3390/act12120446
Chicago/Turabian StyleShahabi, Ebrahim, Behnam Kamare, Francesco Visentin, Alessio Mondini, and Barbara Mazzolai. 2023. "Design of Soft Pneumatic Actuator with Two Oblique Chambers for Coupled Bending and Twisting Movements" Actuators 12, no. 12: 446. https://doi.org/10.3390/act12120446
APA StyleShahabi, E., Kamare, B., Visentin, F., Mondini, A., & Mazzolai, B. (2023). Design of Soft Pneumatic Actuator with Two Oblique Chambers for Coupled Bending and Twisting Movements. Actuators, 12(12), 446. https://doi.org/10.3390/act12120446







