Active Edgewise Blade Damping Control of Large Wind Turbines by Using the Pitch Controller and an Interval Observer
Abstract
1. Introduction
2. Control Law Derivation
2.1. The Control Problem
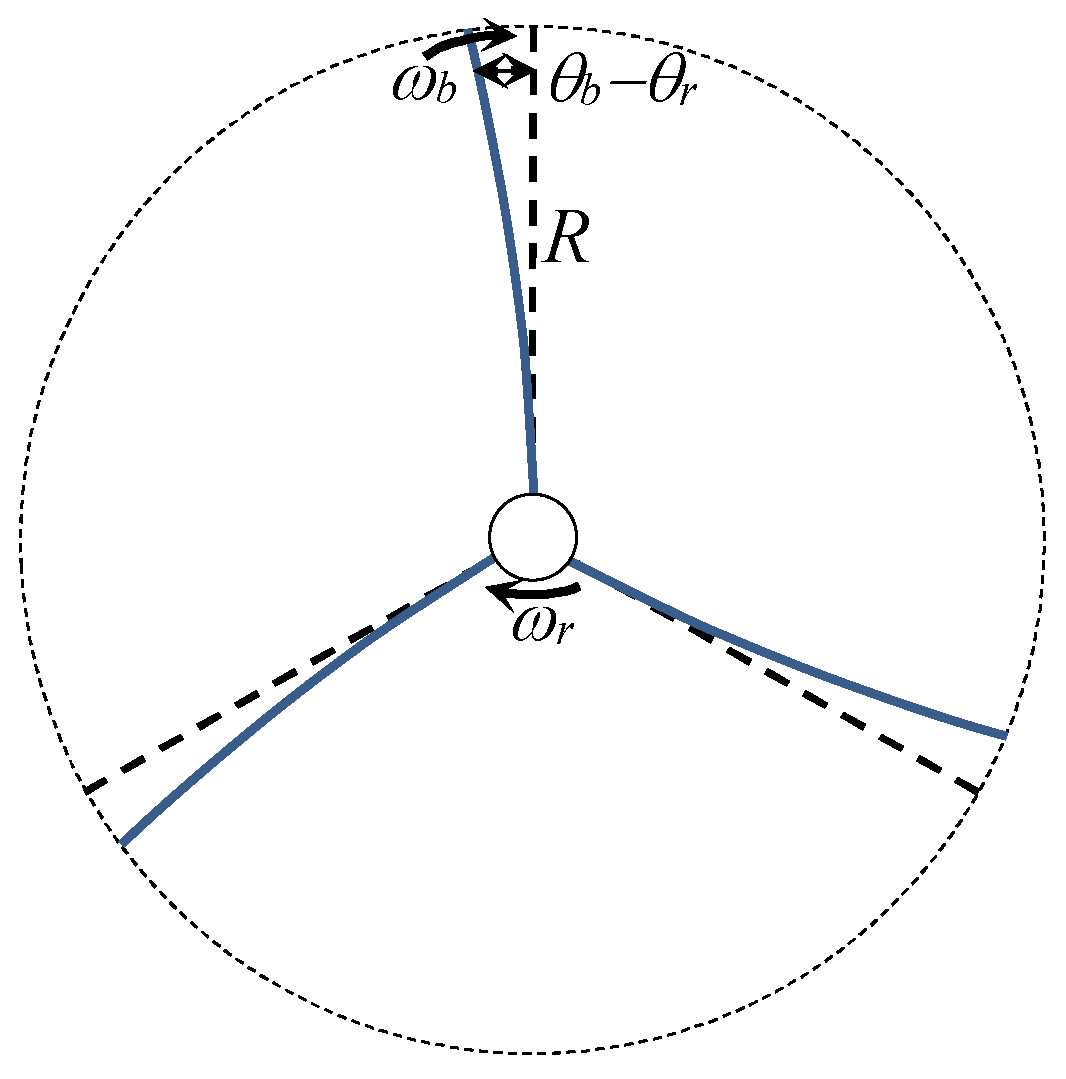
2.2. Active Damping Control
2.3. Collective Pitch Control Loop
2.4. Active Tower Damping Control
2.5. Active Blade Damping Control
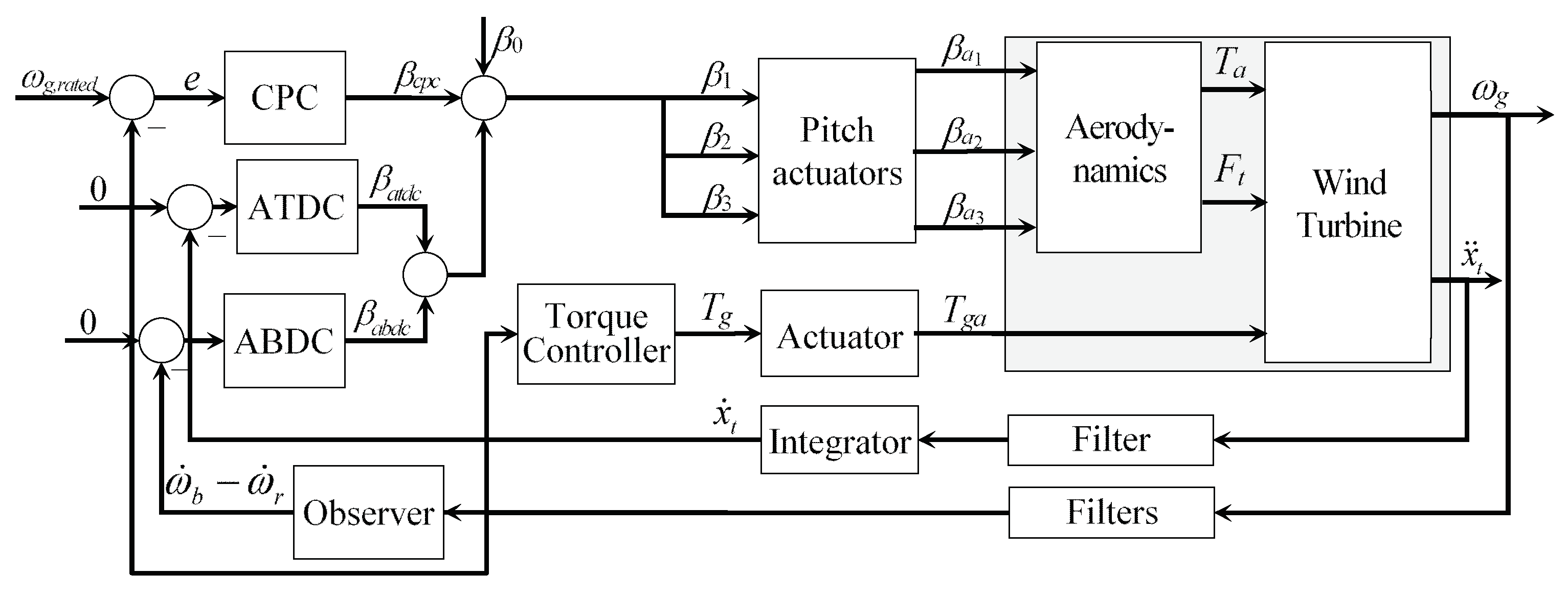
2.6. Pitch Control System with Active Damping Control
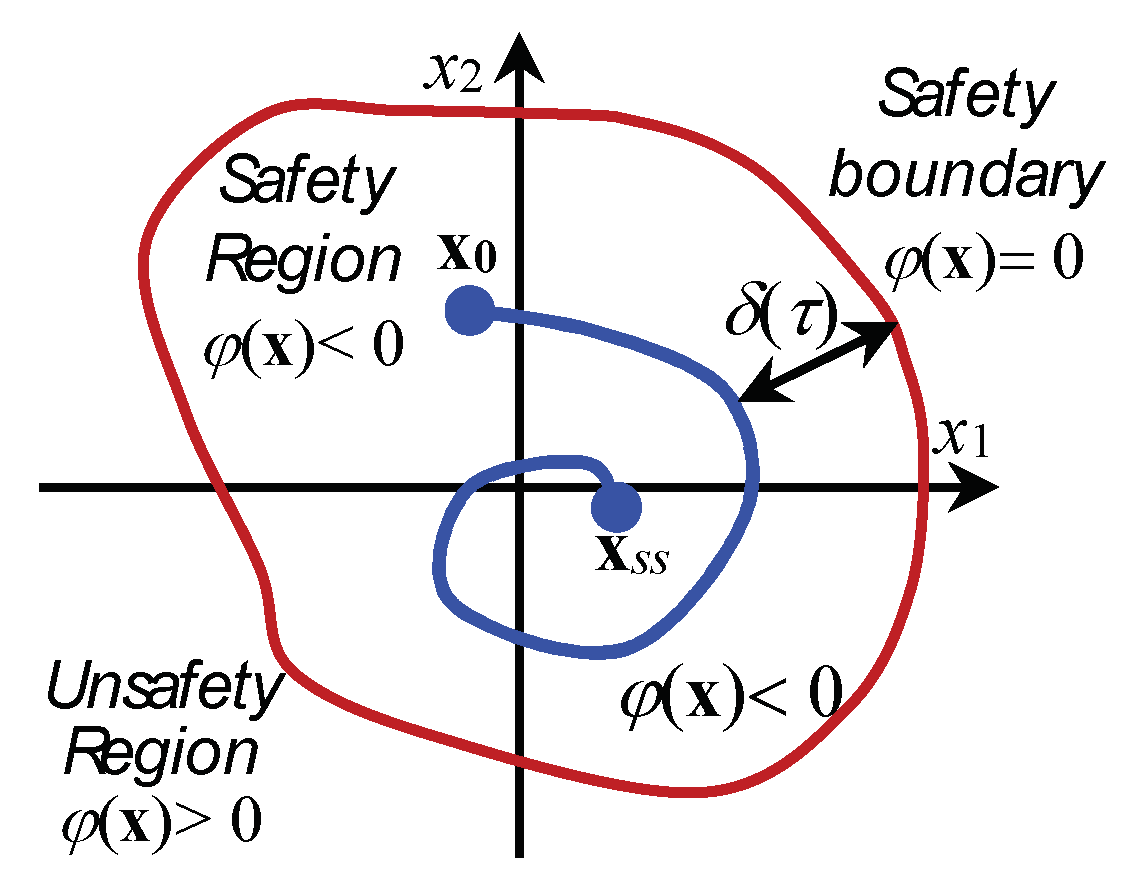
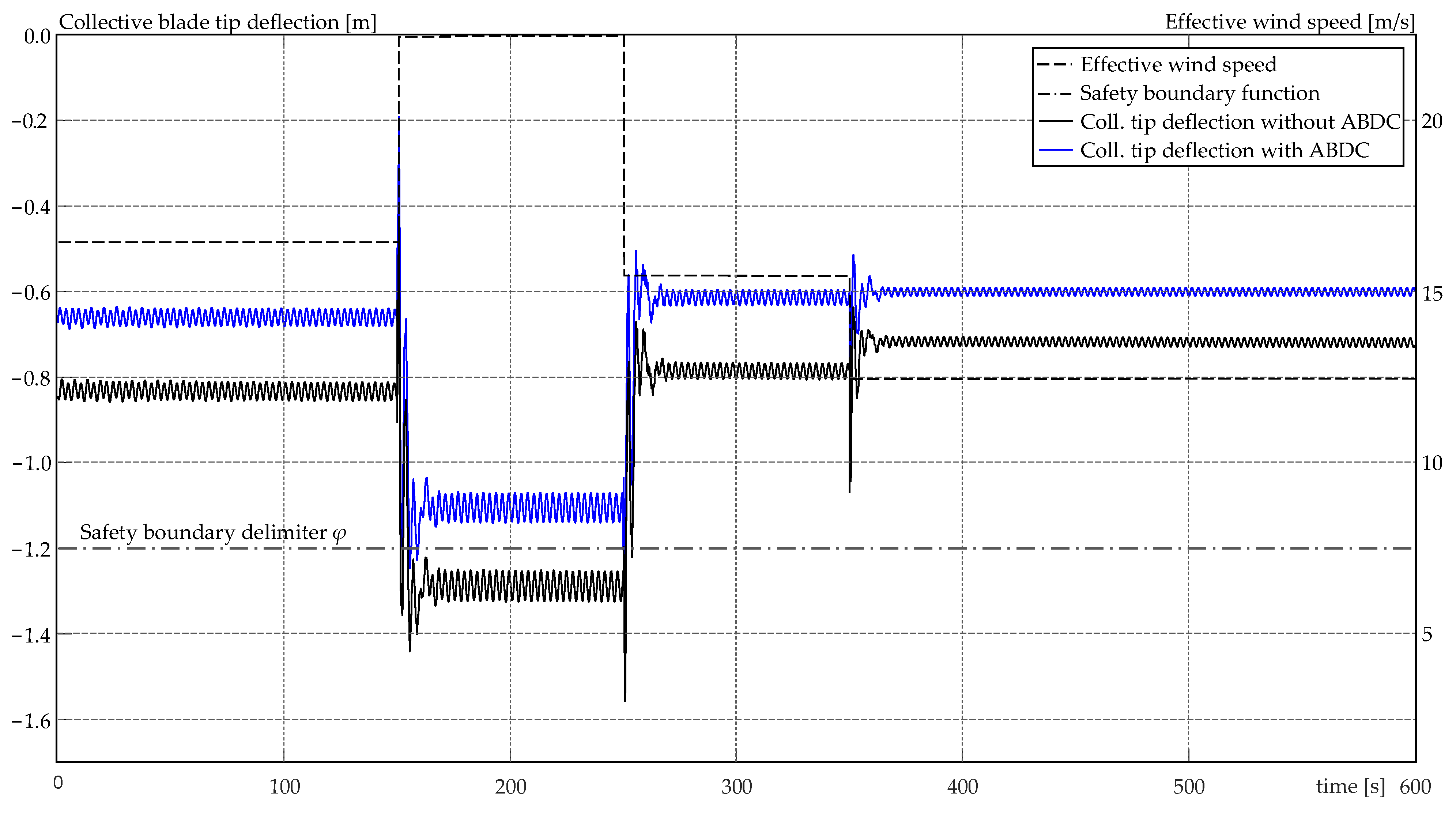
2.7. Application of the Dynamic Safety Marging
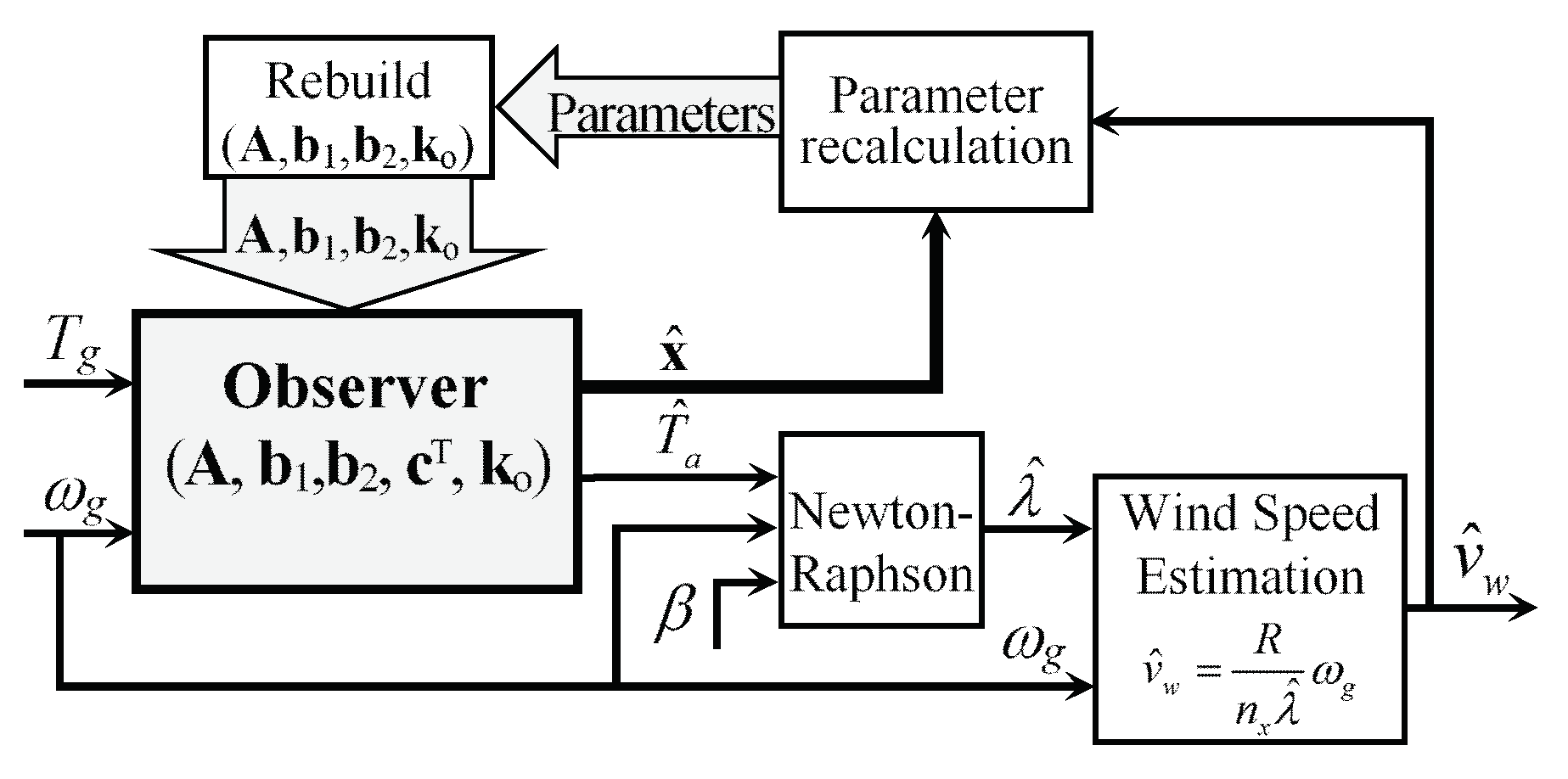
3. Estimation of State Variables
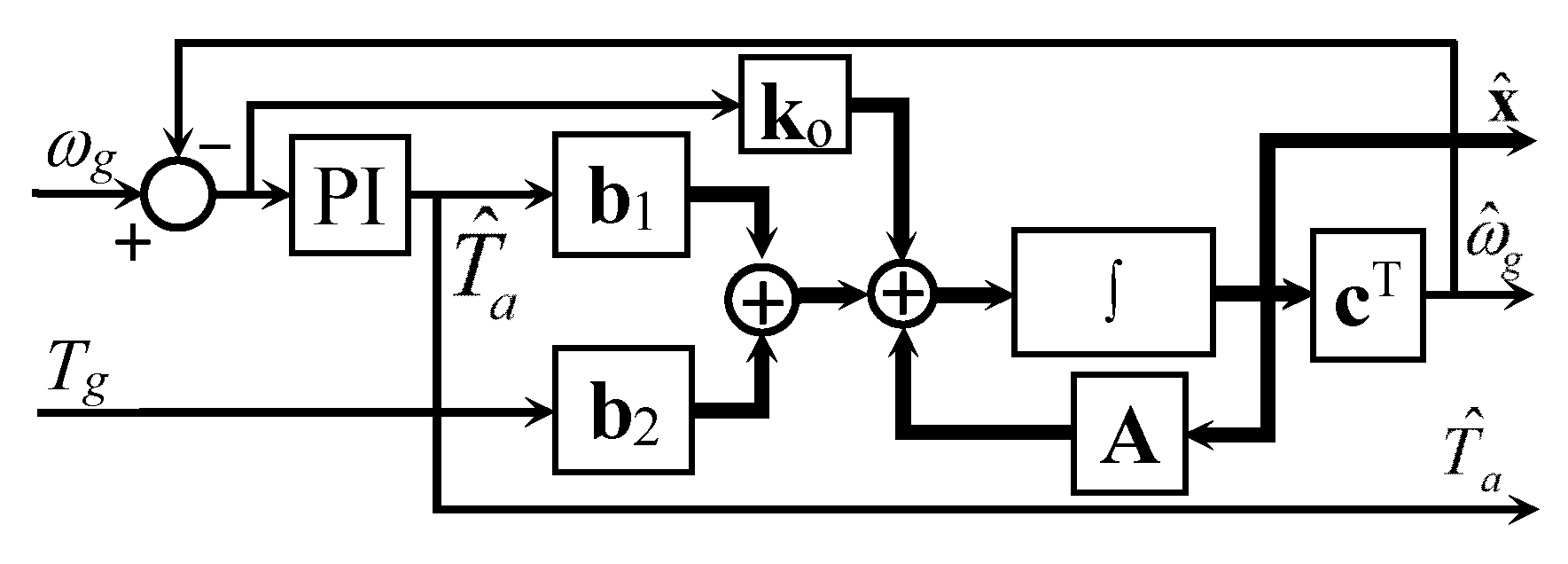
3.1. Observer-Based Estimation of State Variables
3.2. Mathematical Description of the Dynamic System
3.3. Observer Design with Effective Wind Speed Estimation
4. Numerical Study
4.1. Parameters and Rated Values
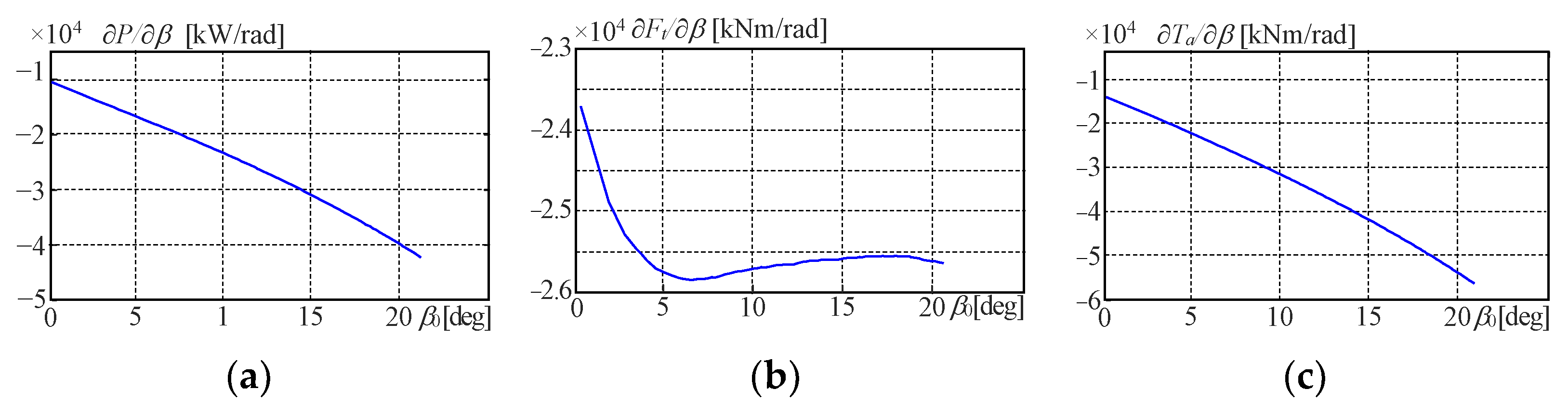
4.2. Sensitivity Functions
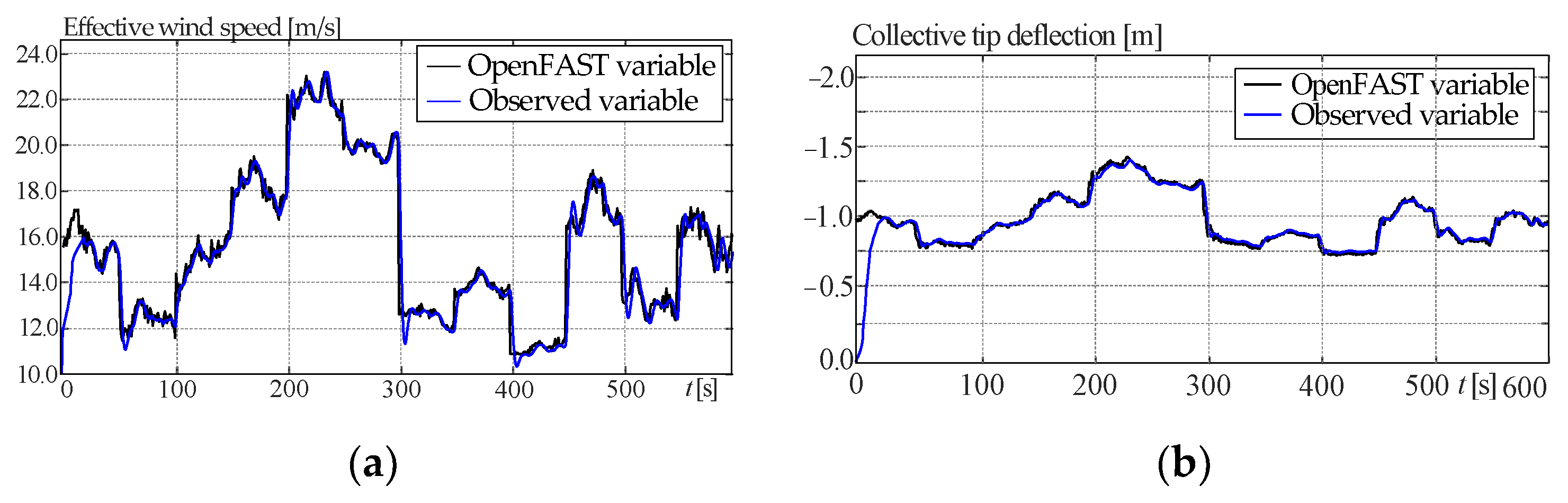
4.3. Experiments for the Simulation Environment
4.4. Observer Performance
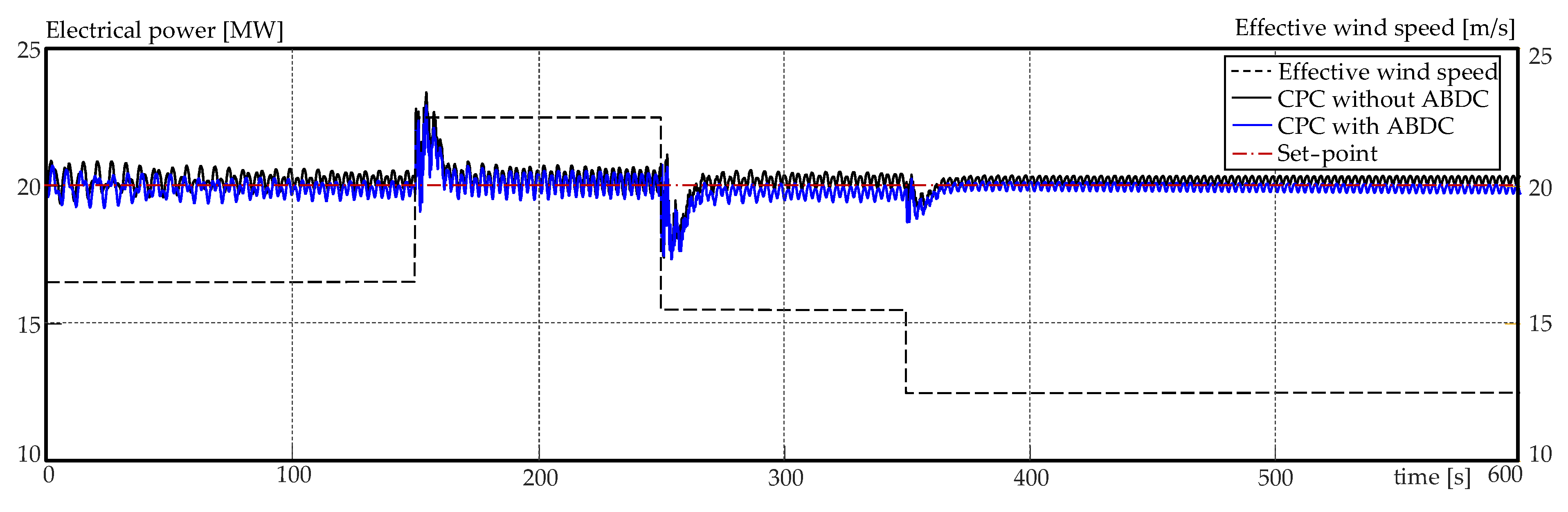
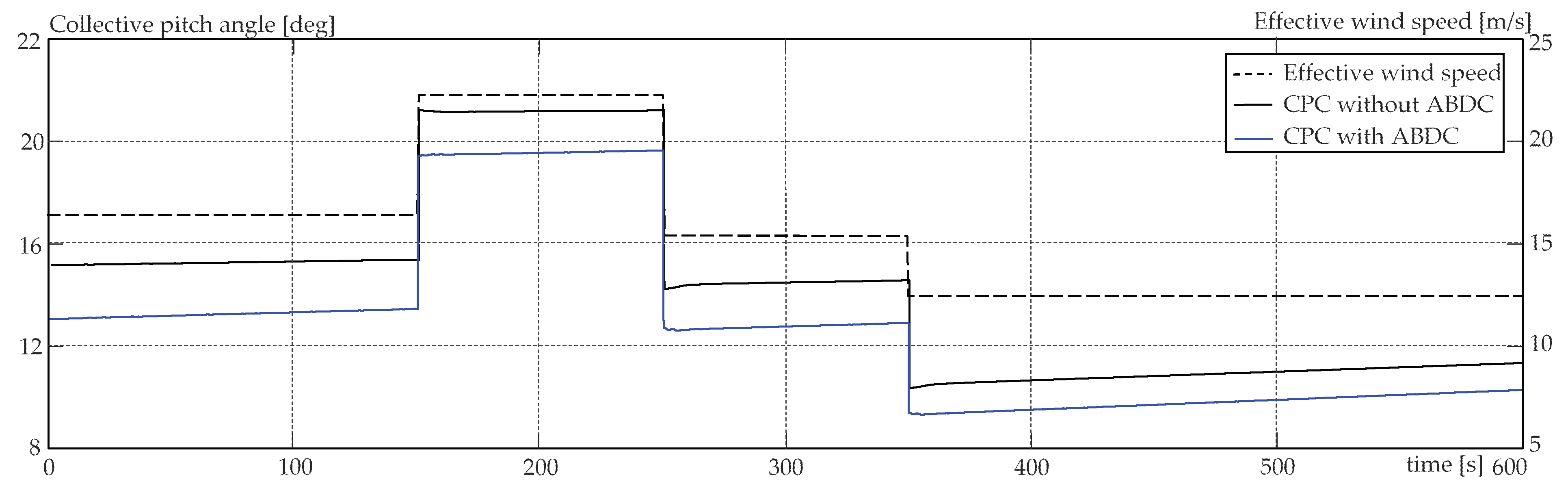
4.5. Simulation Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABDC | Active Blade Damping Control |
| ATDC | Active Tower Damping Control |
| CPC | Collective Pitch Control |
| DSM | Dynamic Safety Margin |
| LQG | Linear Quadratic Gaussian |
| LTI | Linear Time Invariant |
| PD | Proportional Derivative |
| PI | Proportional Integral |
Nomenclature
| Parameters | |
| Bg | Generator viscose friction coefficient, Nm s/rad |
| Be | Equivalent friction coefficient, Nm s/rad |
| Br | Rotor viscose friction coefficient, Nm s/rad |
| Cp | Power coefficient, -- |
| Cp,max | Maximum value of the power coefficient, -- |
| Dlss | Damping coefficient of the low-speed shaft, Nm s/rad |
| Dhss | Damping coefficient of the high-speed shaft, Nm s/rad |
| K | Proportional constant, Nm/(rad/s)2 |
| Klss | Stiffness coefficient for the low-speed shaft, Nm/rad |
| Khss | Stiffness coefficient for the high-speed shaft, Nm/rad |
| Kp, Ki, Ka, Dbc, Kbc | Controller gains |
| Jr | Rotor mass moment of inertia, kg m2 |
| Jg | Generator mass moment of inertia, kg m2 |
| nx | Gearbox ratio, -- |
| Pm,rated | Rated mechanical power, MW |
| R | Rotor radius, m |
| Ta,rated | Rated aerodynamic torque, kg m2 |
| Ta∞ | Steady-state value of the aerodynamic torque, kg m2 |
| Tg,rated | Rated generator torque, kg m2 |
| vci | Cut-in value for the wind speed, m/s |
| vco | Cut-out value for the wind speed, m/s |
| vv,rated | Rated value for the wind speed, m/s |
| ∆θ∞ | Steady-state value for twist angle for the low-speed shaft, rad |
| λ* | Optimal tip-speed ratio |
| ηx, ηg | Efficiency of gearbox and generator |
| ρa | Density of air, kg/m3 |
| ωg,rated | Rated value of the generator speed, rad/s |
| ωr,rated | Rated value of the rotor speed, rad/s |
| ∂Pm/∂β, ∂Ft/∂β, ∂Ta/∂β | Partial derivatives of mechanical power, thrust force, and aerodynamic torque with respect to pitch angle |
| A | System matrix |
| b | Input vector |
| c | Output vector |
| ko | Observer gain |
| aij | Elements of matrix A |
| Variables | |
| Pm | Mechanical power, MW |
| Ta | Aerodynamic torque (on the low-speed shaft), kg m2 |
| Tg | Generator torque (on the low-speed shaft), kg m2 |
| vv | Wind speed, m/s |
| xi | State variables |
| β | Pitch angle, rad |
| β0 | Pitch angle at the operating point, rad |
| Δθ | Twist angle of the low-speed shaft, rad |
| λ | Tip-speed ratio, -- |
| ωg | Generator speed, rad/s |
| ωr | Rotor speed, rad/s |
| Jcpc, Jabdc | Objective factions for control system design |
| e | Control error |
| δ | Dynamic safety margin |
| Functions | |
| f | Controller function |
| φ | Safety boundary delimiter |
| Ψ | Function used to find the tip-speed ratio (Equation (26)) |
References
- Hansen, M.H. Aeroelastic instability problems for wind turbines. Wind. Energy 2007, 10, 551–577. [Google Scholar] [CrossRef]
- Kallesøe, B.S.; Kragh, K.A. Field validation of the stability limit of a multi MW turbine. J. Phys. Conf. Ser. 2016, 753, 042005. [Google Scholar] [CrossRef]
- Jacobson, D.; Laninga, J.; Brandt, R. Wind interconnection in Manitoba. In Proceedings of the CIGRÉ Canada Conference on Power Systems, Montreal, QC, Canada, 1–4 October 2006. [Google Scholar]
- Basu, B.; Staino, A.; Basu, M. Role of flexible alternating current transmission systems devices in mitigating grid fault-induced vibration of wind turbines. Wind. Energy 2014, 17, 1017–1033. [Google Scholar] [CrossRef]
- Staino, A.; Basu, B.; Nielsen, S.R.K. Actuator control of edgewise vibrations in wind turbine blades. J. Sound Vib. 2012, 331, 1233–1256. [Google Scholar] [CrossRef]
- Riziotis, V.A.; Voutsinas, S.G.; Politis, E.S.; Chaviaropoulos, P.K. Aeroelastic stability of wind turbines: The problem, the tethods and the issues. Wind Energy 2004, 7, 373–392. [Google Scholar] [CrossRef]
- Awada, A.; Younes, R.; Ilinca, A. Review of vibration control methods for wind turbines. Energy 2021, 14, 3058. [Google Scholar] [CrossRef]
- Murtagh, P.J.; Basu, B.; Broderick, B.M. Along-wind response of a wind turbine tower with blade coupling. Eng. Struct. 2005, 27, 1209–1219. [Google Scholar] [CrossRef]
- Murtagh, P.J.; Ghosh, A.; Basu, B.; Broderick, B.M. Passive control of wind turbine vibrations including blade/tower interaction and rotationally sampled turbulence. Wind. Energy 2008, 11, 305–317. [Google Scholar] [CrossRef]
- Lackner, M.A.; Rotea, M. Passive structural control of offshore wind turbines. Wind. Energy 2011, 14, 373–388. [Google Scholar] [CrossRef]
- Dinh, V.; Basu, B. Passive control of floating offshore wind turbine nacelle and spar vibrations by multiple tuned mass dampers. Struct. Control Health Monit. 2015, 22, 152–176. [Google Scholar] [CrossRef]
- Mensah, A.F.; Dueñas-Osorio, L. Improved reliability of wind turbine towers with tuned liquid column dampers (TLCDs). Struct Saf. 2014, 47, 78–86. [Google Scholar] [CrossRef]
- Arrigan, J.; Pakrashi, V.; Basu, B.; Nagarajaiah, S. Control of flapwise vibrations in wind turbine blades using semi-active tuned mass dampers. Struct. Control. Health Monit 2011, 18, 840–851. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Basu, B. Active tuned mass damper control of wind turbine nacelle/tower vibrations with damaged foundations. In Proceedings of the 10th International Conference on Damage Assessment of Structures (DAMAS 2013), Dublin, Ireland, 8–10 July 2013; pp. 660–667. [Google Scholar]
- Staino, A.; Basu, B. Emerging trends in vibration control of wind turbines: A focus on a dual control strategy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 1–16. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Nielsen, S.R.K. Edgewise vibration control of wind turbine blades using roller and liquid dampers. J. Phys. Conf. Ser. 2014, 524, 012037. [Google Scholar] [CrossRef]
- Park, S.; Lackner, M.A. Edgewise vibration suppression of multi-megawatt wind turbine blades using passive tuned mass dampers. Wind. Eng. 2021, 45, 1082–1100. [Google Scholar] [CrossRef]
- Andreasen, R.B. Damping of edgewise vibrations of wind turbine blades by smart liquid dampers. Master’s Thesis, Aalborg University, Aalborg, Denmark, 2017. [Google Scholar]
- Biglari, H.; Fakhari, V. Edgewise vibration reduction of small size wind turbine blades using shunt damping. J. Vib. Control 2020, 26, 186–199. [Google Scholar] [CrossRef]
- Yan, B.; Wang, K.; Hu, Z.; Wu, C.; Zhang, X. Shunt Damping Vibration Control Technology: A Review. Appl. Sci. 2017, 7, 494. [Google Scholar] [CrossRef]
- Livne, E. Aircraft active flutter suppression: State of the art and technology maturation needs. J. Aircr. 2018, 55, 410–450. [Google Scholar] [CrossRef]
- Takegaki, M.; Arimoto, S. A new feedback method for dynamic control of manipulators. J. Dyn. Syst. Meas. Control. 1981, 103, 119–125. [Google Scholar] [CrossRef]
- Bossanyi, E.A. The design of closed loop controllers for wind turbines. Wind. Energy 2000, 3, 149–163. [Google Scholar] [CrossRef]
- Leithead, W.E.; Domínguez, S. Analysis of tower/blade interaction in the cancellation of the tower fore-aft mode via control. In Proceedings of the European Wind Energy Conference, London, UK, 22–25 November 2004; pp. 1–10. [Google Scholar]
- Bossanyi, E.A. Wind turbine control for load reduction. Wind. Energy 2003, 6, 229–244. [Google Scholar] [CrossRef]
- Wright, A.D.; Fingersh, L.J. Advanced Control Design for Wind Turbines; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2008. [Google Scholar]
- Gambier, A. Simultaneous design of pitch control and active tower damping of a wind turbine by using multi-objective optimization. In Proceedings of the 1st IEEE Conference on Control Technology and Applications, Kohala Coast, Australia, 27–30 December 2017; pp. 1679–1684. [Google Scholar]
- Gambier, A.; Nazaruddin, Y. Collective pitch control with active tower damping of a wind turbine by using a nonlinear PID approach. IFAC Pap. 2018, 51, 238–243. [Google Scholar] [CrossRef]
- Gambier, A.; Nazaruddin, Y. Wind turbine pitch and active tower damping control using metaheuristic multi-objective bat optimization. In Proceedings of the 19th International Multidisciplinary Modeling & Simulation Multiconference, Rome, Italy, 19–21 September 2022; pp. 1–9. [Google Scholar]
- Imran, R.; Hussain, D.; Soltani, M.; Rafaq, R. Optimal tuning of multivariable disturbance-observer-based control for flicker mitigation using individual pitch control of wind turbine. IET Renew. Power Gener. 2016, 11, 1121–1128. [Google Scholar] [CrossRef]
- Chen, B.; Hua, X.; Zhang, Z.; Nielsen, S.R.K.; Chen, Z. Active flutter control of the wind turbines using double-pitched blades. Renew. Energy 2021, 163, 2081–2097. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, J.; Pang, J.; Wang, B. Research on control methods and technology for reduction of large-scale wind turbine blade vibration. Energy Rep. 2023, 9, 912–923. [Google Scholar] [CrossRef]
- Gambier, A. Evolutionary multiobjective optimization with fractional order integral objectives for the pitch control system design of wind turbines. IFAC-Pap. 2019, 52, 274–279. [Google Scholar] [CrossRef]
- Abdel-Geliel, M.; Badreddin, E.; Gambier, A. Dynamic safety margin in fault-tolerant predictive controller. In Proceedings of the 2005 IEEE Conference on Control Applications, Toronto, ON, Canada, 28–31 August 2005; pp. 803–808. [Google Scholar]
- Gambier, A. Pitch control of three bladed large wind energy converters—A Review. Energies 2021, 14, 8083. [Google Scholar] [CrossRef]
- Stramigioli, S. Creating artificial damping by means of damping injection. In Proceedings of the 1996 ASME International Mechanical Engineering Congress and Exposition, Atlanta, GA, USA, 17–22 November 1996; pp. 601–606. [Google Scholar]
- Ortega, R.; Spong, M.W. Adaptive motion control of rigid robots: A tutorial. Automatica 1989, 25, 877–888. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. PID Controllers: Theory, Design and Tuning; ISA International Society for Measurement and Control: Research Triangle Park, CA, USA, 1995. [Google Scholar]
- Rundqwist, L. Anti-Reset Windup for PID Controllers; Lund Institute of Technology: Lund, Sweden, 1991. [Google Scholar]
- Arrigan, J.; Huang, C.; Staino, A.; Basu, B.; Nagarajaiah, S. A frequency tracking semi-active algorithm for control of edgewise vibrations in wind turbine blades. Smart Struct. Syst. 2014, 13, 177–201. [Google Scholar] [CrossRef]
- Leith, D.J.; Leithead, W.E. Appropriate realization of gain-scheduled controllers with application to wind turbine regulation. Int. J. Control 1996, 65, 223–248. [Google Scholar] [CrossRef]
- Chen, J.-J.; Ji, Z.-C. The gain scheduling control for wind energy conversion system based on LPV model. In Proceedings of the 2010 International Conference on Networking, Sensing and Control, Chicago, IL, USA, 10−12 April 2010; pp. 653–657. [Google Scholar] [CrossRef]
- Gambier, A. Control of Large Wind Energy Systems; Springer Nature: Basel, Switzerland, 2022; ISBN 978-3-030-84894-1. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons: Chichester, UK, 2011; ISBN 978-1-119-99271-4. [Google Scholar]
- Melício, R.; Mendes, V.; Catalao, J. Transient analysis of variable speed wind turbines at wind speed disturbances and a pitch control malfunction. Appl. Energy 2011, 88, 1322–1330. [Google Scholar] [CrossRef]
- Gambier, A. Dynamic modelling of the rotating subsystem of a wind turbine for control design purposes. IFAC-Pap. 2017, 50, 9896–9901. [Google Scholar] [CrossRef]
- Gambier, A. Multiobjective optimal control of wind turbines: A survey on methods and recommendations for the implementation. Energies 2022, 15, 567. [Google Scholar] [CrossRef]
- Luenberger, D.G. Observing the state of a linear system. IEEE Trans. Mil. Electron. 1964, 8, 74–80. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Hou, M.; Müller, P.C. Design of observers for linear systems with unknown inputs. IEEE Trans. Autom. Control 1992, 37, 871–875. [Google Scholar] [CrossRef]
- Abdel-Geliel, M.; Badreddin, E. Adaptive controller using dynamic safety margin for hybrid laboratory plant. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 1443–1448. [Google Scholar]
- Moghaddamjoo, A.; Kirlin, R.L. Robust adaptive Kalman filtering with unknown inputs. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1166–1175. [Google Scholar] [CrossRef]
- Bernard, P. Observer Design for Nonlinear Systems; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Nijmeijer, H.; Fossen, T.I. New Directions in Nonlinear Observer Design; Springer: Berlin, Germany, 1999. [Google Scholar]
- Kim, P. Kalman Filter for Beginners: With MATLAB Examples; CreateSpace: Scotts Valley, CA, USA, 2011. [Google Scholar]
- Condomines, J.-P. Nonlinear Kalman Filter for Multi-Sensor Navigation of Unmanned Aerial Vehicles; ISTE Press—Elsevier: London, UK, 2018. [Google Scholar]
- Doyle, J.C.; Stein, G. Robustness with Observers. IEEE Trans. Autom. Control 1979, 24, 607–611. [Google Scholar] [CrossRef]
- Akpan, E. Robust observer for uncertain linear systems. In Proceedings of the American Control Conference, Arlington, TX, USA; 2001. [Google Scholar]
- Moore, R.E.; Kearfott, R.B.; Cloud, M.J. Introduction to Interval Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar]
- Chen, G.; Wang, J.; Shieh, L.-S. Interval Kalman filtering. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 250–259. [Google Scholar] [CrossRef]
- Efimov, D.; Raïssi, T. Design of interval observers for uncertain dynamical systems. Autom. Remote Control. 2016, 77, 191–225. [Google Scholar] [CrossRef]
- Cacace, F.; Germani, A.; Manes, C. A new approach to design interval observers for linear systems. IEEE Trans. Autom. Control 2015, 60, 1665–1670. [Google Scholar] [CrossRef]
- Wang, K.; Michel, A.N. Necessary and sufficient conditions for the controllability and observability of a class of linear, time-invariant systems with interval plants. IEEE Trans. Autom. Control 1994, 39, 1443–1447. [Google Scholar] [CrossRef]
- Ritter, B.; Schild, A.; Feldt, M.; Konigorski, U. The design of nonlinear observers for wind turbine dynamic state and parameter estimation. J. Phys. Conf. Ser. 2016, 753, 1–12. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Damgaard, C.; Nielsen, R. Unknown input observer based estimation of wind speed for wind turbines control. In Proceedings of the IFAC World Congress, Milan, Italy, 28 August–2 September 2011. [Google Scholar]
- Odgaard, P.F.; Stoustrup, J. Fault tolerant wind speed estimator used in wind turbine controllers. In Proceedings of the 8th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes, Mexico City, Mexico, 29–31 August 2012; pp. 331–336. [Google Scholar]
- Odgaard, P.F.; Damgaard, C.; Nielsen, R. On-line estimation of wind turbine power coefficients using unknown input observers. In Proceedings of the 17th IFAC World Congress, Seoul, Republic of Korea, 6–11 July 2008. [Google Scholar]
- Odgaard, P.F.; Stoustrup, J. Unknown input observer based scheme for detecting faults in a wind turbine converter. In Proceedings of the 7th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes, Barcelona, Spain, 30 June–3 July 2009. [Google Scholar]
- Yuan, Y.; Chen, X.; Tang, J. Disturbance observer based pitch control of wind turbines for disturbance rejection. In Proceedings of the Smart Materials and Nondestructive Evaluation for Energy Systems, Las Vegas, NV, USA, 21–23 March 2016. [Google Scholar]
- Ritter, B.; Konigorski, U. Advanced multivariable control design for modern multi-MW wind turbines. In Proceedings of the 11th EAWE PhD Seminar on Wind Energy in Europe, Stuttgart, Germany, 23–25 September 2015. [Google Scholar]
- Chamoli, S.; Gambier, A. Adaptive interval observer design with application to wind energy converters. In Proceedings of the 20th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2020; pp. 350–355. [Google Scholar] [CrossRef]
- Chamoli, S.; Gambier, A. Modelling, parametrization and observer design of a 20 MW reference wind turbine for control purposes. J. Phys. Conf. Ser. 2020, 1618, 022031. [Google Scholar] [CrossRef]
- Ramtharan, G.; Anaya-Lara, O.; Bossanyi, E.; Jenkins, N. Influence of structural dynamic representations of FSIG wind turbines on electrical transients. Wind. Energy 2007, 10, 293–301. [Google Scholar] [CrossRef]
- Darouach, M.; Zasadzinski, M.; Xu, S.J. Full-order observers for linear systems with unknown inputs. IEEE Trans. Autom. Control 1994, 39, 607–609. [Google Scholar] [CrossRef]
- Østergaard, K.Z.; Brath, P.; Stoustrup, J. Estimation of effective wind speed. J. Phys. Conf. Ser. 2007, 75, 012082. [Google Scholar] [CrossRef]
- Tóth, R. Modeling and Identification of Linear Parameter-Varying Systems, 1st ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Gambier, A.; Nazaruddin, Y.Y. Modelling the wind turbine by using the tip-speed ratio for estimation and control. Energies 2022, 15, 9454. [Google Scholar] [CrossRef]
- Kautsky, J.; Nichols, N.K.; Van Dooren, P. Robust pole assignment in linear state feedback. Int. J. Control. 1985, 41, 1129–1155. [Google Scholar] [CrossRef]
- Ashuri, T.; Martins, J.R.R.A.; Zaaijer, M.B. Aeroservoelastic design definition of a 20 MW common research wind turbine model. Wind. Energy 2016, 19, 2071–2087. [Google Scholar] [CrossRef]
- Gambier, A.; Meng, F. Control system design for a 20 MW reference wind turbine. In Proceedings of the 12th Asian Control Conference, Hong Kong, 19–21 August 2019; pp. 258–263. [Google Scholar] [CrossRef]
- Jonkman, J.; Jonkman, B. FAST modularization framework for wind turbine simulation: Full-system linearization. J. Phys. Conf. Ser. 2016, 753, 082010. [Google Scholar] [CrossRef]

| Variables | Notation | Rated Values | Units |
|---|---|---|---|
| Rated mechanical power | Pm,rated | 21.191 | MW |
| Rated rotor speed | ωr,rated | 7.1567 | rpm |
| Rated generator speed | ωg,rated | 1173.7 | rad/s |
| Cut-in, rated, and cut-out wind speed | vci, vw,rated, vco | 4.48, 10.92, 25 | m/s |
| Rated aerodynamic torque (on the low-speed shaft) | Ta,rated | 28,434.7 | kNm |
| Rated generator torque (on the high-speed shaft) | Tg,rated | 169.76 | kNm |
| Maximum value of the power coefficient Cp | Cp,max | 0.4812 | -- |
| Optimal tip-speed ratio | λ* | 10.115 | -- |
| Density of air | ρa | 1.225 | kg/m3 |
| Parameters | Notation | Values | Units |
|---|---|---|---|
| Rotor mass moment of inertia | Jr | 2919.66 × 106 | kg m2 |
| Generator mass moment of inertia | Jg | 7248.32 | kg m2 |
| Hub mass moment of inertia | Jh | 2.1 × 106 | kg m2 |
| Blade mass moment of inertia | Jb | 972.52 × 106 | kg m2 |
| Rotor radius | R | 138 | m |
| Equivalent shaft spring constant | Kr | 6.94 × 109 | Nm/rad |
| Equivalent shaft damping constant | Dr | 4.97 × 107 | Nm/(rad/s) |
| Generator friction coefficients | Bg | 0.02 | |
| Damping constant of the low-speed shaft | Dlss | 1.99 × 103 | Nm/(rad/s) |
| Damping constant of the high-speed shaft | Dhss | 7.09 × 108 | Nm/(rad/s) |
| Stiffness constant of the low-speed shaft | Klss | ||
| Stiffness constant of the high-speed shaft | Khss | ||
| Gearbox efficiency, generator efficiency | ηx, ηg | 97.8, 96.1 | % |
| Gearbox ratio | nx | 164 | --- |
| First-in-plane blade frequency | 0.6277 | Hz | |
| Structural damping ratio | 0.48 | % | |
| Blade cone angle | 4 | deg |
| Variables | Notation | Inferior Limit | Superior Limit | Units |
|---|---|---|---|---|
| Moment of inertia of all three blades | Jbe | 7.1149 × 105 | 1.2299 × 109 | kg m2 |
| Blade moment of inertia of three rates | J3roots | 2.9168 × 109 | 2.9176 × 109 | kg m2 |
| Damping coefficients of the low-speed shaft | Dlss | |||
| Damping coefficients of the high-speed shaft | Dhss | |||
| Damping coefficient of the blades | Db | 1.5831 × 105 | 2.1216 × 108 | Nm/(rad/s) |
| Stiffness coefficient of the blades | Kb | 3.5227 ×106 | 3.6599 × 109 | Nm/rad |
| Variables | Cross-Correlation | RMSE |
|---|---|---|
| Generator speed | 0.9973 | 0.2671 |
| Aerodynamic torque | 0.9967 | 0.6823 |
| Effective wind speed | 0.9990 | 0.7049 |
| Collective tip deflection | 0.9998 | 0.0234 |
| Parameter | CPC Only | CPC + ABDC |
|---|---|---|
| Kp of CPC | 1.4970 | 0.0201 |
| Ki of CPC | 3.3980 | 0.0134 |
| Kbc of ABDC | ---- | 5.6320 |
| Dbc of ABDC | ---- | 2808.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamoli, S.; Gambier, A. Active Edgewise Blade Damping Control of Large Wind Turbines by Using the Pitch Controller and an Interval Observer. Actuators 2024, 13, 58. https://doi.org/10.3390/act13020058
Chamoli S, Gambier A. Active Edgewise Blade Damping Control of Large Wind Turbines by Using the Pitch Controller and an Interval Observer. Actuators. 2024; 13(2):58. https://doi.org/10.3390/act13020058
Chicago/Turabian StyleChamoli, Suryans, and Adrian Gambier. 2024. "Active Edgewise Blade Damping Control of Large Wind Turbines by Using the Pitch Controller and an Interval Observer" Actuators 13, no. 2: 58. https://doi.org/10.3390/act13020058
APA StyleChamoli, S., & Gambier, A. (2024). Active Edgewise Blade Damping Control of Large Wind Turbines by Using the Pitch Controller and an Interval Observer. Actuators, 13(2), 58. https://doi.org/10.3390/act13020058







