Abstract
Exoskeleton robots hold promising prospects for rehabilitation training in individuals with weakened muscular conditions. However, achieving improved human–machine interaction and delivering customized assistance remains a challenging task. This paper introduces a muscle synergy-based human-in-the-loop (HIL) optimization framework for hip exoskeletons to offer more personalized torque assistance. Initially, we propose a muscle synergy similarity index to quantify the similarity of synergy while walking with and without the assistance of an exoskeleton. By integrating surface electromyography (sEMG) signals to calculate metrics evaluating muscle synergy and iteratively optimizing assistance parameters in real time, a muscle synergy-based HIL optimized torque configuration is presented and tested on a portable hip exoskeleton. Iterative optimization explores the optimal and suboptimal assistance torque profiles for six healthy volunteers, simultaneously testing zero torque and predefined assistance configurations, and verified the corresponding muscle synergy similarity indices through experimental testing. In our validation experiments, the assistance parameters generated through HIL optimization significantly enhance muscle synergy similarity during walking with exoskeletal assistance, with an optimal average of 0.80 ± 0.04 (mean ± std), marking a 6.3% improvement over prior assistive studies and achieving 96.4% similarity compared with free walking. This demonstrates that the proposed muscle synergy-based HIL optimization can ensure robotic exoskeleton-assisted walking as “natural” as possible.
1. Introduction
Wearable devices, such as exoskeleton robots and exosuits, have garnered significant attention in fields such as rehabilitation [1], augmentation [2], and elderly care [3] owing to their potential to offer timely movement guidance or torque assistance to users [4]. Recent advancements in portable walking-assist exoskeletons demonstrate considerable potential in improving the wearers’ mobility, for instance, by reducing metabolic costs [5,6,7,8] or muscular activity [9,10]. Simultaneously, mechanical adaptations, e.g., serial elastic actuator [11] and quasi-direct driver [12], along with cognitive adaptations, such as admittance control [13], have been extensively researched to foster improved human–exoskeleton interactions. Despite the innovations, determining the exertion of forces and torques on the human body and understanding and predicting individual adaptation or response remain unresolved challenges [14,15]. Even for an exoskeleton that applies assistive torques to a single joint during highly cyclic motions such as walking, forecasting variations in an individual’s muscle recruitment and movement patterns poses challenges [16]. Enhancements in somatic sensation due to optimized torque configurations based on human-in-the-loop (HIL) optimization have made significant strides [6,8], thereby garnering increased attention for walking-assist exoskeletons. Beyond metabolic costs and muscular activity, user preferences [17], transferred work [9], and several other physical and physiological signals are also considered cost functions in HIL optimization. However, during the acceptance of the assistance of an exoskeleton, users’ neuromuscular control might undergo alterations. Understanding how users adapt their neuromuscular control in response to external assistance is crucial for guiding the high-level control of wearable devices [18]. In other words, considering the higher-level control of users’ neuromuscular patterns is more likely to achieve a more “natural” gait.
The hypothesis of muscle synergy was initially proposed by Bernstein [19] as an appropriate way to explain the mechanisms of the motor nervous system under multi-degree-of-freedom control. This hypothesis suggests that the central nervous system (CNS) tends to combine muscle groups within low-dimensional modules to achieve efficient and precise motor control, thereby reducing the complexity of CNS control over the musculoskeletal system [20]. Characteristics of muscle synergy have been observed in various movements, such as walking [21], running [22], and turning [23]. Muscle synergy has been employed to investigate the impact of exoskeletons on users, providing guidance for the design of these devices. Exoskeletons can alter muscle recruitment patterns during walking and other tasks. Li et al. [24] quantitatively analyzed the muscle synergy of the lower limbs during walking with hip-knee exoskeleton assistance. The results showed significant alterations in muscle synergy when there was assistance from the exoskeleton. Liu et al. [25] used muscle synergy to identify transitions between different movement patterns, which are crucial for adjusting exoskeleton control to ensure safe and comfortable support for users. Steele et al. [18] demonstrated the feasibility of exoskeleton application in rehabilitation by comparing synergy weights and activations of ankle exoskeletons under different torque and operation modes. Current research primarily focuses on variations in muscle synergy under various exoskeleton assist modes. However, the means of adjusting assistive torque configurations to influence user muscle synergy remains unknown. This work proposes a similarity index to quantify the degree of similarity between muscle synergy patterns, based on which a muscle synergy-based human–exoskeleton interaction optimized hip exoskeleton assistive torque configuration is designed and experimentally validated to guide “natural” walking.
The objective of this study is to establish a HIL optimization framework grounded in muscle synergy for exoskeleton control. This framework aims to offer personalized torque assistance while concurrently minimizing the exertion involved in walking. The baseline muscle synergy, i.e., synergy during free “natural” walking of one subject, can be referred to as a synergy dataset that could be developed by researchers based on statistical analysis. Our contributions are outlined as follows:
On the one hand, we devised a muscle synergy similarity index to quantify the resemblance of synergy between walking with and without exoskeleton assistance. On the other hand, we proposed a human–exoskeleton interaction optimized assistive torque configuration based on muscle synergy and experimentally validated it on a portable hip exoskeleton. Under the personalized optimal torque configurations provided by hip exoskeleton assistance, an enhancement in muscle synergy similarity during walking was observed. To our knowledge, this is the first work to use muscle synergy as a cost function in HIL optimization for assistive torque generation and to investigate it. The findings of this study will contribute to future human–machine collaboration optimization and a better understanding of human neuromuscular control responses under external robotic assistance.
In the remaining sections of this paper, Section 2 introduces the experimental platform and the proposed HIL optimization framework, and Section 3 presents the experimental results of walking with exoskeletal assistance and detailed data analysis. The discussion and conclusions are presented in Section 4 and Section 5, respectively.
2. Methods
2.1. System Overview
The total mass of the hip exoskeleton was 4.95 kg, comprising the powered joint module, interface modules (cuffs and frames), and electrical components (control board and battery), as illustrated in Figure 1A [26]. It was secured to the human body by straps, fixing it around the waist and thighs. The waist’s fixation structure serves to secure the exoskeleton and motor positions, while the leg’s structure connects with the leg link, securing it to the wearer’s thigh for torque transmission. The leg link is constructed from carbon fiber, aiming to minimize the exoskeleton’s weight while ensuring torque transmission, with personalized adjustments in link length to accommodate varying body sizes.
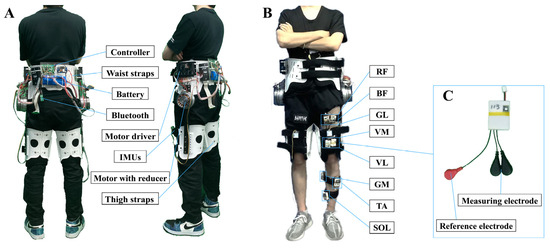
Figure 1.
Exoskeleton and sEMG sensors: (A). Hip exoskeleton; (B). sEMG sensors attached to the muscles (RF: rectus femoris, VM: vastus medialis, VL: vastus lateralis, BF: biceps femoris, GL: gluteus maximus, GM: gastrocnemius, TA: tibialis anterior, SOL: soleus); (C). sEMG sensors.
The powered joint module consisted of servo motors (Maxon EC 90 Flat, Maxon Motor Co., Ltd., Sachseln, Switzerland), customized planetary gear reducers (31.6:1), and motor drivers (ESCON 50/5 module, Maxon Motor Co., Ltd., Switzerland) positioned on the left and right sides of the hips, providing assistance torque ranging from 0 to 23 Nm for hip flexion and extension. Two inertial measurement units (IMU) (Shenzhen Witte Intelligent Technology Co., Ltd., Shenzhen, China), depicted in Figure 1A, were mounted on the front of both thighs, measuring hip flexion/extension angles and velocities. Surface electromyography (sEMG) signal sensors (Customized by College of Biomedical Engineering & Instrument Science, Zhejiang University) were used in the experiments, with a sampling frequency of 2 kHz [27]. Data of real-time transmission to the computer were achieved using WIFI. Multiple threads were employed to receive data from several sensors, parsing the communication data to obtain multi-channel sensor data. As shown in Figure 1B, sEMG sensors were used to capture sEMG signals from eight muscle sites on the left leg of the human body, including rectus femoris (RF), vastus medialis (VM), vastus lateralis (VL), biceps femoris (BF), gluteus maximus (GL), gastrocnemius (GM), tibialis anterior (TA), and soleus (SOL).
2.2. Human-in-the-Loop Optimization Platform
The experimental setup comprises sEMG sensors, a hip exoskeleton, and an upper-level computer housing a human-in-the-loop optimization algorithm. The workflow of the experimental setup is illustrated in Figure 2 [26].
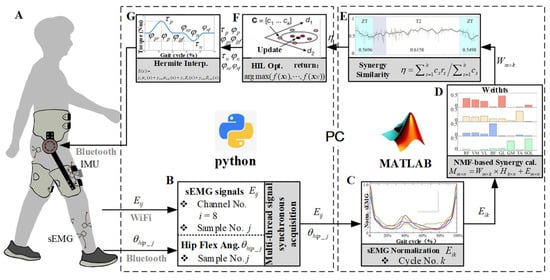
Figure 2.
Human-in-the-loop optimization platform: (A). The subject wearing the hip exoskeleton; (B). Angle and sEMG signal sampling; (C). Signals segmentation and normalization; (D). NMF-based synergy calculation. (E). Synergy similarity calculation. (F). HIL optimization based on synergy similarity; (G). Hermite interpolation for assist torque profile generation.
The sEMG signals and lower-limb kinematic data were transmitted to the upper-level computer via WIFI and Bluetooth, respectively, where all data processing tasks were conducted using MATLAB (MatlabR2020b, MathWorks Inc., Natick, MA, USA). Referring to the data preprocessing method of Zhang et al. [28], parameters were adjusted to preprocess the original sEMG signals. This involved second-order 20–300 Hz Butterworth bandpass filtering, full-wave rectification, and second-order 10 Hz Butterworth low-pass filtering. Subsequently, using kinematic data, such as angles and phases, collected by IMUs, the sEMG signals were segmented based on gait cycles and processed through an optimized Non-negative Matrix Factorization (NMF) method to compute muscle synergy, which is discussed further in Section 2.3. Finally, various gait evaluation parameters were obtained through a comparison with predefined standard assessment metrics in HIL optimization. The mean of the evaluation parameters obtained from multiple gait calculations was considered the evaluation metric for this iteration. In Python, using HIL optimization, iterative calculations yielded eight key parameters for the assistive configuration file. In Section 2.5, these parameters were then used to generate the assistive configuration file for torque control.
2.3. Evaluation Index Based on Muscle Synergy
In this study, the process of analyzing synergies based on human experimental data is illustrated in Figure 3. The raw sEMG signal during walking (Figure 3A) underwent filtering (Figure 3B), and after gait segmentation and normalization, the preprocessed sEMG signal was obtained (Figure 3C), NMF was employed for extracting muscle synergies, ensuring the non-negative attributes of the decomposition matrix [29,30], thereby granting it greater physical interpretability compared with alternative decomposition methodologies. The expression is as follows:
where incorporates sEMG signals sampled across all eight channels (where denotes the number of muscles, and signifies the time frames used to extract muscle synergies). signifies the muscle weight distribution, reflecting the relative contributions of each muscle to the synergies, while embodies the activation profiles, elucidating the temporal dynamics of muscle synergy activation throughout the gait cycle. denotes the reconstruction error, depicting the disparity between the reconstructed and original sEMG signals. The number of muscle synergies, , is determined using the activation profile matrix variability accounted for (VAF) criterion [31], which is defined as the reconstruction error over the original sEMG signals:
In accordance with previous studies, the quantity of muscular synergy effects is determined by two conditions: when adding new muscular synergy effects, the total VAF exceeds 90%, while each additional synergy effect does not exceed 5% [32]. In the present study, as illustrated in Figure 4, when the number of synergies was 3, the VAF exceeded 90%, meeting the first condition. However, when the number of synergies increased to 4, the rise in VAF surpassed 5%. Ultimately, the number of synergies was determined to be 4, indicating that four sets of synergies could describe the muscular activity of the lower limbs during human walking.
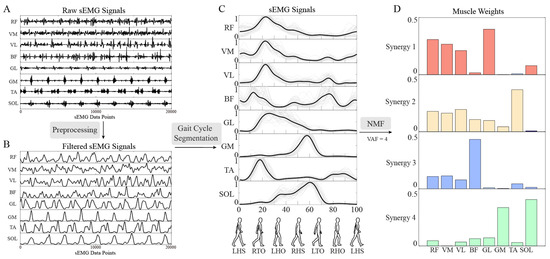
Figure 3.
The flow chart of muscle synergy analysis. (A). Raw sEMG signals; (B). Filtered sEMG signals; (C). The mean value (black line) of preprocessed sEMG signals of different gaits (gray line); (D). Muscle synergy weights.
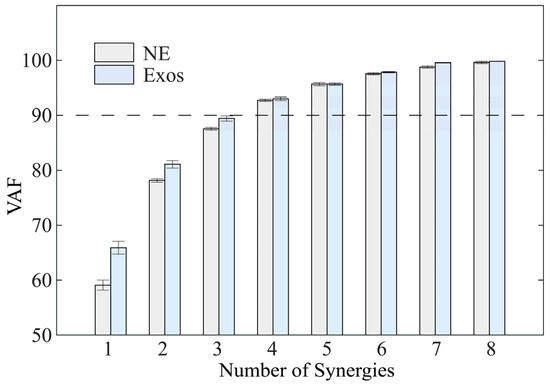
Figure 4.
Total variability accounted for (VAF) versus the number of synergies based on NMF. NE and Exos stand for walking trials without and with exoskeleton, respectively. VAF gradually increased, with an increase in the number of synergies.
To quantify the similarity among human muscle synergies across different conditions, an evaluative measure termed was introduced. was calculated as the summation of the product between the proportion of the s-th synergy and its corresponding Pearson correlation coefficient :
where signifies the correlation coefficient between the s-th synergy and its matched reference synergy, and denotes the activation ratio of the s-th synergy vector. is defined as follows:
where is the product of the k-th column vector of and the k-th row vector of .
2.4. Assistive Torque Profile Generation
The assistive torque configuration was generated using a parameterized approach that allows for online adjustments. The gait cycle serves as the horizontal axis, while the assistive torque represents the vertical axis, with the moment of maximum hip flexion angle set as the starting point of a gait cycle. Previous studies configured the assistive torque within a cycle using four parameter points [33]. However, in the normal human walking process, hip joint flexion and extension torques are not symmetrical. To ensure accuracy in calculating the assistive torque profile and convergence speed, this study determined the assistive torque configuration for each gait cycle using eight parameters. These parameters included peak torque during flexion and extension , peak time of flexion and extension , rise time of flexion and extension , and fall time of flexion and extension .
The segmented cubic Hermite interpolation polynomial was employed to interpolate each profile, thereby linking each parameter to generate the desired torque assistance profile s. The interpolation polynomials can be represented as follows:
where , , , and represent the basis functions of interpolation. The expressions for these basis functions are as follows:
For the sake of simplifying the function expressions, we defined the following:
Substituting Equations (7) and (8) with Equation (6) yields the cubic polynomial of this segment of the profile:
In this study, the expression can be simplified since the derivatives at all connecting points of the profile s are zero:
Considering safety and comfort during assistance, these parameters are only allowed to vary within predefined suitable ranges established through prior testing:
Figure 5 illustrates the interpolation of the configuration files and spatial coverage achieved by generating different parameters’ configuration files.
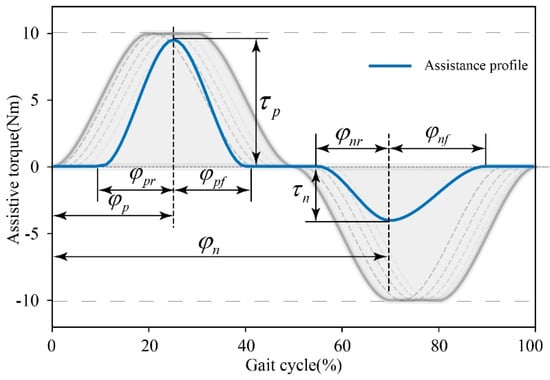
Figure 5.
Parametric assistance profile generation, including assistance profile, control parameters, and the space that profiles can traverse.
2.5. Iterative Process for Optimizing Assistive Torque
The optimization process of HIL employs the Bayesian optimization algorithm [34], achieving a twofold increase in convergence speed compared with traditional gradient descent methods [35]. Table 1 presents the pseudocode for the optimization process.

Table 1.
Optimization process for assistive torque based on the Bayesian optimization algorithm.
The variables involved include as the parameters of the exoskeleton assistive torque profile, which is presented in the form , and as the optimization target, representing the similarity of human muscle synergy. stands for the dataset, denotes the model for the assistance profile and human muscle synergy similarity, represents the hyperparameter search space, signifies the acquisition function, represents the model fitted to dataset , is the initial number of sampling points, and T refers to the number of algorithm iterations. This approach aims to explore the region where the maximum value of the function is expected. After a certain number of iterations, the assistance torque profile parameter values corresponding to the highest attained muscle synergy similarity evaluation index represent the optimal torque.
2.6. Testing Protocol
Six healthy male participants took part in this experiment, and their basic characteristics are presented in Table 2. The experiment comprised two sessions.

Table 2.
Participants information.
The first session involved the HIL optimization experiment. Initially, participants walked for 90 s on a treadmill at a speed of 1 m/s without wearing the exoskeleton (NE) to establish a baseline using data collected from sEMG sensors and IMUs. Subsequently, participants walked on the treadmill at a speed of 1 m/s while wearing the exoskeleton, and tests were randomly conducted according to the conditions outlined in Table 3. Before the experiment, participants had a period of time to acclimatize to the exoskeleton, ensuring no resistance to the assistive torque provided by the exoskeleton during walking. Based on prior experimental findings and testing experiences, each iteration was set for a duration of 90 s [32], with the evaluation metrics calculated using the data from the last 30 s (approximately 20 steps). Additionally, the data processing and synergy analysis using NMF took approximately 3 s, which was compensated for at the beginning of each iteration and did not impact the experimental results. To mitigate the impact of muscle fatigue during human walking on the produced sEMG signals, participants rested for a certain period after completing 10 cycles of optimization, equivalent to 15 min of walking. To expedite the exploration process, the experiment commenced with four sets of different predefined parameters.

Table 3.
The assist torque profile used in the experiment.
The second session involved the evaluation of muscle synergy optimization, scheduled concurrently with the HIL optimization experiment, aiming to minimize the influence of additional factors by requiring participants to maintain a lifestyle consistent with the day of the HIL optimization experiment. Before the experiment, participants had a period to adapt to the exoskeleton. To mitigate the impact of different sensor placements on the experimental results, the surface sEMG sensors were positioned as close as possible to their locations in the previous experiment. Initially, participants walked freely on a treadmill at a speed of 1 m/s in NE mode, and the collected sEMG data were used to calculate a new synergy baseline. Subsequently, participants wore the exoskeleton and were subjected to randomized tests according to the conditions outlined in Table 3 [26]. Finally, participants walked freely on the treadmill at a speed of 1 m/s in NE mode as well, and these data were compared with the baseline data obtained at the beginning of the experiment. The initial and final 10-step data from each experimental condition were removed, and the remaining sEMG data from the gait cycles were used for synergy analysis and similarity calculations. Statistical analysis was conducted using the similarity data obtained from multiple gait cycles.
3. Results
3.1. Human-in-the-Loop Optimization Experiment
The process of HIL optimization based on muscular synergy is depicted in Figure 6. Figure 6A delineates the specifics of the iterative refinement of eight parameters. Figure 6B exhibits auxiliary configuration files generated for each iteration, illustrating the exploration of the optimal auxiliary torque configuration throughout the process. The muscular synergy-based evaluation metrics computed in each iteration are presented in Figure 6C. Taking Subject 2 as an example, a total of 64 iterations were conducted, and at the 35th iteration, the evaluation metric reached its highest value, stabilizing thereafter, thereby establishing it as the optimal parameter set. The optimal auxiliary parameters were determined to be = [2.38, 0.28, 0.19, 0.16, 4.85, 0.76, 0.16, 0.13], with a synergy similarity of 0.84. Of the six participants, the peak assist torque value of Subject 2 was the lowest. During the experiment, when assist torque increased, the gait of Subject 2 slightly changed, leading to an unnatural feeling during walking; thus, the synergy similarity would decrease. After HIL optimization, he felt more natural during the low-assist peak torque pattern. In contrast, the subsequent analysis identified a sub-optimal parameter set at the 53rd iteration, yielding = [4.43, 0.29, 0.17, 0.18, 3.46, 0.73, 0.18, 0.13], with a synergy similarity of 0.82. The iterative optimization results of the assistive parameters for the six subjects are presented in Table 4. The difference between the similarity achieved by all subjects under the optimal assistive torque configuration and the similarity under the sub-optimal configuration was less than 0.015, indicating convergence, despite Subjects 3 and 5 reaching only 35 and 48 iterations, respectively. Compared with the optimal strategy, their similarity decrease was merely 1.33% and 2.17%, respectively. The average similarities for the optimal group (BO1) and the sub-optimal group (BO2) of the six subjects were 0.83 ± 0.09 and 0.81 ± 0.08 (mean ± std), respectively.
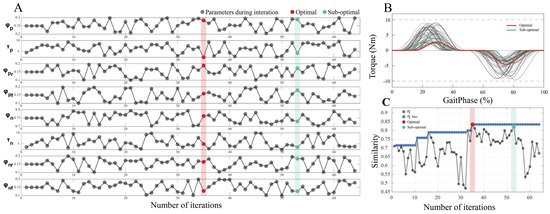
Figure 6.
Human-in-the-loop optimization results: (A) Variation of each parameter with iteration. (B) The assistive torque profiles; (C) Evaluation index calculated in each iteration and optimization of evaluation index.

Table 4.
Iterations of Assistive Parameters to Optimal and Sub-optimal for Six Participants.
Subjects 4 and 5 showcased notable synergy similarities when using hip exoskeleton assistance, reaching 0.91 and 0.92, respectively, in the BO1 mode and surpassing 0.9 even in the BO2 mode. This theoretically suggests a minimal impact of exoskeleton assistance on the muscular synergy structure under the current iterative torque configuration and aligns closely with the “natural” walking of these subjects. S2 and S6 maintained synergy optimization configurations around 0.84. However, Subjects 1 and 3 exhibited lower synergy similarities after assistive optimization, with S1 registering the lowest at 0.69 and 0.69 under the two parameter sets, indicating a substantial impact on the muscular synergy structure despite being optimal assistive parameter configurations. Comprehensive torque configuration data for each iteration are provided in Appendix A.
3.2. Optimized Muscle Synergy
Figure 7 displays the validation outcomes of the HIL optimization experiments. Figure 7A conducts a significant analysis of the experimental similarity among the six subjects, while Figure 7B presents the mean similarity results and their distribution. With the exception of Subject 4, the muscular synergy similarity indices in the two sets of NE mode for all subjects were highest when compared with their own, averaging above 0.83. This suggests that human muscle coordination remains generally consistent in the short term after assistance, making free walking a viable reference. The similarity index for the ZT group was notably lower, averaging only 0.68 ± 0.03. Comparatively, the mean similarity index in the BO1 mode exhibited an increase of approximately 18.0%, averaging 0.80 ± 0.04. Similarly, the BO2 mode demonstrated a 12.3% increase, averaging 0.76 ± 0.03. In contrast to the PD mode, the similarity indices increased by 6.3% and 1.2% for optimal and sub-optimal parameters, respectively. Moreover, when compared with free walking, the mean similarity index of the BO1 mode decreased by only 3.6%, demonstrating an 80.3% improvement over the ZT mode and a 61.5% enhancement over the PD mode, indicating a better alignment of the iteratively optimized assistive torque profile with the human muscular synergy structure. Furthermore, the similarity indices obtained from the validation experiments closely mirrored the average optimal and sub-optimal similarity indices obtained from the HIL optimization experiments, differing by only 2.5% and 6.2%, respectively, signifying good overall stability in the assistive torque parameter configurations derived from the HIL optimization process.
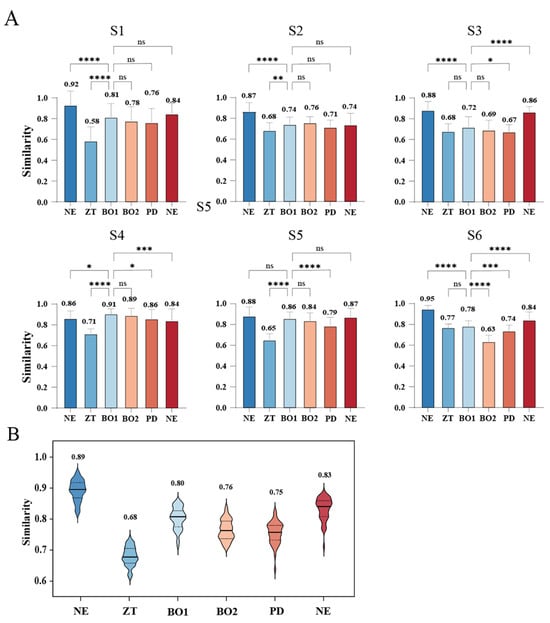
Figure 7.
Evaluation of muscle synergy optimization: (A) Analysis of similarity indices under various individual conditions and their significance differences. Significance levels are denoted by asterisks: ns (p ≥ 0.05), * (p < 0.05), ** (p < 0.01), *** (p < 0.001), and **** (p < 0.0001); (B) Average similarity results among the subjects.
In Figure 7A, aligned with the HIL optimization experiments at an individual level, S4 and S5 exhibited relatively high similarity, while S1 and S6 demonstrated comparatively lower similarity. In the validation experiment results, a significant difference analysis was conducted between the similarity of each subject under the optimal assistive configuration and under other conditions, demonstrating significant differences for p < 0.05. Apart from Subject 6, there were almost no significant differences between the optimal and sub-optimal configurations in terms of similarity values, indicating the convergence of the HIL iterative optimization. It is worth noting that S6 did not perform well in the BO2 mode during the evaluation session. This may be caused by a difference in sEMG sensor location between the optimization session and the evaluation session, which could lead to a difference in sEMG signals, making the synergy similarity of BO2 poor. S1, S2, S4, and S5 showed significantly lower similarity in the BO1 mode compared with free walking. Despite S3 and S6 exhibiting significant differences in free walking, their overall similarity was higher than that of the other groups. This suggests that HIL optimization enables subjects to walk more naturally under the primary assistance of an exoskeleton. For each subject, synergy similarities of the two NE modes were different to a certain extent. In particular, for S1, S3, S4, and S5, the differences were negligible. This confirmed that the synergy in this experiment was relatively stable.
4. Discussion
4.1. Strategy for Torque Generation
While torque assistance based on a database seems straightforward [34,35], its stability in accommodating external condition changes is poor. Mere scaling of biomechanical joint torques proves insufficient in achieving convincing torque assistance. Ding et al. parameterized the timing and values of assistive torque peaks, showcasing the superiority of their approach [35]. Collins et al. introduced metabolism as a feedback signal, creating cubic spline profiles for torque assistance based on four configuration parameters: rise time, fall time, peak time, and peak torque. This significantly reduced human energy consumption, albeit with a longer optimization convergence time [28]. In our previous research, we employed sEMG as a metabolic representation for feedback, using Bayesian and Covariance Matrix Adaptive Evolution Strategy to optimize the same four parameter configurations and enhance the convergence speed of the optimal torque profile [33]. Considering potential differences in amplitude and phase between torque profiles during flexion and extension, this study expanded the torque configuration parameters to eight and used Hermite interpolation to generate assistive profiles. Despite several trials, participants did not notably report increased comfort compared with the assistive profiles used in the previous study. Nevertheless, in this study, the optimal similarity index surpassed the predefined similarity, indicating that the four parameters—rise time, fall time, peak time, and peak torque—adequately characterized the torque assistance profile.
4.2. Evaluation Index Based on Muscle Synergy
The NMF algorithm exhibits greater robustness in extracting muscle synergies compared with ICA and FA [36,37]. Collins et al. employed NMF to compute synergistic effects in each experiment, requiring 64 min of walking time to optimize four control parameters based on metabolic consumption [18]. In this study, the algorithm was refined by implementing a faster updating iterative method using the projected gradient approach for NMF. Additionally, sEMG was employed to swiftly characterize metabolism as the evaluation function for the HIL optimization process. These optimizations allowed for convergence in a shorter duration (less than 1 h) despite doubling the number of parameter configurations. To quantify the similarity of human muscle synergy under different conditions, a novel evaluation index, η, was introduced, providing a more detailed representation than the evaluation metrics proposed by Collins et al. [18].
4.3. The Experiments and Evaluation of Human-in-the-Loop Optimization
The preliminary analysis of both the HIL optimization and validation experiments was conducted to obtain the aforementioned results. The similarity under the ZT condition appears to be consistently lower, potentially due to the exoskeleton acting as an additional load on the human body in this mode. Moreover, achieving an ideal zero torque mode without torque sensors is challenging due to the reliance on exoskeleton-driven joint friction compensation. Consequently, walking experiments under this condition altered the human body’s synergy pattern, resulting in decreased similarity.
S1, S2, S4, and S5 displayed significant differences between BO1 and ZT, indicating that the synergy structures of these subjects are susceptible to external factors (unpowered exoskeletons here) but can be restored to high synergy similarity by wearing exoskeletons, highlighting the superiority of HIL optimization. In contrast, the similarity of S3 and S6 under the optimal configuration did not significantly differ from ZT and closely resembled PD, potentially linked to the high sensitivity of locomotion control to external robotic assistance of these subjects.
Subject 4 achieved the highest similarity of 0.9054 under the optimal assistive parameters, close to the similarity in the HIL optimization experiments and significantly higher than the unassisted mode. Even the sub-optimal assistive profile reached a similarity of 0.8899, both surpassing the similarity in free walking. However, this contradicts the theoretical similarity of S4 being highest in free walking, possibly due to the minimal torque variations throughout the optimization process (with a maximum peak of only 3.6744 Nm with optimal configuration, in Table A1, and 3.19 Nm with sub-optimal configuration, in Table A2). This suggests that Subject 4 may be more accustomed to walking with lower torque, resulting in minimal or even improved impact on the muscular synergy structure. Subject 2 did not achieve the highest muscular synergy similarity with the optimal torque configuration, showing a decrease of 2.2% compared with the sub-optimal configuration, despite generally having the highest similarity with the BO1 mode across subjects after excluding the NE group. This discrepancy might be attributed to oscillations in the muscular synergy similarity under a particular assistive torque configuration observed during the experiment and arising from unstable physiological signals, specifically sEMG. Subject 6 displayed significantly lower similarity under the sub-optimal assistive configuration than ZT and PD, potentially due to the stochastic nature of collaborative computation during the closed-loop optimization experiment, resulting in some outlier data.
Table 5 illustrates a comparison of HIL optimizations for exoskeleton assist torque profile generation. Both the Collins group [28] and the Walsh group [6] used metabolic cost as a cost function, which would take 2~4 min to estimate the metabolic cost for each iteration. Our former work adopted muscle activity as a cost function to reduce muscle effort during exoskeleton-assisted walking, making a reduction of rectus femoris muscle activation to 33.5%. The presented work used muscle synergy as a cost function, which reduced time cost per iteration to 30 s and sped up the whole HIL optimization. Meanwhile, an average synergy similarity increase of 18.3% compared with ZT mode shows a promising solution for natural robotic walking assistance.

Table 5.
Comparison of HIL optimizations for exoskeletons.
4.4. Study Limitations
One major limitation of this study is that, despite the positive findings obtained from the participation of six volunteers with homogeneous gender and age in the experiment, the inclusion of more subjects, especially female participants and participants with a wider range of ages, is necessary to establish more detailed patterns. Moreover, due to the prolonged duration of HIL optimization, some participants experienced sweating while wearing the exoskeleton, which affected the quality of the sEMG signal to some extent, although this phenomenon was observed only during the experiment of S6. Structural and algorithmic optimizations of the exoskeleton are needed to improve breathability and shorten convergence time. Moreover, free walking trials should be conducted instead of treadmill walking with a constant speed since, in real life, humans would constantly adjust their walking speed and perform more natural and relaxed musculoskeletal states.
5. Conclusions
This study proposes a quantification method for muscular synergy similarity, investigating the degree of similarity in muscular synergy during walking both with and without exoskeleton assistance. Moreover, based on this quantification, it introduces a human–machine collaborative optimization framework grounded in muscular synergy to generate personalized torque assistance configurations validated on a portable hip exoskeleton platform. The research findings indicate that incorporating quantified human physiological signals and neuromuscular control into robot feedback control and subsequently obtaining optimal torque configurations through iterative optimization significantly enhance muscular synergy during exoskeleton-assisted walking. This achievement allows for a more rational and “natural” torque assistance, presenting a novel, feasible approach for exoskeleton-assisted strategies.
Author Contributions
Conceptualization, D.L. and Y.M.; methodology, Y.M. and D.L.; software, L.Y.; validation, D.L., L.G. and W.Y.; formal analysis, L.G. and Z.Y.; investigation, W.Y.; resources, L.Y.; data curation, Z.Y.; writing—original draft preparation, Y.M. and D.L.; writing—review and editing, Y.M., D.L. and W.Y; visualization, L.Y.; supervision, C.Y.; project administration, W.Y.; funding acquisition, W.Y. and C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Key Research and Development Project of Zhejiang Province (No. 2022C03029), in part by the Ningbo Public Welfare Project (No. 2021S082), in part by the Scientific Research Fund of Zhejiang Provincial Education Department (No. Y202353520), in part by the Scientific Research Fund of Zhejiang University (No. XY2023046), and in part by the Zhejiang Public Welfare Project (No. LTGY23H170002).
Data Availability Statement
All data for this study have been included in this paper, and there are no other unpublished data.
Acknowledgments
We appreciate the invaluable contributions of the volunteers involved in dataset preparation and our experimental work.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This section provides a detailed account of the optimal and sub-optimal torque assistance profiles obtained from the HIL optimization for six participants. S1, S2, and S4 exhibited peak values ( and ) lower than 5 Nm for both optimal and sub-optimal torques. This indicates a preference for lower levels of assistive torque among these three participants. Conversely, S3, S5, and S6 demonstrated a preference for higher levels of assistance, with Subject 3 notably displaying a peak extension torque () at the hip joint of 9.5760 Nm.

Table A1.
Optimal assistive parameters of six participants.
Table A1.
Optimal assistive parameters of six participants.
| Subjects | ||||||||
|---|---|---|---|---|---|---|---|---|
| S1 | 0.25 | 4.54 Nm | 0.17 | 0.14 | 0.73 | 3.42 Nm | 0.10 | 0.14 |
| S2 | 0.28 | 2.38 Nm | 0.19 | 0.16 | 0.76 | 4.85 Nm | 0.16 | 0.13 |
| S3 | 0.24 | 7.85 Nm | 0.16 | 0.13 | 0.79 | 9.58 Nm | 0.18 | 0.13 |
| S4 | 0.30 | 3.67 Nm | 0.10 | 0.18 | 0.80 | 2.40 Nm | 0.20 | 0.10 |
| S5 | 0.25 | 7.95 Nm | 0.15 | 0.15 | 0.75 | 6.81 Nm | 0.15 | 0.15 |
| S6 | 0.25 | 6.28 Nm | 0.18 | 0.15 | 0.75 | 5.98 Nm | 0.19 | 0.17 |

Table A2.
Sub-Optimal assistive parameters of six participants.
Table A2.
Sub-Optimal assistive parameters of six participants.
| Subjects | ||||||||
|---|---|---|---|---|---|---|---|---|
| S1 | 0.25 | 4.54 Nm | 0.15 | 0.15 | 0.75 | 3.41 Nm | 0.15 | 0.15 |
| S2 | 0.29 | 4.25 Nm | 0.17 | 0.18 | 0.73 | 3.46 Nm | 0.18 | 0.13 |
| S3 | 0.25 | 5.13 Nm | 0.20 | 0.19 | 0.71 | 6.83 Nm | 0.14 | 0.18 |
| S4 | 0.25 | 3.19 Nm | 0.14 | 0.13 | 0.75 | 3.37 Nm | 0.16 | 0.17 |
| S5 | 0.28 | 9.27 Nm | 0.12 | 0.19 | 0.78 | 6.64 Nm | 0.18 | 0.10 |
| S6 | 0.26 | 2.79 Nm | 0.13 | 0.13 | 0.72 | 9.75 Nm | 0.14 | 0.14 |
References
- Wei, Q.; Li, Z.; Zhao, K.; Kang, Y.; Su, C.-Y. Synergy-Based Control of Assistive Lower-Limb Exoskeletons by Skill Transfer. IEEE/ASME Trans. Mechatron. 2020, 25, 705–715. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Li, T.; Yan, Y.; Jiang, D. Gait Prediction and Variable Admittance Control for Lower Limb Exoskeleton with Measurement Delay and Extended-State-Observer. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 8693–8706. [Google Scholar] [CrossRef]
- Jayaraman, C.; Embry, K.R.; Mummidisetty, C.K.; Moon, Y.; Giffhorn, M.; Prokup, S.; Lim, B.; Lee, J.; Lee, Y.; Lee, M.; et al. Modular Hip Exoskeleton Improves Walking Function and Reduces Sedentary Time in Community-Dwelling Older Adults. J. NeuroEng. Rehabil. 2022, 19, 144. [Google Scholar] [CrossRef]
- Yang, C.; Yu, L.; Xu, L.; Yan, Z.; Hu, D.; Zhang, S.; Yang, W. Current Developments of Robotic Hip Exoskeleton toward Sensing, Decision, and Actuation: A Review. Wearable Technol. 2022, 3, e15. [Google Scholar] [CrossRef]
- Seo, K.; Kim, K.; Park, Y.J.; Cho, J.-K.; Lee, J.; Choi, B.; Lim, B.; Lee, Y.; Shim, Y. Adaptive Oscillator-Based Control for Active Lower-Limb Exoskeleton and Its Metabolic Impact. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6752–6758. [Google Scholar]
- Kim, J.; Lee, G.; Heimgartner, R.; Arumukhom Revi, D.; Karavas, N.; Nathanson, D.; Galiana, I.; Eckert-Erdheim, A.; Murphy, P.; Perry, D.; et al. Reducing the Metabolic Rate of Walking and Running with a Versatile, Portable Exosuit. Science 2019, 365, 668–672. [Google Scholar] [CrossRef] [PubMed]
- Gordon, D.F.N.; McGreavy, C.; Christou, A.; Vijayakumar, S. Human-in-the-Loop Optimization of Exoskeleton Assistance Via Online Simulation of Metabolic Cost. IEEE Trans. Robot. 2022, 38, 1410–1429. [Google Scholar] [CrossRef]
- Slade, P.; Kochenderfer, M.J.; Delp, S.L.; Collins, S.H. Personalizing Exoskeleton Assistance While Walking in the Real World. Nature 2022, 610, 277–282. [Google Scholar] [CrossRef] [PubMed]
- Tu, X.; Li, M.; Liu, M.; Si, J.; Huang, H.H. A Data-Driven Reinforcement Learning Solution Framework for Optimal and Adaptive Personalization of a Hip Exoskeleton. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 10610–10616. [Google Scholar]
- Wang, W.; Chen, J.; Ji, Y.; Jin, W.; Liu, J.; Zhang, J. Evaluation of Lower Leg Muscle Activities During Human Walking Assisted by an Ankle Exoskeleton. IEEE Trans. Ind. Inf. 2020, 16, 7168–7176. [Google Scholar] [CrossRef]
- Qian, Y.; Han, S.; Wang, Y.; Yu, H.; Fu, C. Toward Improving Actuation Transparency and Safety of a Hip Exoskeleton with a Novel Nonlinear Series Elastic Actuator. IEEE/ASME Trans. Mechatron. 2023, 28, 417–428. [Google Scholar] [CrossRef]
- Nesler, C.; Thomas, G.; Divekar, N.; Rouse, E.J.; Gregg, R.D. Enhancing Voluntary Motion with Modular, Backdrivable, Powered Hip and Knee Orthoses. IEEE Robot. Autom. Lett. 2022, 7, 6155–6162. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Tran, M.; Huang, H. Admittance Shaping-Based Assistive Control of SEA-Driven Robotic Hip Exoskeleton. IEEE/ASME Trans. Mechatron. 2019, 24, 1508–1519. [Google Scholar] [CrossRef]
- Uchida, T.K.; Seth, A.; Pouya, S.; Dembia, C.L.; Hicks, J.L.; Delp, S.L. Simulating Ideal Assistive Devices to Reduce the Metabolic Cost of Running. PLoS ONE 2016, 11, e0163417. [Google Scholar] [CrossRef]
- Wang, L.T.; Van Asseldonk, E.H.F.; Van Der Kooij, H. Model Predictive Control-Based Gait Pattern Generation for Wearable Exoskeletons. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–6. [Google Scholar]
- Cain, S.M.; Gordon, K.E.; Ferris, D.P. Locomotor Adaptation to a Powered Ankle-Foot Orthosis Depends on Control Method. J. NeuroEng. Rehabil. 2007, 4, 48. [Google Scholar] [CrossRef]
- Ingraham, K.A.; Remy, C.D.; Rouse, E.J. The Role of User Preference in the Customized Control of Robotic Exoskeletons. Sci. Robot. 2022, 7, eabj3487. [Google Scholar] [CrossRef]
- Steele, K.M.; Jackson, R.W.; Shuman, B.R.; Collins, S.H. Muscle Recruitment and Coordination with an Ankle Exoskeleton. J. Biomech. 2017, 59, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, M.B. The Co-ordination and Regulation of Movements. J. Neuropathol. Exp. Neurol. 1968, 27, 348. [Google Scholar] [CrossRef]
- d’Avella, A.; Saltiel, P.; Bizzi, E. Combinations of Muscle Synergies in the Construction of a Natural Motor Behavior. Nat. Neurosci. 2003, 6, 300–308. [Google Scholar] [CrossRef] [PubMed]
- Chvatal, S.A.; Ting, L.H. Common Muscle Synergies for Balance and Walking. Front. Comput. Neurosci. 2013, 7, 48. [Google Scholar] [CrossRef] [PubMed]
- Bach, M.M.; Daffertshofer, A.; Dominici, N. Muscle Synergies in Children Walking and Running on a Treadmill. Front. Hum. Neurosci. 2021, 15, 637157. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Kim, Y.; Kim, M.; Yoon, B. Muscle Synergies for Turning During Human Walking. J. Mot. Behav. 2019, 51, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, H.; Yin, Z.; Chen, K. Muscle Synergy Alteration of Human During Walking with Lower Limb Exoskeleton. Front. Neurosci. 2019, 12, 1050. [Google Scholar] [CrossRef]
- Liu, Y.-X.; Gutierrez-Farewik, E.M. Joint Kinematics, Kinetics and Muscle Synergy Patterns During Transitions Between Locomotion Modes. IEEE Trans. Biomed Eng. 2023, 70, 1062–1071. [Google Scholar] [CrossRef]
- Yang, W.; Yan, Z.; Yu, L.; Feng, L.; Gui, L.; Yang, C. Muscle Synergy-Based Human-in-the-Loop Optimization for Personalized Hip Exoskeleton Control. In Proceedings of the 2023 International Conference on Advanced Robotics and Mechatronics (ICARM), Sanya, China, 8–10 July 2023; pp. 73–78. [Google Scholar]
- Zhou, C.; Yang, L.; Liao, H.; Liang, B.; Ye, X. Ankle Foot Motion Recognition Based on Wireless Wearable sEMG and Acceleration Sensors for Smart AFO. Sens. Actuators A Phys. 2021, 331, 113025. [Google Scholar] [CrossRef]
- Zhang, J.; Fiers, P.; Witte, K.A.; Jackson, R.W.; Poggensee, K.L.; Atkeson, C.G.; Collins, S.H. Human-in-the-Loop Optimization of Exoskeleton Assistance during Walking. Science 2017, 356, 1280–1284. [Google Scholar] [CrossRef]
- Hu, L.; Luo, X.; Tang, S.; Wu, X.; Chen, L.; Zheng, X.; Hou, W. Research on Power-Assisted Strategy and Device Based on Muscle Synergy. In Proceedings of the 2019 IEEE International Conference on Computational Intelligence and Virtual Environments for Measurement Systems and Applications (CIVEMSA), Tianjin, China, 14–16 June 2019; pp. 1–5. [Google Scholar]
- Rabbi, M.F.; Pizzolato, C.; Lloyd, D.G.; Carty, C.P.; Devaprakash, D.; Diamond, L.E. Non-Negative Matrix Factorisation Is the Most Appropriate Method for Extraction of Muscle Synergies in Walking and Running. Sci. Rep. 2020, 10, 8266. [Google Scholar] [CrossRef]
- Chia Bejarano, N.; Pedrocchi, A.; Nardone, A.; Schieppati, M.; Baccinelli, W.; Monticone, M.; Ferrigno, G.; Ferrante, S. Tuning of Muscle Synergies During Walking Along Rectilinear and Curvilinear Trajectories in Humans. Ann. Biomed Eng. 2017, 45, 1204–1218. [Google Scholar] [CrossRef]
- Clark, D.J.; Ting, L.H.; Zajac, F.E.; Neptune, R.R.; Kautz, S.A. Merging of Healthy Motor Modules Predicts Reduced Locomotor Performance and Muscle Coordination Complexity Post-Stroke. J. Neurophysiol. 2010, 103, 844–857. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Liu, X.; Chen, Y.; Yu, L.; Yan, Z.; Yang, C.; Zhou, C.; Yang, W. Reducing the Muscle Activity of Walking Using a Portable Hip Exoskeleton Based on Human-in-the-Loop Optimization. Front. Bioeng. Biotechnol. 2023, 11, 1006326. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Kim, M.; Kuindersma, S.; Walsh, C.J. Human-in-the-Loop Optimization of Hip Assistance with a Soft Exosuit during Walking. Sci. Robot. 2018, 3, eaar5438. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Galiana, I.; Asbeck, A.T.; De Rossi, S.M.M.; Bae, J.; Santos, T.R.T.; De Araujo, V.L.; Lee, S.; Holt, K.G.; Walsh, C. Biomechanical and Physiological Evaluation of Multi-Joint Assistance with Soft Exosuits. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Tresch, M.C.; Cheung, V.C.K.; d’Avella, A. Matrix Factorization Algorithms for the Identification of Muscle Synergies: Evaluation on Simulated and Experimental Data Sets. J. Neurophysiol. 2006, 95, 2199–2212. [Google Scholar] [CrossRef] [PubMed]
- Lambert-Shirzad, N.; Van Der Loos, H.F.M. On Identifying Kinematic and Muscle Synergies: A Comparison of Matrix Factorization Methods Using Experimental Data from the Healthy Population. J. Neurophysiol. 2017, 117, 290–302. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).