Distributed Fixed-Time Leader-Following Consensus for Multi-Agent Systems: An Event-Triggered Mechanism

Abstract

In this work, a fixed-time leader-following event-triggered (ET) consensus problem for multi-agent systems (MASs) with external disturbances is investigated. A distributed observer is developed to achieve the estimated state of the leader. By means of the observation information, the consensus error system for multi-agents is reformulated into a tracking error system, wherein individual follower agent aims to track the leader agent. Building upon Lyapunov technology and fixed-time stability theory, a new ET protocol is introduced to mitigate communication wastes. Notably, the proposed controller incorporates a strong robust fixed-time control form with lower complexity, and a reliable dynamic triggering condition also ensures the excellent performance of the system. Rigorous demonstrations underscore the stability and robustness of the ET method, while guaranteeing the avoidance of Zeno behavior. Finally, several numerical simulations are provided to underscore the efficacy of the proposed protocols.

1. Introduction

In the dynamic landscape of multi-agent systems (MASs), the paradigm of cooperative control has witnessed a surge of interest and consequential breakthroughs in recent years. Noteworthy achievements span diverse domains, including but not limited to sensor network deployment [1], encirclement hunting guidance [2], forest fire monitoring [3], transportation [4], and so on. Consensus control stands as one of fundamental problems in cooperative control, aiming to devise the appropriate control strategy such that a collective of agents to attain a desired agreement on states or outputs.

To fulfill the objective of consensus for MASs, various methods were designed that attuned to interactive information among the agents. A sign rigidity theory was introduced in [5], where a distributed consensus algorithm based on displacement and distance was designed to achieve formation control in two-dimensional space. Additionally, incorporating area constraints helped eliminate formation specification singularities. In [6], the consensus problem for MASs with time delays was investigated, and an average state feedback was devised to ensure the robustness of the system. In [7], the investigation addressed the consensus problem under jointly connected topologies and temporal delays, a Lyapunov–Krasovskii function describing the current and past dynamics was constructed to guaranteed convergence of MASs.

Leader-following consensus, heralded for its efficiency in communication reinforcement, takes precedence in consensus control. In contrast to leaderless consensus [8,9,10], the leader-following approach not only elevates collaborative efficiency, but also adapts more readily to diverse environmental and task-specific demands, providing a flexible and reliable solution for practice applications. In [11], the leader-following consensus problem of second-order MASs was investigated, a feedback tracking control protocol was proposed to enhance convergence accuracy in terms of the distinct input delays. In [12], the partial differential equations/ordinary differential equation-based MASs was analyzed with a leaderless and leader-following model, wherein the corresponding coupling strengths were determined and controllers are designed to ensure consensus. In [13], a concise solution for achieving leader-following consensus in MASs was introduced by employing a distributed observer and dynamic gain controller to ensure fast convergence of a high-order system. Focusing on a leader-following MAS within a directed communication graph, a reset consensus controller was introduced in [14]. By transforming the regularity problem into a continuous Skolem problem, this controller contributed to an improvement in transient performance and resource utilization.

Time-scheduled control methods are commonly utilized in practical control systems due to their well-established theoretical framework. Conversely, event-based control methods, responsive to specific events, confer practical advantages for achieving consensus in MASs by enhancing adaptability to real-time dynamics and fostering improved system responsiveness. Certain limitations arise from noncontinuous measurement, including inadequate computation resources and calculation accuracy, as sensors often provide sampled signals [15]. To address these challenges, implementing sampling control becomes crucial. This approach effectively lowered the communication update frequency, thereby mitigating control costs. A dynamic event-triggered mechanism was introduced in [16] to a co-designed distributed controller, which incorporated a dynamic parameter and effectively reduced the trigger frequency of events. In [17], an adaptive event-triggered (ET) controller was proposed, which enhanced the self-regulating capability of the ET mechanism. Ref. [18] employed composite ET conditions to achieve distributed consensus in a leader–follower scenario. This method extended its applicability to a bounded control strategy encompassing with general directed graphs.

Within the domain of MAS consensus research, most results showcase progressive convergence [19,20]. Notably, these investigations consistently tie the convergence time to the initial state of a single agent, highlighting a prolonged convergence when the initial state becomes large. Fortunately, the fixed-time control theory offers a novel solution, which ensures the system converges within a bound time independent of the initial states [21]. Moreover, in diverse fields like aerospace systems [22,23] and vehicle systems [24,25], fixed-time control theory has gained significant traction. Meanwhile, its capacity for strong integration with other methods, including observer control [26,27], optimal control [28], fault-tolerant control [29], and so on. Additionally, the ET controller can obtain better convergence accuracy and convergence speed under the fixed-time mechanism. In [30], a fixed-time consensus control strategy was proposed for MASs with nonlinear dynamics, which utilized a discontinuous ET method to reduce controller power consumption. In [31], an ET controller based on axis-angle attitude representation was introduced under the switching topologies, in which attitude consensus was achieved by fixed time. In [32], a ET control scheme was proposed to address the formation problem of MASs with multi-dimensional dynamics and disturbances, thus realizing time-varying formation control. The nonlinear uncertainties were considered in [33], and a comprehensive analysis of MASs was conducted by combining centralized and distributed strategies to examine the fixed-time ET method.

In light of the aforementioned discussions, it is significant to strike a balance between computation resources and convergence performance. Fortunately, there have been preliminary investigations into the fixed-time ET strategy. Nevertheless, problems like frequent triggering frequencies and complex controller forms persist in fixed-time ET theory. To address these problems, a new fixed-time consensus algorithm combined with an ET mechanism is proposed for MASs with respect to external disturbances in this work. The primary contributions can be encapsulated as:

(1) A reasonable structure for solving the multi-agent ET consensus problem is built. Based on observer theory, the consensus system is transformed into a leader’s state estimation system and a tracking control system. A new form of fixed-time controller is proposed to deal with external disturbances directly.

(2) According to the information on continuous triggering condition monitoring, a optimized ET mechanism is proposed. Compared with [33,34], the optimized dynamic trigger function is constrained by a fixed threshold, which can ensure a more stable trigger frequency while guaranteeing the fixed-time convergence performance. In addition, the trigger time is independent for each follower agent under the distributed controller.

Notation 1.

The following symbols are used in this work. The definition of symbol $\lceil ·\rfloor$ is introduced as ${\lceil \mathit{\eta }\rfloor }^{\alpha }\triangleq {\left[|{\eta }_1{|}^{\alpha }\mathrm{sign}\left({\eta }_1\right),|{\eta }_2{|}^{\alpha }\mathrm{sign}\left({\eta }_2\right),\dots ,{\left|{\eta }_m\right|}^{\alpha }\mathrm{sign}\left({\eta }_m\right)\right]}^{\mathrm{T}}$, with positive number α. $\lambda \left(P\right)$ and ${\lambda }_{min}\left(P\right)$ denote the eigenvalue and the smallest eigenvalue of the matrix P, respectively. Constant vector ${\mathbf{1}}_m=[\underset{\underset{m}{︸}}{1,1,\dots ,1}]\in {\mathbb{R}}^m$.

2. Preliminaries

In the following, a compilation of graph theory, lemmas and problem description are presented, contributing to aspects of the proposed consensus strategy.

2.1. Description of Algebraic Graph Theory

To depict information communication among one leader agent and follower agents, fundamental concepts in graph theory are used. In the context of an undirected graph $\mathcal{G}=\left(\mathcal{V},\mathcal{E},\mathcal{A}\right)$, which consists of vertices $\mathcal{V}=\left\{v_1,v_2,\dots ,v_N\right\}$ and an index set of edges $\mathcal{E}=\left\{(v_i,v_j)|v_i,v_j\in \mathcal{V}\right\}$. $\mathcal{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ stands for the adjacency matrix, with $a_{ij}=1$ for $(j,i)\in \mathcal{E}$, $j\ne i$, otherwise $a_{ij}=0$. The in-degree matrix is defined as $\mathcal{D}=\mathrm{diag}(d_1,d_2,$$\dots ,d_n)\in {\mathbb{R}}^{N\times N}$, and its elements $d_i={\displaystyle \sum _{j=1}^n}{a}_{ij}$. Furthermore, the Laplacian matrix $\mathcal{L}=\left[l_{ij}\right]\in {\mathbb{R}}^{N\times N}$ can be calculated by $\mathcal{L}=\mathcal{D}-\mathcal{A}$. The diagonal matrix $\mathcal{B}\in {\mathbb{R}}^{N\times N}$ represents the connectivity between the ith follower and the leader, which is defined as $\mathcal{B}=\mathrm{diag}(b_1,b_2,\dots ,b_n)$, $b_i\ge 0$. To streamline the depiction, define $\mathcal{L}+\mathcal{B}=\mathcal{H}$.

Assumption 1.

The augmented graph $\mathcal{G}$ stands as an undirected structure, while containing a spanning tree rooted at the leader node.

2.2. Lemmas

Lemma 1

([35]). For arbitrary ${\zeta }_i\ge 0$ $(i=1,2,\dots ,N)$, the subsequent inequalities are satisfied

$$\begin{array}{c}\hfill N^{1-r}{\left(\sum _{i=1}^N{\zeta }_i\right)}^r\le \sum _{i=1}^N{\zeta }_i^r\le {\left(\sum _{i=1}^N{\zeta }_i\right)}^r,\\ \hfill {\left(\sum _{i=1}^N{\zeta }_i^{p_2}\right)}^{\frac{1}{p_2}}\le {\left(\sum _{i=1}^N{\zeta }_i^{q_2}\right)}^{\frac{1}{q_2}}.\end{array}$$

where $r>1$ and $0<q_2<p_2$.

Lemma 2

([36]). For any scalar y,

$$ytanh\left(by\right)\ge \left|y\right|-\frac{\delta }{b}.$$

where $b>0$ and $\delta =0.2785$.

Lemma 3

([37]). Suppose a positive definite and continuous radially unbounded function V obeys $\dot{V}\le -p_1{V}^{q_1}-p_2{V}^{q_2}$ with $p_1>0$, $p_2>0$, $0<q_1<1$ and $1<q_2$. Then, the globally fixed-time stability can be achieved, and the settling-time $T_f$ is bounded by

$$T_f<\frac{1}{p_1\left(1-q_1\right)}+\frac{1}{p_2\left(q_2-1\right)}.$$

Furthermore, if $r_1\triangleq \frac{q_2-1}{1-q_1}\le 1$, a more accurate time estimation of $T_f$ is

$$\begin{array}{c}\hfill T_f\le T_{max}\le \frac{1}{1-q_1}\left(\frac{1}{\sqrt{p_1{p}_2}}{tan}^{-1}\sqrt{\frac{p_2}{p_1}}+\frac{1}{p_2{r}_1}\right)\end{array}$$

Lemma 4

([38]). In the other case, the Lyapunov function satisfies $\dot{V}\le -p_3{V}^{q_3}-p_4{V}^{q_4}+{\vartheta }_p$ when ${\vartheta }_p$ is a small known positive number, $p_3>0$, $p_4>0$, $0<q_3<1$ and $q_4>1$. Then, the practical fixed-time stability can be achieved, and the settling-time $T_p$ is bounded by

$$T_p<\frac{1}{{\gamma }_p{p}_3\left(1-q_3\right)}+\frac{1}{{\gamma }_p{p}_4\left(q_5-1\right)},$$

with $0<{\gamma }_p<1$, and the residual set of states is denoted as

$$\varsigma =\left\{V|V\le min\left\{{\left(\frac{{\vartheta }_p}{(1-{\gamma }_p)p_3}\right)}^{\frac{1}{q_3}},{\left(\frac{{\vartheta }_p}{(1-{\gamma }_p)p_4}\right)}^{\frac{1}{q_4}}\right\}\right\}.$$

Lemma 5.

Suppose a positive definite symmetric matrix $\mathit{P}$. There exists a vector $\mathit{X}$ satisfying ${\left(\mathit{P}\mathit{X}\right)}^{\mathrm{T}}\mathit{P}\mathit{X}={\mathit{X}}^{\mathrm{T}}\mathit{P}\mathit{P}\mathit{X}\ge {\lambda }_{min}\left(\mathit{P}\right){\mathit{X}}^{\mathrm{T}}\mathit{P}\mathit{X}$.

Proof. 

An orthogonal decomposition for matrix $\mathit{P}$ yields $\mathit{P}=\mathit{Q}\Lambda {\mathit{Q}}^{\mathrm{T}}$ with ${\mathit{Q}}^{\mathrm{T}}\mathit{Q}=\mathit{I}$ and $\Lambda =\mathrm{diag}\left({\lambda }_i\left(\mathit{P}\right)\right)$.

$${\mathit{X}}^{\mathrm{T}}\mathit{P}\mathit{P}\mathit{X}={\mathit{X}}^{\mathrm{T}}\mathit{Q}\Lambda {\mathit{Q}}^{\mathrm{T}}\mathit{Q}\Lambda {\mathit{Q}}^{\mathrm{T}}\mathit{X}={\mathit{X}}^{\mathrm{T}}\mathit{Q}{\Lambda }^2{\mathit{Q}}^{\mathrm{T}}\mathit{X}={\mathit{X}}^{\mathrm{T}}\mathit{Q}{\Lambda }^{\frac{1}{2}}\Lambda {\Lambda }^{\frac{1}{2}}{\mathit{Q}}^{\mathrm{T}}\mathit{X}.$$

According to the eigenvalue inequality, one has

$${\mathit{X}}^{\mathrm{T}}\mathit{Q}{\Lambda }^{\frac{1}{2}}\Lambda {\Lambda }^{\frac{1}{2}}{\mathit{Q}}^{\mathrm{T}}\mathit{X}\ge {\lambda }_{min}(\Lambda ){\mathit{X}}^{\mathrm{T}}\mathit{Q}{\Lambda }^{\frac{1}{2}}{\Lambda }^{\frac{1}{2}}{\mathit{Q}}^{\mathrm{T}}\mathit{X}={\lambda }_{min}\left(\mathit{P}\right){\mathit{X}}^{\mathrm{T}}\mathit{P}\mathit{X}.$$

□

Lemma 6

([39]). Within the framework of the leader-following scenario, it is imperative that the team leader plays the role of the spanning tree’s root. The communication matrix $\mathcal{H}=\mathcal{L}+\mathcal{B}$ has positive real parts if and only if a globally reachable value exists in $\mathcal{G}$. That means there is a reachable communication path between the leader and each follower.

Remark 1.

According to Lemma 6 and Assumption 1 of this work, under the leader-following communication structure, the matrix $\mathcal{H}$ satisfies the following:

(1) 

$\mathcal{H}$ is a positive definite matrix and its eigenvalues ${\lambda }_i\left(\mathcal{H}\right)>0$, $i=1,2,\dots ,N$.

(2) 

There exists a vector $\mathit{X}$ satisfying ${\mathit{X}}^{\mathrm{T}}\mathcal{H}\mathit{X}\ge {\lambda }_{\min }\left(\mathcal{H}\right){\mathit{X}}^{\mathrm{T}}\mathit{X}$

2.3. Problem Description

Considering a MAS with N agents and one leader, which is represented by

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\dot{x}}_0\left(t\right)& =u_0\left(t\right),\hfill \\ \hfill {\dot{x}}_i\left(t\right)& =u_i\left(t\right)+d_i\left(t\right).\hfill \end{array}\hfill \end{array}\right.$$

(1)

where $i=1,2,\dots ,N$. $x_i\left(t\right)\in \mathbb{R}$ and $x_0\in \mathbb{R}$ are the system state and the leader state, respectively. $u_i\left(t\right)\in \mathbb{R}$ is the control input of agent i. $d_i\left(t\right)\in \mathbb{R}$ is the exogenous disturbance.

In the context of autonomous systems, such as vehicle systems and robotic systems, which typically exhibit nonlinear and underactuated characteristics. However, the work focuses on first-order systems with respect to position for simplicity. Meanwhile, the stability of the system (1) is proved rigorously by means of Lyapunov method.

Assumption 2.

For MAS (1), the unknown exogenous disturbance $d_i\left(t\right)$ is satisfied $|d_i\left(t\right)|\le D$, with D is a positive constant.

Assumption 3.

The control input $u_0\left(t\right)$ of leader is dynamic and unknown, subject to an upper limit $|u_0\left(t\right)|\le u_{0M}$, with $u_{0M}$ is a positive constant.

Definition 1.

The system (1) is said to achieve the practical fixed-time consensus when there exists an inequation $|x_i\left(t\right)-x_0\left(t\right)|\le {\delta }_1$, $t\ge T$ for arbitrary initial conditions $x_i\left(t_0\right)$, with T is a solvable constant and ${\delta }_1$ is a small positive constant.

3. Main Results

For this part, a new distributed control method is formulated to address the fixed-time leader-following consensus problem in MASs. The devised procedure comprises two steps. Firstly, each follower agent is equipped with a distributed observer to estimate the leader’s state. Subsequently, an ET tracking controller is employed to guarantee the synchronization of the states of each agent with the leader’s state estimation. It is noteworthy that both steps converge within a fixed time.

3.1. Distributed Fixed-Time Observer

Distributed observers are meticulously designed for follower agents, aimed at estimating the leader’s state. It is crucial to emphasize that the information communication between leader-following agents is intimately linked with the graph theory structure expounded in Section 2.1. The following observation structure is adopted:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill {\dot{\widehat{z}}}_i\left(t\right)& =-k_1\mathrm{sign}\left(y_i\left(t\right)\right)-k_2{\lceil y_i\left(t\right)\rfloor }^{{\beta }_1},\hfill \\ \hfill y_i\left(t\right)& =\sum _{j=1}^N{a}_{ij}\left({\widehat{z}}_i\left(t\right)-{\widehat{z}}_j\left(t\right)\right)+b_i\left({\widehat{z}}_i\left(t\right)-x_0\left(t\right)\right).\hfill \end{array}\hfill \end{array}\right.$$

(2)

where $k_1>0$, $k_2>0$ and ${\beta }_1>1$. The variable ${\widehat{z}}_i\left(t\right)$ is each agent’s observation for the leader’s state $x_0\left(t\right)$.

Theorem 1.

Let the observation error ${\tilde{z}}_i\left(t\right)={\widehat{z}}_i\left(t\right)-x_0\left(t\right)$. If the observation design follows the form of (2), then the observation error ${\tilde{z}}_i\left(t\right)$ will converge to the origin within a fixed time.

Proof. 

Under the protocol (2), the observed states can be rewritten into a compact form. Define $\mathit{Y}\left(t\right)={\left[y_1\left(t\right),y_2\left(t\right),\dots ,y_N\left(t\right)\right]}^{\mathrm{T}}$ and $\widehat{\mathit{Z}}\left(t\right)={\left[{\widehat{z}}_1\left(t\right),{\widehat{z}}_2\left(t\right),\dots ,{\widehat{z}}_N\left(t\right)\right]}^{\mathrm{T}}$. Thus, $\tilde{\mathit{Z}}\left(t\right)=\widehat{\mathit{Z}}\left(t\right)-{\mathbf{1}}_N{x}_0\left(t\right)$ and $\mathit{Y}\left(t\right)=\mathcal{H}\tilde{\mathit{Z}}\left(t\right)$.

In order to demonstrate that the observation error ${\tilde{z}}_i\left(t\right)$ can converge within a fixed time, choose the Lyapunov function

$$\begin{array}{cc}\hfill V_1=& \frac{1}{2}\sum _{i=1}^N{\tilde{z}}_i\left(t\right)y_i\left(t\right)\hfill \\ \hfill =& \frac{1}{2}{\tilde{\mathit{Z}}}^{\mathrm{T}}\mathcal{H}\tilde{\mathit{Z}}\hfill \end{array}$$

(3)

By differentiating (3), one has

$$\begin{array}{cc}\hfill {\dot{V}}_1& ={\tilde{\mathit{Z}}}^{\mathrm{T}}\mathcal{H}\dot{\tilde{\mathit{Z}}}\hfill \\ \hfill & ={\mathit{Y}}^{\mathrm{T}}\left(t\right)\left[-k_1\mathrm{sign}\left(\mathit{Y}\left(t\right)\right)-k_2{\lceil \mathit{Y}\left(t\right)\rfloor }^{{\beta }_1}-{\mathbf{1}}_N{u}_0\left(t\right)\right]\hfill \\ \hfill & \le -(k_1-u_{0M})\sum _{i=1}^N|y_i\left(t\right)|-k_2\sum _{i=1}^N{|y_i\left(t\right)|}^{1+{\beta }_1}\hfill \\ \hfill & \le -(k_1-u_{0M})\sum _{i=1}^N\left|y_i\left(t\right)\right|-k_2{N}^{-{\beta }_1}{\left(\sum _{i=1}^N\left|y_i\left(t\right)\right|\right)}^{1+{\beta }_1}.\hfill \end{array}$$

(4)

By means of Lemmas 1 and 5, one has

$$\sum _{i=1}^N\left|y_i\left(t\right)\right|\ge {\left(\sum _{i=1}^N{y}_i^2\left(t\right)\right)}^{\frac{1}{2}}={\left({\left(\mathcal{H}\tilde{\mathit{Z}}\left(t\right)\right)}^{\mathrm{T}}\mathcal{H}\tilde{\mathit{Z}}\left(t\right)\right)}^{\frac{1}{2}}.$$

Thus, (4) can be transformed as

$$\begin{array}{cc}\hfill {\dot{V}}_1& \le -(k_1-u_{0M}){\left({\left(\mathcal{H}\tilde{\mathit{Z}}\left(t\right)\right)}^{\mathrm{T}}\mathcal{H}\tilde{\mathit{Z}}\left(t\right)\right)}^{\frac{1}{2}}-k_2{N}^{-{\beta }_1}{\left({\left(\mathcal{H}\tilde{\mathit{Z}}\left(t\right)\right)}^{\mathrm{T}}\mathcal{H}\tilde{\mathit{Z}}\left(t\right)\right)}^{\frac{1+{\beta }_1}{2}}\hfill \\ \hfill & \le -(k_1-u_{0M}){\left({\lambda }_{min}((\mathcal{H})\tilde{\mathit{Z}}{(t))}^{\mathrm{T}}\mathcal{H}\tilde{\mathit{Z}}(t)\right)}^{\frac{1}{2}}-k_2{N}^{-{\beta }_1}{\left({\lambda }_{min}((\mathcal{H})\tilde{\mathit{Z}}{(t))}^{\mathrm{T}}\mathcal{H}\tilde{\mathit{Z}}(t)\right)}^{\frac{1+{\beta }_1}{2}}\hfill \\ \hfill & \le -(k_1-u_{0M})\sqrt{2{\lambda }_{min}(\mathcal{H})}{V}_1^{\frac{1}{2}}-k_2{N}^{-{\beta }_1}{\left(2{\lambda }_{min}\left(\mathcal{H}\right)\right)}^{\frac{1+{\beta }_1}{2}}{V}_1^{\frac{1+{\beta }_1}{2}}\hfill \\ \hfill & \le -{\alpha }_1{V}_1^{\frac{1}{2}}-{\alpha }_2{V}_1^{\frac{1+{\beta }_1}{2}}.\hfill \end{array}$$

with ${\alpha }_1=(k_1-u_{0M})\sqrt{2{\lambda }_{min}\left(\mathcal{H}\right)}$ and ${\alpha }_2=k_2{N}^{-{\beta }_1}{\left(2{\lambda }_{min}\left(\mathcal{H}\right)\right)}^{\frac{1+{\beta }_1}{2}}$. Thus, with the aid of Lemma 3, the observer system will converge to zero in fixed time $T_1$, which can be computed as

$$T_1\le 2\left(\frac{1}{{\alpha }_1{\alpha }_2}{tan}^{-1}\sqrt{\frac{{\alpha }_2}{{\alpha }_1}}+\frac{1}{{\alpha }_2({\beta }_1-1)}\right).$$

□

3.2. Event-Triggered Tracking Control

On the basis of Observation (2), by defining the tracking error $e_i\left(t\right)=x_i\left(t\right)-{\widehat{z}}_i\left(t\right)=x_i\left(t\right)-x_0\left(t\right)-{\tilde{z}}_i\left(t\right)$, one obtains

$$\begin{array}{cc}\hfill {\dot{e}}_i\left(t\right)=& {\dot{x}}_i\left(t\right)-{\dot{\widehat{z}}}_i\left(t\right)=u_i\left(t\right)+d_i\left(t\right)+k_1\mathrm{sign}\left(y_i\left(t\right)\right)+k_2{\lceil y_i\left(t\right)\rfloor }^{{\beta }_1}.\hfill \end{array}$$

(5)

When the observation error converges, that is ${\tilde{z}}_i\left(t\right)=0$ and $y_i\left(t\right)=0$, then the error dynamic model (5) can be simplified as

$$\begin{array}{c}\hfill {\dot{e}}_i\left(t\right)=u_i\left(t\right)+d_i\left(t\right).\end{array}$$

(6)

With the aim of reducing control costs and enhancing convergence speed, for each follower agent in the system (6), the fixed-time ET consensus protocol is designed as follows:

$$\begin{array}{cc}\hfill u_i\left(t\right)=& -k_{3}tanh\left(\frac{e_i\left(t_k^i\right)}{ϵ}\right)-k_4{\lceil e_i\left(t_k^i\right)\rfloor }^{{\beta }_2},\hfill \end{array}$$

(7)

with $k_3>0$, $k_4>0$, ${\beta }_2>1$, and $ϵ$ is a small positive number. $t_k^i$ represents the k-th ET moment of the agent i.

Theorem 2.

Define measurement error ${\xi }_i\left(t\right)$

$$\begin{array}{cc}\hfill {\xi }_i\left(t\right)=& k_{3}tanh\left(\frac{e_i\left(t_k^i\right)}{ϵ}\right)+k_4{\lceil e_i\left(t_k^i\right)\rfloor }^{{\beta }_2}-k_{3}tanh\left(\frac{e_i\left(t\right)}{ϵ}\right)-k_4{\lceil e_i\left(t\right)\rfloor }^{{\beta }_2}.\hfill \end{array}$$

then, the controller (7) can be morphed into:

$$\begin{array}{cc}\hfill u_i\left(t\right)=& -{\xi }_i\left(t\right)-k_{3}tanh\left(\frac{e_i\left(t\right)}{ϵ}\right)-k_4{\lceil e_i\left(t\right)\rfloor }^{{\beta }_2}.\hfill \end{array}$$

(8)

Give the trigger function $F\left(t\right)=\left|{\xi }_i\left(t\right)\right|-{\kappa }_{1}tanh\left(\frac{|e_i\left(t\right)|}{ϵ}\right)-{\kappa }_2$.

$$\begin{array}{c}\hfill t_k^i=\inf \{t>t_k^i:F\left(t\right)\ge 0\},i=1,2,\dots ,N.\end{array}$$

(9)

Under the control protocol (8) and Assumption 2, if the controller parameter $k_3$ satisfies $k_3>{\kappa }_1+{\kappa }_2+D$, the practical leader-following consensus can be achieved within a fixed time, and Zeno behavior is excluded.

Proof. 

For each follower agent, the distributed controller (7) is updated when the event is triggered. Then, the trigger function satisfies $|{\xi }_i\left(t\right)|=0$. Consider the case where the event is not triggered, which is $|{\xi }_i\left(t\right)|<{\kappa }_{1}tanh\left(\frac{|e_i\left(t\right)|}{ϵ}\right)+{\kappa }_2$. Furthermore, select the following Lyapunov candidate function:

$$\begin{array}{c}\hfill V_2=\frac{1}{2}\sum _{i=1}^N{e}_i^2\left(t\right).\end{array}$$

(10)

By taking the derivative of (10), one can obtain

$$\begin{array}{cc}\hfill {\dot{V}}_2=& \sum _{i=1}^N{e}_i\left(t\right){\dot{e}}_i\left(t\right)\hfill \\ \hfill =& \sum _{i=1}^N{e}_i\left(t\right)\left[-{\xi }_i\left(t\right)-k_{3}tanh\left(\frac{e_i\left(t\right)}{ϵ}\right)-k_4{\lceil e_i\left(t\right)\rfloor }^{{\beta }_2}+d_i\left(t\right)\right]\hfill \\ \hfill \le & \sum _{i=1}^N|e_i\left(t\right)||{\xi }_i\left(t\right)|-{\kappa }_1\sum _{i=1}^N|e_i\left(t\right)|tanh\left(\frac{|e_i\left(t\right)|}{ϵ}\right)-\left(k_3-{\kappa }_1\right)\sum _{i=1}^N|e_i\left(t\right)|\hfill \\ \hfill & +\left(k_3-{\kappa }_1\right)N\delta ϵ-k_4\sum _{i=1}^N|e_i{\left(t\right)|}^{{\beta }_2+1}+\sum _{i=1}^N|e_i\left(t\right)||d_i\left(t\right)|\hfill \end{array}$$

(11)

By means of Assumption 2, one has

$$\begin{array}{cc}\hfill {\dot{V}}_2\le & -\left(k_3-{\kappa }_1-{\kappa }_2-D\right)\sum _{i=1}^N|e_i\left(t\right)|-k_4\sum _{i=1}^N{|e_i\left(t\right)|}^{{\beta }_2+1}+\left(k_3-{\kappa }_1\right)N\delta ϵ\hfill \\ \hfill & +\sum _{i=1}^N|e_i\left(t\right)|\left(|{\xi }_i\left(t\right)|-{\kappa }_{1}tanh\left(\frac{|e_i\left(t\right)|}{ϵ}\right)-{\kappa }_2\right)\hfill \\ \hfill \le & -\left(k_3-{\kappa }_1-{\kappa }_2-D\right){\left(\sum _{i=1}^N{e}_i^2\left(t\right)\right)}^{\frac{1}{2}}-k_4{N}^{\frac{1-{\beta }_2}{2}}{\left(\sum _{i=1}^N{e}_i^2\left(t\right)\right)}^{\frac{{\beta }_2+1}{2}}\hfill \\ \hfill & +\left(k_3-{\kappa }_1\right)N\delta ϵ\hfill \\ \hfill \le & -{\alpha }_3{V}_2^{\frac{1}{2}}-{\alpha }_4{V}_2^{\frac{{\beta }_2+1}{2}}+\nu ,\hfill \end{array}$$

(12)

with ${\alpha }_3=\left(k_3-{\kappa }_1-{\kappa }_2-D\right)\sqrt{2}$, ${\alpha }_4=k_4{N}^{\frac{1-{\beta }_2}{2}}{2}^{\frac{{\beta }_2+1}{2}}$ and $\nu =\left(k_3-{\kappa }_1\right)N\delta ϵ$. Moreover, the solution of system will reach $V_2={\varsigma }_1$, ${\varsigma }_1=\left\{V_2|V_2\le min\left\{{\left(\frac{\nu }{(1-\gamma ){\alpha }_3}\right)}^2,{\left(\frac{\nu }{(1-\gamma ){\alpha }_4}\right)}^{\frac{2}{{\beta }_2+1}}\right\}\right\}$ in fixed time $T_2$ with $0<\gamma <1$.

$$T_2<\frac{2}{\gamma {\alpha }_3}+\frac{2}{\gamma {\alpha }_4\left({\beta }_2-1\right)},$$

Zeno behavior denotes the occurrence of events at an exceptionally high frequency within a brief time interval, resulting in undesirable consequences. The following demonstrates that the system, under the specified ET control protocol, avoids exhibiting Zeno behavior. According to (10) and (12), we have ${\displaystyle \sum _{i=1}^N}{e}_i^2\left(t\right)=2V_2\le 2V_2\left(t_0\right)$, so $|e_i\left(t\right)|\le 2V_2\left(t_0\right)$. Take the time derivative of $|{\xi }_i\left(t\right)|$

$$\begin{array}{cc}\hfill |{\xi }_i{\left(t\right)|}^{{}^{\prime }}& =k_3{\left(tanh\left(\frac{|e_i\left(t\right)|}{ϵ}\right)\right)}^{{}^{\prime }}+k_4{\beta }_2{\lceil e_i\left(t\right)\rfloor }^{{\beta }_2-1}{\dot{e}}_i\left(t\right).\hfill \end{array}$$

(13)

in which

$$\begin{array}{cc}\hfill & {\left(tanh\left(\frac{|e_i\left(t\right)|}{ϵ}\right)\right)}^{{}^{\prime }}=\frac{\mathrm{sign}\left(e_i\left(t\right)\right)}{ϵ}\left(1-{tanh}^2\left(\frac{e_i\left(t\right)}{ϵ}\right)\right){\dot{e}}_i\left(t\right)\le \frac{|{\dot{e}}_i\left(t\right)|}{ϵ}.\hfill \end{array}$$

(14)

Therefore, substituting (14) into (13) yields

$$\begin{array}{cc}\hfill |{\xi }_i{\left(t\right)|}^{{}^{\prime }}& \le \frac{k_3\left|{\dot{e}}_i\left(t\right)\right|}{ϵ}+k_4{\beta }_2|e_i{\left(t\right)|}^{{\beta }_2-1}\left|{\dot{e}}_i\left(t\right)\right|\hfill \\ \hfill & \le {\gamma }_1|u_i\left(t\right)+d_i\left(t\right)|\hfill \\ \hfill & \le {\gamma }_1\left(k_3+k_4{\left|e_i\left(t_k^i\right)\right|}^{{\beta }_2}+D\right),\hfill \end{array}$$

in which ${\gamma }_1=\frac{k_3}{ϵ}+k_4{\beta }_2{\left(2V_2\left(t_0\right)\right)}^{{\beta }_2-1}$. If $t_k^i$ represents the ith agent’s latest trigger moment, then ${\xi }_i\left(t_k^i\right)=0$.

$$\begin{array}{cc}\hfill |{\xi }_i\left(t\right)|\le & {\int }_{t_k^i}^t{\left|{\xi }_i\left(s\right)\right|}^{{}^{\prime }}\mathrm{d}s\hfill \\ \hfill \le & {\int }_{t_k^i}^t{\gamma }_1\left(k_3+k_4{\left|e_i\left(s_k^i\right)\right|}^{{\beta }_2}+D\right)\mathrm{d}s.\hfill \end{array}$$

According to (12), discrete tracking error variable $e_i\left(t_{k+1}^i\right)$ is the monotonic subtraction of the triggered moment. It is reasonable to assume that $e_i\left(t_{k+1}^i\right)$ has an upper bound $|e_i\left(t_{k+1}^i\right)|\le 2V_2\left(t_0\right)$. By using the triggering condition $|{\xi }_i\left(t\right)|={\kappa }_{1}tanh\left(\frac{|e_i\left(t\right)|}{ϵ}\right)+{\kappa }_2$ for the next moment $t_{k+1}^i$, one has

$$\begin{array}{cc}\hfill |{\xi }_i\left(t_{k+1}^i\right)|& ={\kappa }_{1}tanh\left(\frac{|e_i\left(t_{k+1}^i\right)|}{ϵ}\right)+{\kappa }_2\hfill \\ \hfill & \le {\int }_{t_k^i}^{t_{k+1}^i}{\gamma }_1\left(k_3+k_4{\left|2V_2\left(t_0\right)\right|}^{{\beta }_2}+D\right)\mathrm{d}s.\hfill \end{array}$$

Continuing to simplify the formula yields

$$\begin{array}{cc}\hfill t_{k+1}^i-t_k^i& \ge \frac{{\kappa }_{1}tanh\left(\frac{|e_i\left(t_{k+1}^i\right)|}{ϵ}\right)+{\kappa }_2}{{\gamma }_1\left(k_3+k_4{\left|2V_2\left(t_0\right)\right|}^{{\beta }_2}+D\right)}\hfill \\ \hfill & \ge \frac{{\kappa }_2}{{\gamma }_1\left(k_3+k_4{\left|2V_2\left(t_0\right)\right|}^{{\beta }_2}+D\right)}.\hfill \end{array}$$

Hence, there exists a constant time interval between any two trigger instants, thereby affirming the absence of Zeno behavior in the proposed control protocol. □

According to Theorems 1 and 2 and Definition 1, the leader-following system (1) can achieve the consensus in fixed time $T=T_1+T_2$ under the distributed observer (2) and improved ET mechanism (9).

Remark 2.

It is worth noting that the state $x_i\left(t\right)$ of System (1) does not converge to zero, but to a small region ${\varsigma }_1$. According to the ET mechanism (9), the design process optimizes the triggered frequency of events, which does not contradict the threshold of ET condition. The result is consistent with the practical fixed-time stability theory, which is expressed in Lemma 4.

Remark 3.

It can be deduced from (9) that the measurement error $|{\xi }_i\left(t\right)|$ is compared with a dynamic function ${\kappa }_{1}tanh\left(\frac{|e_i\left(t\right)|}{ϵ}\right)+{\kappa }_2$ related to the error state. The dynamic function exists with a reasonable upper and lower bound of ${\kappa }_1+{\kappa }_2$ and ${\kappa }_2$, respectively, which improves the stability of the system and reduces the computational resource consumption of the control.

Remark 4.

Compared with the traditional fixed-time strategy [23,24], the sign(·) function term in the fixed-time observer (2) can directly enhance the robustness of the fixed-time form, which simplifies the design process. In contrast, the fixed-time ET controller (7) employs the tanh(·) function instead of the sign(·) function, which is intended to mitigate controller chattering [26]. In the ET strategy, this approach is also able to optimize the triggering frequency.

4. Simulations and Results

In this section, the proposed controller designed in Section 3 is validated through simulation, specifically using MATLAB/Simulink for the testing process to showcase the efficacy of the controller. As depicted in Figure 1, the communication graph features one leader agent and five follower agents, which are described by node 0 and nodes 1–5, respectively. The Laplace matrix can be obtained as follows:

$$\begin{array}{c}\hfill L=\left[\begin{array}{ccccc}\hfill 1& \hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 2& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 2& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 2& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 1\end{array}\right].\end{array}$$

and the leader accessibility matrix is $\mathcal{B}=\mathrm{diag}\{1,0,0,0,0\}$. The control input for the leader is denoted as $u_0\left(t\right)=2cos(2t-\pi /3),u_0\left(0\right)=-1.5$ in the simulation. The external disturbance is chosen as $d_i\left(t\right)=0.1isin(5t+(i-1)\pi /5)+(0.5-0.1i)cos(5t+$$(i-1)\pi /5),i=1,\dots ,5$ following the assumption provided in the work. The initial values are $\mathit{X}\left(0\right)={\left[6,4,2,-4,-6\right]}^{\mathrm{T}}$. Building upon the aforementioned model, in the context of the distributed ET consensus algorithm, the control parameters are chosen as $k_1=2,k_2=0.2,k_3=3,k_4=1.2,{\beta }_1=1.01,{\beta }_2=1.1,ϵ=0.05,{\kappa }_1=0.3,{\kappa }_2=0.5$.

The simulation employs the Euler method with a fixed integration step of ${10}^{-3}$. Results of the simulation are presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Figure 2, Figure 3 and Figure 4 present the time histories of the follower agent’s state estimations for the leader agent, the state observation errors and the follower agent’s tracking errors for leader’s observation state, respectively. Furthermore, over an extended duration, the observation errors are consistently brought into convergence, ensuring sustained precision in tracking. In Figure 2 and Figure 3, it is evident that each follower agent can rapidly achieve precise information of the leader agent within a short time, approximately $0.5$ s. Moreover, the observation error chatters in a small range after convergence, which aligns with the intended effect of the sign function in observation (2). As depicted in Figure 4, leveraging accurate observation information of leader enables fast tracking, which can be achieved even if the initial errors of each follower agent are substantial. This tracking proficiency persists over an extended period of time, showcasing the good convergence performance of the proposed strategy. Meanwhile, in Figure 5, the states of the leader and followers are able to reach consensus quickly, although the initial errors are large. This can be attributed to the effectiveness of the fixed-time controller, which can obtain an estimated convergence time independent of the system’s initial state. From Figure 6, under the influence of the ET mechanism, the system strikes a good balance between convergence performance and computational resource consumption. Moreover, the convergence error of the system remains within the acceptable range of $0.1$ with respect to external disturbances.

Aside from the aforementioned results of consensus tracking performance, ET controllers also bring a lower frequency of refresh counts to the system. Unlike the time-triggered control method, the ET control scheme updates control signals in response to triggered events. The triggering instants of follower agents are depicted in Figure 7. As anticipated, the triggering times of each agent are independent, and Zeno behavior is excluded. In detail, as shown in

Table 1. The number of event times of followers during the simulation time.

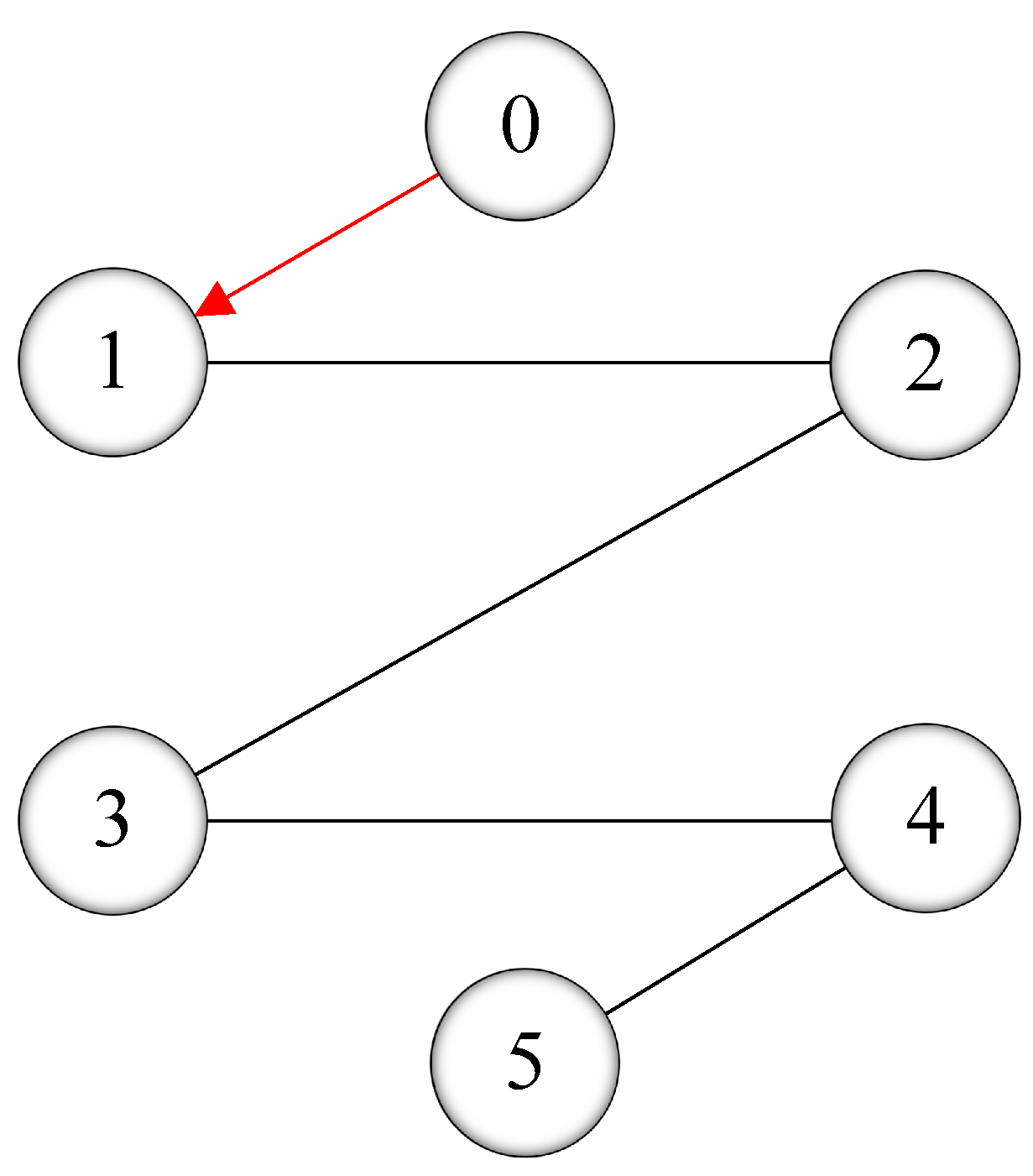
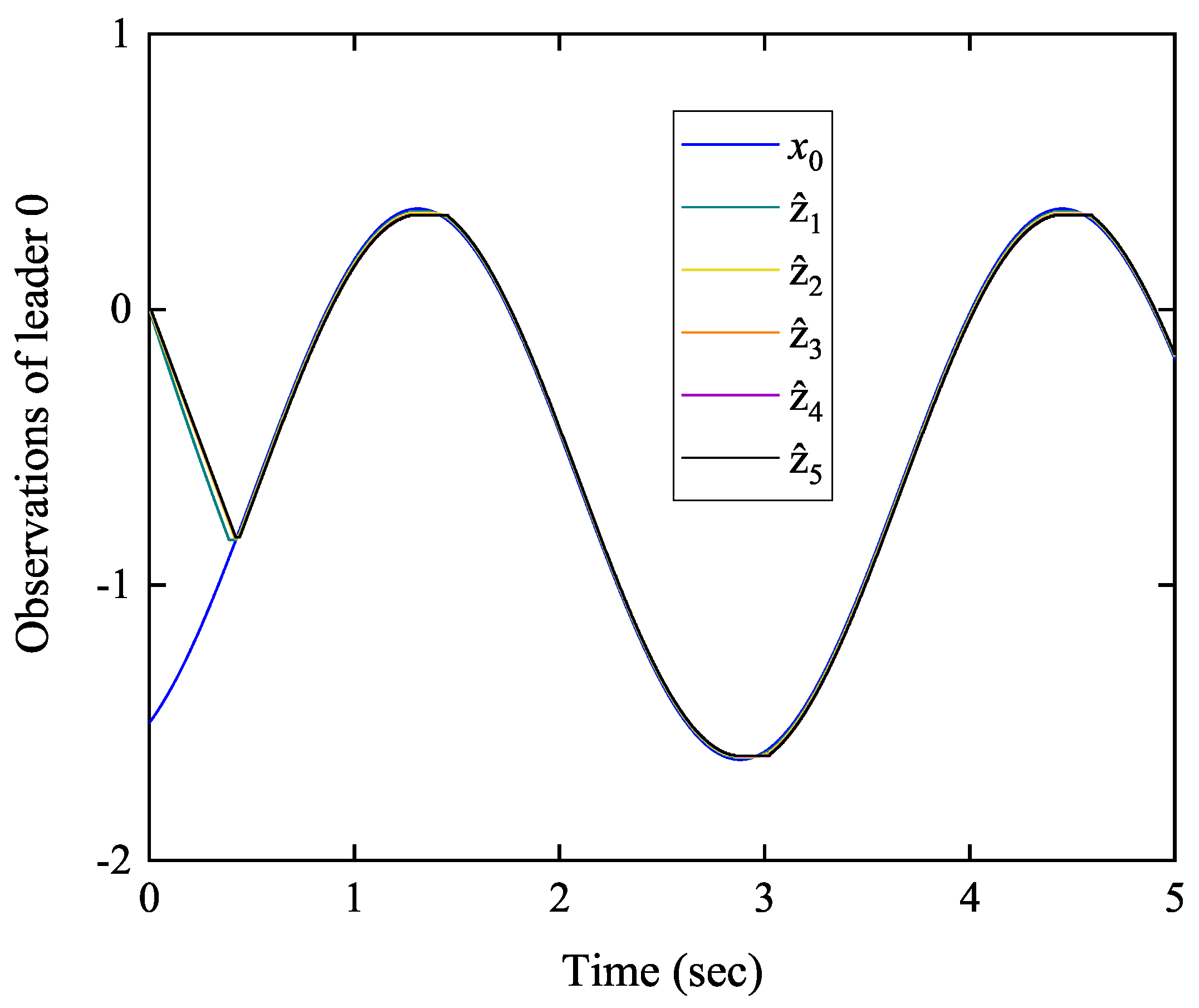
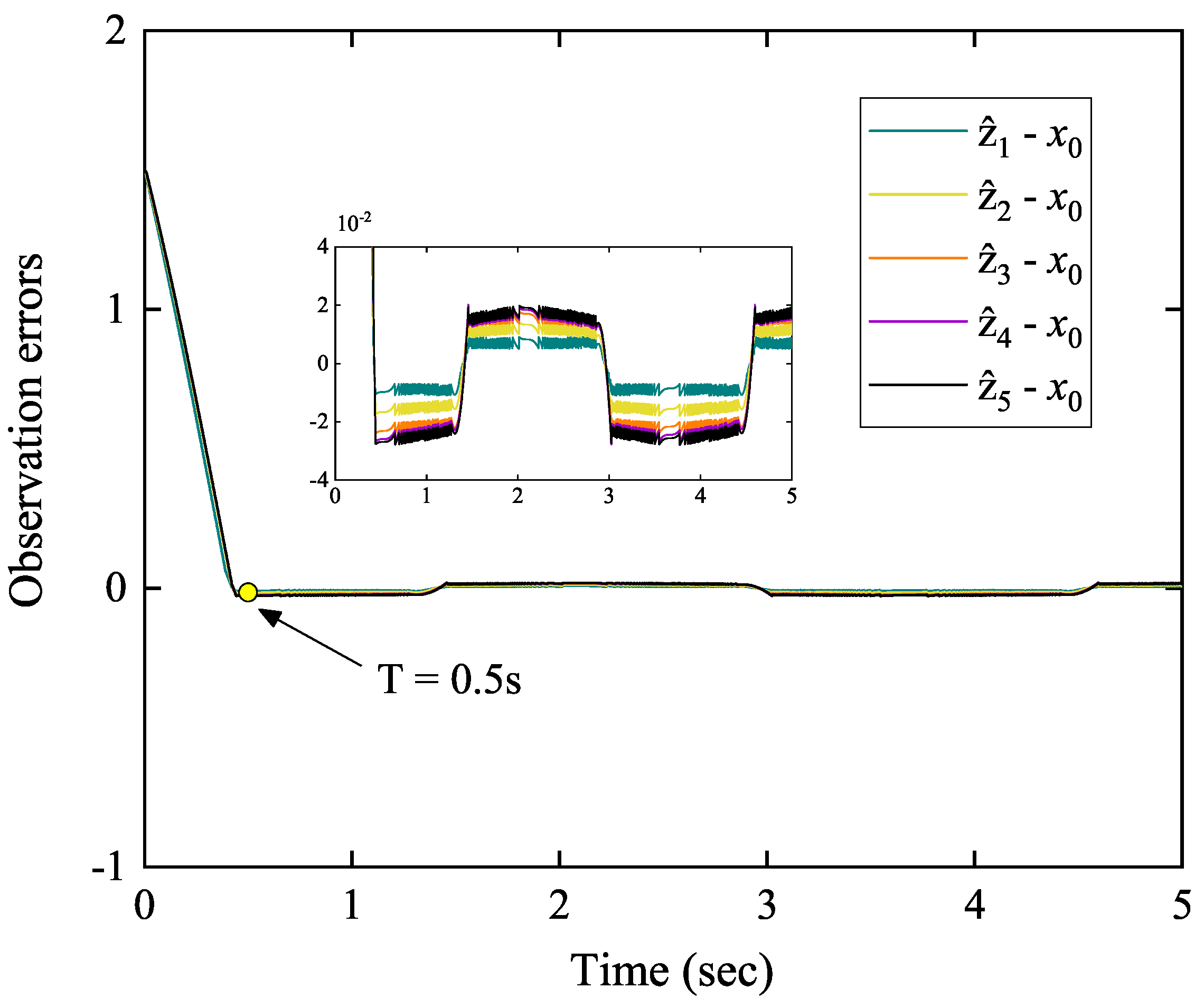
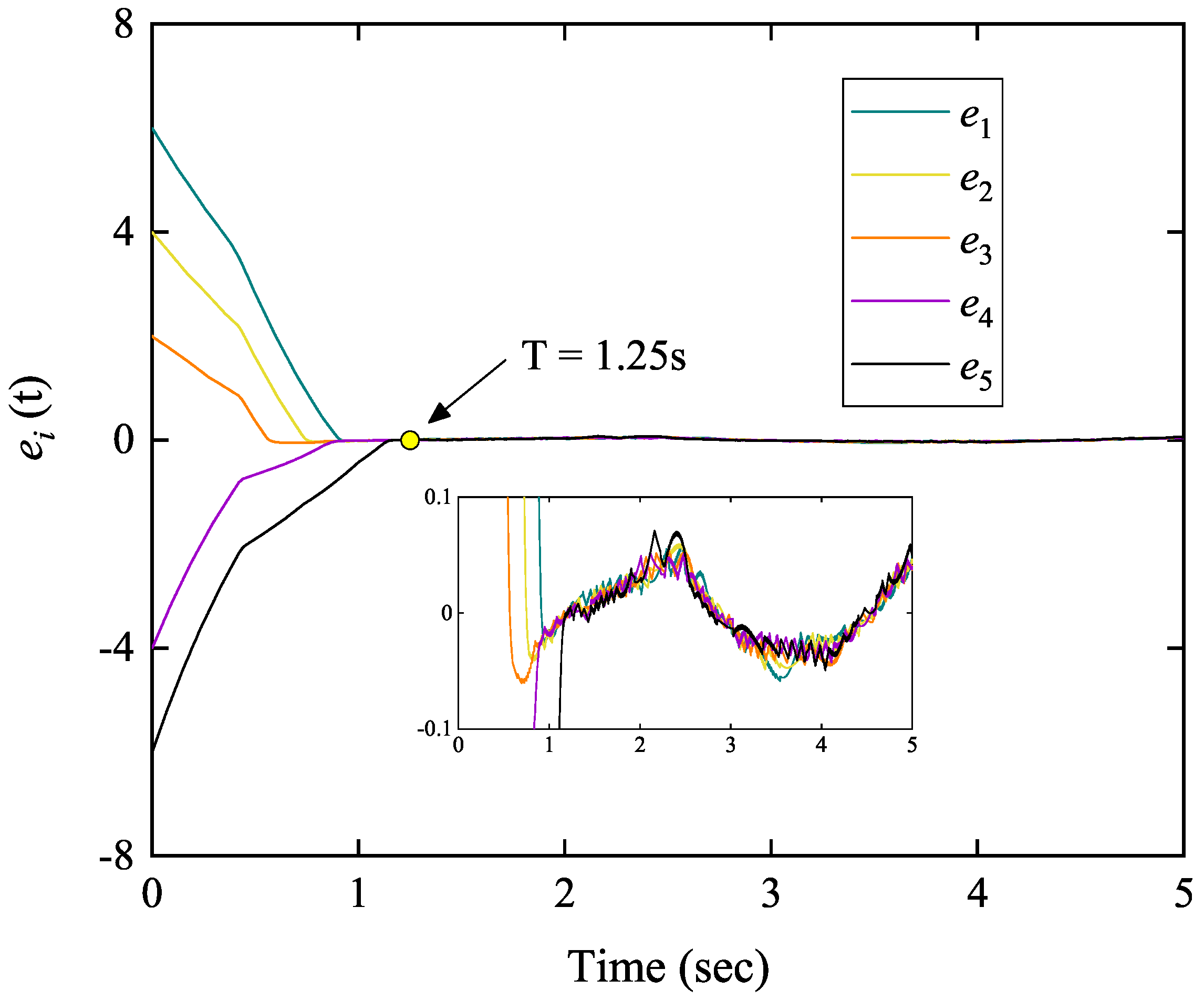
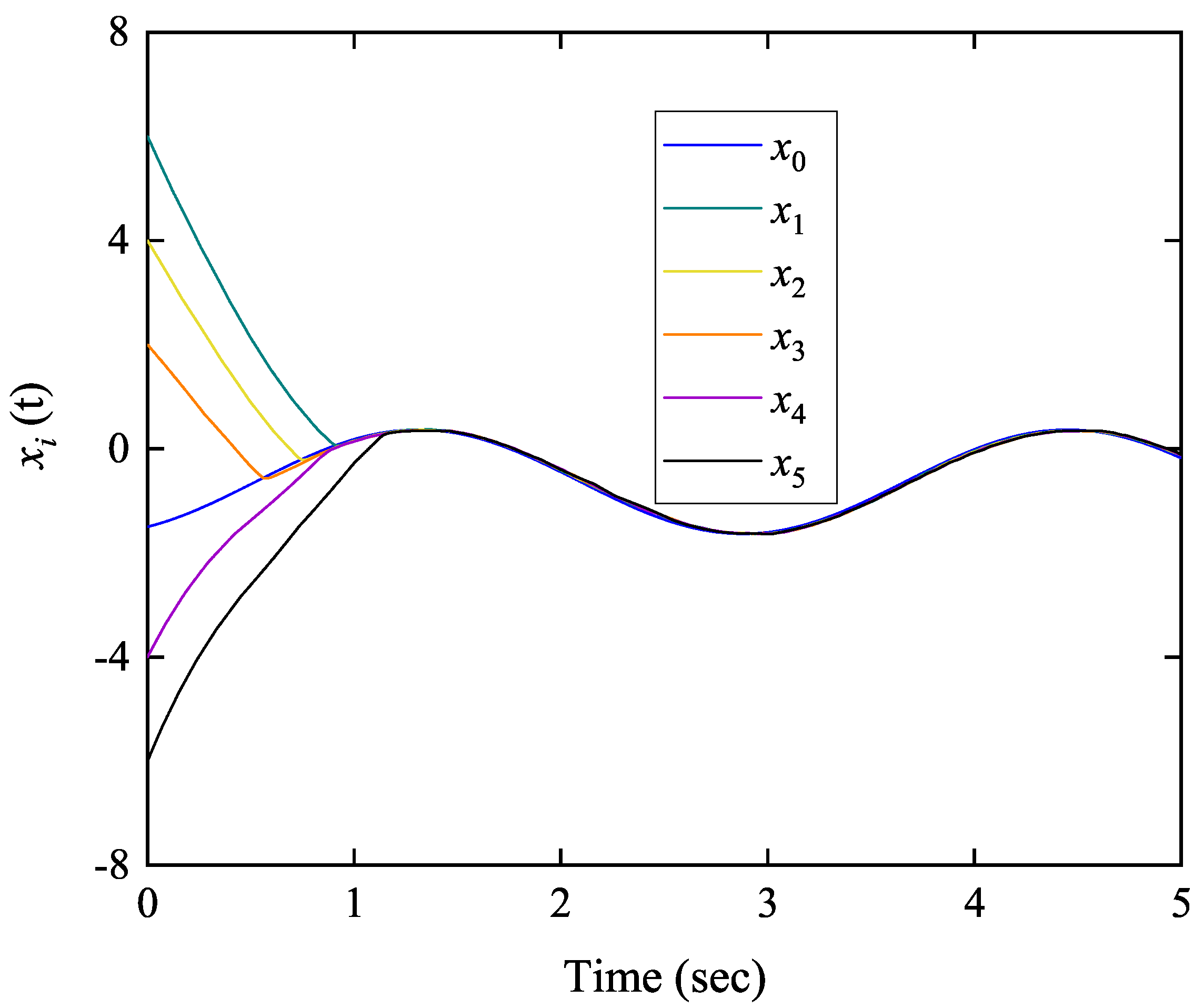
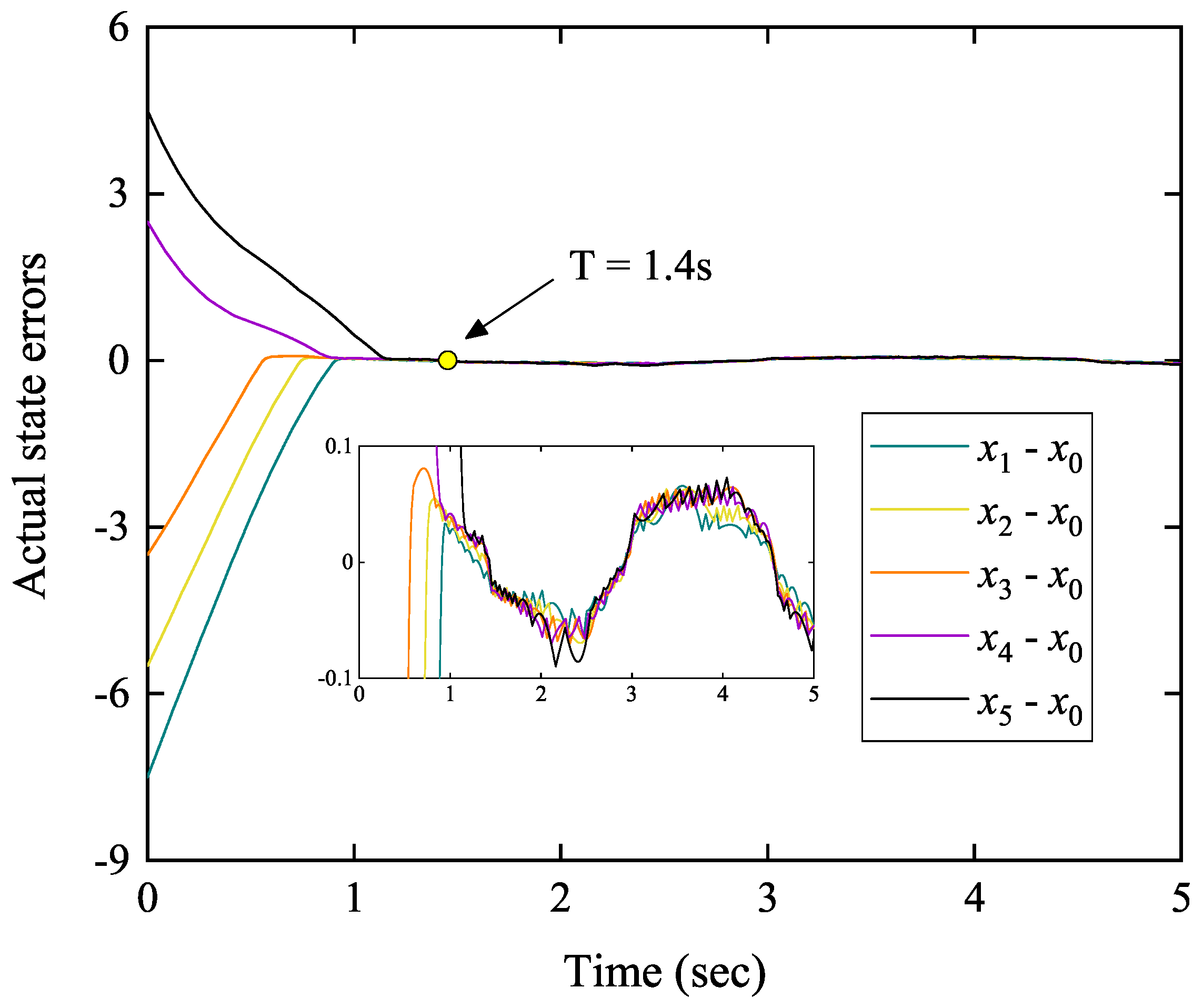
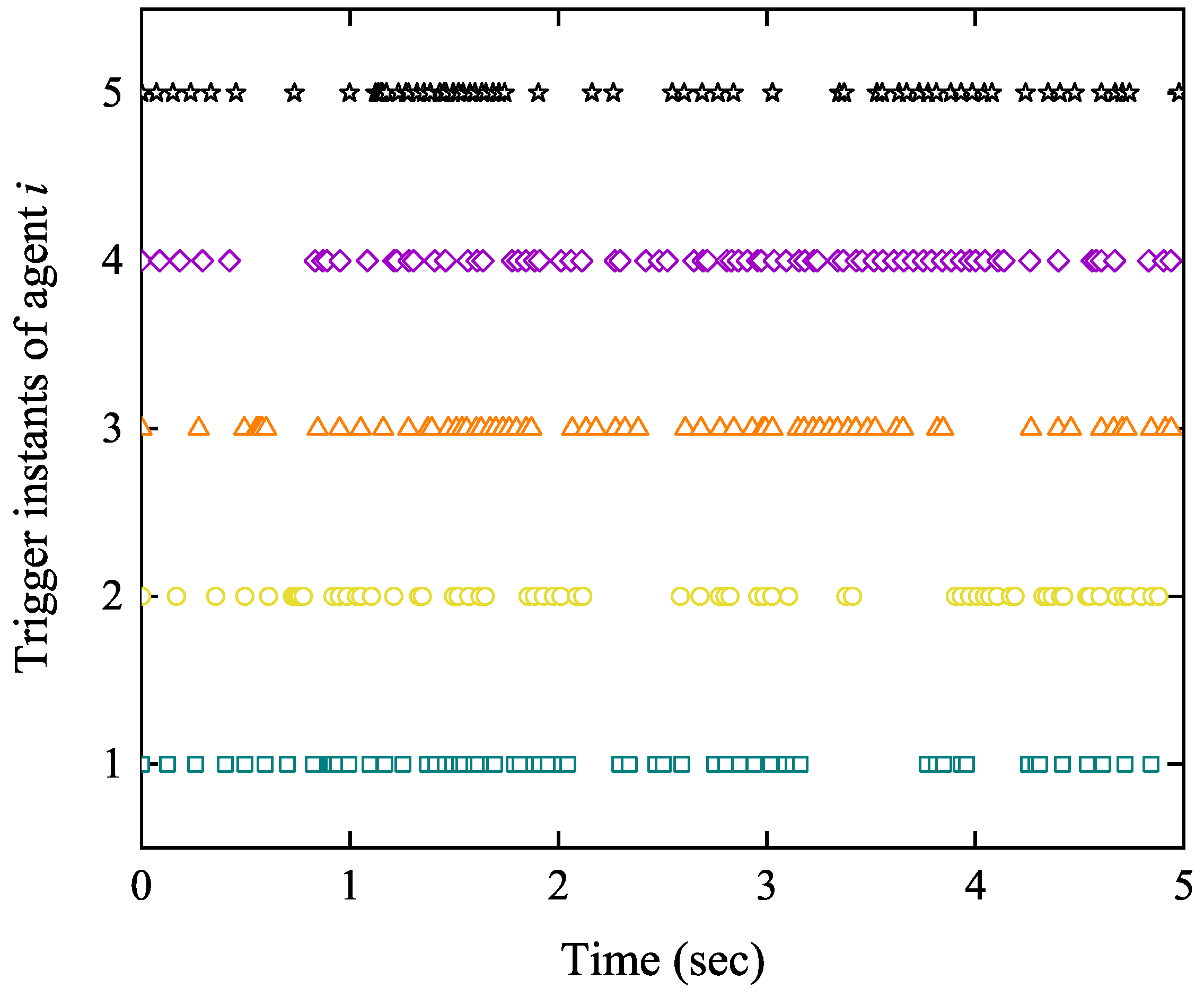
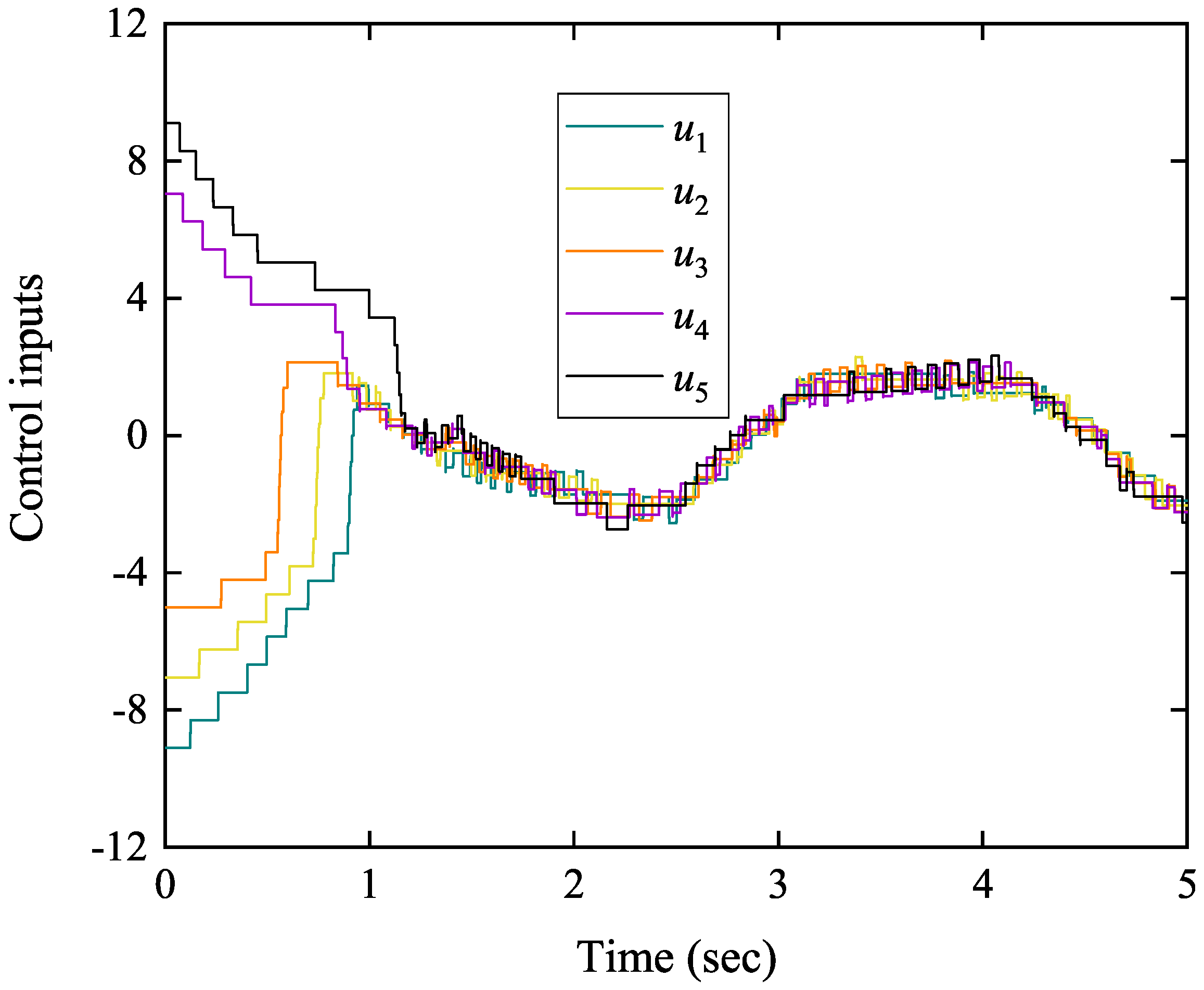
Follower Agent i	Number of Trigger Times	Total Number of Sample Times
Agent 1	61
Agent 2	67
Agent 3	68	5000 (Sample time = 0.001 s)
Agent 4	75
Agent 5	64

, the triggering times for the five follower agents are 61, 67, 68, 75 and 64, respectively. These values are significantly lower than the total sampling times within time interval of 5 s, demonstrating a distinct advantage of the low-frequency triggering in the proposed controller (7). Furthermore, Figure 8 provides a clearly illustration of the control inputs under ET conditions. It can be inferred that the proposed strategy leads to substantial resource savings in control expenditure.

5. Conclusions

This work focuses on addressing the distributed fixed-time ET control strategy using observer protocols for nonlinear MASs with external disturbances. The aim is to design a control scheme that is both simple and high-performing. In pursuit of achieving consensus objectives, a comprehensive model analysis is conducted for the MASs. A distributed fixed-time observer is introduced to give rise to a tracking control framework with the leader’s state as the target. Furthermore, the observation error model between the leader and followers is formalized. To strike a balance between consensus control performance and control cost, distributed ET controller is designed for each follower agent. Optimized ET conditions are proposed, further reducing trigger frequency and communication burden. By utilizing a Lyapunov function, the stability of this control protocol is rigorously proven. Additionally, there is no Zeno behavior exhibited throughout the entire consensus process. In summary, the proposed strategy enhances the efficiency of consensus but also mitigates unnecessary communication expenditure. In a future work, the communication delays and switching topologies in MASs will be taken into account, and the proposed scheme will be applied to a general system for validation.