A Soft Sensor Model for Predicting the Flow of a Hydraulic Pump Based on Graph Convolutional Network–Long Short-Term Memory
Abstract
1. Introduction
- (1)
- We proposed a novel soft sensor model for predicting the flow of hydraulic pumps by combining a GCN and LSTM. We used a GCN to capture the spatial features of the process variable and LSTM to capture their temporal features;
- (2)
- We collected a first-of-its-kind real-world dataset of a hydraulic shovel with actual operational conditions and showed that our proposed GCN-LSTM model was also able to outperform current deep learning approaches for predicting the flow of hydraulic pumps in practical settings;
- (3)
- We validated the proposed GCN-LSTM model on two public datasets and showed that our GCN-LSTM model outperformed current deep learning approaches for other complex engineering operations.
2. Methods
2.1. Principles of GCN
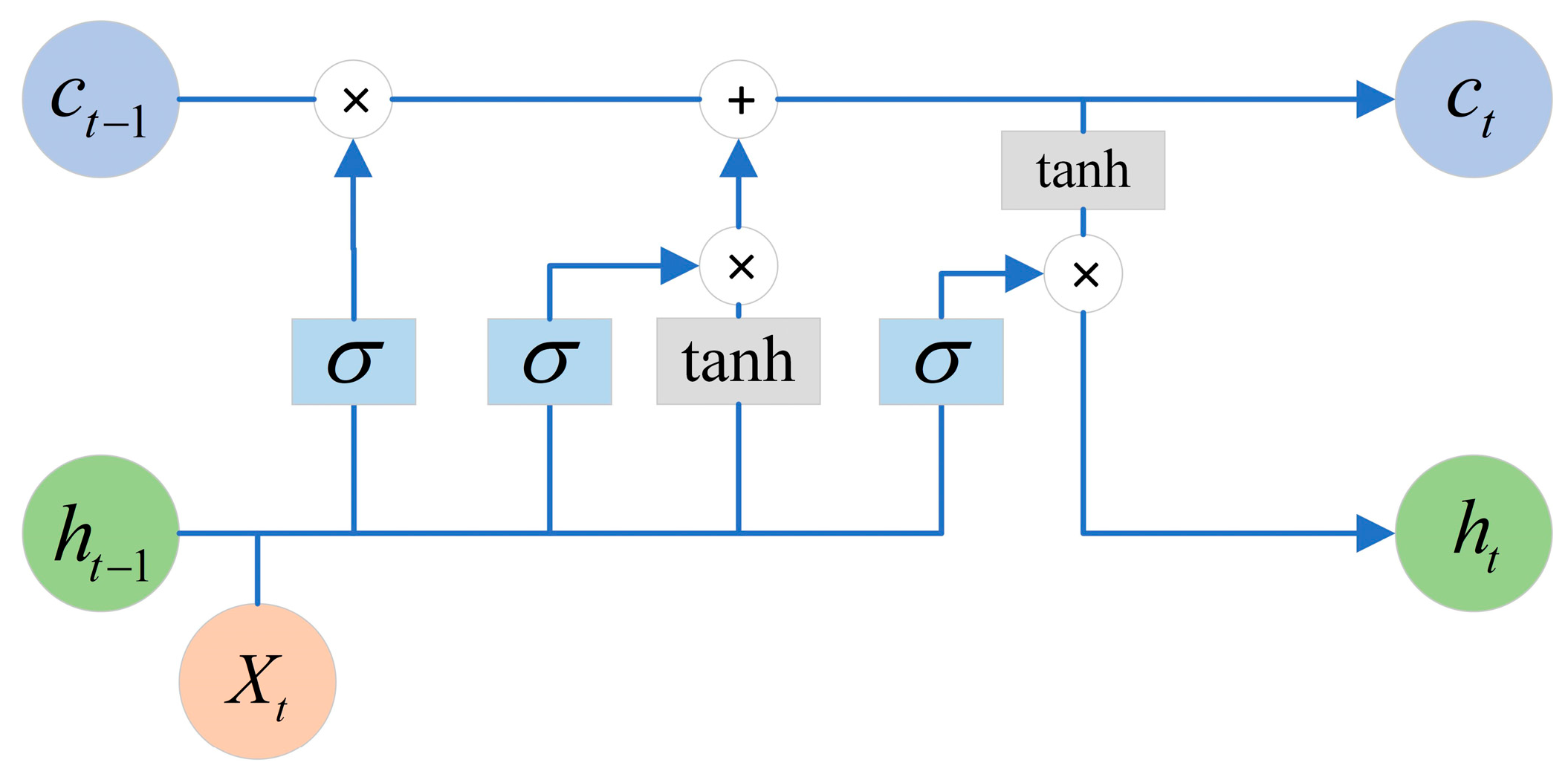
2.2. Principles of LSTM
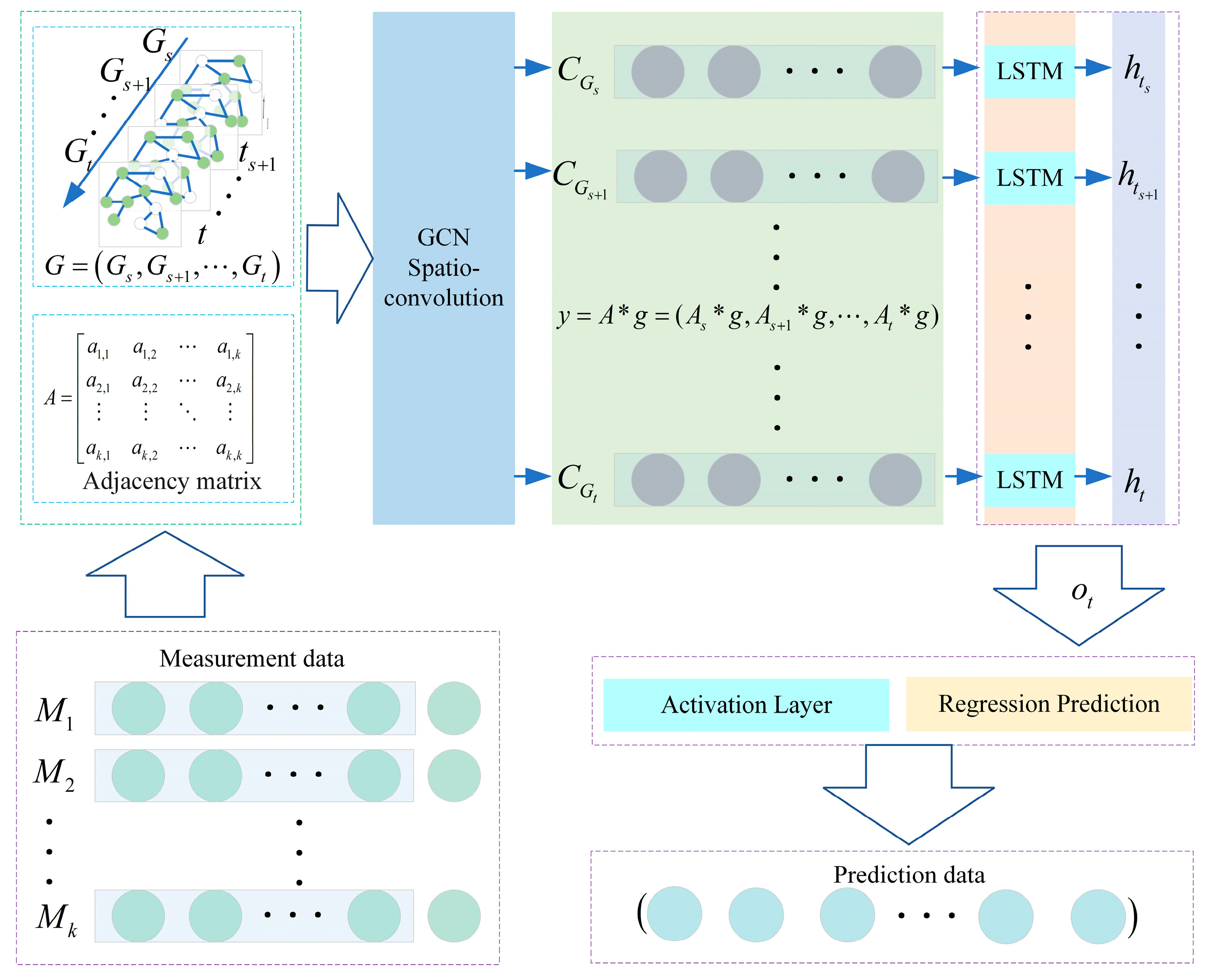
2.3. GCN-LSTM Model
3. Case Studies: Hydraulic Pump
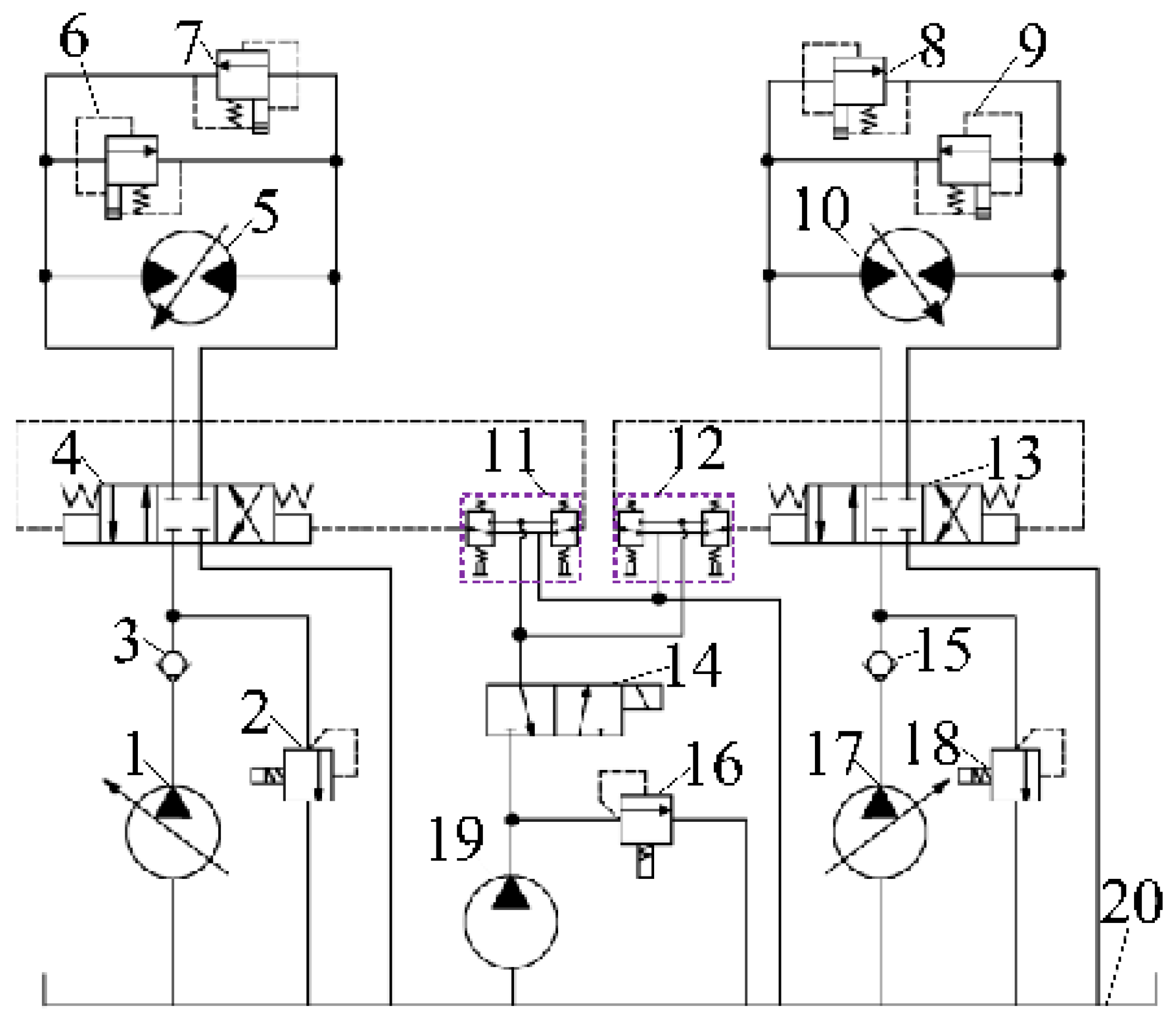
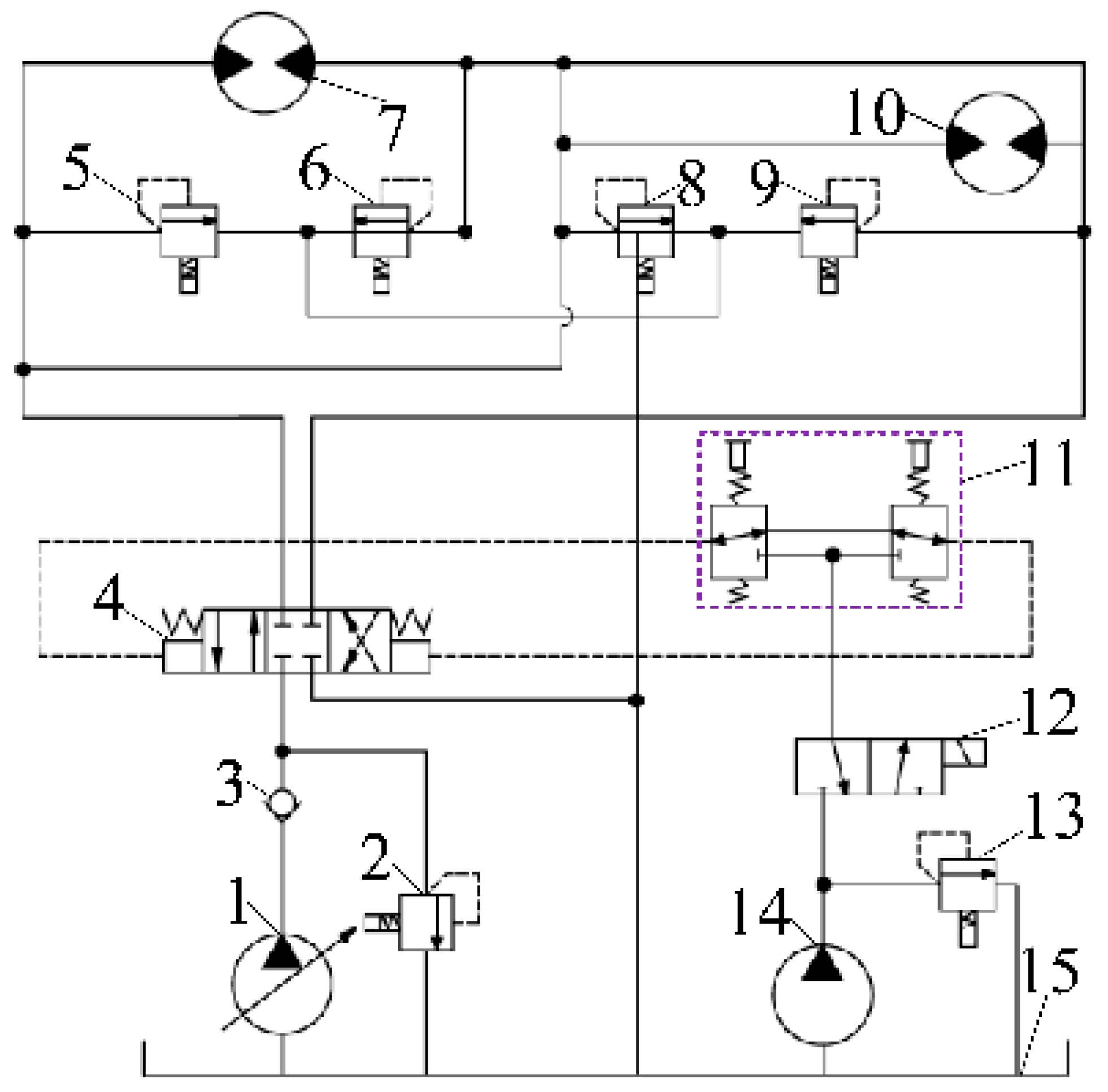
3.1. Experimental Setup
3.2. Pump Flow Prediction under Swing Action
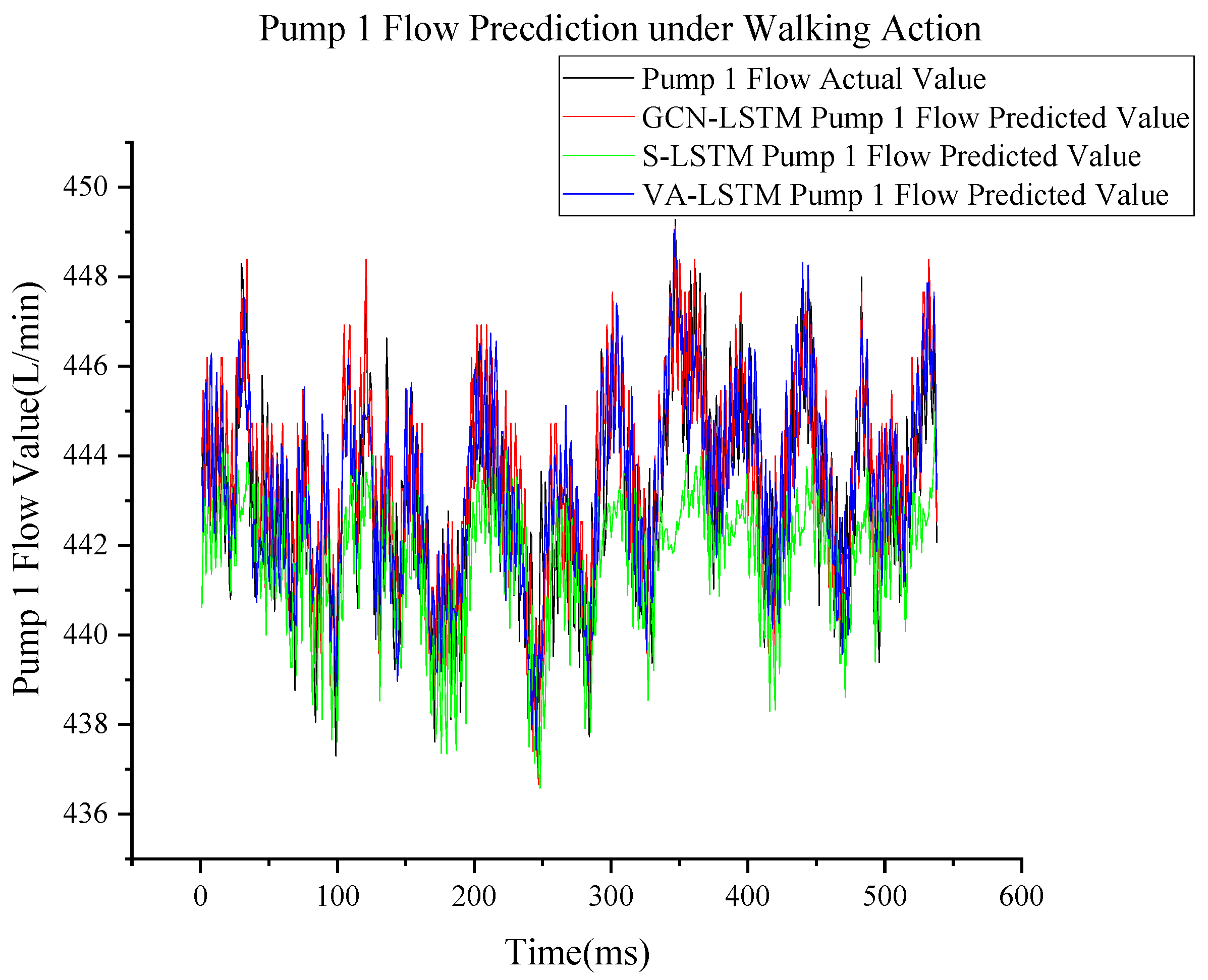
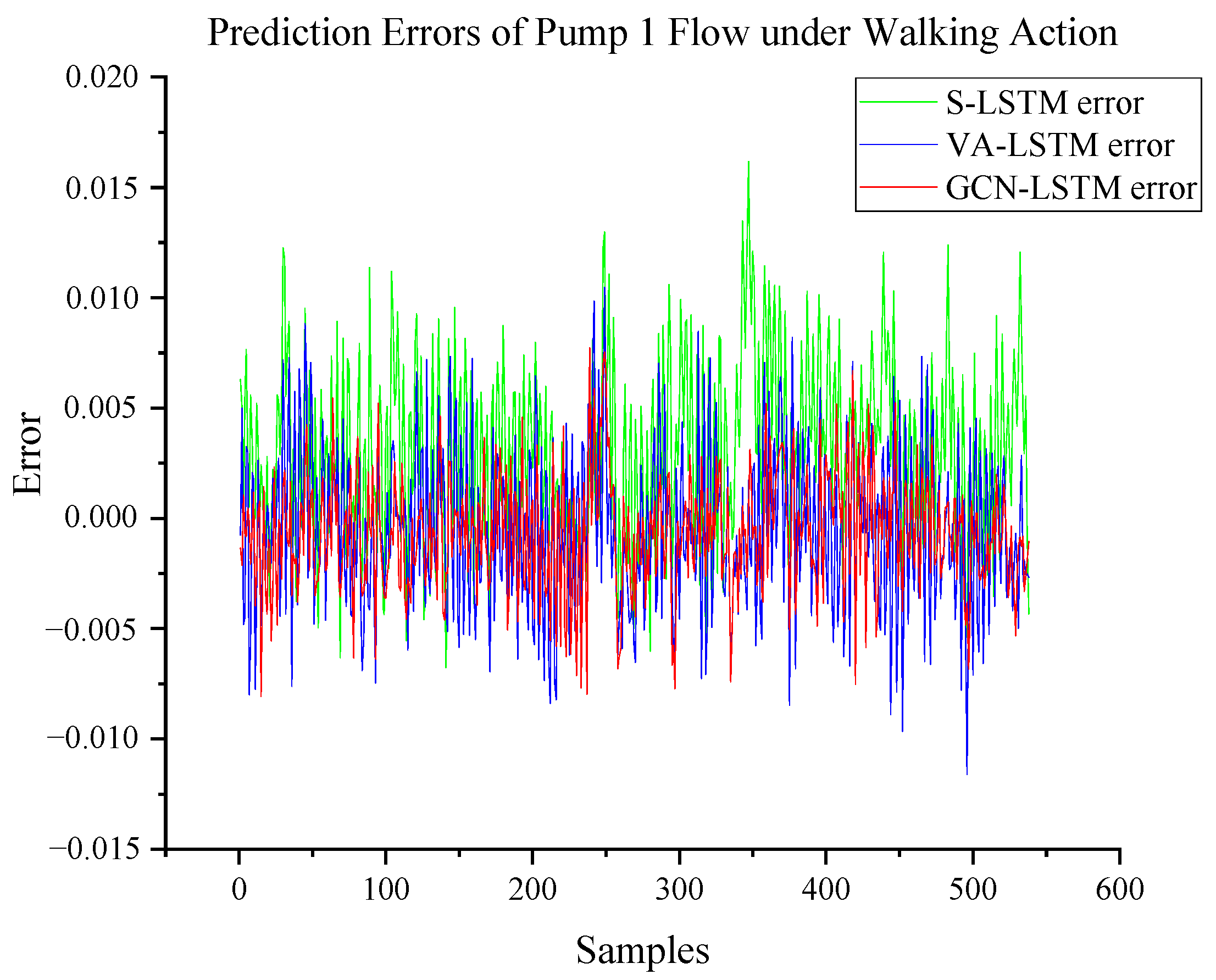
3.3. Pump Flow Prediction under Walking Action
3.4. Pump Flow Prediction under Composite Action
3.4.1. Pump 1 Flow Prediction
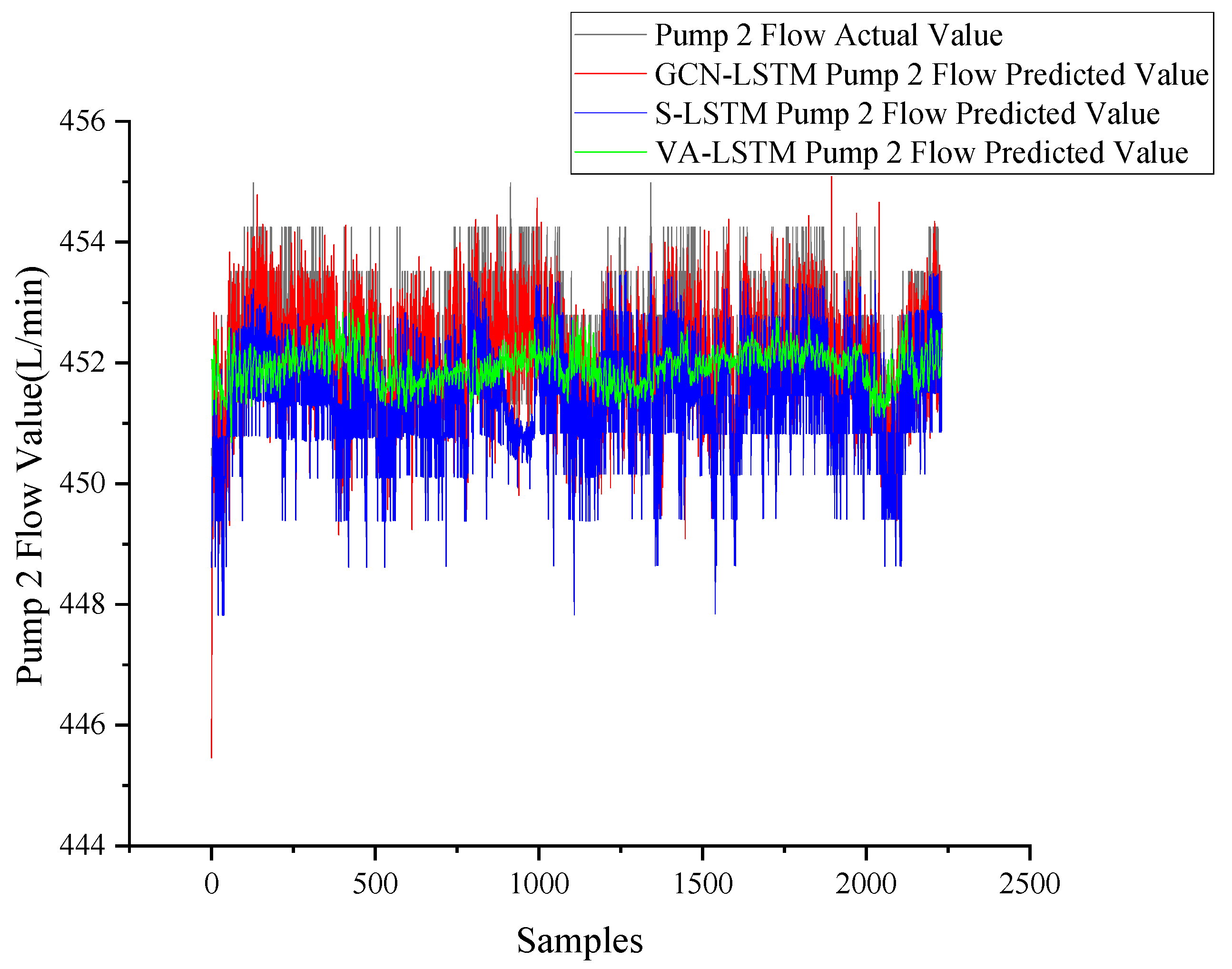
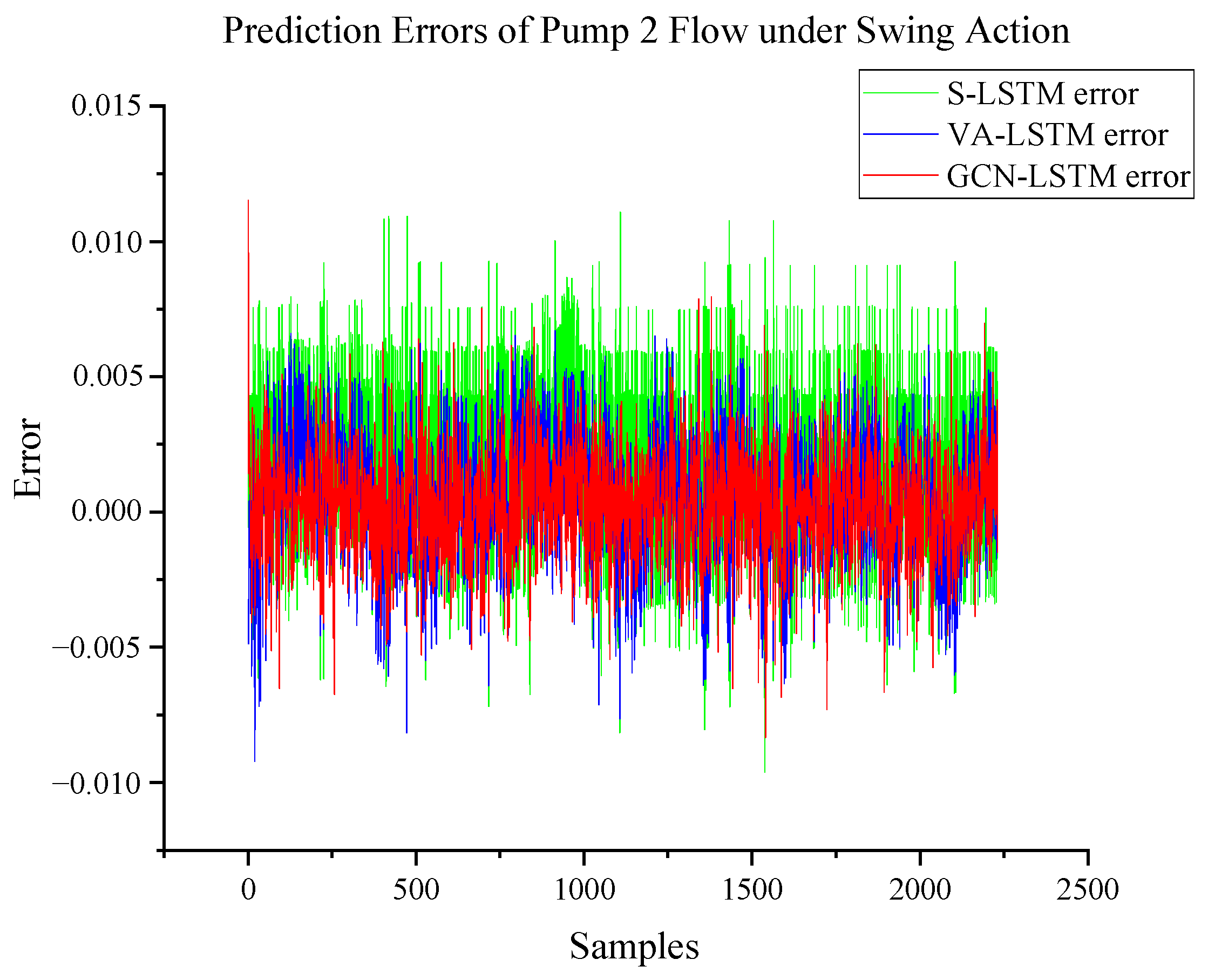
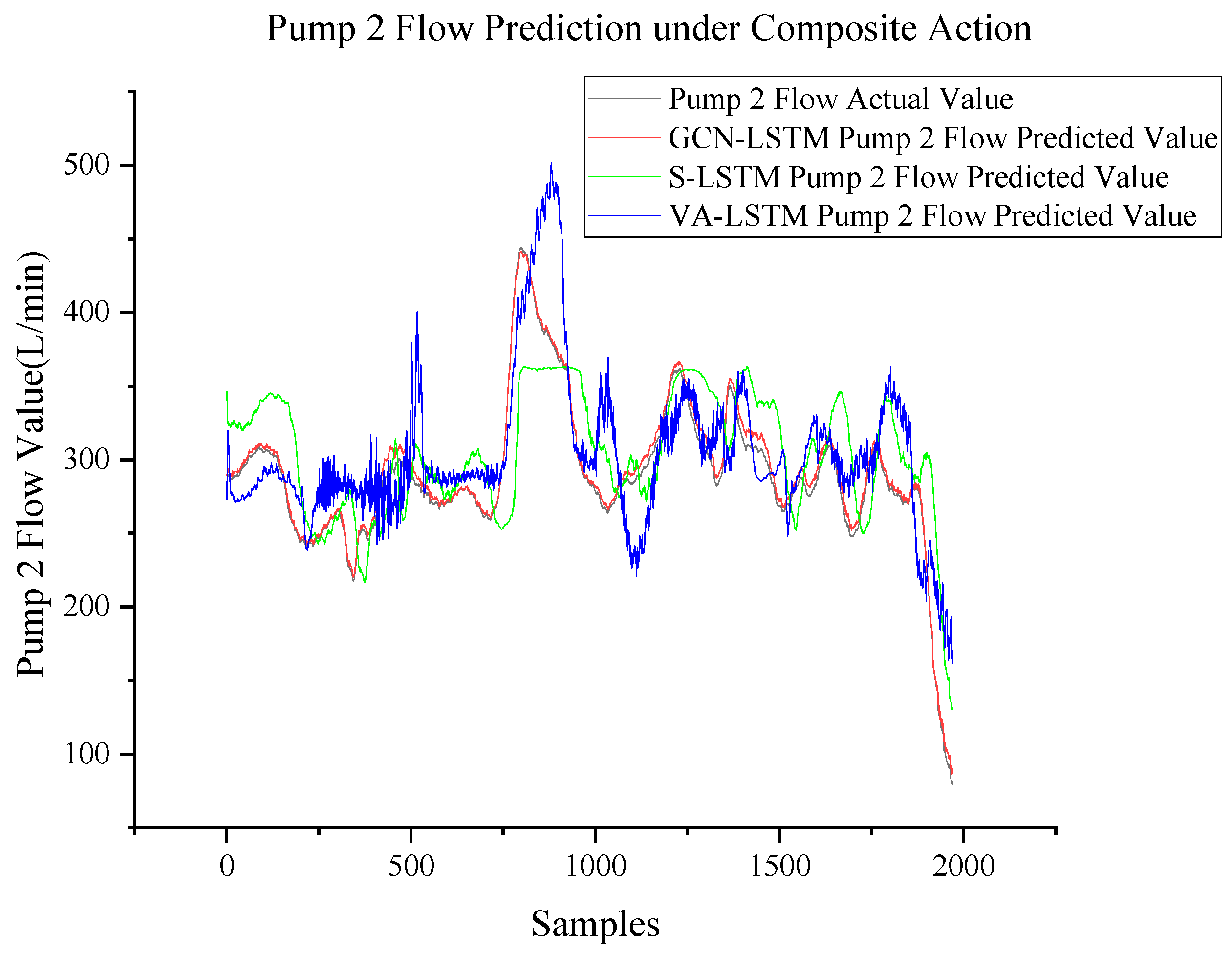
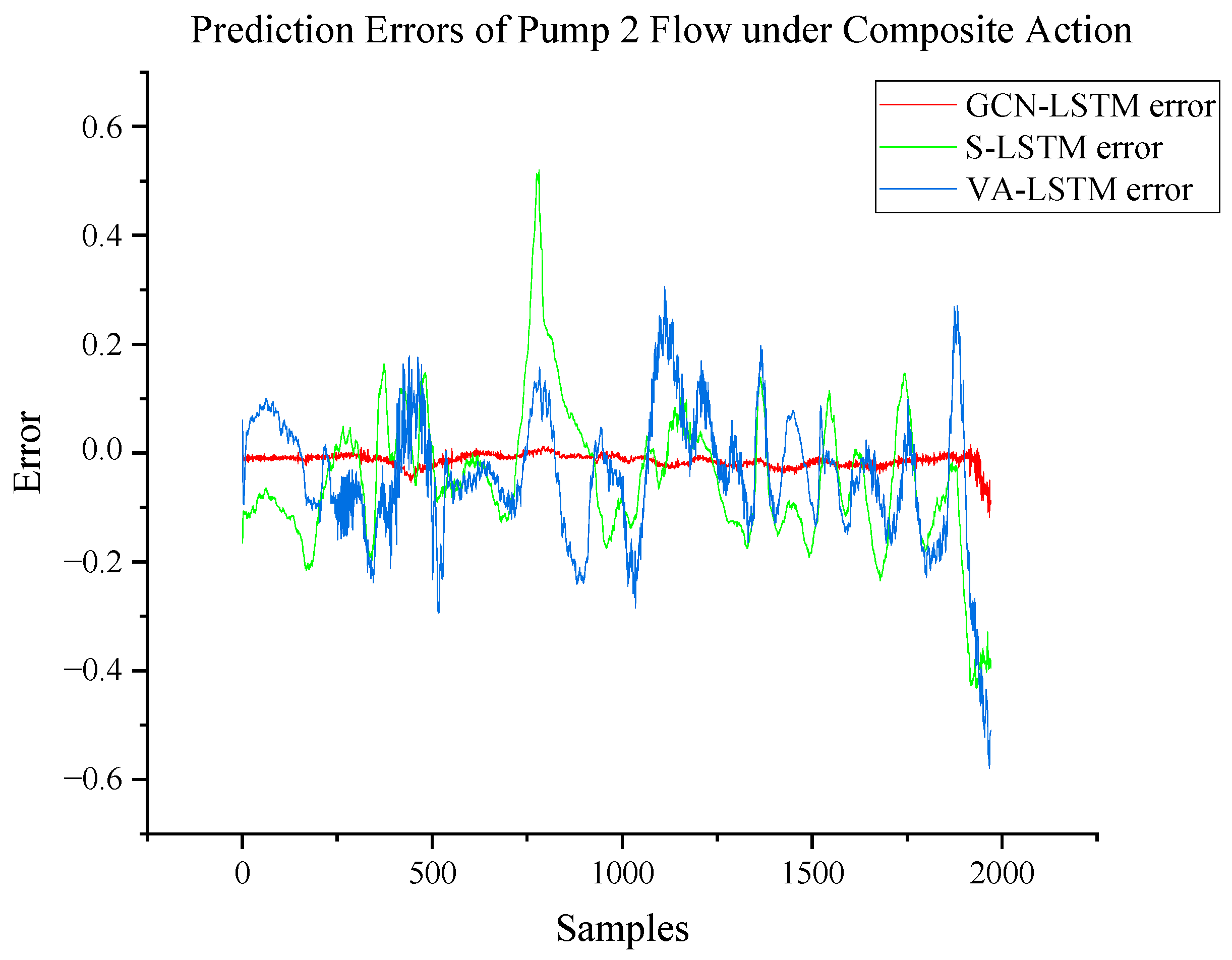
3.4.2. Pump 2 Flow Prediction
3.5. Public Datasets
4. Discussion and Results
5. Conclusions
- (1)
- The GCN-LSTM model outperformed the S-LSTM and VA-LSTM models in predicting the flow of hydraulic pumps under steady-state conditions (swing and walking actions) and variable operating conditions (composite action);
- (2)
- The GCN-LSTM model demonstrated superior predictive performance in the sulfur recovery and debutanizer column datasets compared to the S-LSTM and VA-LSTM models.
- (1)
- The GCN-LSTM model is highly sensitive to the quality and quantity of data. Therefore, the introduction of more advanced data preprocessing techniques to reduce noise interference in the data is an area that requires further research;
- (2)
- Given the high computational complexity of the GCN-LSTM model, optimizing its structure to reduce the number of parameters is an important direction for future research.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.H.; Xiang, J.W.; Zhong, Y.T. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Signal Process. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- He, Y.; Tang, H.S.; Kumar, A. A deep multi-signal fusion adversarial model-based transfer learning and residual network for axial piston pump fault diagnosis. Measurement 2022, 192, 110889. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.P.; Wang, R. Intelligent fault diagnosis of hydraulic piston pump combining improved LeNet-5 and PSO hyperparameter optimization. Appl. Acoust. 2021, 183, 108336. [Google Scholar] [CrossRef]
- Yu, H.; Li, H.R.; Li, Y.L. Vibration signal fusion using improved empirical wavelet transform and variance contribution rate for weak fault detection of hydraulic pumps. ISA Trans. 2020, 107, 385–401. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.R.; Liu, H.; Nikitas, N. Internal pump leakage detection of the hydraulic systems with highly incomplete flow data. Adv. Eng. Inform. 2023, 56, 101974. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Wu, D.H.; Fei, M.H. Application of GA-BPNN on estimating the flow rate of a centrifugal pump. Eng. Appl. Artif. Intel. 2023, 119, 105738. [Google Scholar] [CrossRef]
- Yao, L.; Shen, B.B.; Cui, L.L. Semi-Supervised Deep Dynamic Probabilistic Latent Variable Model for Multimode Process Soft Sensor Application. IEEE Trans. Ind. Inform. 2023, 19, 6056–6068. [Google Scholar] [CrossRef]
- Gao, S.W.; Qiu, S.L.; Ma, Z.Y. SVAE-WGAN-Based Soft Sensor Data Supplement Method for Process Industry. IEEE Sens. J. 2022, 22, 601–610. [Google Scholar] [CrossRef]
- Nie, L.; Ren, Y.Z.; Wu, R.H. Sensor Fault Diagnosis, Isolation, and Accommodation for Heating, Ventilating, and Air Conditioning Systems Based on Soft Sensor. Actuators. 2023, 12, 389. [Google Scholar] [CrossRef]
- Gao, S.W.; Zhang, Q.S.; Tian, R. Collaborative Apportionment Noise-Based Soft Sensor Framework. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Yuan, X.F.; Li, L.; Wang, Y.L. Deep Learning with Spatiotemporal Attention-Based LSTM for Industrial Soft Sensor Model Development. IEEE Trans. Ind. Electron. 2021, 68, 4404–4414. [Google Scholar] [CrossRef]
- Guo, R.Y.; Liu, H.; Xie, G. A Self-Interpretable Soft Sensor Based on Deep Learning and Multiple Attention Mechanism: From Data Selection to Sensor Modeling. IEEE Trans. Ind. Inform. 2023, 19, 6859–6871. [Google Scholar] [CrossRef]
- Xie, W.; Wang, J.S.; Xing, C. Variational Autoencoder Bidirectional Long and Short-Term Memory Neural Network Soft-Sensor Model Based on Batch Training Strategy. IEEE Trans. Ind. Inform. 2023, 17, 5325–5334. [Google Scholar] [CrossRef]
- Mannering, F.; Bhat, C.R.; Shankar, V. Big data, traditional data and the tradeoffs between prediction and causality in highway-safety analysis. Anal. Methods Accid. Res. 2020, 25, 100113. [Google Scholar] [CrossRef]
- Shen, B.W.; Yao, L.; Ge, Z. Nonlinear probabilistic latent variable regression models for soft sensor application: From shallow to deep structure. Control Eng. Pract. 2020, 94, 100113. [Google Scholar] [CrossRef]
- Ferreira, J.; Pedemonte, M.; Torres, A.I. Development of a machine learning-based soft sensor for an oil refinery’s distillation column. Comput. Chem. Eng. 2022, 161, 107756. [Google Scholar] [CrossRef]
- Xibilia, M.G.; Latino, M.; Marinkovic, Z. Soft sensors based on deep neural networks for applications in security and safety. IEEE Trans. Instrum. Meas. 2020, 69, 7869–7876. [Google Scholar] [CrossRef]
- Zheng, J.H.; Song, Z.H. Semisupervised learning for probabilistic partial least squares regression model and soft sensor application. J. Process Control 2018, 64, 123–131. [Google Scholar] [CrossRef]
- Herceg, S.; Andriji’c, Ž.U.; Bolf, N. Development of soft sensors for isomerization process based on support vector machine regression and dynamic polynomial models. Chem. Eng. Res. Design 2019, 149, 95–103. [Google Scholar] [CrossRef]
- Wang, G.M.; Jia, Q.S.; Zhou, M.C. Artificial neural networks for water quality soft-sensing in wastewater treatment: A review. Artif. Intell. Rev. 2021, 55, 565–587. [Google Scholar] [CrossRef]
- Zhu, P.B.; Liu, X.Y.; Wang, B. Mixture semisupervised Bayesian principal component regression for soft sensor modeling. IEEE Access. 2018, 6, 40909–40919. [Google Scholar] [CrossRef]
- Li, W.Q.; Yang, C.H.; Jabari, S.E. Nonlinear traffic prediction as a matrix completion problem with ensemble learning. Transp. Sci. 2022, 56, 52–78. [Google Scholar] [CrossRef]
- Lima, J.M.M.; Araujo, F.M.U. Ensemble deep relevant learning framework for semi-supervised soft sensor modeling of industrial processes. Neurocomputing 2021, 462, 154–168. [Google Scholar] [CrossRef]
- Chai, Z.; Zhao, C.H.; Huang, B. A Deep Probabilistic Transfer Learning Framework for Soft Sensor Modeling with Missing Data. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7598–7609. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.Q.; Ge, Z.Q. A survey on deep learning for data-driven soft sensors. IEEE Trans. Ind. Informat. 2021, 17, 5853–5866. [Google Scholar] [CrossRef]
- Zheng, J.H.; Wu, C.; Sun, Q.Q. Deep learning of complex process data for fault classification based on sparse probabilistic dynamic network. J. Taiwan Inst. Chem. Eng. 2022, 138, 104498. [Google Scholar] [CrossRef]
- Yuan, X.F.; Qi, S.B.; Wang, Y.L. A dynamic CNN for nonlinear dynamic feature learning in soft sensor modeling of industrial process data. Control Eng. Pract. 2020, 104, 104614. [Google Scholar] [CrossRef]
- Gilbert Chandra, D.; Vinoth, B.; Srinivasulu Reddyb, U. Recurrent Neural Network based Soft Sensor for flow estimation in Liquid Rocket Engine Injector calibration. Flow Meas. Instrum. 2022, 83, 102105. [Google Scholar]
- Ke, W.S.; Huang, D.X.; Yang, F. Soft sensor development and applications based on LSTM in deep neural networks. Proc. IEEE Symp. Ser. Comput. Intell. 2017, 12, 1–6. [Google Scholar]
- Sun, Q.Q.; Ge, Z.Q. Gated Stacked Target-Related Autoencoder: A Novel Deep Feature Extraction and Layerwise Ensemble Method for Industrial Soft Sensor Application. IEEE Trans. Cybern. 2022, 52, 3457–3468. [Google Scholar] [CrossRef]
- Fan, W.; Si, F.Q.; Ren, S.J. Integration of continuous restricted Boltzmann machine and SVR in NOx emissions prediction of a tangential firing boiler. Chemom. Intell. Lab. Syst. 2019, 195, 103870. [Google Scholar] [CrossRef]
- Yuan, X.F.; Qi, S.B.; Wang, Y.L. Soft sensor model for dynamic processes based on multichannel convolutional neural network. Chemom. Intell. Lab. Syst. 2020, 203, 104050. [Google Scholar] [CrossRef]
- Alghamdi, W.Y. A novel deep learning method for predicting athletes’ health using wearable sensors and recurrent neural networks. Decis. Anal. J. 2023, 7, 100213. [Google Scholar] [CrossRef]
- Jorge, L.B.; Heo, S.K.; Yoo, C.K. Soft sensor validation for monitoring and resilient control of sequential subway indoor air quality through memory-gated recurrent neural networks-based autoencoders. Control Eng. Pract. 2020, 97, 104330. [Google Scholar]
- Zhu, K.; Zhao, C.H. Dynamic Graph-Based Adaptive Learning for Online Industrial Soft Sensor with Mutable Spatial Coupling Relations. IEEE Trans. Ind. Electron. 2023, 70, 9614–9622. [Google Scholar] [CrossRef]
- Song, P.Y.; Zhao, C.H. Slow down to go better: A survey on slow feature analysis. IEEE Trans. Neural Netw. Learn. Syst. 2022, 326, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Chen, X.Q. A novel reinforced dynamic graph convolutional network model with data imputation for network-wide traffic flow prediction. Transp. Res. C Emerg. Technol. 2022, 143, 103820. [Google Scholar] [CrossRef]
- Wang, G.T.; Zhang, Z.R.; Bian, Z.P. A short-term voltage stability online prediction method based on graph convolutional networks and long short-term memory networks. Int. J. Elec. Power. 2021, 127, 103820. [Google Scholar] [CrossRef]
- Ta, X.X.; Liu, Z.H.; Hu, X. Adaptive Spatio-temporal Graph Neural Network for traffic forecasting. Knowl.-Based Syst. 2022, 242, 108199. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.T.; Zhu, Z.X. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. In Proceedings of the IJCAI-27, 27th International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar]
- Wang, X.; Zhu, M.Q.; Bo, D.Y. AM-GCN: Adaptive Multi-channel Graph Convolutional Networks. In Proceedings of the KDD-20, 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 1243–1253. [Google Scholar]
- Zhou, K.B.; Yang, C.Y.; Liu, J. Dynamic graph-based feature learning with few edges considering noisy samples for rotating machinery fault diagnosis. IEEE Trans. Ind. Electron. 2022, 69, 10595–10604. [Google Scholar] [CrossRef]
- Yang, C.Y.; Liu, J.; Zhou, K.B. An improved multi-channel graph convolutional network and its applications for rotating machinery diagnosis. Measurement 2022, 190, 110720. [Google Scholar] [CrossRef]
- Jiang, Y.C.; Yin, S.; Dong, J.W. A Review on Soft Sensors for Monitoring, Control, and Optimization of Industrial Processes. IEEE Sens. J. 2021, 21, 12868–12881. [Google Scholar] [CrossRef]
- Li, X.T.; Michael, K.N.; Xu, G.N. Multi-channel fusion graph neural network for multivariate time series forecasting. Neural Netw. 2023, 161, 343–358. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.N.; Dong, Y.X.; Wang, K.S. GPT-GNN: Generative Pre-Training of Graph Neural Networks. In Proceedings of the KDD-20, 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 6–10 July 2020; Volume 56, pp. 1857–1867. [Google Scholar]
- Park, M.Y.; Geum, Y.J. Two-stage technology opportunity discovery for firm-level decision making: GCN-based link-prediction approach. Technol. Forecast. Soc. Chang. 2022, 183, 121934. [Google Scholar] [CrossRef]
- Lui, C.F.; Liu, Y.; Xie, M. A Supervised Bidirectional Long Short-Term Memory Network for Data-Driven Dynamic Soft Sensor Modeling. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Huang, D.Y.; Liu, H.; Bi, T.S. GCN-LSTM spatiotemporal-network-based method for post-disturbance frequency prediction of power systems. Glob. Energy Interconnect. 2022, 5, 96–107. [Google Scholar] [CrossRef]
- Yuan, X.F.; Huang, B.; Wang, Y.L. Deep Learning-Based Feature Representation and Its Application for Soft Sensor Modeling with Variable-Wise Weighted SAE. IEEE Trans. Ind. Inform. 2018, 14, 3235–3243. [Google Scholar] [CrossRef]
- Yuan, X.F.; Li, L.; Wang, Y.L. Nonlinear dynamic soft sensor modeling with supervised long short-term memory network. IEEE Trans. Ind. Inform. 2019, 16, 3168–3176. [Google Scholar] [CrossRef]
- Yuan, X.F.; Li, L.; Wang, Y.L. Deep learning for quality prediction of nonlinear dynamic processes with variable attention- based long short-term memory network. Can. J. Chem. Eng. 2020, 98, 1377–1389. [Google Scholar] [CrossRef]
- Fortuna, L.; Rizzo, A.; Sinatra, M. Soft analyzers for a sulfur recovery unit. Control Eng. Pract. 2003, 11, 1491–1500. [Google Scholar] [CrossRef]
- Yuan, X.F.; Ou, C.; Wang, Y.L. A novel semi-supervised pre-training strategy for deep networks and its application for quality variable prediction in industrial processes. Chem. Eng. Sci. 2020, 2017, 115509. [Google Scholar] [CrossRef]


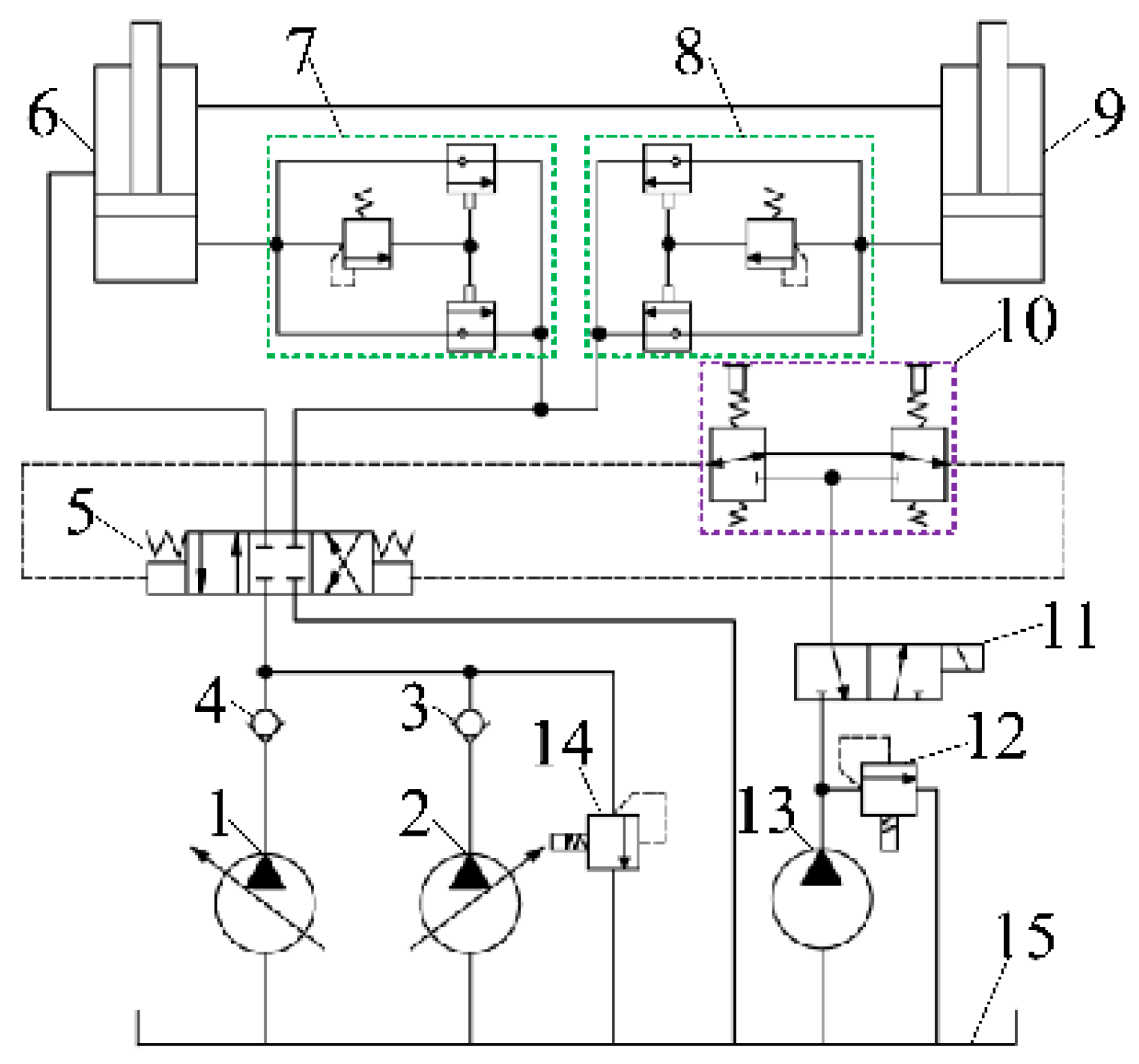
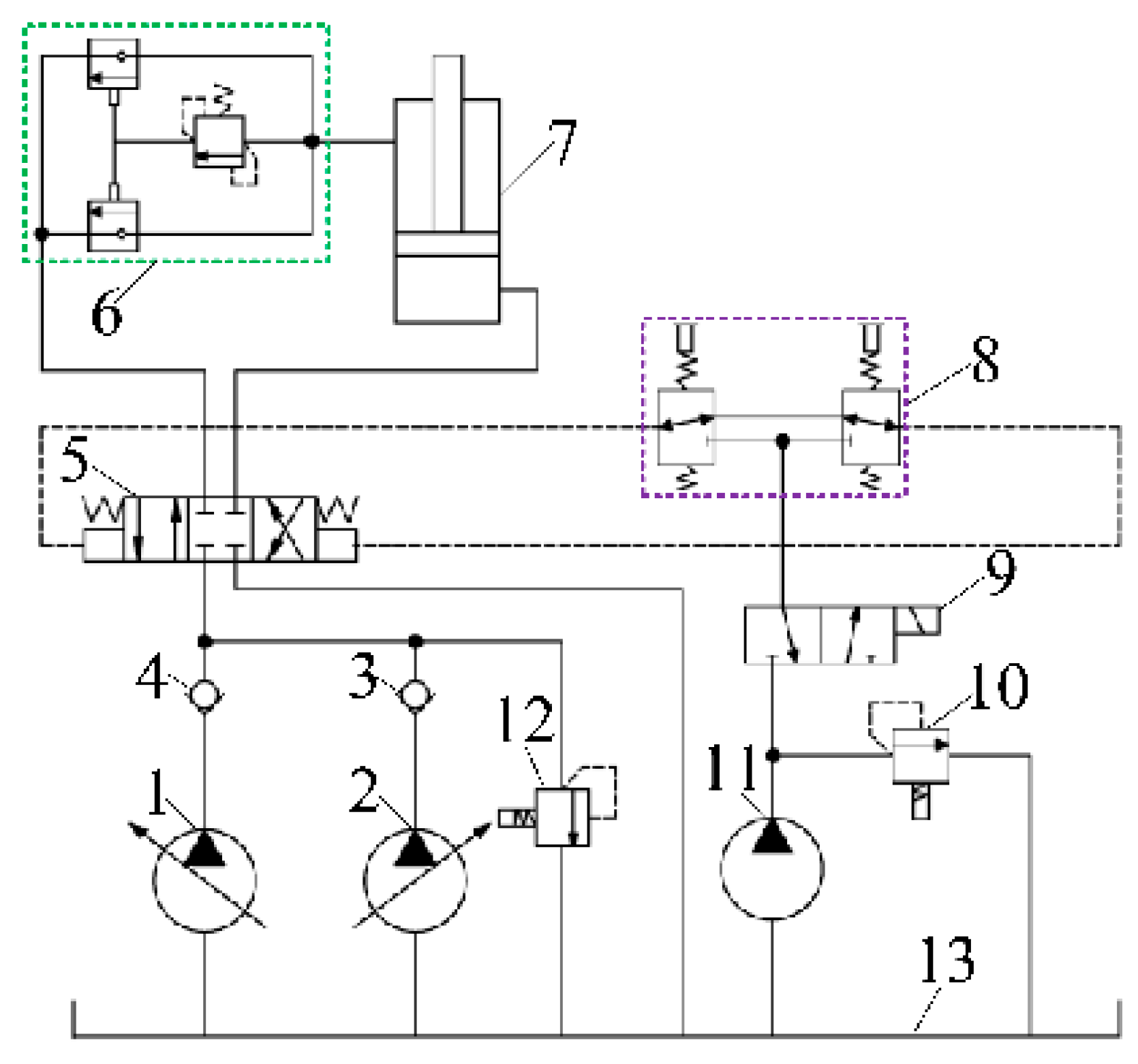





| Variables | Description |
|---|---|
| x1 | Pump 2 oil temperature |
| x2 | Pump 2 pressure |
| x3 | Bucket small chamber pressure |
| x4 | Bucket large chamber pressure |
| x5 | Boom large chamber pressure |
| x6 | Boom small chamber pressure |
| x7 | Swing motor pressure |
| x8 | Swing motor flow |
| x9 | Arm large chamber pressure |
| x10 | Arm small chamber pressure |
| x11 | Pump 1 pressure |
| x12 | Walking motor flow |
| x13 | Walking motor pressure |
| x14 | Swing pilot pressure |
| x15 | Left walking pilot pressure |
| x16 | Right walking pilot pressure |
| x17 | Arm inward pilot pressure |
| x18 | Arm outward pilot pressure |
| x19 | Boom inward pilot pressure |
| x20 | Boom outward pilot pressure |
| x21 | Bucket inward pilot pressure |
| x22 | Bucket outward pilot pressure |
| x23 | Engine speed |
| x24 | Engine torque percentage |
| y1 | Pump 1 flow |
| y2 | Pump 2 flow |
| Name | Main Parameters |
|---|---|
| LSTM | n = 50, dropout = 0.2 |
| LSTM | n = 50, dropout = 0.2 |
| Dense | 1 |
| Dropout | 0.2 |
| Epochs | 200 |
| Batch size | 30 |
| Target Variables | Indicators | S-LSTM | VA-LSTM | GCN-LSTM |
|---|---|---|---|---|
| Swing action pump 2 flow | RMSE R2 | 0.1027 0.726 | 0.1262 0.703 | 0.0916 0.857 |
| Walking action pump 1 flow | RMSE R2 | 0.1047 0.364 | 0.0921 0.754 | 0.0782 0.898 |
| Composite action pump 1 flow | RMSE R2 | 0.0745 0.579 | 0.0903 0.386 | 0.0109 0.987 |
| Composite action pump 2 flow | RMSE R2 | 0.0532 0.767 | 0.0742 0.547 | 0.0109 0.990 |
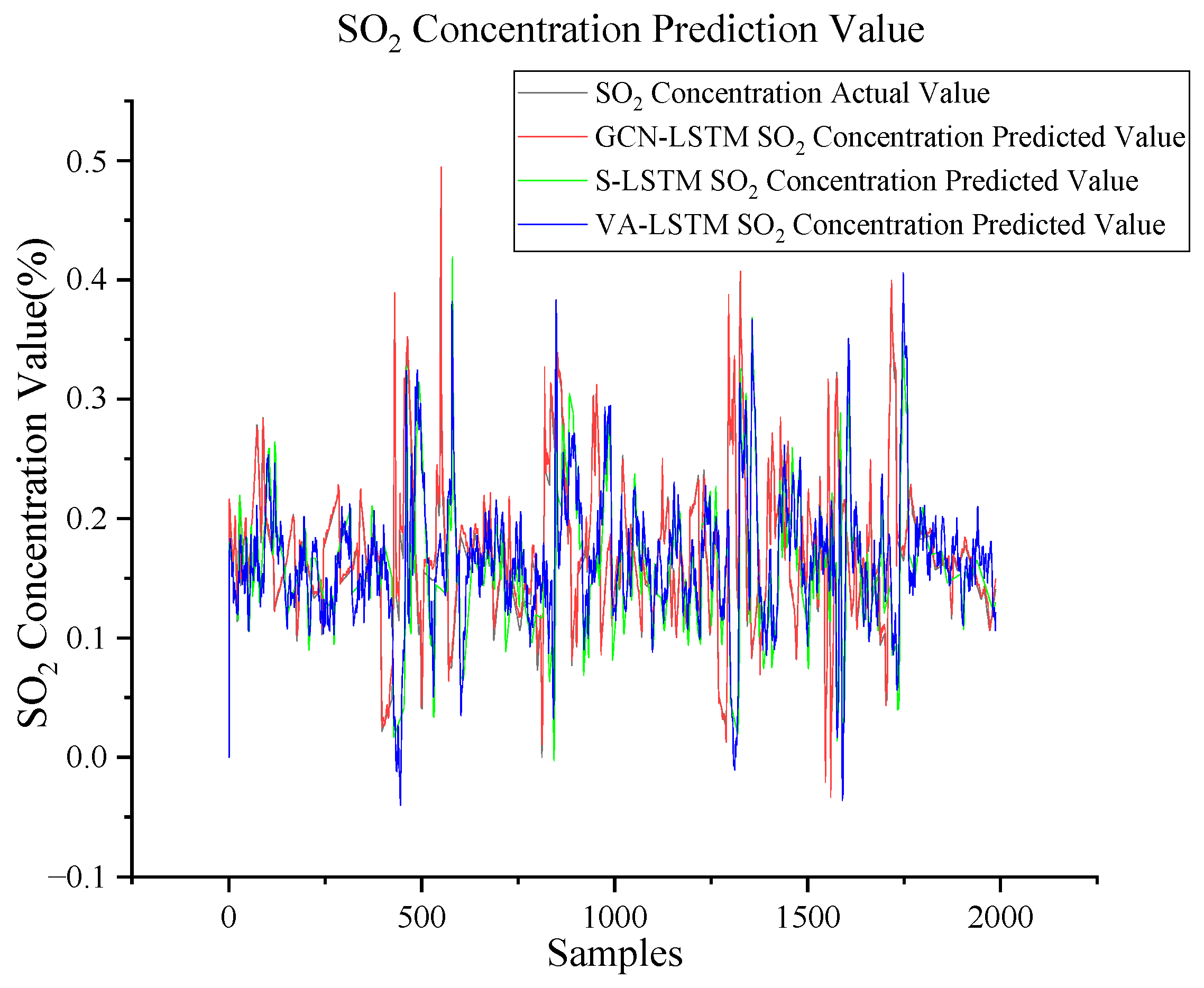
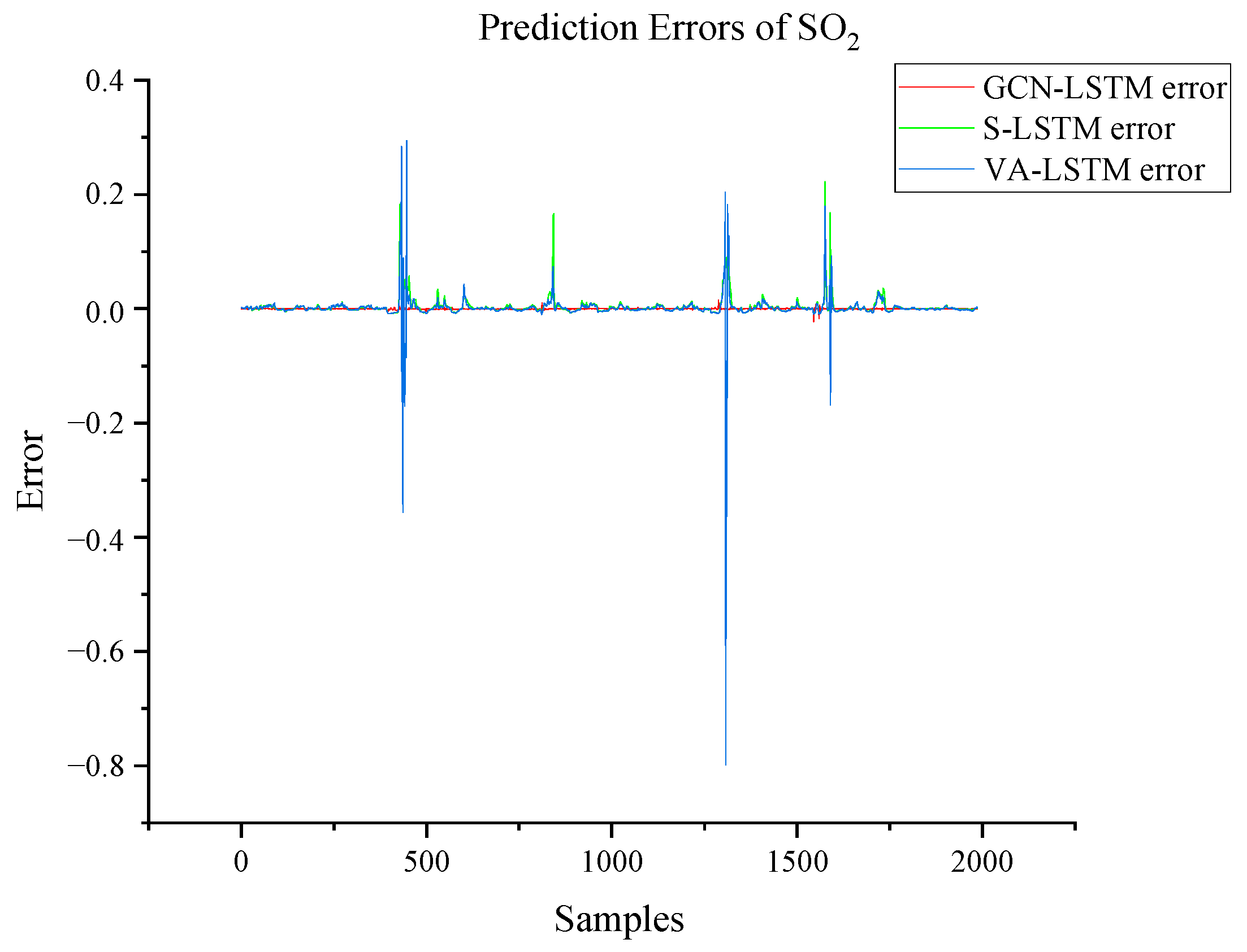
| SO2 | RMSE R2 | 0.0188 0.894 | 0.0236 0.833 | 0.0114 0.962 |
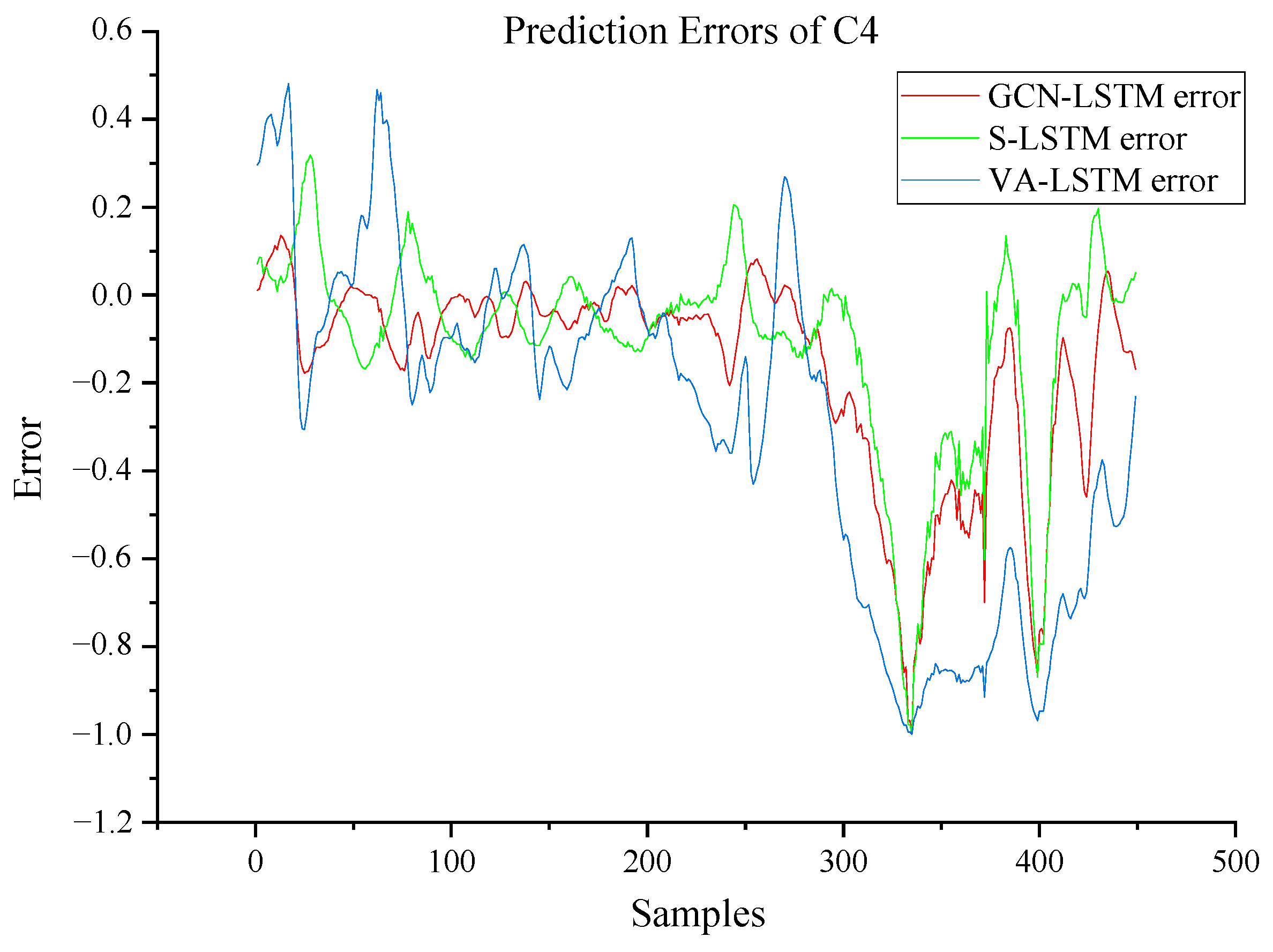
| C4 | RMSE R2 | 0.0404 0.962 | 0.1617 0.393 | 0.0357 0.971 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, S.; Li, W.; Wang, Y.; Zhang, B.; Ng, S.-K. A Soft Sensor Model for Predicting the Flow of a Hydraulic Pump Based on Graph Convolutional Network–Long Short-Term Memory. Actuators 2024, 13, 38. https://doi.org/10.3390/act13010038
Ji S, Li W, Wang Y, Zhang B, Ng S-K. A Soft Sensor Model for Predicting the Flow of a Hydraulic Pump Based on Graph Convolutional Network–Long Short-Term Memory. Actuators. 2024; 13(1):38. https://doi.org/10.3390/act13010038
Chicago/Turabian StyleJi, Shengfei, Wei Li, Yong Wang, Bo Zhang, and See-Kiong Ng. 2024. "A Soft Sensor Model for Predicting the Flow of a Hydraulic Pump Based on Graph Convolutional Network–Long Short-Term Memory" Actuators 13, no. 1: 38. https://doi.org/10.3390/act13010038
APA StyleJi, S., Li, W., Wang, Y., Zhang, B., & Ng, S.-K. (2024). A Soft Sensor Model for Predicting the Flow of a Hydraulic Pump Based on Graph Convolutional Network–Long Short-Term Memory. Actuators, 13(1), 38. https://doi.org/10.3390/act13010038






