Design, Manufacturing, and Open-Loop Control of a Soft Pneumatic Arm
Abstract
1. Introduction
2. Related Works
2.1. Pneumatic Actuation
2.2. Pneumatic Arms
2.3. Control of Soft Robots
3. PAUL: Design and Manufacturing
3.1. Robot Design
- The resulting robot must consist of three independently actuated segments, each with three degrees of freedom.
- The actuation of the segments that make up the robot must be pneumatic.
- The segments must be made of flexible silicone.
- These segments must allow easy assembly and disassembly as well as a modular design.
- The pneumatic tubes must be completely embedded in the body of the robot to avoid breakage and to allow more complex movements.
3.2. Material Selection
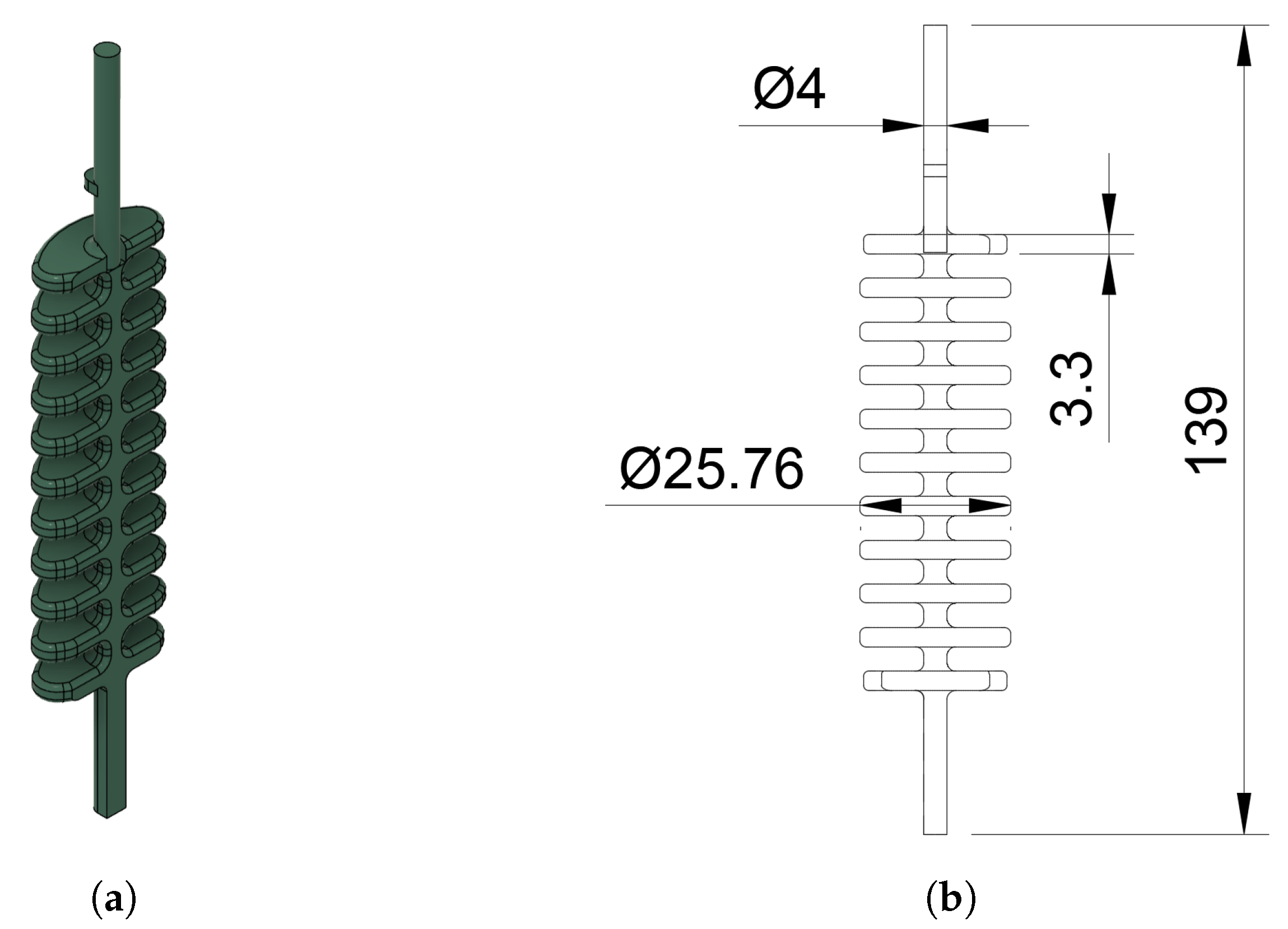
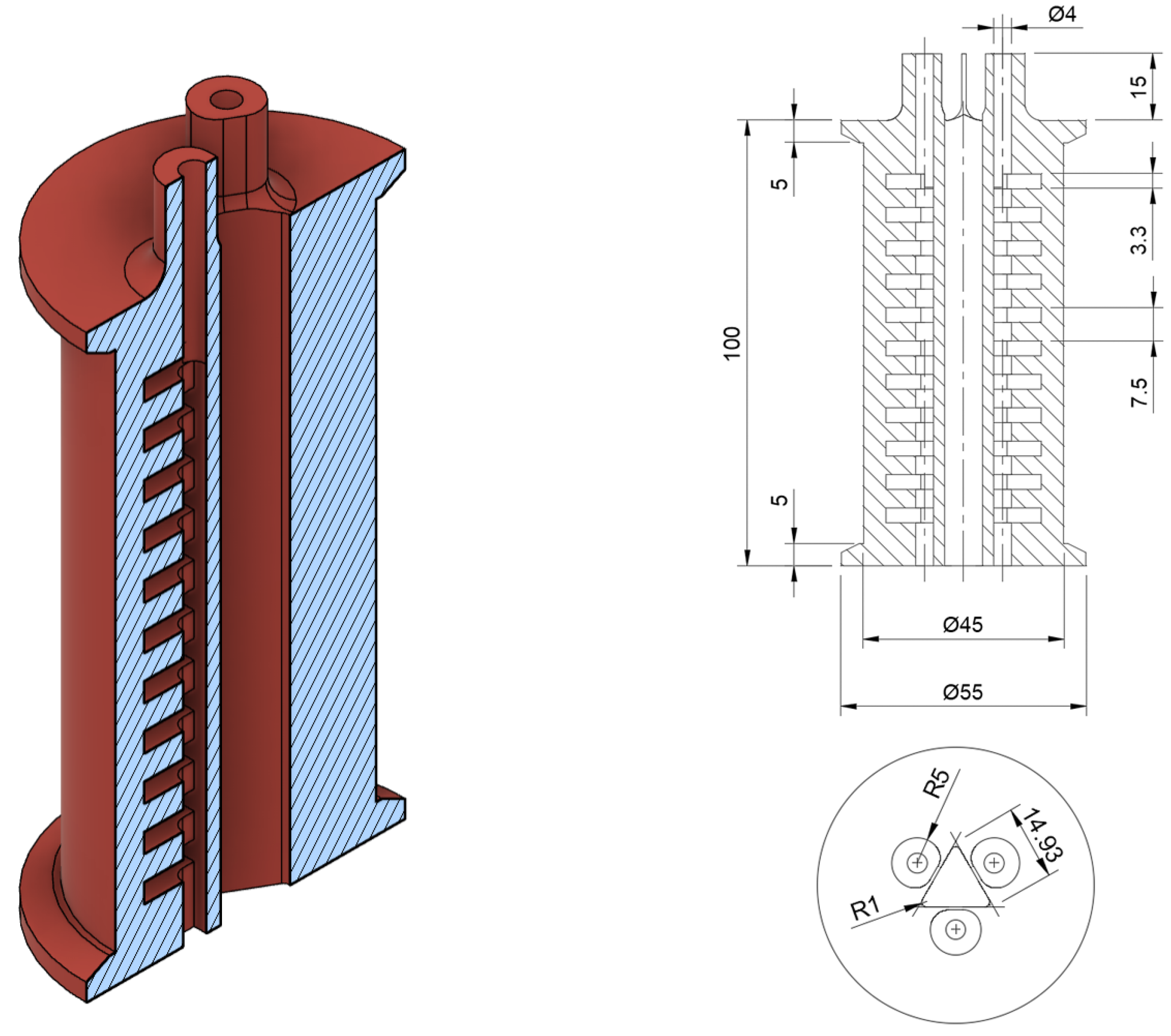
3.3. Manufacturing
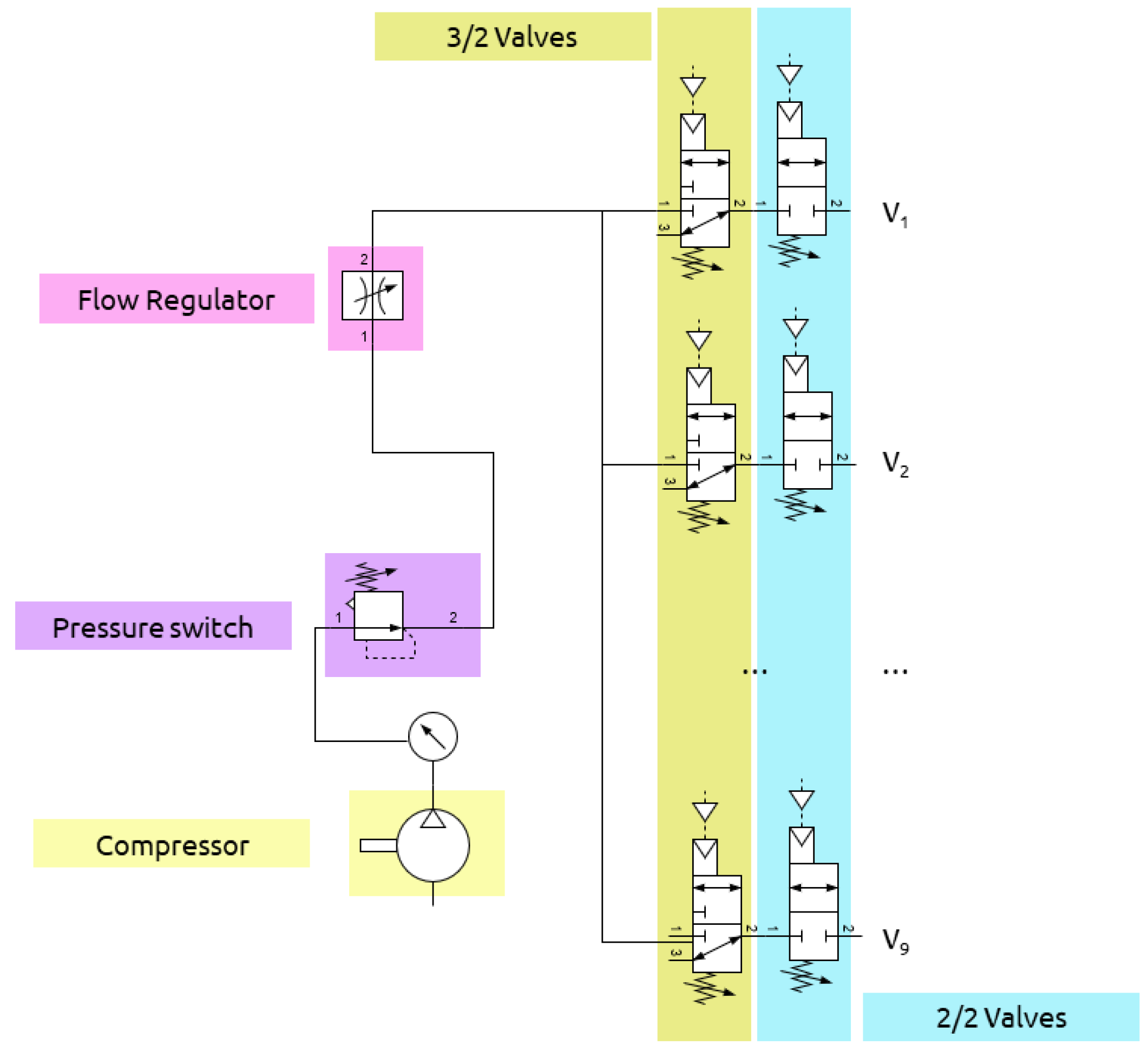
3.4. Actuation Bank
4. Data Acquisition and Open-Loop Control
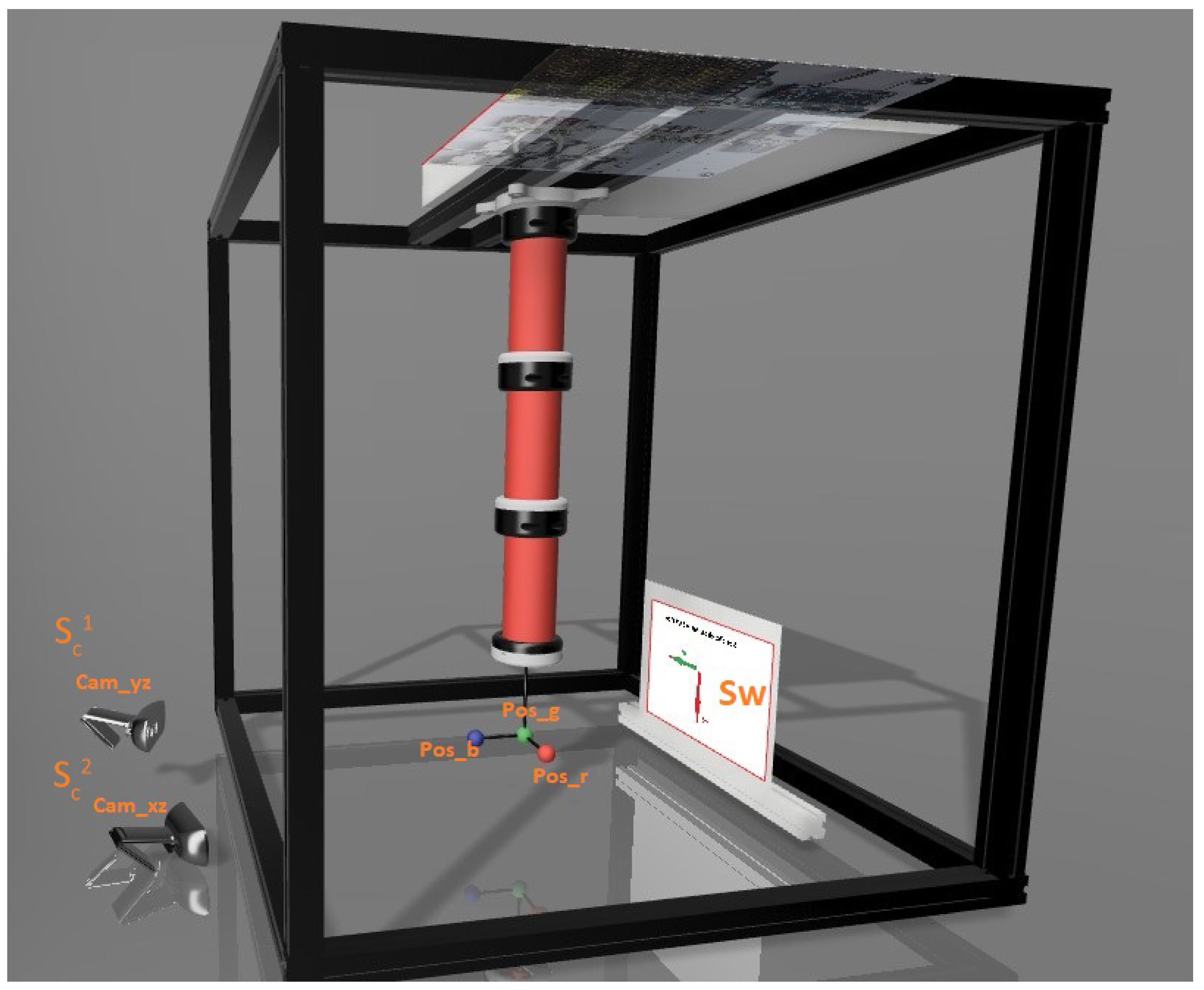
4.1. Hardware Setup
4.2. Vision Capture System
- corresponds to the depth of the camera (the distance from camera to the detected sphere), which is unknown.
- denotes the camera intrinsic parameters matrix, on which the focal lengths ( and ) and offsets ( and ) are reflected. These parameters are specific to each camera. In order to obtain them, it is necessary to perform some kind of intrinsic calibration the first time the camera is used. In this case, we have used the default calibration in Matlab, which consists of taking several pictures of the chessboard in Figure 11a at different angles and then calculating the distortion in each one of them. Latest null column has been inserted in the matrix to fit with the dimensions of .
- contains the rotation matrix () and the translation vector () from the real-world system to the camera system. As this matrix depends both on the position of the coordinate origin and on the position of the camera, which can easily be moved due to accidental slippage, it is necessary to recalibrate it at the beginning of each working session. For this purpose, the extrinsic calibration protocol, also available by default in Matlab, is used, and the grid in Figure 11a, whose lower-left corner is taken as the origin of the real-world reference system. From the dimensions of the squares, the translation and rotation with respect to their reference frame can be estimated. Subsequently, in the first measurement, the green sphere is taken as the origin of the real-world reference frame.
4.3. Dataset Generation: Table-Based Models
4.4. Open-Loop Control
5. Results
5.1. Final PAUL Version
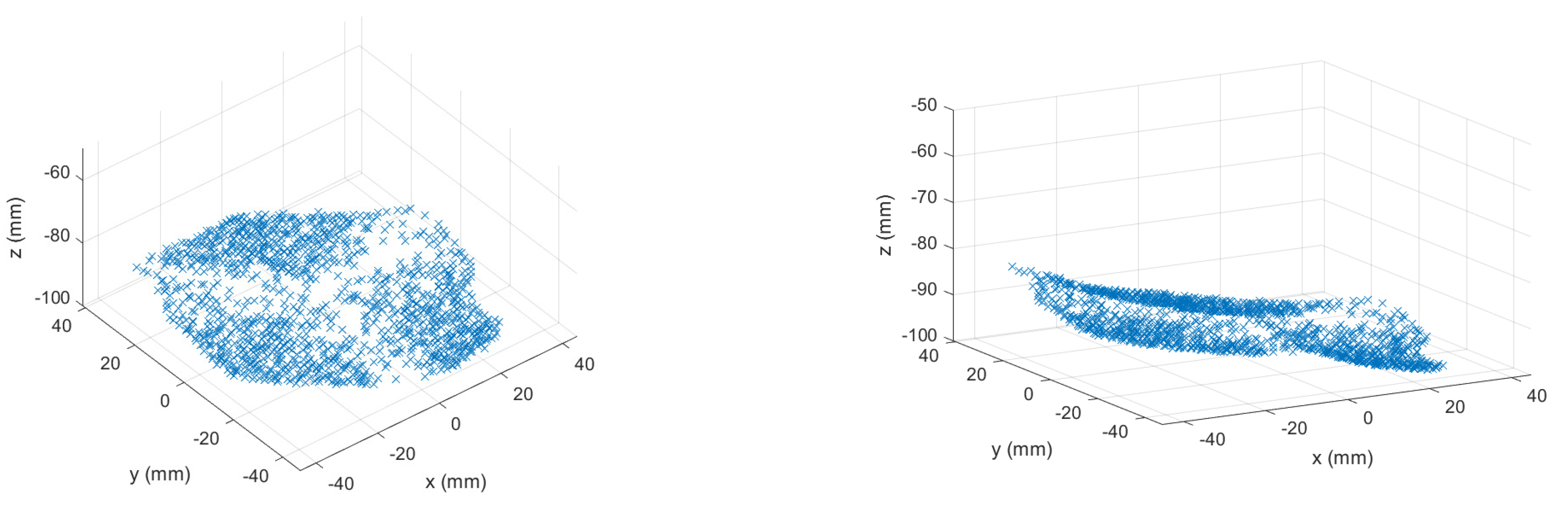
5.2. Workspace Analysis
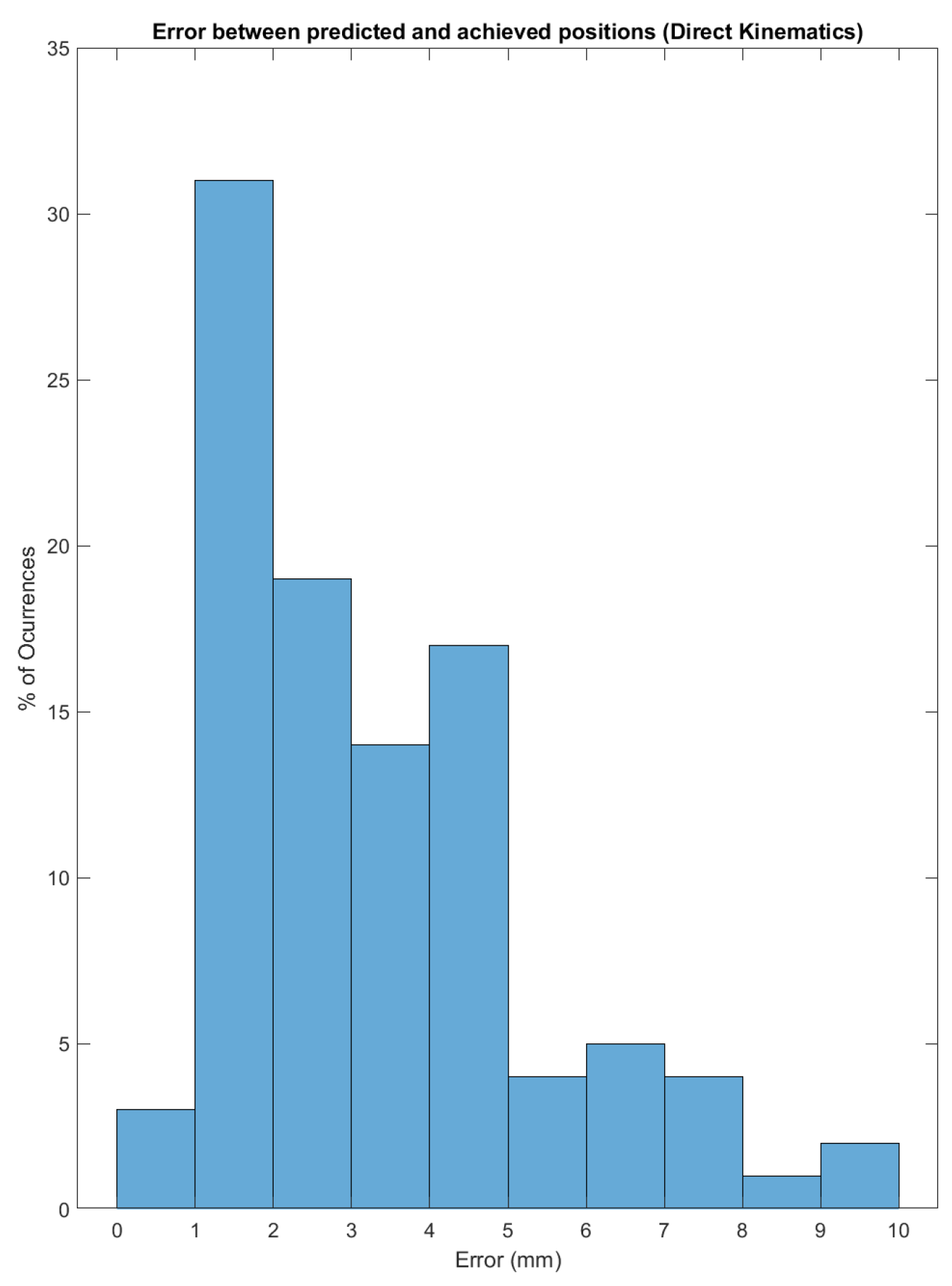
5.3. Performance of the Table-Based Models
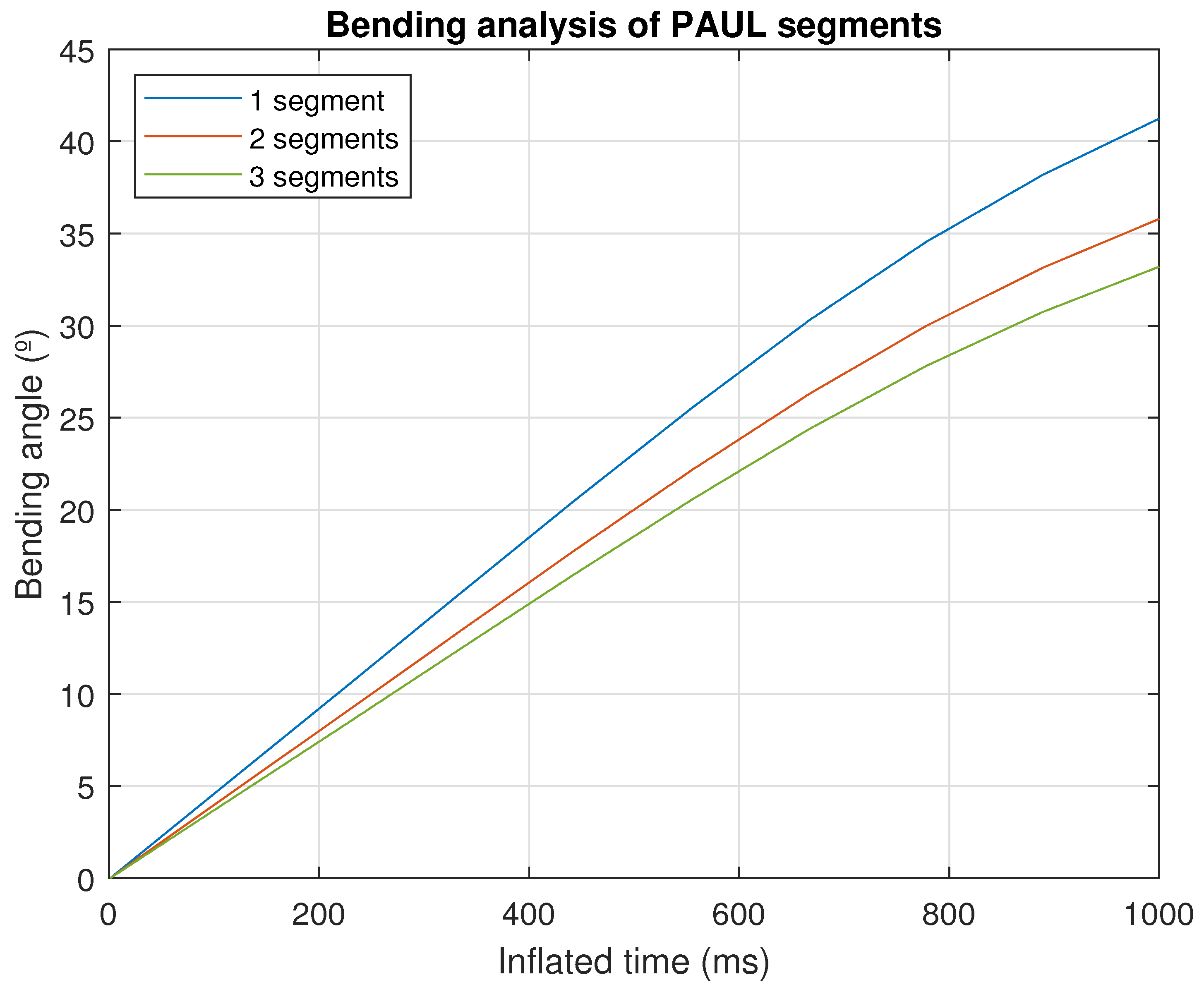
5.4. Bending Experiments
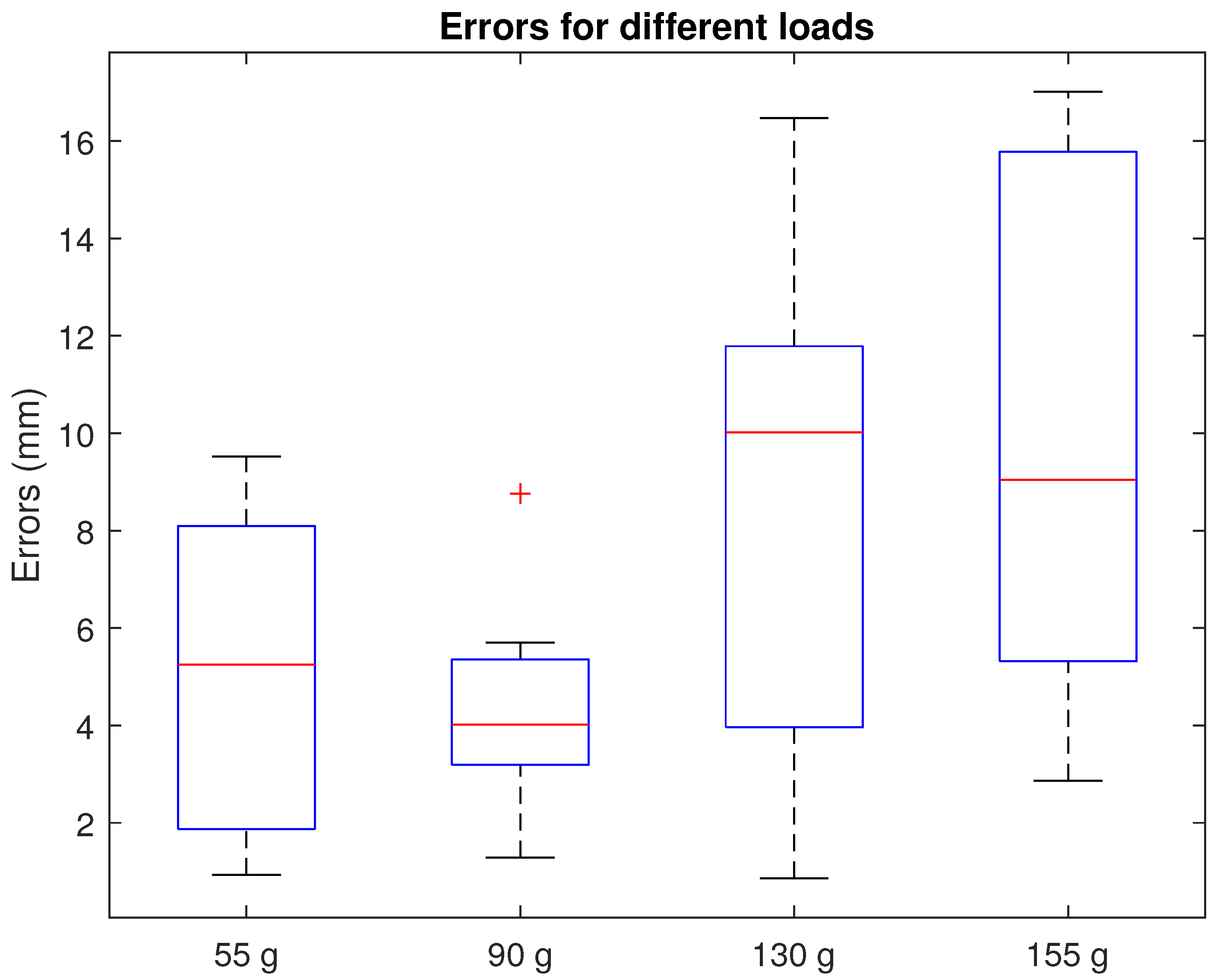
5.5. Weight Carrying Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOF | Degrees of Freedom |
| EAP | Electroactive Polymer |
| FEM | Finite Elements Method |
| FFNN | Feedforward Neural Network |
| HPN | Honeycomb Pneumatic Network |
| ML | Machine Learning |
| MSER | Maximally Stable External Regions |
| PAM | Pneumatic Artificial Muscle |
| PAUL | Pneumatic Articulated Ultrasoft Limb |
| PCC | Piecewise Constant Curvature |
| SMA | Shape Memory Alloys |
| TCA | Twisted and Coiled Actuators |
Appendix A. Conducted Experiments
References
- Manti, M.; Pratesi, A.; Falotico, E.; Cianchetti, M.; Laschi, C. Soft assistive robot for personal care of elderly people. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; pp. 833–838. [Google Scholar] [CrossRef]
- Carrasco Martínez, S.; Gamboa Montero, J.J.; Maroto Gómez, M.; Alonso Martín, F.; Salichs, M.A. Applying psychological and social strategies to increase engagement in human-robot interaction. Rev. Iberoam. Autom. Inform. Ind. 2023, 20, 199–212. [Google Scholar] [CrossRef]
- Paternò, L.; Lorenzon, L. Soft robotics in wearable and implantable medical applications: Translational challenges and future outlooks. Front. Robot. AI 2023, 10, 1075634. [Google Scholar] [CrossRef]
- Huang, H.; Tang, S.; Chai, W.; Sun, F.; Wu, D.; Miao, S.; Zhong, D.; Hou, H.; Dong, M. MCSG: A morphology configurable soft gripper with self-adaption modular composite finger. IEEE Trans. Ind. Electron. 2023, 71, 708–717. [Google Scholar] [CrossRef]
- Holsten, F.; Darkner, S.; Engell-Nørregård, M.P.; Erleben, K. Data Driven Inverse Kinematics of Soft Robots using Local Models. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montréal, QC, Canada, 20–24 May 2019; pp. 6251–6257. [Google Scholar] [CrossRef]
- Continelli, N.A.; Nagua, L.F.; Monje, C.A.; Balaguer, C. Modeling of a soft robotic neck using machine learning techniques. Rev. Iberoam. Autom. Inform. Ind. 2023, 20, 282–292. [Google Scholar] [CrossRef]
- Kalinsky, T.; Drotman, D.; Shih, B.; Aronoof-Spencer, E. Differential pressure control of 3D printed soft fluidic actuators. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Maksimkin, A.V.; Dayyoub, T.; Telyshev, D.V.; Gerasimenko, A.Y. Electroactive Polymer-Based Composites for Artificial Muscle-like Actuators: A Review. Nanomaterials 2022, 12, 2272. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Tian, C.; Mao, L.; Meng, X.; Shen, X.; Hao, B.; Wang, X.; Xie, H.; Zhang, L. Reconfigurable Magnetic Slime Robot: Deformation, Adaptability, and Multifunction. Adv. Funct. Mater. 2022, 32, 2112508. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Z.; Wu, J.; Zhang, Y.; Su, C.Y. Modelling and model-based tracking control of soft twisted and coiled actuators. Control Eng. Pract. 2023, 141, 105722. [Google Scholar] [CrossRef]
- Cruz Ulloa, C.; Terrile, S.; Barrientos, A. Soft underwater robot actuated by shape-memory alloys “jellyrobcib” for path tracking through fuzzy visual control. Appl. Sci. 2020, 10, 7160. [Google Scholar] [CrossRef]
- Terrile, S.; López, A.; Barrientos, A. Use of Finite Elements in the Training of a Neural Network for the Modeling of a Soft Robot. Biomimetics 2023, 8, 56. [Google Scholar] [CrossRef] [PubMed]
- Seleem, I.A.; El-Hussieny, H.; Ishii, H. Recent Developments of Actuation Mechanisms for Continuum Robots: A Review. Int. J. Control. Autom. Syst. 2023, 21, 1592–1609. [Google Scholar] [CrossRef] [PubMed]
- Terrile, S.; Argüelles, M.; Barrientos, A. Comparison of Different Technologies for Soft Robotics Grippers. Sensors 2021, 21, 3253. [Google Scholar] [CrossRef]
- Li, X.A.; Yue, H.; Yang, D.; Sun, K.; Liu, H. A Large-Scale Inflatable Robotic Arm Toward Inspecting Sensitive Environments: Design and Performance Evaluation. IEEE Trans. Ind. Electron. 2023, 70, 12486–12499. [Google Scholar] [CrossRef]
- Coad, M.M.; Blumenschein, L.H.; Cutler, S.; Zepeda, J.A.R.; Naclerio, N.D.; El-Hussieny, H.; Mehmood, U.; Ryu, J.H.; Hawkes, E.W.; Okamura, A.M. Vine Robots: Design, Teleoperation, and Deployment for Navigation and Exploration. IEEE Robot. Autom. Mag. 2020, 27, 120–132. [Google Scholar] [CrossRef]
- Martinez-Sanchez, D.E.; Sandoval-Castro, X.Y.; Cruz-Santos, N.; Castillo-Castaneda, E.; Ruiz-Torres, M.F.; Laribi, M.A. Soft Robot for Inspection Tasks Inspired on Annelids to Obtain Peristaltic Locomotion. Machines 2023, 11, 779. [Google Scholar] [CrossRef]
- Eslami, M.; Pirmoradian, M.; Mokhtarian, A.; Baghaei, S. Design and manufacture of a soft robot with dual-interaction in virtual reality. Heliyon 2023, 9, e19997. [Google Scholar] [CrossRef]
- Zhang, C.; Li, M.; Chen, Y.; Yang, Z.; He, B.; Li, X.; Xie, J.; Xu, G. An Anthropomorphic Robotic Hand With a Soft-Rigid Hybrid Structure and Positive-Negative Pneumatic Actuation. IEEE Robot. Autom. Lett. 2023, 8, 4346–4353. [Google Scholar] [CrossRef]
- Cerrillo, D.; Barrientos, A.; Del Cerro, J. Kinematic Modelling for Hyper-Redundant Robots—A Structured Guide. Mathematics 2022, 10, 2891. [Google Scholar] [CrossRef]
- Stilli, A.; Wurdemann, H.A.; Althoefer, K. Shrinkable, stiffness-controllable soft manipulator based on a bio-inspired antagonistic actuation principle. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2476–2481. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Li, Y.; Chen, M.Z.; Wei, Y. Bioinspired robotic fingers based on pneumatic actuator and 3D printing of smart material. Soft Robot. 2017, 4, 147–162. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. Pneumatic Artificial Muscles: Actuators for robotics and automation. Eur. J. Mech. Environ. Eng. 2002, 47, 10–21. [Google Scholar]
- Hawkes, E.W.; Christensen, D.L.; Okamura, A.M. Design and implementation of a 300% strain soft artificial muscle. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 4022–4029. [Google Scholar] [CrossRef]
- Sun, W.; Akashi, N.; Kuniyoshi, Y.; Nakajima, K. Physics-Informed Recurrent Neural Networks for Soft Pneumatic Actuators. IEEE Robot. Autom. Lett. 2022, 7, 6862–6869. [Google Scholar] [CrossRef]
- Liu, G.; Sun, N.; Yang, T.; Fang, Y. Reinforcement Learning-Based Prescribed Performance Motion Control of Pneumatic Muscle Actuated Robotic Arms With Measurement Noises. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 1801–1812. [Google Scholar] [CrossRef]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.; Whitesides, G. Pneumatic Networks for Soft Robotics that Actuate Rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Batsuren, K.; Yun, D. Soft robotic gripper with chambered fingers for performing in-hand manipulation. Appl. Sci. 2019, 9, 2967. [Google Scholar] [CrossRef]
- Sierra, E.M.; Ordoñez-Ávila, J.L. Mathematical Modeling of a Multi-Chamber Pneumatic Soft Actuator. Actuators 2022, 11, 221. [Google Scholar] [CrossRef]
- Terrile, S.; Miguelañez, J.; Barrientos, A. A Soft Haptic Glove Actuated with Shape Memory Alloy and Flexible Stretch Sensors. Sensors 2021, 21, 5278. [Google Scholar] [CrossRef]
- Shiva, A.; Stilli, A.; Noh, Y.; Faragasso, A.; Falco, I.D.; Gerboni, G.; Cianchetti, M.; Menciassi, A.; Althoefer, K.; Wurdemann, H.A. Tendon-Based Stiffening for a Pneumatically Actuated Soft Manipulator. IEEE Robot. Autom. Lett. 2016, 1, 632–637. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, J. Modeling, Characterization, and Application of Soft Bellows-Type Pneumatic Actuators for Bionic Locomotion. Acta Mech. Solida Sin. 2023, 36, 1–12. [Google Scholar] [CrossRef]
- Deimel, R.; Brock, O. A Novel Type of Compliant, Underactuated Robotic Hand for Dexterous Grasping. Int. J. Robot. Res. 2014, 35, 161–185. [Google Scholar] [CrossRef]
- Babu, S.P.; Sadeghi, A.; Mondini, A.; Mazzolai, B. Antagonistic pneumatic actuators with variable stiffness for soft robotic applications. In Proceedings of the RoboSoft 2019—2019 IEEE International Conference on Soft Robotics, Seoul, Republic of Korea, 14–18 April 2019; pp. 283–288. [Google Scholar] [CrossRef]
- Heung, K.H.; Li, H.; Wong, T.W.; Ng, S.S. Assistive robotic hand with bi-directional soft actuator for hand impaired patients. Front. Bioeng. Biotechnol. 2023, 11, 1188996. [Google Scholar] [CrossRef]
- Brown, E.; Rodenberg, N.; Amend, J.; Mozeika, A.; Steltz, E.; Zakin, M.R.; Lipson, H.; Jaeger, H.M. Universal robotic gripper based on the jamming of granular material. Proc. Natl. Acad. Sci. USA 2010, 107, 18809–18814. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Kan, Z.; Zeng, J.; Wang, M.Y. Hybrid Jamming for Bioinspired Soft Robotic Fingers. Soft Robot. 2020, 7, 292–308. [Google Scholar] [CrossRef]
- Yang, H.; Yuan, L.; Yao, X.F.; Fang, D.N. Piezoresistive response of graphene rubber composites considering the tunneling effect. J. Mech. Phys. Solids 2020, 139, 103943. [Google Scholar] [CrossRef]
- Tondu, B.; Ippolito, S.; Guiochet, J.; Daidie, A. A Seven-degrees-of-freedom robot-arm driven by pneumatic artificial muscles for humanoid robots. Int. J. Robot. Res. 2005, 24, 257–274. [Google Scholar] [CrossRef]
- Ohta, P.; Valle, L.; King, J.; Low, K.; Yi, J.; Atkeson, C.G.; Park, Y.L. Design of a Lightweight Soft Robotic Arm Using Pneumatic Artificial Muscles and Inflatable Sleeves. Soft Robot. 2018, 5, 204–215. [Google Scholar] [CrossRef]
- Oh, N.; Lee, J.G.; Rodrigue, H. Torsional Pneumatic Actuator Based on Pre-Twisted Pneumatic Tubes for Soft Robotic Manipulators. IEEE/ASME Trans. Mechatron. 2023, 28, 3191–3201. [Google Scholar] [CrossRef]
- Oh, N.; Rodrigue, H. Toward the Development of Large-Scale Inflatable Robotic Arms Using Hot Air Welding. Soft Robot. 2023, 10, 88–96. [Google Scholar] [CrossRef]
- Park, M.J.; Kim, W.; Yu, S.Y.; Cho, J.; Kang, W.; Byun, J.; Jeong, U.; Cho, K.J. Deployable Soft Origami Modular Robotic Arm With Variable Stiffness Using Facet Buckling. IEEE Robot. Autom. Lett. 2023, 8, 864–871. [Google Scholar] [CrossRef]
- Alessi, C.; Falotico, E.; Lucantonio, A. Ablation Study of a Dynamic Model for a 3D-Printed Pneumatic Soft Robotic Arm. IEEE Access 2023, 11, 37840–37853. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, Z.; Liu, X.; Chen, X.; Jin, Y.; You, X.; Chen, X. A two-level approach for solving the inverse kinematics of an extensible soft arm considering viscoelastic behavior. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 6127–6133. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, Z.; Jin, Y.; Chen, X.; Li, P.; Gan, Y.; Lin, S.; Chen, X. Design, Control, and Applications of a Soft Robotic Arm. arXiv 2019, arXiv:2107.05842v1. [Google Scholar]
- Thuruthel, T.G.; Falotico, E.; Renda, F.; Laschi, C. Model-Based Reinforcement Learning for Closed-Loop Dynamic Control of Soft Robotic Manipulators. IEEE Trans. Robot. 2019, 35, 127–134. [Google Scholar] [CrossRef]
- Cianchetti, M.; Ranzani, T.; Gerboni, G.; De Falco, I.; Laschi, C.; Menciassi, A. STIFF-FLOP surgical manipulator: Mechanical design and experimental characterization of the single module. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3576–3581. [Google Scholar] [CrossRef]
- Toshimitsu, Y.; Wong, K.W.; Buchner, T.; Katzschmann, R. SoPrA: Fabrication and Dynamical Modeling of a Scalable Soft Continuum Robotic Arm with Integrated Proprioceptive Sensing. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021. [Google Scholar]
- Katzschmann, R.K.; Santina, C.D.; Toshimitsu, Y.; Bicchi, A.; Rus, D. Dynamic motion control of multi-segment soft robots using piecewise constant curvature matched with an augmented rigid body model. In Proceedings of the RoboSoft 2019—2019 IEEE International Conference on Soft Robotics, Seoul, Republic of Korea, 14–18 April 2019; pp. 454–461. [Google Scholar] [CrossRef]
- Borja, P.; Dabiri, A.; Santina, C.D. Energy-based shape regulation of soft robots with unactuated dynamics dominated by elasticity. In Proceedings of the 2022 IEEE 5th International Conference on Soft Robotics, RoboSoft 2022, Edinburgh, UK, 4–8 April 2022; pp. 396–402. [Google Scholar] [CrossRef]
- Schegg, P.; Duriez, C. Review on generic methods for mechanical modeling, simulation and control of soft robots. PLoS ONE 2022, 17, e02510594. [Google Scholar] [CrossRef] [PubMed]
- Della Santina, C. The Soft Inverted Pendulum with Affine Curvature. In Proceedings of the IEEE Conference on Decision and Control, Jeju, Republic of Korea, 14–18 December 2020; pp. 4135–4142. [Google Scholar] [CrossRef]
- Coevoet, E.; Escande, A.; Duriez, C. Soft robots locomotion and manipulation control using FEM simulation and quadratic programming. In Proceedings of the RoboSoft 2019—2019 IEEE International Conference on Soft Robotics, Seoul, Republic of Korea, 14–18 April 2019; pp. 739–745. [Google Scholar] [CrossRef]
- Ding, L.; Niu, L.; Su, Y.; Yang, H.; Liu, G.; Gao, H.; Deng, Z. Dynamic Finite Element Modeling and Simulation of Soft Robots. Chin. J. Mech. Eng. Engl. Ed. 2022, 35, 24. [Google Scholar] [CrossRef]
- Cangan, B.G.; Navarro, S.E.; Yang, B.; Zhang, Y.; Duriez, C.; Katzschmann, R.K. Model-Based Disturbance Estimation for a Fiber-Reinforced Soft Manipulator using Orientation Sensing. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Kyoto, Japan, 23–27 October 2022; pp. 9424–9430. [Google Scholar] [CrossRef]
- Dubied, M.; Michelis, M.Y.; Spielberg, A.; Katzschmann, R.K. Sim-to-Real for Soft Robots Using Differentiable FEM: Recipes for Meshing, Damping, and Actuation. IEEE Robot. Autom. Lett. 2022, 7, 5015–5022. [Google Scholar] [CrossRef]
- Baysal, C.V. An Inverse Dynamics-Based Control Approach for Compliant Control of Pneumatic Artificial Muscles. Actuators 2022, 11, 111. [Google Scholar] [CrossRef]
- Li, P.; Wang, G.; Jiang, H.; Jin, Y.; Gan, Y.; Chen, X.; Ji, J. A Q-learning Control Method for a Soft Robotic Arm Utilizing Training Data from a Rough Simulator. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics, ROBIO 2021, Sanya, China, 27–31 December 2021; pp. 839–845. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Hassan, T.; Falotico, E.; Ansari, Y.; Cianchetti, M.; Laschi, C. Closed loop control of a braided-structure continuum manipulator with hybrid actuation based on learning models. In Proceedings of the 2019 IEEE International Conference on Cyborg and Bionic Systems, CBS 2019, Munich, Germany, 18–20 September 2019; pp. 116–122. [Google Scholar] [CrossRef]
- Centurelli, A.; Arleo, L.; Rizzo, A.; Tolu, S.; Laschi, C.; Falotico, E. Closed-Loop Dynamic Control of a Soft Manipulator Using Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2022, 7, 4741–4748. [Google Scholar] [CrossRef]
- Fang, G.; Tian, Y.; Yang, Z.X.; Geraedts, J.M.; Wang, C.C. Efficient Jacobian-Based Inverse Kinematics With Sim-to-Real Transfer of Soft Robots by Learning. IEEE/ASME Trans. Mechatron. 2022, 27, 5296–5306. [Google Scholar] [CrossRef]
- Almanzor, E.; Ye, F.; Shi, J.; Thuruthel, T.G.; Wurdemann, H.A.; Iida, F. Static Shape Control of Soft Continuum Robots Using Deep Visual Inverse Kinematic Models. IEEE Trans. Robot. 2023, 39, 2973–2988. [Google Scholar] [CrossRef]
- Yip, M.C.; Camarillo, D.B. Model-less feedback control of continuum manipulators in constrained environments. IEEE Trans. Robot. 2014, 30, 880–889. [Google Scholar] [CrossRef]
- Bruder, D.; Gillespie, B.; David Remy, C.; Vasudevan, R. Modeling and Control of Soft Robots Using the Koopman Operator and Model Predictive Control. arXiv 2019, arXiv:1902.02827. [Google Scholar] [CrossRef]
- Yang, Y.S. Measurement of Dynamic Responses from Large Structural Tests by Analyzing Non-Synchronized Videos. Sensors 2019, 19, 3520. [Google Scholar] [CrossRef]
- Martin-Barrio, A.; Terrile, S.; Diaz-Carrasco, M.; del Cerro, J.; Barrientos, A. Modelling the Soft Robot Kyma Based on Real-Time Finite Element Method. Comput. Graph. Forum 2020, 39, 289–302. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Falotico, E.; Manti, M.; Laschi, C. Stable Open Loop Control of Soft Robotic Manipulators. IEEE Robot. Autom. Lett. 2018, 3, 1292–1298. [Google Scholar] [CrossRef]













| Parameter | Mould | Connectors |
|---|---|---|
| Layer Height | ||
| Infill | 5% | 14% |
| Number of Perimeters | 2 | 3 |
| Extrusion Temperature | 195 | 195 |
| Bed Temperature | 200 | 200 |
| Property | PlatSil FS10 | EasyPlat 0030 | TinSil 8015 |
|---|---|---|---|
| Type | Platinum | Platinum | Til |
| Shore Hardness | A13 | 00-30 | A15 |
| Curing Time | 12 | 4 | 24 |
| Viscosity | 3 | 12 | |
| Density | / | / | / |
| Dataset Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Number of Samples | 100 | 100 | 100 | 500 | 6 | 200 | 200 |
| Total Time (s) | 695 | 697 | 712 | 3884 | 38 | 1210 | 1199 |
| Time per Sample (s) | 6.95 | 6.97 | 7.13 | 7.77 | 6.47 | 6.05 | 6.00 |
| Reference | Actuation Type | Control Methodology | Robot Length | Error |
|---|---|---|---|---|
| [12] | SMA | FEM + FFNN | 240 | 4 |
| [67] | Tendon-driven | FEM | 1200 | 20 |
| [60] | Tendon-driven | Reinforcement Learning | 418 | |
| [45] (3 segment, open-loop) | Pneumatic (HPN) | FFNN | 630 | |
| [59] | Pneumatic (HPN) | Reinforcement Learning | 630 | 20 |
| [68] | Pneumatic (3D printed) | Reinforcement Learning | 400 | 22 |
| [56] | Pneumatic (STIFF-FLOP based) | FEM | 300 | |
| PAUL | Pneumatic (STIFF-FLOP based) | Table-Based | 390 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Samartín, J.F.; Rieker, A.; Barrientos, A. Design, Manufacturing, and Open-Loop Control of a Soft Pneumatic Arm. Actuators 2024, 13, 36. https://doi.org/10.3390/act13010036
García-Samartín JF, Rieker A, Barrientos A. Design, Manufacturing, and Open-Loop Control of a Soft Pneumatic Arm. Actuators. 2024; 13(1):36. https://doi.org/10.3390/act13010036
Chicago/Turabian StyleGarcía-Samartín, Jorge Francisco, Adrián Rieker, and Antonio Barrientos. 2024. "Design, Manufacturing, and Open-Loop Control of a Soft Pneumatic Arm" Actuators 13, no. 1: 36. https://doi.org/10.3390/act13010036
APA StyleGarcía-Samartín, J. F., Rieker, A., & Barrientos, A. (2024). Design, Manufacturing, and Open-Loop Control of a Soft Pneumatic Arm. Actuators, 13(1), 36. https://doi.org/10.3390/act13010036







