Design and Analysis of Brake-by-Wire Unit Based on Direct Drive Pump–Valve Cooperative
Abstract
:1. Introduction
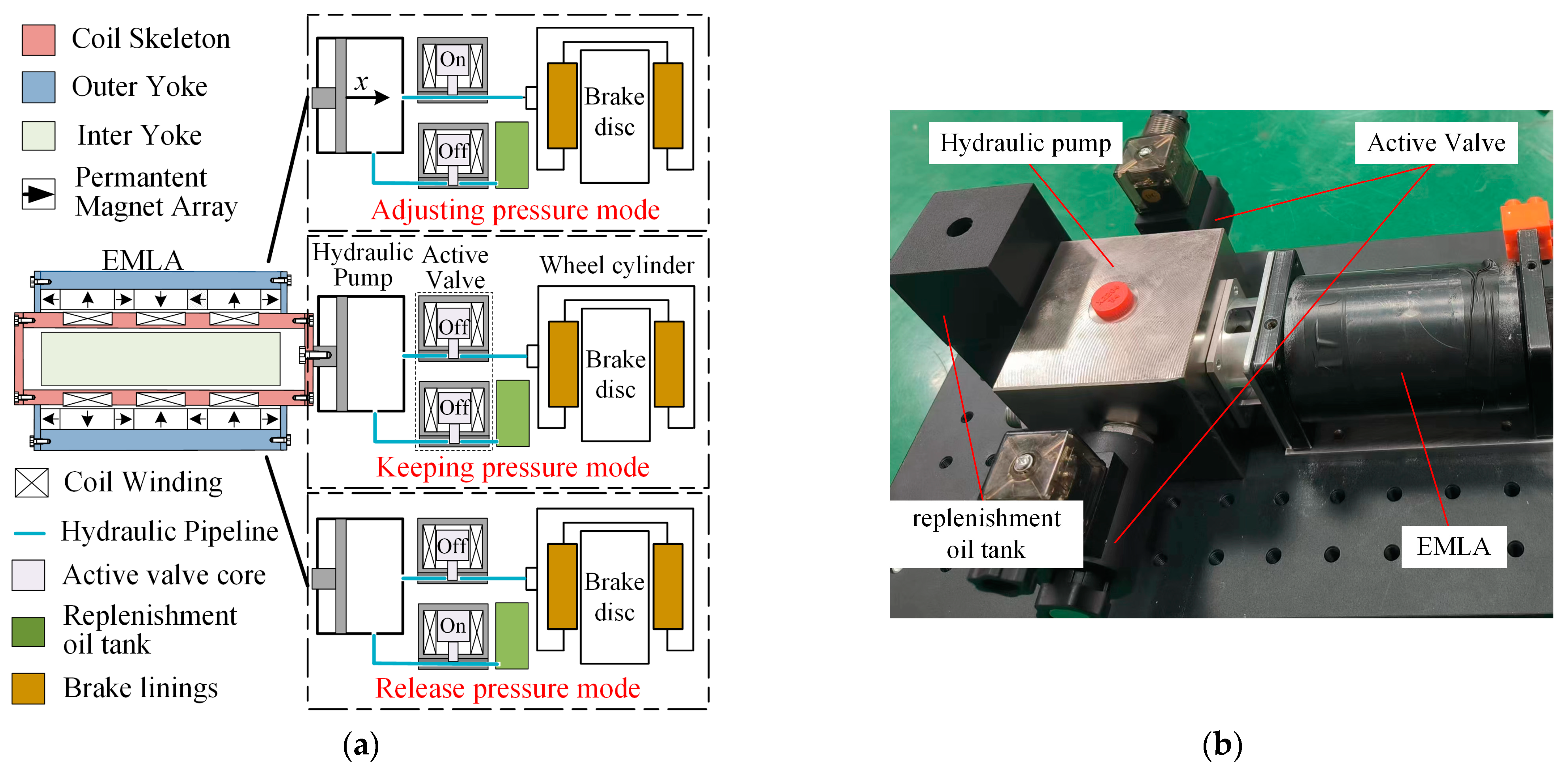
2. System Scheme and Principle
3. Parameter Matching Design
4. System Modeling
4.1. Modeling of the EMLA
4.2. Hydraulic System Modeling
4.3. Quarter-Car Dynamics Model Establishment
4.4. Co-Simulation Model Construction
5. Results and Analysis
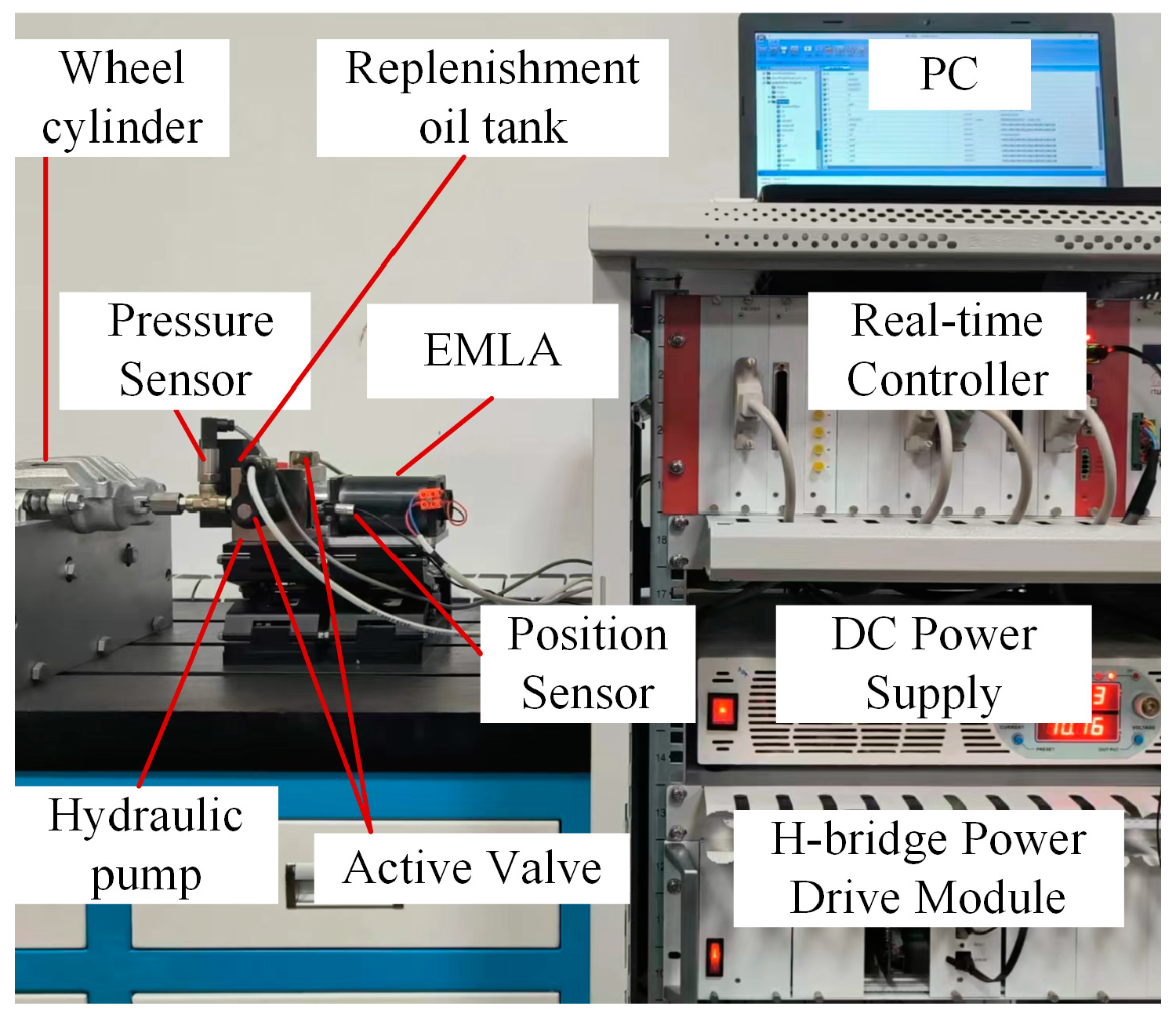
5.1. The Experimental Platform
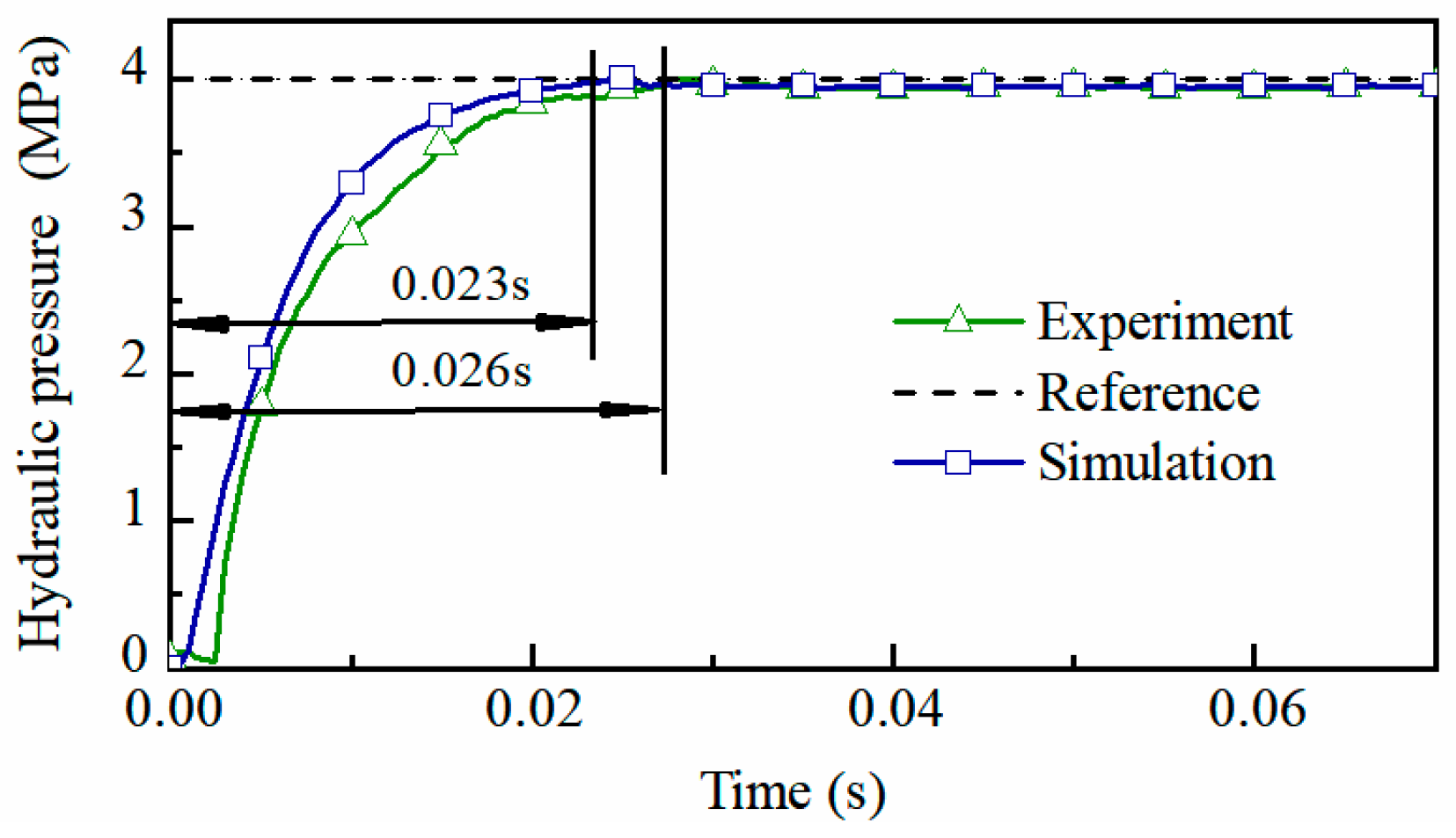
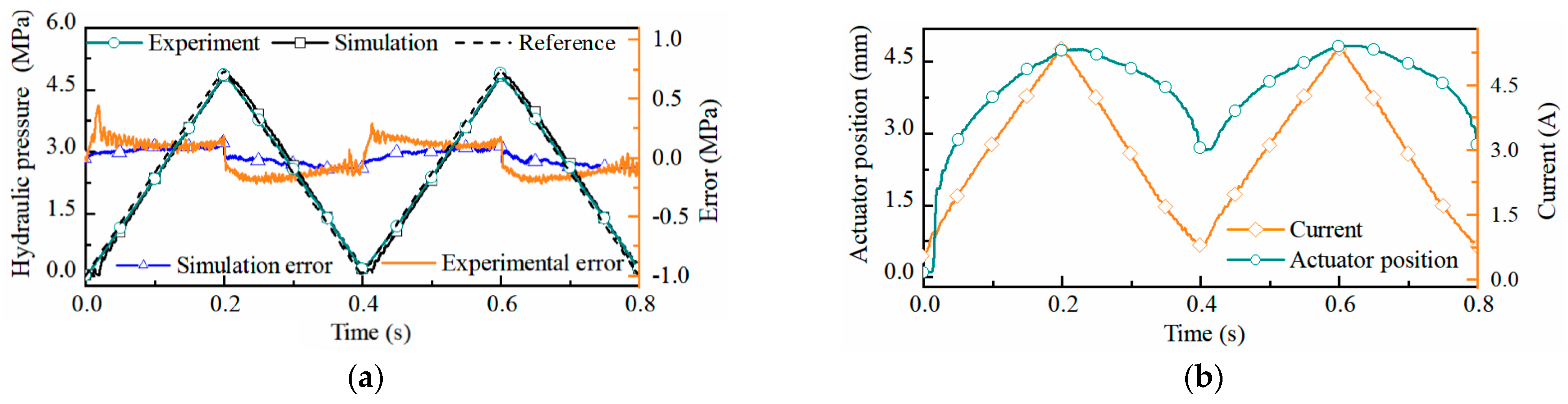
5.2. Analysis of Hydraulic Pressure Response Performance
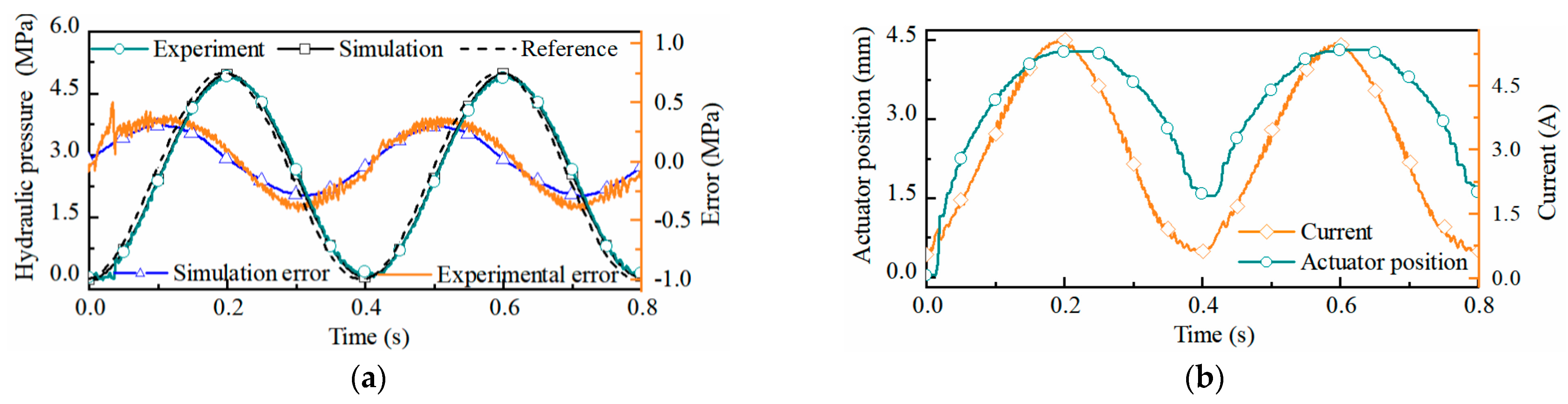
5.3. Analysis of Hydraulic Pressure Tracking Performance
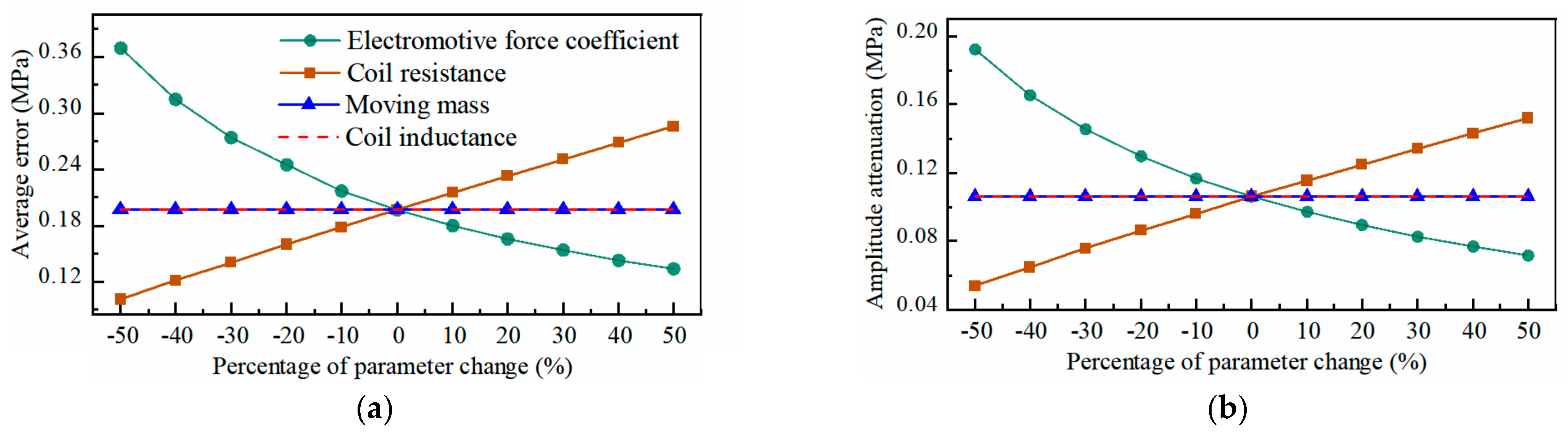
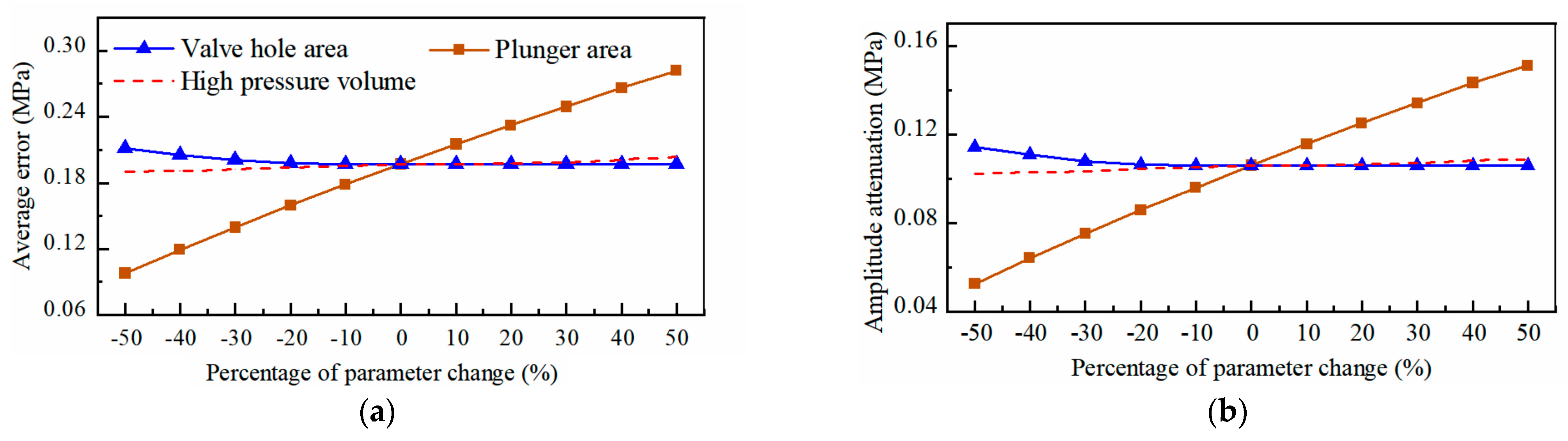
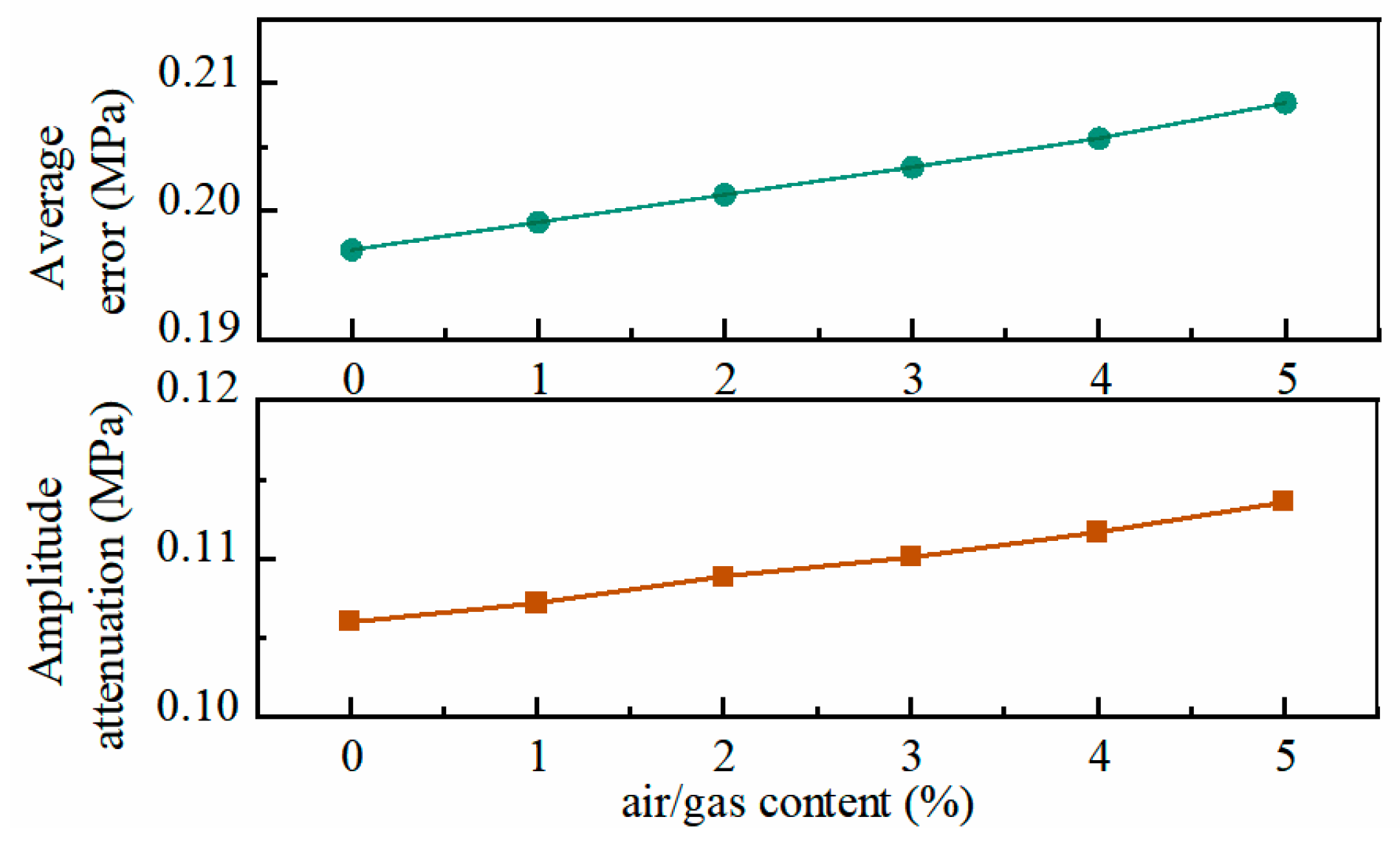
5.4. Analysis of the Impact of Parameters on System Performance
5.4.1. Actuator Parameter
5.4.2. Hydraulic System Parameter
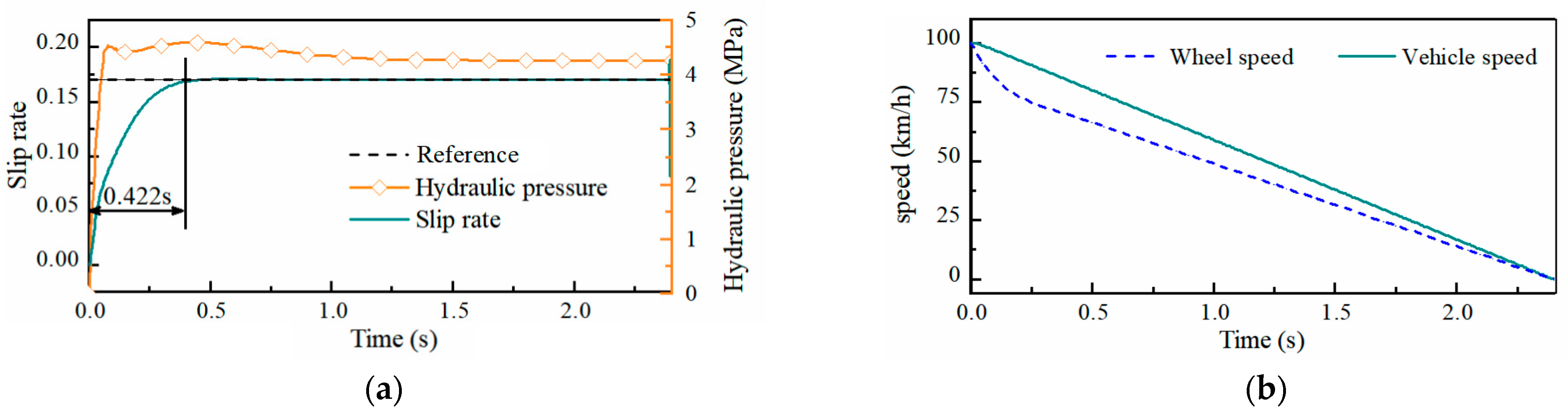
5.5. ABS Performance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ji, Y.; Zhang, J.; He, C.; Ma, R.; Hu, X. Constraint performance pressure tracking control with asymmetric continuous friction compensation for booster based brake-by-wire system. Mech. Syst. Signal Process. 2022, 174, 109083. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhou, L.; Zhang, J.; Zhu, Q.; Hedrick, J.K. Distributed and self-adaptive vehicle speed estimation in the composite braking case for four-wheel drive hybrid electric car. Veh. Syst. Dyn. 2017, 55, 750–773. [Google Scholar] [CrossRef]
- Mingde, G.; Hailong, W. Full power hydraulic brake system based on double pipelines for heavy vehicles. Chin. J. Mech. Eng. 2011, 24, 790. [Google Scholar]
- Todeschini, F.; Corno, M.; Panzani, G.; Fiorenti, S.; Savaresi, S.M. Adaptive cascade control of a brake-by-wire actuator for sport motorcycles. IEEE/ASME Trans. Mechatron. 2014, 20, 1310–1319. [Google Scholar] [CrossRef]
- Tang, Q.; Yang, Y.; Luo, C.; Yang, Z.; Fu, C. A novel electro-hydraulic compound braking system coordinated control strategy for a four-wheel-drive pure electric vehicle driven by dual motors. Energy 2022, 241, 122750. [Google Scholar] [CrossRef]
- Xiong, L.; Han, W.; Yu, Z. Adaptive sliding mode pressure control for an electro-hydraulic brake system via desired-state and integral-antiwindup compensation. Mechatronics 2020, 68, 102359. [Google Scholar] [CrossRef]
- Han, W.; Xiong, L.; Yu, Z. Braking pressure control in electro-hydraulic brake system based on pressure estimation with nonlinearities and uncertainties. Mech. Syst. Signal Process. 2019, 131, 703–727. [Google Scholar] [CrossRef]
- Todeschini, F.; Formentin, S.; Panzani, G.; Corno, M.; Savaresi, S.M.; Zaccarian, L. Nonlinear pressure control for BBW systems via dead-zone and antiwindup compensation. IEEE Trans. Control Syst. Technol. 2015, 24, 1419–1431. [Google Scholar] [CrossRef]
- Pei, X.; Pan, H.; Chen, Z.; Guo, X.; Yang, B. Coordinated control strategy of electro-hydraulic braking for energy regeneration. Control Eng. Pract. 2020, 96, 104324. [Google Scholar] [CrossRef]
- Savitski, D.; Ivanov, V.; Schleinin, D.; Augsburg, K.; Pütz, T.; Lee, C.F. Advanced control functions of decoupled electro-hydraulic brake system. In Proceedings of the 2016 IEEE 14th International Workshop on Advanced Motion Control, Auckland, New Zealand, 22–24 April 2016. [Google Scholar]
- Oshima, T.; Fujiki, N.; Nakao, S.; Kimura, T.; Ohtani, Y.; Ueno, K. Development of an electrically driven intelligent brake system. SAE Int. J. Passeng. Cars-Mech. Syst. 2011, 4, 399–405. [Google Scholar] [CrossRef]
- Li, L.; Zhang, T.; Sun, B.; Wu, K.; Sun, Z.; Zhang, Z.; Lin, L.; Xu, H. Research on electro-hydraulic ratios for a novel mechanical-electro-hydraulic power coupling electric vehicle. Energy 2023, 270, 126970. [Google Scholar] [CrossRef]
- Pugi, L.; Pagliai, M.; Nocentini, A.; Lutzemberger, G.; Pretto, A. Design of a hydraulic servo-actuation fed by a regenerative braking system. Appl. Energy 2017, 187, 96–115. [Google Scholar] [CrossRef]
- Gong, X.; Ge, W.; Yan, J.; Zhang, Y.; Gongye, X. Review on the development, control method and application prospect of brake-by-wire actuator. Actuators 2020, 9, 15. [Google Scholar] [CrossRef]
- Tan, C.; Ren, H.; Li, B.; Lu, J.; Li, D.; Tao, W. Design and analysis of a novel cascade control algorithm for braking-by-wire system based on electromagnetic direct-drive valves. J. Frankl. Inst. 2022, 359, 8497–8521. [Google Scholar] [CrossRef]
- Picasso, B.; Caporale, D.; Colaneri, P. Braking control in railway vehicles: A distributed preview approach. IEEE Trans. Autom. Control 2017, 63, 189–195. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, Z.; Wang, M. Brake force cooperative control and test for integrated electro-hydraulic brake system. J. Jilin Univ. 2016, 46, 718–724. [Google Scholar]
- Liu, Z.; Long, Y.; Li, Y.; Tan, X.; Wu, G. Study on the Design and Parameter Matching of Integrated Electro-Hydraulic Braking System. Automot. Eng. 2022, 44, 1416–1424. [Google Scholar]
- Joa, E.; Yi, K.; Sohn, K.; Bae, H. Four-wheel independent brake control to limit tire slip under unknown road conditions. Control Eng. Pract. 2018, 76, 79–95. [Google Scholar] [CrossRef]
- Lee, C.F.; Manzie, C. Active brake judder attenuation using an electromechanical brake-by-wire system. IEEE/ASME Trans. Mechatron. 2016, 21, 2964–2976. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, L.; Wang, Z.; Zuo, L.; Song, J. All-wheel braking force allocation during a braking-in-turn maneuver for vehicles with the brake-by-wire system considering braking efficiency and stability. IEEE Trans. Veh. Technol. 2015, 65, 4752–4767. [Google Scholar] [CrossRef]
- Yu, D.; Wang, W.; Zhang, H.; Xu, D. Research on anti-lock braking control strategy of distributed-driven electric vehicle. IEEE Access 2020, 8, 162467–162478. [Google Scholar] [CrossRef]
- Henderson, J.P.; Plummer, A.; Johnston, N. An electro-hydrostatic actuator for hybrid active-passive vibration isolation. Int. J. Hydromechatron. 2018, 1, 47–71. [Google Scholar] [CrossRef]
- Fu, Y.F.; Hu, X.H.; Wang, W.R.; Ge, Z. Simulation and experimental study of a new electromechanical brake with automatic wear adjustment function. Int. J. Automot. Technol. 2020, 21, 227–238. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, L.; You, C.; Wang, Y.; Song, J. Fail-safe control allocation for a distributed brake-by-wire system considering the driver’s behaviour. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 1547–1567. [Google Scholar] [CrossRef]
- Gong, X.; Qian, L.; Ge, W.; Yan, J. Research on electronic brake force distribution and anti-lock brake of vehicle based on direct drive electro hydraulic actuator. Int. J. Automot. Eng. 2020, 11, 22–29. [Google Scholar] [CrossRef]
- Xiao, F.; Gong, X.; Lu, Z.; Qian, L.; Zhang, Y.; Wang, L. Design and control of new brake-by-wire actuator for vehicle based on linear motor and lever mechanism. IEEE Access 2021, 9, 95832–95842. [Google Scholar] [CrossRef]
- Zheng, H.Y.; He, R.; Zong, C.F. Research of electric vehicle regenerative braking control strategy based on EHB system. Adv. Mater. Res. 2013, 724, 1436–1439. [Google Scholar] [CrossRef]
- Han, W.; Xiong, L.; Yu, Z. Analysis and optimization of minimum hydraulic brake-by-wire system for wheeled vehicles based on queueing theory. IEEE Trans. Veh. Technol. 2021, 70, 12491–12505. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, J.; Zhang, J.; He, C.; Hou, X.; Han, J. Constraint performance slip ratio control for vehicles with distributed electrohydraulic brake-by-wire system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023. [Google Scholar] [CrossRef]
- Lu, Y.; Tan, C.; Ge, W.; Zhao, Y.; Wang, G. Adaptive disturbance observer-based improved super-twisting sliding mode control for electromagnetic direct-drive pump. Smart Mater. Struct. 2022, 32, 017001. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, M.; Zhang, G.; Hou, Z.; Lin, Q.; Yuan, H. Study on high frequency response characteristics of a moving-coil-type linear actuator using the coils combinations. Int. J. Hydromechatron. 2022, 5, 226–242. [Google Scholar] [CrossRef]
- Li, B.; Liu, Y.; Tan, C.; Qin, Q.; Lu, Y. Review on electro-hydrostatic actuator: System configurations, design methods and control technologies. Int. J. Mechatron. Manuf. Syst. 2020, 13, 323–346. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, B.; Wang, Q. Accurate motion control of linear motors with adaptive robust compensation of nonlinear electromagnetic field effect. IEEE/ASME Trans. Mechatron. 2012, 18, 1122–1129. [Google Scholar] [CrossRef]
- Shi, Q.; He, L. A Model Predictive Control Approach for Electro-Hydraulic Braking by Wire. IEEE Trans. Ind. Inform. 2022, 19, 1380–1388. [Google Scholar] [CrossRef]


| Item | Value | Unit |
|---|---|---|
| Mass at full load | 300 | kg |
| Wheel radius | 228 | mm |
| Brake type | Disc brake | |
| Cross-sectional radius of the piston | 19 | mm |
| Effective radius of friction plate | 110 | mm |
| Friction coefficient of friction plate | 0.38 | |
| Components | Item | Value | Unit |
|---|---|---|---|
| Hydraulic pump | Plunger area | 28 | mm2 |
| Length of pump chamber | 16 | mm | |
| EMLA | Coil resistance | 1.40 | Ω |
| Coil inductance | 0.91 | mH | |
| Back EMF constant | 24.61 | Vs/m | |
| Electromagnetic force coefficient | 24.61 | N/A | |
| Active valve | Valve core diameter | 4 | mm |
| Valve hole diameter | 8 | mm | |
| Opening time | 2 | ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, P.; Sun, Z.; Xu, H.; Ren, Y.; Tan, C. Design and Analysis of Brake-by-Wire Unit Based on Direct Drive Pump–Valve Cooperative. Actuators 2023, 12, 360. https://doi.org/10.3390/act12090360
Yu P, Sun Z, Xu H, Ren Y, Tan C. Design and Analysis of Brake-by-Wire Unit Based on Direct Drive Pump–Valve Cooperative. Actuators. 2023; 12(9):360. https://doi.org/10.3390/act12090360
Chicago/Turabian StyleYu, Peng, Zhaoyue Sun, Haoli Xu, Yunyun Ren, and Cao Tan. 2023. "Design and Analysis of Brake-by-Wire Unit Based on Direct Drive Pump–Valve Cooperative" Actuators 12, no. 9: 360. https://doi.org/10.3390/act12090360
APA StyleYu, P., Sun, Z., Xu, H., Ren, Y., & Tan, C. (2023). Design and Analysis of Brake-by-Wire Unit Based on Direct Drive Pump–Valve Cooperative. Actuators, 12(9), 360. https://doi.org/10.3390/act12090360







