Mining Electric Shovel Working Device Configuration Synthesis and Performance Analysis
Abstract
1. Introduction
2. Mining Electric Shovel Working Device Configuration Synthesis Based on Screw Theory
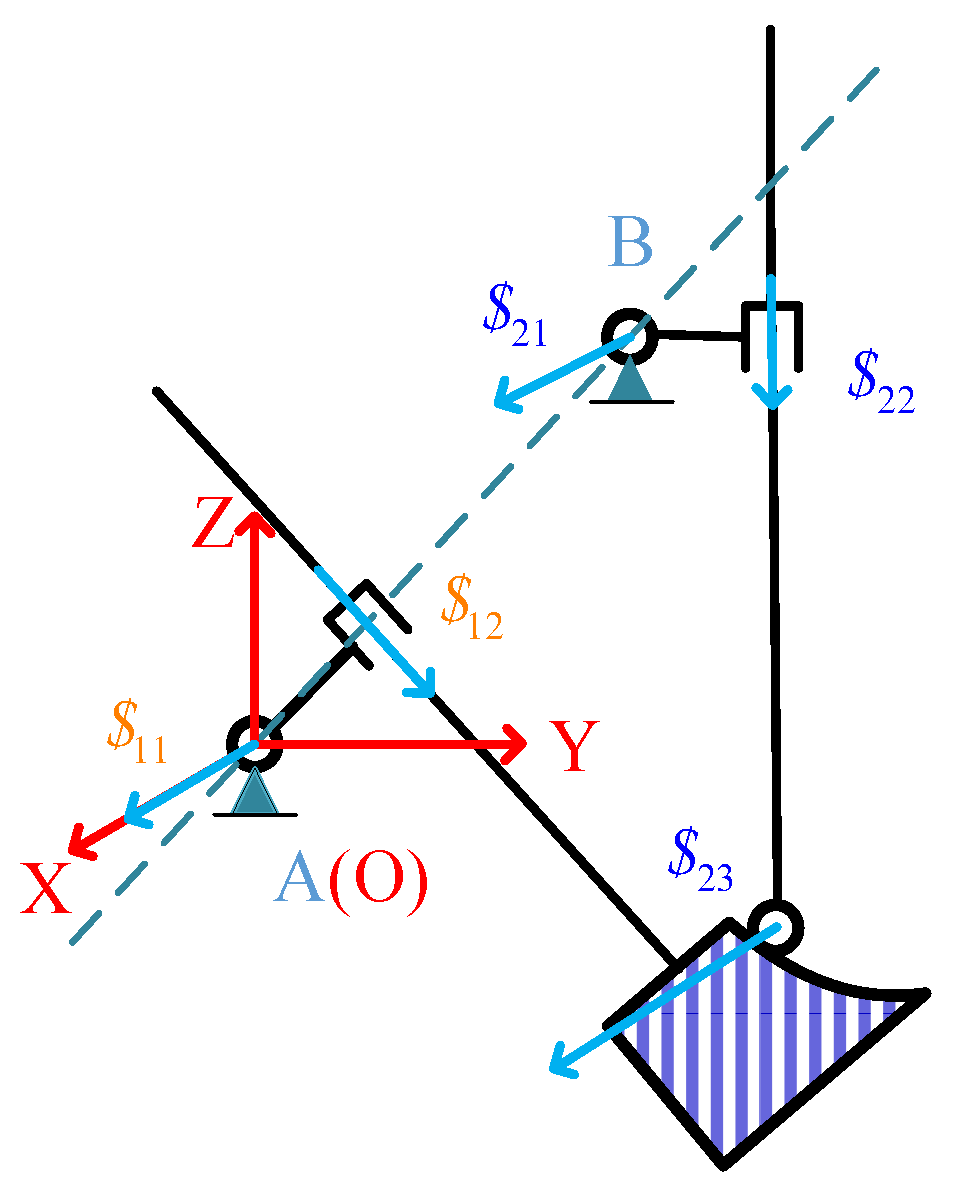
2.1. Overview of the Screw Theory
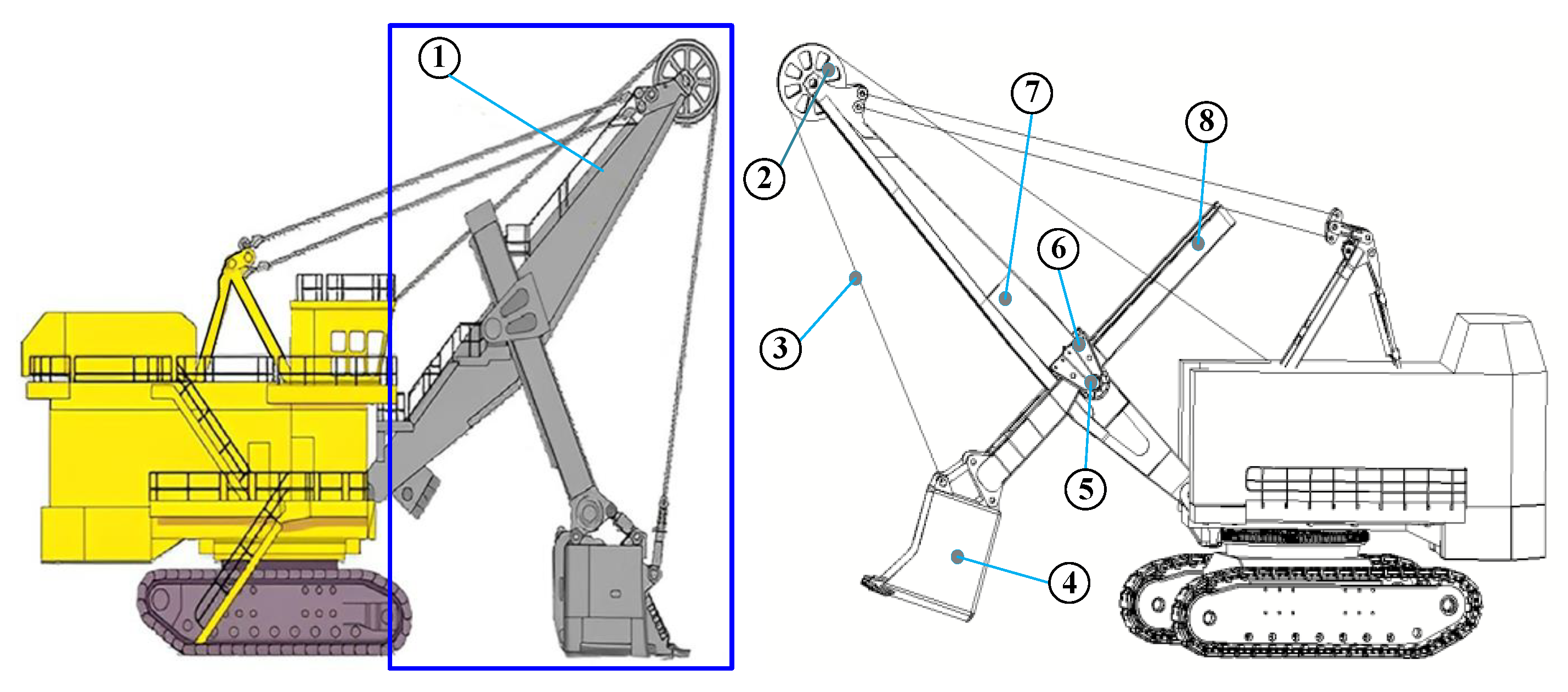
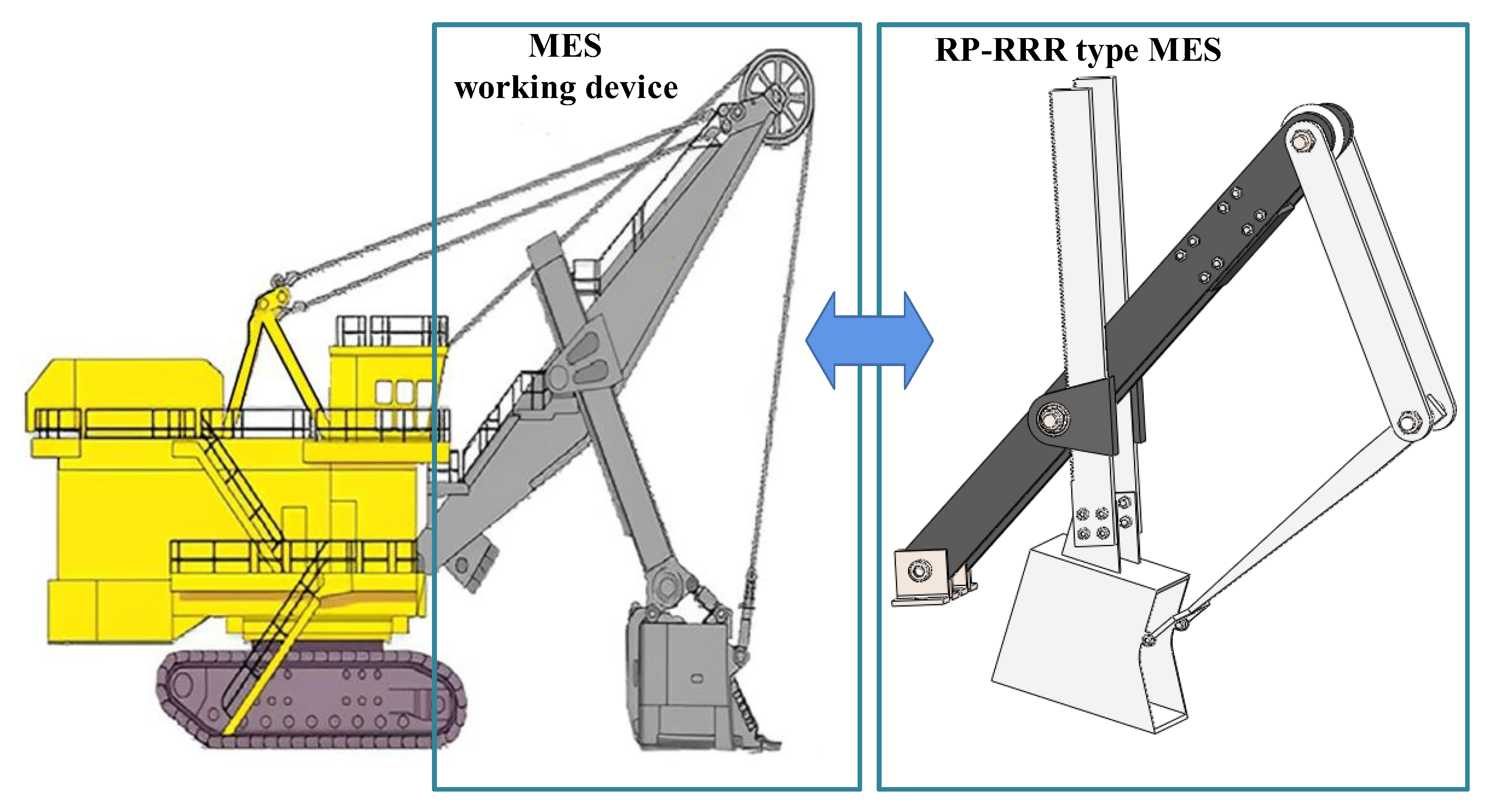
2.2. Analysis of Mining Electric Shovels: A Working Device
2.3. Configuration Synthesis of MES, in a Working Device
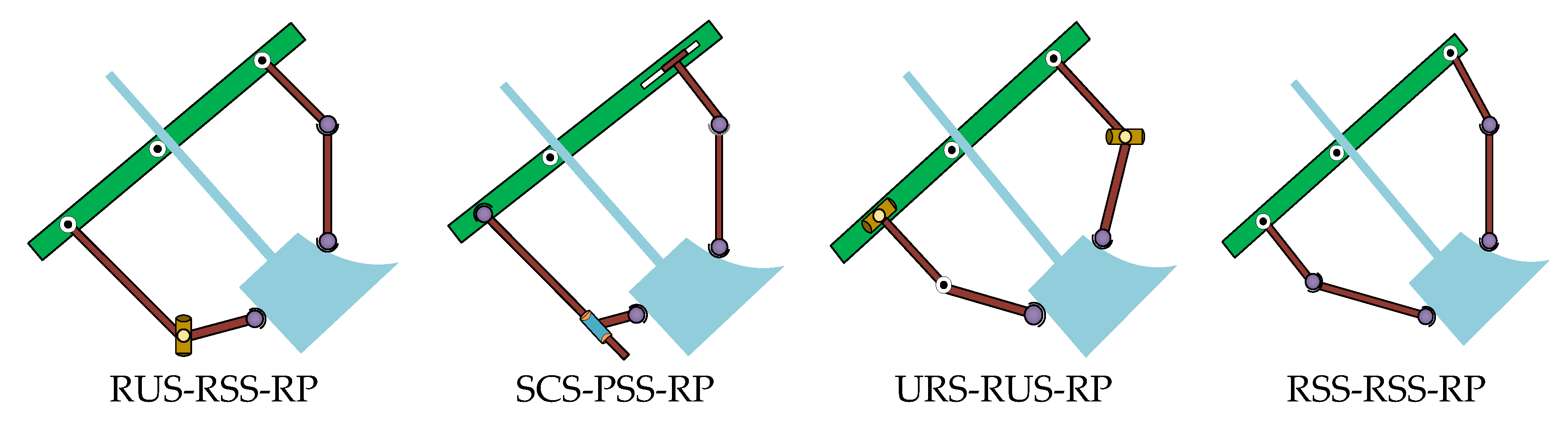
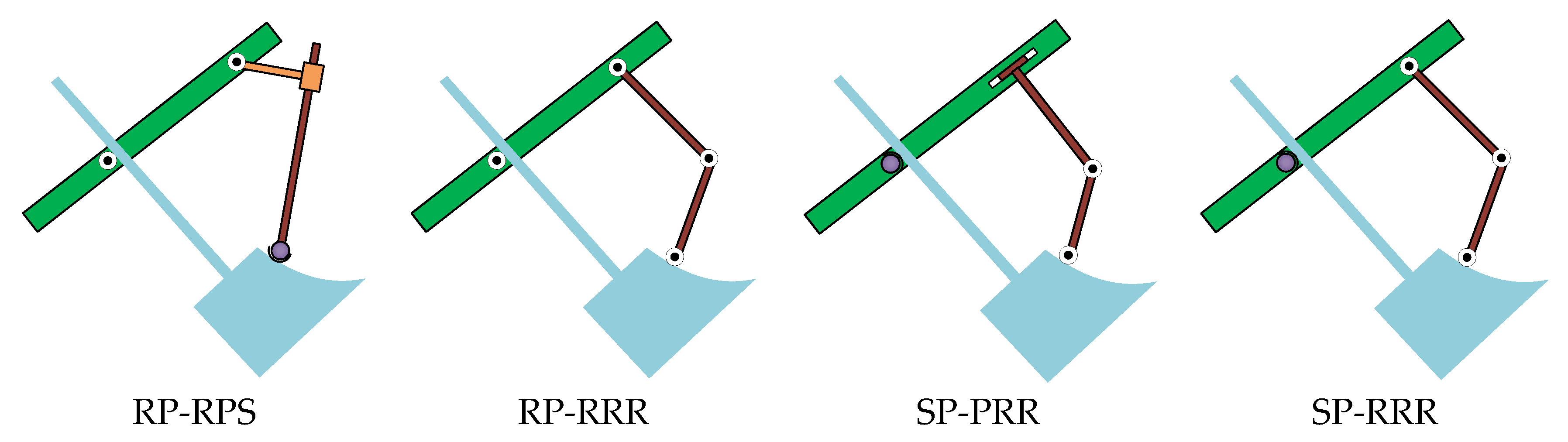
2.3.1. Synthesis Scheme I
2.3.2. Synthesis Scheme II
3. Workspace Analysis
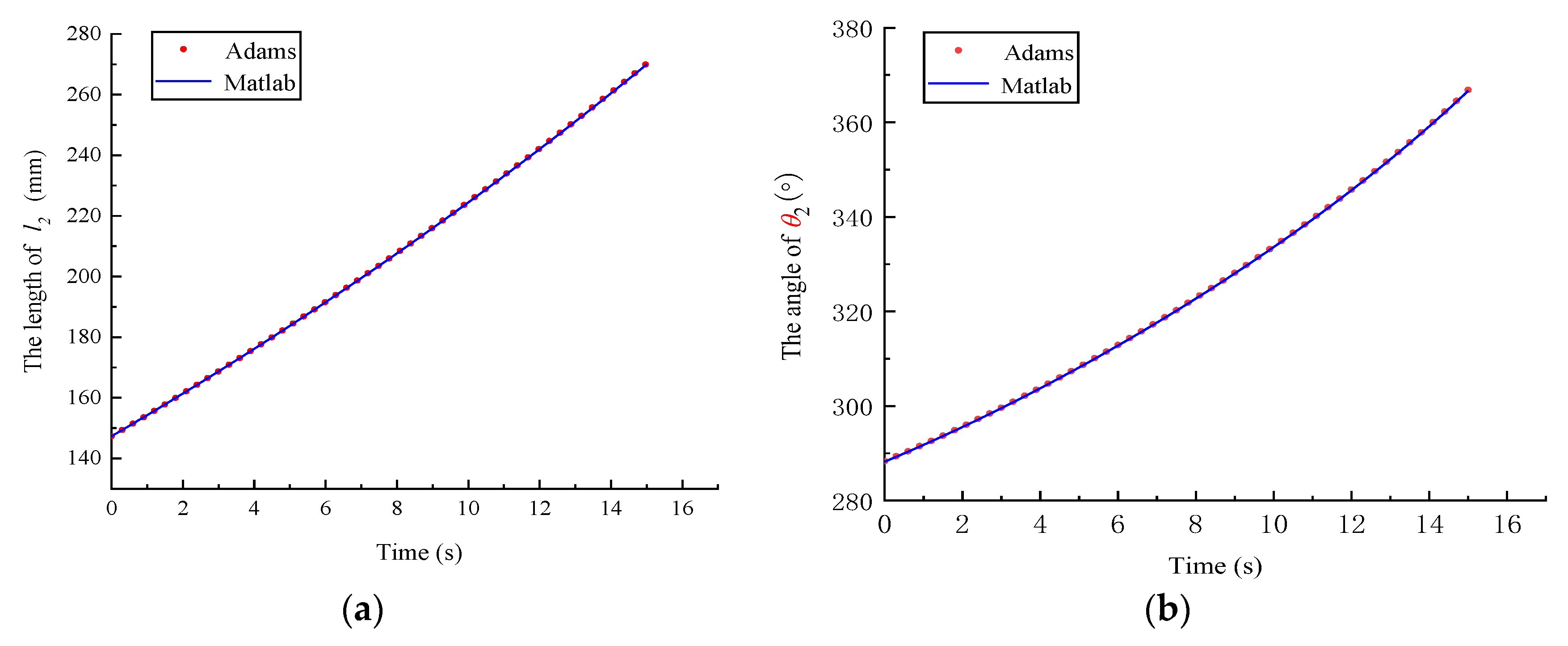
3.1. Location Analysis and Simulation Verification
| Parameter (Unit) | Value | Parameter (Unit) | Value |
|---|---|---|---|
| L0 (mm) | 290 | lBP (mm) | 72.45 |
| l1 (mm) | 24.5 | lAP (mm) | 133.71 |
| l3 (mm) | 270 | θ0 (°) | 45 |
| l4 (mm) | 263 | β1 (°) | 16.85 |
| lAB (mm) | 68.09 | β2 (°) | 17.78 |
3.2. Constraints on the Workspace
3.2.1. Constraints of Revolute Pairs
3.2.2. Constraints of Prismatic Pairs
3.2.3. Interference Constraints between Adjacent Rods
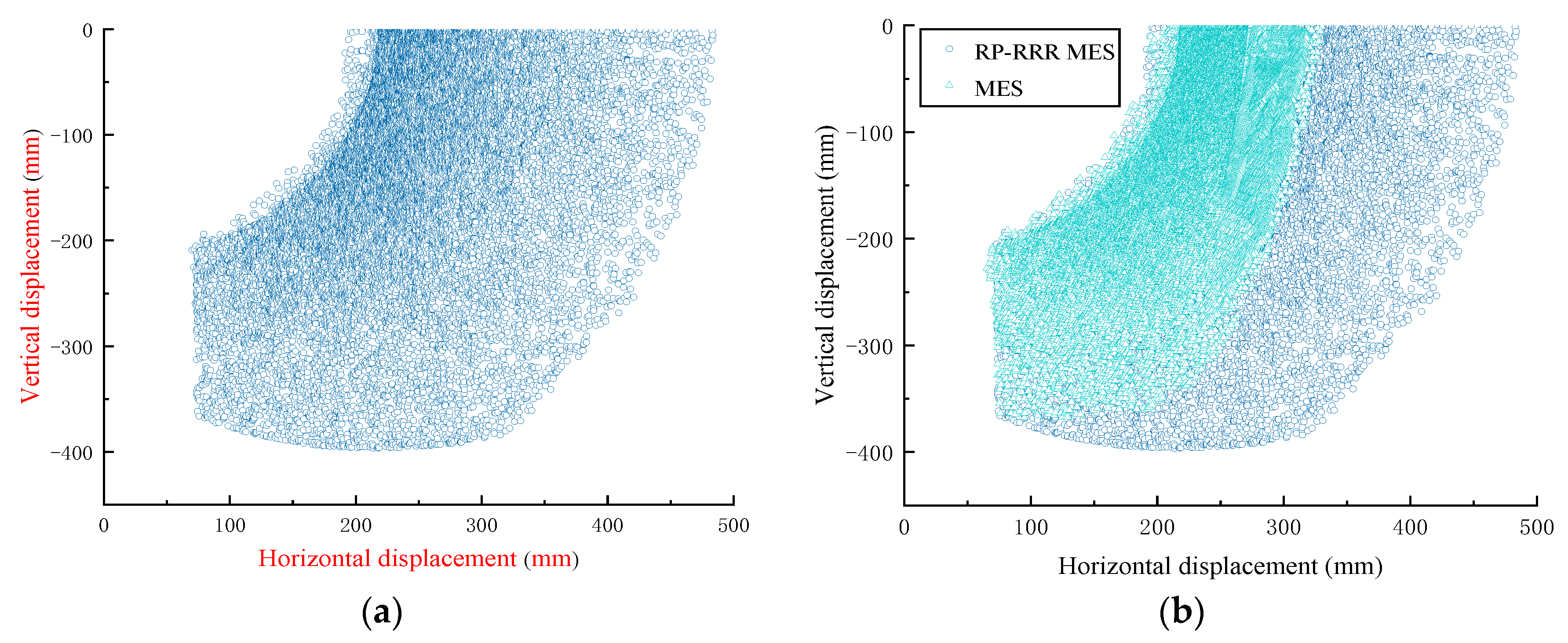
3.3. Workspace Analysis
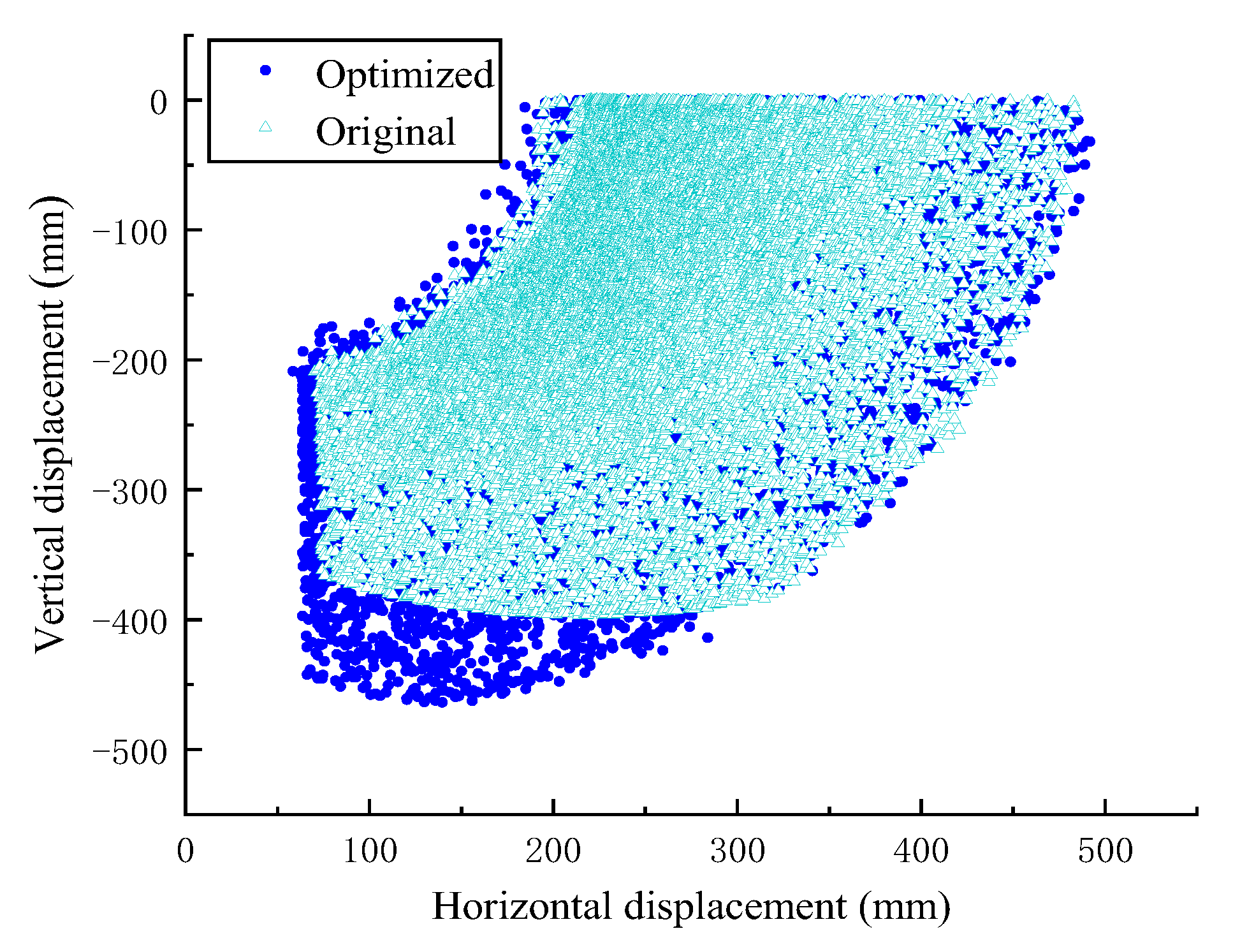
4. Optimization of Rod Parameters
4.1. Influence of Rod Size Parameters on the Working Space
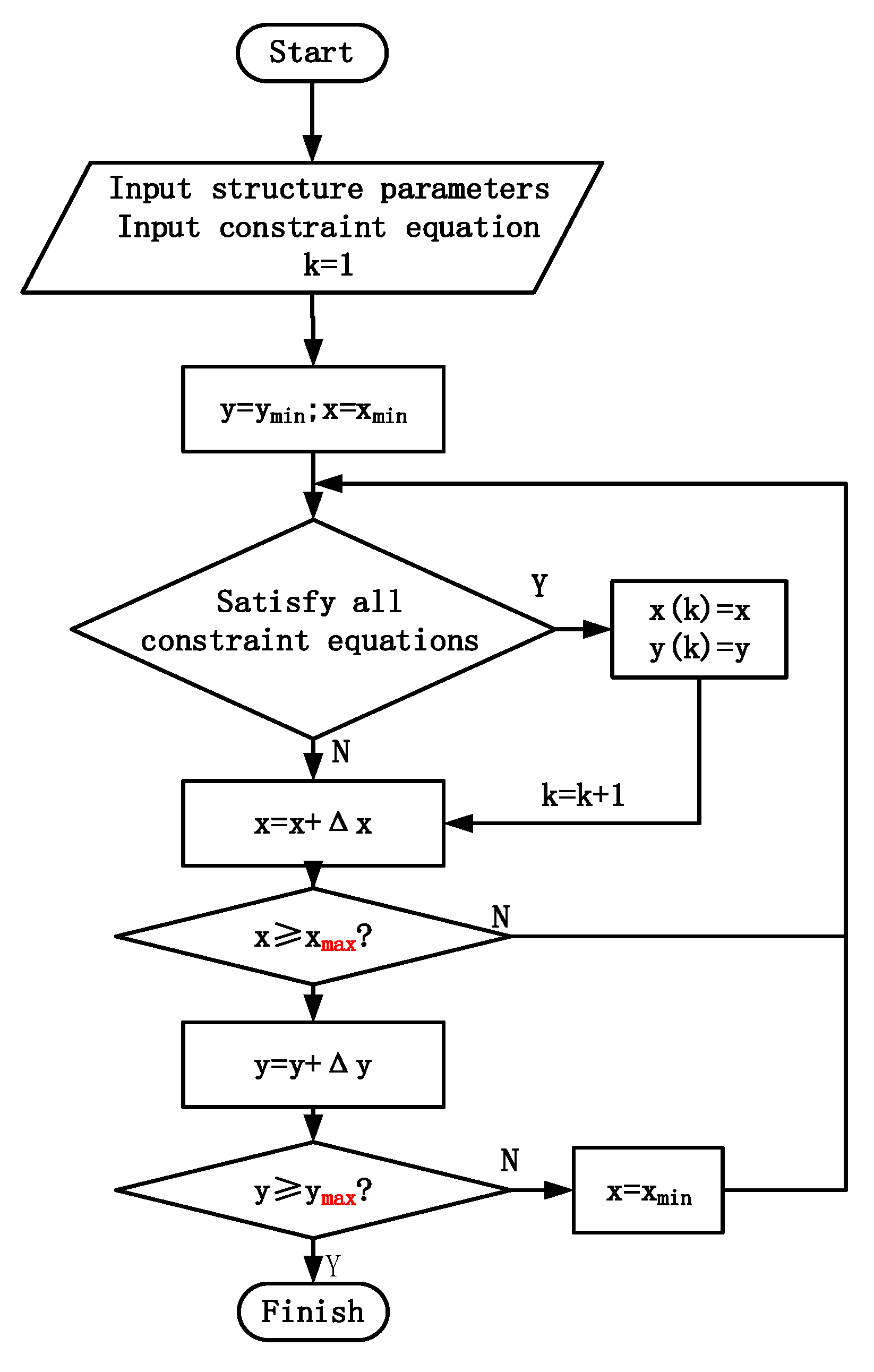
4.2. Optimization Model for Working Devices
4.3. Optimization Analysis of RP-RRR-Type MES Working Devices
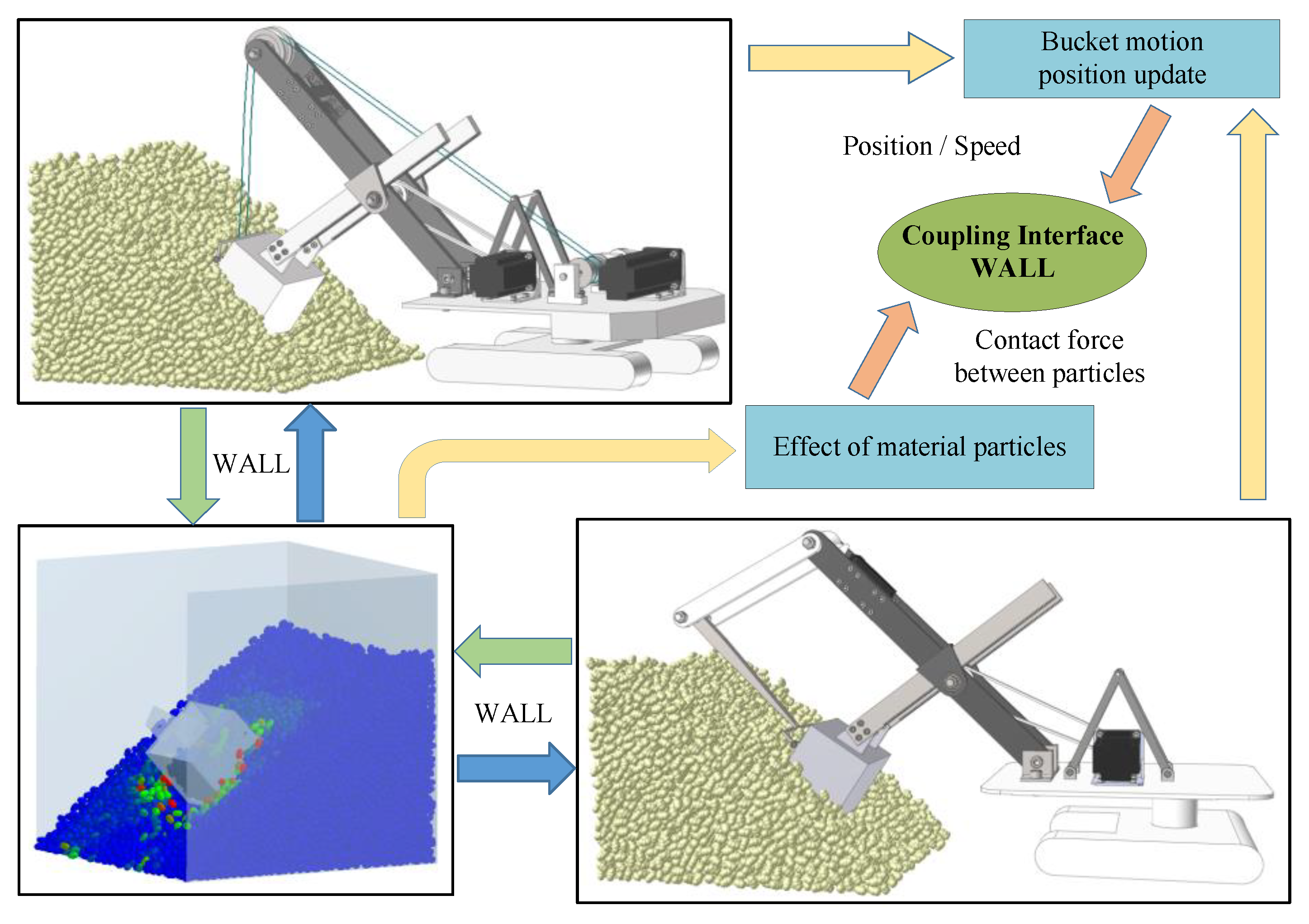
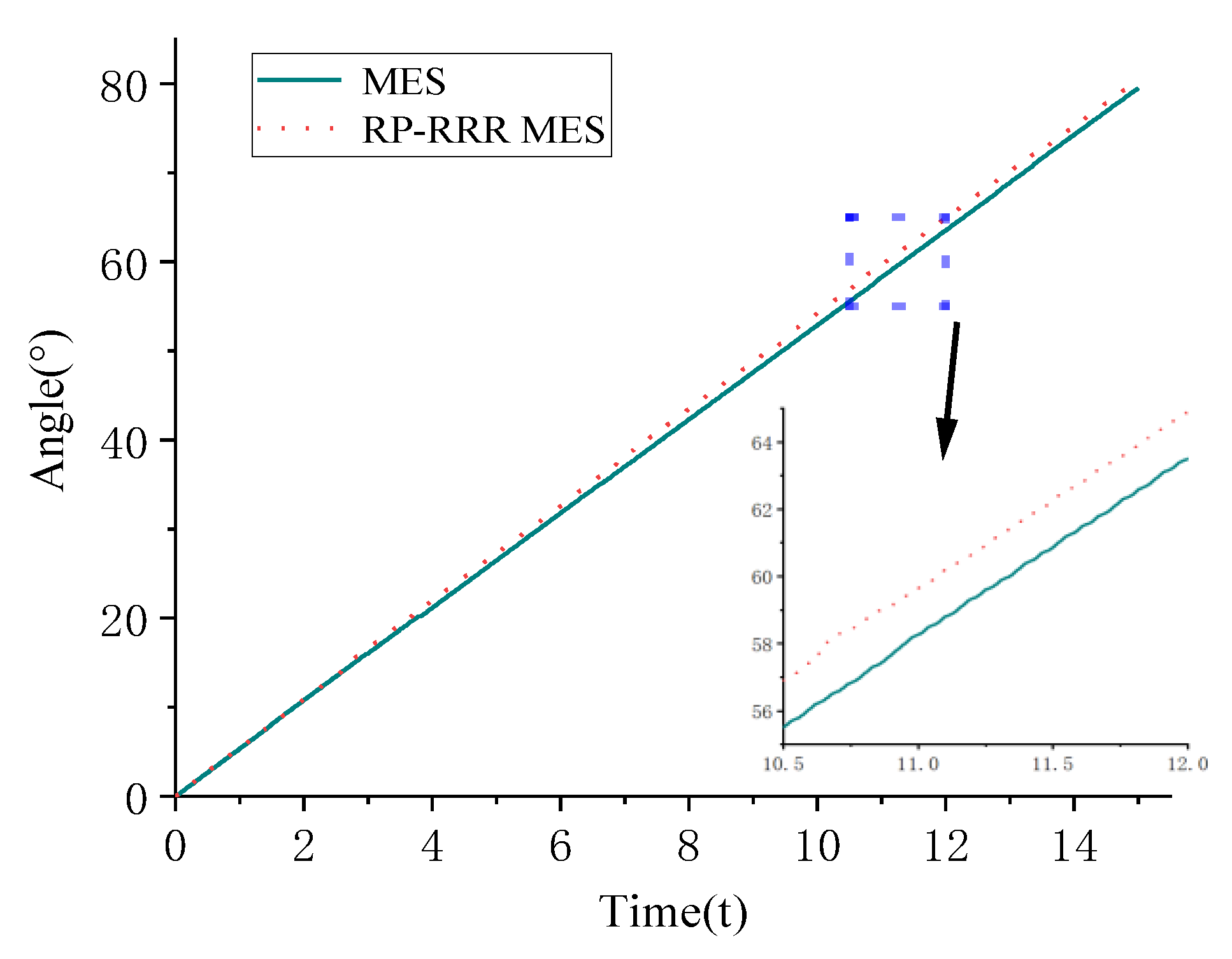
5. Simulation Analysis and Experimental Verification
5.1. EDEM and RecurDyn Bidirectional Coupling Simulation Analysis
5.2. Experimental Verification of the MES Working Device
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, B.; Gao, F.; Chen, J.; He, J.; Wu, S.; Song, Q. Mechanics performance of three-degree-of-freedom excavating mechanism of an electric shovel. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 1443–1457. [Google Scholar] [CrossRef]
- Hervé, J. The Lie group of rigid body displacements, a fundamental tool for mechanism design. Mech. Mach. Theory 1999, 34, 719–730. [Google Scholar] [CrossRef]
- Li, Q.; Huang, Z.; Hervé, J. Type synthesis of 3R2T 5-DOF parallel mechanisms using the lie group of displacements. IEEE Trans. Rob. Autom. 2004, 20, 173–180. [Google Scholar] [CrossRef]
- Meng, J.; Liu, G.F.; Li, Z.X. A geometric theory for analysis and synthesis of Sub-6 DOF parallel manipulators. IEEE Trans. Rob. 2007, 23, 625–649. [Google Scholar] [CrossRef]
- Gogu, G. Structural Synthesis of Parallel Robots: Part 2: Translational Topologies with Two and Three Degrees of Freedom; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Gogu, G. Structural Synthesis of Parallel Robots: Part 3: Topologies with Planar Motion of the Moving Platform; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Gogu, G. Structural Synthesis of Parallel Robots: Part 4: Other Topologies with Two and Three Degrees of Freedom; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Yang, T.; Liu, A.; Shen, H.; Hang, L.; Ge, Q. Composition principle based on single-open-chain unit for general spatial mechanisms and its application—In conjunction with a review of development of mechanism composition principles. ASME J. Mech. Robot. 2018, 10, 051005. [Google Scholar] [CrossRef]
- Kong, X.W.; Gosselin, C.M. Type synthesis of 3-DOF translational parallel manipulators based on screw theory. J. Mech. Des. 2004, 126, 83–92. [Google Scholar] [CrossRef]
- Kong, X.W.; Gosselin, C.M. Type synthesis of 4-DOF SP-equivalent parallel manipulators: A virtual chain approach. Mech. Mach. Theory 2006, 41, 1306–1319. [Google Scholar] [CrossRef]
- Han, B.; Xu, Y.; Yao, J.; Zheng, D.; Guo, X.; Zhao, Y. Configuration synthesis of hoop truss deployable mechanisms for space antenna based on screw theory. AIP Adv. 2019, 9, 085201. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, F.; Chen, C.; Jin, L.; Li, J.; Zhang, X.; Lu, X. Inverse kinematics and trajectory Planning for a Hyper-redundant bionic Trunk-like robot. Int. J. Robotics Autom. 2020, 35, 229–241. [Google Scholar] [CrossRef]
- Wang, Y.; Lyu, C.; Liu, J. Kinematic Analysis and Verification of a New 5-DOF Parallel Mechanism. Appl. Sci. 2021, 11, 8157. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Q.; Ge, Y.F.; Qin, X.R.; Sun, Y.T. Dynamic analysis of an over-constrained parallel mechanism with the principle of virtual work. Math. Comput. Model. Dyn. Syst. 2021, 27, 347–372. [Google Scholar] [CrossRef]
- Kang, H.; Deng, Z.; Luo, L. Workspace analysis of 6-PTRT parallel robot. J. Liaoning Univ. Petrochem. Technol. 2019, 39, 82–89. [Google Scholar]
- Hao, F.; Merlet, J.P. Multi-criteria optimal design of parallel manipulators based on interval analysis. Mech. Mach. Theory 2005, 40, 157–171. [Google Scholar] [CrossRef]
- Lei, J.; Wang, J. Orientation Workspace Analysis and Parameter Optimization of 3-RRPS Parallel Robot for Pelvic Fracture Reduction. J. Mech. Robot. 2023, 15, 051003. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, K.; Li, X.; Zhang, Y. Accurate Numerical Methods for Computing 2D and 3D Robot Workspace. Int. J. Adv. Robot. Syst. 2011, 8, 76. [Google Scholar] [CrossRef]
- Behera, L.; Rybak, L.; Malyshev, D.; Khalapyan, S. Numerical simulation of the workspace of robots with moving bases in the multi-agent system. Procedia Comput. Sci. 2021, 186, 431–439. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, J.; Guo, H.; Liu, R.; Kou, Z. Design of a 2T1R-Type Parallel Mechanism: Performance Analysis and Size Optimization. Actuators 2022, 11, 262. [Google Scholar] [CrossRef]
- Zhu, S.; Huang, Z. Eighteen fully symmetrical 5-DoF 3R2T parallel manipulators with better actuating modes. Inter-Natl. J. Adv. Manuf. Technol. 2007, 34, 406–412. [Google Scholar] [CrossRef]
- Chen, C.; Li, T.; Tang, Y. Configuration Synthesis of Generalized Mechanism Based on Screw Theory. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 1013–1021. [Google Scholar] [CrossRef]
- Li, Q.; Huang, Z. Mobility analysis of lower-mobility parallel manipulators based on screw theory. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; Volume 1, pp. 1179–1184. [Google Scholar]
- Feng, Y.; Wu, J.; Guo, C.; Lin, B. Numerical simulation and experiment on excavating resistance of an electric cable shovel based on edem-recurdyn bidirectional coupling. Machines 2022, 10, 1203. [Google Scholar] [CrossRef]
- Fan, R.; Li, Y.; Yang, L. Trajectory Planning Based on Minimum Input Energy for the Electro-Hydraulic Cable Shovel. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020. [Google Scholar]
- Fan, R.; Li, Y.; Yang, L. Multiobjective trajectory optimization of intelligent electro-hydraulic shovel. Front. Mech. Eng. 2022, 17, 50. [Google Scholar] [CrossRef]




| Kinematic Screw | Constraint Screw | |
|---|---|---|
| Subchain I | ||
| Subchain II |
| Structure Type | 6-DOF Branched Chain Structure |
|---|---|
| I | RUS, RSU, PUS, PSU |
| SPU, UPS, SRU, SUR | |
| URS, USR, SUP, USP | |
| II | RSS, PSS, SPS |
| SRS, SSR, SSP | |
| III | CRS, CPS, UCU, CUU |
| CUS, CSU, UCS, SCU | |
| CSS, SCS, RCS, SCR | |
| PCS, SCH, CSR, CSP |
| The Structure Type of Branch I | The Structure Type of Branch II |
|---|---|
| RP | RSR, RPS, PPS |
| RCR, PCR | |
| RRR, RRP, PRR | |
| SP | RCR, PCR |
| RRR, RRP, RPR, PRR |
| No. | Design Variables | Optimization Results | |||
|---|---|---|---|---|---|
| L0 | l1 | l3 | l4 | ||
| 1 | 256.6881 | 27.6433 | 247.2907 | 277.1148 | −0.8379% |
| 2 | 344.9432 | 26.8493 | 268.3057 | 282.5948 | −5.7994% |
| 3 | 343.4026 | 22.4208 | 244.9275 | 284.2629 | −6.1360% |
| 4 | 299.7904 | 28.9187 | 248.2934 | 250.2538 | 3.7150% |
| 5 | 334.3502 | 27.2155 | 245.0065 | 290.1873 | −1.1705% |
| 6 | 262.7021 | 24.8517 | 294.0936 | 291.2911 | 13.4789% |
| 7 | 258.9309 | 24.0451 | 254.7247 | 243.3277 | −1.7839% |
| 8 | 301.4956 | 22.4725 | 284.6440 | 297.4211 | 3.2607% |
| 9 | 295.2182 | 26.8182 | 260.2839 | 274.5947 | −0.0586% |
| 10 | 297.3883 | 25.3067 | 288.2746 | 267.9916 | 1.8651% |
| Simulation Data | Experimental Data | Excavation Quality Difference | |
|---|---|---|---|
| MES working device | 1.815 kg | 1.779 kg | 2.02% |
| RP-RRR-type MES device | 1.808 kg | 1.769 kg | 2.20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Wu, J.; Feng, Y.; Wang, X.; Wang, Y. Mining Electric Shovel Working Device Configuration Synthesis and Performance Analysis. Actuators 2023, 12, 317. https://doi.org/10.3390/act12080317
Guo C, Wu J, Feng Y, Wang X, Wang Y. Mining Electric Shovel Working Device Configuration Synthesis and Performance Analysis. Actuators. 2023; 12(8):317. https://doi.org/10.3390/act12080317
Chicago/Turabian StyleGuo, Chenhao, Juan Wu, Yinnan Feng, Xin Wang, and Yuliang Wang. 2023. "Mining Electric Shovel Working Device Configuration Synthesis and Performance Analysis" Actuators 12, no. 8: 317. https://doi.org/10.3390/act12080317
APA StyleGuo, C., Wu, J., Feng, Y., Wang, X., & Wang, Y. (2023). Mining Electric Shovel Working Device Configuration Synthesis and Performance Analysis. Actuators, 12(8), 317. https://doi.org/10.3390/act12080317





