Balancing Control of an Absolute Pressure Piston Manometer Based on Fuzzy Linear Active Disturbance Rejection Control
Abstract
1. Introduction
2. Theoretical Modeling of an Absolute Pressure Piston Manometer
2.1. The Working Principle of the Absolute Pressure Piston Manometer
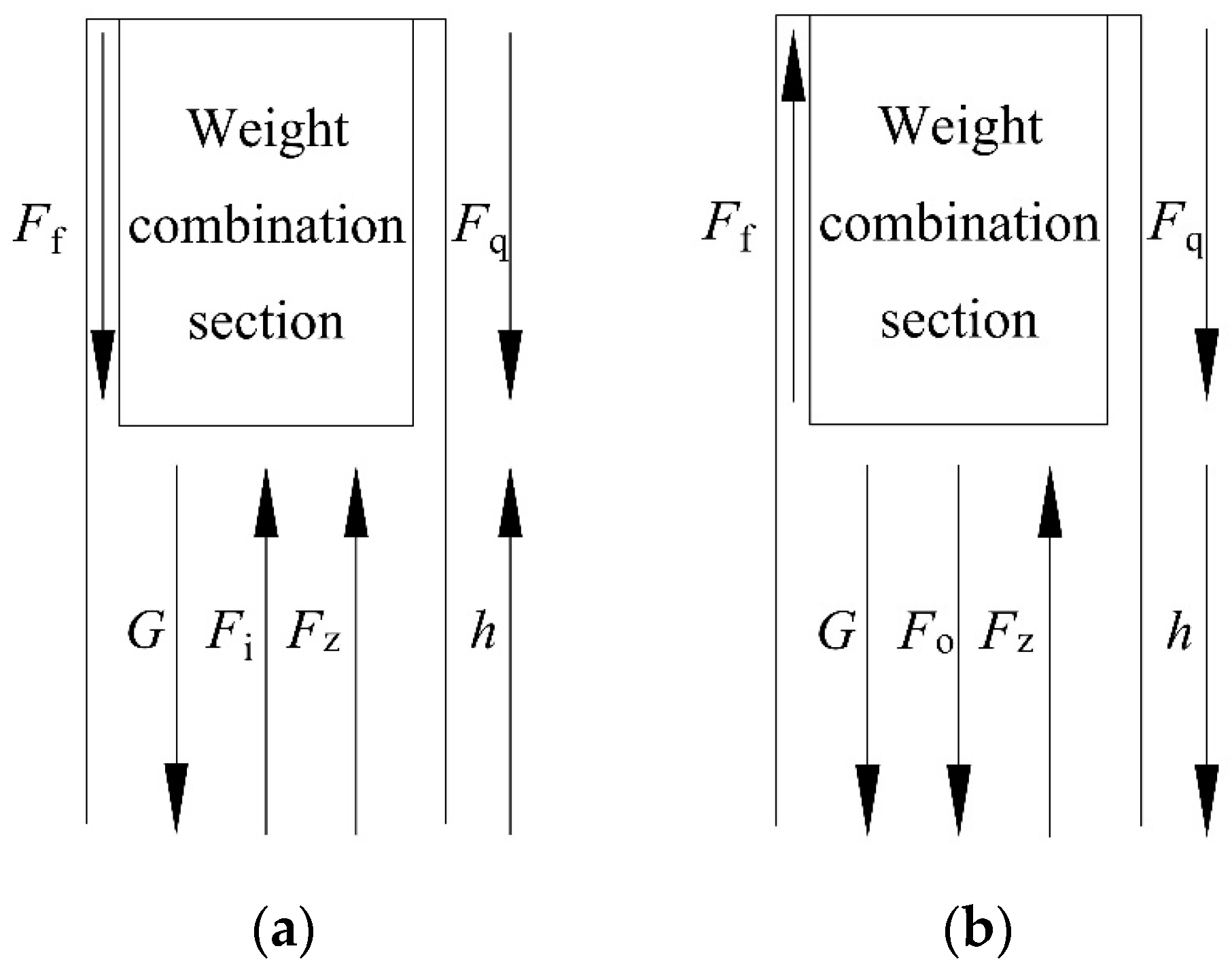
2.2. Kinetic Analysis of the Weight Combination Section
2.3. Flow Analysis of Switching Valves
2.4. Analytical Correction of Other Uncertainties
2.4.1. Analytical Correction of Piston Effective Area
2.4.2. Analytical Correction of Gas Leakage Volumes
2.5. Establishment of the Differential Equilibrium Equations of the System
3. Design of the Controller
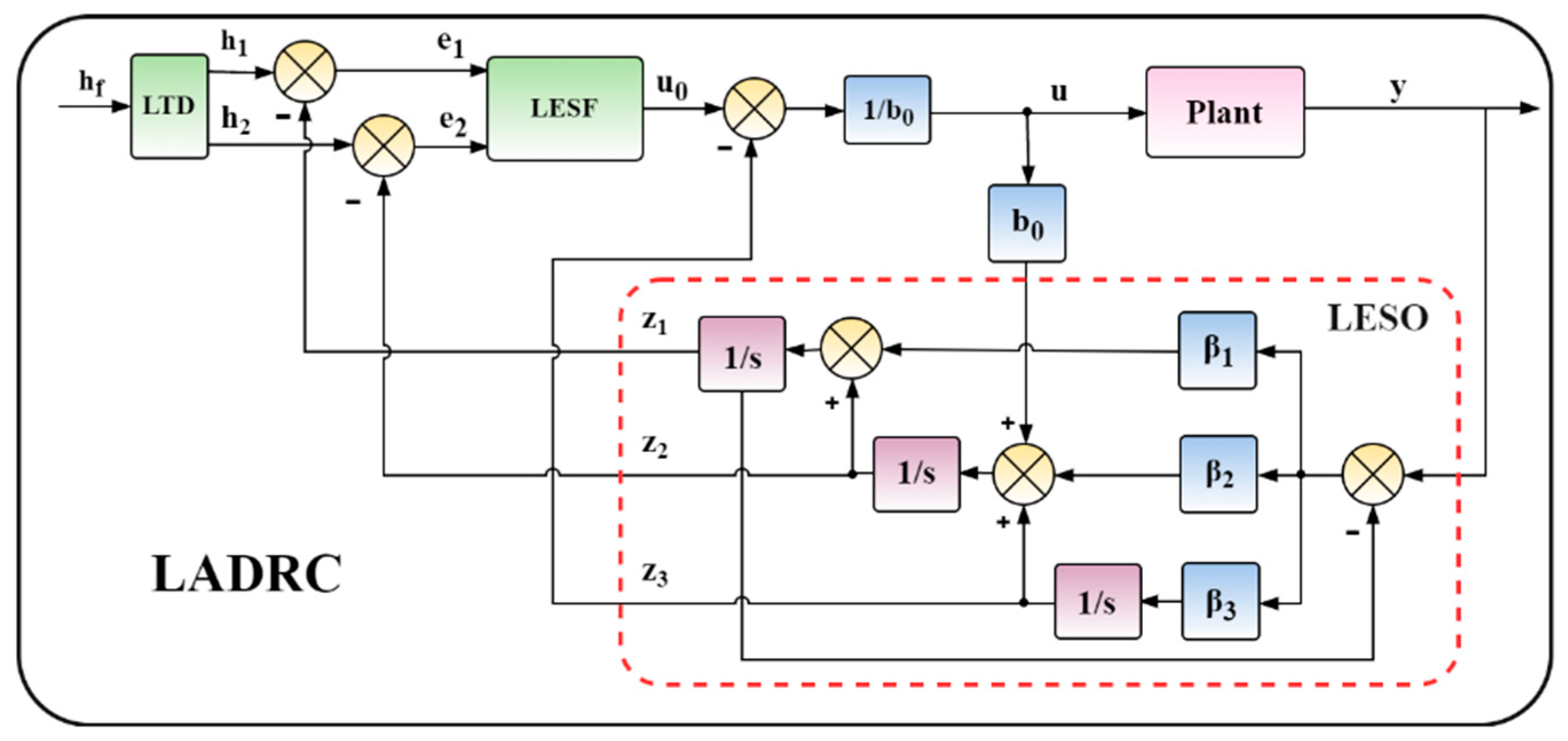
3.1. Design of the LADRC
3.1.1. Structure of the LADRC
3.1.2. Design of the LTD
3.1.3. Design of the LESO
3.1.4. Design of the LESF
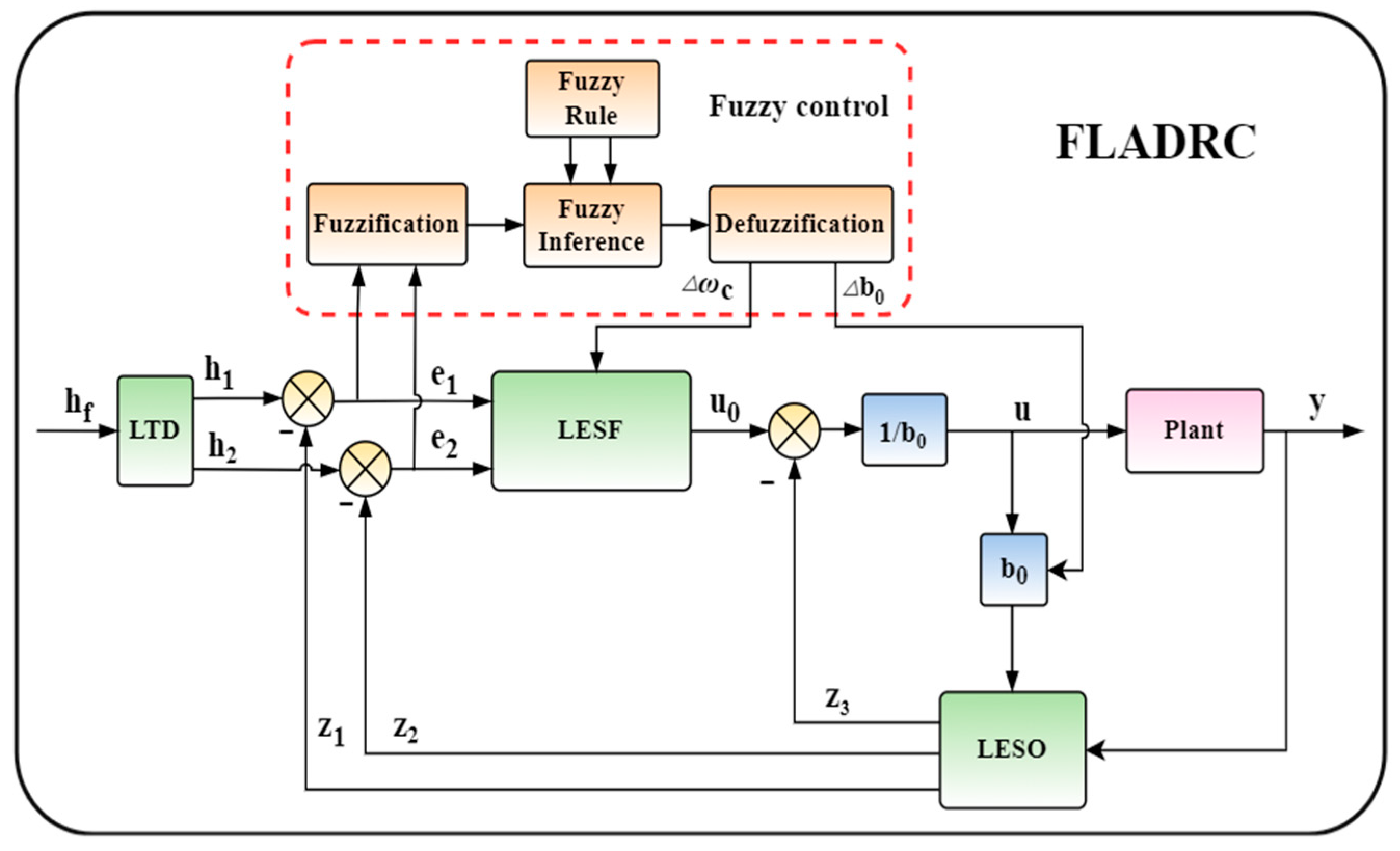
3.2. Design of the FLADRC
3.2.1. Structure of the FLADRC
3.2.2. Design of the Fuzzy Controller
3.3. Stability Analysis
4. Simulation Results and Analysis
4.1. Experimental Parameter Settings
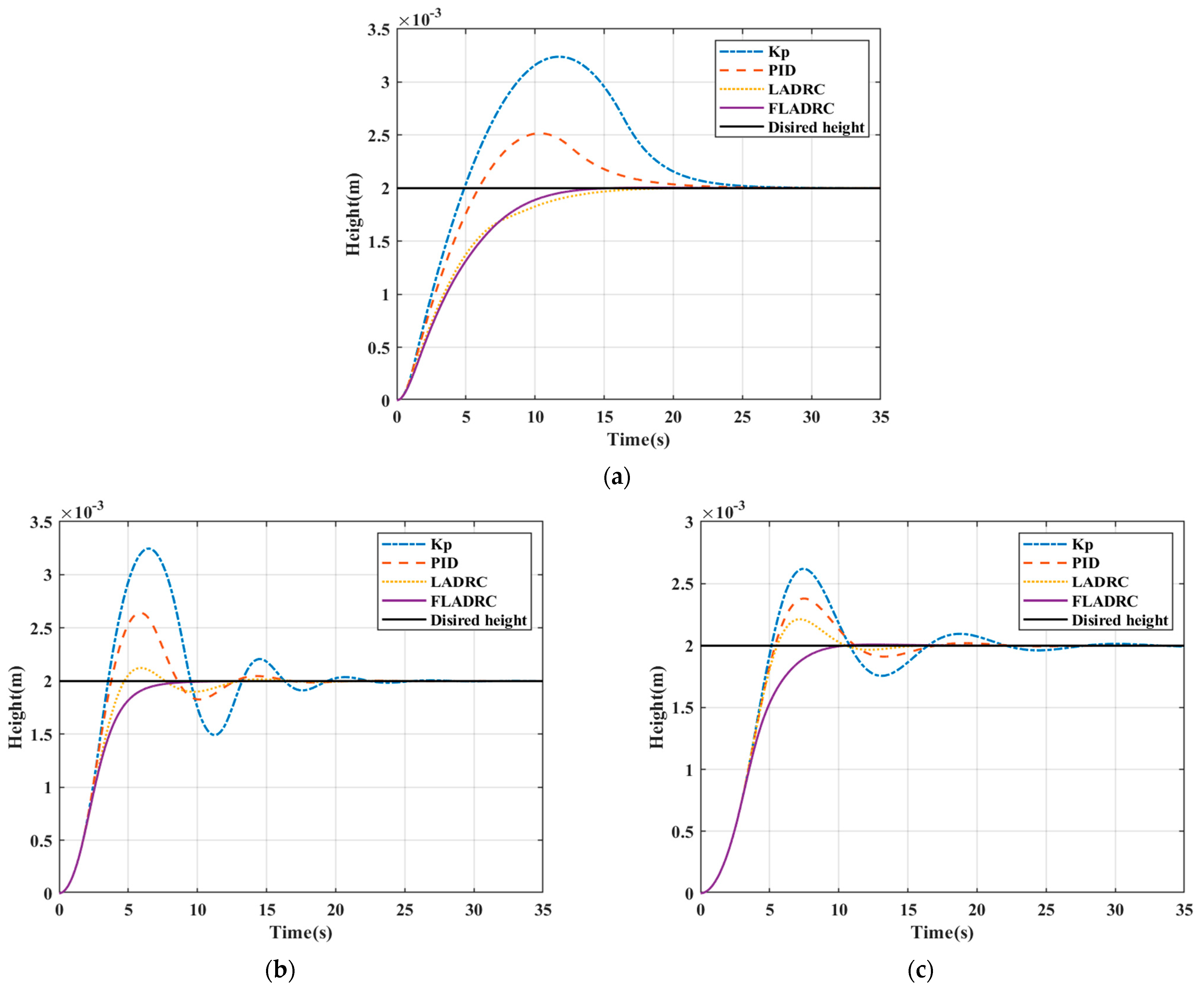
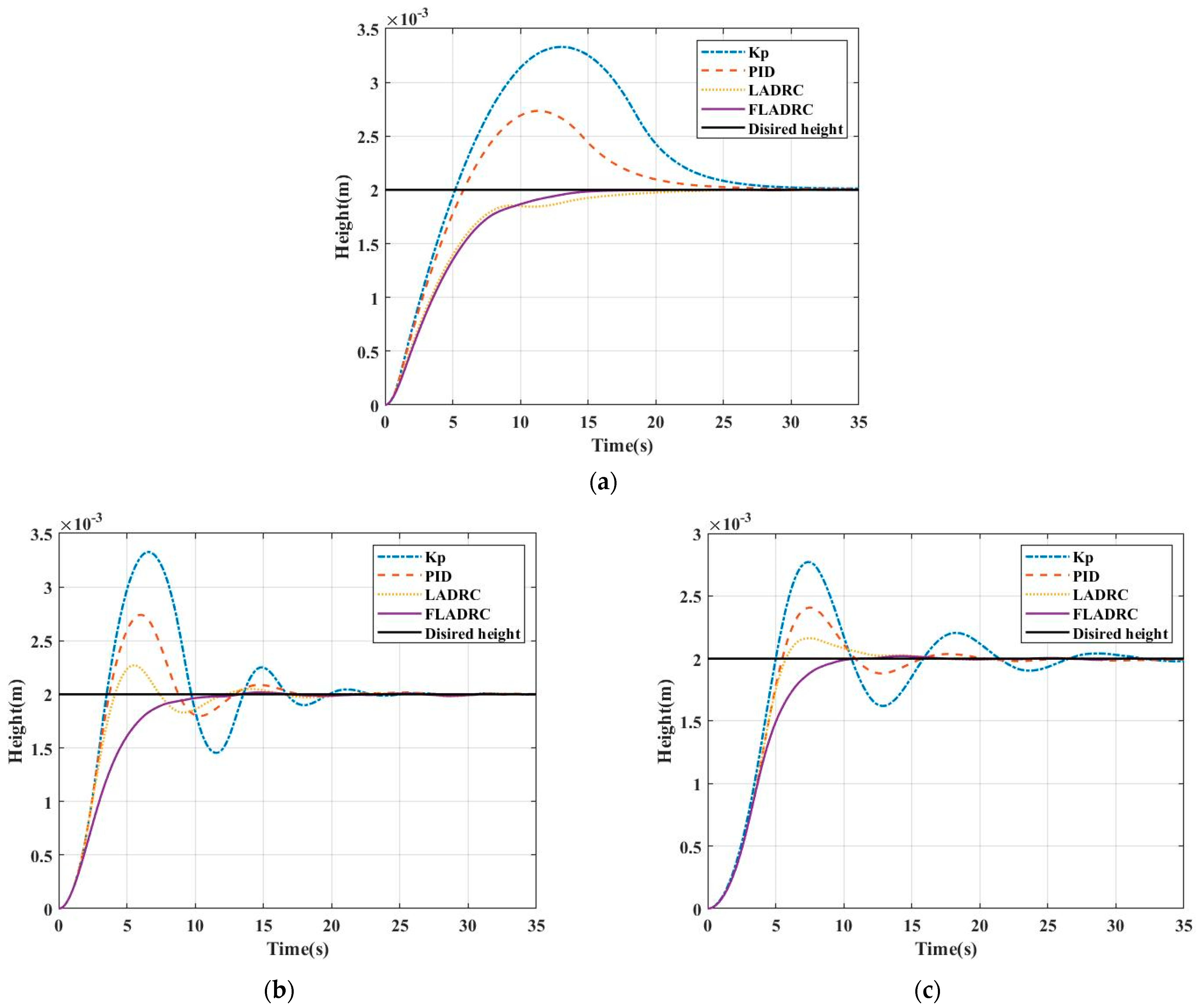
4.2. Experimental Analysis of Stability Performance
4.3. Experimental Analysis of Interference Immunity Performance
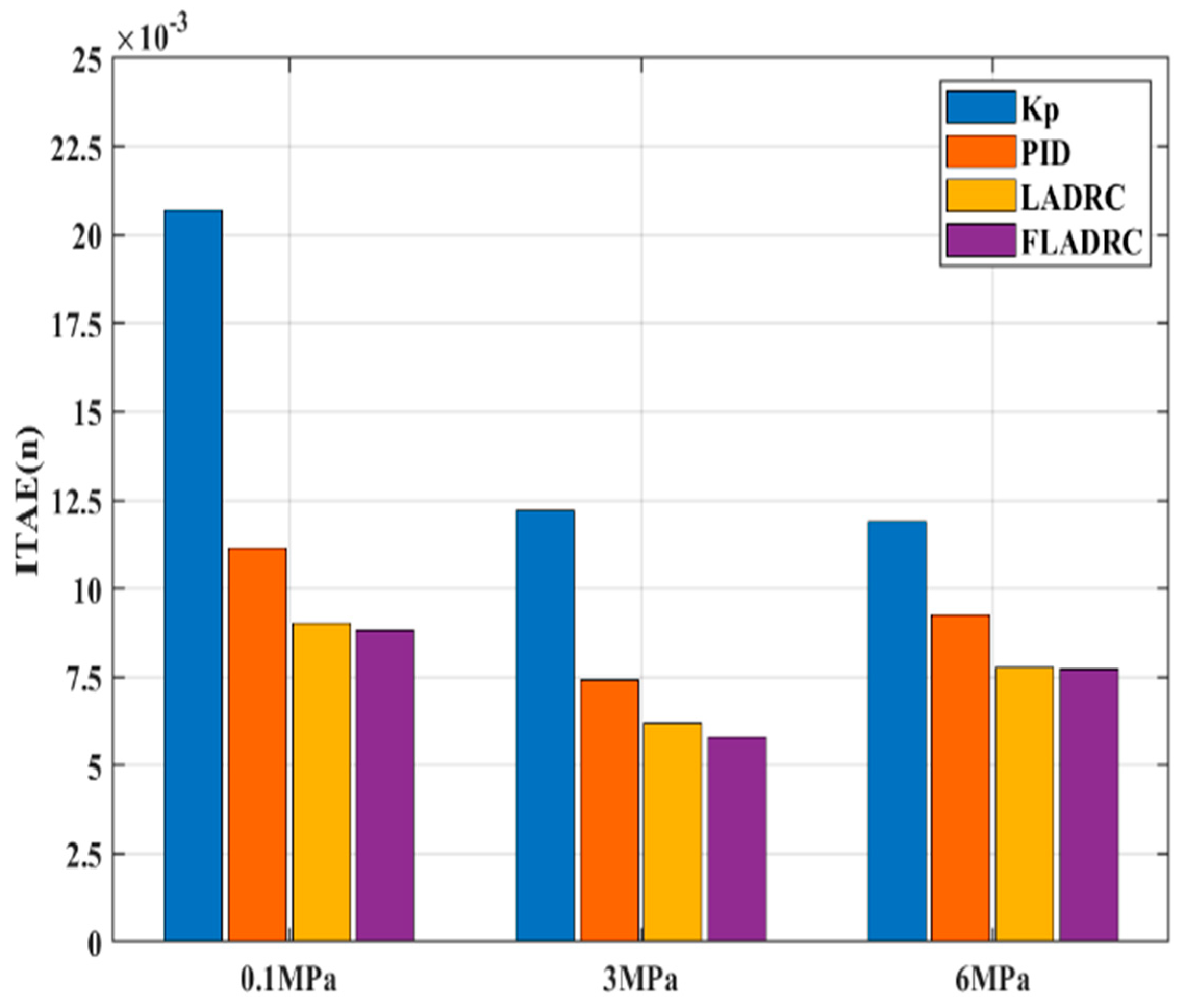
4.4. Experimental Analysis of Engineering Energy Consumption
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Driver, R.G.; Quintavalle, J.S.; Scherschligt, J.; Schlatter, K.; Ricker, J.E.; Strouse, G.F.; Olson, D.A.; Hendricks, J.H. An integrated and automated calibration system for pneumatic piston gauges. Measurement 2018, 134, 1–5. [Google Scholar] [CrossRef]
- Schmidt, J.W.; A Tison, S.; Ehrlich, C.D. Model for drag forces in the crevice of piston gauges in the viscous-flow and molecular-flow regimes. Metrologia 1999, 36, 565–570. [Google Scholar] [CrossRef]
- Welch, B.; Edsinger, R.; Bean, V.; Ehrlich, C. The reduction of uncertainties for absolute piston gauge pressure measurements in the atmospheric pressure range. J. Res. Natl. Inst. Stand. Technol. 1989, 94, 343–346. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Jing, H.; Bao, J.; Sun, S.; Wang, R. Robust H∞ fault tolerant control for quadrotor attitude regulation. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 1302–1313. [Google Scholar] [CrossRef]
- Romero, A.; Sun, S.; Foehn, P.; Scaramuzza, D. Model Predictive Contouring Control for Time-Optimal Quadrotor Flight. IEEE Trans. Robot. 2022, 38, 3340–3356. [Google Scholar] [CrossRef]
- Wang, X.; Dong, H.; Sun, X.; Yao, X. PD control of inverted pendulum based on adaptive fuzzy compensation. J. Intell. Fuzzy Syst. 2016, 31, 3013–3019. [Google Scholar] [CrossRef]
- Sharma, A.K.; Bhushan, B. Comparison of various fuzzy sliding mode based controller on single link inverted pendulum. J. Intell. Fuzzy Syst. 2022, 42, 679–688. [Google Scholar] [CrossRef]
- Semenov, M.E.; Solovyov, A.M.; Popov, M.A.; Meleshenko, P.A. Coupled inverted pendulums: Stabilization problem. Arch. Appl. Mech. 2017, 88, 517–524. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Wang, T.; Zhang, Y.; Li, X. Nonlinear dynamics modeling and simulation of two-wheeled self-balancing vehicle. Int. J. Adv. Robot. Syst. 2016, 13, 156–171. [Google Scholar] [CrossRef]
- Huang, C.-N. The Development of Self-Balancing Controller for One-Wheeled Vehicles. Engineering 2010, 2, 212–219. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. Active-Disturbance-Rejection-Based Sliding-Mode Current Control for Permanent-Magnet Synchronous Motors. IEEE Trans. Power Electron. 2020, 36, 751–760. [Google Scholar] [CrossRef]
- Tarczewski, T.; Grzesiak, L.M. Constrained State Feedback Speed Control of PMSM Based on Model Predictive Approach. IEEE Trans. Ind. Electron. 2015, 63, 3867–3875. [Google Scholar] [CrossRef]
- Lee, D.; Cheon, Y.; Ryu, J.-H.; Lee, I.-B. An MCFC operation optimization strategy based on PID auto-tuning control. Int. J. Hydrogen Energy 2017, 42, 25518–25530. [Google Scholar] [CrossRef]
- Rakhtala, S.; Roudbari, E.S. Fuzzy PID control of a stand-alone system based on PEM fuel cell. Int. J. Electr. Power Energy Syst. 2016, 78, 576–590. [Google Scholar] [CrossRef]
- Gün, A. Attitude control of a quadrotor using PID controller based on differential evolution algorithm. Expert Syst. Appl. 2023, 229, 412–424. [Google Scholar] [CrossRef]
- Nocoń, Ł.; Koruba, Z. Modified linear-quadratic regulator used for controlling anti-tank guided missile in vertical plane. J. Theor. Appl. Mech. 2020, 58, 723–732. [Google Scholar] [CrossRef]
- Borrelli, F.; Keviczky, T. Distributed LQR Design for Identical Dynamically Decoupled Systems. IEEE Trans. Autom. Control 2008, 53, 1901–1912. [Google Scholar] [CrossRef]
- Tingting, Y.; Aijun, L.; Taimoor, M.; Amin, R.U. High AOA short landing robust control for an aircraft. Aircr. Eng. Aerosp. Technol. 2018, 91, 38–49. [Google Scholar] [CrossRef]
- Pan, S. Robust control of gyro stabilized platform driven by ultrasonic motor. Sens. Actuators A Phys. 2017, 261, 280–287. [Google Scholar] [CrossRef]
- Abbasi, S.M.M.; Jalali, A. Fuzzy tracking control of fuzzy linear dynamical systems. ISA Trans. 2020, 97, 102–115. [Google Scholar] [CrossRef]
- Yoon, J.H.; Bak, G.-M.; Bae, Y. Fuzzy Control for Chaotic Confliction Model. Int. J. Fuzzy Syst. 2020, 22, 1961–1971. [Google Scholar] [CrossRef]
- Lu, Y. Adaptive-fuzzy control compensation design for direct adaptive fuzzy control. IEEE Trans. Fuzzy Syst. 2018, 26, 3222–3231. [Google Scholar] [CrossRef]
- Canciello, G.; Cavallo, A.; Cucuzzella, M.; Ferrara, A. Fuzzy scheduling of robust controllers for islanded DC microgrids applications. Int. J. Dyn. Control. 2019, 7, 690–700. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Z.; He, W.; Hong, K.-S.; Li, H.-X. Boundary adaptive fault-tolerant control for a flexible Timoshenko arm with backlash-like hysteresis. Automatica 2021, 130, 109690. [Google Scholar] [CrossRef]
- Sang, H.; Zhou, Y.; Sun, X.; Yang, S. Heading tracking control with an adaptive hybrid control for under actuated underwater glider. ISA Trans. 2018, 80, 554–563. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Vázquez, A.J.; Fernández-Anaya, G.; Meléndez-Vázquez, F.; Torres, J.D.S. Generalised conformable sliding mode control. Math. Methods Appl. Sci. 2021, 45, 1687–1699. [Google Scholar] [CrossRef]
- Ma, H.; Wu, J.; Xiong, Z. Discrete-time sliding-mode control with improved quasi-sliding-mode domain. IEEE Trans. Ind. Electron. 2016, 63, 6292–6304. [Google Scholar] [CrossRef]
- Canciello, G.; Cavallo, A.; Schiavo, A.L.; Russo, A. Multi-objective adaptive sliding manifold control for More Electric Aircraft. ISA Trans. 2020, 107, 316–328. [Google Scholar] [CrossRef]
- Nichols, G.P.; Fontenot, J.D.; Gibbons, J.P.; Sanders, M. Evaluation of volumetric modulated Arc therapy for postmastectomy treatment. Radiat. Oncol. 2014, 9, 66. [Google Scholar] [CrossRef]
- Wang, F.; Chen, K.; Zhen, S.; Zheng, H.; Chen, X.; Chen, F. Optimal design of Udwadia–Kalaba theory-based adaptive robust control for permanent magnet linear synchronous motor. J. Vib. Control 2023, 10775463221149086. [Google Scholar] [CrossRef]
- Nadda, S.; Swarup, A. On adaptive sliding mode control for improved quadrotor tracking. J. Vib. Control 2017, 24, 3219–3230. [Google Scholar] [CrossRef]
- Jain, A.; Sharma, A.; Jately, V.; Azzopardi, B.; Choudhury, S. Real-Time Swing-Up Control of Non-Linear Inverted Pendulum Using Lyapunov Based Optimized Fuzzy Logic Control. IEEE Access 2021, 9, 50715–50726. [Google Scholar] [CrossRef]
- Luo, Z.; Xu, L. Research on LQR controller of control torque gyro self-balancing vehicle based on QPSO optimization. J. Phys. Conf. Ser. 2022, 2258, 012071. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar] [CrossRef]
- Yuan, C.; Zhou, X.; Ma, Y.; Gao, Z.; Zhou, Y.; Wang, C. Improved Application of Third-Order LADRC in Wind Power Inverter. Energies 2020, 13, 4412. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, T. Based on robust sliding mode and linear active disturbance rejection control for attitude of quadrotor load UAV. Nonlinear Dyn. 2022, 108, 3485–3503. [Google Scholar] [CrossRef]
- Zeng, J.; Huang, Z.; Huang, Y.; Qiu, G.; Li, Z.; Yang, L.; Yu, T.; Yang, B. Modified linear active disturbance rejection control for microgrid inverters: Design, analysis, and hardware implementation. Int. Trans. Electr. Energy Syst. 2019, 29, e12060. [Google Scholar] [CrossRef]
- Ramasamy, K.; Rathinasamy, S.; Kwon, O.M.; Palanisamy, S. Robust tracking control design for fractional-order interval type-2 fuzzy systems. Nonlinear Dyn. 2021, 107, 3611–3628. [Google Scholar] [CrossRef]
- Qiu, T.; Dai, H.; Lei, Y.; Liu, Y. Effects of valve needle speed on flow characteristics in control valve for unit pump fuel system. Adv. Mech. Eng. 2018, 10, 378–389. [Google Scholar] [CrossRef]
- Kavikumar, R.; Kwon, O.-M.; Kaviarasan, B.; Sakthivel, R. Antidisturbance Control Design for Interval Type-2 Fuzzy Stochastic Systems with Input Quantization. IEEE Trans. Fuzzy Syst. 2022, 31, 1806–1818. [Google Scholar] [CrossRef]
- Bobovnik, G.; Kutin, J. Correlation of the leakage flow rate with pressure changes in a clearance-sealed piston prover. Flow Meas. Instrum. 2020, 74, 101785. [Google Scholar] [CrossRef]
- Yu, B.; Shen, A.; Chen, B.; Luo, X.; Tang, Q.; Xu, J.; Zhu, M. A Compensation Strategy of Flux Linkage Observer in SPMSM Sensorless Drives Based on Linear Extended State Observer. IEEE Trans. Energy Convers. 2021, 37, 824–831. [Google Scholar] [CrossRef]
- Liang, Q.; Wang, C.; Pan, J.; Wei, Y.; Wang, Y. Identification of linear self-adjoint control parameters b0 and parameter tuning laws. Control Decis. Mak. 2015, 30, 1691–1695. [Google Scholar]
- Ren, Q.; Bigras, P. A Highly Accurate Model-Free Motion Control System with a Mamdani Fuzzy Feedback Controller combined with a TSK Fuzzy Feed-forward Controller. J. Intell. Robot. Syst. 2017, 86, 367–379. [Google Scholar] [CrossRef]



| e1 | e2 | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB | PB | PM | PM | PS | PS | ZO |
| NM | PB | PB | PM | PM | PS | ZO | ZO |
| NS | PM | PM | PM | PS | ZO | NS | NM |
| ZO | PM | PS | PS | ZO | NS | NM | NM |
| PS | PS | PS | ZO | NS | NS | NM | NM |
| PM | ZO | ZO | NS | NM | NM | NM | NB |
| PB | ZO | NS | NS | NM | NM | NB | NB |
| e1 | e2 | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | NS | NS | ZO | ZO | PS | ZO | NB |
| NM | PS | PS | PS | PS | PS | ZO | PS |
| NS | PB | PB | PM | PS | PS | ZO | NS |
| ZO | PB | PM | PM | PS | ZO | ZO | NS |
| PS | PB | PM | PS | PS | NS | ZO | NS |
| PM | PM | PS | PS | PS | NS | ZO | NS |
| PB | NS | ZO | ZO | ZO | NS | ZO | NB |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Cd | 0.9 | ac | 4.5 × 10−5 °C−1 |
| ρ | 1.25 kg/m3 | ae | 4.5 × 10−5 °C−1 |
| λ | 7.1 × 10−7 MPa−1 | θ | 21 °C |
| 6 × 10−7 m | T | 294 k | |
| R | 296.8 J/(kg∙K) | μ | 1.741 × 10−2 N·s·m−2 |
| Z | 0.292 | A1 | 7.85 × 10−9 m2 |
| V0 | 3.7 × 10−7 m3 | A0 | 5 × 10−5 m2 |
| Parameters | Value | ||
|---|---|---|---|
| 0.1 MPa | 3 MPa | 6 MPa | |
| m1 | 2.94 × 10−9 kg | 3.53 × 10−10 kg | 1.12 × 10−9 kg |
| m2 | 2.23 × 10−9 kg | 1.93 × 10−9 kg | 2.73 × 10−9 kg |
| mw | 0.5 kg | 16 kg | 32 kg |
| Controllers | Value | ||
|---|---|---|---|
| 0.1 MPa | 3 MPa | 6 MPa | |
| Kp | 55 | 65 | 90 |
| PID | Kp = 26, Ki = 0.55, K1d = 7.5 | K1p = 30, K1i = 0.5, K1d = 7 | K1p = 40, K1i = 0.9, K1d = 8 |
| LADRC | r = 4, ωc = 46, b0 = 0.22 | r = 4, ωc = 77, b0 = 0.37 | r = 4, ωc = 65, b0 = 0.25 |
| FLADRC | Range1 = [−4, 4] Range2 = [−0.022, 0.022] | Range1 = [−7, 7] Range2 = [−0.037, 0.037] | Range1 = [−6, 6] Range2 = [−0.025, 0.025] |
| Conditions | Kp | PID | LADRC | FLADRC |
|---|---|---|---|---|
| 0.1 MPa | 23.36 | 19.58 | 14.87 | 12.37 |
| 3 MPa | 18.72 | 14.76 | 11.84 | 8.54 |
| 6 MPa | 20.98 | 15.79 | 12.04 | 8.67 |
| Conditions | Kp | PID | LADRC | FLADRC |
|---|---|---|---|---|
| 0.1 MPa | 27.62 | 22.48 | 17.09 | 13.26 |
| 3 MPa | 21.67 | 16.28 | 14.85 | 9.87 |
| 6 MPa | 25.33 | 22.03 | 13.07 | 10.41 |
| Conditions | Kp | PID | LADRC | FLADRC |
|---|---|---|---|---|
| 0.1 MPa | 18.23% | 18.95% | 14.92% | 7.19% |
| 3 MPa | 15.76% | 12.06% | 11.74% | 10.77% |
| 6 MPa | 21.97% | 13.29% | 8.33% | 6.22% |
| Conditions | Kp | PID | LADRC | FLADRC |
|---|---|---|---|---|
| 0.1 MPa | 19.21% | 10.44% | 3.35% | 1.51% |
| 3 MPa | 15.34% | 9.16% | 7.63% | 2.68% |
| 6 MPa | 16.47% | 9.79% | 4.44% | 1.24% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhai, X.; Gao, T.; Wang, N.; Zhao, Z.; Pang, G. Balancing Control of an Absolute Pressure Piston Manometer Based on Fuzzy Linear Active Disturbance Rejection Control. Actuators 2023, 12, 275. https://doi.org/10.3390/act12070275
Wu H, Zhai X, Gao T, Wang N, Zhao Z, Pang G. Balancing Control of an Absolute Pressure Piston Manometer Based on Fuzzy Linear Active Disturbance Rejection Control. Actuators. 2023; 12(7):275. https://doi.org/10.3390/act12070275
Chicago/Turabian StyleWu, Hongda, Xianyi Zhai, Teng Gao, Nan Wang, Zongsheng Zhao, and Guibing Pang. 2023. "Balancing Control of an Absolute Pressure Piston Manometer Based on Fuzzy Linear Active Disturbance Rejection Control" Actuators 12, no. 7: 275. https://doi.org/10.3390/act12070275
APA StyleWu, H., Zhai, X., Gao, T., Wang, N., Zhao, Z., & Pang, G. (2023). Balancing Control of an Absolute Pressure Piston Manometer Based on Fuzzy Linear Active Disturbance Rejection Control. Actuators, 12(7), 275. https://doi.org/10.3390/act12070275








