Abstract
Valve switching is one of the most important power losses in digital hydraulics. In this paper, a dynamic Zero-Flowrate-Switching (ZFS) control method is developed for hydraulic/pneumatic systems. The proposed control strategy is to actively reduce the flowrate passing through the valve to zero before switching off the valve. To realize it, an accessory line, in which a RLC oscillator is applied to generate a sinusoidal flowrate, is allocated parallel to the main control line for flowrate regulation. The pressure, with high frequency and small amplitude wave outputs from a regular piston pump, is used to drive the RLC oscillator. To evaluate the performance of this strategy, mathematical models for switching power loss and pressure pulses are developed and characteristic analysis is conducted. The results show that the energy loss of the system when applying the dynamic ZFS controller is reduced to 16% compared to that of a normal hydraulic system without a dynamic ZFS controller; moreover, pressure pulses in a dynamic ZFS system are much more minor than those in a Hard-Switching system.
1. Introduction
Digital hydraulic systems, which apply a number of fast-switching valves switching at high frequencies [1,2,3,4,5,6], show higher theoretical efficiency and better controllability than traditional servo/proportional ones. In principle, applying fast switching valves in digital hydraulic systems could efficiently avoid energy consumptions that go over the valves. However, the response time of physical valves can only achieve between 1–2 ms; during a switching-off process, a certain switching power loss will be generated, since a pressure difference and flowrate exist before the valve is completely switched off. Moreover, when the valve is suddenly switched off, the fluid with a large kinetic energy will generate large pressure pulses, which lead to vibrations and noises and make the system less efficient and accurate [7].
In recent years, many works in digital hydraulics have been conducted to improve system efficiency and eliminate pressure pulses [8,9,10,11,12]. For example, the Fibonacci coding method is proposed to ease the pressure pulses by decreasing the quantity of digital valves switching at the same time compared to binary coding in a PCM method [8]. A flatness-based controller is designed for the Hydraulic Buck Converter (HBC), which aims to attenuate pressure ripples and oscillatory response [9]. In addition, Johnston et al. proposed some analytical models for a switched inertance hydraulic system in a four-port high-speed switching valve configuration [10,11,12]. These models provide promising ways to understand the characteristics of a four-port hydraulic system that includes a flowrate/pressure response. With these models, they analyzed the performance of a flow booster with a high-speed rotary valve, which is designed to minimum the pressure/flow loss through the valve orifice. They also proposed an active method for pressure pulsation cancellation by superimposing an anti-phase control signal. In [13] Y. Alexander C. and V. James D. proposed a soft-switching method in a switched inertance hydraulic circuit. In the proposed method, the flow that would otherwise be throttled across the transitioning valve is stored in a capacitive element and bypassed through check valves in parallel with the switching valves. This method aims to reduce the switching power loss caused by the overlap of the directional valves. In [14], a monotube was applied to absorb pressure shock.
The nature of control valves is to throttle flowrate and yield pressure pulses. All the research above was to passively improve system efficiency, while none of the studies focused on the reason for pressure pulses and energy consumption. In [15], we firstly proposed the concept of the Zero-Flowrate-Switching controller, which reduces energy loss by reducing the flowrate of the switcher to zero when it is time to shut off the switcher. In this way, it is possible to greatly depress pressure pulses and ultimately reduce energy consumption. The ZFS control method for hydraulic applications is inspired by electronic soft-switching techniques [16,17,18,19]. A resonant line is based on a RLC oscillator and assisted by other potential lines to achieve the purpose. A theoretical framework of a ZFS controller for a basic one-direction actuation system was mathematically modeled. In [15], the frequency and amplitude of the supply pressure were assumed as 50 Hz and 1 bar to validate the feasibility of the ZFS controller in a simple one-direction hydraulic line; however, there is a key problem in the application of the ZFS controller: a ZFS controller needs an AC supplier while the DC source is employed in hydraulic systems. To solve this problem, the authors figured out a new measuring method—the fiber brag measuring method—to measure the output pressures of an actual pump (Hydroleduc W12) [20,21]. In the following publication [22], we validated the feasibility of the output pressure waves of the actual pump as the supplier of a ZFS controller, and the result was positive. Additionally, we analyzed the characteristics of this ZFS controller in a double-direction hydraulic line. The results presented a 14.7% switching power loss compared to that of a Hard-Switching (HS) control system in a double-direction hydraulic system.
However, the characteristics of hydraulic systems are different from that of electronic counterparts. The performance is complex in the valve start-up process [23]. Many hydraulic problems should be resolved before a real hydraulic ZFS model is developed. Linear hydraulic components such as the inductance/capacitance should be investigated in a RLC resonator; unexpected hydraulic capacitance needs to be properly considered, since dynamic load forces have an impact on pressure/flowrate response and system capacitance. In this paper, a dynamic ZFS control method for a 4-port hydraulic system is proposed. In the dynamic ZFS controller presented in this paper, dynamic load forces are applied in the model; in the meantime, the impact of the dynamic load forces on the cylinder chamber pressures/flowrates and system capacitance is also considered in this advanced model.
The paper is organized as follows. The second section explains how the switching power loss and pressure pulses are generated in a switching system; the third section presents the schematic of a ZFS control system where two ZFS controllers are used for both extension and drawing back motions of the cylinder in a typical four-port switching system; the principle of a ZFS controller is introduced in this section; after that, mathematic models are built in Section 4; in Section 5, a dynamic load is modeled, cylinder capacitance is investigated, and the switching power loss and pressure pulses are also modeled. After that, simulation results are presented in Section 6. At the end of the paper comes the conclusions for this proposed hydraulic control method.
2. Statement of the Problems and Principle of the ZFS Control Method
2.1. Statement of the Problems
As presented in Figure 1, a typical digital hydraulic system actuates the hydraulic cylinder by several fast-switching valves. When the piston of the cylinder is extending, the fluid flows, as indicated by the red arrows; when extracting, the circuit works in the way presented by the white arrows.
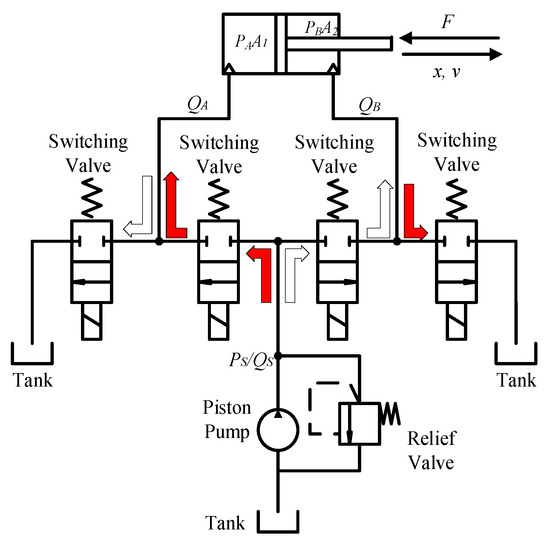
Figure 1.
Schematic of a digital hydraulic system.
When the cylinder is extending, the control line between the power unit and the cylinder is simplified, as Figure 2 shows. The power source PS supplies the load (pressure PA and flowrate QA) through a fast-switching valve. The fast-switching valve is powered by a PWM controller which actuates the valve to switch at a high frequency. Switching off the valve introduces switching power loss and pressure pulses which make the system response less smooth and less efficient. Moreover, it results in noises and vibrations that do harm to the system. Referring to the concept of the ZFS controller, this line is referred to as ‘a Hard-Switching (HS) Controller’.
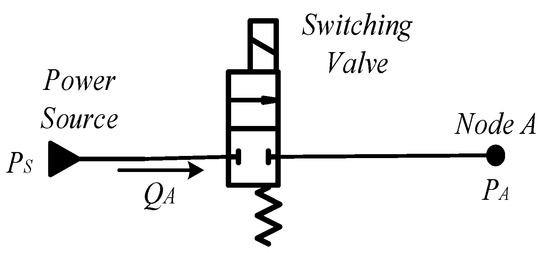
Figure 2.
A hydraulic line for extending motion (HS Controller).
2.1.1. Switching Power Loss
Theoretically, the fast-switching valve works only in ON and OFF states; the switching power loss is supposed to be zero. However, physical switching valves are not ideal ones. It is assumed that the flowrate-to-time is linear for the valve opening of valve 1 and valve 2, thus the orifice coefficient of the valve opening is
where t is time, t0 is the initial moment to switch the valve and TS is the switching time of the valve. During the switching process, both the flowrate and pressure difference are none-zero. The switching power loss for the switching valve in Figure 2 is derived as
where T is the time period of the pressure waves; N = 0, 1, 2, 3…; as presented in Figure 3, at the beginning of the switching-off process, PS(t) − PA(t) is small but the value of QA(t) is close to required flowrate; at the end of the switching-off process, PS(t) − PA(t) is equal to PS(t), which is a large value, while Q(t) is small. A certain level of power loss is observed during this process.
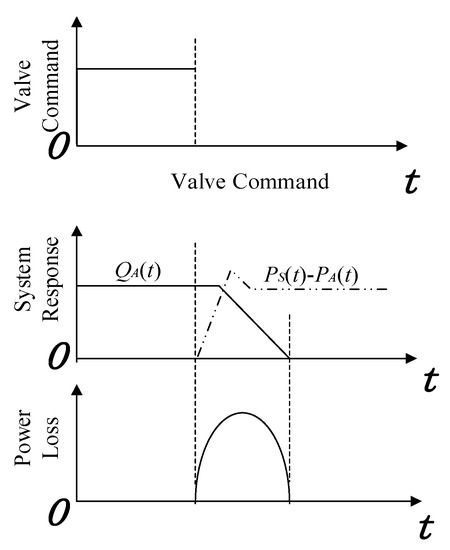
Figure 3.
Switching power loss for a simple hydraulic line.
As indicated in Equation (2), a high switching frequency fPWM, large flowrate QA or pressure difference will give rise to switching power loss, which is a serious problem in the applications with high frequent switching, large system flowrate or large pressure difference.
2.1.2. Pressure Pulses
When the switching valve shuts off suddenly, the fluid energy before the valve fulfills
where the kinetic energy Ek and the potential energy Ep [24] are
where ρ is the density of hydraulic fluid; Lpipe is the length of the pipe between the pump and the valve; A is the area of the pipe; v0 is the velocity of the fluid; E is the elastic bulk of the fluid and Ppulse is the peak value of the pressure pulses. According to Equations (3)–(5), the larger the flowrate is, the higher the pressure pulses are. Pressure pulses are normally found in systems with large flowrates.
2.2. Why the ZFS Control Method?
As stated above, systems with large flowrates can suffer both switching power loss and pressure pulses; reducing the flowrate before the pressure goes up to a certain level is a solution for both problems (shown in Figure 4). A Zero-Flowrate-Switching (ZFS) control method is a way to make the flowrate through the switching valve as small as possible during the switching-off process. In this way, it restrains pressure pulses and reduces switching power loss for high switching-frequency hydraulic systems.
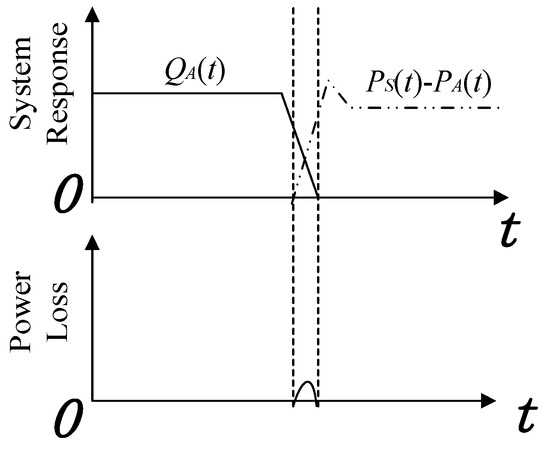
Figure 4.
Switching power loss for a ZFS system.
2.3. The Principle of the ZFS Control Method
2.3.1. A ZFS Controller
In this paper, the ZFS control method is proposed to actively reduce switching power loss and restrain the pressure pulses for a typical four-port switching system—shown in Figure 1—to achieve a more efficient and smoother performance. The four-port switching hydraulic system controlled by the ZFS controllers is shown in Figure 5. The groups covered by red sheets are two ZFS controllers: one is to regulate extension motion and the other is for the drawing back of the cylinder. A ZFS controller includes a main control valve and a resonant line; the resonant line consists of a switching valve, a hydraulic inductance and a hydraulic capacitance.
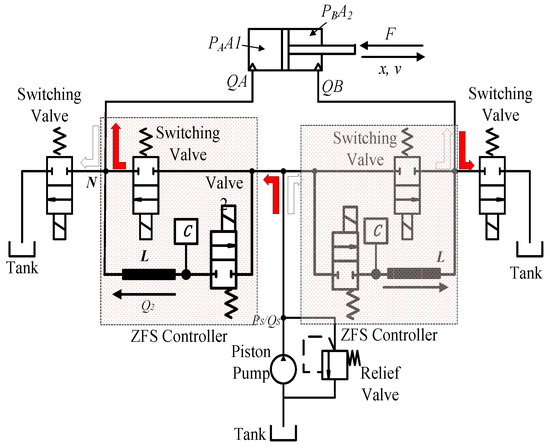
Figure 5.
A 4-port switching system controlled by ZFS controllers.
The ZFS control method is to regulate the flowrate of the switching valve to zero right before the valve switches off. Figure 6 presents a hydraulic schematic of a ZFS controller. It consists of a main control line and a resonant line. The main control line is to supply the pressure and flowrate for the load. When it is about to close the main control line, it opens the resonant line, and then the flowrate of the resonant line starts to increase. Accordingly, the flowrate of the main control line falls down until it is zero. Then, the main control line is closed. This is the principle of a ZFS controller.
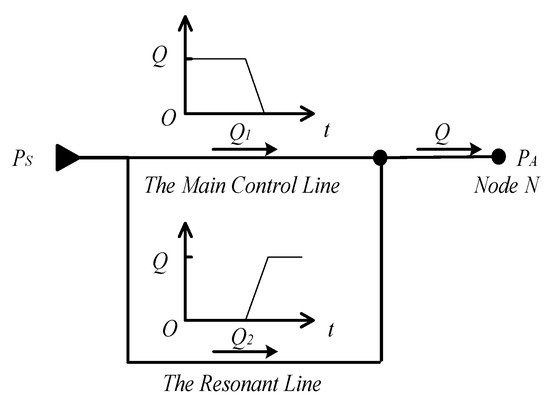
Figure 6.
Schematic of a ZFS control system.
2.3.2. A Resonant Line
An electronic RLC resonator, shown in Figure 7a, consists of resistance, inductance and capacitance. When the inductance is equal to the capacitive reactance, the electronic flow will resonate with the excitation of an AC source.
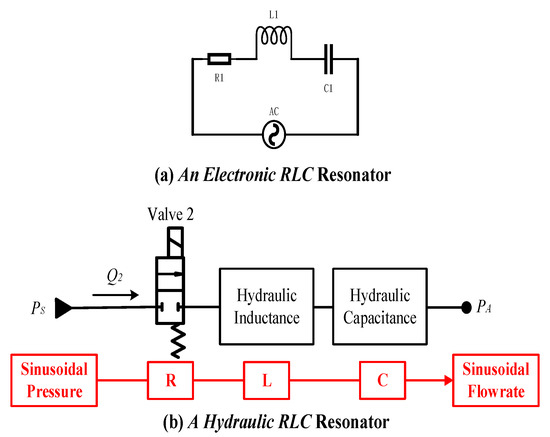
Figure 7.
Comparison of an electronic RLC resonator and a hydraulic RLC resonator.
In a hydraulic counterpart, the resonant line is composed of a fast-switching valve, hydraulic inductance and hydraulic capacitance (shown in Figure 7). The power supplier is a regular piston pump which outputs constant pressure with tiny amplitude waves.
where PS0 is the average value of the supplied pressure; PSa is the amplitude of the pressure waves and ω is the angular speed of the pressure waves. The term is used to generate the sinusoidal resonant flowrate Qres. When the RLC resonator works, the pressure waves distributed along the line are represented as
where Qres is resonant flowrate and C is number for the hydraulic capacitance. For this case, the relationship between the pressure drop p and flowrate q of the valve is assumed to be linear
Differentiating and dividing by L leads to the second order differential equation
when
the output flowrate Qres is derived as
To make the ZFS controller work, Qres fulfills
3. Mathematic Model of a ZFS Control System
In this section, a ZFS control model with a dynamic load force will be introduced. In [20], the authors have proposed a basic ZFS model. As shown in Figure 8, valve 1 is the control valve which stays open when the control line (the line between power source and PA) is working. When the control line is required to stop, valve 1 will not switch off immediately; instead, the resonant line will start to participate in order to switch off the control line until the control line is ultimately switched off. There are four modes during the whole switching-off process: mode 1, mode 2, mode 3 and mode 4. The working principle for the four modes is explained in [20]; the related flowrates for each of the modes are presented in Table 1.
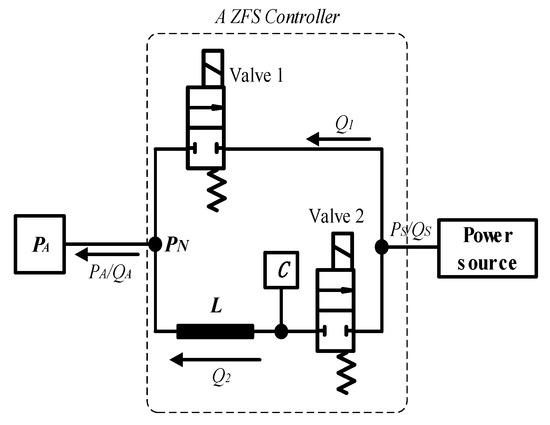
Figure 8.
ZFS Control strategy for extending motion.

Table 1.
State matrix of the valves.
3.1. Dynamic Load of the ZFS Controller
Based on the model in Figure 8, the system characteristics with dynamic loads will be further discussed in this work. In the model described in Figure 8, the piston is moving with a constant velocity and varied load force, thus the input pressure of the cylinder is
The tank pressure is zero, thus the pressure PB can be regarded as the pressure difference across the valve, and is derived as follows
where Cq is flow coefficient and ρ is the density of the fluid. Hence, PA is derived as
3.2. Dynamic Capacitance of the Cylinder
In a ZFS controller, the resonant line generates flowrate waves to make the flowrate through the valves reduce to zero. Theoretically, the valve switches off at the zero-flowrate moment, and the power loss is thus zero. However, the switching-off moment of the valve cannot exactly match the zero-flowrate moment in a real hydraulic system. The error between the switching-off moment and the zero-flowrate moment will lead to some power loss. The larger the error is, the more the power loss is. Therefore, accurately simulating zero-flowrate moments is very important to improve system efficiency.
Normally, the input flowrate of a cylinder is calculated with the piston velocity timing and piston area. However, the capacitance of the input chamber of a cylinder has an influence on its flowrates. When the system load force is various, cylinder capacitance can be complex. To better simulate the input flowrate of the cylinder, the influence of the capacitance on the cylinder input flowrate is modeled. When the load force is changing, the cylinder chamber works as the capacitance Ccyl; the following relationship is derived using Equation (13)
where cylinder capacitance Ccyl is determined by the dimensions of the cylinder chamber and the pipe between the control valve and the cylinder input port.
Then, the flowrate change due to the load change is obtained.
where QA is
3.3. Switching Power Loss
Switching power loss exists due to the pressure difference and flowrate during the switching-off process. Physical switching valves are not ideal ones which transfer directly from an ON state to an OFF state. Actually, the orifice of the valve is gradually closed until the valve is completely switched off.
In a ZFS controller, two switching valves are located in the circuit. Theoretically, two switching valves are designed to switch off at the zero-flowrate moment.
The switching power loss for valve 1 is
The switching power loss for valve 2 is
Total switching loss for a ZFS controller is
It is assumed that pressure pulses happen after the switching-off process of the valves. The total value of the fluid energy before and after the switching-off process is kept constant, which fulfills Equation (3). By substituting Equations (4) and (5) with Equation (3), it is obtained that
The switching pulse for valve 1 is derived by substituting Equation (21) for Equation (24)
The switching pulse for valve 2 is derived by substituting Equation (22) for Equation (25)
4. Stateflow Controller
Figure 9 shows the schematic of the electronic controller for a ZFS control system. Position of the cylinder piston, flowrate of hydraulic lines, and system pressures are collected by the transducers and sent to a PC. When it is ready to switch off the control line, the PC sends a command to a stateflow controller. At the same time, the flowrate of Q1 and Q2 are also sent to the stateflow controller.
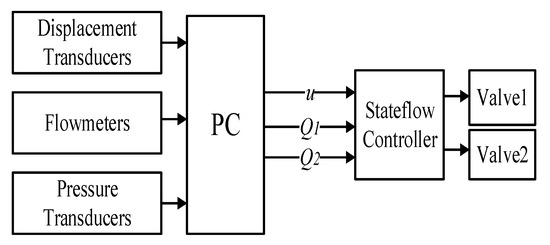
Figure 9.
Schematic of the electronic controller for a ZFS System.
The stateflow chart (shown in Figure 10) determines the running mode of the system. When the stateflow controller receives command u from the PC, the system automatically runs in mode 1; when u = 1 is true, the controller is switched to mode 2; when Q1 = 0 is true, the controller is switched from mode 2 to mode 3; when Q2 = 0 is true, the controller is switched to mode 4. The conditions are defined as:
Mode 1_feas: u = 0,
Mode 2_feas: u = 1,
Mode 3_feas: Q1 = 1,
Mode 4_feas: Q2 = 1,
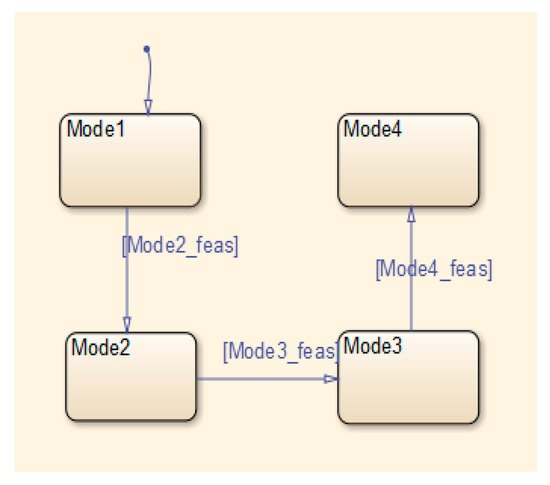
Figure 10.
Schematic of the stateflow chart characteristics of a ZFS Controller.
Figure 11 shows the relationship between the performance of a ZFS controller and some parameters of the system. The power source provides PS/QS as an input of the ZFS controller. Most piston pumps are feasible options to pressurize the system with proper pressure waves due to the reciprocating movement of the pistons. The output of the ZFS controller is defined by system parameters: the PA is required by the velocity and dimensions of the cylinder, as well as the exerted load force on the cylinder rod. The QA basically adapts the velocity of the cylinder. The capacitance of the cylinder would also have an effect on the QA, since a large derivation of the load force creates a certain flowrate within a fixed volume (the cylinder chamber can be regarded as a fixed volume when the time derivation is very small). A stateflow controller is employed to detect zero-flowrate moments and make decisions about when to switch the valves.
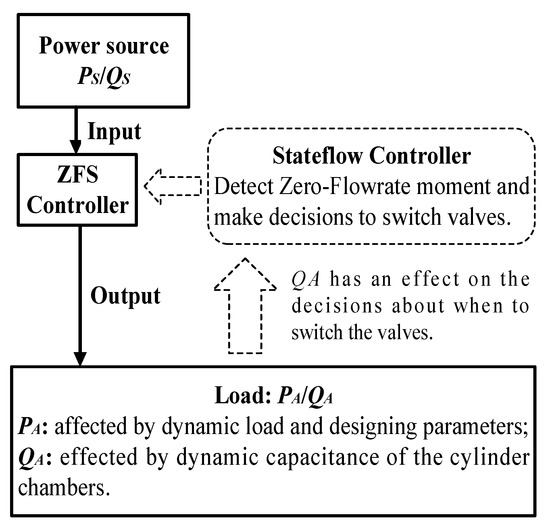
Figure 11.
Parameters that have an effect on the performance of a ZFS controller for the extension motion of the cylinder.
In this section, the output PA and QA are modeled taking into consideration the dynamic load of the system and the dynamic capacitance of the cylinders. The models of switching power loss are built for both valves in the ZFS controller based on a linear characteristic of the valve opening. The pressure pulses are modeled for both valves in a ZFS controller according to the principle of fluid energy. All the models are built based on the following assumptions:
- (1)
- The pump outputs sinusoidal pressures at one frequency.
- (2)
- All the valves switch at zero-flowrate moments.
- (3)
- The opening of the valves changes linearly during switching processes.
5. System Evaluation
A dynamic ZFS controller (shown in Figure 12a,b) and a Hard-Switching (HS) system (shown in Figure 12c,d) are built for evaluation. A hydraulic inductance is realized by a piece of pipe with a length of 0.2 m and diameter of 0.008 m. A hydraulic capacitance is realized by an accumulator with a linear spring; the volume of the accumulator is 0.8 L.
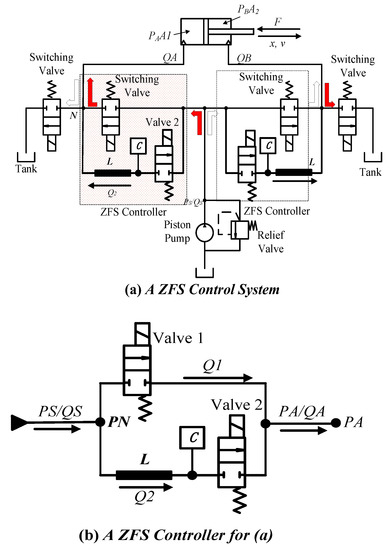
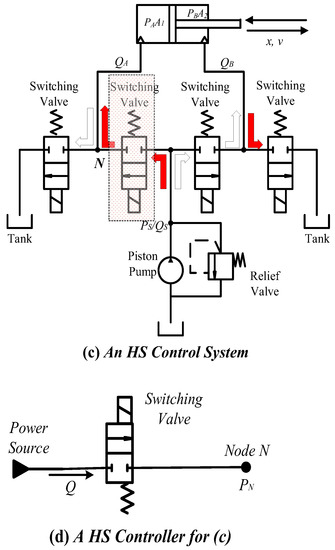
Figure 12.
A ZFS control system and a HS control system.
The characteristics of the two systems are evaluated in this section. The dynamic capacitance, switching power loss and pressure pulses due to the switching-off of the valves are analyzed, respectively.
The tested systems are operated to drive a load at the speed of 0.06 m/s and with a load force of 40,000 N. The system pressure is 205 bar with waves whose amplitude and frequency are 2 bar and 113 Hz, respectively. The maximum flowrate of the pump is 7.5 L/min. Other parameters of the systems are presented in Table 2.

Table 2.
System parameters.
5.1. Dynamic Capacitance of the Cylinder
When the piston of the cylinder is moving, the volume of the cylinder chamber is varied; the varied chamber shows capacitance when the load force is changing. Such dynamic capacitance leads to flowrate change. According to Equation (12), the pipe volume and piston area have an effect on the flowrate change. Figure 13 presents a linear relationship between the position of piston x and the derivation of flowrate dQ. The piston area is 0.002 m2, the diameter of the pipe of 0.012 m and the length of the pipe is 1 m. As the position of piston x increases from 0 m to 0.2 m, the derivation of flowrate dQ linearly increases correspondingly. When dF is 200 N, the derivation of flowrate dQ is relatively small and the slope of the curve is small; as dF increases, both dQ and the slope of the curve respond to this increase.
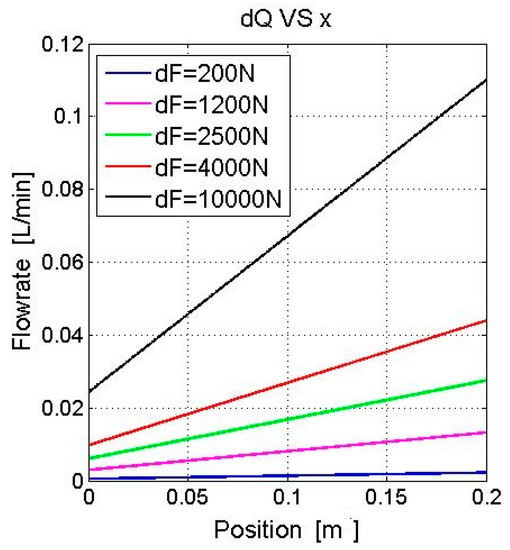
Figure 13.
Parameters that have an effect on the flowrate change (lpipe = 1 m; dpipe = 0.012 m; Apis = 0.002 m2).
Figure 14 presents the relationship between the piston area and the flowrate change when the position of piston x = 0.2 m. When dF is fixed, it shows that the smaller the area of the piston is, the larger the derivation of the flowrate is. When the flowrate change dQ becomes infinitely large, then the area of the piston Apis becomes infinitely small.
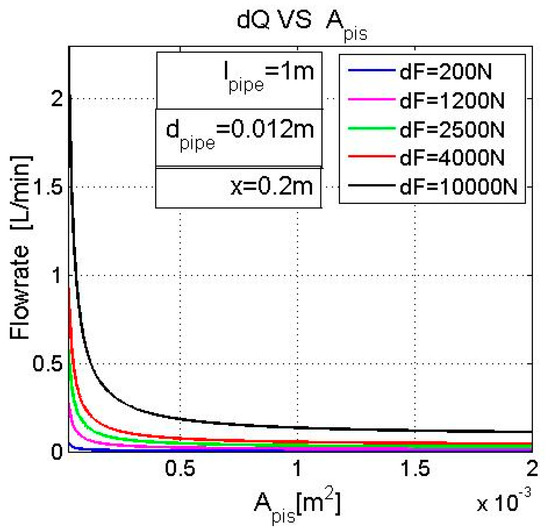
Figure 14.
Parameters that have an effect on the flowrate change (lpipe = 1 m; dpipe = 0.012 m; x = 0.2 m).
When the area of the piston is Apis fixed, the derivation of flowrate dQ changes as the derivation of force dF increases. Take Apis = 5 m2, for example; the derivations of the flowrates are dQ = 0.0038 L/min when dF = 200 N, 0.023 L/min for when dF = 1200 N, 0.053 L/min when dF = 2500 N, 0.073 L/min when dF = 4000 N and 0.2 L/min when dF = 10,000 N.
A similar effect, the one the area of piston Apis has on the derivation of flowrate dQ, is found in Figure 15. For a fixed pipe length lpipe, the smaller the area of piston Apis is, the larger the derivation of flowrate dQ is. Figure 14 also presents the relationship between the piston area Apis and the flowrate change dQ. When dF changes from 200 N to 10,000 N, generally speaking, dQ increases as the length of the pipe lpipe increases. When lpipe is 0 m, the line is flat and straight; when lpipe is larger, Apis has more of an effect on dQ in small, scaled devices. By comparing the five figures with each other, a larger dF leads to a larger dQ. When dF is 10,000 N and Apis is 0.002 m2, dQ is 0.1 L/min.

Figure 15.
Parameters that have an effect on the flowrate change (dF = 10,000 N; dpipe = 0.012 m; x = 0.2 m).
5.2. Switching Power Loss
The switching power loss is also investigated for the two models. Figure 16 and Figure 17 show the system responses for the dynamic ZFS system and HS system. In Figure 16, valve 2 is switched on at the end of mode 2. Then, the flowrate of the accessory line Q1 decreases as the flowrate of the main line Q2 increases. Q1 falls down to zero and then valve 1 stays closed. Q2 keeps going up and then falls down until its value is less than the load flowrate QA. Then, the supply flowrate supplies the system together with the resonant flowrate. The resonant flowrate falls down to zero and then goes in the opposite direction. Once the value of the resonant flowrate achieves the maximum supply flowrate QSmax, the flowrate Q2 starts to decrease from QA until it reaches zero. Then, valve 2 is switched off. Q2 finally stays at zero after valve 2 is completely switched off.
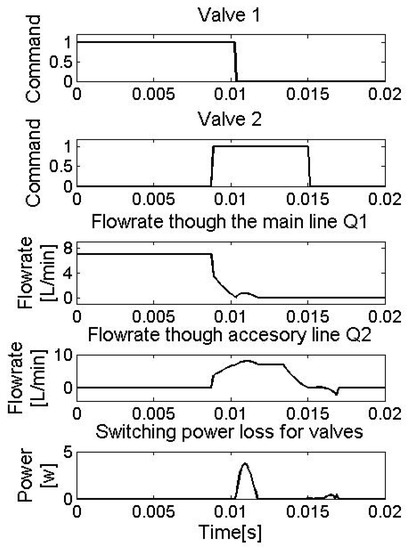
Figure 16.
System response of a ZFS System.
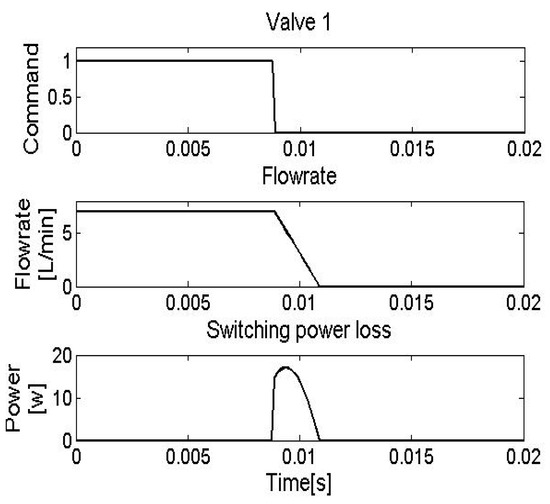
Figure 17.
System response of a HS System.
According to the fifth plot in Figure 16, switching power loss occurs during two stages: one is for valve 1 and the other is for valve 2. The peak power losses are 4 w and 0.4 w for the two stages, respectively, compared to 17 w for the HS system (shown in Figure 17). Table 3 presents the energy consumptions of the two systems. The total switching power loss consumed by the ZFS system is 32 J versus 203 J consumed by the HS system (shown in Figure 18 and Table 3).

Table 3.
Switching power loss for two systems.
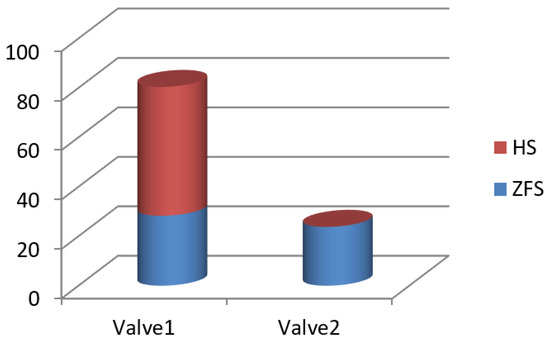
Figure 18.
Switching power loss for two systems.
5.3. Pressure Pulses
As shown in Figure 19 and Table 4, one switch in a normal HS controller excites pressure pulses with a peak value of 1.1 × 106 Pa, while the peaks of the pressure pulse are 1.1 × 104 Pa and 2.3 × 105 Pa for valve 1 and valve 2, respectively. Pressure pulses in a ZFS system are much minor than those in a HS system.
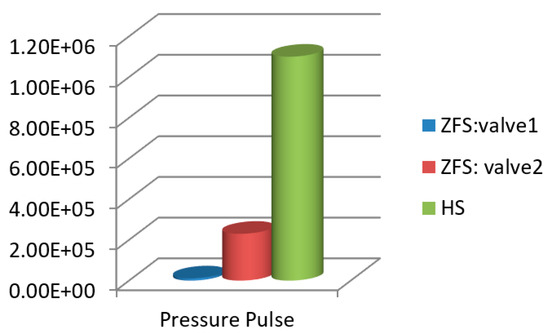
Figure 19.
Pressure pulses for two systems.

Table 4.
Pressure pulses for two systems.
6. Conclusions
In hydraulic applications, the switching-off of fast-switching valves leads to considerable switching power loss and pressure pulses. In this work, a dynamic ZFS controller is proposed to switch off valves at zero-flowrate moments. With the novel controller, the system achieves small switching power loss and suffers minor pressure pulses.
To better simulate zero-flowrate moments and make the switching power loss as small as possible, this paper takes into account the models of dynamic load forces and cylinder capacitance. In the following applications, dynamic load forces and cylinder capacitance should be considered when running a ZFS controller:
- (1)
- Applications where the cylinder stroke is large.
- (2)
- Applications where the derivation of load forces is large.
- (3)
- Applications where the piston/rod areas of the cylinders are small.
- (4)
- Applications where the pipe length between the output of the ZFS controller and the input of the cylinder is large.
The results show the advantage of a dynamic ZFS system in relation to its energy saving performance. The total switching power loss consumed by the ZFS system is 32 J versus 203 J consumed by the HS system. The system applying the dynamic ZFS controller consumes only 16% of the energy that is consumed by a normal HS system.
Moreover, the system with a dynamic ZFS controller leads to minor pressure pulses. One switch in a normal HS controller excites pressure pulses with a peak value of 1.1 × 106 Pa, while the peaks of the pressure pulse are 1.1 × 104 Pa and 2.3 × 105 Pa for valve 1 and valve 2, respectively. Pressure pulses in a dynamic ZFS system are much minor than those in a HS system.
It can be concluded that the dynamic ZFS controller provides a solution to achieve better efficiency performance and make pressure pulses as minor as possible in typical four-ports hydraulic systems. Besides in typical 4-ports hydraulic systems, switching also exists in traditional proportional/servo hydraulic systems where high frequency-switching happens. The ZFS control method provides a potential solution for those systems with large switching power loss and unsmooth pressure response caused by valve switching.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Peng, S.; Branson, D.; Guglielmino, E.; Caldwell, D.G. Simulated performance assessment of different digital hydraulic configurations for use on the HyQ. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 36–41. [Google Scholar]
- Liu, S.; Yao, B. Coordinate control of energy saving programmable valves. IEEE Trans. Control. Syst. Technol. 2008, 16, 34–45. [Google Scholar] [CrossRef]
- Kogler, H.; Scheil, R. Two basic concepts of hydraulic switching converters. In Proceedings of the First Workshop on Digital Fluid Power, Tampere, Finland, 3 October 2008. [Google Scholar]
- Peng, S.; Kogler, H.; Guglielmino, E.; Scheidl, R.; Branson, D.T.; Caldwell, D.G. The use of a hydraulic DC-DC converter in the actuator of a robotic leg. In Proceedings of the IEEE/RSJ International Conference Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Muto, T.; Yamada, H.; Suematsu, Y. PWM-Digital control of hydraulic actuator utilizing 2-way solenoid valves. J. Jpn. Hydraul. Pheumatica Soc. 1988, 19, 564–571. (In Japanese) [Google Scholar]
- Mattila, J.; Virvalo, T. Energy-efficient motion control of a hydraulic manipulator. In Proceedings of the International Conference Robotics & Automation, San Francisco, CA, USA, 24–28 April 2000. [Google Scholar]
- Karpenko, M.; Prentkovskis, O.; Šukevičius, Š. Research on high-pressure hose with repairing fitting and influence on energy parameter of the hydraulic drive. Eksploat. I Niezawodn. 2022, 24, 25–32. [Google Scholar] [CrossRef]
- Laamanen, A.; Linjama, M.; Vilenlius, M. Pressure peak phenomenon in digital hydraulic systems—A theoretical study. In Proceedings of the Power Transmission and Motion Control, Bath, UK, 7–9 September 2005. [Google Scholar]
- Kogler, H.; Winkler, B.; Scheidl, R. Flatness based control of a fast switching hydraulic drive. In Proceedings of the International Conference Computer Methods in Fluid Power, Aalborg, Denmark, 21–24 September 2006. [Google Scholar]
- Johnston, N.; Pan, M.; Plummer, A.; Yang, H. Theoretical studies of a switched inertance hydraulic system in a four-port valve configuration. In Proceedings of the The Seventh Workshop on Digital Fluid Power, Linz, Austria, 26–27 February 2015. [Google Scholar]
- Pan, M.; Johnston, N.; Plummer, A.; Yang, H. Experimental Investigation of a switched inertance hydraulic system with a high-speed rotary valve. J. Dyn. Syst. Meas. Control 2015, 137, 121003. [Google Scholar] [CrossRef]
- Pan, M.; Johnston, N.; Hillis, A. Active control of pressure pulsation in a switched inertance hydraulic system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2013, 227, 610–620. [Google Scholar] [CrossRef]
- Alexander, C.Y.; James, D.V. Soft switching in Switched Inertance Hydraulic Circuits. J. Dyn. Sys. Meas. Control 2017, 139, 121007. [Google Scholar]
- Skrickij, V.; Savitski, D.; Ivanov, V.; Skačkauskas, P. Investigation of cavitation process in monotube shock absorber. Int. J. Automot. Technol. 2018, 19, 801–810. [Google Scholar] [CrossRef]
- Peng, S. The concept of a zero-flowrate-switching controller. In Proceedings of the Eighth Workshop on Digital Fluid Power, Tampere, Finland, 24–25 May 2016. [Google Scholar]
- Bellar, M.; Wu, T.; Tchamdj, A. A review of soft-switched da-ac converters. IEEE Trans. Ind. Appl. 1998, 34, 847–860. [Google Scholar] [CrossRef]
- Ruan, X.; Zhou, L.; Yan, Y. Soft-switching PWM three-level converters. IEEE Trans. Power Electron. 2001, 16, 612–622. [Google Scholar] [CrossRef]
- Yao, G.; Chen, A.; He, X. Soft switching circuit for interleaved boost converters. IEEE Trans. Power Electron. 2007, 22, 80–86. [Google Scholar] [CrossRef]
- Hua, G.; Lee, F.C. Soft switching techniques in PWM converters. IEEE Trans. Insutrial Electron. 1995, 42, 595–603. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Z.; Peng, S.; Tan, Y.; Zhou, Z. A Ring-Type Fiber Bragg Grating Sensor and Its Closure Method. Patent No. CN201510253458.2, 22 March 2017. [Google Scholar]
- Liu, M.; Zhang, Z.; Zhou, Z.; Peng, S.; Tan, Y. A new method on Fiber Bragg grating sensor for the milling force measurement. IEEE Trans. Mechatron. 2015, 31, 22–29. [Google Scholar] [CrossRef]
- Peng, S. An Zero-Flowrate-Switching (ZFS) control Method Applied in a digital hydraulic system. In Proceedings of the 15th Scandinavian International Conference on Fluid Power, Linköping, Sweden, 7–9 June 2017; Linköping University Electronic Press: Linköping, Sweden, 2017; pp. 172–177. [Google Scholar]
- Bury, P.; Stosiak, M.; Urbanowicz, K.; Kodura, A.; Kubrak, M.; Malesińska, A. A Case Study of Open- and Closed-Loop Control of Hydrostatic Transmission with Proportional Valve Start-Up Process. Energies 2022, 15, 1860. [Google Scholar] [CrossRef]
- Merritt, H. Hydraulic Control System; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).