Abstract
A multi-head-attention-network-based method is proposed for effective information extraction from multidimensional data to accurately predict the remaining useful life (RUL) of gradually degrading equipment. The multidimensional features of the desired equipment were evaluated using a comprehensive evaluation index, constructed of discrete coefficients, based on correlation, monotonicity, and robustness. For information extraction, the optimal feature subset, determined by the adaptive feature selection method, was input into the multi-head temporal convolution network–bidirectional long short-term memory (TCN-BILSTM) network. Each feature was individually mined to avoid the loss of information. The effectiveness of our proposed RUL prediction method was verified using the NASA IMS bearings dataset and C-MAPSS aeroengines dataset. The results indicate the superiority of our method for the RUL prediction of gradually degrading equipment compared to other mainstream machine learning methods.
1. Introduction
With the rapid development of the industrial economy, the maintenance cost of machinery and ensuring equipment safety and reliability is an important issue. An accurate prediction of the remaining useful life (RUL) can reduce equipment maintenance downtime, increasing productivity and lowering production costs. In general, the theoretical failure models for mechanical equipment are based on degradation due to performance failure. However, in practical engineering applications, it is often difficult to accurately predict the RUL of gradually degrading equipment.
From the research point of view, several models exist for RUL predictions. These can be classified into three main categories, namely physical [1], data-driven [2,3,4], and hybrid models [5]. Traditional prediction techniques require accurate theoretical and physical models to characterize the degradation process. However, often it is quite difficult to establish such universal models for the actual production of the equipment, resulting in a loss of time and labor. With the development of data storage technologies, there is an increasing demand to evaluate the health of machinery according to their historically available working status data. The data-driven model uses the sensor monitoring parameters to effectively mine information. It extracts useful feature information through data analysis and characterizes the health status of the equipment to achieve high-precision RUL prediction. The hybrid model offers better accuracy theoretically, owing to the combined advantage of both physical and data-driven models. However, to function properly, it requires a reasonably well-constructed physical model. This is often the most challenging task in RUL prediction, at times even impossible for complex mechanical systems. Therefore, data-driven models are the most extensively applied models in the present age.
Generally speaking, data-driven equipment RUL prediction for equipment consists of two important steps: (1) extracting features that can characterize the equipment’s degradation state; and (2) building appropriate predictive models using machine learning methods, such as support vector machine (SVM) [6], grey forecasts model (GM (1, 1)) [7], hidden Markov model (HMM) [8], and so on.
It is necessary to extract features that conform to the equipment degradation trend to characterize the degradation process and predict the RUL. Guo et al. [9] used statistical features extracted from the original vibration signal of a rolling bearing to characterize its degradation state. However, some features unrelated to the bearing degradation process also tend to be extracted in practical applications. Such features need to be screened and rejected to simplify the prediction model and reduce errors, improving the calculation accuracy and efficiency. Mi et al. [10] proposed a double-layer feature selection method to screen out a subset from the candidate features and improve the sensitivity of the degradation trend by eliminating redundancy. Based on this method, it is necessary to build an appropriate model for the time-series RUL prediction. Saufi et al. [11] built a long short-term memory (LSTM) model by integrating the Laplacian score (LS), random search optimization, and LSTM to achieve an accurate RUL analysis for the rolling bearings. Behera et al. [12] proposed a novel RUL prediction method based on a multiscale deep bidirectional gated recurrent neural network (MDBGRU) for large and complex equipment. This method overcomes the pre-expertise requirement on multiple subcomponents of the system and realizes automatic learning both local and global information. Zhang et al. [13] proposed a dual-task network structure based on bidirectional gated recurrent unit (BiGRU) and multigate mixture-of-experts (MMoE), which simultaneously evaluates the HS and predict the RUL of aeroengines. In order to well mine the degradation trend in aeroengines in different levels, Xiang et al. [14] constructs a novel variant LSTM called multicellular LSTM (MCLSTM), which is used to extract the health indicators of aeroengines from raw data.
In order to accurately characterize the degradation process, the characteristic features of the equipment operation process should be extracted to the fullest extent. Feature extraction in practical applications can have several problems such as large dimensions, data redundancy, and high time costs due to manual screening. Consequently, a comprehensive evaluation index was constructed to screen multidimensional features. For improved information mining of the selected features, we propose a prediction method based on a multi-head attention mechanism for improved accuracy and enhanced generalization.
Initially, for multidimensional features, the noise was reduced through exponential smoothing. Subsequently, based on correlation, monotonicity, and robustness, a comprehensive evaluation index J was constructed using the discrete coefficients. The optimal feature subset was obtained by replacing manual screening with adaptive feature selection to improve the working efficiency. Finally, a temporal convolution network–bidirectional long short-term memory (TCN-BILSTM) network, based on the multi-head attention mechanism, was applied to effectively mine and extract information from the optimal feature subset. Different features were modeled individually to realize parallel processing and maximize data integrity preservation, while improving the network’s computational efficiency. The results demonstrated higher prediction accuracy and better generalization of our proposed method compared to other mainstream machine learning methods.
2. Methodology
As mechanical equipment operates over time, depending on its health status, different sensor monitoring signals are produced. Different sensor signals can be regarded as different features. Based on the RUL analysis incorporated with the adaptive feature selection method, we constructed a multichannel prediction network to analyze and process the different features and retain the useful information of the multidimensional features to the highest possible extent. The framework of the method is shown in Figure 1. This method is divided into two main steps: (1) data processing and (2) prediction model construction.
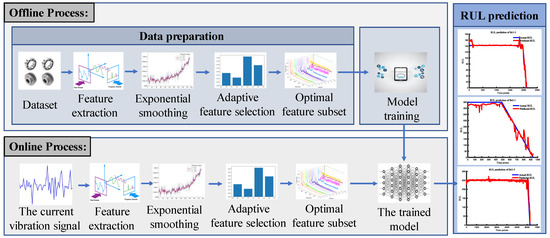
Figure 1.
RUL prediction process.
2.1. Data Preprocessing
2.1.1. Exponential Smoothing
Since the correlation between the current parameters of the equipment features and their surrounding values decreases with the increase in the number of sample groups, it is feasible to use the exponential smoothing method for noise reduction [15]. The current value is expressed as the weighted average of the actual current value and the parameter value at the previous moment.
where is the observed value at the t moment, represents the observed value at the moment of , is the true value of the t moment, and is a smoothing constant in the range of 0 to 1.
2.1.2. Adaptive Feature Selection
- (I) Feature evaluation indices
The equipment degradation process is essentially a random process of continuous change. An excellent feature should basically meet three particular conditions:
- There exists a correlation between the features and the time series of the RUL; features change with the degradation of the equipment.
- Features should be monotonical owing to degradation being an irreversible process.
- Features should have good anti-interference properties against random noise.
In this study, correlation, monotony, and robustness [16] are taken as the feature evaluation indices for the adaptive feature selection process. With performance degradation being a random process, good degradation features can be broken down into the actual trend and the residual parts. The exponential weighted moving average method is used to decompose the features into the stationary trend and the random margin term :
where represents the feature value obtained at the time , and represents the instance of time.
Correlation, monotony, and robustness are calculated as shown in Equations (3)–(5). Corr represents the linearity between the measured feature and time; Mon represents the monotonous trend in the evaluated feature; and Rob represents the tolerance of the feature to outliers. The values of the aforementioned features evaluation indices range from [0,1]; the larger the index value, the better the performance of the feature.
where represents the stationary trend, represents the random margin term, represents the feature value obtained at the time , represents the instance of time, and is a unit step function.
- (II) Feature selection
Individual indices can only provide a one-sided measurement of the health of alternative features. In order to compute the three evaluation indices of each alternative feature, a linear combination can be constructed as the final comprehensive evaluation criterion
where J belongs to [0,1] represents a comprehensive criterion, Ω represents a set of alternative features, and represents the weight of each performance evaluation metric. The features with high J-values should be retained in order to effectively predict the RUL.
For the selection of weights in Equation (6), we used the dispersion coefficient (CV) to evaluate the degree of dispersion of the three features indices
where CV is dispersion coefficient, is standard deviation, and is the average value.
Using Equations (3)–(5), the weights of the three evaluation indices were calculated as
where ωc, ωm, ωr, are the weights of Corr, Mon and Rob in Equation (6), and , and the mean values of the CVs for the Corr, Mon and Rob, respectively.
If the comprehensive evaluation index J of all the alternative features is sorted in decreasing order, and the first m number of features with the larger J-value are directly selected as the optimal feature subset, it may lead to feature redundancy. With increased redundancy, the RUL prediction model gradually becomes more complex with reduced prediction efficiency. Therefore, the adaptive optimal order search algorithm can be used to improve the search efficiency, and automatically determine the optimal feature subset. The algorithm screens out an optimal feature from k alternative features each time and introduces a random Gaussian white noise ε to keep the original number of features unchanged. This process reiterates until the screened optimal feature subset is nothing but the introduced Gaussian white noise (process explained in Section 2.1.3). The specific process is shown in Figure 2:

Figure 2.
adaptive sequential optimal feature selection.
2.1.3. RUL Target Function
When mechanical equipment first begins to operate, due to negligible wear of its mechanical components, it is said to be in a healthy state. The RUL target function for the equipment is defined as follows:
where is the number of cycles of the measured point, is the maximum number of cycles, and is the critical degradation value.
2.2. Prediction Model Construction
2.2.1. Basic Theory
- (I) Temporal Convolutional Network
TCN combines dilated causal convolution (DCC) and residual connections (RC) to solve timing problems [17]. Causal convolution is a time-constrained model that is unable to obtain future information. This increases the training costs while enhancing the memory of historical information on the network. On the other hand, by using dilated convolution with RC, the model enables a large, efficient receptive field. This field is able to accept more historical data while avoiding the problem caused by the very deep network. For the multidimensional features in this study, TCN can not only solve the problem that traditional convolutional neural networks (CNNs) are limited by (due to convolutional kernels), but also avoid the problem of gradient disappearance or explosion of recurrent neural networks (RNN). The RC is a constituent unit of the TCN and is illustrated in Figure 3.
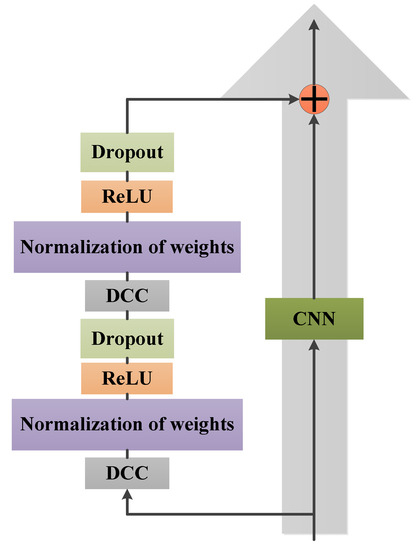
Figure 3.
TCN residual block structure.
- (II) Bidirectional Long Short-Term Memory
In order to extrapolate the health status of the equipment from the degradation law of the signal over time, the BILSTM algorithm is used to concatenate the hidden front and back layer vectors. This model fully considers the bidirectional information of the features, while improving the validity of time series prediction.
The BILSTM network (Figure 4) adds a reverse layer to the (LSTM) network, allowing fuller use of the effective information from the optimal feature subset. This network combines the output of the front and back layers at each moment to obtain the final output as
where x represents the input layer, hR represents the forward layer, hL represents the backward layer, h represents the output layer, w represents the weights, and f represents the function.

Figure 4.
BILSTM loop structure diagram.
- (III) Multi-head Attention
To account for the independent multidimensional equipment features, we utilized a multi-headed attention mechanism to process the different features parallelly (model structure shown in Figure 5).
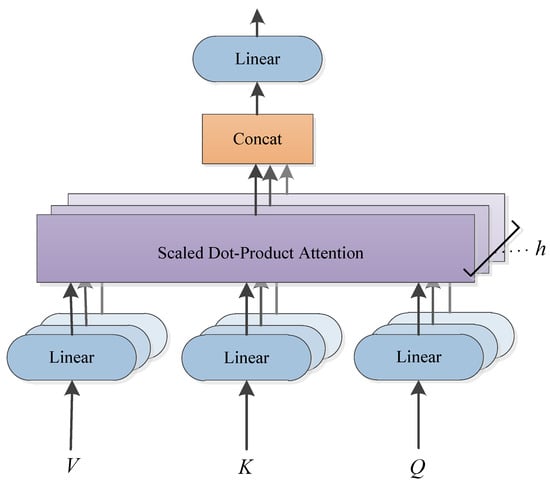
Figure 5.
Multi-head attention model.
The multi-head attention mechanism, based on the transformer, simultaneously attended to different parameters. The obtained results were stitched together to realize the final attention as
where Q is a query matrix, K is a key matrix, and V is a values matrix, and , , and represent the weight matrices containing the weights of Q, K, and V in the ith attention head, respectively. The output of the multi-head attention mechanism is spliced by the merge layer.
Multihead (Q, K, V) = Concat (head1, head2, ⋯, headn)W
2.2.2. Metrics
In this study, we evaluate the proposed method using 3 indices, namely root mean square error (RMSE), mean absolute percentage error (MAPE), and SCORE:
- RMSE: It is a commonly used metric for evaluating prediction models in various fields, including machine learning, statistics, and engineering. It measures the differences between predicted values and actual values by computing the square root of the average squared difference between them. This metric provides a way to quantify the magnitude of the errors in the predictions and can be used to compare the performance of different prediction models.
- MAPE: It is another commonly used evaluation metric for predicting RUL. MAPE measures the percentage difference between predicted values and actual values, which makes it useful for assessing the accuracy of predictions when the scale of the data varies widely.
- SCORE: Early prediction is often more important and effective than later prediction for gradually degrading equipment, such as aircraft engines, bearings, etc., which experience gradual deterioration within their operational life cycle, and their failures typically develop gradually, causing progressive damage to the equipment over a period of time. By setting a penalty for later predictions compared to early predictions, the score function can better capture the preference for early predictions. This is particularly useful for capturing the early warning signs of equipment degradation and preventing catastrophic failures.
where is the RUL prediction value at moment i and is the RUL true value at moment i.
2.2.3. Proposed Model
In order to make full use of the optimal feature subset, we propose a multichannel prediction model of TCN-BILSTM based on the multi-head attention mechanism. This model introduces TCN to improve the computational efficiency of the network, while ensuring the integrity of the long-term sequence. Further, BILSTM is used to extract bidirectional sequence information, and achieve parallel processing of multiple features through the multichannel network structure. The specific structure is shown in the following Figure 6. The detailed model parameters are listed in Table 1.

Figure 6.
Network structure based on multi-head attention and TCN-BILSTM.

Table 1.
Network parameters based on TCN-BILSTM and multi-head attention.
3. Case Studies
3.1. Case Study1: Intelligent Maintenance System (IMS) Bearing Dataset
3.1.1. Dataset Description
The experimental data were procured from the Rolling Bearing Life Cycle Experiment of the Intelligent Maintenance System (IMS) at the University of Cincinnati, USA [18]. In the experimental device (shown in Figure 7), the DC motor drives the rotation of the four Rexnord ZA-2115 rolling bearings on the shaft. Each bearing is installed with a 353B33 high-sensitivity quartz acceleration sensor in both radial and axial directions. A constant radial load of 26.67 KN was applied to each bearing at a constant speed of 2000 r/min. The vibration signal was measured every 10 min during the experiment. The spindle speed was kept at a constant 2000 r/min. The sampling frequency was 20 kHz, and each sample contained 20,480 data points. Therefore, in order to maintain the internal information integrity of a single training sample, while greatly reducing the amount of computation, each sensor trains with an initial set of 10,240 data points, with the final set of 10,240 points being the actual test data. This dataset contains the sub-datasets of the three experiments (specific bearing data shown in Table 2).

Figure 7.
Experimental device diagram of bearing life cycle.

Table 2.
Description of IMS datasets.
3.1.2. Data Preparation
In order to find the degradation law for the bearings and to improve the RUL prediction accuracy, a variety of features were extracted on the basis of the original bearing vibration signal. Fourteen features including the maximum, standard deviation, and root mean square (RMS) values were extracted from the time domain range. Simultaneously, four features, namely center of gravity frequency, average frequency, RMS frequency, and frequency standard deviation, were extracted from the frequency domain range. As shown in Figure 8, using the adaptive feature selection method, these 18-dimensional features were extracted for three types of bearings: Br1-3, Br2-1, and Br3-3.
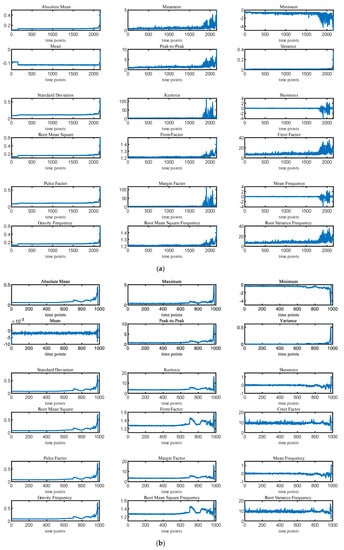
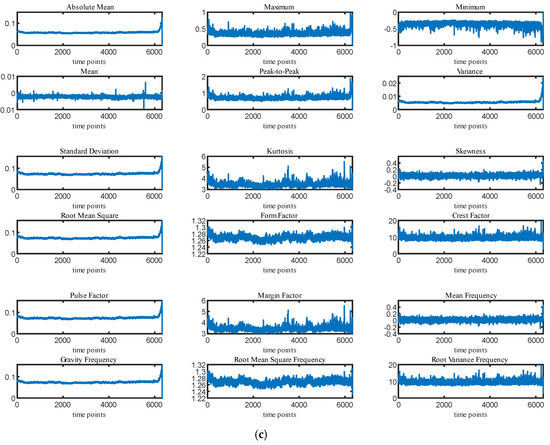
Figure 8.
(a) Feature extraction results of Br1-3; (b) feature extraction results of Br2-1; (c) feature extraction results of r3-3.
The value of α in the exponential smoothing method determines the degree of smoothing. The larger the α, the greater the influence of the recent data on the prediction results; the smaller the α, the smoother the data. When the data remain unchanged in the long term, α can be taken within 0.1 to 0.5 [19]. We selected α-values of 0.1, 0.3, and 0.5 to treat the 18-dimensional features of the three bearings separately. A random feature of each bearing was selected to demonstrate the exponential smoothing (Figure 9). For all three bearings, the effect of the different α-values on the RUL prediction results are compared and displayed in Figure 10.
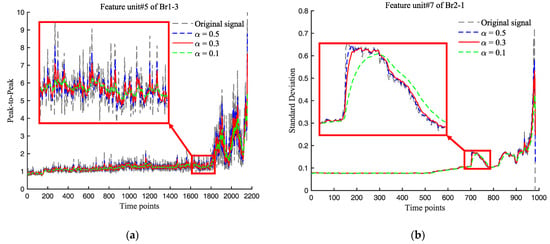
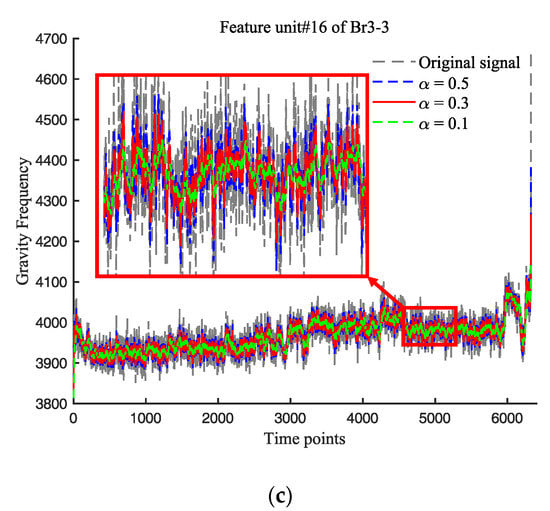
Figure 9.
(a) Performance of ES on peak-to-peak of Br1-3; (b) performance of ES on standard deviation of Br2-1; (c) 3; (b) performance of ES on gravity frequency of Br3-3.
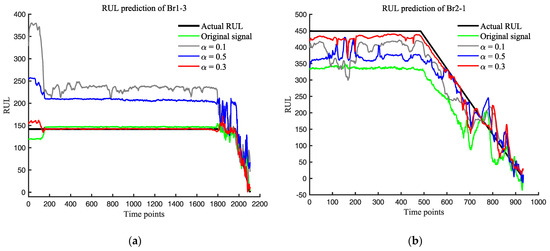
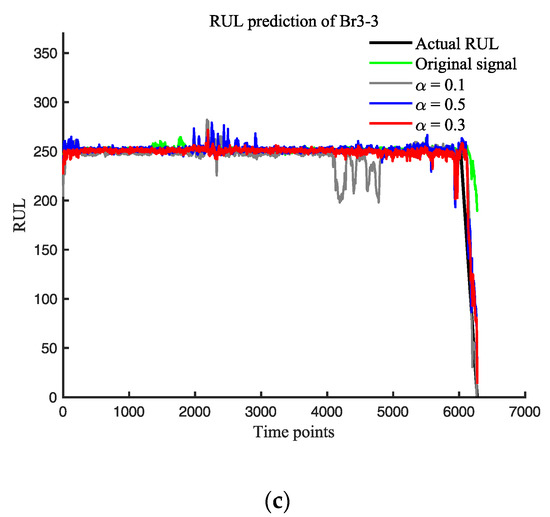
Figure 10.
(a) RUL prediction of different α on Br1-3; (b) RUL prediction of different α on Br2-1; (c) RUL prediction of different α on Br3-3.
According to several studies, the early degradation points of Br1-3, Br2-1, and Br3-3 were determined to be 2015, 536, and 6074 [20], respectively. The critical degradation values of R were found to be 142, 449 and 251, respectively. Figure 10 and Table 3 display the significant impact of varying the α-value on the RUL predictions.

Table 3.
Evaluation indexes for different α.
As shown in Figure 10, the use of different smoothing constants has varying effects on the RUL prediction of bearings. The selection of smoothing constant significantly impacts the prediction performance of Br1-3. When α = 0.1, a considerable amount of noise is removed, but this also affects the network’s prediction accuracy, suggesting that excessive noise removal can reduce the network’s robustness and, consequently, the prediction accuracy. On the other hand, when α = 0.5, excessive redundant noise is retained, leading to a decrease in the prediction accuracy. However, when α = 0.3, RMSE, SCORE, and MAPE were optimized by 43.23%, 73.69%, and 57.14%, respectively.
For the prediction results of Br2-1, the original data contain a large number of environmental interference factors, and the introduction of exponential smoothing can effectively improve the prediction performance. The optimal prediction performance is achieved when α = 0.3, with RMSE, SCORE, and MAPE optimized by 73.59%, 97.19%, and 58.33%, respectively.
Regarding the prediction results of Br3-3, it can be observed that the original data perform well in predicting the bearing in a healthy state, while the prediction performance of the bearing in a degraded state is poor. However, the introduction of exponential smoothing significantly improves the prediction performance for the bearing in the degraded state. The prediction performance for the Br3-3 in the healthy state decreases, whether α = 0.1 or α = 0.5. Nonetheless, the optimal prediction performance is achieved when α = 0.3, with RMSE, SCORE, and MAPE optimized by 57.71%, 99.99%, and 70.57%, respectively.
3.1.3. Optimal Feature Subset
The Corr, Mon, and Rob of the 18-dimensional features of the three bearings were obtained using Equations (3)–(5), and the weights of the three evaluation indices were calculated to be ωc = 0.15, ωm = 0.64, and ωr = 0.21, using Equations (8)–(10) (Table 4).

Table 4.
Dispersion Coefficient.
Based on the adaptive selection method explained in Section 2.1.2, using Equation (6), the 18-dimensional features of the three bearings were screened down to an 11-dimensional optimal feature subset. To test the validity of this subset, we compared the effects of the screened 11-dimensional features (subset 1), original 18-dimensional features (subset 2), and the first 11-dimensional features with a large J-value (subset 3), on their bearing RUL predictions (Figure 11 and Table 5).

Figure 11.
(a) RUL prediction of different feature subsets on Br1-3; (b) RUL prediction of different feature subsets on Br2-1; (c) RUL prediction of different feature subsets on Br3-3.

Table 5.
Different feature subsets.
From Figure 11, it can be seen that subset 1 shows a better RUL prediction for the three bearings, displaying the highest and lowest impact on the prediction for bearings Br2-1 and Br1-3, respectively. The quantitative analysis (Table 6) shows a superiority in the prediction performance of subset 1 over that of subsets 2 and 3 for the three evaluation indices. This indicates that the adaptive feature selection method can efficiently screen the features of the bearings, and the optimal feature subset can effectively reduce prediction errors.

Table 6.
Evaluation indexes for different feature subsets.
3.1.4. Discussion and Comparison
In order to verify the superiority of our model, we constructed several commonly used deep learning models: CNN, TCN, LSTM, BILSTM, BIGRU, CNN-LSTM, TCN-BIGRU, and TCN-BILSTM. To validate the comparison, the optimal prediction results of each model were selected, implying possible variations in the datasets of the different models. The prediction results of the different models are shown in Figure 12, and the error analysis is displayed in Table 7.
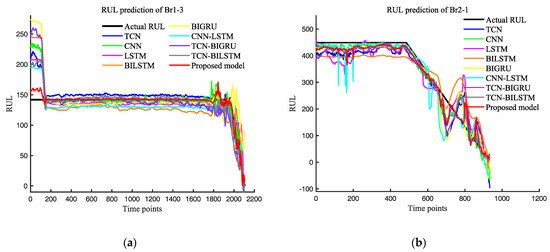
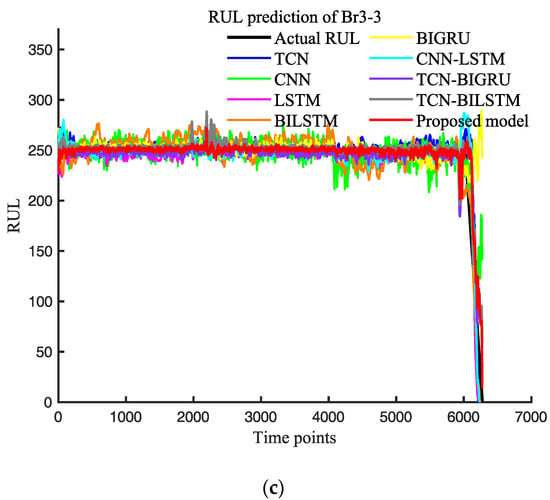
Figure 12.
(a) RUL prediction of different feature models on Br1-3; (b) RUL prediction of different feature models on Br2-1; (c) RUL prediction of different feature models on Br3-3.

Table 7.
Evaluation indexes for different models.
Based on the prediction results, the proposed model can accurately predict the remaining useful life (RUL) of the three bearings. Among them, the prediction performance of Br1-3 is the best, and all three evaluation indices show good performance. For Br3-3, it can be accurately predicted in both healthy and degraded stages, and the prediction performance is good. As shown in Table 2, the life cycle of Br2-1 is the shortest among the three bearings, which means that compared with the other bearings, there are less full-life cycle data available for training on Br2-1. Therefore, the model has learned less relevant information on Br2-1, resulting in relatively poor prediction performance for Br2-1.
3.2. Case Study2: C-MAPSS Aeroengines Dataset
3.2.1. Dataset Description
In this section, we discuss the use of NASA’s C-MAPSS dataset to generalize the prediction effect of our proposed method for aeroengines. The dataset contains four sub-datasets, each containing the training set, the test set, and the RUL true value. Both the training and test datasets contain 21-dimensional feature parameters. For each engine, the process goes through the initial healthy state to the final failure state. The test dataset contains 100 engines that run a certain number of cycles before they fail [21,22]. The work in this section is mainly based on the dataset under the FD001 operating conditions (shown in Table 8 and Table 9).

Table 8.
FD001 data description.

Table 9.
C-MAPSS outputs to measure system response.
3.2.2. Data Preparation
We chose 21 sensor detection features for the 100 engines. These were processed with exponential smoothing coefficient (α-values of 0.1, 0.3, and 0.5, and two sensor detection datasets were randomly selected for plotting. The processed data are shown in Figure 13.

Figure 13.
(a,b) Performance of ES on sensors #11 and #14 of FD001.
From the above figure, we can observe that when (i) α = 0.1, it is not possible to perform a good trend fitting in the later periods of the cycle; (ii) α = 0.5, the environmental noise is not completely eliminated; and α = 0.3, the environmental noise interference is avoided to the highest extent, while ensuring a good fit of the degradation curve of the cycle. Therefore, when α = 0.3, we have the most optimal smoothing effect on the sensor detection features of the aeroengine.
3.2.3. Optimal Feature Subset
Based on Equations (3)–(5) and (8)–(10), the weights of ωc, ωm, and ωr of the C-MAPSS data were calculated as 0.29, 0.43, and 0.28, respectively. The 21-dimensional sensor detection features of the C-MAPSS data were filtered using the adaptive feature selection method (Section 2.1.2), and finally, an optimal feature subset consisting of 12-dimensional features was obtained. As shown in Table 10, in order to verify the effectiveness of the optimal feature subset, two other feature subsets were constructed (in the same manner as Section 3.1.3) for the comparative testing of aeroengine RUL prediction (Figure 14).

Table 10.
Different feature subsets.

Figure 14.
RUL prediction of different feature subsets.
From Figure 14, we can observe that subset 1 achieves the most accurate prediction of the aeroengine RUL. The comparison with the other subsets is based on two commonly used evaluation indices of C-MAPSS, i.e., RMSE and SCORE. The prediction effect of subset 1 is seen to be significantly better than the other two subsets on the two evaluation indices (Table 11).

Table 11.
Evaluation indexes for different feature subsets.
3.2.4. Discussion and Comparison
The NASA C-MAPSS data are a widely used public dataset for RUL prediction, by which many researchers achieved exciting results. Thakkar et al. [23] developed a deep layer recurrent neural network (DL-RNN) model to predict the RUL of aeroengines and the results showed this DL-RNN model achieved high prediction accuracy. As to our model, it aims to realize relatively satisfactory RUL prediction for various types of gradually degrading equipment, with a focus on enhancing the generalization and versatility of the prediction model. In order to verify the effectiveness of our proposed method for the RUL prediction of aeroengines, we compared it with the mainstream machine learning methods (Table 12). Our method improves on and vastly outperforms other methods tested on the C-MAPSS dataset, with both RMSE and SCORE values reduced by 6%. The RUL prediction comparison results are visually displayed by choosing 3 engines randomly out of the set of 100 engines (Figure 15).

Table 12.
Evaluation indexes for different models.

Figure 15.
(a) RUL prediction results for engine units #52 of FD001; (b) RUL prediction results for engine units #81 of FD001; (c) RUL prediction results for engine units #100 of FD001.
4. Conclusions
Based on the multi-head attention mechanism, a novel RUL prediction method for gradually degrading equipment was proposed, which uses discrete coefficients to construct evaluation indices for obtaining the optimal feature subset. This method effectively eliminates redundant features and improves the prediction accuracy of the model. The TCN-BILSTM network based on the multi-head attention mechanism was used to perform individual feature mining to maximize information integrity and avoid information loss. In addition, the proposed method was verified using the IMS bearing dataset and the C-MAPSS aeroengines dataset. The results indicate that the proposed method has a higher prediction accuracy and greater generalization than other machine learning methods for different types of mechanical equipment. With multidimensional features being generally used to improve the RUL prediction accuracy, our method, in particular, demonstrates great advantages in the case of such input features, providing an effective guide for future mechanical equipment maintenance.
Author Contributions
Conceptualization, L.N.; methodology, L.N. and S.X.; investigation, L.Z. and S.X.; software, S.X.; validation, L.Z.; writing—original draft preparation, S.X.; writing—review and editing, L.N., S.X. and L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China Program (No. 51975191).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, Y.; Li, Q.; Liang, S.Y. Physics-based intelligent prognosis for rolling bearing with fault feature extraction. Int. J. Adv. Manuf. Technol. 2018, 97, 611–620. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Jin, Y.; Dang, X.; Deng, W. Feature Extraction for Data-Driven Remaining Useful Life Prediction of Rolling Bearings. IEEE Trans. Instrum. Meas. 2021, 70, 3511910. [Google Scholar] [CrossRef]
- Gao, T.; Li, Y.; Huang, X.; Wang, C. Data-Driven Method for Predicting Remaining Useful Life of Bearing Based on Bayesian Theory. Sensors 2021, 21, 182. [Google Scholar] [CrossRef] [PubMed]
- Que, Z.; Jin, X.; Xu, Z. Remaining Useful Life Prediction for Bearings Based on a Gated Recurrent Unit. IEEE Trans. Instrum. Meas. 2021, 70, 3511411. [Google Scholar] [CrossRef]
- Kai, G.; Celaya, J.; Sankararaman, S.; Roychoudhury, I.; Saxena, A. Prognostics: The Science of Making Predictions; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2017. [Google Scholar]
- Shen, F.; Yan, R. A New Intermediate-Domain SVM-Based Transfer Model for Rolling Bearing RUL Prediction. IEEE/ASME Trans. Mechatron. 2022, 27, 1357–1369. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Liu, C.; Li, H.; Han, Q. Remaining Useful Life Prediction Method of Rolling Bearings Based on Pchip-EEMD-GM(1,1) Model. Shock Vib. 2018, 2018, 3013684. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, N.; Shen, C. A new data-driven transferable remaining useful life prediction approach for bearing under different working conditions. Mech. Syst. Signal Process. 2020, 139, 106602. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Mi, J.; Liu, L.; Zhuang, Y.; Bai, L.; Li, Y.-F. A Synthetic Feature Processing Method for Remaining Useful Life Prediction of Rolling Bearings. IEEE Trans. Reliab. 2022, 72, 125–136. [Google Scholar] [CrossRef]
- Saufi, M.S.R.M.; Hassan, K.A. Remaining useful life prediction using an integrated Laplacian-LSTM network on machinery components. Appl. Soft Comput. 2021, 112, 107817. [Google Scholar] [CrossRef]
- Behera, S.; Misra, R.; Sillitti, A. Multiscale deep bidirectional gated recurrent neural networks based prognostic method for complex non-linear degradation systems. Inf. Sci. 2021, 554, 120–144. [Google Scholar] [CrossRef]
- Zhang, Y.; Xin, Y.; Liu, Z.-W.; Chi, M.; Ma, G. Health status assessment and remaining useful life prediction of aero-engine based on BiGRU and MMoE. Reliab. Eng. Syst. Saf. 2022, 220, 108263. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Luo, J.; Pu, H.Y.; Tang, B.P. Multicellular LSTM-based deep learning model for aero-engine remaining useful life prediction. Reliab. Eng. Syst. Saf. 2021, 216, 107927. [Google Scholar] [CrossRef]
- Zhang, N.; Wu, L.; Wang, Z.; Guan, Y. Bearing Remaining Useful Life Prediction Based on Naive Bayes and Weibull Distributions. Entropy 2018, 20, 944. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Zhang, L.; Xu, J. Degradation Feature Selection for Remaining Useful Life Prediction of Rolling Element Bearings. Qual. Reliab. Eng. Int. 2016, 32, 547–554. [Google Scholar] [CrossRef]
- Pan, M.; Hu, P.; Gao, R.; Liang, K. Multistep prediction of remaining useful life of proton exchange membrane fuel cell based on temporal convolutional network. Int. J. Green Energy 2022, 20, 408–422. [Google Scholar] [CrossRef]
- Ding, H.; Yang, L.; Cheng, Z.; Yang, Z. A remaining useful life prediction method for bearing based on deep neural networks. Measurement 2020, 172, 108878. [Google Scholar] [CrossRef]
- Niu, T.; Zhang, L.; Zhang, B.; Yang, B.; Wei, S. An Improved Prediction Model Combining Inverse Exponential Smoothing and Markov Chain. Math. Probl. Eng. 2020, 2020, 6210616. [Google Scholar] [CrossRef]
- Lv, M.; Liu, S.; Su, X.; Chen, C. Early degradation detection of rolling bearing based on adaptive variational mode decomposition and envelope harmonic to noise ratio. J. Vib. Shock 2021, 40, 271–280. [Google Scholar] [CrossRef]
- Cheng, Y.; Wu, J.; Zhu, H.; Or, S.W.; Shao, X. Remaining Useful Life Prognosis Based on Ensemble Long Short-Term Memory Neural Network. IEEE Trans. Instrum. Meas. 2021, 70, 3503912. [Google Scholar] [CrossRef]
- Wu, J.Y.; Min, W.; Chen, Z.; Li, X.L.; Yan, R. Degradation-Aware Remaining Useful Life Prediction With LSTM Autoencoder. IEEE Trans. Instrum. Meas. 2021, 70, 3511810. [Google Scholar] [CrossRef]
- Thakkar, U.; Chaoui, H. Remaining Useful Life Prediction of an Aircraft Turbofan Engine Using Deep Layer Recurrent Neural Networks. Actuators 2022, 11, 67. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, L.; Liu, C. Uncertainty prediction of remaining useful life using long short-term memory network based on bootstrap method. In Proceedings of the 2018 IEEE International Conference on Prognostics and Health Management (ICPHM), Seattle, WA, USA, 11–13 June 2018; pp. 1–8. [Google Scholar]
- Zhang, C.; Lim, P.; Qin, A.K.; Tan, K.C. Multiobjective Deep Belief Networks Ensemble for Remaining Useful Life Estimation in Prognostics. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2306–2318. [Google Scholar] [CrossRef] [PubMed]
- Shuai, Z.; Ristovski, K.; Farahat, A.; Gupta, C. Long Short-Term Memory Network for Remaining Useful Life estimation. In Proceedings of the 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA, 19–21 June 2017. [Google Scholar]
- Sateesh Babu, G.; Zhao, P.; Li, X.-L. Deep Convolutional Neural Network Based Regression Approach for Estimation of Remaining Useful Life. In Proceedings of the Database Systems for Advanced Applications, Cham, Switzerland, 25 March 2016; pp. 214–228. [Google Scholar]
- Gu, Y.; Wylie, B.K.; Boyte, S.P.; Picotte, J.; Howard, D.M.; Smith, K.; Nelson, K.J. An Optimal Sample Data Usage Strategy to Minimize Overfitting and Underfitting Effects in Regression Tree Models Based on Remotely-Sensed Data. Remote Sens. 2016, 8, 943. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).