Abstract
Terrain adaptation research can significantly improve the motion performance of hexapod robots. In this paper, we propose a method that combines reinforcement learning with a central pattern generator (CPG) to enhance the terrain adaptation of hexapod robots in terms of gait planning. The hexapod robot’s complex task presents a high-dimensional observation and action space, which makes it challenging to directly apply reinforcement learning to robot control. Therefore, we utilize the CPG algorithm to generate the rhythmic gait while compressing the action space dimension of the agent. Additionally, the proposed method requires less internal sensor information, which exhibits strong applicability. Finally, we conduct experiments and deploy the proposed framework in the simulation environment. The results show that the terrain adaptation policy trained in our framework enables the hexapod robot to move more smoothly and efficiently on rugged terrain compared to the traditional CPG method.
1. Introduction
The movement path of the legged robot is formed by discrete landing points. In uneven terrain environments, legged robots have a stronger motion potential than regular wheeled or tracked mobile robots and can meet task requirements in more complex environments. Among them, the good motion stability of the hexapod robot makes it have greater advantages and application value in the fields of rescue, transportation exploration, and so on [1,2,3]. However, redundant actuators increase the difficulty of modeling and motion planning. In order to make robots move smoothly on irregular ground, complex control systems and algorithms usually need to be designed [4,5,6]. At present, the research on adaptive motion control technology of hexapod robots mainly includes (1) model-based motion optimization [7,8,9,10,11,12,13]; (2) bio-inspired methods [14,15,16,17,18]; and (3) machine learning [19,20,21,22].
The hexapod robots in [7,8,10] use external sensing sensors, such as depth sensors [8], stereo cameras [7], and LIDAR [10], to model the surrounding, so that the robot can determine a reasonable landing point position and leg trajectory through planning algorithms and realize the crossing of obstacles and balancing the body. Such methods can significantly improve the motion performance of robots but require expensive sensors and large computational resources to ensure efficiency. The method proposed in [9,13] only relies on the legs of the robot to sense the environment and adjusts the joint positions through the balance algorithm to maintain the body posture. This class of algorithms has low implementation cost, but it requires a large amount of prior knowledge, and the improvement in robot motion performance is limited. In [18], a new biologically inspired adaptive neuroendocrine control approach was proposed, which combined the three modules of CPG control, an artificial hormone network, and unsupervised input-related learning so as to make effective adjustment of legs in continuous motion. Moreover, the method does not require a robot model and is therefore general. In [21,22], the authors adopted the hierarchical control framework and reinforcement learning method to improve the adaptive motion ability of the hexapod robot. The policy network obtained by iteratively training a hexapod robot in a stochastic simulation environment has a certain generalization capability, which is an effective approach to solve the control problem of complex nonlinear systems in an unknown environment.
Motion control based on CPG offers the advantages of simple design and low computational complexity. However, the performance of CPG-based motion control is poor in rough terrain. At the same time, directly controlling the joint angles of hexapod robots with reinforcement learning to achieve terrain-adapted walking is challenging. On the one hand, this is because the hexapod robot has many joints, which means that as the dimension of the output layer of the policy network increases, there are more parameters to learn in the network. On the other hand, we need the hexapod robot to converge to a regular walking pattern instead of swinging its legs in a haphazard manner, which requires a lot of effort in the design of the reward function. Imitation learning and reinforcement learning are usually combined to make the robot learn a specific behavior pattern.
Therefore, this paper focuses on designing a novel terrain-adapted gait generation method for hexapod robots by combining CPG and reinforcement learning, with leg contact feedback as the primary means of environment sensing. The signal coupling of oscillators simplifies gait design and reduces the action space dimension of reinforcement learning, making it easier to converge. First, a network comprising of six Hopf oscillators generates the basic rhythmic gait signal. Then, the mapping function transforms the signal into the foot coordinates. Finally, the inverse kinematic (IK) module computes the angle of motion of the joints. The key point of this approach is that the parameters of the mapping function, corresponding to the oscillator of each leg, are variable and their values are determined by the policy network trained by reinforcement learning. The parameters are modified to change the trajectory of the foot, and the body pose adjusts during the walk to improve the motion performance in rough terrain.
The rest of the paper is organized as follows: Section 2 introduces the hexapod robot platform and the method of generating rhythmic gait using the CPG network. Section 3 proposes a terrain-adaptive gait generation framework that fuses reinforcement learning and CPG networks (RL-CPG) and describes the design and training details of the policy network. Section 4 presents experiments to validate the effectiveness and feasibility of the proposed framework. Finally, the conclusions and avenues for future research are presented in Section 5.
2. Rhythmic Gait Generation by the CPG Network
In this section, we briefly introduce the used hexapod robot platform. Then, a network composed of Hopf oscillators for generating rhythmic gaits is described in detail.
2.1. Hexapod Robot
The work in this paper uses a hexapod robot model built in Pybullet [23], as shown in Figure 1. The six legs are evenly distributed around the body and each has three joints: the hip, knee, and ankle joints. The robot is blind because it does not carry external sensors such as radar and camera, and the robot can only sense its own state information, body attitude angle, acceleration, foot-tip collision, etc. External precision sensors have a high probability of damage, and in the absence of such sensor information, we would like the hexapod robot to still have some terrain adaptation capability; hence, we initiated a related study on blind hexapod robot platforms.
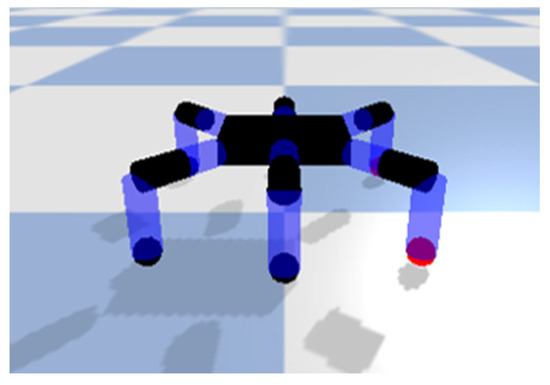
Figure 1.
Simulated prototype of the hexapod robot.
2.2. CPG Network
The CPG algorithm is used to output a stable periodic signal. Classical oscillation models include the Matsuoka neuron oscillator model [24,25], the Van der Pol (VDP) relaxation oscillator [26,27], the Kuramoto phase oscillator [28], etc. The Hopf harmonic oscillator model [29,30] has the advantages of high stability, few parameters, clear physical meaning, and easy tuning. Therefore, the Hopf oscillator is chosen as the signal source in this paper and its basic mathematical model is as follows:
where , are the output of the oscillator; , are convergence rate coefficients; is the square of the output signal amplitude; is the frequency of the oscillator. When the hexapod robot walks with different gaits, the support time and swing time of the legs are not the same. In order to make the rising section of the oscillator output correspond to the swing phase of the leg and the falling section correspond to the support phase of the leg, the coverage coefficient is added to adjust the value of , which has the following relationship:
where and are stance phase frequency and swing phase frequency, respectively; is a positive coefficient ( in this paper) that determines the rate of transition of the frequency ω between and . The coefficient of common gait on land occupancy is shown in the Table 1 below.

Table 1.
Common gaits corresponding to the coverage coefficient.
In this paper, each leg is controlled using signals generated by a single oscillator unit, and the whole robot uses six oscillator units to form a coupled network to generate a rhythmic gait. As shown in Figure 2, the network is performed by bidirectional coupling of neighboring oscillatory units.
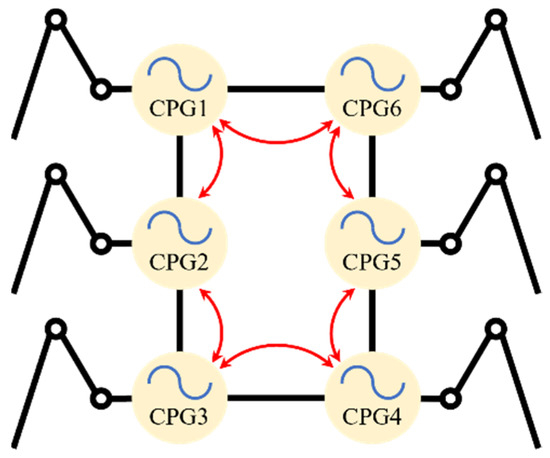
Figure 2.
Circularly bidirectionally coupled CPG network.
In order to realize coupling, the signals generated by different oscillators, the coupling term is added to Equation (1), and the final mathematical model is given by
where represents the coupling strength coefficient between oscillators ( in this paper), and if its value is too large, it will cause the curve to appear blurred; the output signal compensation and are used to adjust the center position of the output signal to meet the needs of different gaits. The coupling way of the network determines the expression of the coupling term as follows:
where represents the phase difference between oscillators, and the phase difference between legs corresponding to common gaits is shown in Figure 3.
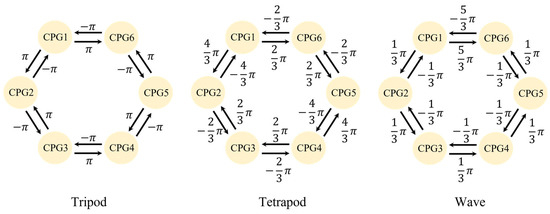
Figure 3.
The phase difference corresponding to common gaits.
The transition from the output signal of the oscillator to the control signal of the robot joint requires a mapping that transforms the signal into a foot trajectory and then computes the joint angle via inverse kinematics. The mapping function is defined as follows:
where is the initial position of the foot; , , are the scaling coefficients, depending on the workspace of the specific robot; is the z-axis compensation and is the direction of the stride. In summary, Equations (2)–(5) form the basic part of the adaptive gait generator in this paper, and with appropriate gait parameters, the hexapod robot will move with a rhythmic gait generated by the CPG algorithm. Figure 4 shows the robot moving in a tripod gait on flat ground with the mapping parameters set to , , and .
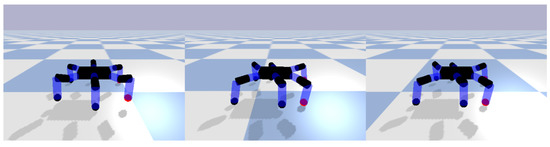
Figure 4.
Hexapod robot walks with a tripod gait generated by the CPG algorithm.
3. Terrain-Adaptive Gait Generation
3.1. Problem Description
Here we consider the robot interacting with the environment in discrete time steps. At each time step, the robot state (position, attitude, velocity, angular velocity, angular acceleration, torque, etc.) and environmental information (terrain height, ground friction coefficient, etc.) can be completely described by a set of state vectors . By definition, this vector contains the information needed to select the operation at the current time step. The robot obtains the information from and performs an action to interact with the environment. At the next time step, the state vector is updated and state-transition distribution is denoted by . The reward function evaluates the quality of each state-action transition.
The above process can be described as a Markov decision process (MDP) and satisfies the basic Markov property; that is, in a sequential process, the state at time only depends on the state at time and has nothing to do with the state before time . When the state is not fully observable, that is , we refer to the process as a partially observable MDP (POMDP).
In this paper, it is obvious that the robot cannot observe all the information about the environment, so we treat the learning problem as a POMDP. The agent selects the appropriate action by the policy network . The parameter denotes the weights of the neural network. Our goal is to find policy parameters such that the reward is maximized over a finite time horizon using the observation , according to the following objective:
where is a discount factor, is the expected value, and is the optimal policy parameters. The architecture of the terrain-adaptive gait generator designed in this paper is shown in Figure 5.
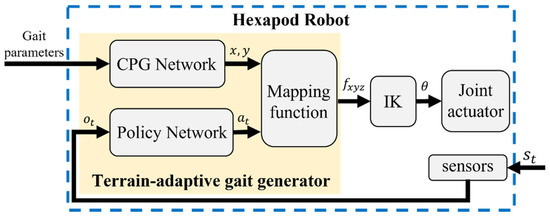
Figure 5.
Terrain-adaptive gait generation framework.
In our framework, the terrain-adaptive gait generator with RL-CPG algorithm adjusts the position of the foot by using different mapping parameters. This is a simple and practical way to adjust the body balance, regardless of which rhythmic gait the robot is walking with. As a result, in the reinforcement learning task, we adopt an action that is a 7-D vector. represents the turning direction of the robot, where the robot turns by adjusting the stride difference between the legs on both sides of the body. The larger the absolute value of , the larger the stride difference. is the variable in the mapping function of each leg.
As mentioned above, our research is based on the blind hexapod robot platform. This means that there is a limit to what the robot can observe. Considering future deployments on real robots, we choose the observation . is the Euler angle of the body. , are the angular and linear velocities of the body, respectively. is a 6-D Boolean vector representing the touchdown of each leg. and are the joint torques and angular velocities, respectively.
3.2. Reward Function
The reward design encourages the robot to adjust the position of its foot according to the terrain and its own motion state to keep the fuselage as smooth as possible while maintaining the forward direction. Therefore, we design the following rules of reward:
- (1)
- In our work, the robot does not have sensors to sense the terrain ahead, so it cannot make a plan in advance. However, the robot is able to level the tilted body by compensating for joint positions, and this behavior deserves a reward. Thus, the expression for is given bywhere means that each element of the two vectors is multiplied separately. encourages actions that help the robot recover its balance.
- (2)
- In order to avoid the robot taking advantage of the first rule to obtain a large number of rewards and behaving in an undesired way, we need to design a negative reward as follows:where and are the weighting factors.
- (3)
- The reward for robot motion is necessary, and we expect the robot to keep moving forward in rough terrain. The expression iswhere is the forward speed of the robot, and is the forward distance of the robot.
- (4)
- In this paper, we expect to perturb the gait trajectory as little as possible. The energy consumption penalty is the penalty for gait motion efficiency and energy consumption. The expression we designed iswhere is the joint torque, and is the joint angular velocity.
3.3. Termination Condition
Certain termination conditions are set to avoid the policy network falling into local minima and improve the sampling efficiency. When the following condition occurs, the agent will terminate the training and start again from the initial state.
- (1)
- The robot is involved in a self-collision.
- (2)
- The pitch, roll, or yaw of the base exceeds the allowed range.
- (3)
- The base height is less than the set threshold.
- (4)
- The distance the robot moves exceeds the set threshold.
3.4. Policy Training
In this paper, the augmented random search (ARS) [31] method is used to train a policy to maximize the expected reward return as shown in Equation (6). ARS uses a random parameter search policy optimization technique which is more simplified than the current reinforcement learning algorithm and can improve the sample efficiency. We chose a linear policy so that it could reduce the application cost in the future. Thus, for each ARS optimization step, we deploy 8 rollouts per iteration with a parameter learning rate of 0.015 and parameter exploration noise of 0.05. During the training process, a new rugged ground is generated by a random seed at each episode. The height of the ground varies by a maximum of 75% of the height of the raised leg.
After the training is completed, we can obtain a policy network with fixed parameters. The flow chart of the robot for terrain-adapted walking using the RL-CPG algorithm is shown in Figure 6. First, the coupled rhythmic signals with specified gait parameters, which are the basis for the hexapod robot to move in a regular pattern, are output by the oscillator network. Then, the currently obtained observations of the robot are fed into the policy network to obtain the mapping parameters and bring them into the mapping function. Next, the signal is mapped to the foot-end trajectory using the mapping function. Finally, the IK module calculates the desired angle for each joint and sends them to the joint actuators to move the hexapod robot.
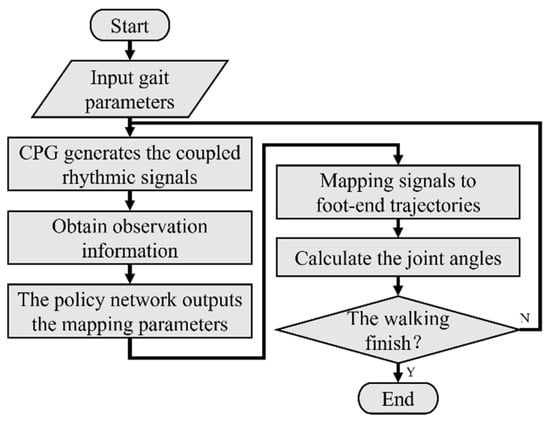
Figure 6.
Flowchart of the robot walking with the RL-CPG algorithm.
4. Experiments and Results
4.1. Motion Verification
In this experiment, we validate the trained policy network. The height of the robot is initialized to be 0.147 m. We set the positive y-axis direction of the world coordinate frame as the forward direction. The robot is set to walk with a tripod gait, and the strategy network slightly adjusts the mapping parameters in real time. Figure 7 shows the process of the hexapod robot walking on rough ground. From the results, we can see that when a leg lands on the raised ground, the output of the policy network for that leg is large to compensate for the height of the leg landing earlier. The movement of the hexapod robot performs well on rough ground.
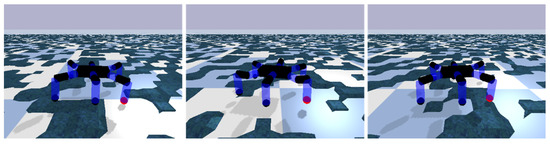
Figure 7.
The hexapod robot uses the RL-CPG algorithm to walk on rough ground.
During motion, the roll and pitch angles reflect the degree of body sway. Figure 8 records the roll and pitch angles during the movement of the robot using RL-CPG algorithm. The results show that the shaking amplitude of the robot is about 3 degrees, and the performance is smooth. This also indicates that the proposed terrain-adapted gait generator is feasible and capable of making the hexapod robot move in rough terrain.
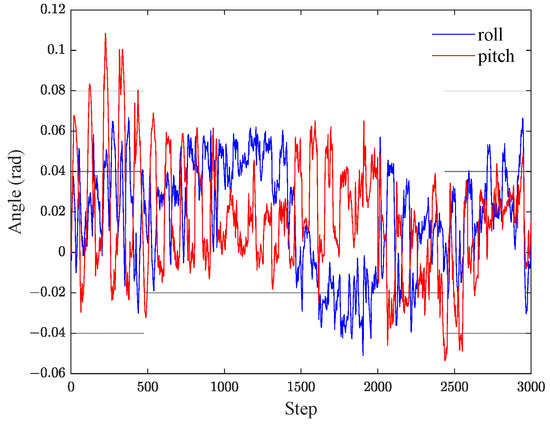
Figure 8.
The roll and pitch angles of the robot in motion.
4.2. Motion Performance Comparison
In order to compare the direct control of robot joint motion using RL baseline algorithm and the gait generation method using RL-CPG algorithm and CPG algorithm, we performed 100 experiments, and each experiment randomly generated rugged terrain. The fixed time step is set to 5000. The motion states of the hexapod robot with these different algorithms are compared under the same terrain, as shown in Table 2.

Table 2.
Statistics of the experimental data of RL-CPG algorithm and traditional CPG algorithm.
We compared the average forward distance, the average offset, the mean of the absolute value of the roll and pitch angle, and the number of early terminations. We expect the robot to walk in the forward direction as much as possible. It is found that the method of using RL baseline to directly control the joint motion of the hexapod robot fails to make the robot learn a regular motion pattern and walk on rough ground under the same training conditions. From the results, it can be seen that the robot using RL-CPG algorithm walks farther in the y direction than that using CPG algorithm, and the offset in the x direction is smaller; that is, the walking efficiency is higher. In addition, the robot using the RL-CPG algorithm terminates significantly fewer times early.
However, the degree of body sway is not obvious from the mean comparison. The absolute values of the body roll angle and pitch angle of the robot at each time step in all experiments were counted, and their distribution was observed as shown in Figure 9. It can be seen that with the RL-CPG algorithm, the robot body has a smaller amplitude range and its motion is more stable.
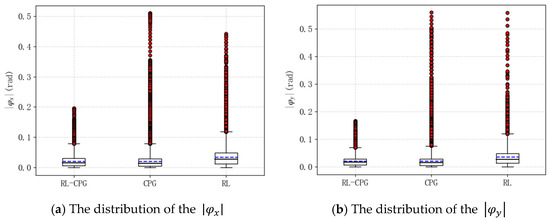
Figure 9.
Comparison of the distribution of and between CPG and RL-CPG algorithm.
5. Conclusions
In this paper, a terrain-adaptive gait generation framework with RL-CPG algorithm is proposed to improve robot terrain adaptation. The CPG algorithm reduces the difficulty of applying reinforcement learning to the hexapod robot, and the application of reinforcement learning makes the CPG algorithm more flexible and suitable for walking on rough ground. In addition, the algorithm relies on fewer sensors, so the algorithm has more stable performance and strong versatility. Despite the low deployment cost of the proposed algorithm, the current study only considers rugged terrain, and it is the focus of future work to consider more complex terrain and apply the algorithm to real robots. However, the study of terrain adaptation in this paper is only for rugged ground, and it will be our main work in the future to consider more complex ground situations.
Author Contributions
All authors contributed to this work. Conceptualization, D.L.; methodology, D.L.; software, D.L.; validation, D.L. and W.W.; writing—original draft, D.L.; writing—review and editing, Z.Q. and D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China [Grant Nos. 61573148, 61603358] and the Science and Technology Planning Project of Guangdong Province, China [Grant Nos. 2015B010919007, 2019A050520001].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy and ethical restrictions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Belter, D.; Skrzypczyński, P. Rough terrain mapping and classification for foothold selection in a walking robot. J. Field Robot. 2011, 28, 497–528. [Google Scholar] [CrossRef]
- Isvara, Y.; Rachmatullah, S.; Mutijarsa, K.; Prabakti, D.E.; Pragitatama, W. Terrain adaptation gait algorithm in a hexapod walking robot. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; pp. 1735–1739. [Google Scholar] [CrossRef]
- Bjelonic, M.; Kottege, N.; Beckerle, P. Proprioceptive control of an over-actuated hexapod robot in unstructured terrain. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 2042–2049. [Google Scholar] [CrossRef]
- Hu, N.; Li, S.; Zhu, Y.; Gao, F. Constrained model predictive control for a hexapod robot walking on irregular terrain. J. Intell. Robot. Syst. 2019, 94, 179–201. [Google Scholar] [CrossRef]
- Qazani, M.R.C.; Asadi, H.; Nahavandi, S. A model predictive control-based motion cueing algorithm with consideration of joints’ limitations for hexapod motion platform. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 708–713. [Google Scholar] [CrossRef]
- Gao, Y.; Wei, W.; Wang, X.; Li, Y.; Wang, D.; Yu, Q. Feasibility, planning and control of ground-wall transition for a suctorial hexapod robot. Appl. Intell. 2021, 51, 5506–5524. [Google Scholar] [CrossRef]
- Bjelonic, M.; Kottege, N.; Homberger, T.; Borges, P.; Beckerle, P.; Chli, M. Weaver: Hexapod robot for autonomous navigation on unstructured terrain. J. Field Robot. 2018, 35, 1063–1079. [Google Scholar] [CrossRef]
- Murata, Y.; Inagaki, S.; Suzuki, T. Development of an adaptive hexapod robot based on Follow-the-contact-point gait control and Timekeeper control. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 3321–3327. [Google Scholar] [CrossRef]
- Faigl, J.; Čížek, P. Adaptive locomotion control of hexapod walking robot for traversing rough terrains with position feedback only. Robot. Auton. Syst. 2019, 116, 136–147. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, F.; Sun, Q.; Yin, Y. Terrain classification and adaptive locomotion for a hexapod robot Qingzhui. Front. Mech. Eng. 2021, 16, 271–284. [Google Scholar] [CrossRef]
- Fukuhara, A.; Suda, W.; Kano, T.; Kobayashi, R.; Ishiguro, A. Adaptive Interlimb Coordination Mechanism for Hexapod Locomotion Based on Active Load Sensing. Front. Neurorobotics 2022, 16, 645683. [Google Scholar] [CrossRef]
- Hua-yong, W. Obstacle avoidance path optimization method of multi-legged robot based on virtual reality technology. In Proceedings of the International Conference of Social Computing and Digital Economy (ICSCDE), Chongqing, China, 28–29 August 2021; pp. 215–218. [Google Scholar] [CrossRef]
- Fućek, L.; Kovačić, Z.; Bogdan, S. Analytically founded yaw control algorithm for walking on uneven terrain applied to a hexapod robot. Int. J. Adv. Robot. Syst. 2019, 16, 1–17. [Google Scholar] [CrossRef]
- Tieck, J.C.V.; Rutschke, J.; Kaiser, J.; Schulze, M.; Buettner, T.; Reichard, D.; Roennau, A.; Dillmann, R. Combining spiking motor primitives with a behaviour-based architecture to model locomotion for six-legged robots. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4161–4168. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, X.; Chen, B. Matsuoka’s CPG with desired rhythmic signals for adaptive walking of humanoid robots. IEEE Trans. Cybern. 2018, 50, 613–626. [Google Scholar] [CrossRef]
- Yu, H.; Gao, H.; Deng, Z. Enhancing adaptability with local reactive behaviors for hexapod walking robot via sensory feedback integrated central pattern generator. Robot. Auton. Syst. 2020, 124, 103401. [Google Scholar] [CrossRef]
- Mokhtari, M.; Taghizadeh, M.; Ghaf-Ghanbari, P. Adaptive second-order sliding model-based fault-tolerant control of a lower-limb exoskeleton subject to tracking the desired trajectories augmented by CPG algorithm. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 423. [Google Scholar] [CrossRef]
- Homchanthanakul, J.; Manoonpong, P. Continuous online adaptation of bioinspired adaptive neuroendocrine control for autonomous walking robots. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 1833–1845. [Google Scholar] [CrossRef] [PubMed]
- Cully, A.; Clune, J.; Tarapore, D.; Mouret, J.-B. Robots that can adapt like animals. Nature 2015, 521, 503–507. [Google Scholar] [CrossRef] [PubMed]
- Hwangbo, J.; Lee, J.; Dosovitskiy, A.; Bellicoso, D.; Tsounis, V.; Koltun, V.; Hutter, M. Learning agile and dynamic motor skills for legged robots. Sci. Robot. 2019, 4, 5872. [Google Scholar] [CrossRef] [PubMed]
- Azayev, T.; Zimmerman, K. Blind hexapod locomotion in complex terrain with gait adaptation using deep reinforcement learning and classification. J. Intell. Robot. Syst. 2020, 99, 659–671. [Google Scholar] [CrossRef]
- Ouyang, W.; Chi, H.; Pang, J.; Liang, W.; Ren, Q. Adaptive locomotion control of a hexapod robot via bio-inspired learning. Front. Neurorobot. 2021, 15, 627157. [Google Scholar] [CrossRef]
- Panerati, J.; Zheng, H.; Zhou, S.Q.; Xu, J.; Prorok, A.; Schoellig, A.P. Learning to fly-a gym environment with pybullet physics for reinforcement learning of multi-agent quadcopter control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Prague, Czech Republic, 27 September–1 October 2021; pp. 7512–7519. [Google Scholar] [CrossRef]
- Matsuoka, K. Sustained oscillations generated by mutually inhibiting neurons with adaptation. Biol. Cybern. 1985, 52, 367–376. [Google Scholar] [CrossRef]
- Matsuoka, K. Mechanisms of frequency and pattern control in the neural rhythm generators. Biol. Cybern. 1987, 56, 345–353. [Google Scholar] [CrossRef]
- Pol, B.V.D.; Mark, J.V.D. The heartbeat considered as a relaxation-oscillation, and an electrical model of the heart. Philos. Mag. 1929, 6, 763–775. [Google Scholar] [CrossRef]
- Bay, J.S.; Hemami, H. Modeling of a neural pattern generator with coupled nonlinear oscillators. IEEE Trans. Biomed. Eng. 1987, BME-34, 297–306. [Google Scholar] [CrossRef]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137. [Google Scholar] [CrossRef]
- Righetti, L.; Ijspeert, A.J. Pattern generators with sensory feedback for the control of quadruped locomotion. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 819–824. [Google Scholar] [CrossRef]
- Righetti, L.; Buchli, J.; Ijspeert, A.J. From Dynamic Hebbian Learning for Oscillators to Adaptive Central Pattern Generators; Verlag ISLE: Ilmenau, Germany, 2005; pp. 1–6. [Google Scholar]
- Mania, H.; Guy, A.; Recht, B. Simple random search provides a competitive approach to reinforcement learning. arXiv 2018. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).