Design and Analysis of Electromagnetic Linear Actuation-Energy-Reclaiming Device Applied to a New-Type Energy-Reclaiming Suspension
Abstract
1. Introduction
2. Overall Design of the New Suspension
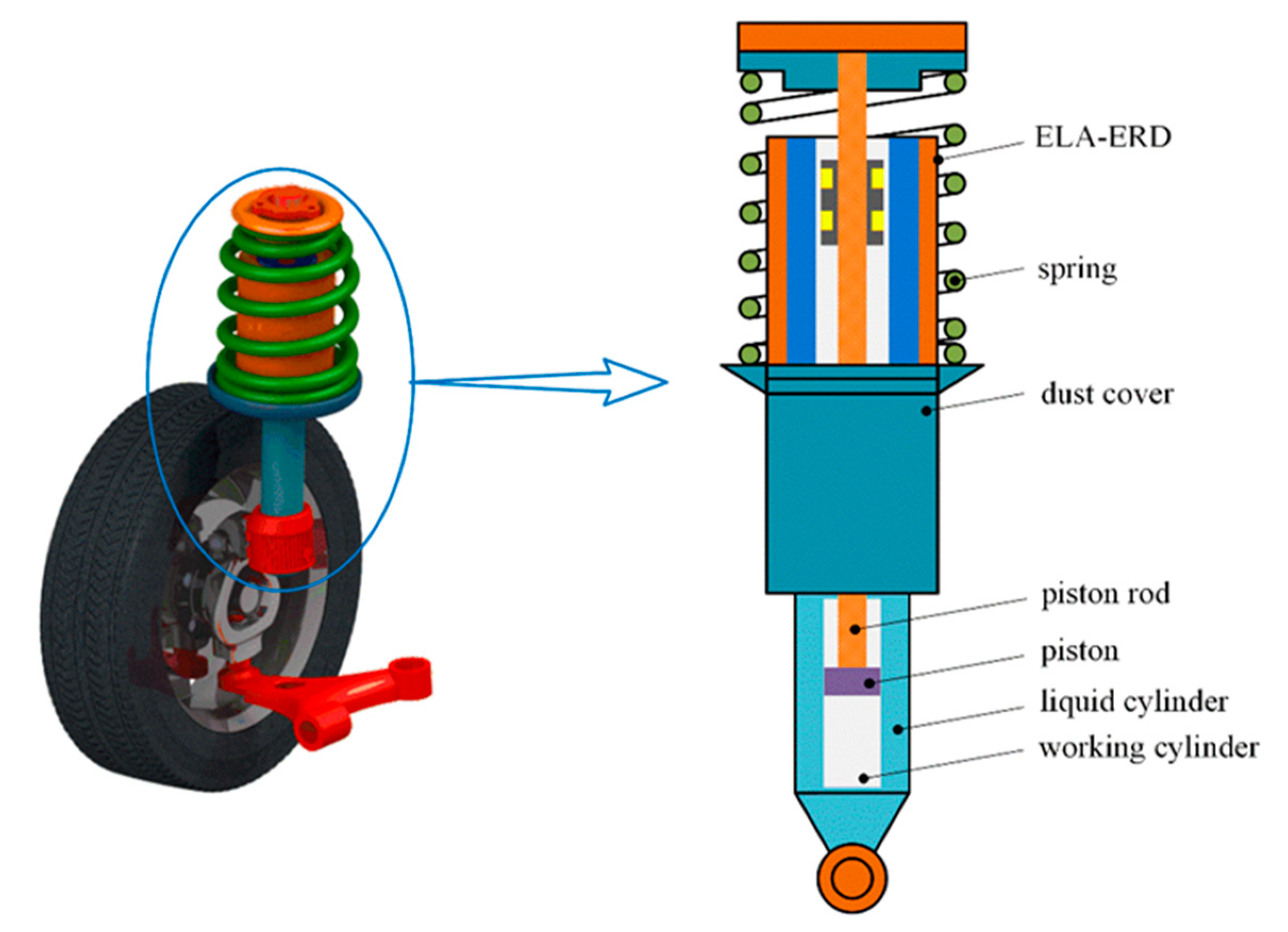
2.1. Suspension Scheme
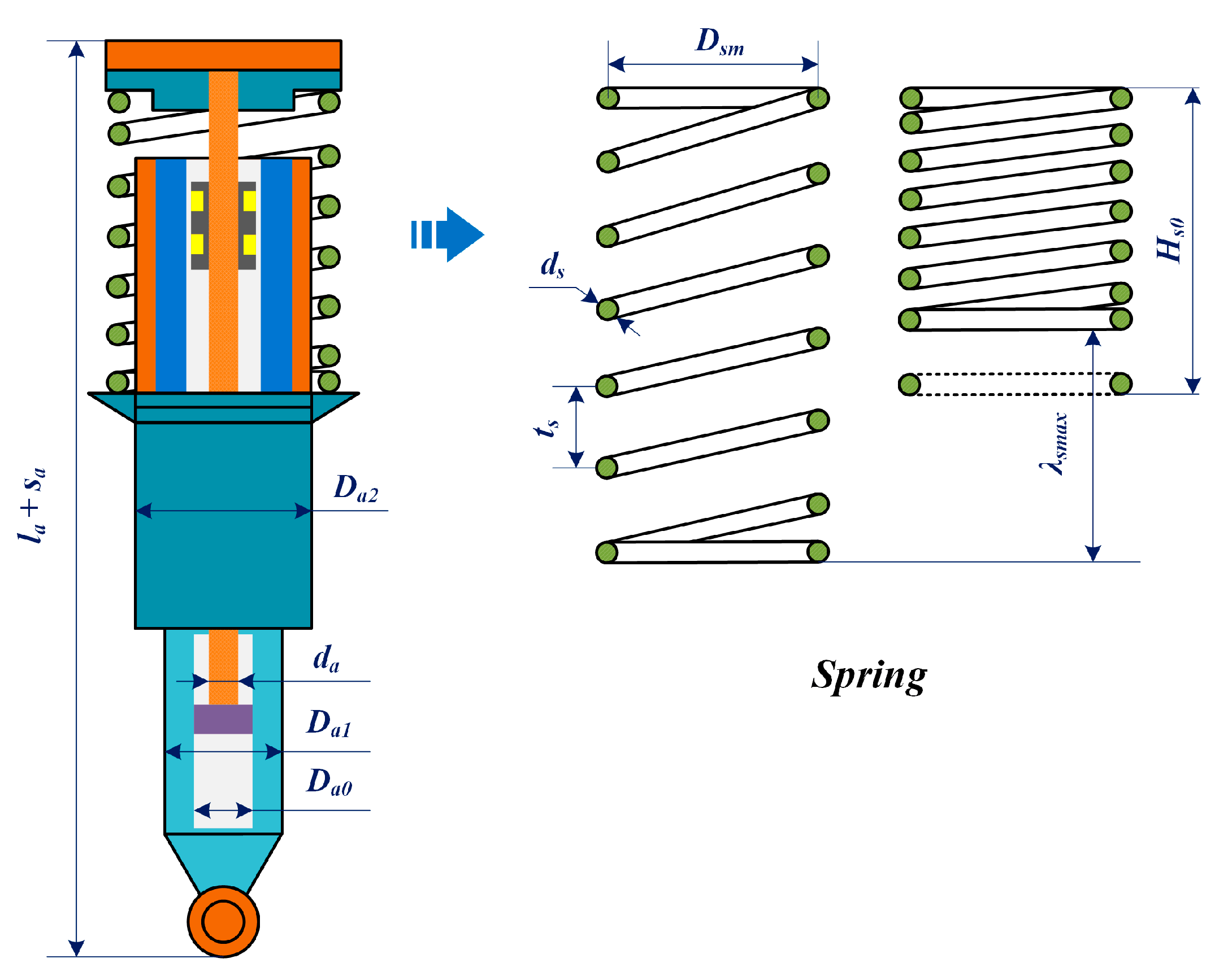
2.2. Parameters Determination
3. Design of ELA-ERD
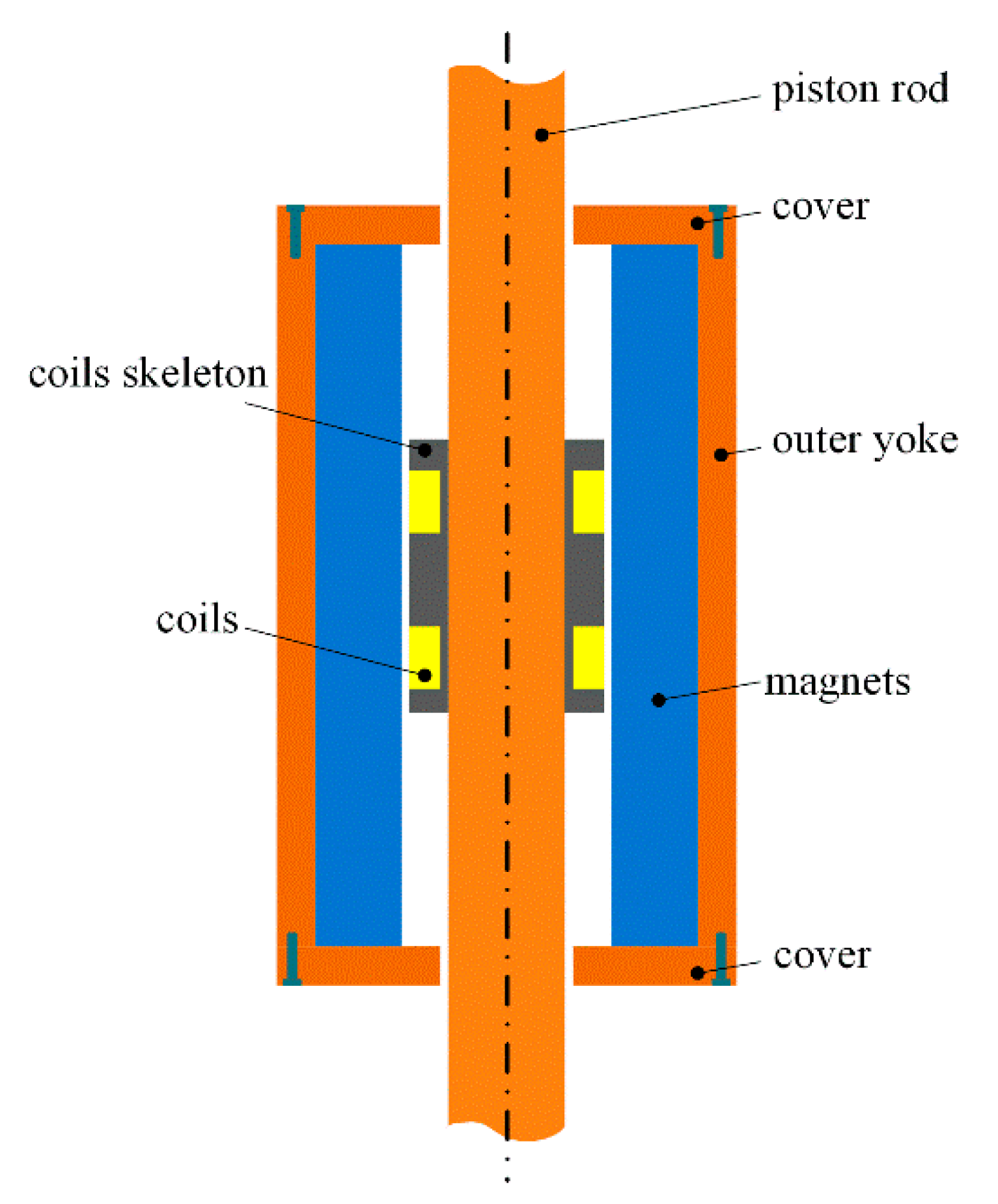
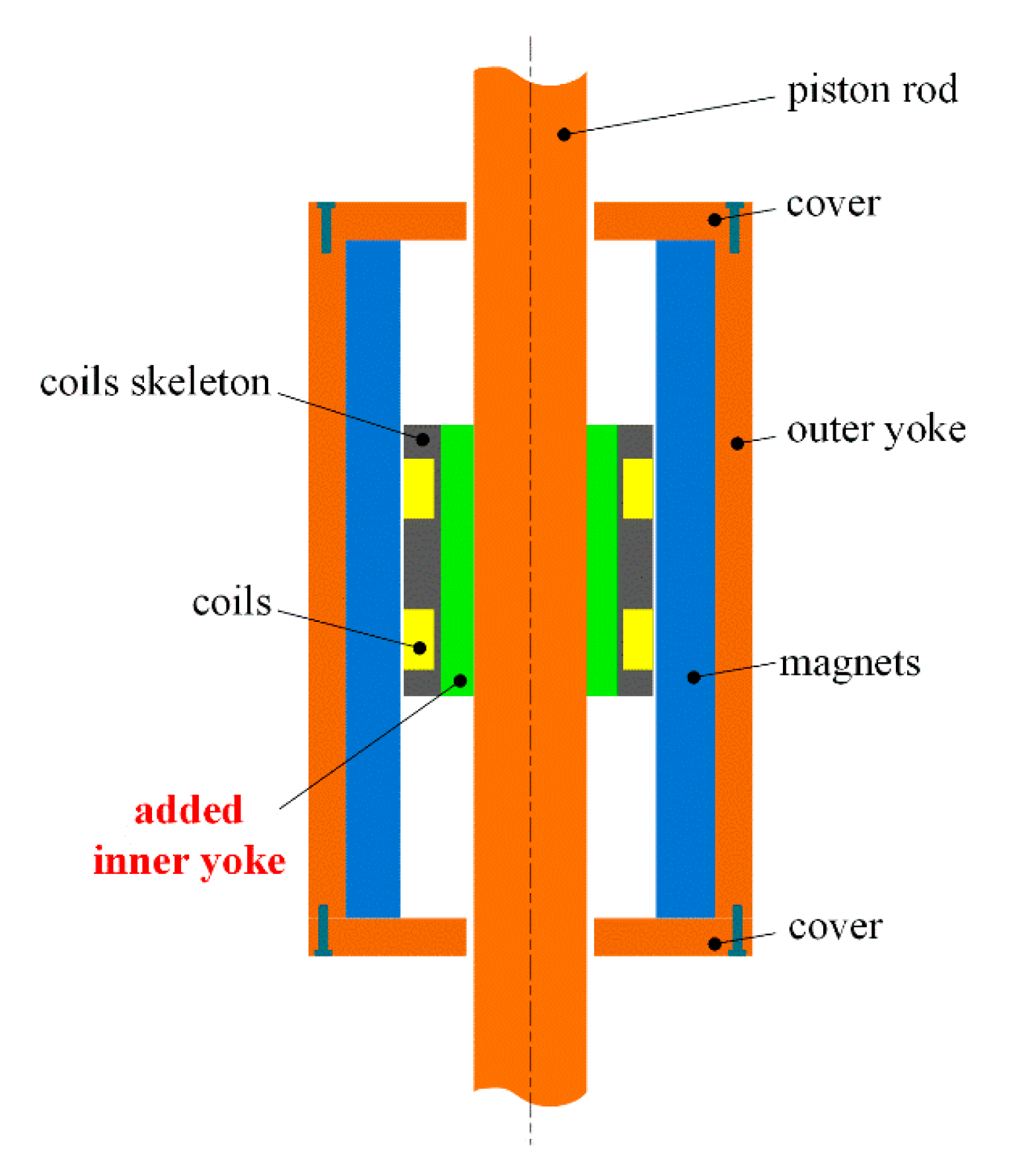
3.1. Basic Structure and Working Principle
3.2. Determination of Dimension and Material
3.3. Winding Design
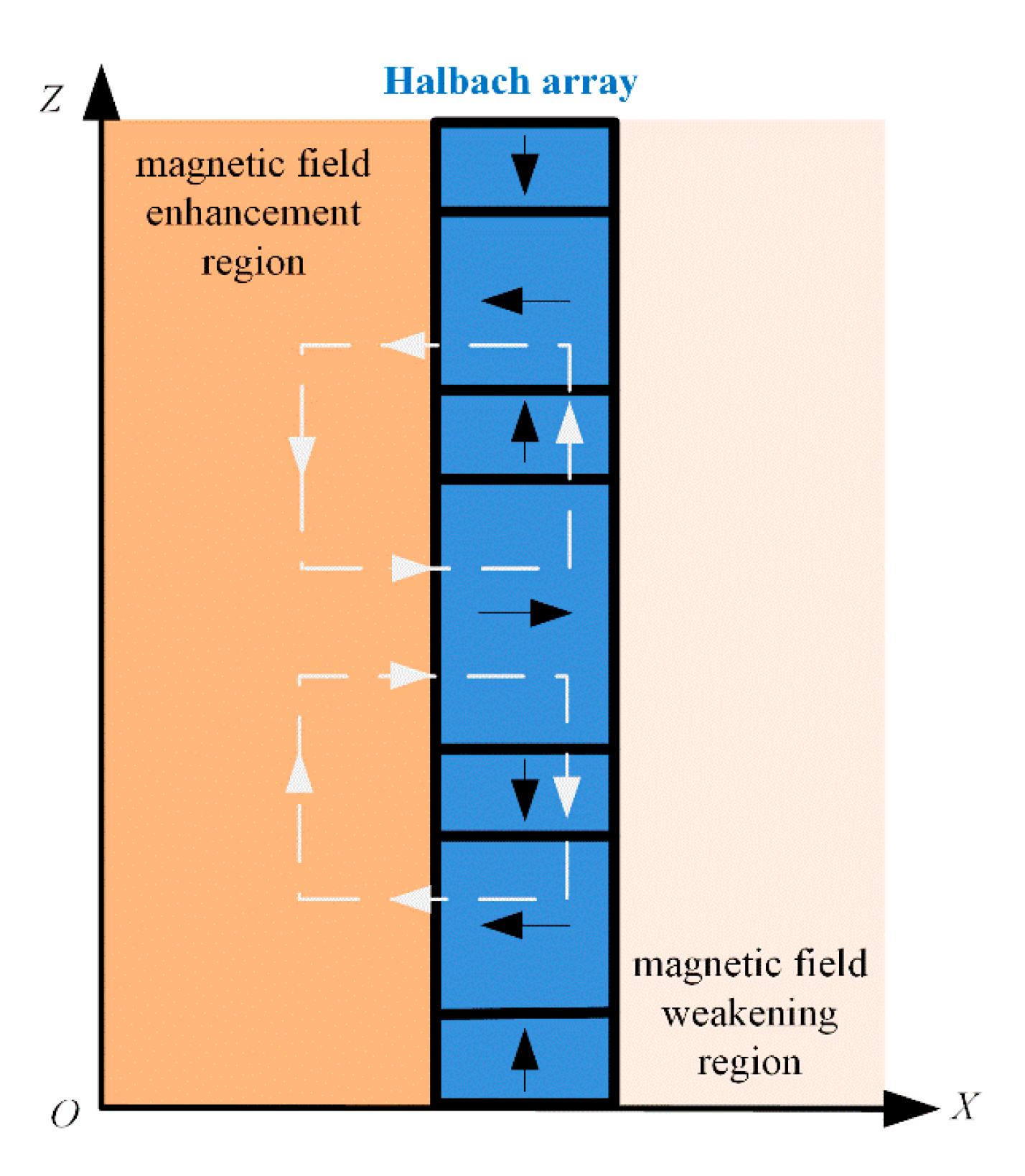
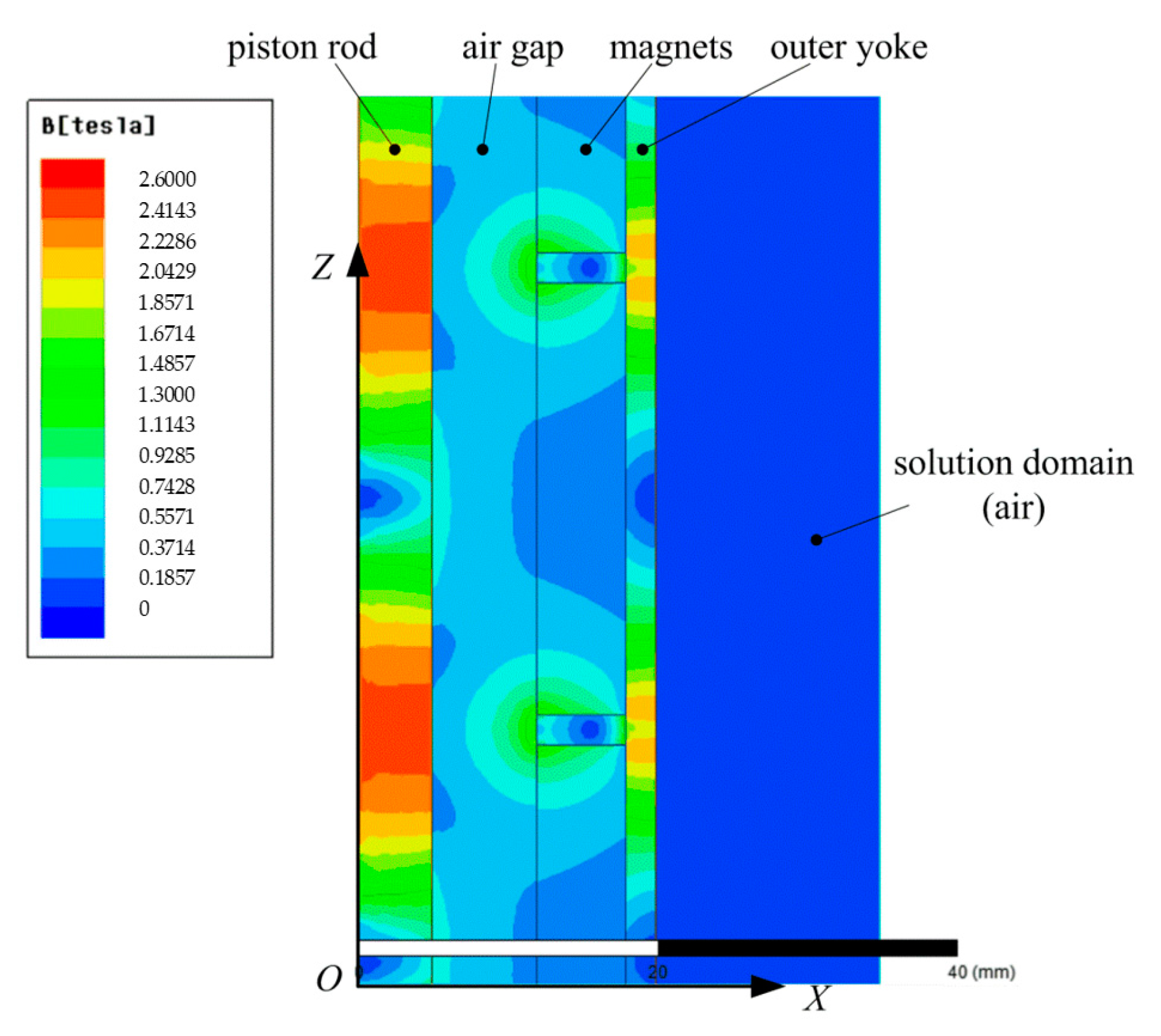
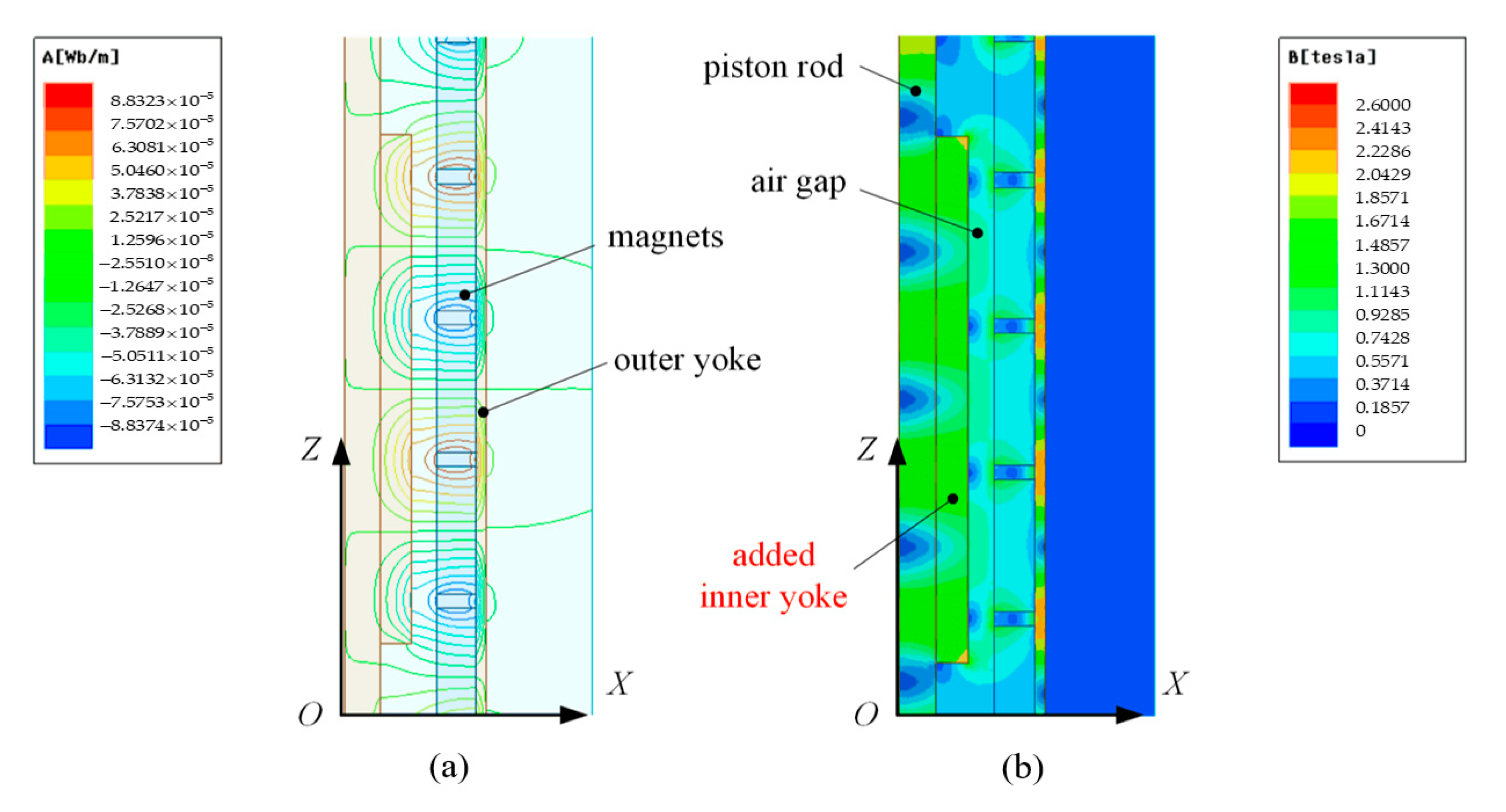
3.4. Improvement of Magnetic Circuit
4. Analysis of Energy-Reclaiming Characteristics of ELA-ERD
4.1. Analysis of Energy-Reclaiming Effect
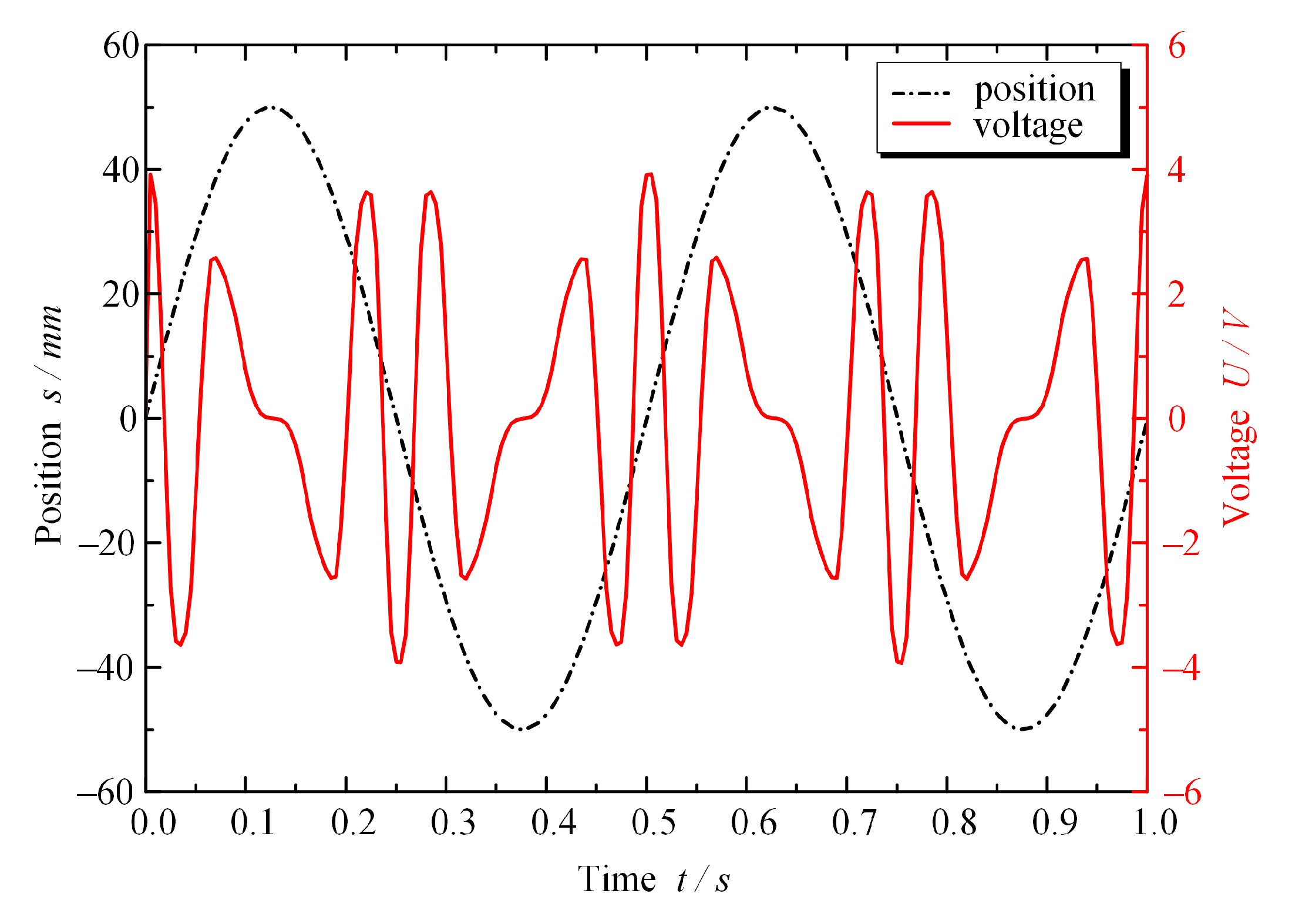
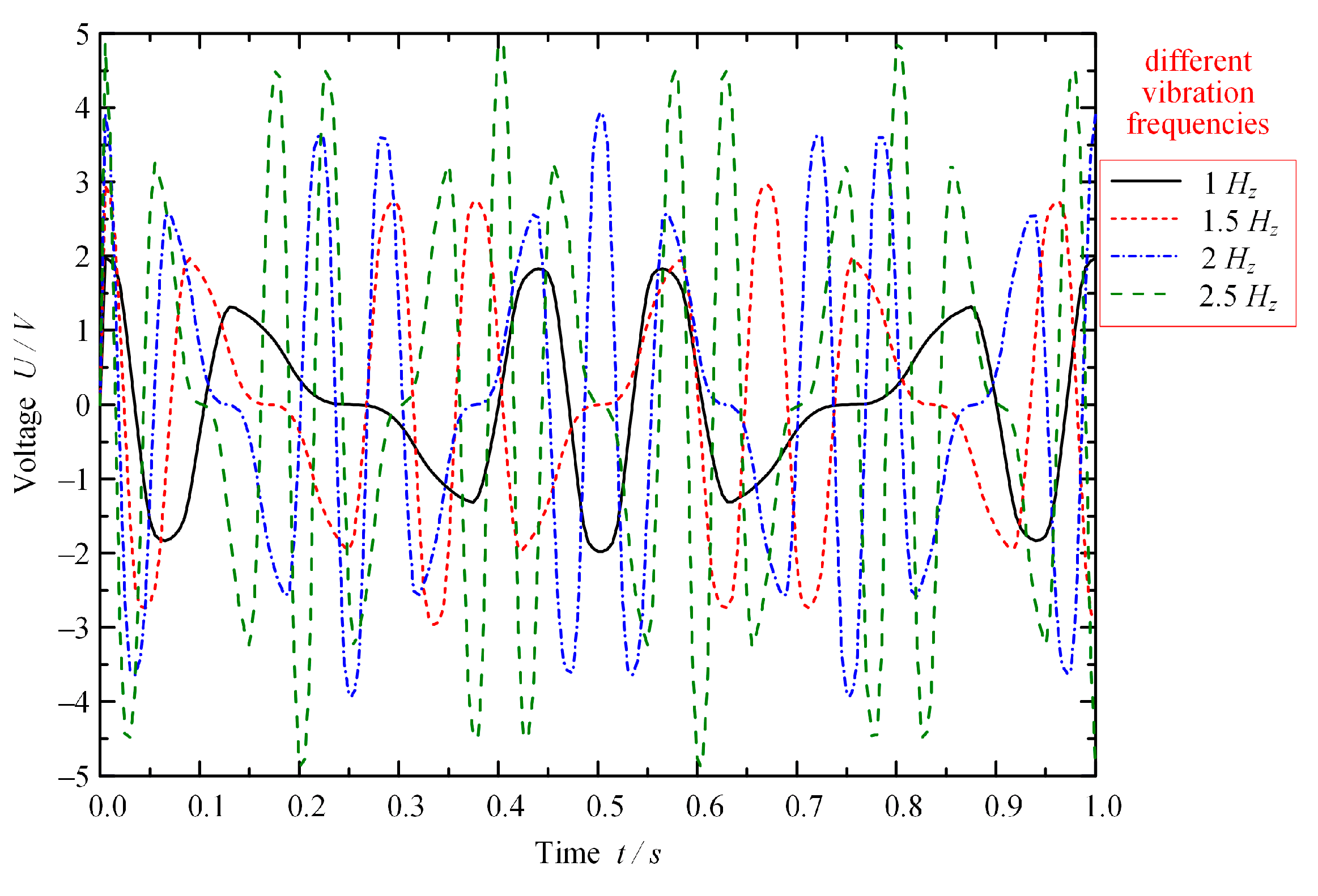
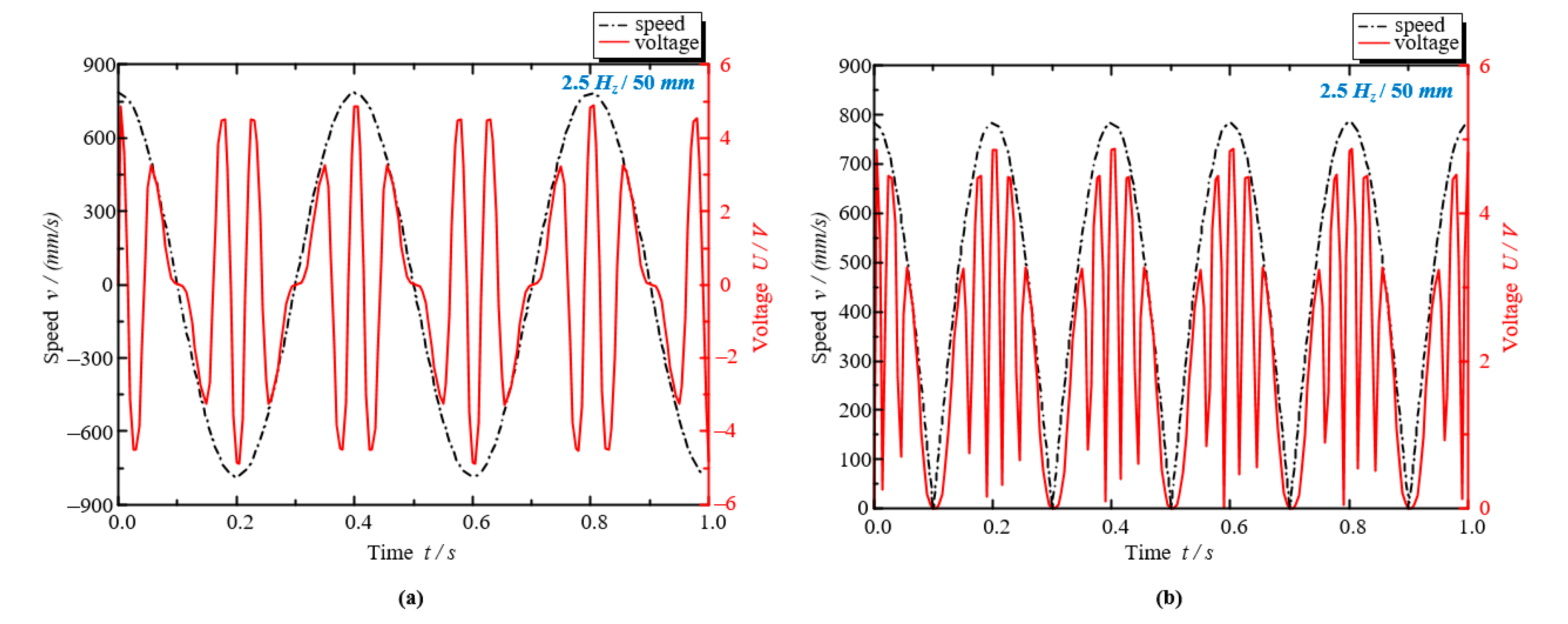
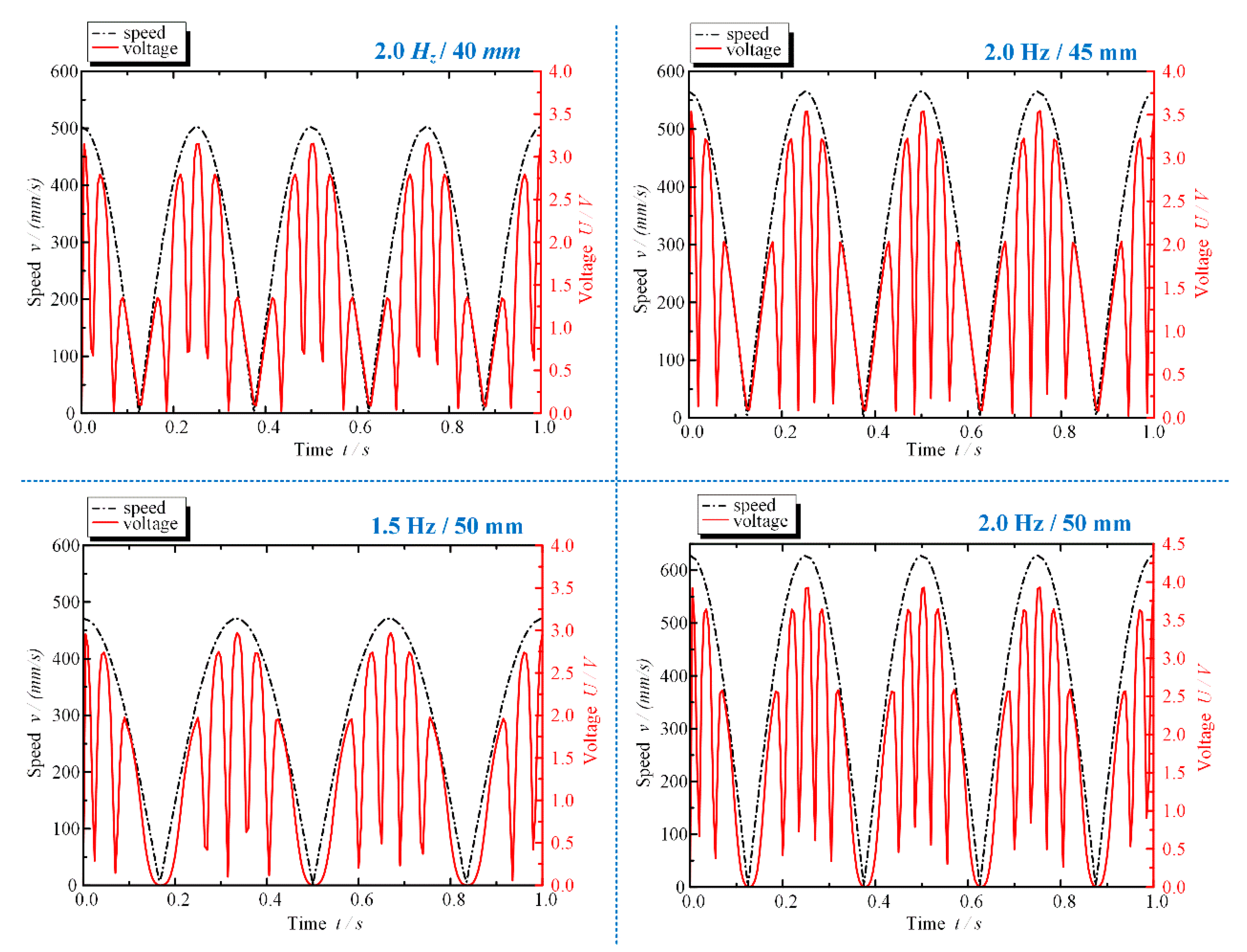
4.2. Study of Energy-Reclaiming Law
5. Conclusions
- A novel electromagnetic linear energy-reclaiming suspension based on the McPherson independent suspension is proposed in this study. The suspension has the advantages of compact structure, easy modification, and high reliability. Even if ELA-ERD fails, the normal operation of the suspension will not be affected, showing obvious advantages over other electromagnetic energy-reclaiming suspension.
- The ELA-ERD applied to the novel suspension was designed to realize passive energy reclaiming and active control. This device adopts the piston rod of the shock absorber as the inner yoke and organically integrates the structural characteristics of the suspension. The permanent magnets are arranged in Halbach array pattern to enhance the magnetic density within the work field.
- To solve the problem of magnetic density oversaturation of the inner yoke in the initial design phase, the magnetic circuit of ELA-ERD is optimized by increasing the size of the inner yoke in the effective working area of the moving coils. The simulation results show that this measure effectively improved the electromagnetic performance of ELA-ERD.
- The simulation analysis showed that the energy-reclaiming power of ELA-ERD reached 42 W under vibration amplitude of 50 mm and vibration frequency of 2 Hz. Therefore, the electromagnetic linear energy-reclaiming suspension with ELA-ERD has considerable potential for energy reclaiming.
- The factors influencing the energy-reclaiming law of ELA-ERD were analyzed from the perspectives of the changes of vibration amplitude and vibration frequency, and then the most fundamental influencing factor, vibration velocity, was further explored. According to Equation (14), the energy-reclaiming voltage coefficient was defined. Through comparison of a large number of data, the energy-reclaiming voltage coefficient of the ELA-ERD designed in this paper was derived, which lays a theoretical foundation for the subsequent research of ELA-ERD.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdelkareem, M.A.; Xu, L.; Ali, M.K.A.; Elagouz, A.; Mi, J.; Guo, S.; Liu, Y.; Zuo, L. Vibration energy harvesting in automotive suspension system: A detailed review. Appl. Energy 2018, 229, 672–699. [Google Scholar] [CrossRef]
- Zheng, P.; Gao., J.; Wang, R.; Dong, J.; Diao, J. Review on the Research of Regenerative Shock Absorber. In Proceedings of the 2018 24th International Conference on Automation and Computing (ICAC), Newcastle upon Tyne, UK, 6–7 September 2018; pp. 1–12. [Google Scholar]
- Zhang, Y.; Guo, K.; Wang, D.; Chen, C.; Li, X. Energy conversion mechanism and regenerative potential of vehicle suspensions. Energy 2017, 119, 961–970. [Google Scholar] [CrossRef]
- Čorić, M.; Deur, J.; Kasać, J.; Tseng, H.E.; Hrovat, D. Optimisation of active suspension control inputs for improved vehicle handling performance. Veh. Syst. Dyn. Int. J. Veh. Mech. Mobil. 2016, 54, 1574–1600. [Google Scholar] [CrossRef]
- Gong, M.; Yan, X. Robust Control Strategy of Heavy Vehicle Active Suspension Based on Road Level Estimation. Int. J. Automot. Technol. 2021, 22, 141–153. [Google Scholar] [CrossRef]
- Zheng, X.; Yu, F. Study on the potential benefits of an energy-regenerative active suspension for vehicles. SAE Trans. 2005, 114, 242–245. [Google Scholar]
- Lato, T.; Zhao, H.; Lin, Z.; He, Y. An Energy-Regenerative Suspension System. In Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition IMECE 2018, Pittsburg, PA, USA, 9–15 November 2018. [Google Scholar]
- Zheng, P.; Wang, R.; Gao, J. A Comprehensive Review on Regenerative Shock Absorber Systems. J. Vib. Eng. Technol. 2020, 8, 225–246. [Google Scholar] [CrossRef]
- Long, G.; Ding, F.; Zhang, N.; Zhang, J.; Qin, A. Regenerative active suspension system with residual energy for in-wheel motor driven electric vehicle. Appl. Energy 2020, 260, 114180. [Google Scholar] [CrossRef]
- Salman, W.; Qi, L.; Zhu, X.; Pan, H.; Zhang, X.; Bano, S.; Zhang, Z.; Yuan, Y. A high-efficiency energy regenerative shock absorber using helical gears for powering low-wattage electrical device of electric vehicles. Energy 2018, 159, 361–372. [Google Scholar] [CrossRef]
- Fu, C.; Lu, J.; Ge, W.; Tan, C.; Li, B. A Review of Electromagnetic Energy Regenerative Suspension System & Key Technologies. Comput. Model. Eng. Sci. 2022, 135. [Google Scholar] [CrossRef]
- Tvrdić, V.; Podrug, S.; Jelaska, D.; Perkušić, M. A Concept of the Novel Regenerative Hydraulic Suspension: The Prototype Description. In Proceedings of the 2018 3rd International Conference on Smart and Sustainable Technologies (SpliTech), Split, Croatia, 26–29 June 2018; pp. 1–6. [Google Scholar]
- He, X.; Xiao, G.; Hu, B.; Tan, L.; Tang, H.; He, S.; He, Z. The applications of energy regeneration and conversion technologies based on hydraulic transmission systems: A review. Energy Convers. Manag. 2020, 205, 0196–8904. [Google Scholar] [CrossRef]
- Dai, J.G.; Wang, C.; Liu, Z.F.; Zhu, J.H.; Hu, X.M. Review of energy reclaiming suspension technology. Sci. Technol. Eng. 2018, 18, 131–139. [Google Scholar]
- Bose Automotive Systems (China). BOSE’s innovative suspension system. Auto Accessories 2012, 12, 38–39. [Google Scholar]
- Boduroglu, A.; Gulec, M.; Demir, Y.; Yolacan, E.; Aydin, M. A New Asymmetric Planar V-Shaped Magnet Arrangement for A Linear PM Synchronous Motor. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Lv, X.; Ji, Y.; Zhao, H.; Zhang, J.; Zhang, G.; Zhang, L. Research Review of a Vehicle Energy-Regenerative Suspension System. Energies 2020, 13, 441. [Google Scholar] [CrossRef]
- Gysen, B.L.; Paulides, J.J.; Janssen, J.L.; Lomonova, E.A. Active electromagnetic suspension system for improved vehicle dynamics. IEEE Trans. Veh. Technol. 2010, 59, 1156–1163. [Google Scholar] [CrossRef]
- Gysen, B.L.; van der Sande, T.P.; Paulides, J.J.; Lomonova, E.A. Efficiency of a regenerative direct-drive electromagnetic active suspension. IEEE Trans. Veh. Technol. 2010, 60, 1384–1393. [Google Scholar] [CrossRef]
- Gysen, B.L.; Janssen, J.L.; Paulides, J.J.; Lomonova, E.A. Design aspects of an active electromagnetic suspension system for automotive applications. In Proceedings of the Industry Applications Society Meeting, Houston, TX, USA, 4–8 October 2009; IEEE: New York, NY, USA, 2009; pp. 1–8. [Google Scholar]
- Vijayakumara, P.; Mallikarjuna, D.C.; Suresh, R. Generating of power suspension shock absorber. Int. J. Adv. Eng. Res. Dev. 2017, 4, 713–721. [Google Scholar]
- Deng, Z.; Lai, F. Vehicle Active suspension Electromagnetic linear actuator Finite element analysis. Chin. J. Mech. Eng. Engl. Ed. 2011, 47, 121–128. [Google Scholar] [CrossRef]
- Chen, X.; Luo, H.; Deng, Z. Design of an energy-regenerative suspension control systemusing linear motor and energy recovery analysis. J. Vib. Shock. 2012, 31, 124–129. [Google Scholar]
- Deubel, C.; Prokop, G. Friction of a MacPherson suspension system at various load cases. J. Vib. Control. 2022, 2022, 10775463221140324. [Google Scholar] [CrossRef]
- Xiao-dong, S.U.N.; Feng, C.A.I.; Ying-feng, C.A.I.; Long, C.H.E.N. Improved Model Predictive Thrust-force Control of Linear Motors for Active Suspensions. China J. Highw. Transp. 2021, 34, 85–100. [Google Scholar]
- Yang, M.; Yu, J.; Guo, Y. Present Situation and Development Tendency of Shock Absorbers in Vehicle Suspensions. Eng. Test 2019, 59, 97–100 + 103. [Google Scholar]
- Yu, L.; Zhang, M.; Xue, W.; Luo, W.; He, J.; Tian, H. A Comprehensive Review of Permanent Magnet Synchronous Linear Motors in automotive electromagnetic suspension system. In Proceedings of the 2021 IEEE 4th Advanced Information Management Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; pp. 792–796. [Google Scholar]
- Dai, J.; Zhao, Z.; Xu, S.; Wang, C.; Zhu, J.; Fan, X. Inhibition of iron loss of the inner yoke in electromagnetic linear actuator. IET Electr. Power Appl. 2019, 13, 419–425. [Google Scholar] [CrossRef]
- Dai, J.; Xia, J.; Wang, C.; Xu, S. Thermal analysis of an electromagnetic linear actuator. Adv. Mech. Eng. 2017, 9, 1687814017745387. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Q.; Liu, B.; Gong, Z. Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array. Actuators 2021, 10, 231. [Google Scholar] [CrossRef]



| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Unladen mass | 1220 kg | The load distributed by the front axle under no-load condition | 60% |
| Wheelbase | 2610 mm | Wheel specification | 205/55 R16 |
| Max power | 81 kw | Max speed | 188 km/h |
| Max torque | 155 N·m | Displacement | 1598 mL |
| Parameters | Value |
|---|---|
| Diameter of working Cylinder | 20 mm |
| Base length | 80 mm |
| Oil tank diameter | 34 mm |
| Piston stroke | 100 mm |
| Outer diameter of dust Cover | 40 mm |
| Diameter of piston rod | 10 mm |
| Parameters | Value |
|---|---|
| Pitch diameter | 112 mm |
| Steel wire diameter | 14 mm |
| Number of active coils | 10 |
| Unsupported height | 420 mm |
| Pitch of teeth | 39.2 mm |
| Max deflection | 201.6 mm |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Height | 200 mm | Air gap thickness | 0.15 mm |
| Outer diameter | 40 mm | Radial thickness of permanent magnet | 5.5 mm |
| Stroke | 110 mm | Radial thickness of the outer yoke | 1.5 mm |
| Inner yoke diameter (diameter of piston rod ) | 10 mm | Axial thickness of end cover | 9 mm |
| Component | Material | Component | Material |
|---|---|---|---|
| Outer cover | Steel-1008 | Permanent magnets | N45 H |
| End cover | Steel-1008 | Coil skeleton | Teflon |
| Inner yoke (piston rod) | Steel-1008 | Coils | Copper-core enameled wire |
| Vibration Frequency | Vibration Amplitude | |
|---|---|---|
| 1 Hz | 35 mm | 4.47 |
| 1 Hz | 40 mm | 4.56 |
| 1 Hz | 45 mm | 4.46 |
| 1 Hz | 50 mm | 4.49 |
| 1.5 Hz | 35 mm | 4.41 |
| 1.5 Hz | 40 mm | 4.53 |
| 1.5 Hz | 45 mm | 4.59 |
| 1.5 Hz | 50 mm | 4.47 |
| 2 Hz | 35 mm | 4.22 |
| 2 Hz | 40 mm | 4.45 |
| 2 Hz | 45 mm | 4.58 |
| 2 Hz | 50 mm | 4.38 |
| 2.5 Hz | 35 mm | 4.42 |
| 2.5 Hz | 40 mm | 4.40 |
| 2.5 Hz | 45 mm | 4.45 |
| 2.5 Hz | 50 mm | 4.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Chang, L.; Qin, Y.; Wang, C.; Zhu, J.; Zhu, J.; Zhu, J. Design and Analysis of Electromagnetic Linear Actuation-Energy-Reclaiming Device Applied to a New-Type Energy-Reclaiming Suspension. Actuators 2023, 12, 142. https://doi.org/10.3390/act12040142
Dai J, Chang L, Qin Y, Wang C, Zhu J, Zhu J, Zhu J. Design and Analysis of Electromagnetic Linear Actuation-Energy-Reclaiming Device Applied to a New-Type Energy-Reclaiming Suspension. Actuators. 2023; 12(4):142. https://doi.org/10.3390/act12040142
Chicago/Turabian StyleDai, Jianguo, Lv Chang, Youning Qin, Cheng Wang, Jianhui Zhu, Jun Zhu, and Jingxuan Zhu. 2023. "Design and Analysis of Electromagnetic Linear Actuation-Energy-Reclaiming Device Applied to a New-Type Energy-Reclaiming Suspension" Actuators 12, no. 4: 142. https://doi.org/10.3390/act12040142
APA StyleDai, J., Chang, L., Qin, Y., Wang, C., Zhu, J., Zhu, J., & Zhu, J. (2023). Design and Analysis of Electromagnetic Linear Actuation-Energy-Reclaiming Device Applied to a New-Type Energy-Reclaiming Suspension. Actuators, 12(4), 142. https://doi.org/10.3390/act12040142






