A Novel Cooling Design for an Agonistic–Antagonistic SMA Tendon-Driven Actuator
Abstract
:1. Introduction
2. Design Concepts of SMA Actuator
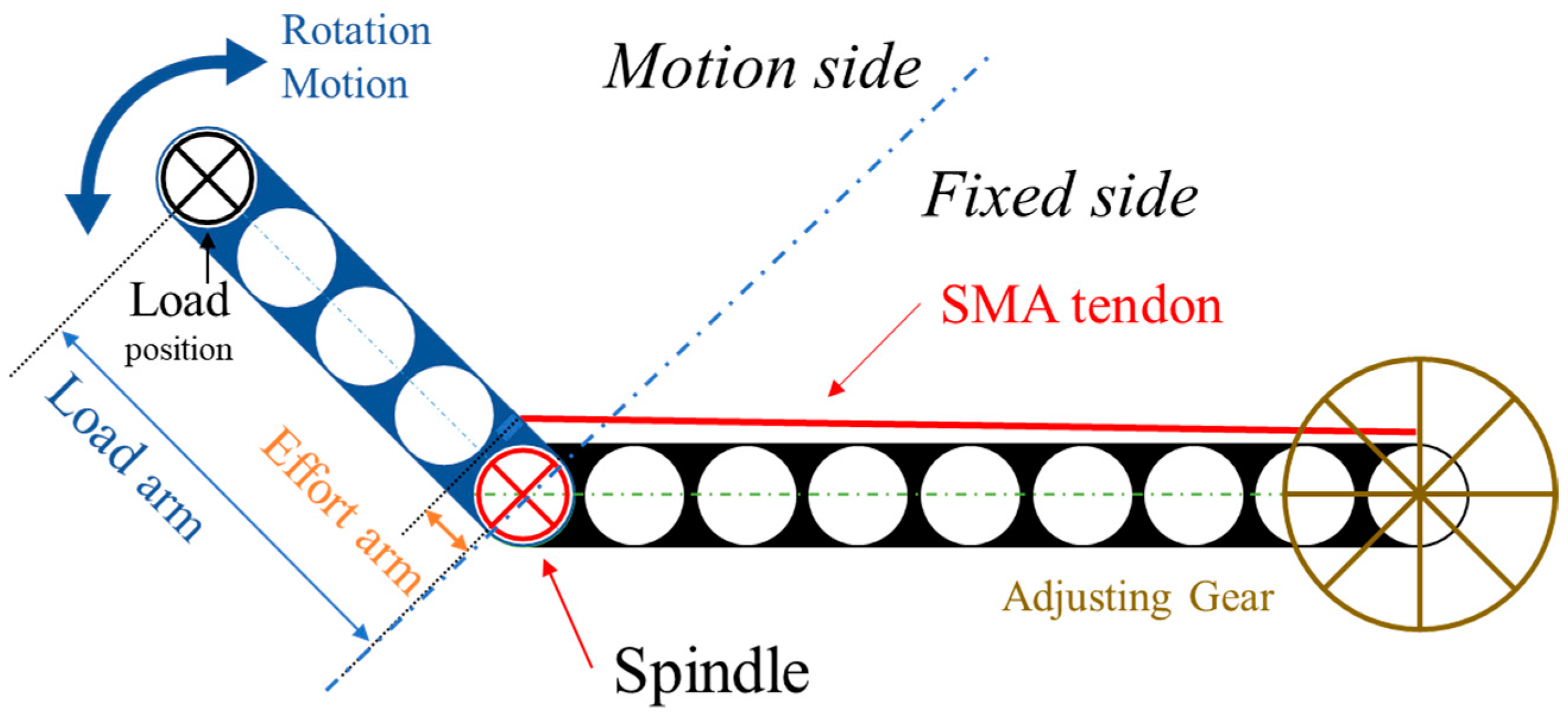
2.1. SMA-Tendon-Driven Actuator
2.2. Improved Cooling Concept
3. SMA-Based Tendon-Driven Actuator
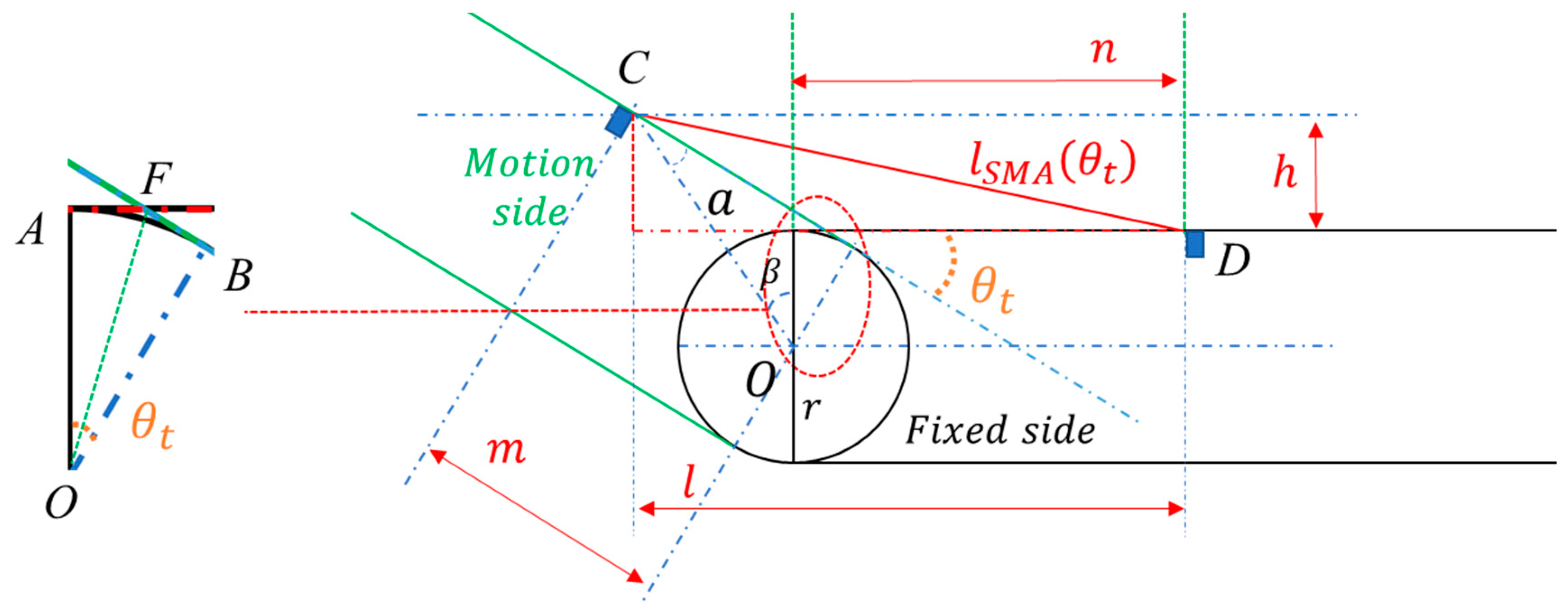
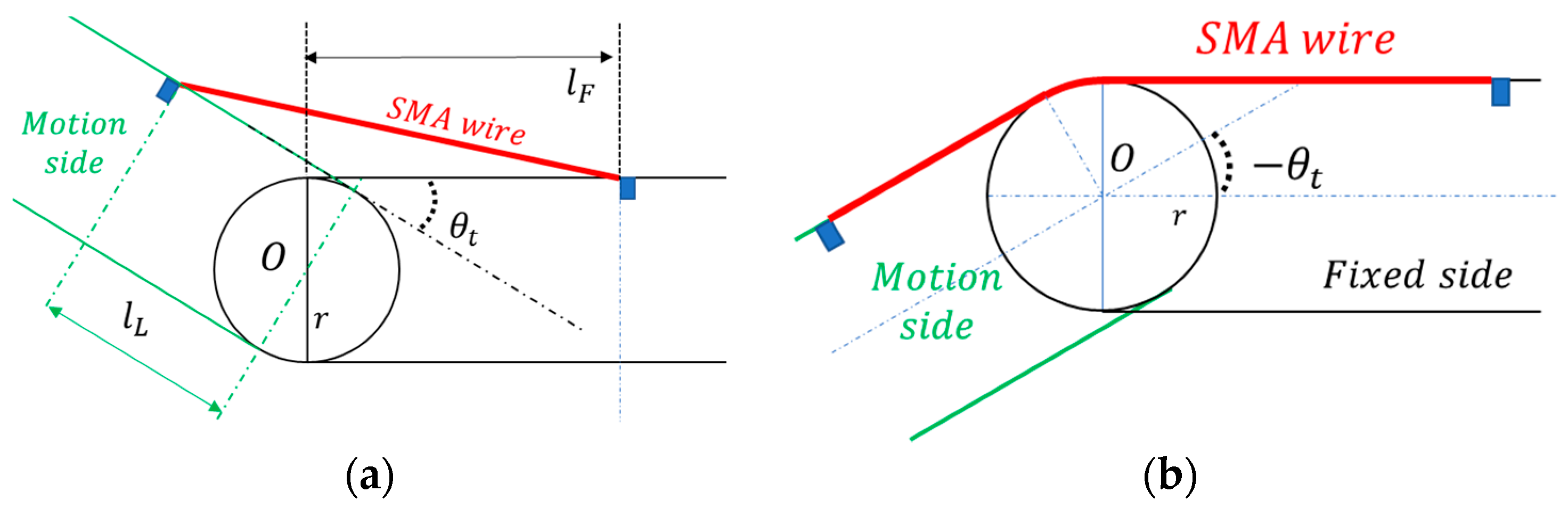
3.1. Single Joint Actuator
3.2. Prototype for Agonistic–Antagonistic Actuation
4. Sensing and Controlling Methodology
4.1. Controlling and Sensoing Circuits
4.2. Controlling Methodology
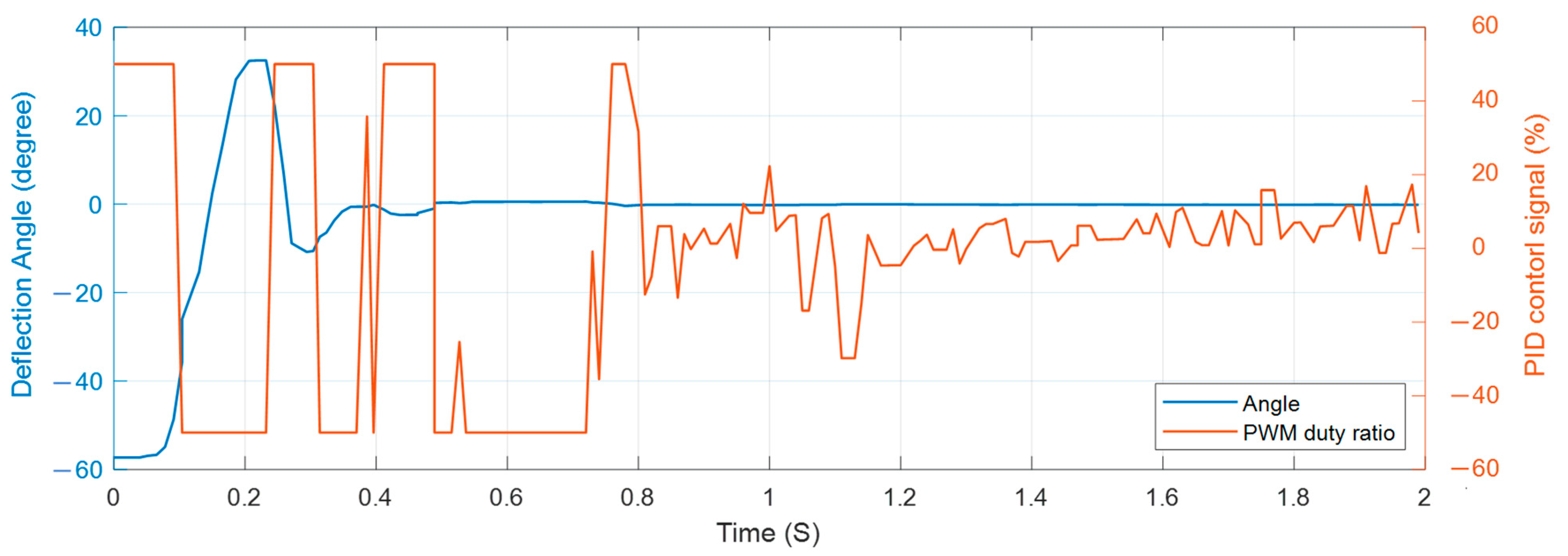
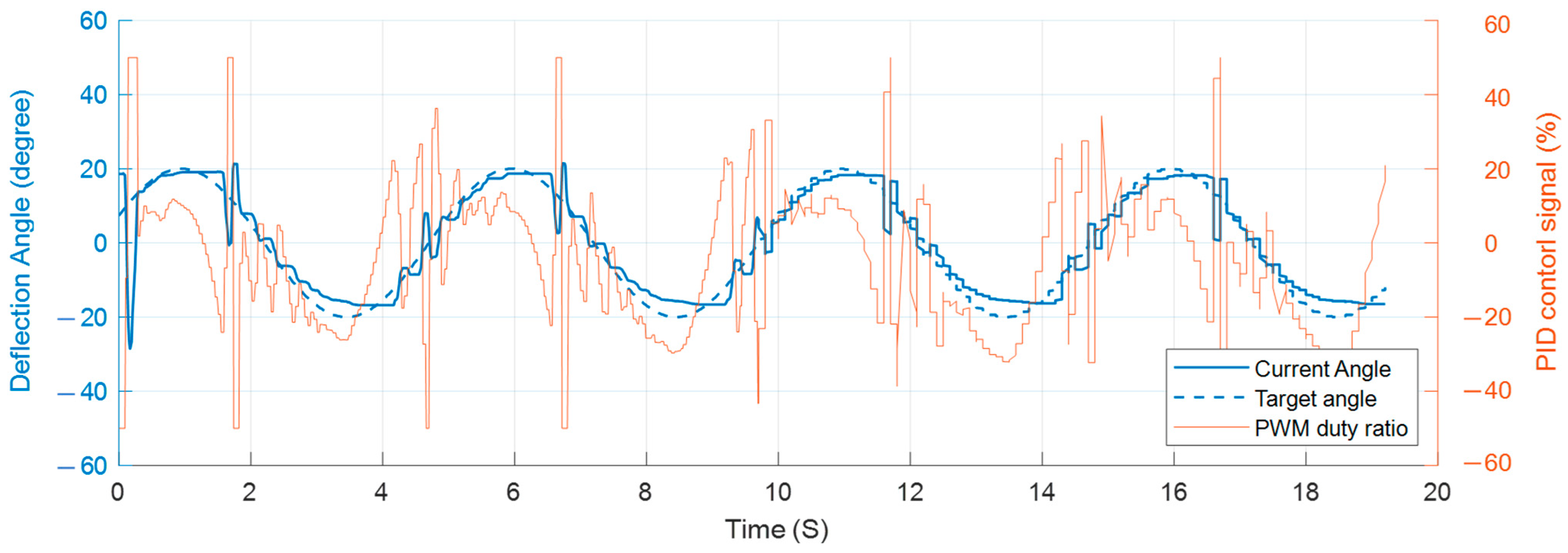
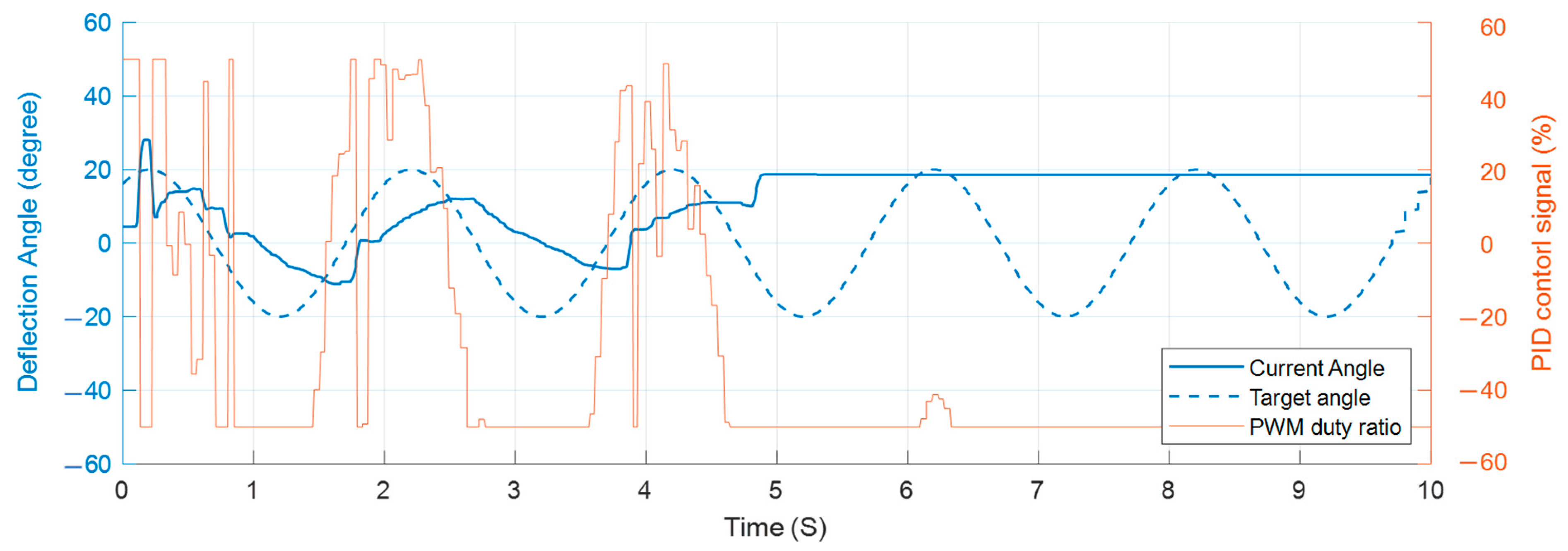
5. Evaluation and Discussion
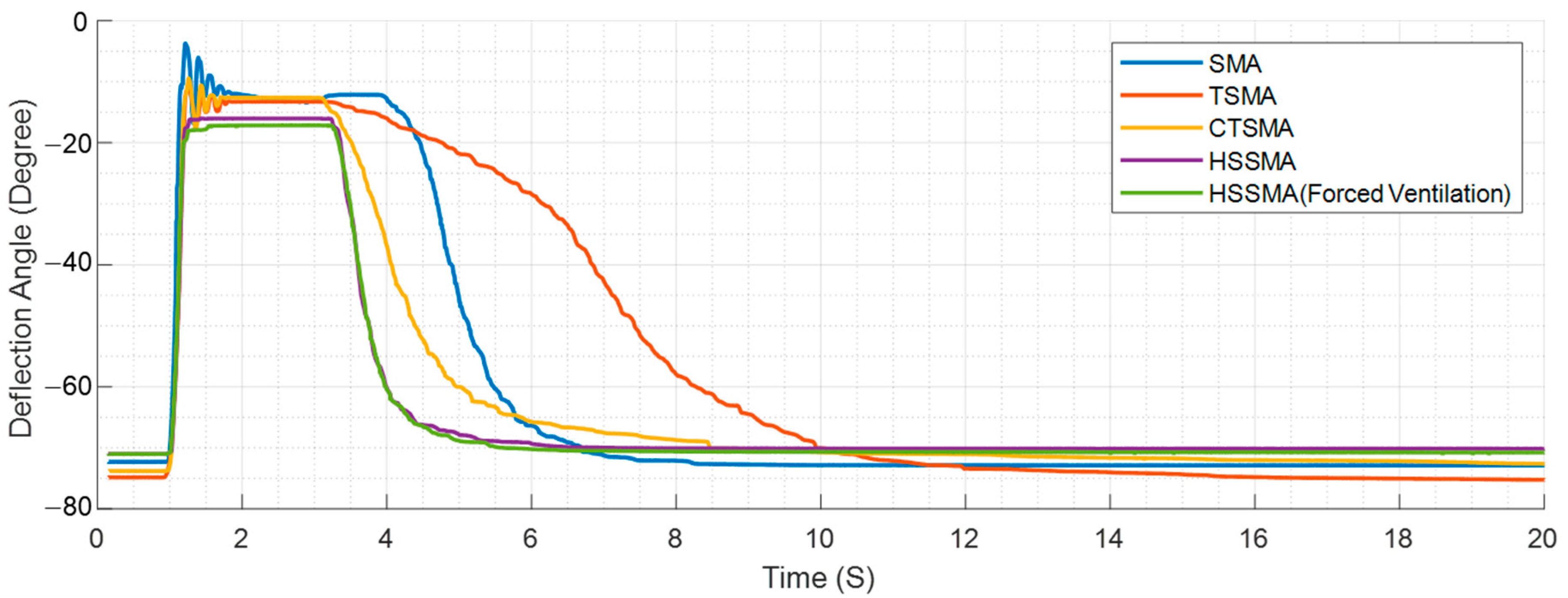
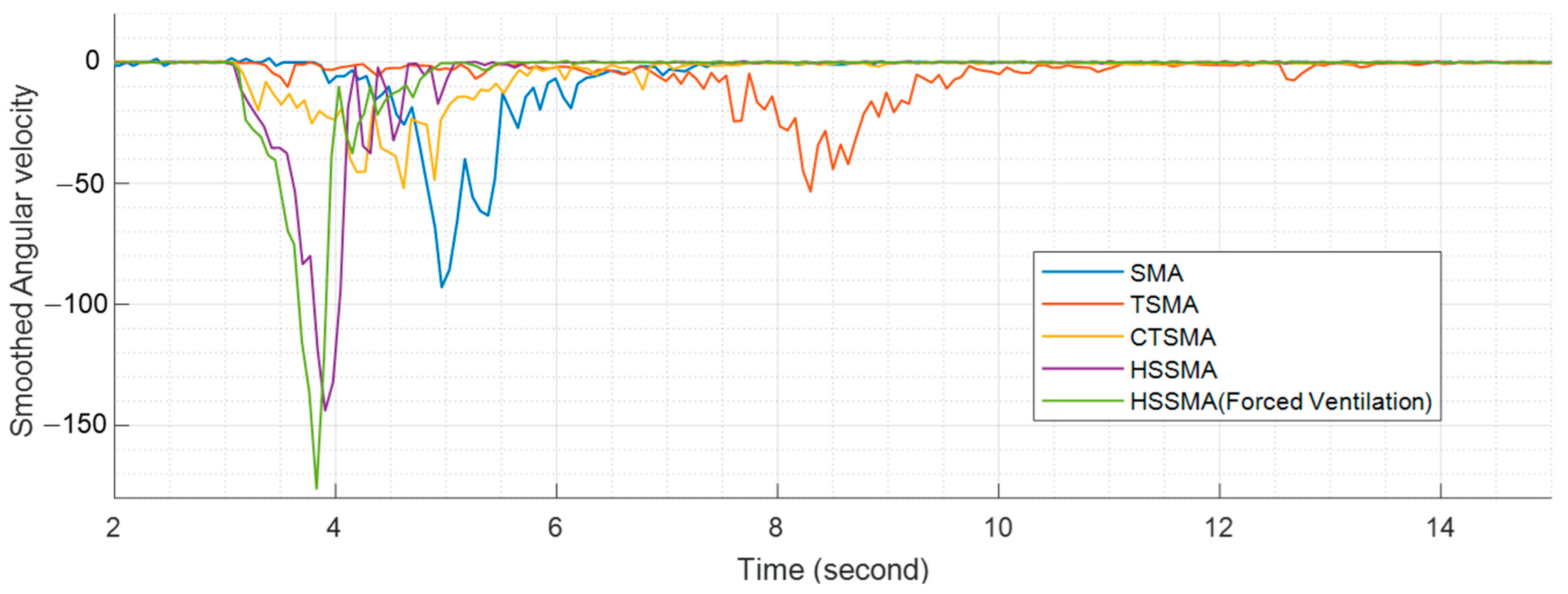
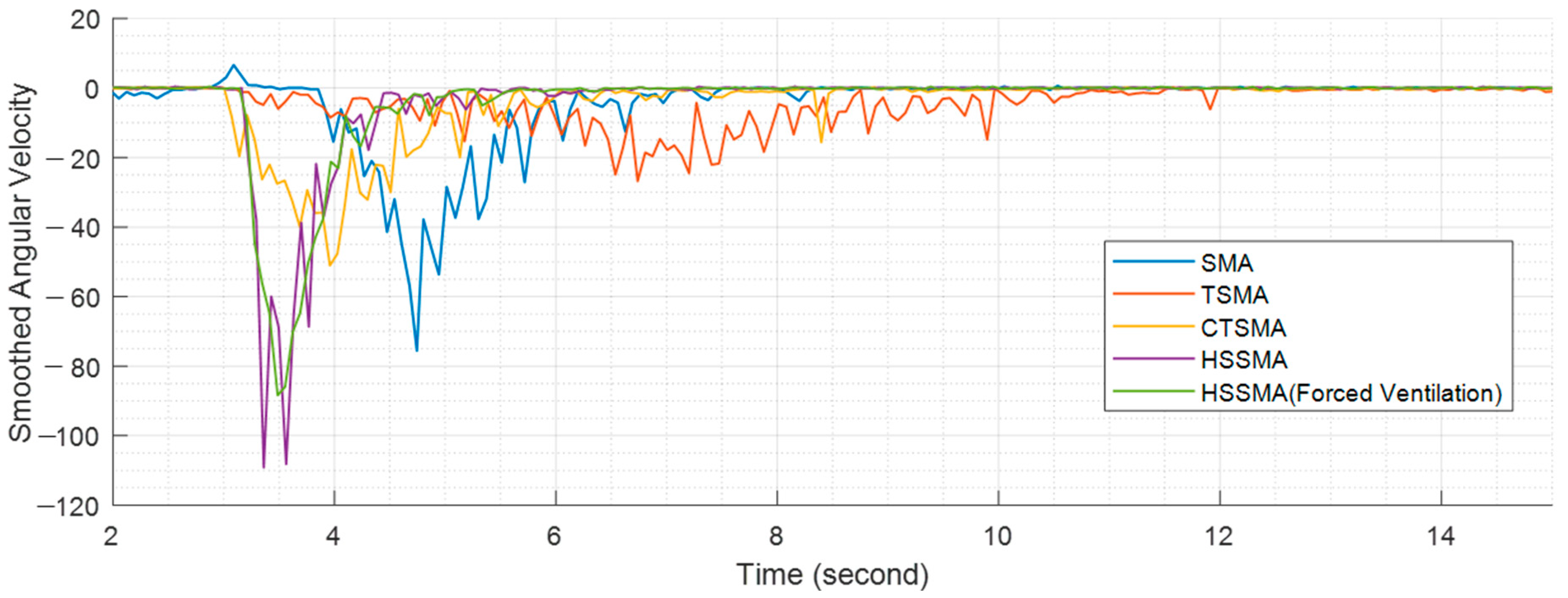
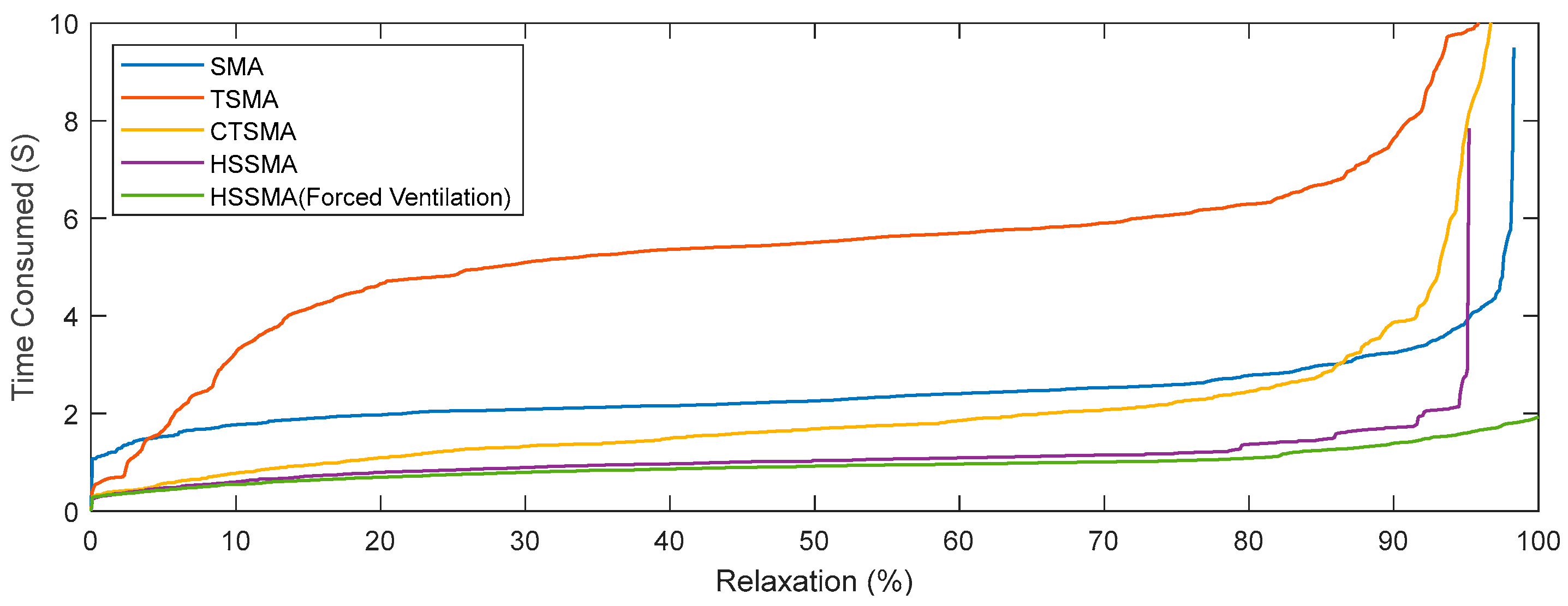
5.1. Relaxation Evaluation by Single Wire Actuator
5.2. Responding Performance
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Relaxation Percentage * (Degree) |
SMA (Second) |
TSMA (Second) |
CTSMA (Second) |
HSSMA Passive (Second) |
HSSMA Forced Ventilation (Second) |
|---|---|---|---|---|---|
| 0 | 0.100 | 0.005 | 0.013 | 0.002 | 0.001 |
| 1 | 1.160 | 0.643 | 0.370 | 0.310 | 0.325 |
| 5 | 1.530 | 1.658 | 0.563 | 0.469 | 0.422 |
| 10 | 1.760 | 3.248 | 0.773 | 0.593 | 0.545 |
| 25 | 2.050 | 4.828 | 1.229 | 0.840 | 0.748 |
| 50 | 2.260 | 5.505 | 1.685 | 1.032 | 0.918 |
| 75 | 2.590 | 6.081 | 2.236 | 1.184 | 1.031 |
| 90 | 3.240 | 7.627 | 3.865 | 1.711 | 1.388 |
| 95 | 3.880 | 9.822 | 7.825 | 2.766 | 1.594 |
| 99 | -- | 14.644 | 16.729 | -- | 1.842 |
| 100 | -- | -- | -- | -- | 1.925 |
| Relaxation Percentage * (Degree) |
SMA (Second) |
TSMA (Second) |
CTSMA (Second) |
HSSMA Passive (Second) |
HSSMA Forced Ventilation (Second) |
|---|---|---|---|---|---|
| 0 | 0.005 | 0.002 | 0.003 | 0.001 | 0.001 |
| 1 | 1.168 | 0.482 | 0.245 | 0.349 | 0.361 |
| 5 | 1.392 | 1.131 | 0.422 | 0.438 | 0.431 |
| 10 | 1.504 | 1.730 | 0.543 | 0.476 | 0.481 |
| 25 | 1.763 | 3.131 | 0.851 | 0.564 | 0.603 |
| 50 | 2.044 | 4.177 | 1.230 | 0.733 | 0.765 |
| 75 | 2.484 | 5.292 | 1.945 | 1.026 | 1.003 |
| 90 | 3.114 | 6.863 | 4.216 | 1.481 | 1.455 |
| 95 | 3.666 | 7.790 | 7.123 | 2.298 | 1.985 |
| 99 | 4.472 | 11.788 | -- | -- | 3.650 |
| 100 | 5.291 | 13.284 | -- | -- | -- |
References
- Ölander, A. An Electrochemical Investigation of Solid Cadmium-Gold Alloys. J. Am. Chem. Soc. 1932, 54, 3819–3833. [Google Scholar] [CrossRef]
- Tanaka, K.; Kobayashi, S.; Sato, Y. Thermomechanics of transformation pseudoelasticity and shape memory effect in alloys. Int. J. Plast. 1986, 2, 59–72. [Google Scholar] [CrossRef]
- Furuya, Y.; Shimada, H. Shape memory actuators for robotic applications. Mater. Des. 1991, 12, 21–28. [Google Scholar] [CrossRef]
- Chang-Jun, Q.; Pei-Sun, M.; Qin, Y. A prototype micro-wheeled-robot using SMA actuator. Sens. Actuators A Phys. 2004, 113, 94–99. [Google Scholar] [CrossRef]
- Veeramani, A.S.; Buckner, G.D.; Owen, S.B.; Cook, R.C.; Bolotin, G. Modeling the dynamic behavior of a shape memory alloy actuated catheter. Smart Mater. Struct. 2008, 17, 015037. [Google Scholar] [CrossRef]
- Singh, K.; Sirohi, J.; Chopra, I. An Improved Shape Memory Alloy Actuator for Rotor Blade Tracking. J. Intell. Mater. Syst. Struct. 2003, 14, 767–786. [Google Scholar] [CrossRef]
- Karakalas, A.A.; Machairas, T.T.; Saravanos, D.A. Effect of shape memory alloys partial transformation on the response of morphing structures encompassing shape memory alloy wire actuators. J. Intell. Mater. Syst. Struct. 2019, 30, 1682–1698. [Google Scholar] [CrossRef]
- Benafan, O.; Moholt, M.R.; Bass, M.; Mabe, J.H.; Nicholson, D.E.; Calkins, F.T. Recent Advancements in Rotary Shape Memory Alloy Actuators for Aeronautics. Shap. Mem. Superelasticity 2019, 5, 415–428. [Google Scholar] [CrossRef]
- Bishay, P.L.; Finden, R.; Recinos, S.; Alas, C.; Lopez, E.; Aslanpour, D.; Flores, D.; Gonzalez, E. Development of an SMA-based camber morphing UAV tail core design. Smart Mater. Struct. 2019, 28, 075024. [Google Scholar] [CrossRef]
- Bishay, P.L.; Aguilar, C.; Amirbekyan, A.; Vartanian, K.; Arjon-Ramirez, M.; Pucio, D. Design of a lightweight shape memory alloy stroke-amplification and locking system in a transradial prosthetic arm. In 2021 ASME Conference on Smart Materials, Adaptive Structures and Intelligent Systems (SMASIS) Proceedings; SMASIS2021-68248, V001T05A015; ASME: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Andrianesis Tzes, A. Development and Control of a Multifunctional Prosthetic Hand with Shape Memory Alloy Actuators. J. Intell. Robot Syst. 2015, 78, 257–289. [Google Scholar] [CrossRef]
- Soriano-Heras, E.; Blaya-Haro, F.; Molino, C.; de Agustín del Burgo, J.M. Rapid prototyping prosthetic hand acting by a low-cost shape-memory-alloy actuator. J. Artif. Organs. 2018, 21, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Bishay, P.L.; Fontana, J.; Raquipiso, B.; Rodriguez, J.; Borreta, M.J.; Enos, B.; Gay, T.; Mauricio, K. Development of a biomimetic transradial prosthetic arm with shape memory alloy muscle wires. Eng. Res. Express 2020, 2, 035041. [Google Scholar] [CrossRef]
- Bundhoo, V.; Haslam, E.; Birch, B.; Park, E.J. A shape memory alloy-based tendon-driven actuation system for biomimetic artificial fingers, part I: Design and evaluation. Robotica 2009, 27, 131–146. [Google Scholar] [CrossRef]
- Gilardi, G.; Haslam, E.; Bundhoo, V.; Park, E.J. A shape memory alloy based tendon-driven actuation system for biomimetic artificial fingers, part II: Modelling and control. Robotica 2010, 28, 675–687. [Google Scholar] [CrossRef]
- Cheng, S.S.; Kim, Y.; Desai, J.P. Modeling and characterization of shape memory alloy springs with water cooling strategy in a neurosurgical robot. J. Intell. Mater. Syst. Struct. 2017, 28, 2167–2183. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J.; Choi, K.; Rodrigue, H.; Park, C.H. Soft Exosuit Based on Fabric Muscle for Upper Limb Assistance. IEEE/ASME Trans. Mechatron. 2023, 28, 26–37. [Google Scholar] [CrossRef]
- Park, S.J.; Choi, K.; Rodrigue, H.; Park, C.H. Fabric muscle with a cooling acceleration structure for upper limb assistance soft exosuits. Sci. Rep. 2022, 12, 11398. [Google Scholar] [CrossRef]
- Liu, R.; Sawada, H. An SMA Wire-based Tendon Actuator and its Application on Robotic Fingers. In Proceedings of the 2023 IEEE International Conference on Mechatronics and Automation (ICMA), Harbin, China, 6–9 August 2023; IEEE: New York, NY, USA, 2023; pp. 681–686. [Google Scholar]

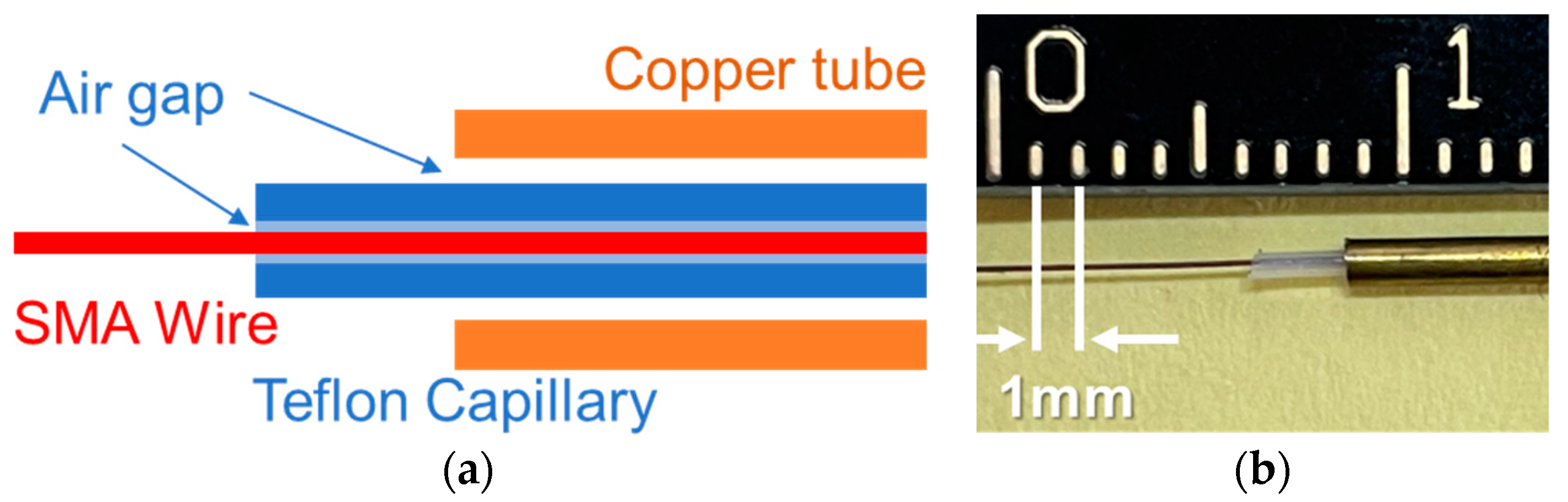


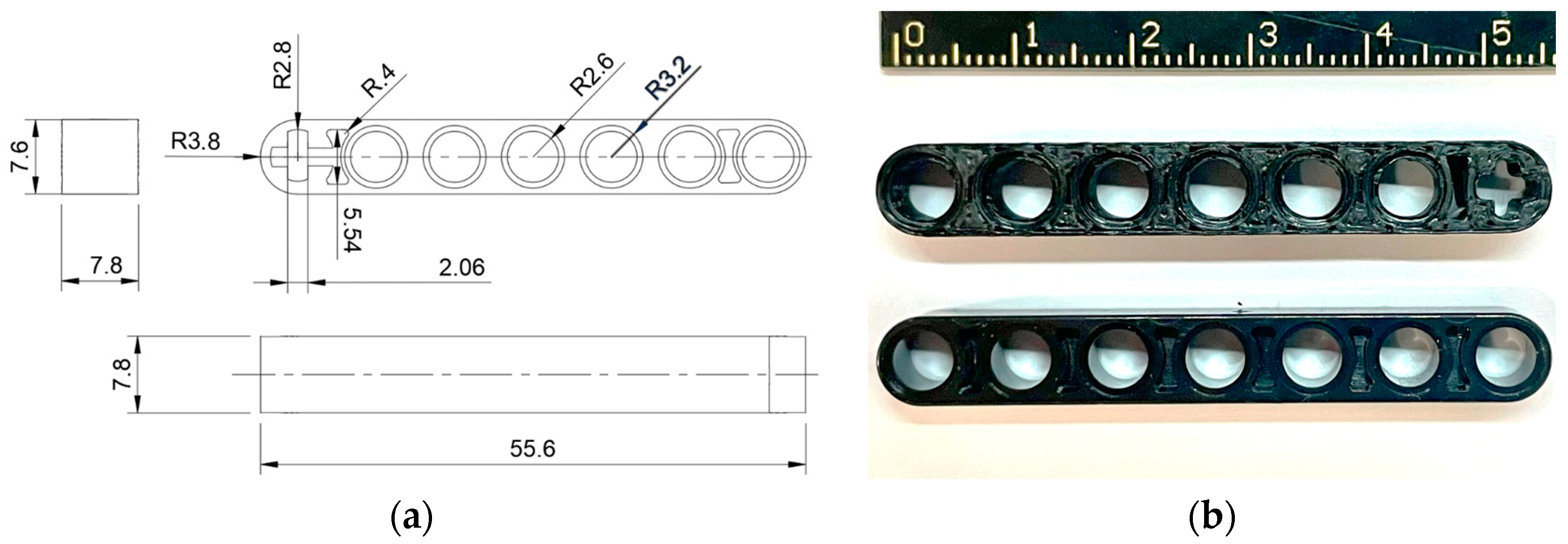



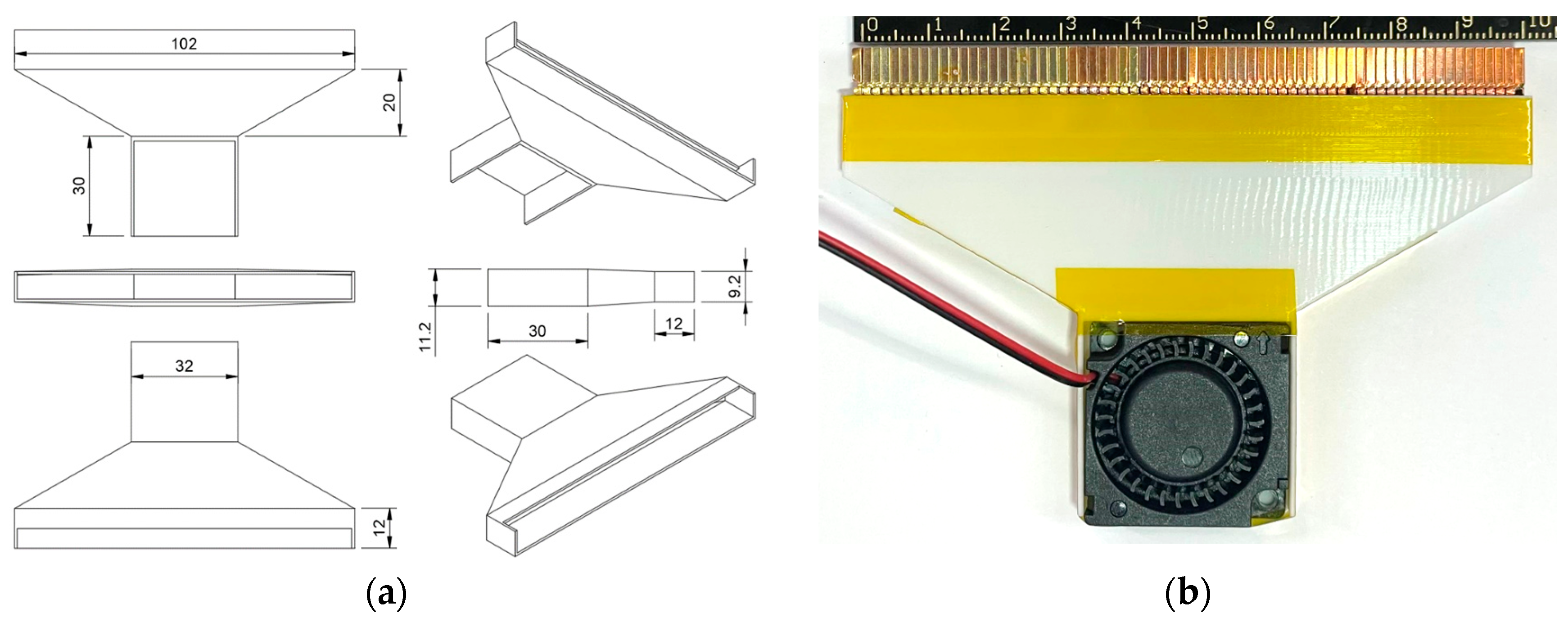
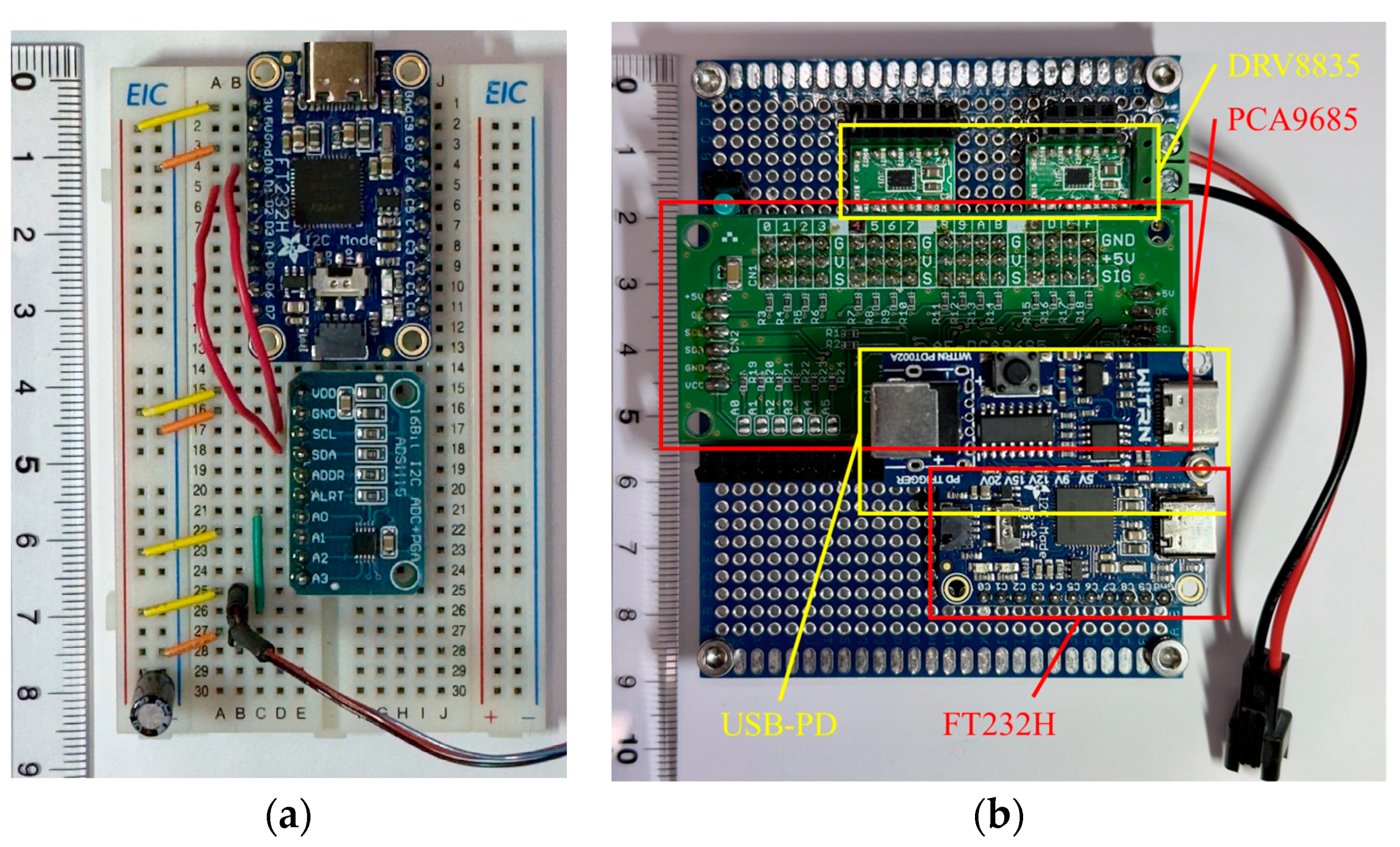


| Parts | Diameter | Value |
|---|---|---|
| SMA wire | Inner | - |
| Outer | ||
| Teflon Capillary | Inner | |
| Outer | ||
| Copper Tube | Inner | |
| Outer |
| Feature | Value | Unit |
|---|---|---|
| Diameter | 0.15 | |
| Weight | 112 | |
| Standard Resistance | 61 | |
| Standard Driving Voltage | 20.7 | |
| Standard Driving Current | 0.34 | |
| Standard Power Consumption | 7.05 | |
| Practical Strain | 4.0 | % |
| Practical Life Cycles (Under 80 Mpa) | times | |
| Destruction Force | 1.8 |
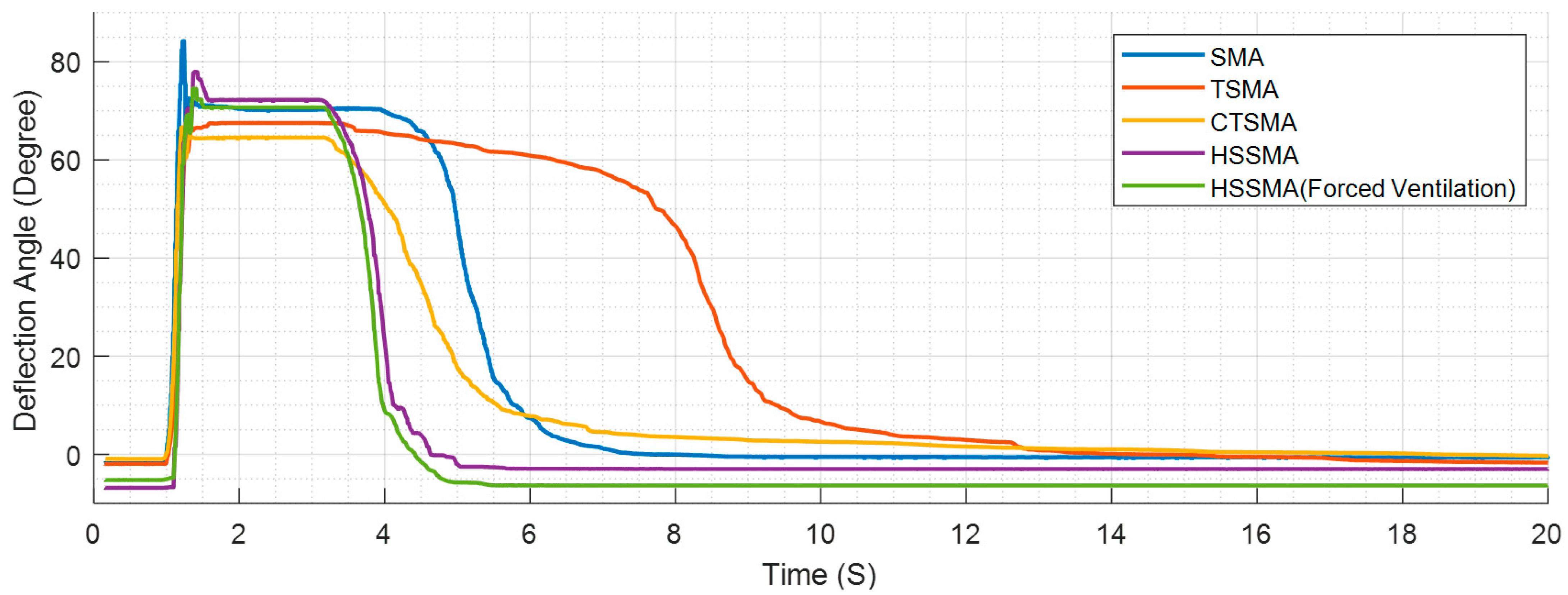
| Angle | SMA | TSMA | CTSMA | HSSMA Passive | HSSMA Forced Ventilation |
|---|---|---|---|---|---|
| Initial Deflection (at 0 S) | −1.841 | −1.948 | −0.936 | −6.829 | −5.248 |
| Maximum Deflection | 70.204 | 67.522 | 64.536 | 72.236 | 70.704 |
| Final Deflection (at 20 S) | −0.608 | −1.635 | −0.220 | −3.021 | −6.370 |
| Deflection Range | 72.045 | 69.470 | 65.472 | 79.065 | 75.952 |
| Relaxation Range | 70.812 | 69.157 | 64.756 | 75.257 | 77.073 |
| Angle | SMA | TSMA | CTSMA | HSSMA Passive | HSSMA Forced Ventilation |
|---|---|---|---|---|---|
| Initial Deflection (at 0 S) | −72.298 | −74.835 | −73.795 | −71.008 | −71.003 |
| Maximum Deflection | −13.207 | −13.265 | −12.619 | −16.027 | −17.146 |
| Final Deflection (at 20 S) | −72.866 | −75.188 | −72.532 | −70.138 | −70.764 |
| Deflection Range | 59.091 | 61.571 | 61.177 | 54.981 | 53.857 |
| Relaxation Range | 59.659 | 61.923 | 59.913 | 54.111 | 53.619 |
| Relaxation Performance | SMA | TSMA | CTSMA | HSSMA Passive | HSSMA Forced Convection |
|---|---|---|---|---|---|
| Flexor side | 2.720 | 9.179 | 7.454 | 2.456 | 1.269 |
| Extensor side | 2.497 | 7.308 | 6.877 | 1.949 | 1.624 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Zhang, S.; Baba, Y.; Sawada, H. A Novel Cooling Design for an Agonistic–Antagonistic SMA Tendon-Driven Actuator. Actuators 2023, 12, 415. https://doi.org/10.3390/act12110415
Liu R, Zhang S, Baba Y, Sawada H. A Novel Cooling Design for an Agonistic–Antagonistic SMA Tendon-Driven Actuator. Actuators. 2023; 12(11):415. https://doi.org/10.3390/act12110415
Chicago/Turabian StyleLiu, Renke, Shuyao Zhang, Yusuke Baba, and Hideyuki Sawada. 2023. "A Novel Cooling Design for an Agonistic–Antagonistic SMA Tendon-Driven Actuator" Actuators 12, no. 11: 415. https://doi.org/10.3390/act12110415
APA StyleLiu, R., Zhang, S., Baba, Y., & Sawada, H. (2023). A Novel Cooling Design for an Agonistic–Antagonistic SMA Tendon-Driven Actuator. Actuators, 12(11), 415. https://doi.org/10.3390/act12110415






