Abstract
The external gear pump, like any other hydraulic component, is vulnerable to failure, which may lead to downtime as well as the failure of other components linked to it, thereby causing production loss. Therefore, establishing a condition monitoring system is crucial in identifying failure at an early stage. Traditional condition monitoring approaches rely on experimental data that are collected by means of sensors. However, the sensors utilized in the experiments may have calibration issues, which lead to inaccurate measurements. The availability of experimental data is also limited as it is difficult and expensive to create and detect a fault in a component. Hence, it is essential to develop a simulation model that mimics the performance of the actual system. The data generated from the model can be utilized to create the data source required for automated condition monitoring. A new methodology based on a detailed geometric model for simulating the External Gear Pump is described and compared to two models analyzed in the authors’ previous work, namely Schlosser’s loss model and simple geometric model. In this paper, the three models are compared with experimental data and the method utilized for fault injection. Schlosser’s loss model, as well as the detailed geometric model, are found to be suitable in terms of validation; however, the latter is a better candidate in terms of fault injection. Hence, the detailed geometric model can be implemented as a tool to generate the data source for condition monitoring applications.
1. Introduction
External Gear Pumps (EGPs) can be found in several stationary as well as mobile machine applications due to their low cost, simple, and robust design. EGP, like any other component in the system, is susceptible to failure. There are four main modes of failure, namely, internal leakage [1], external leakage [2], severe pressure ripples [3], and overheating of the pump [4]. They occur due to the presence of cavitation [5], wear [6], fluid contamination [7], and design and assembly errors. The unexpected failure of a pump may lead to substantial production delays because of machine downtime. Therefore, it is essential to develop an onboard condition monitoring system that can identify faults at an incipient stage, thereby making the system more reliable.
Earlier methods of condition monitoring relied on data sources developed with the aid of sensors. The sensors utilized are accelerometers [8], pressure transducers [9], flow meters [10], and displacement sensors [11] to name a few. The sensors, however, are expensive, prone to failure, difficult to incorporate into existing system design, and lead to overfitting of condition monitoring model [12]. Furthermore, there has been an attempt to develop fault-tolerant control for an electro/hydraulic servo system that compensates for sensor faults [13]. The development of an experimental setup that is suitable for fault injection also poses some challenges, such as the fault may lead to failure of other components within the system, high cost of setup, and introducing realistic fault can consume time and resources. Therefore, it is essential to develop an automated condition monitoring system that is capable of utilizing existing information, such as data from sensors within the system, electric drive, and data source generated with the aid of a robust simulation model for situations where it is difficult to obtain experimental data.
The required complexity of the simulation model to generate data sources for condition monitoring applications is rarely investigated. It is expected that a detailed model can represent an actual system more accurately. However, it is important to note that the required parameters for a detailed model are higher than those required for a simple model. According to a study performed in [14], the higher the complexity of a model, the higher the accuracy of the model in most scenarios; however, there are a few instances where the opposite is also true. A previous attempt at investigating the effect of model complexity demonstrated in [15] that a simplified model performed better than the detailed model of an EGP. However, it was addressed that the measurement of certain parameters might not have been accurate and that further investigation is required regarding the detailed model.
Upon the development of a robust simulation model, the next step is to build an AI-based condition-monitoring algorithm that can identify faults at an early stage. Simulation data with data augmentation has been demonstrated in [16] as a tool to generate data for condition monitoring of a variable displacement axial piston pump. A check valve failure simulation model has been utilized in [17] for generating data to classify various faults at different levels. The mixing of domain databases by combining data from a hydraulic press and a simulation model is investigated in [18]. Simulation-driven fault classification of bearing faults utilizing machine learning is demonstrated in [19]. A sparse linear parameter varying vector auto-regression model was proposed and demonstrated high accuracy in the fault detection of gearboxes under variable speed conditions [20]. Apart from applications in condition monitoring strategies, the development of a robust simulation model can aid in the development of a database that extends to better maintenance strategies such as predictive and prescriptive maintenance [21].
Considering the challenges addressed, the main contributions of this paper can be summarized as follows:
- (1)
- A new approach, which relies on a detailed geometric model for simulating the EGP, is proposed.
- (2)
- The approach is assessed by comparing two models that were previously examined, with each model being validated against experimental data from the study case of an electrified reach truck.
- (3)
- A test classifier is developed to assess the data reliability from the top-performing model for automated condition monitoring of EGP.
The remainder of the paper is organized as follows: Section 2 describes the methods implemented and includes the description of EGP models, the electric reach truck co-simulation model, and the experimental setup. Section 3 discusses and compares the results obtained on performing model validation as well as the results obtained from a test classifier. Finally, Section 4 contains the conclusion and future developments.
2. Methods
In this section, the mathematical models of EGPs are defined first. Next, the case of an electrified reached truck is chosen, and the schematic and simulation model setup is described. Finally, the experimental setup utilized to compare and validate the levels of complexity of the simulation model is defined.
2.1. External Gear Pump Models
The first level of complexity model uses the displacement and efficiency data given by the pump’s manufacturer coupled with Schlosser’s loss coefficient model [22] to evaluate the laminar and turbulent leakages. The resulting volumetric flow equation is:
where is the volumetric displacement of EGP, is the rotational speed, is the laminar slip coefficient, is the delivery pressure, is the dynamic viscosity, is the turbulent slip coefficient, and 𝜌 is the density.
The second level of the complexity model implements the same Schlosser’s loss coefficient model to evaluate the leakages but coupled with a more detailed volumetric displacement equation that requires actual geometric parameters of the pump, such as the outer diameter of the gear, the gears width, and the gears center distance:
where is the gear width, is the outside diameter of gear, and is the distance between the gear centers.
Further details about these two models can be found in the authors’ previous work [15]. The third level of complexity is the model deeply analyzed in this work that was subject to the new proposed methodology. In the previous work, the higher complexity model coupled with Schlosser’s loss coefficient model produced lower accuracy than expected, even lower than the intermediate model used. This unexpected result led to consider the Schlösser’s loss coefficient model not being a good match for the volumetric displacement equation implemented for the higher complexity model. The new methodology proposed models the laminar and turbulent leakages by specific equations while using the same volumetric displacement equation used in the highest complexity model of the previous work.
The volumetric displacement equation Is based on the geometrical parameters of the gear pump and evaluates the displacement volume of a tooth pair [23]:
where b is the axial width of the gears, ri is the pitch diameter of each gear, z is the number of teeth, rhi is the outer diameter of the gear, and t0 is the base pitch. These parameters could be either from measuring the physical components after disassembly or from CAD files.
The new proposed methodology couples this volumetric displacement equation with three different equations to model the internal leakages of the pump and obtain the flow rate of the pump. The first equation models the radial leakages, which are the leakages in the clearance between the front faces of the gears under the root diameter and the front surface of the wear plates, as shown in Figure 1.
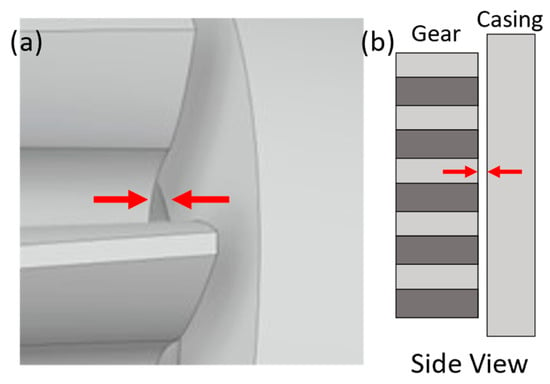
Figure 1.
Physical representation of the radial leakages inside an EGP (Distance exaggerated for better visual representation): (a) 3D representation, (b) 2D representation.
The clearance that leads to radial leakage is modeled as a laminar rectangular orifice, and for a couple of teeth, this results in a net flow rate equal to [24]:
where bl is the arc length between two adjacent teeth on the root diameter, hr is the gap clearance between the gears and the wear plates, µ is the dynamic viscosity, lr is the difference between the root and the shaft radius, and Δp is the pressure difference between the delivery and the suction line. The total flow rate for this type of leakage is the following:
where n is the number of rotations of the pump, z is the number of teeth. The two constant factors encompass the two gears and the front and rear faces of the gears. Factor k1 considers the fraction of the gears’ rotation where the couple of teeth is in connection with the inlet part where the pressure difference is zero, thus giving no contribution. This factor is equal to:
where ε is the angle between the start and the end of the suction zone, as shown in Figure 2.
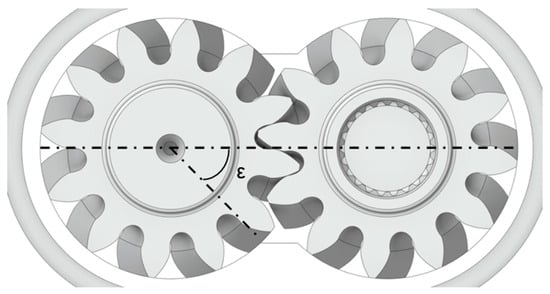
Figure 2.
Definition of the rotation suction angle ε.
The second typology of leakage considered is the leakages acting over the tip of the teeth. This is a very important type of leakage that greatly influences the behavior of the pump and is very difficult to model due to the many phenomena to consider. The flow rate for each tooth is modeled as composed of a Poiseuille flow part (pressure-related) and a Couette flow part (speed-related) [25,26]:
where h is the variable gap distance between the tip and the housing, lt is the tip width, and ut is the tangential speed. To obtain a correct representation of the event, it is necessary to consider the variability of the gap distance along the sealing zone. This variability is due to the eccentricity between the gears and the housing center created using pressure forces acting on the gears. The modeled equation is again based on an equivalent rectangular orifice geometry, so, for this reason, some evaluations are needed. The first is the need to evaluate an equivalent value of the gap clearance along the sealing zone for a single rotation. To obtain this equivalent parameter, an integral average is implemented based on geometric and trigonometric techniques [23]:
where ε is the angle between the start and the end of the outlet zone, equal to the inlet one. The other parameters are illustrated in Figure 3, where the outer circle represents the housing while the inner circle represents the outer diameter of the gears.
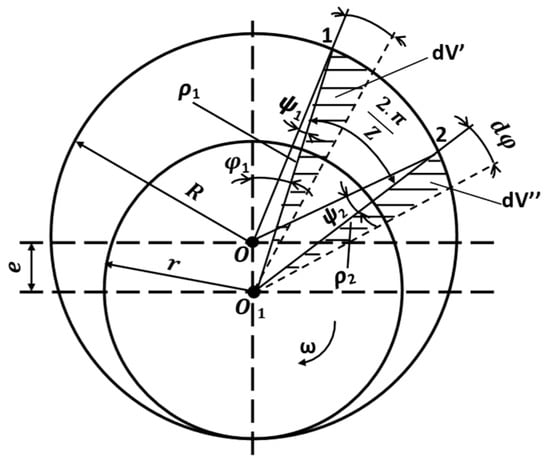
Figure 3.
Parameter definition for the evaluation of havg for the tip leakages.
The factor w represents the minimum value of the gap and is the fundamental parameter to control and simulate the wearing of the pump. The second and last evaluation to be done is the linearization of the circular arc that encompasses the interaction between the tooth tip and the housing inside the sealing zone. This is achieved by the following equations:
The total flow rate for this type of leakage is the following:
Finally, the last equation implemented estimates the lateral leakages concerning the leakages between the gears’ teeth and the wear plate faces. This type of leakage is modeled as a laminar orifice with an equivalent rectangular geometry, like the radial typology. The net flow rate for a single tooth is:
where bl is the difference between the outer and the root radius, ll is the tooth thickness on the pitch diameter. The choice of tooth thickness is an overestimation of the true value, but it permits considerable simplification and streamlines the evaluation without losing too much accuracy. The total flow rate for this leakage is the following:
The implemented leakages equation also allows us to evaluate in a simple way the effect of the wearing of the pump on the performances. In fact, each of these equations implements some tuning parameters that allow the simulation of the wearing of the pump. Both radial and lateral leakages can simulate the progressive wearing using the variation of the h parameter in Equations (4) and (12). This parameter represents the value of the gap between the faces of the gears and the surfaces of the wear plate that increases over time due to the wearing process. For tip leakages, the parameter w allows the simulation of the progressive wearing of the housing due to the milling of the gears’ teeth, increasing thus the gap and the relative leakages. Naturally, these parameters do not reflect the actual measurement of the wearing, being tuning parameters, but can be associated with more realistic values via validation with experimental tests and measurements. Finally, thanks to these equations and tuning parameters, it is possible to implement a simplistic form of fault injection, altering their values to simulate in the numerical model the effect of specific pump faults on the performance. It is possible to simulate excessive wear of both the front surface of the wear plates and of the housing at the start of the sealing zone. Both faults are responsible for increasing the leakages, resulting in an unacceptable reduction of the volumetric efficiency of the pump. The new proposed model permits the simulation of this process and analyzes its impact on the performances of the EGPs.
2.2. Case
An electrified reach truck system is chosen as a case to implement the levels of complexity into the simulation model and for validation. To simplify the system, the lifting functionality of the electrified reach truck is only considered. The hydraulic schematic of the electrified reach truck is illustrated in Figure 4.
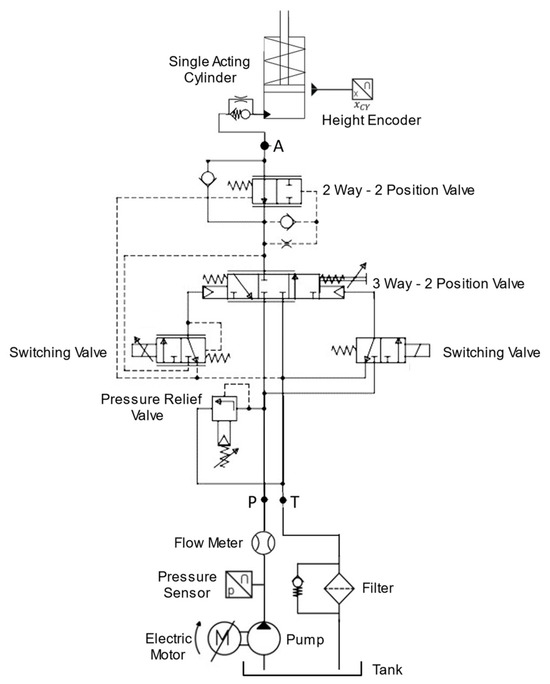
Figure 4.
Hydraulic Schematic of the Reach Truck.
An electric motor drives the fixed displacement external gear pump, which in turn delivers oil from the tank to the three-by-two valve via a switching valve. A single-acting cylinder is attached to the forks and is controlled by the three-by-two valve. The pump is operational only during the lifting phase, while the lowering phase is controlled using a load-holding valve. A pressure sensor, a flow sensor, and a height encoder are the sensors present in the system.
MATLAB/Simulink environment is utilized to model the hydraulic system, electric motor, and controller. The kinematics of the reach truck are modeled in a multi-body system simulation software called Mevea and were realized in [27] by utilizing a multi-physics co-simulation model. The co-simulation functionality is implemented with a functional mockup interface (FMI) that enables simulation models to share parameters across different software. In Figure 5, the co-simulation structure is illustrated. The reference speed of the electric motor is calculated by feeding the joystick control input to the controller. Considering the load applied to the system, the electric motor calculates the actual speed. The cylinder force is calculated using the hydraulics model by utilizing the actual speed from the electric motor model and the cylinder displacement and velocity from the Mevea kinematics model. The cylinder force is then fed to the Mevea kinematics model to complete the loop.
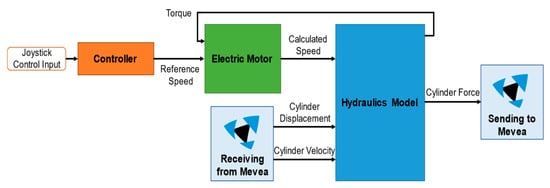
Figure 5.
Co-simulation Structure of System.
The translational load between the chassis, mast, and chain wheel is considered to calculate the cylinder displacement and velocity in the Mevea model. The Runge Kutta method is implemented in the solvers of Mevea and MATLAB/Simulink to solve ordinary differential equations with a timestep of 0.2 ms and 0.1 ms, respectively. The Mevea software is implemented as the controller, while MATLAB/Simulink is the agent. Additionally, the parameters such as the viscosity and bulk modulus are set to a constant value for all operating conditions of the simulation. Thermal effects are not considered in the simulation model.
2.3. Experimental Setup
The experimental setup is illustrated in Figure 6. It consists of the electric reach truck, sensors, and data acquisition system. The sensors include a pressure transducer from Trafag with a measuring range of up to 250 bar, a flow meter from Kracht with a measuring capacity of up to 80 L/min, and a height encoder from SICK with a range of up to 10 m. The sensor location can be found in Figure 4. A National Instrument (NI) based data acquisition system that consists of a CompactRIO Controller 9045 coupled with two 9229 modules is utilized. The system has a sampling rate of up to 50 kHz and supports simultaneous sampling. A program based on Functional Programmable Gateway Arrays (FPGA) was developed in LabVIEW software to acquire all sensor data. The duty cycle is defined as lifting the forks of the reach truck with a load of 1000 kg and returning to the home position. To avoid experimental uncertainty, the measurements are repeated several times, and the average of multiple acquisitions is utilized as the experimental data for the validation of simulation models. The systematic errors, however, have not been considered in this work thanks to the proven experience in performing experiments with the utilized test rig. The required geometric parameters of the pump are acquired from the manufacturer data sheet as well as by detaching the pump from the system and measuring the parameters of interest. The reference pump used to perform tests is an EGP with a die-cast aluminum body and cast-iron front and rear covers. This construction permits high working operating pressures while maintaining a compact size, relatively low weight, and low production cost. The specific pump tested has a displacement of about 14.6 cm3/rev.
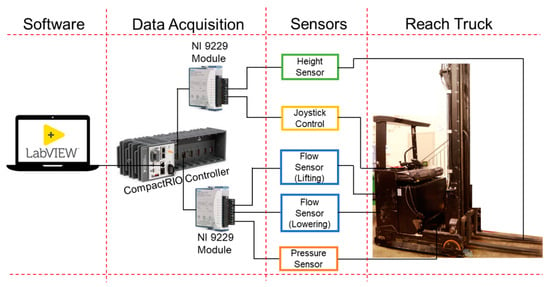
Figure 6.
Experimental setup for simulation model validation.
3. Results and Discussion
In this section, the results from the model validation are illustrated and discussed by comparing the three levels of complexity of the external gear pump simulation model. Furthermore, a test classifier is developed and tested to identify if it is possible to utilize the data generated from the simulation model as a reliable data source for condition monitoring applications.
3.1. Model Validation
The validation of the model is performed by comparing the results with experimental data. The cylinder displacement, system pressure, and pump volumetric flow rate are analyzed. The lifting phase involves the operation of the pump; however, the lowering is controlled by a load balancing valve as a single-acting cylinder is present in the reach truck.
The pump installed on the reach truck has a volumetric displacement of 14.6 cc, as indicated by the manufacturer. In the level 1 model of complexity, the simulation model applies Equation (1). In the level 2 model of complexity, the simulation model applies Equation (2) to calculate the volumetric displacement. The level 3 model utilizes Equation (3) for displacement calculation. The required parameters of the external gear pump for geometric calculations are obtained from the manufacturers’ data sheet as well as by disassembling the pump and performing measurements. A vernier caliper of 0.01 mm precision is utilized for the measurements. The volumetric displacement for the simple geometric and the complex geometric models are calculated to be 15.47 cm3/rev and 14.79 cm3/rev, respectively.
Figure 7 illustrates the comparison plot of cylinder displacement between the experimental data and all levels of complexity of the simulation model. The experimental data is represented by the blue solid line, the level 1 model is represented by the green dotted line, the level 2 model is represented by the black dashed line, and the level 3 model is represented by the red dash-dotted line, respectively. A consistent format is implemented for the upcoming plots of system pressure and volumetric flow. It can be noticed that the cylinder displacement is closest to the experimental data in the case of both level 1 and level 3 models. The level 2 model is higher throughout the duty cycle when compared to experimental data, which indicates that the calculated volumetric displacement is inaccurate and has a value larger than that of the actual pump. At peak displacement, it is evident that the level 1 model is slightly lower than the measured data while the level 3 model is slightly higher, as can be visualized in the zoomed-in plot.
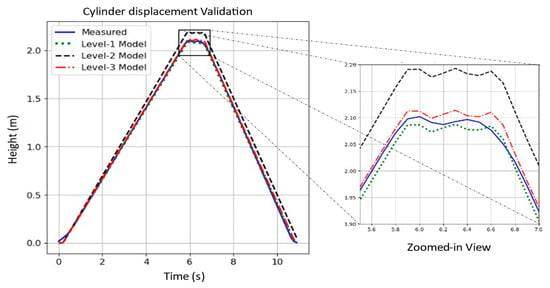
Figure 7.
Model validation for the three levels of complexity based on cylinder displacement. The blue solid line is the measured data; the green dotted line is the level 1 model, the black dashed line is the level 2 model, and the red dash-dotted line is the level 3 model.
In Figure 8, a comparison plot of system pressure between the experimental data and all levels of complexity of the simulation model is illustrated. Based on the visual comparison, it can be noted that the pressure signals in all simulation models have some oscillations at the beginning. This is because the forks are touching the load in the case of simulation while the forks are located a little lower than the load pallet. The oscillations stop prior to one second, and the pressure values seem to be higher than the measured value during the lifting phase, which indicates that the simulation model requires further tuning. The region beyond 7 s is not of interest as the pump is non-operational during this phase of the cycle. Visually, all the simulation models tend to follow a similar trend, and it is not distinguishable without performing other data analysis techniques. Upon zooming into the plot, we can notice that the highest deviation from measured data is the level 2 model, followed by level 3 and level 1 models, respectively.
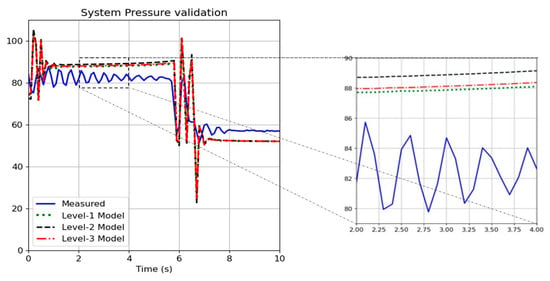
Figure 8.
Model validation for all levels of complexity based on system pressure.
Figure 9 illustrates a comparison plot of the volumetric flow rate between the measured and all levels of complexity of the simulation model. Like the case of cylinder displacement, the volumetric flow rate also seems to be closer to measured data in the case of level 1 and level 3 models. The level 2 model is higher throughout the duty cycle when compared to experimental data, which indicates that the calculated volumetric displacement is inaccurate and has a value larger than that of the actual pump. Throughout the lifting phase, it is evident that the level 1 model is slightly lower than the measured data, while the level 3 model is slightly higher.
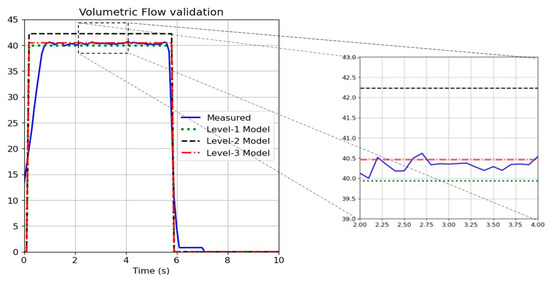
Figure 9.
Model validation for all levels of complexity based on volumetric flow.
To get a better understanding of the deviation from the measured data, a few evaluation metrics, such as mean squared error (MSE) and root mean squared error (RMSE), are calculated for several experiments with variation in the rotation speed of the pump. The average MSE and RMSE of all experiments are compared for all models with respect to the measured data for the complete duration of the duty cycle and tabulated in Table 1.

Table 1.
Calculated average of MSE and RMSE for all levels of the simulation model.
The level 1 model has the least MSE and RMSE in comparison to all models with respect to cylinder displacement and volumetric flow rate, while the level 3 model has the least error in terms of system pressure. This implies that both level 1 and level 3 models are good models that closely represent the actual system. However, in terms of fault injection, the level 3 model is the best option as the developed equations to inject lateral, radial, and tip leakage in the external gear pump are better in terms of understanding the level of fault injected. In the level 1 model, the slip coefficients need to be obtained to avoid any errors in the calculation. The slip coefficients also pose the challenge of varying drastically at different rotation speeds of the pump. The limitation of the level 3 model is the high number of gear parameter measurements required, which in this work was obtained from the manufacturer data and few measurements. However, the implementation of a level 3 model on another pump could be difficult in case the required gear parameters are difficult to obtain.
3.2. Test Classifier
The validation of different complexity levels of simulation is performed to identify the best model that can mimic the behavior of the actual system as well as to generate data sources suitable for AI-based condition monitoring applications. From the results of the model validation, it is evident that the level 3 model is the best choice to generate the data source. The data source is fed to a test classifier to identify if it is reliable for condition monitoring. Time series data is generated from the simulation model and includes the cylinder displacement, volumetric flow, and system pressure signals, respectively.
The sampling rate of the simulation model is 10 kHz, while the measured signals from the experiment have a sampling rate of 100 Hz. Prior to feeding the data into the classifier, the data requires some pre-processing to make the signals to be of similar format as well as to extract features from the signals that may aid in classifying the data better. The sampling rate of the simulation data is reduced from 10 kHz to 100 Hz by implementing down sampling. Feature extraction is performed by calculating a total of 16 statistical parameters for each signal by selecting an appropriate window size and applying the sliding window technique. The selected window size is 100 data points, which is equivalent to one second of the duty cycle, and the slide is made for every 10 data points. The parameters are the minimum, maximum, mean, median, standard deviation, variance, skewness, kurtosis, argmin, argmax, first location of minimum, first location of maximum, last location of minimum, last location of maximum, sum of values, absolute energy, absolute sum of changes, and mean absolute change. A total of 48 features are extracted per second of the duty cycle.
The classification task requires the implementation of a machine learning or deep learning-based algorithm. Linear discriminant analysis (LDA), decision tree (DT), random forest (RF), K-nearest neighbor (KNN), and a deep learning-based neural network multi-layer perceptron (MLP) are selected to develop the test classifier. The evaluation metric selected is a balanced accuracy score to compare the algorithm performance. The advantage of a balanced accuracy score is that it can work with imbalanced datasets and calculate the average recall for each class. Recall is defined as the number of true positive scenarios over the number of true positive and false negative outcomes.
The test classifier is trained by feeding data from one cycle of measured healthy data, one cycle of simulated healthy data, two cycles of simulated data with tip leakages, and two cycles of simulated data with radial leakages. The total number of data points is 2793. The data is split into training and testing sets, where 85% of the data is selected for training, and 15% of the data is selected for testing, respectively. The test classifier is a multi-class classifier and differentiates between the healthy, tip leakage fault, and radial leakage fault. The results of the balanced accuracy scores obtained for all the tested algorithms are tabulated in Table 2.

Table 2.
Balanced Accuracy Scores of selected classifier algorithms.
From Table 2, it is evident that the best classifier based on the balanced accuracy score is the RF classifier, followed by the DT classifier. The neural network-based classifier, MLP, did not perform well as neural networks as they require a large training dataset. The hyperparameters utilized in the MLP classifier were also tuned; however, the performance was not affected significantly. The tuned hyperparameters include the number of hidden layers, the number of neurons in each hidden layer, the activation function, and the solver.
The RF classifier has a balanced accuracy score of 88.95%. This implies that 88.95% of the 419 test data points were classified accurately by the classifier, which was trained on 2374 training data points. To have a better understanding, a confusion matrix is plotted in Figure 10 to visualize the same.
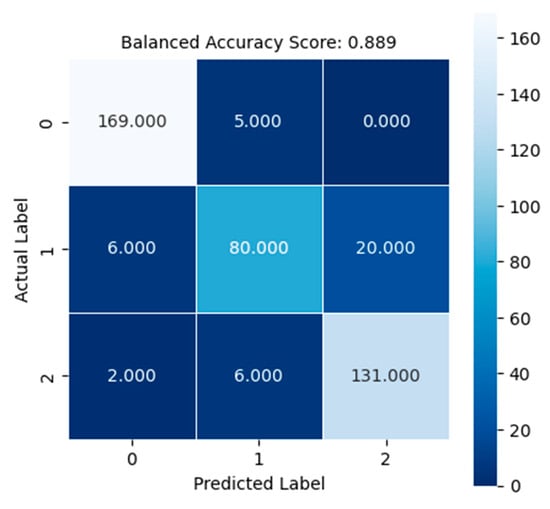
Figure 10.
Confusion matrix for random forest classifier.
In Figure 10, the labels 0, 1, and 2 represent the healthy case, tip leakage case, and radial leakage case, respectively. It can be noticed that in five instances, the healthy data was misclassified as tip leakage. The tip leakage was misclassified in six instances as healthy and in 20 instances as radial leakage. The radial leakage was misclassified in two instances as healthy and in six instances as tip leakage. The misclassification could be due to idle states in the duty cycle, which would reflect the data to have a similar appearance. Overall, we can notice that the misclassification rate is quite small, and hence, the data source generated using the simulation model is quite robust. However, to ensure that the data source is reliable, faulty experimental data should also be tested. To generate faulty experimental data, an accelerated life test rig for an EGP is under development in which aluminum oxide particles will be introduced to accelerate the pump’s wear and obtain faulty measured data. Furthermore, an additional test utilizing experimental data that was not utilized to train the classifier is tested to evaluate the performance. It was found that a balanced accuracy score of 100% was obtained upon testing. This proves that the classifier is capable of predicting the actual state of the EGP; however, further testing with faulty experimental data is essential to guarantee the robustness of the classifier.
4. Conclusions
This paper described a new approach to investigate the effect of model complexity of an external gear pump for artificial intelligence (AI) based classification. The new methodology allows an increase in the level of complexity and a higher degree of flexibility in the choice of parameters to tweak to inject fault in the external gear pump. A simulation model of an external gear pump at three levels of complexity is developed using MATLAB Simulink, which is later validated using an experimental test campaign. The levels of the simulation model are characterized by the method used to evaluate the volumetric displacement of the pump. The first level applies the displacement assigned by the pump manufacturer coupled with a model to calculate the total laminar and turbulent losses. The second level estimates the volumetric displacement through a simple geometric equation coupled with the same losses model of the previous level. The third level determines the pump volumetric displacement, applying a more detailed geometric equation paired with specific equations to evaluate the internal leakages. Data analysis is performed to validate the simulation model by comparing the data generated on the model with measured data on an electric reach truck equipped with the reference external gear pump. The results from the data analysis show that the level 1 and level 3 models were close in representing the measured data. However, in terms of fault injection capabilities, the better model would be the level 3 model. The only limitation of the level 3 model would be in terms of the higher number of gear parameter measurements required, which in this work was obtained from manufacturer data and few measurements.
A test classifier was developed by implementing various machine learning and deep learning algorithms and was evaluated using the balanced accuracy score metric. The data fed to the training algorithm included one cycle of measured healthy data, one cycle of simulated healthy data, two cycles of simulated data with tip leakages, and two cycles of simulated data with radial leakages. The faults were injected by varying the tip leakage parameter and radial leakage parameter on the level 3 model, respectively. The total number of data points was 2793. The data is split into training and testing sets, where 85% of the data is selected for training, and 15% of the data is selected for testing, respectively. The test classifier was a multi-class classifier and differentiates between the healthy, tip leakage fault, and radial leakage fault. The best classifier based on the balanced accuracy was found to be the random forest classifier, with an accuracy score of 88.95%.
As for future development, several pumps of known operational hours will be tested on the electrified reach truck to obtain more measured data to further validate the simulation model. The information will also be utilized to build a relation between the operational hour of the pump and the rate of wearing process on the planned accelerated life test rig for the external gear pump. This, in turn, will aid in identifying the remaining useful life of the pump and extend the data generation for predictive and prescriptive maintenance applications. Furthermore, additional fault-injecting techniques to apply to the simulation model will be explored.
Author Contributions
Conceptualization, A.A.A. and P.M.; methodology, A.A.A. and P.M.; software, A.A.A.; validation, A.A.A.; formal analysis, A.A.A. and P.M.; investigation, A.A.A. and P.M.; resources, A.A.A., E.F., A.S., and T.M.; data curation, A.A.A.; writing—original draft preparation, A.A.A. and P.M.; writing—review and editing, A.A.A., P.M., T.M, E.F., and A.S.; visualization, A.A.A. and P.M. and supervision, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was enabled by the financial support of the Academy of Finland (project ESTV), internal funding from the Department of Automation Technology and Mechanical Engineering, the IHA group at Tampere University, Finland, and PhD program funding supported by the MUR (Ministero dell’Università e della Ricerca) of the Italian Government.
Data Availability Statement
The simulation and experimental data sets generated and analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| CAD | Computer Aided Drafting |
| DT | Decision Tree |
| EGP | External Gear Pump |
| FMI | Functional Mockup Interface |
| FPGA | Functional Programmable Gateway Arrays |
| KNN | K-Nearest Neighbor |
| LDA | Linear Discriminant Analysis |
| MLP | Multi-Layer Perceptron |
| MSE | Mean Squared Error |
| RF | Random Forest |
| RMSE | Root Mean Squared Error |
Nomenclature
| Symbol | Description | Unit |
| 𝑏 | Gear Width | [m] |
| bl bl | Root arc length | [m] |
| 𝐶𝑠 | Laminar Slip Coefficient | |
| 𝐶𝑠𝑡 | Turbulent Slip Coefficient | |
| e | Eccentricity | |
| h h | Tooth tip gap clearance | [m] |
| havg | Mean value of Tooth tip gap clearance | [m] |
| hr hr | Radial gap clearance | [m] |
| k1 k1 | Rotational Inlet fraction | |
| k2 k2 | Sealing zone rotational factor | |
| Ll ll | Lateral orifice length | [m] |
| lr | Radial orifice length | [m] |
| lt | Tooth Tip orifice length | [m] |
| 𝑛 | Rotational Speed | [rad/s] |
| 𝑟1 | Pitch Diameter of Gear 1 | [m] |
| 𝑟2 | Pitch Diameter of Gear 2 | [m] |
| 𝑟ℎ | Outside Diameter of Gear | [m] |
| 𝑟ℎ1 | Outside Diameter of Gear 1 | [m] |
| 𝑟ℎ2 | Outside Diameter of Gear 2 | [m] |
| R | Housing Diameter | [m] |
| 𝑄 | Volumetric Flow | [m3/s] |
| 𝑃 | Pressure | [Pa] |
| 𝑡0 | Base Pitch | [m] |
| ut | Tangential speed | [m/s] |
| 𝑉 | Volumetric Displacement | [m3/rev] |
| 𝑉𝑔 | Geometric Displacement Volume | [m3/rev] |
| 𝑉𝑔𝑖 | Geometric Displacement Volume of tooth pair | [m3/rev] |
| w | Housing Wear parameter | [m] |
| z | Number of Teeth | |
| Greek letter | Description | Unit |
| ε | Suction angle | [rad] |
| φ | Rotational angle | [rad] |
| 𝜇 | Dynamic Viscosity | [Kg/ms] |
| 𝜂𝑣 | Volumetric Efficiency | |
| 𝜌 | Density | [Kg/m3] |
References
- Kun, W.; Mingwei, W. Servo Model of Internal Leakage and Volume Efficiency Simulation for External Gear Pumps or Motors. J. Mech. Transm. 2023, 47, 69–73. [Google Scholar]
- Sedri, F.; Riasi, A. Investigation of leakage within an external gear pump with new decompression slots: Numerical and experimental study. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 224. [Google Scholar] [CrossRef]
- Hao, X.; Zhou, X.; Liu, X.; Sang, X. Pressure ripple of gear pumps affected by air content on trapped volume. J. Vibroeng. 2016, 18, 4033–4041. [Google Scholar] [CrossRef]
- Borghi, M.; Zardin, B.; Specchia, E. External Gear Pump Volumetric Efficiency: Numerical and Experimental Analysis; SAE Technical Papers; SAE: Warrendale, PA, USA, 2009. [Google Scholar]
- del Campo, D.; Castilla, R.; Raush, G.; Montero, P.J.G.; Codina, E. Numerical Analysis of External Gear Pumps Including Cavitation. J. Fluids Eng. 2012, 134, 81105–81112. [Google Scholar] [CrossRef]
- Guo, R.; Li, Y.; Shi, Y.; Li, H.; Zhao, J.; Gao, D. Research on identification method of wear degradation of external gear pump based on flow field analysis. Sensors 2020, 20, 4058. [Google Scholar] [CrossRef] [PubMed]
- Webster, R.L.; Evans, D.J.; Rawson, P.M. A method for the identification and quantitation of hydraulic fluid contamination of turbine engine oils by gas chromatography-chemical ionisation mass spectrometry. Lubr. Sci. 2012, 24, 373–381. [Google Scholar] [CrossRef]
- Ahmed, H.; Nandi, A.K. Condition Monitoring with Vibration Signals: Compressive Sampling and Learning Algorithms for Rotating Machines; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Zhang, J.; Li, N.; Chen, Y.; Zhai, J.; Han, Q.; Hou, Z. A method of in-situ monitoring multiple parameters and blade condition of turbomachinery by using a single acoustic pressure sensor. Mech. Syst. Signal Process. 2022, 173, 109051. [Google Scholar] [CrossRef]
- Liu, M.; Kim, G.; Bauckhage, K.; Geimer, M. Data-Driven Virtual Flow Rate Sensor Development for Leakage Monitoring at the Cradle Bearing in an Axial Piston Pump. Energies 2022, 15, 6115. [Google Scholar] [CrossRef]
- Li, H.; Xu, G.; Gui, X.; Liang, L. A Double FBGs Temperature Self-Compensating Displacement Sensor and Its Application in Subway Monitoring. Materials 2022, 15, 6831. [Google Scholar] [CrossRef] [PubMed]
- Keller, N.; Sciancalepore, A.; Vacca, A. Demonstrating a Condition Monitoring Process for Axial Piston Pumps with Damaged Valve Plates. Int. J. Fluid Power 2022, 23, 205–236. [Google Scholar] [CrossRef]
- Phan, V.D.; Ahn, K.K. Fault-tolerant control for an electro-hydraulic servo system with sensor fault compensation and disturbance rejection. Nonlinear Dyn. 2023, 111, 10131–10146. [Google Scholar] [CrossRef]
- Robinson, S. Exploring the relationship between simulation model accuracy and complexity. J. Oper. Res. Soc. 2022, 74, 1992–2011. [Google Scholar] [CrossRef]
- Azeez, A.A.; Minav, T. The effect of model complexity on an external gear pump for AI-based condition monitoring applications. In Proceedings of the Scandinavian International Conference on Fluid Power, Tampere, Finland, 30 May–1 June 2023. [Google Scholar]
- Azeez, A.A.; Vuorinen, E.; Minav, T.; Casoli, P. AI-based condition monitoring of a variable displacement axial piston pump. In Proceedings of the 13th International Fluid Power Conference, Aachen, Germany, 13–15 June 2022. [Google Scholar]
- Azeez, A.A.; Han, X.; Zakharov, V.; Minav, T. AI-based condition monitoring of hydraulic valves in zonal hydraulics using simulated electric motor signals. In Proceedings of the ASME/BATH 2021 Symposium on Fluid Power and Motion Control, Online, 19–21 October 2021. [Google Scholar]
- Makansi, F.; Schmitz, K. Fault Detection and Diagnosis for a Hydraulic Press by Use of a Mixed Domain Database. In Proceedings of the BATH/ASME 2022 Symposium on Fluid Power and Motion Control, Bath, UK, 14–16 September 2022. [Google Scholar]
- Sobie, C.; Freitas, C.; Nicolai, M. Simulation-driven machine learning: Bearing fault classification. Mech. Syst. Signal Process. 2018, 99, 403–419. [Google Scholar] [CrossRef]
- Chen, Y.; Zuo, M.J. A sparse multivariate time series model-based fault detection method for gearboxes under variable speed condition. Mech. Syst. Signal Process. 2022, 167, 108539–108558. [Google Scholar] [CrossRef]
- Gordon, C.A.K.; Pistikopoulos, E.N. Data-driven prescriptive maintenance toward fault-tolerant multiparametric control. AIChE J. 2022, 68, e17489. [Google Scholar] [CrossRef]
- Torrent, M.; Gamez-Montero, P.J.; Codina, E. Parameterization, Modeling, and Validation in Real Conditions of an External Gear Pump. Sustainability 2021, 13, 3089. [Google Scholar] [CrossRef]
- Ivantysyn, J. Hydrostatic Pumps and Motors: Principles, Design, Performance, Modelling, Analysis, Control and Testing, 1st ed.; Akademia Books International: New Delhi, India, 2001. [Google Scholar]
- Siemens Industry Software, Inc. Simcenter Amesim Reference Manual; Siemens Digital Industries Software: Plano, TX, USA, 2020. [Google Scholar]
- Mazzei, P.; Frosina, E.; Senatore, A. Helical Gear Pump: A Comparison between a Lumped Parameter and a Computational Fluid Dynamics-Based Approaches. Fluids 2023, 8, 193. [Google Scholar] [CrossRef]
- Marinaro, G.; Frosina, E.; Senatore, A. A numerical analysis of an innovative flow ripple reduction method for External Gear Pumps. Energies 2021, 14, 471. [Google Scholar] [CrossRef]
- Azeez, A.A.; Zakharov, V.; Orifjonov, A.; Niemela, J.; Minav, T. Multi-physics Co-simulation of an Electric Reach Truck. In Proceedings of the 13th International Fluid Power Conference, Aachen, Germany, 13–15 June 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).