Adaptive Super-Twisting Sliding Mode Control of Underwater Mechanical Leg with Extended State Observer
Abstract
:1. Introduction
2. Models and Problem Formulation
2.1. Kinematic Model
2.2. Dynamic Model
2.3. Control Objective
3. Observer Design
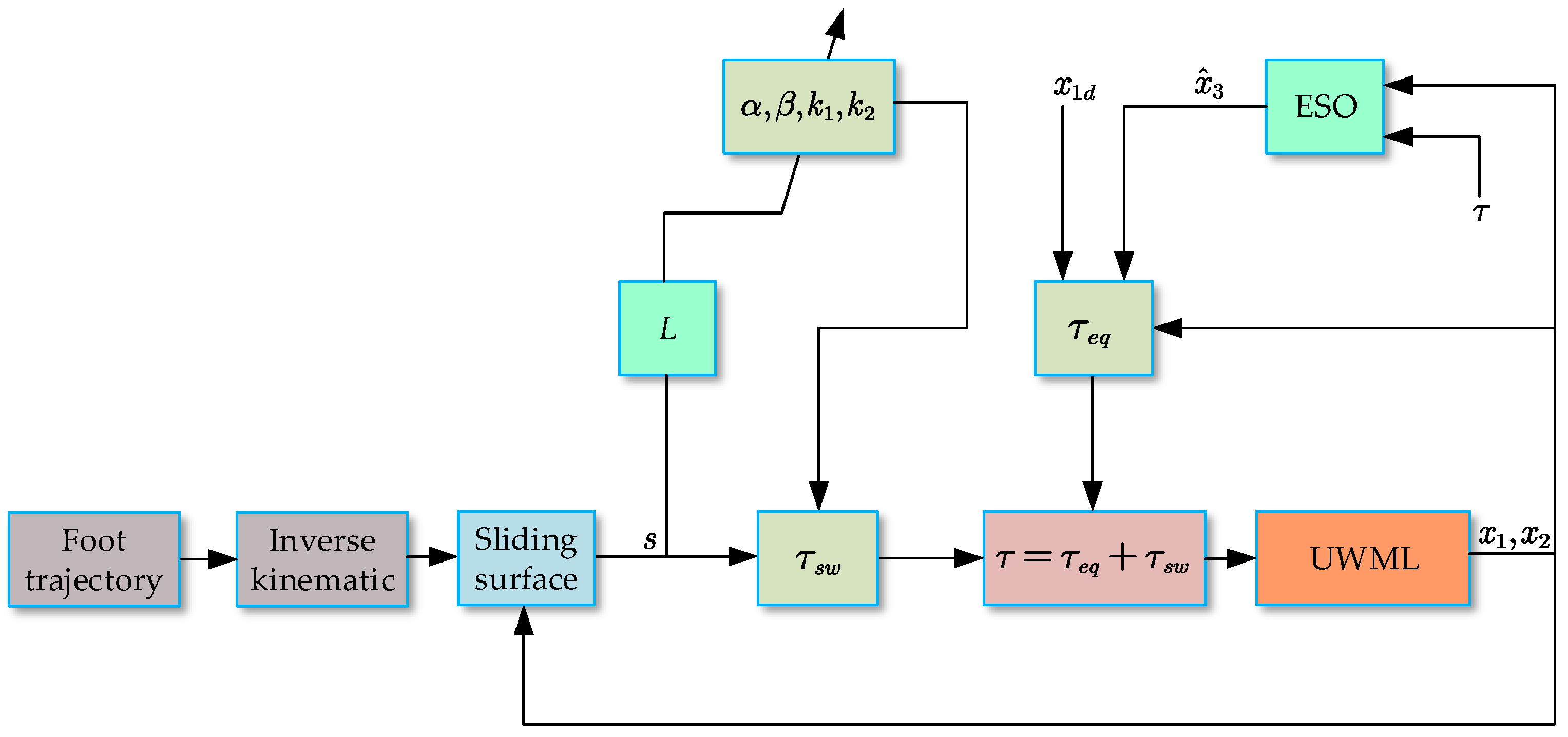
4. Controller Design
4.1. Design of SMC-ESO Controller
4.2. Design of ASTSMC-ESO Controller
4.3. Controller Stability Analysis
4.4. Design of the Adaptive Function
5. Simulation Results
5.1. Simulation Model
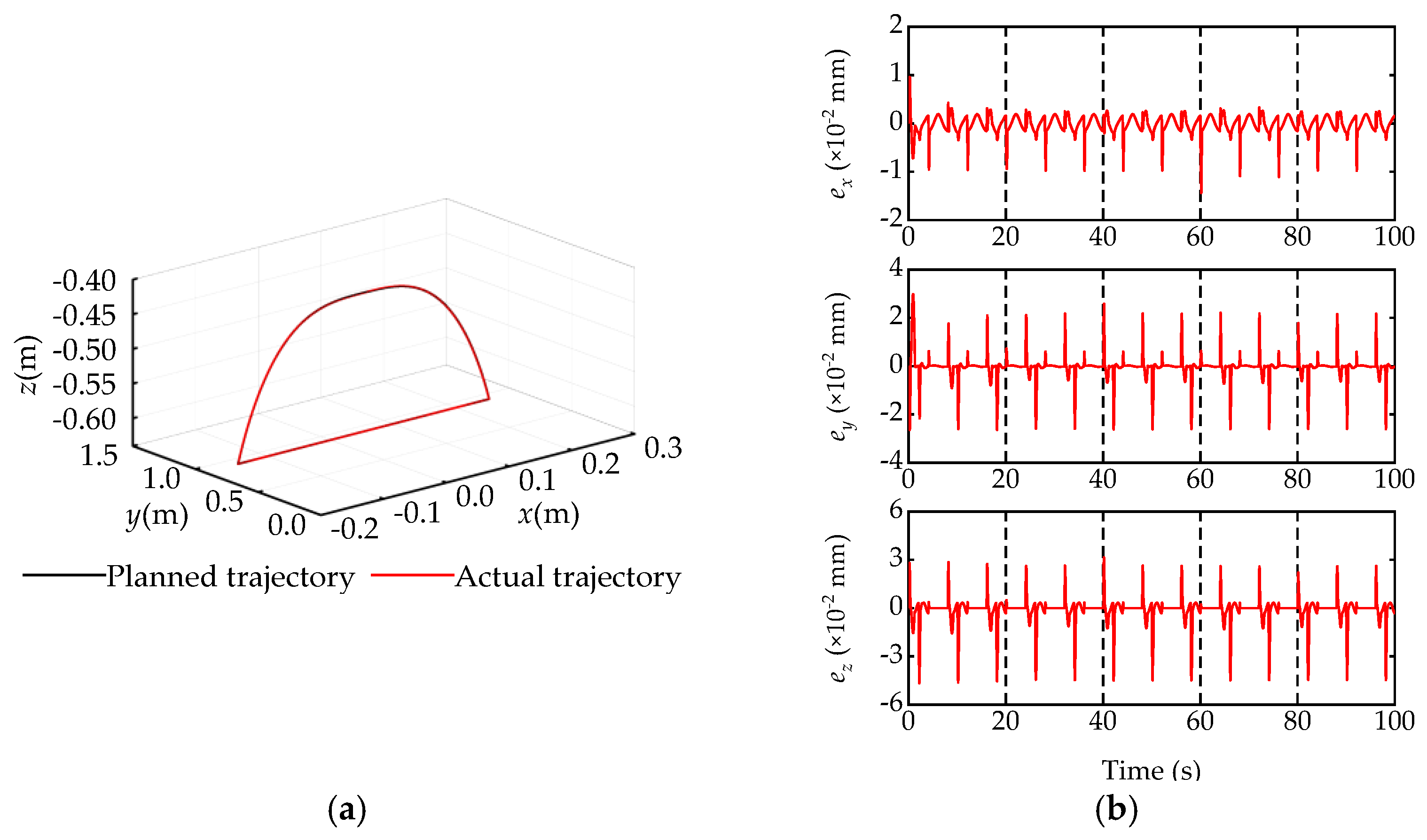
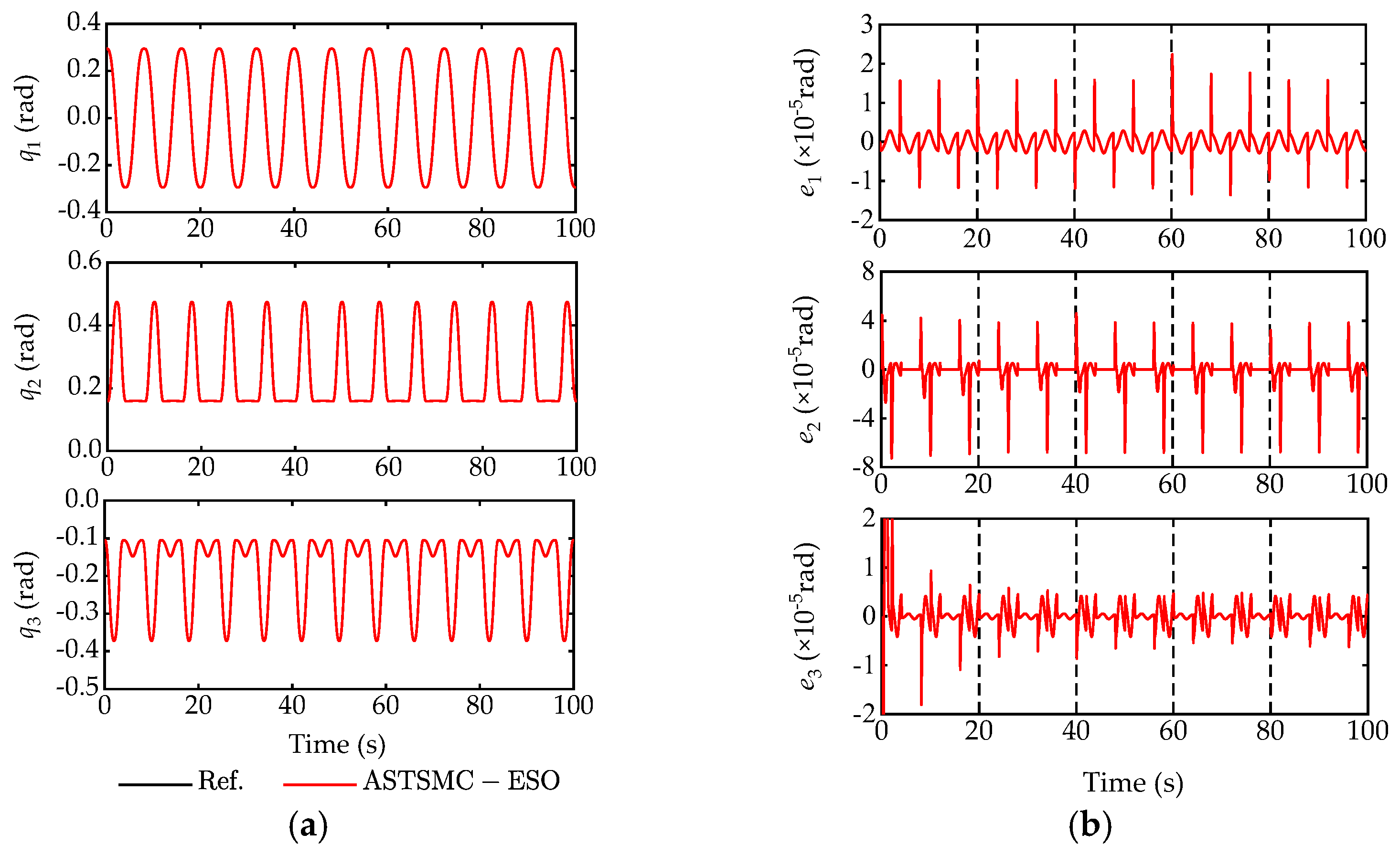
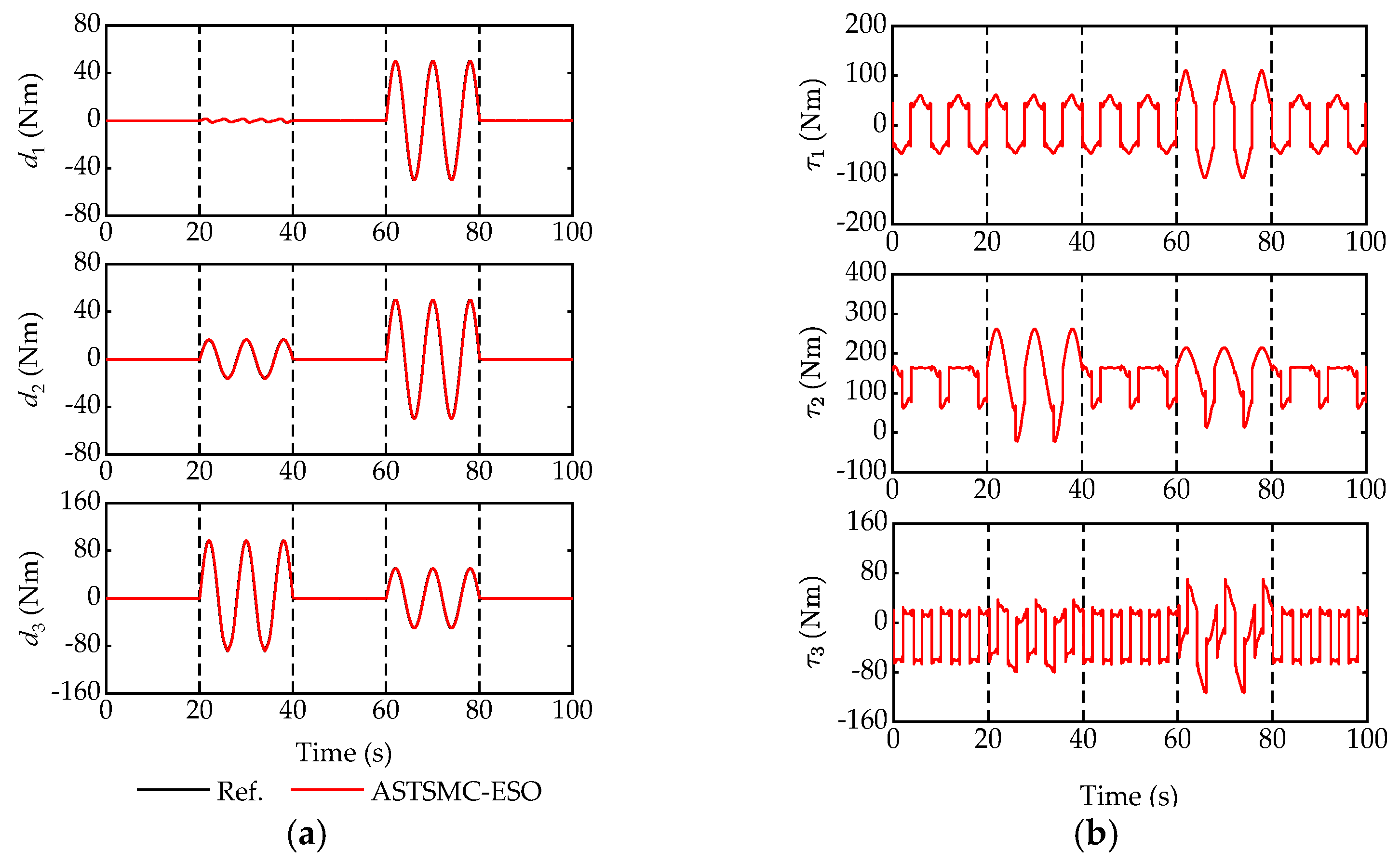
5.2. Simulation Study
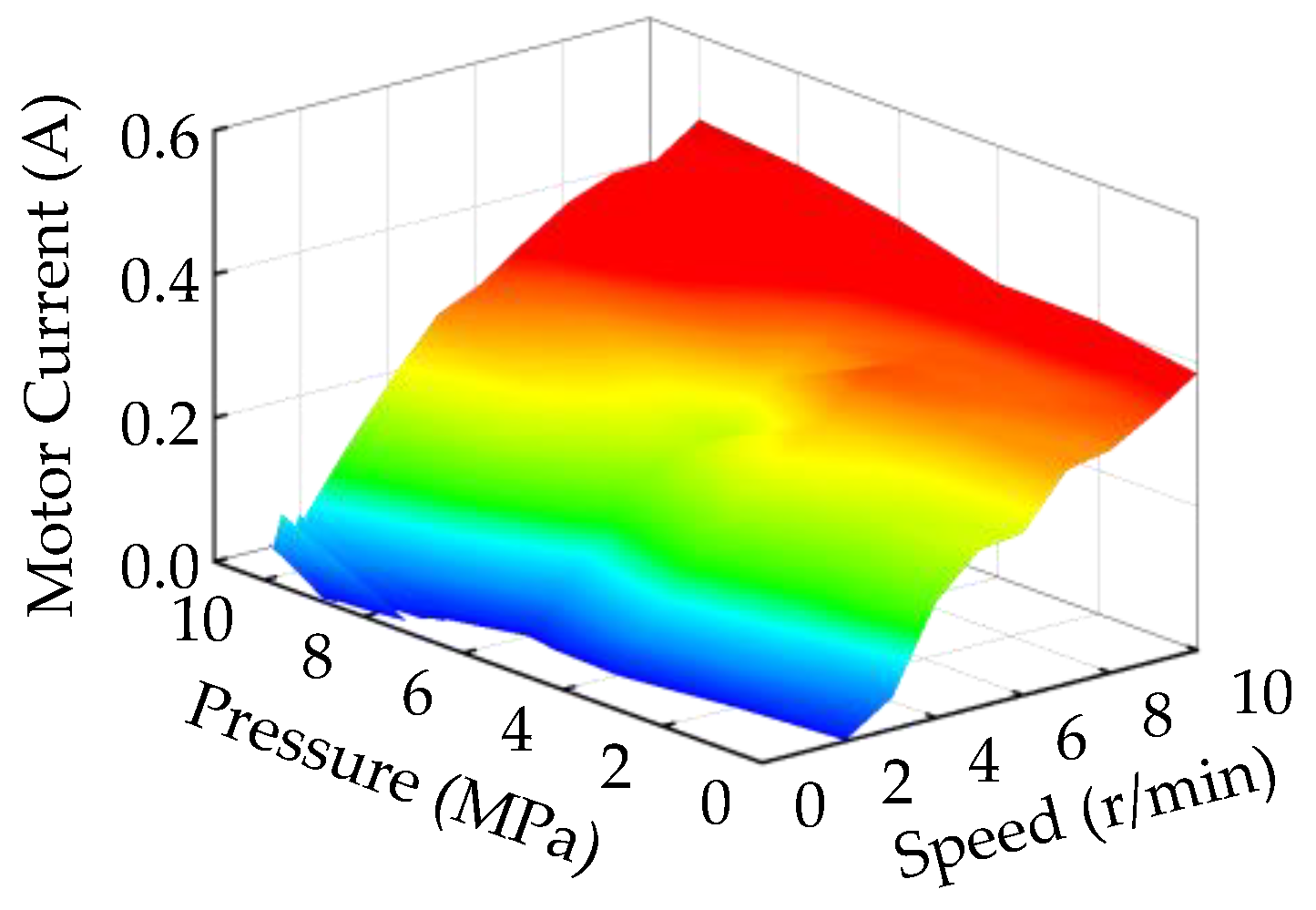
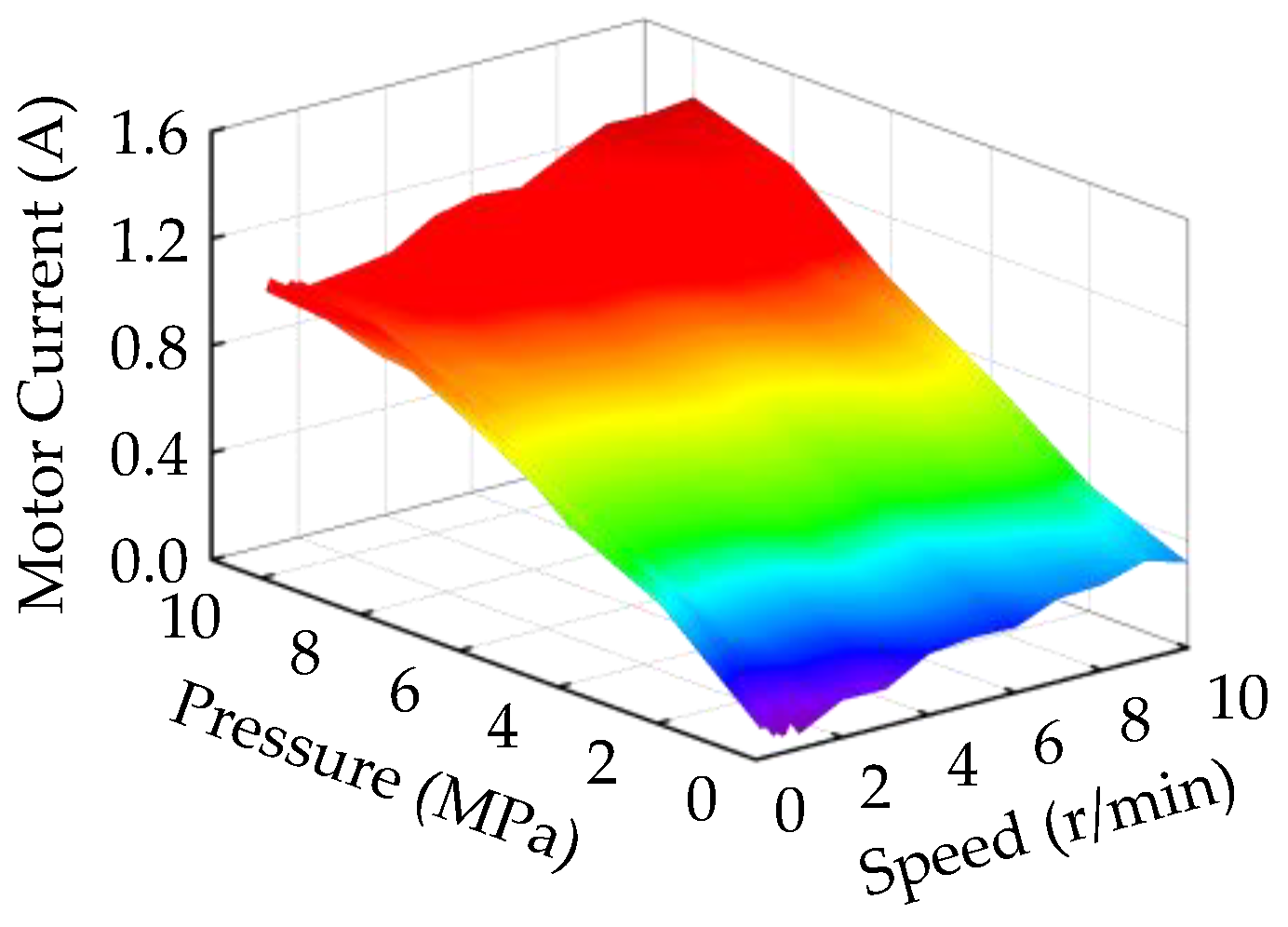
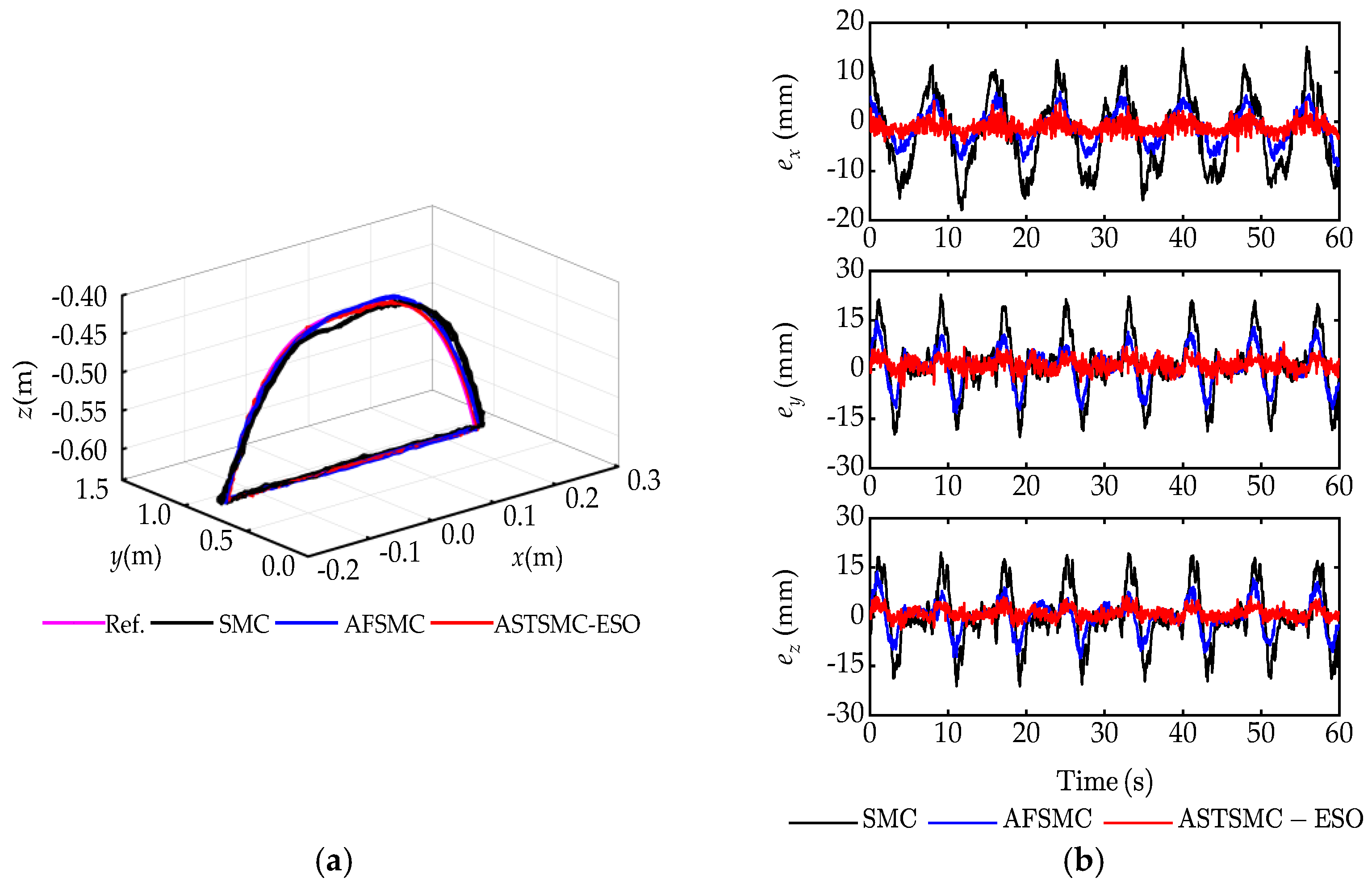
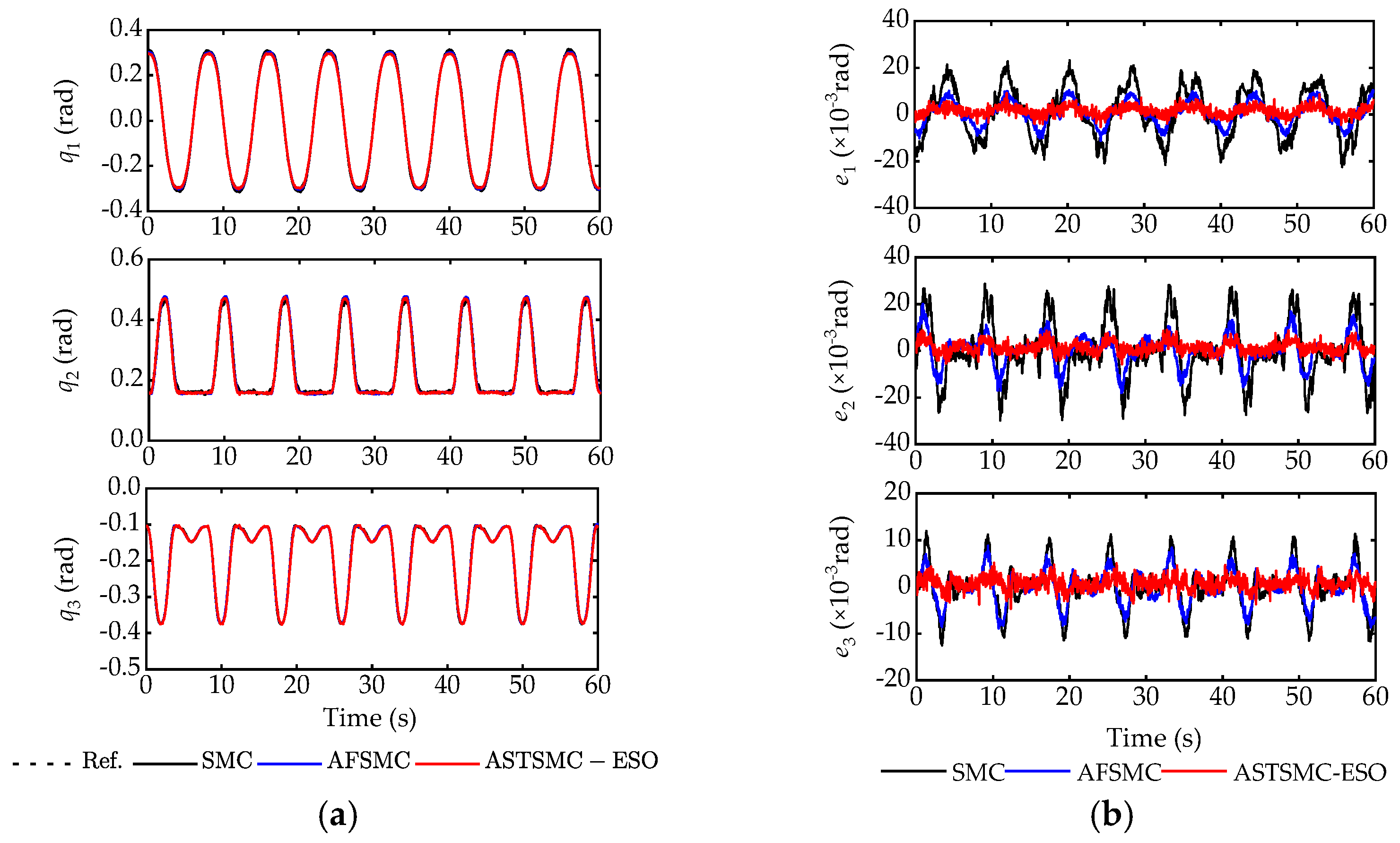
6. Comparative Experimental Results
6.1. Comparison Controllers
6.2. Experimental Study
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 2
References
- Xu, S.; He, B.; Hu, H. Research on Kinematics and Stability of a Bionic Wall-Climbing Hexapod Robot. Appl. Bionics Biomech. 2019, 2019, 6146214. [Google Scholar] [CrossRef]
- Guizzo, E. By leaps and bounds: An exclusive look at how Boston dynamics is redefining robot agility. IEEE Spectr. 2019, 56, 34–39. [Google Scholar] [CrossRef]
- Carlo, J.D.; Wensing, P.M.; Katz, B.; Bledt, G.; Kim, S. Dynamic Locomotion in the MIT Cheetah 3 through Convex Model-Predictive Control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar]
- Shim, H.; Yoo, S.Y.; Ju, B.H.; Kang, H. Development of arm and leg for seabed walking robot CRABSTER200. Ocean Eng. 2016, 116, 55–67. [Google Scholar] [CrossRef]
- Yang, C.; Yao, F.; Zhang, M.J.; Zhang, Z.Q.; Wu, Z.Z.; Dan, P.J. Adaptive Sliding Mode PID Control for Underwater Manipulator Based on Legendre Polynomial Function Approximation and Its Experimental Evaluation. Appl. Sci. 2020, 10, 1728. [Google Scholar] [CrossRef]
- Yao, J.J.; Wang, C.J. Model reference adaptive control for a hydraulic underwater manipulator. J. Vib. Control 2011, 18, 893–902. [Google Scholar] [CrossRef]
- Lee, M.; Choi, H.S. A Robust Neural Controller for Underwater Robot Manipulators. IEEE Trans. Neural Netw. 2000, 11, 1465–1470. [Google Scholar]
- Zhou, Z.C.; Tang, G.Y.; Huang, H.; Han, L.J.; Xu, R.K. Adaptive nonsingular fast terminal sliding mode control for underwater manipulator robotics with asymmetric saturation actuators. Control Theory Technol. 2020, 18, 81–91. [Google Scholar] [CrossRef]
- Zhou, Z.C.; Tang, G.Y.; Xu, R.K.; HAN, L.J.; Cheng, M.L. A Novel Continuous Nonsingular Finite-Time Control for Underwater Robot Manipulators. J. Mar. Sci. Eng. 2021, 9, 269. [Google Scholar] [CrossRef]
- Chatchanayuenyong, T.; Parnichkun, M. Neural network based-time optimal sliding mode control for an autonomous underwater robot. Mechatronics 2006, 16, 41–87. [Google Scholar] [CrossRef]
- Yao, B.; Tomizuka, M. Adaptive robust motion and force tracking control of robot manipulators in contact with compliant surfaces with unknown stiffness. J. Dyn. Syst. Meas. Control 1998, 120, 232–240. [Google Scholar] [CrossRef]
- Sabanovic, A. Variable structure systems with sliding modes in motion control—A survey. IEEE Trans. Ind. Inform. 2011, 2, 212–223. [Google Scholar] [CrossRef]
- Doulgeri, Z. Sliding regime of a nonlinear robust controller for robot manipulators. IEE Proc. Control Theory Appl. 1999, 146, 493–498. [Google Scholar] [CrossRef]
- Goel, A.; Swarup, A. Adaptive fuzzy high-order super-twisting sliding mode controller for uncertain robotic manipulator. J. Intell. Syst. 2017, 26, 697–715. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Nagesh, I.; Edwards, C. A multivariable super-twisting sliding mode approach. Automatica 2014, 50, 984–988. [Google Scholar] [CrossRef]
- Polyakov, A.; Poznyak, A. Reaching time estimation for ‘‘super-twisting’’ second order sliding mode controller via Lyapunov function designing. IEEE Trans. Autom. Control 2009, 54, 1951–1955. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, S. A new modified super-twisting algorithm with double closed-loop feedback regulation. Trans. Inst. Meas. Control 2017, 39, 1603–1612. [Google Scholar] [CrossRef]
- Boiko, I.; Fridman, L. Analysis of chattering in continuous sliding-mode controllers. IEEE Trans. Autom. Control 2005, 50, 1442–1446. [Google Scholar] [CrossRef]
- Edwards, C.; Shtessel, Y. Adaptive dual-layer super-twisting control and observation. Int. J. Control 2016, 89, 1759–1766. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S. Adaptive Fuzzy Integral Sliding-Mode Control for Robust Fault-Tolerant Control of Robot Manipulators with Disturbances Observer. IEEE Trans. Fuzzy Syst. 2021, 29, 284–1296. [Google Scholar] [CrossRef]
- Zhu, Y.K.; Qiao, J.Z.; Guo, L. Adaptive Sliding Mode Disturbances Observer-Based Composite Control with Prescribed Performance of Space Manipulators for Target Capturing. IEEE Trans. Ind. Electron. 2019, 66, 1973–1983. [Google Scholar] [CrossRef]
- Xi, R.; Xiao, X.; Ma, T.; Yang, Z. Adaptive Sliding Mode Disturbances Observer Based Robust Control for Robot Manipulators Towards Assembly Assistance. IEEE Robot. Autom. Lett. 2022, 7, 6139–6146. [Google Scholar] [CrossRef]
- Xu, B.; Ji, S.; Zhang, C.; Chen, C.; Ni, H.; Wu, X. Linear-extended-state-observer-based prescribed performance control for trajectory tracking of a robotic manipulator. Ind. Robot Int. J. Robot. Res. Appl. 2021, 48, 544–555. [Google Scholar] [CrossRef]
- Tran, D.T.; Jin, M.; Ahn, K.K. Nonlinear Extended State Observer Based on Output Feedback Control for a Manipulator with Time-Varying Output Constraints and External Disturbances. IEEE Access 2019, 7, 156860–156870. [Google Scholar] [CrossRef]
- Wu, X.; Wang, C.; Hua, S. Adaptive extended state observer-based nonsingular terminal sliding mode control for the aircraft skin inspection robot. J. Intell. Robot. Syst. 2020, 98, 721–732. [Google Scholar] [CrossRef]
- Yao, J.Y.; Jiao, Z.X.; Ma, D.W. Adaptive robust control of DC motors with extended state observer. IEEE Trans. Ind. Electron. 2013, 61, 3630–3637. [Google Scholar] [CrossRef]
- Liao, L.H.; Li, B.R.; Wang, Y.Y.; Xi, Y.; Zhang, D.J.; Gao, L.L. Adaptive fuzzy robust control of a bionic mechanical leg with a high gain observer. IEEE Access 2021, 9, 134037–134051. [Google Scholar] [CrossRef]
- Liao, L.H.; Li, B.R.; Zhang, D.J.; Ngwa, M.; Gao, L.P.; Du, J.M. Research on the Influence of Underwater Environment on the Dynamic Performance of the Mechanical Leg of a Deep-sea Crawling and Swimming Robot. arXiv 2023, arXiv:2308.14393. [Google Scholar]
- Zheng, Q.; Gao, L.; Gao, Z. On stability analysis of active disturbances rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3501–3506. [Google Scholar]
- Yang, Y.J.; Liao, Y.; Yin, D.W.; Zheng, Y.X. Adaptive dual layer fast super twisting control algorithm. Control Theory Appl. 2016, 33, 1119–1127. [Google Scholar]
- Zhang, M.; Guan, Y.; Zhao, W. Adaptive super-twisting sliding mode control for stabilization platform of laser seeker based on extended state observer. Optik 2019, 199, 163337. [Google Scholar] [CrossRef]
- Luo, G.S. Research on Subsea 7 Function Maser-Slave Hydraulic Manipulator and Its Nonlinear Robust Control. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2013. [Google Scholar]
- Zhong, Y.G.; Yang, F. Dynamic Modeling and adaptive fuzzy sliding mode control for multi-link underwater manipulators. Ocean Eng. 2019, 187, 106202. [Google Scholar]
- Yao, J.Y.; Deng, W.X.; Jiao, Z.X. Adaptive Control of Hydraulic Actuators with LuGre Model-Based Friction Compensation. IEEE Trans. Ind. Electron. 2015, 62, 6469–6477. [Google Scholar] [CrossRef]
- Wang, Z. Adaptive smooth second-order sliding mode control method with application to missile guidance. Trans. Inst. Meas. Control 2017, 39, 848–860. [Google Scholar] [CrossRef]
- Tan, J.; Zhou, Z.; Zhu, X.P.; Xu, X.P. Fast super twisting algorithm and its application to attitude control of flying wing UAV. Control Decis. 2016, 31, 143–148. [Google Scholar]
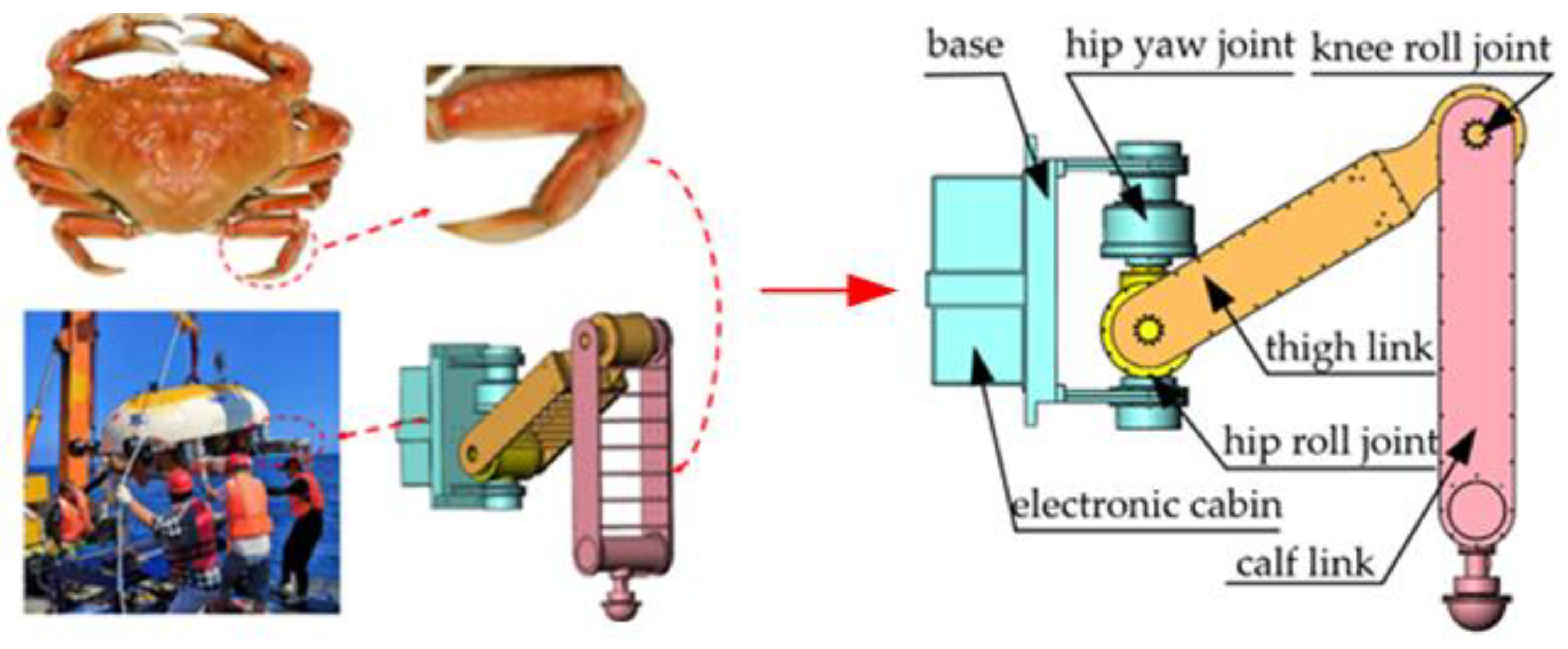
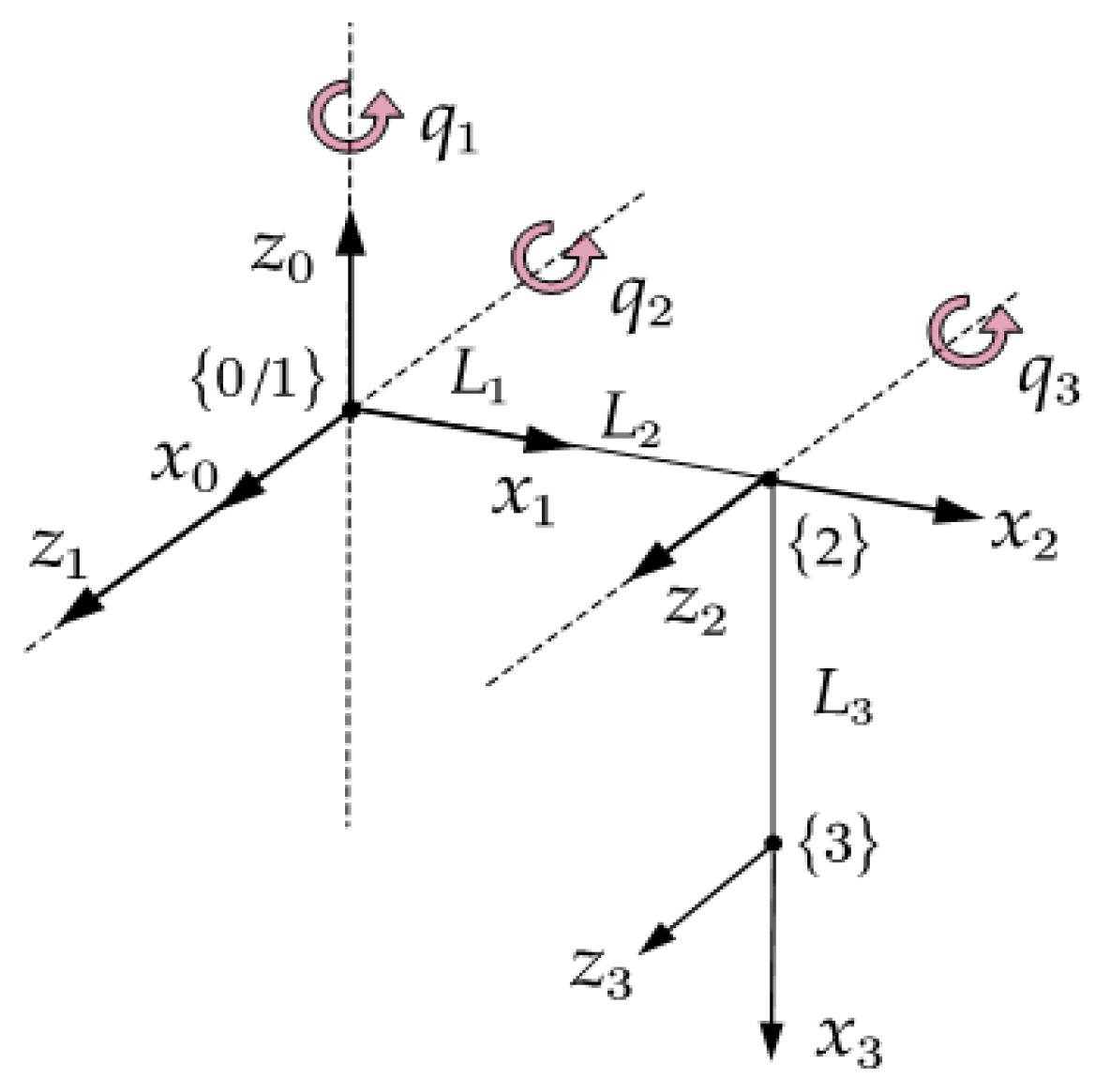

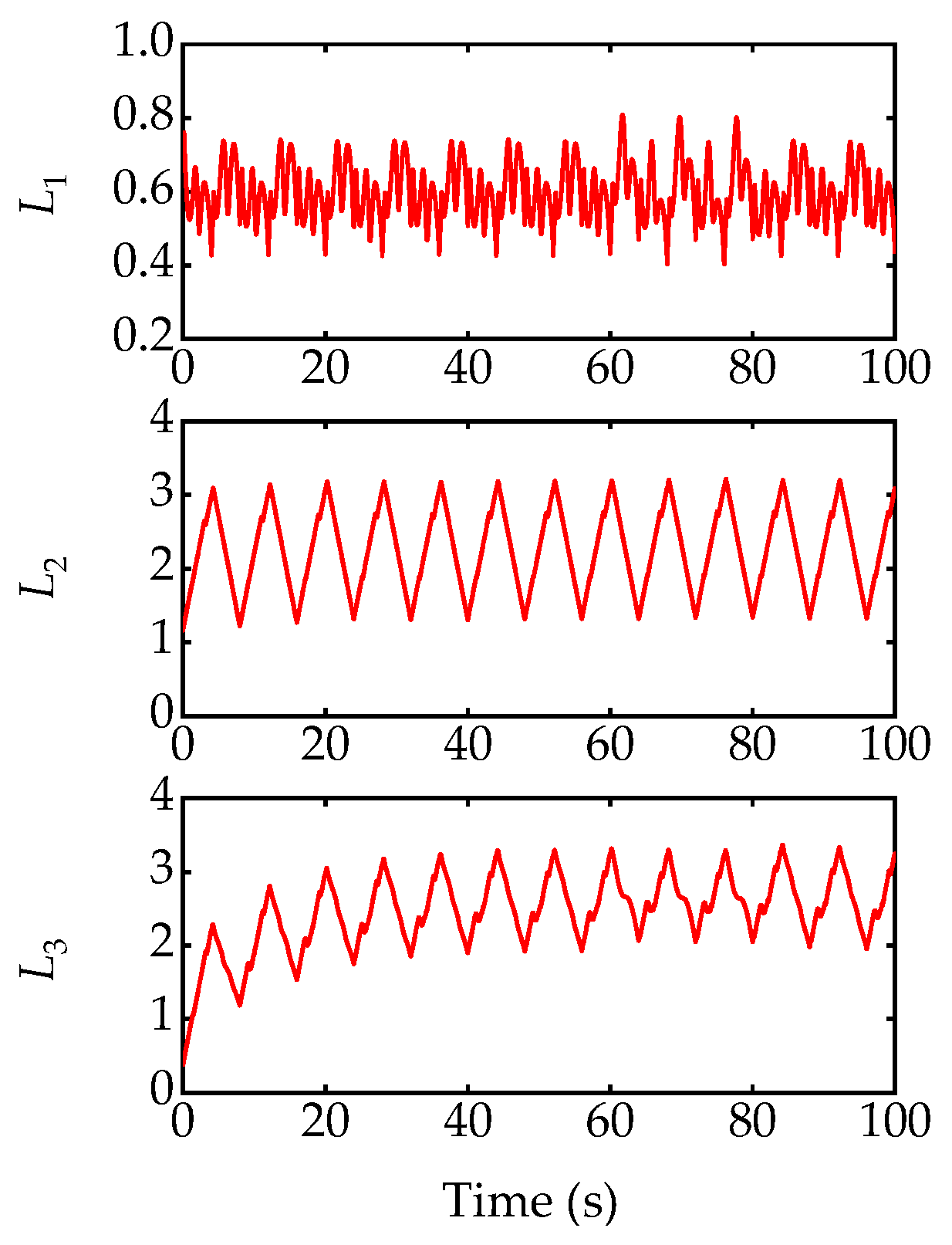


| # | q | d | a | α |
|---|---|---|---|---|
| 0–1 | q1 | 0 | L1 (0 m) | 90° |
| 1–2 | q2 | 0 | L2 (0.66 m) | 0° |
| 2–3 | q3 | 0 | L3 (0.85 m) | 0° |
| Link | Mass (kg) | Center of Mass (m) | Inertia Matrix (kg·m2) |
|---|---|---|---|
| 1 | 10.758 | [0, 0.001, −0.017]T | diag{0.044, 0.039, 0.032} |
| 2 | 19.261 | [−0.154, 0, −0.014]T | diag{0.135, 1.455, 1.375} |
| 3 | 10.375 | [−0.391, 0, −0.045]T | diag{0.138, 2.437, 2.327} |
| Controller | Parameters |
|---|---|
| ASTSMC-ESO | , , , , |
| Name | Specification | Name | Specification |
|---|---|---|---|
| Motor for joint 1/2/3 | Kollmorgen TBMS-7646-A | Velocity sensor of joint 2 | Tamagawa S2620N271E14 |
| Reducer for joint 1/2/3 | Benrun BHS32-160 | Position sensor of joint 3 | Tamagawa S2640N321E64 |
| Motor driver for joint 1/2/3 | Elmo G-SOLTWI15/100ER1 | Velocity sensor of joint 3 | Tamagawa S2620N271E14 |
| Position sensor of joint 1 | Tamagawa TS2660N31E148 | Motion controller | Beckhoff CX5140 PLC |
| Velocity sensor of joint 1 | Tamagawa TS2620N271E14 | Main power | DC48V |
| Position sensor of joint 2 | Tamagawa TS2620N271E14 | Control power | DC24V |
| Condition | Conclusion |
|---|---|
| IF si is NB | THEN λri is NB |
| IF si is NS | THEN λri is NS |
| IF si is ZE | THEN λri is ZE |
| IF si is PS | THEN λri is PS |
| IF si is PB | THEN λri is PB |
| Controller | Parameters |
|---|---|
| SMC | , |
| AFSMC | |
| ASTSMC-ESO | , , , , |
| Controller | Me (mm) | μe (mm) | σe (mm) |
|---|---|---|---|
| SMC | [17.90, 22.76, 21.15] | [6.42, 6.52, 6.17] | [4.25, 6.05, 5.78] |
| AFSMC | [8.94, 14.67, 13.73] | [2.79, 4.32, 3.44] | [2.01, 3.91, 3.04] |
| ASTSMC-ESO | [5.92, 8.28, 6.26] | [1.42, 1.96, 1.54] | [0.91, 1.49, 1.28] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, L.; Gao, L.; Ngwa, M.; Zhang, D.; Du, J.; Li, B. Adaptive Super-Twisting Sliding Mode Control of Underwater Mechanical Leg with Extended State Observer. Actuators 2023, 12, 373. https://doi.org/10.3390/act12100373
Liao L, Gao L, Ngwa M, Zhang D, Du J, Li B. Adaptive Super-Twisting Sliding Mode Control of Underwater Mechanical Leg with Extended State Observer. Actuators. 2023; 12(10):373. https://doi.org/10.3390/act12100373
Chicago/Turabian StyleLiao, Lihui, Luping Gao, Mboulé Ngwa, Dijia Zhang, Jingmin Du, and Baoren Li. 2023. "Adaptive Super-Twisting Sliding Mode Control of Underwater Mechanical Leg with Extended State Observer" Actuators 12, no. 10: 373. https://doi.org/10.3390/act12100373
APA StyleLiao, L., Gao, L., Ngwa, M., Zhang, D., Du, J., & Li, B. (2023). Adaptive Super-Twisting Sliding Mode Control of Underwater Mechanical Leg with Extended State Observer. Actuators, 12(10), 373. https://doi.org/10.3390/act12100373






