Workspace Description and Evaluation of Master-Slave Dual Hydraulic Manipulators
Abstract
1. Introduction
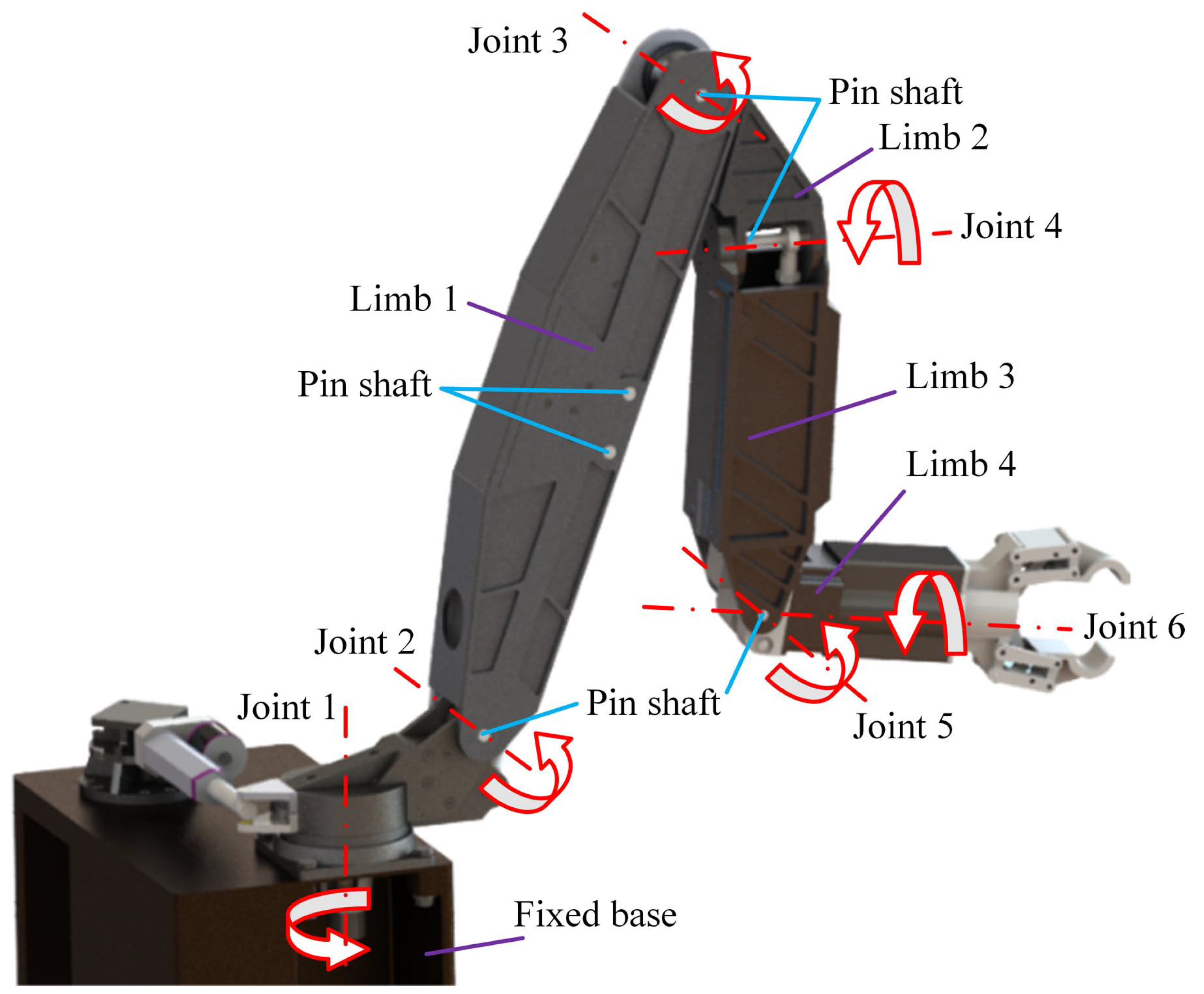
2. NPPER
2.1. Task Requirements
- 1
- To facilitate the disposal of radioactive materials that have leaked, the opening and closing of valves, and the removal of large impediments, a single robotic arm with an end load of 25 kg is required. The manipulator must also be flexible and have a reasonable working space to achieve the required movements to ensure that the emergency response is carried out smoothly.
- 2
- To investigate accident scenes, the robot should be compact and able to travel through single passageways and doors to enter inside regions such as control rooms for investigation or operation.
- 3
- The high radiation intensity at the site of a nuclear accident can be extremely damaging to humans. The robot has been developed to keep the operator away from the dangerous environment, so the robot’s dual robotic arms need to have remote control capabilities.
- 4
- Nuclear accidents produce smoke, vapor, and radioactive substances. Robotic arms are necessary to be resistant to radiation and interference as well as highly dependable while avoiding excessive costs.
- 5
- The technique of operation should be easily comprehended and learned by the operator, hence boosting the operability and simplicity of the double robotic arm’s operation and minimizing the risk of adverse outcomes resulting from faulty operation.
- 6
- The control algorithm of NPPERs employed in nuclear accident relief must have rapid kinematic calculation speed and efficient and intuitive obstacle avoidance methods to enable real-time master and slave motion following, safety, and intuitive operation.
2.2. Preliminary Planning of the Workspace
3. Workspace Generation Algorithms
3.1. Monte Carlo Approach
3.2. OAAS Algorithm
- (1)
- Calculating the positive kinematics of the SRM, providing the conversion formula from joint space to Cartesian space.Substituting the known DH parameters into Equation (2) results in a function between the robot end position coordinates and the joint variables as follows:withwhere , and denote the x, y, and z coordinates of the end-effector of the manipulator, respectively.
- (2)
- A set of points with number n is generated using the Monte Carlo approach (see Equation (1)).
- (3)
- The value of the discriminant radius controls the fineness of the border; the smaller the value, the finer the boundary.
- (4)
- Draw a circle with radius through any two points and from the set of points obtained in step 2. If there are no further data points within either circle, the points and are designated boundary points and their connecting lines are boundary line segments.
- (5)
- If the distance between and exceeds , step 4 is skipped. Thus, a significant number of outliers can be excluded.
- (6)
- Repeat the preceding steps for each point to obtain the solution.
- (7)
- Hide all connection lines and display the region around all connection points.
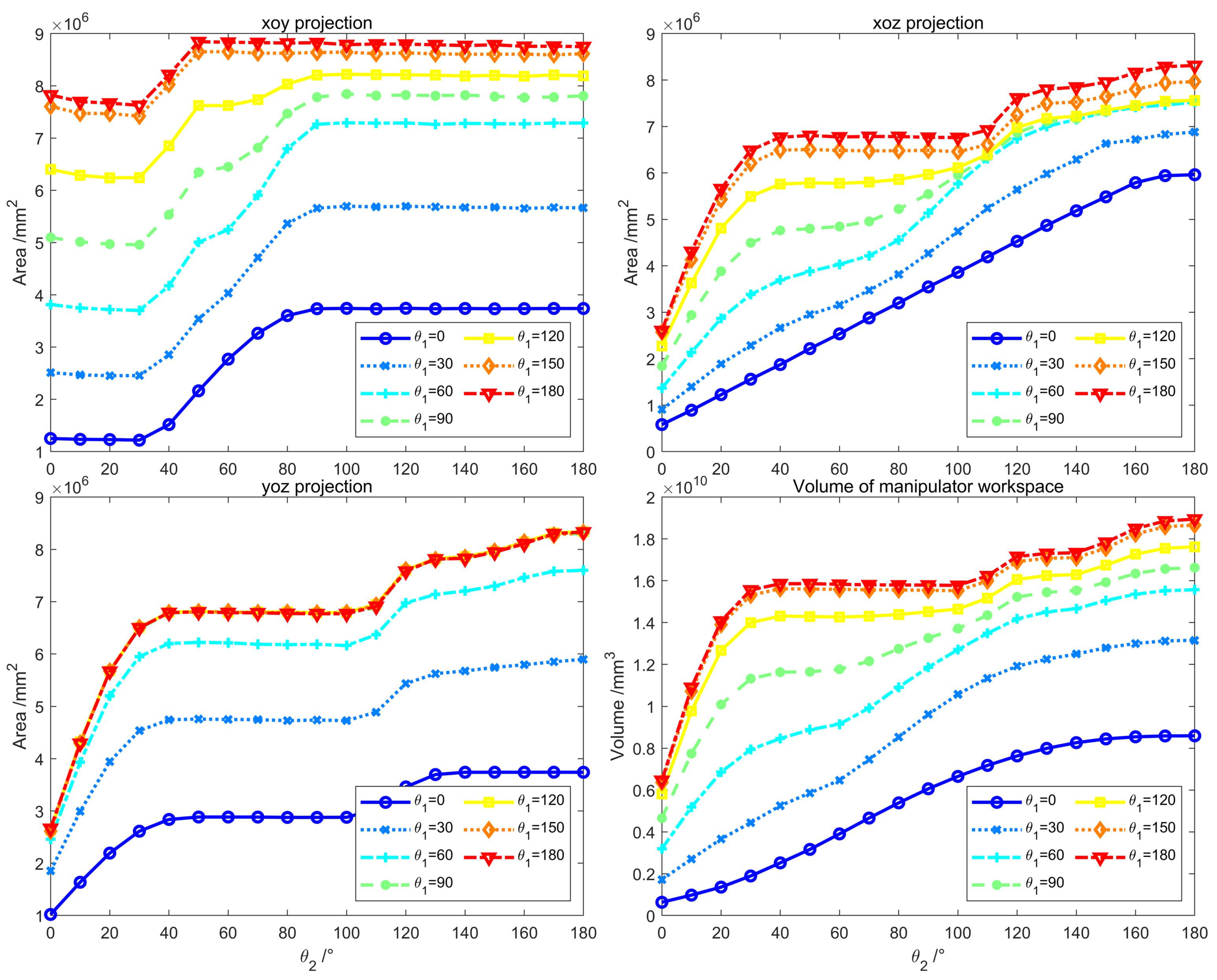
4. Three-Dimensional (D) Workspace Evaluation
4.1. Convex Hull Algorithm
- 1
- Four non-coplanar points (, and ) in are chosen to form a tetrahedron as the initial convex package .
- 2
- Initialize the convex hull and orient the faces into a right-handed system orientation for visible locations outside the envelope. That is, the four-point numbers are changed and reordered so that
- 3
- Take a permutation at random of the remaining points: . Iterate through each point individually and dynamically maintain the convex packet. Determine whether or not is within . According to the hyperplane separation theorem, points and are on the same side of the hyperplane in which is located when the following conditions are satisfiedwithwhere n represents the normals of the faces formed by the points , and . Transforming (5) yieldsAccording to the Vandermonde determinant theorem, the transformation of Equation (7) givesIt follows from Equation (8) and the construction of simplex forms that is in the interior of when the following conditions are satisfied
- 3.1.
- When satisfies Equation (9), let .
- 3.2.
- When does not satisfy Equation (9), then is outside of . A depth search traverses to find the horizon and the plane in which the point is on the convex package .
- 3.3.
- Remove all faces within the visible region of on the convex envelope and join them along the horizon to form a new face. Maintain its orientation and join it to the convex envelope to form the new convex envelope .
- 4
- Repeat step 3 until every point has been handled. Then, we have
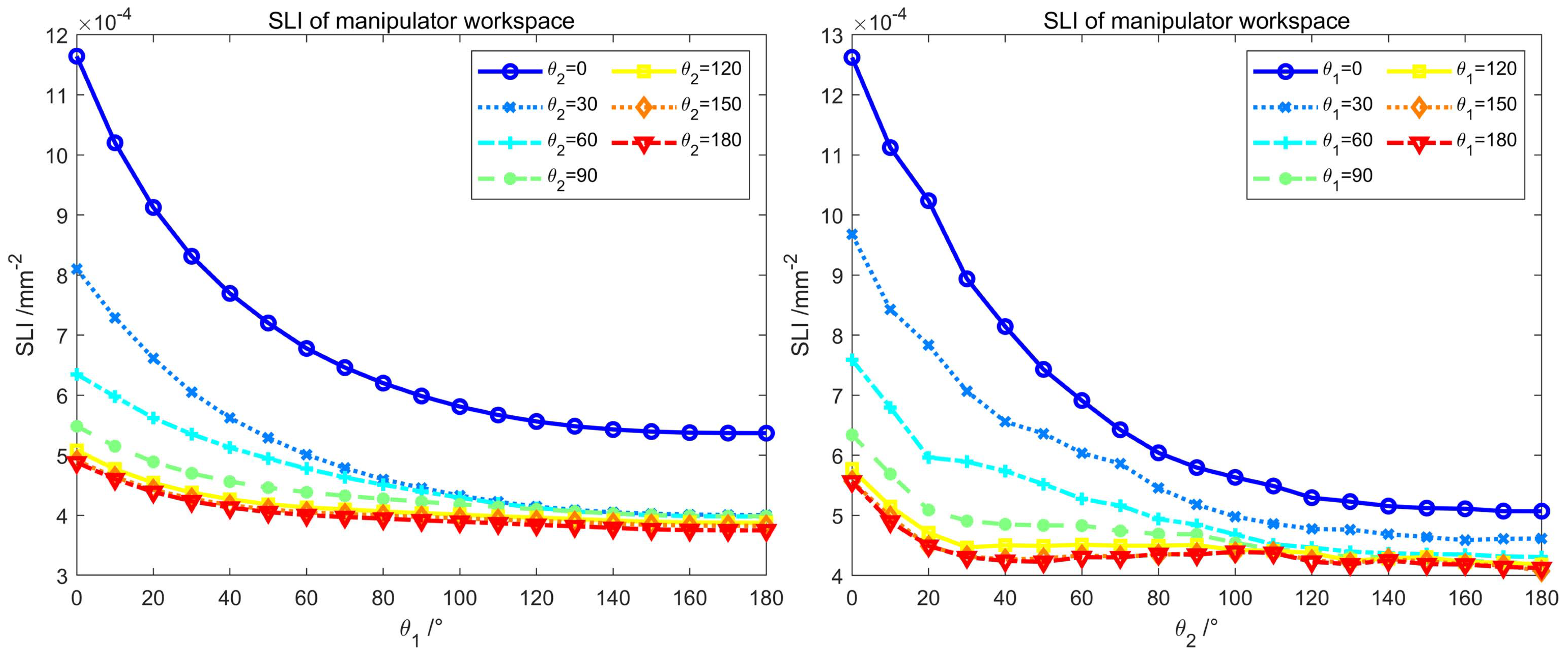
4.2. Structural Length Index of the Manipulator
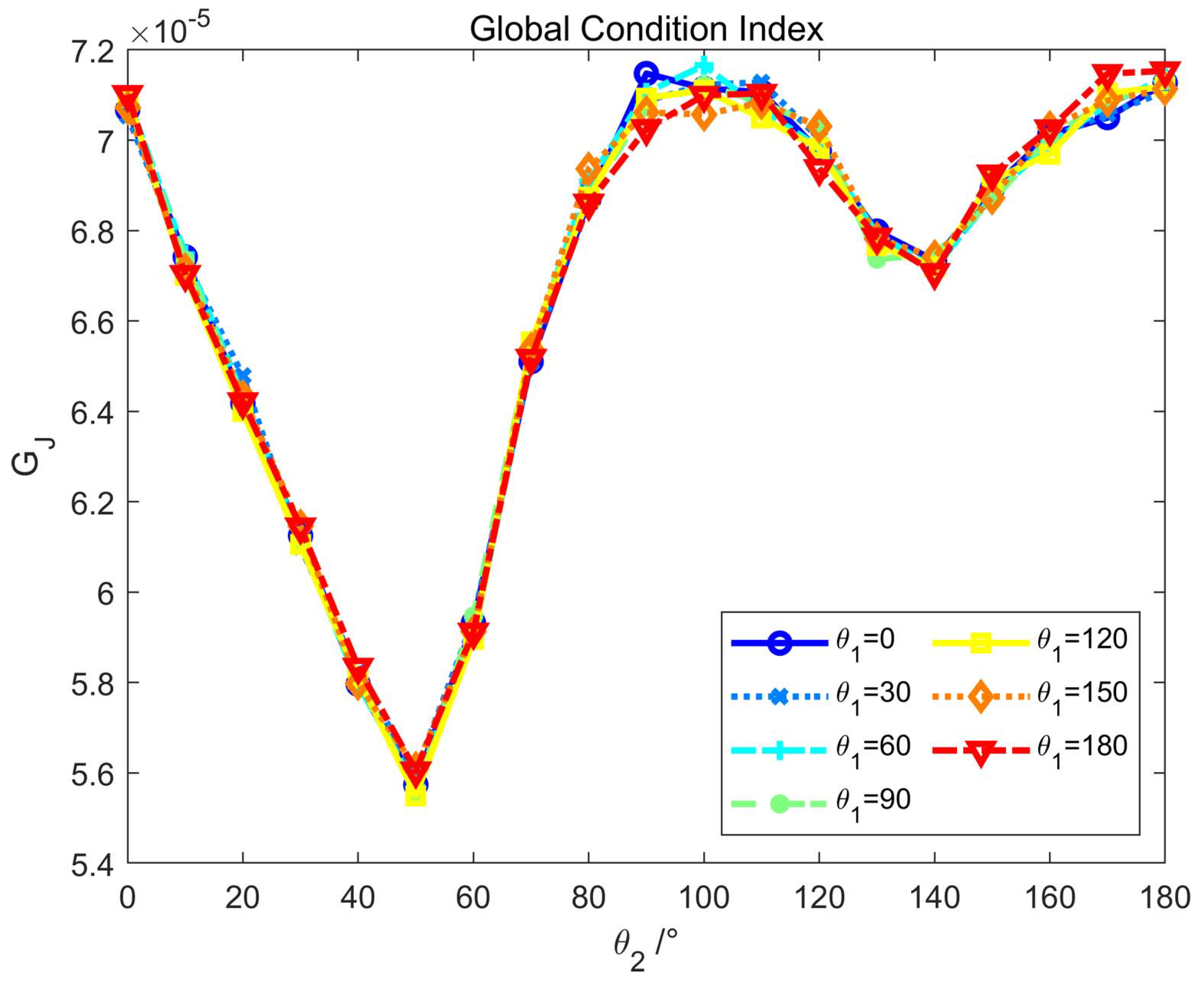
4.3. Global Condition Index of the Manipulator
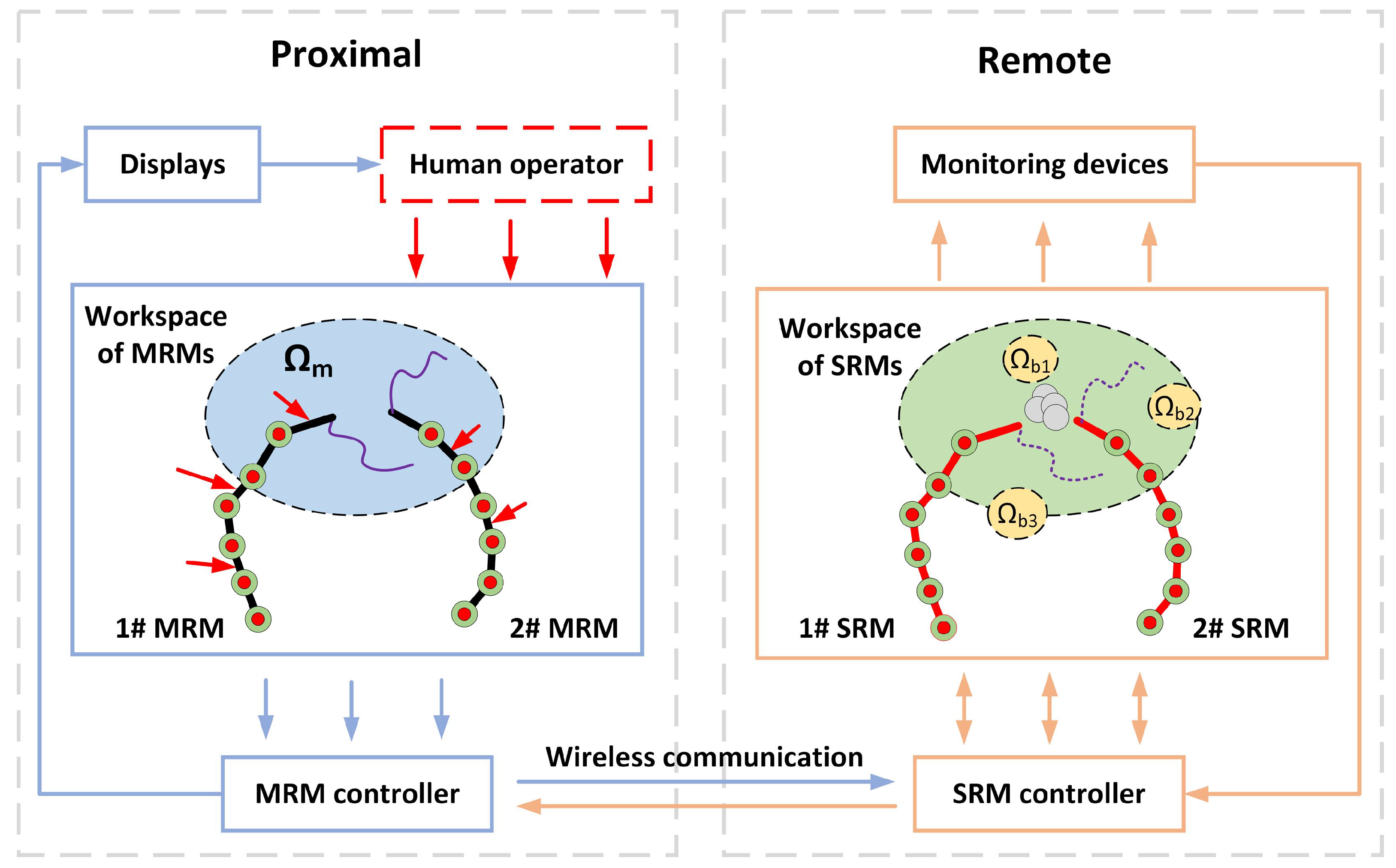
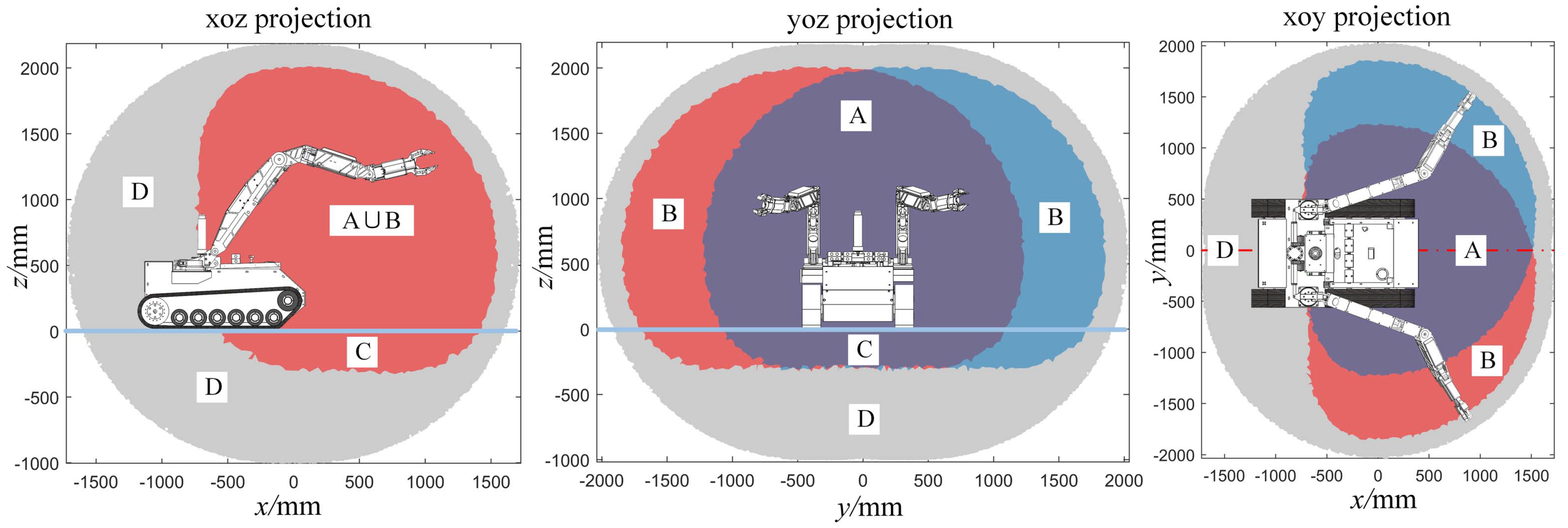
5. Master-Slave Workspace Design
5.1. Master-Slave Control Systems
5.2. Workspace Design of SRM
5.3. Workspace Design of MRM
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, M.; Li, J.; Chou, W. Depth control of ROV in nuclear power plant based on fuzzy PID and dynamics compensation. Microsyst. Technol. 2020, 26, 811–821. [Google Scholar] [CrossRef]
- Cho, B.H.; Byun, S.H.; Shin, C.H.; Yang, J.B.; Song, S.I.; Oh, J.M. KeproVt: Underwater robotic system for visual inspection of nuclear reactor internals. Nucl. Eng. Des. 2004, 231, 327–335. [Google Scholar] [CrossRef]
- Fu, X.; Yan, G.; Yan, B.; Liu, H. A new robot system for auto-inspection of intersected welds of pipes used in nuclear power stations. Int. J. Adv. Manuf. Technol. 2006, 28, 596–601. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, H.; Chen, Y.; Cheng, L.; Zhang, B. Patrol robot path planning in nuclear power plant using an interval multi-objective particle swarm optimization algorithm. Appl. Soft Comput. 2022, 116, 108192. [Google Scholar] [CrossRef]
- Zhonglin, Z.; Bin, F.; Liquan, L.; Encheng, Y. Design and function realization of nuclear power inspection robot system. Robotica 2021, 39, 165–180. [Google Scholar] [CrossRef]
- Nagatani, K.; Kiribayashi, S.; Okada, Y.; Otake, K.; Yoshida, K.; Tadokoro, S.; Nishimura, T.; Yoshida, T.; Koyanagi, E.; Fukushima, M.; et al. Emergency response to the nuclear accident at the Fukushima Daiichi Nuclear Power Plants using mobile rescue robots. J. Field Robot. 2013, 30, 44–63. [Google Scholar] [CrossRef]
- Kim, I.S.; Choi, Y.; Jeong, K.M. A new approach to quantify safety benefits of disaster robots. Nucl. Eng. Technol. 2017, 49, 1414–1422. [Google Scholar] [CrossRef]
- Otaki, M. Environmental monitoring robots for nuclear emergencies. Adv. Robot. 2002, 16, 501–504. [Google Scholar] [CrossRef]
- Chengze, L.; Zhi, Y.; Jingshan, D.; Baojun, Z.; Lei, G. Study on accident response robot for nuclear power plant and analysis of key technologies. Chin. J. Nucl. Sci. Eng. 2013, 33, 97–105. [Google Scholar]
- Han, Y.; Luan, W.; Jiang, Y.; Zhang, X. Protection of electronic devices on nuclear rescue robot: Passive thermal control. Appl. Therm. Eng. 2016, 101, 224–230. [Google Scholar] [CrossRef]
- Kim, J.S.; Jang, Y.H. Development of stable walking robot for accident condition monitoring on uneven floors in a nuclear power plant. Nucl. Eng. Technol. 2017, 49, 632–637. [Google Scholar] [CrossRef]
- Kim, D.; Kim, Y.S.; Noh, K.; Jang, M.; Kim, S. Wall-climbing robot with active sealing for radiation safety of nuclear power plants. Nucl. Sci. Eng. 2020, 194, 1162–1174. [Google Scholar] [CrossRef]
- Yin, G.; Fuying, H.; Li, Z.; Ling, J. Workspace description and simulation of a backhoe device for hydraulic excavators. Autom. Constr. 2020, 119, 103325. [Google Scholar] [CrossRef]
- Merlet, J.P. Parallel Robots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 128. [Google Scholar]
- Bohigas, O.; Manubens, M.; Ros, L. A complete method for workspace boundary determination on general structure manipulators. IEEE Trans. Robot. 2012, 28, 993–1006. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J. Parallel Kinematics; Springer Tracts in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Guan, Y.; Yokoi, K. Reachable space generation of a humanoid robot using the monte carlo method. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 1984–1989. [Google Scholar]
- Guan, Y.; Yokoi, K.; Zhang, X. Numerical methods for reachable space generation of humanoid robots. Int. J. Robot. Res. 2008, 27, 935–950. [Google Scholar] [CrossRef]
- Pisla, D.; Szilaghyi, A.; Vaida, C.; Plitea, N. Kinematics and workspace modeling of a new hybrid robot used in minimally invasive surgery. Robot. Comput.-Integr. Manuf. 2013, 29, 463–474. [Google Scholar] [CrossRef]
- Burgner-Kahrs, J.; Gilbert, H.B.; Granna, J.; Swaney, P.J.; Webster, R.J. Workspace characterization for concentric tube continuum robots. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1269–1275. [Google Scholar]
- Badescu, M.; Mavroidis, C. New performance indices and workspace analysis of reconfigurable hyper-redundant robotic arms. Int. J. Robot. Res. 2004, 23, 643–659. [Google Scholar] [CrossRef]
- Rastegar, J.; Fardanesh, B. Manipulation workspace analysis using the Monte Carlo method. Mech. Mach. Theory 1990, 25, 233–239. [Google Scholar] [CrossRef]
- Alciatore, D.G.; Ng, C.C.D. Determining manipulator workspace boundaries using the Monte Carlo method and least squares segmentation. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, Minneapolis, MN, USA, 11–14 September 1994; Volume 12860, pp. 141–146. [Google Scholar]
- Wang, L.; Wu, J.; Tang, D. Research on workspace of manipulator with complicated constraints. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 995–999. [Google Scholar]
- Liu, Z.; Liu, H.; Luo, Z.; Zhang, X. Improvement on Monte Carlo method for robot workspace determination. Nongye Jixie Xuebao (Trans. Chin. Soc. Agric. Mach.) 2013, 44, 230–235. [Google Scholar]
- Cao, Y.; Lu, K.; Li, X.; Zang, Y. Accurate numerical methods for computing 2d and 3d robot workspace. Int. J. Adv. Robot. Syst. 2011, 8, 76. [Google Scholar] [CrossRef]
- Peidró, A.; Reinoso, Ó.; Gil, A.; Marín, J.M.; Payá, L. An improved Monte Carlo method based on Gaussian growth to calculate the workspace of robots. Eng. Appl. Artif. Intell. 2017, 64, 197–207. [Google Scholar] [CrossRef]
- Cao, Y.; Qi, S.; Lu, K.; Zang, Y.; Yang, G. Shape and size computation of planar robot workspace. In Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, Los Angeles, CA, USA, 31 March–2 April 2009; Volume 2, pp. 126–130. [Google Scholar]
- Bader, A.M.; Maciejewski, A.A. A hybrid approach for estimating the failure-tolerant workspace size of kinematically redundant robots. IEEE Robot. Autom. Lett. 2020, 6, 303–310. [Google Scholar] [CrossRef]
- Hoover, R.C.; Roberts, R.G.; Maciejewski, A.A.; Naik, P.S.; Ben-Gharbia, K.M. Designing a failure-tolerant workspace for kinematically redundant robots. IEEE Trans. Autom. Sci. Eng. 2014, 12, 1421–1432. [Google Scholar] [CrossRef]
- Wang, S.; Chen, Z.; Li, J.; Wang, J.; Li, J.; Zhao, J. Flexible motion framework of the six wheel-legged robot: Experimental results. IEEE/ASME Trans. Mechatronics 2021, 27, 2246–2257. [Google Scholar] [CrossRef]
- Kohlbrecher, S.; Stryk, O.V. From RoboCup Rescue to supervised autonomous mobile robots for remote inspection of industrial plants. KI-Künstliche Intell. 2016, 30, 311–314. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Manipulator performance measures-a comprehensive literature survey. J. Intell. Robot. Syst. 2015, 77, 547–570. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, B. Modelling and optimisation of a 4-DOF hybrid robotic manipulator. Int. J. Comput. Integr. Manuf. 2017, 30, 1179–1189. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. A global performance index for the kinematic optimization of robotic manipulators. J. Mech. Des. 1991, 113, 220–226. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Wan, Y.; Ma, H.; Liang, X. Workspace Description and Evaluation of Master-Slave Dual Hydraulic Manipulators. Actuators 2023, 12, 9. https://doi.org/10.3390/act12010009
Sun Y, Wan Y, Ma H, Liang X. Workspace Description and Evaluation of Master-Slave Dual Hydraulic Manipulators. Actuators. 2023; 12(1):9. https://doi.org/10.3390/act12010009
Chicago/Turabian StyleSun, Yao, Yi Wan, Haifeng Ma, and Xichang Liang. 2023. "Workspace Description and Evaluation of Master-Slave Dual Hydraulic Manipulators" Actuators 12, no. 1: 9. https://doi.org/10.3390/act12010009
APA StyleSun, Y., Wan, Y., Ma, H., & Liang, X. (2023). Workspace Description and Evaluation of Master-Slave Dual Hydraulic Manipulators. Actuators, 12(1), 9. https://doi.org/10.3390/act12010009










