Natural Characteristics Analysis for the Spacecraft Equipped with Constructed Cantilever Solar Panels
Abstract
:1. Introduction
2. Power Series Constraining Method
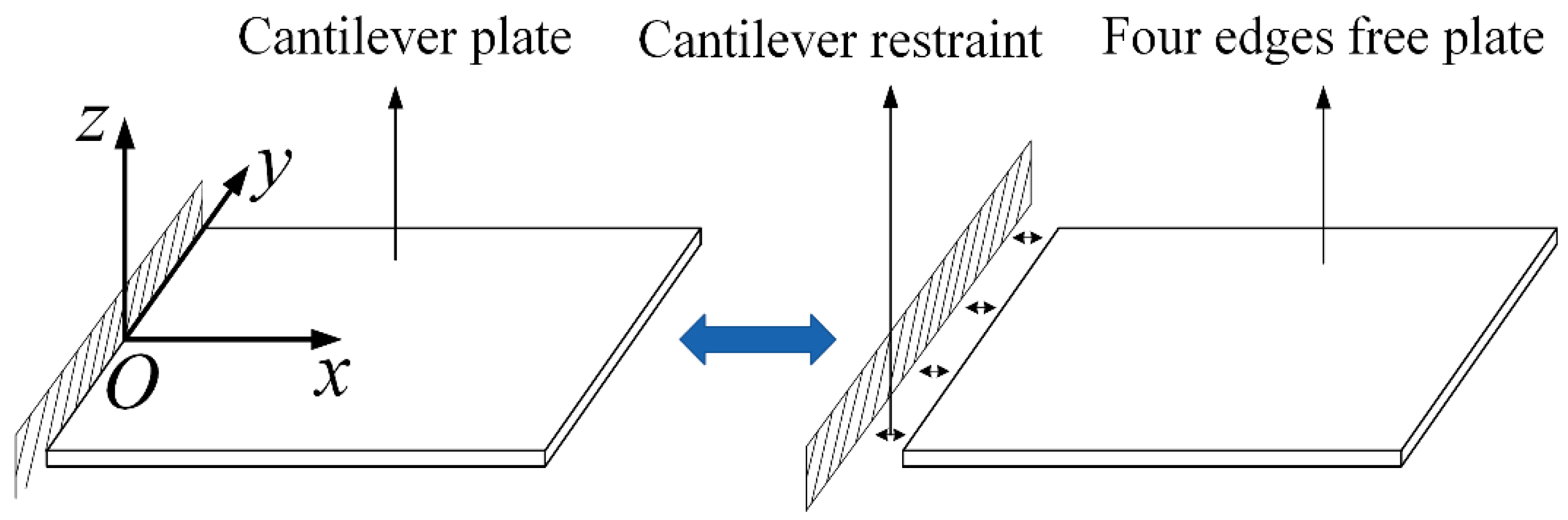
2.1. Displacement Field of the Plate
2.2. Constraining by Power Series Multiplier
3. Dynamical Model of the Flexible Spacecraft with Solar Panels
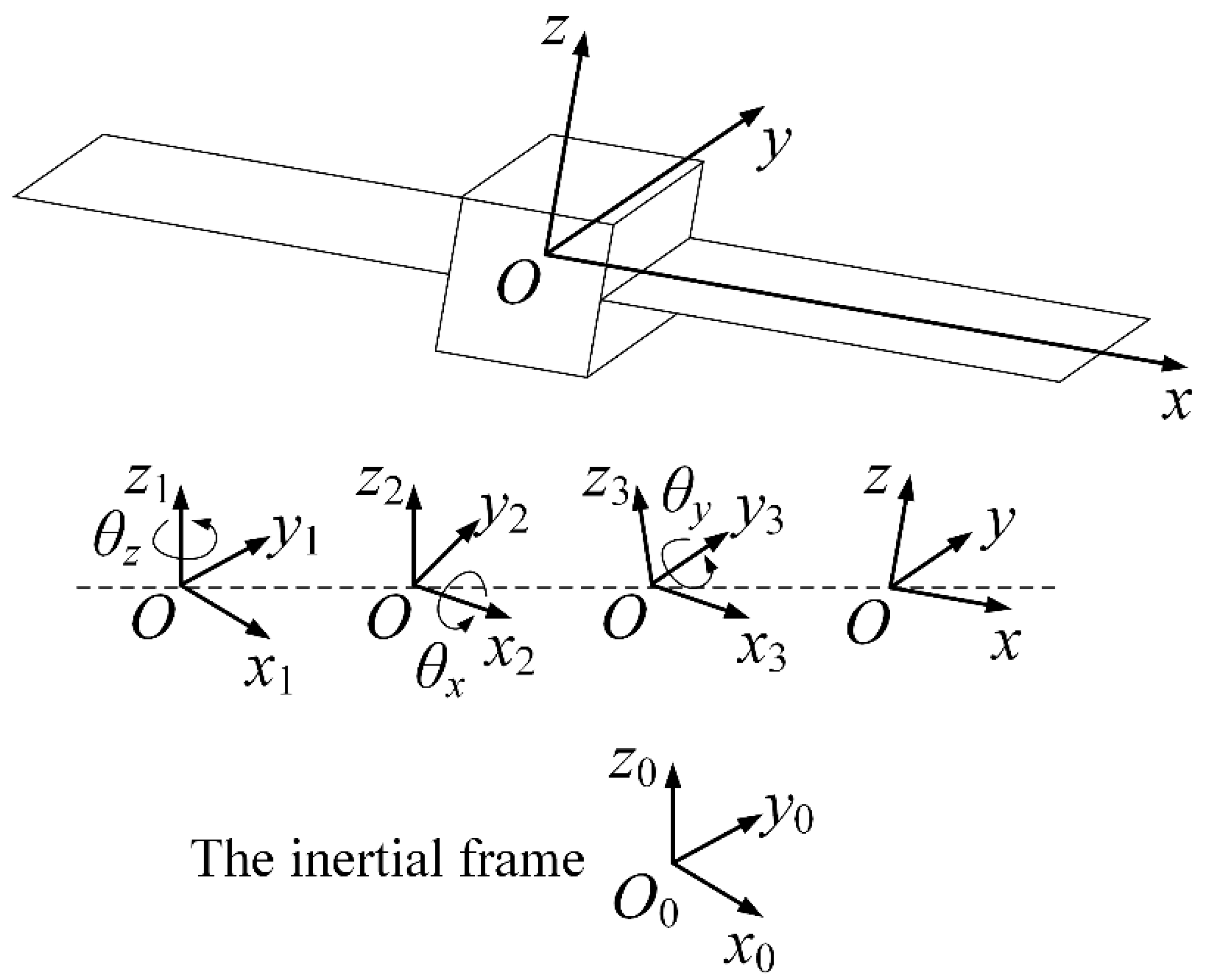
3.1. Geometric Description of the Model
3.2. Characteristic Equation of the Spacecraft
4. Numerical Simulation and Discussion
4.1. Validity Verification and Convergence Analysis of the Method
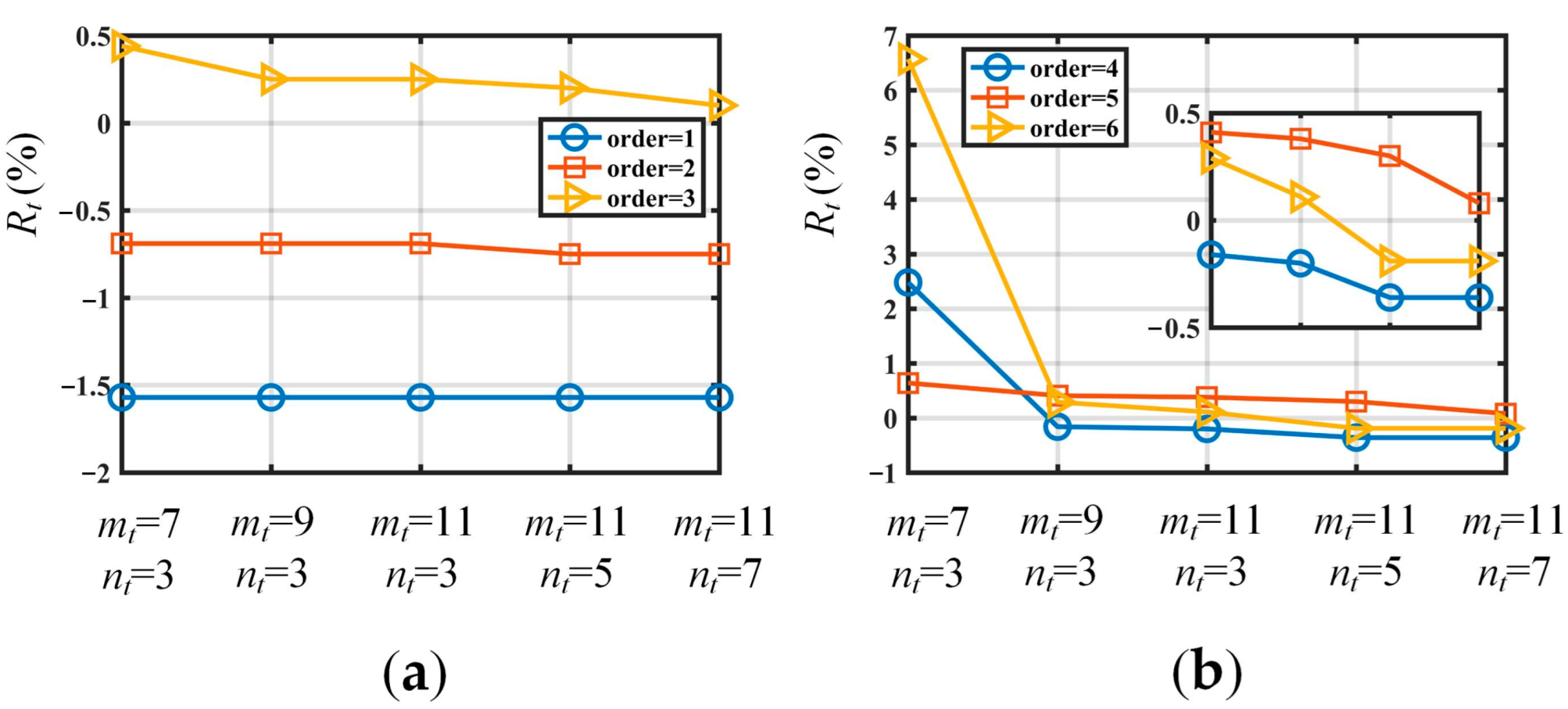
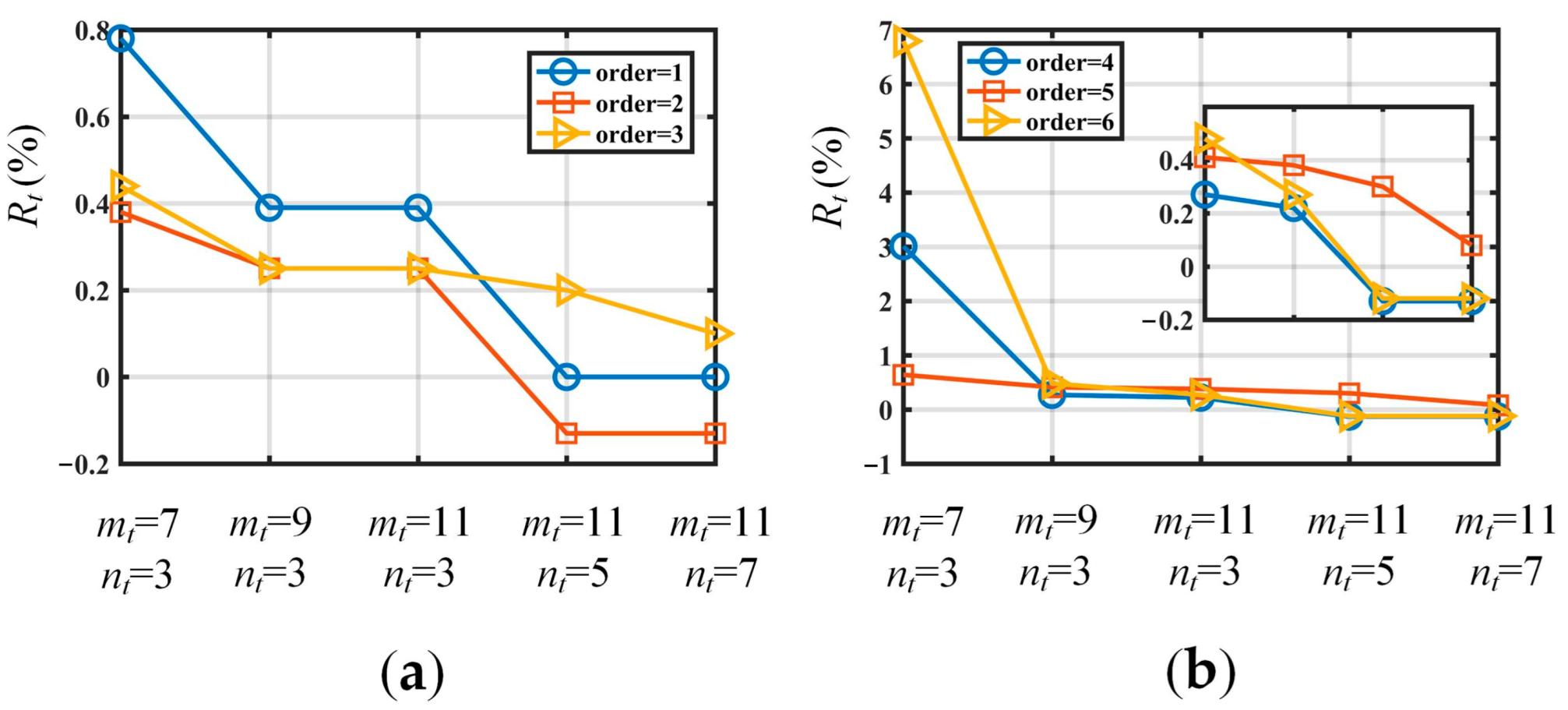
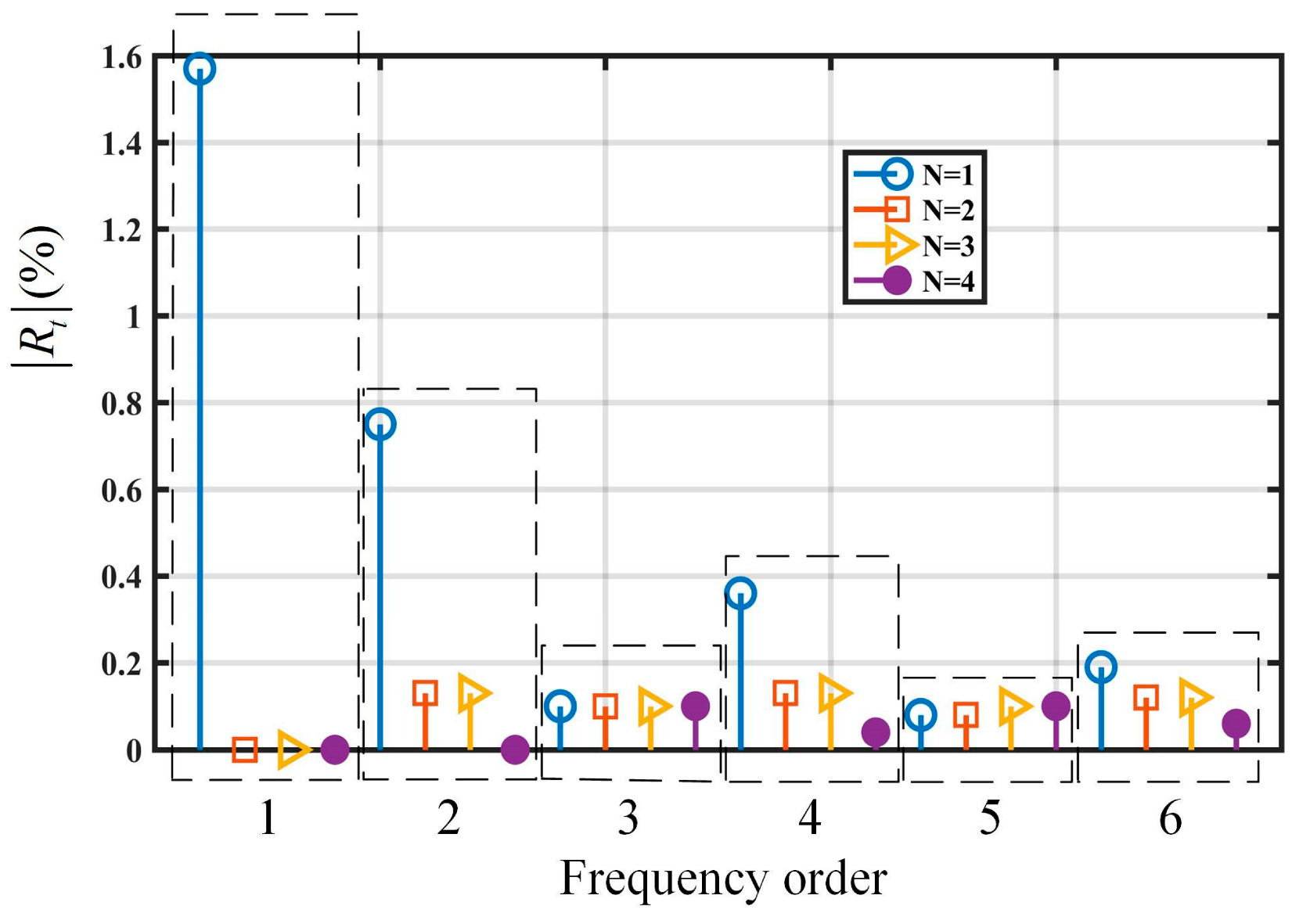
4.2. Study of the Order of Power Series Multipliers
4.3. Study on the Frequency of Flexible Spacecraft by This Method
5. Conclusions
- (1).
- Through the study of the natural characteristics of the cantilever plate, it can be known that the convergence of the method is good and the computational efficiency is high in this the power series multiplier order N = 2. Under this condition, when the length of the clamped edge is shorter than that of the adjacent edge, the result is reasonable and accurate. On the contrary, if the length of the clamped edge is obviously longer than that of the adjacent edge, the result is imprecise.
- (2).
- The method can be extended to a flexible spacecraft equipped with a pair of solar panels symmetrically. By comparing the result with the reference, it can be known that the presented method is not only fit for the single plate, but also feasible for the rigid-flexible coupling structure. It should be mentioned that when the solar panel is so long that it presents as a beam, the convergence of this method is much better. The proposed method can be adopted to the structure, with edges subjected to discontinuous constraints.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Cao, D.Q.; Wei, J.; Tan, X.J.; Yu, T.H. Rigid-Flexible Coupling Dynamic Modeling and Vibration Control for a Three-Axis Stabilized Spacecraft. J. Vib. Acoust. 2017, 139, 041006. [Google Scholar] [CrossRef]
- Li, Q.; Ma, X.R.; Wang, T.S. Reduced Model for Flexible Solar Sail Dynamics. J. Spacecr. Rocket. 2011, 48, 446–453. [Google Scholar] [CrossRef]
- Liu, L.; Sun, S.P.; Cao, D.Q.; Liu, X.Y. Thermal-structural analysis for flexible spacecraft with single or double solar panels: A comparison study. Acta Astronaut. 2019, 154, 33–43. [Google Scholar] [CrossRef]
- Li, Y.Y.; Yang, Y.; Li, M.; Liu, Y.F.; Huang, Y.F. Dynamics analysis and wear prediction of rigid-flexible coupling deployable solar array system with clearance joints considering solid lubrication. Mech. Syst. Signal Processing 2022, 162, 108059. [Google Scholar] [CrossRef]
- Li, Y.Y.; Wang, Z.L.; Wang, C.; Huang, W.H. Planar rigid-flexible coupling spacecraft modeling and control considering solar array deployment and joint clearance. Acta Astronaut. 2018, 142, 138–151. [Google Scholar] [CrossRef]
- Li, Y.Y.; Li, M.; Liu, Y.F.; Geng, X.Y.; Cui, C.B. Parameter optimization for torsion spring of deployable solar array system with multiple clearance joints considering rigid–flexible coupling dynamics. Chin. J. Aeronaut. 2022, 35, 509–524. [Google Scholar] [CrossRef]
- Pan, K.Q.; Liu, J.Y. Investigation on the choice of boundary conditions and shape functions for flexible multi-body system. Acta Mech. Sin. 2011, 28, 180–189. [Google Scholar] [CrossRef]
- Zhang, J.L.; Lu, S.B.; Zhao, L.Y. Modeling and disturbance suppression for spacecraft solar array systems subject to drive fluctuation. Aerosp. Sci. Technol. 2021, 108, 106398. [Google Scholar] [CrossRef]
- Yang, J.Y.; Liu, F. Coupled Structure Vibration–Attitude Dynamics Evolution and Control of China’s Space Station. Int. J. Aeronaut. Space Sci. 2019, 20, 126–138. [Google Scholar] [CrossRef]
- Nicassio, F.; Fattizzo, D.; Giannuzzi, M.; Scarselli, G.; Avanzini, G. Attitude dynamics and control of a large flexible space structure by means of a minimum complexity model. Acta Astronaut. 2022, 198, 124–134. [Google Scholar] [CrossRef]
- Wei, J.; Cao, D.Q.; Liu, L.; Huang, W.H. Global mode method for dynamic modeling of a flexible-link flexible-joint manipulator with tip mass. Appl. Math. Model. 2017, 48, 787–805. [Google Scholar] [CrossRef]
- Wei, J.; Cao, D.Q.; Huang, H.; Wang, L.C.; Huang, W.H. Dynamics of a multi-beam structure connected with nonlinear joints: Modelling and simulation. Arch. Appl. Mech. 2018, 88, 1059–1074. [Google Scholar] [CrossRef]
- Fang, B.; Cao, D.Q.; Chen, C.; Chen, S. Nonlinear dynamic modeling and responses of a cable dragged flexible spacecraft. J. Frankl. Inst. 2022, 359, 3238–3290. [Google Scholar] [CrossRef]
- Liu, L.; Cao, D.Q.; Tan, X.J. Studies on global analytical mode for a three-axis attitude stabilized spacecraft by using the Rayleigh–Ritz method. Arch. Appl. Mech. 2016, 86, 1927–1946. [Google Scholar] [CrossRef]
- Liu, L.; Cao, D.Q.; Wei, J. Rigid-flexible coupling dynamic modeling and vibration control for flexible spacecraft based on its global analytical modes. Sci. China Technol. Sci. 2018, 62, 608–618. [Google Scholar] [CrossRef]
- Chen, L.H.; Cui, S.J.; Jing, H.; Zhang, W. Analysis and modeling of a flexible rectangular cantilever plate. Appl. Math. Model. 2020, 78, 117–133. [Google Scholar] [CrossRef]
- Cao, Y.T.; Cao, D.Q.; Huang, W.H. Dynamic modeling and vibration control for a T-shaped bending and torsion structure. Int. J. Mech. Sci. 2019, 157–158, 773–786. [Google Scholar] [CrossRef]
- Cao, Y.T.; Cao, D.Q.; Liu, L.; Huang, W.H. Dynamical modeling and attitude analysis for the spacecraft with lateral solar arrays. Appl. Math. Model. 2018, 64, 489–509. [Google Scholar] [CrossRef]
- Cao, Y.T.; Cao, D.Q.; He, G.Q.; Liu, L. Thermal alternation induced vibration analysis of spacecraft with lateral solar arrays in orbit. Appl. Math. Model. 2020, 86, 166–184. [Google Scholar] [CrossRef]
- He, G.Q.; Cao, D.Q.; Cao, Y.T.; Huang, W.H. Investigation on global analytic modes for a three-axis attitude stabilized spacecraft with jointed panels. Aerosp. Sci. Technol. 2020, 106, 106087. [Google Scholar] [CrossRef]
- Xing, W.C.; Wang, Y.Q. Vibration characteristics analysis of rigid-flexible spacecraft with double-direction hinged solar arrays. Acta Astronaut. 2022, 193, 454–468. [Google Scholar] [CrossRef]
- He, G.Q.; Cao, D.Q.; Wei, J.; Cao, Y.T.; Chen, Z.G. Study on analytical global modes for a multi-panel structure connected with flexible hinges. Appl. Math. Model. 2021, 91, 1081–1099. [Google Scholar] [CrossRef]
- He, G.Q.; Cao, D.Q.; Cao, Y.T.; Huang, W.H. Dynamic modeling and orbit maneuvering response analysis for a three-axis attitude stabilized large scale flexible spacecraft installed with hinged solar arrays. Mech. Syst. Signal Processing 2022, 162, 108083. [Google Scholar] [CrossRef]
- Cao, Y.T.; Cao, D.Q.; He, G.Q.; Ge, X.S.; Hao, Y.X. Modelling and vibration analysis for the multi-plate structure connected by nonlinear hinges. J. Sound Vib. 2021, 492, 115809. [Google Scholar] [CrossRef]
- Xing, W.C.; Wang, Y.Q. Vibration characteristics of thin plate system joined by hinges in double directions. Thin-Walled Struct. 2022, 175, 109260. [Google Scholar] [CrossRef]
- Bhat, R.B. Natural frequencies of rectangular plates using characteristic orthogonal polynomials in Rayleigh–Ritz method. J. Sound Vib. 1985, 102, 493–499. [Google Scholar] [CrossRef]
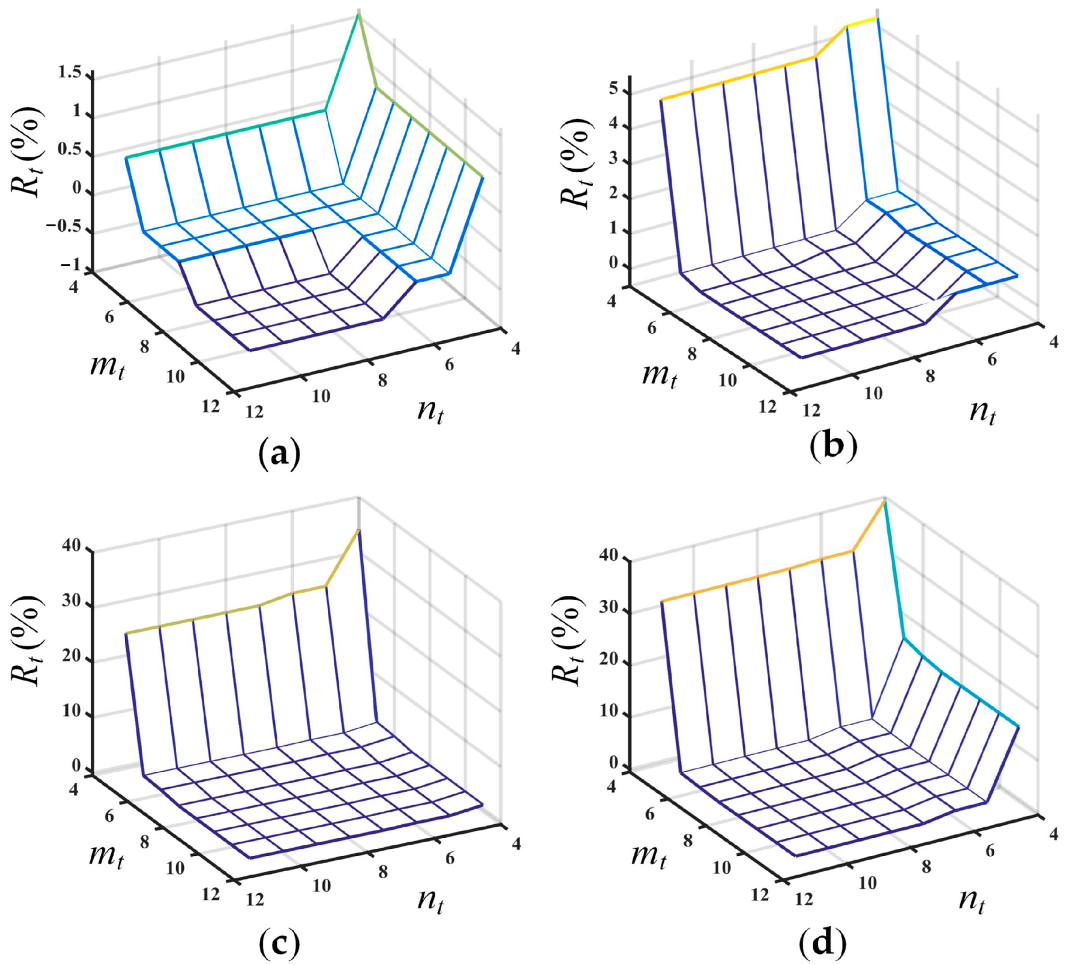
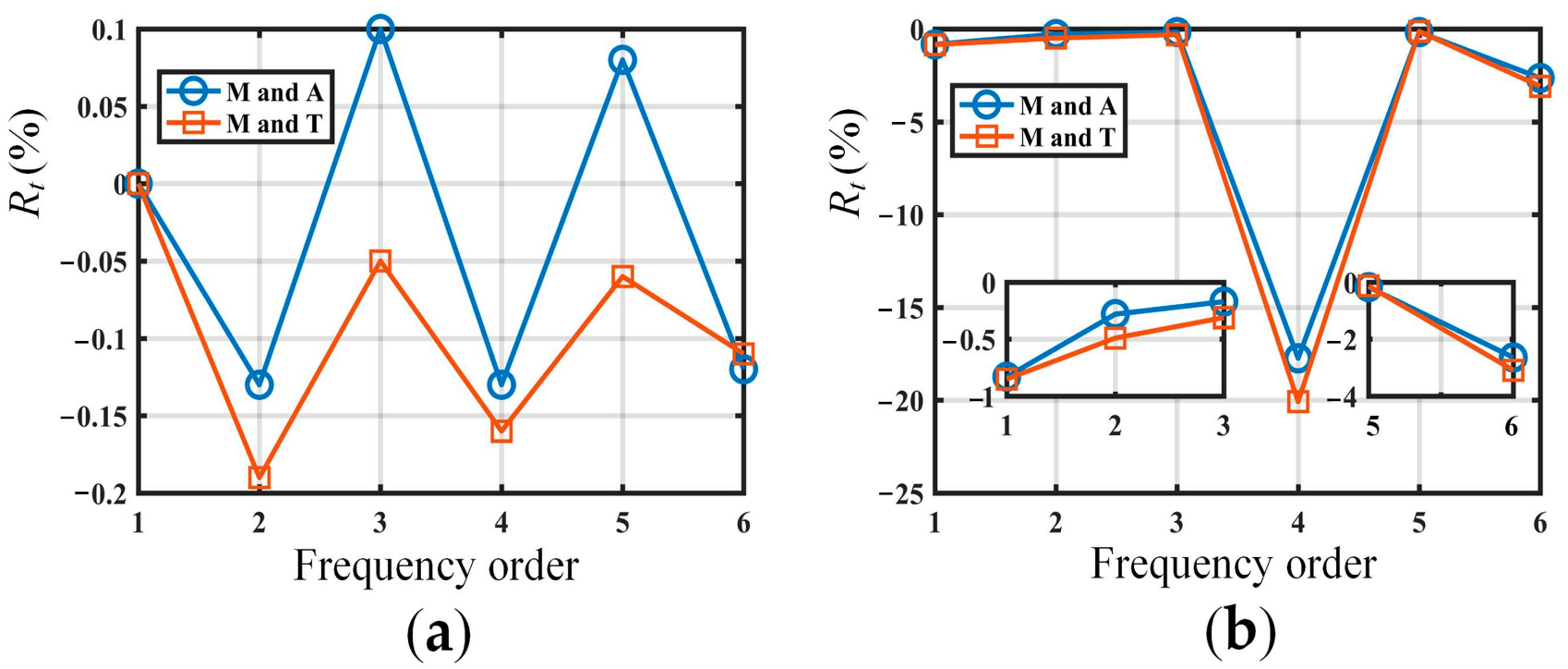
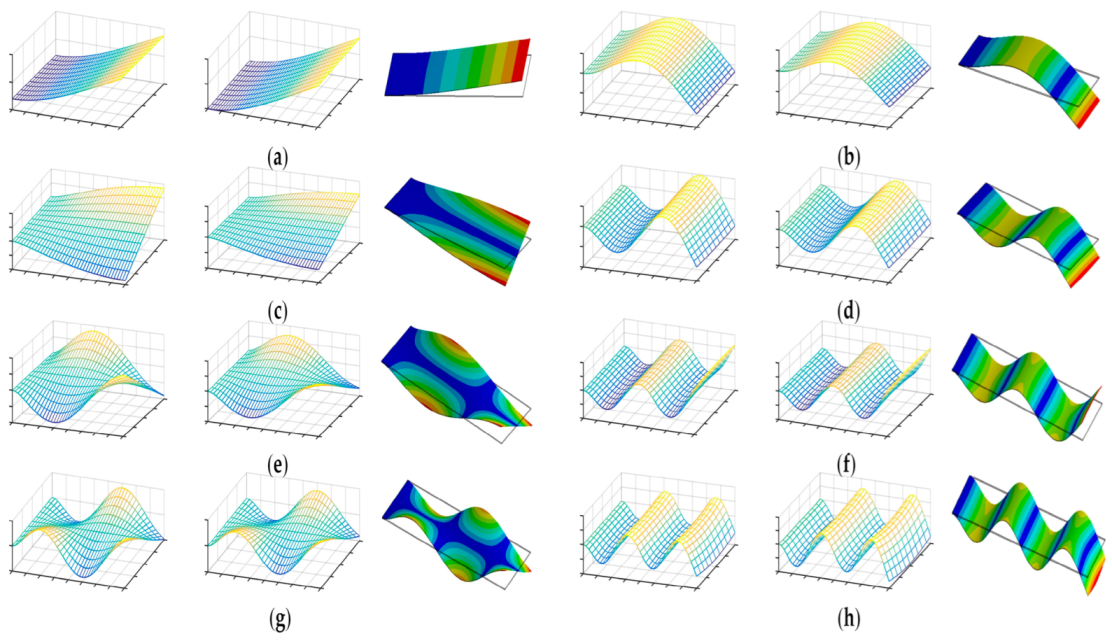

| Order | 2b = 2 m | 2b = 4 m | 2b = 8 m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ANSYS | Method | Rt (%) | ANSYS | Method | Rt (%) | ANSYS | Method | Rt (%) | |
| 1 | 0.255 | 0.255 | 0.00 | 0.258 | 0.257 | −0.39 | 0.261 | 0.259 | −0.77 |
| 2 | 1.595 | 1.593 | −0.13 | 1.095 | 1.095 | 0.00 | 0.631 | 0.630 | −0.16 |
| 3 | 2.031 | 2.033 | 0.10 | 1.607 | 1.604 | −0.19 | 1.593 | 1.590 | −0.19 |
| 4 | 4.482 | 4.476 | −0.13 | 3.575 | 3.573 | −0.06 | 2.043 | 2.041 | −0.10 |
| 5 | 6.278 | 6.283 | 0.08 | 4.511 | 4.505 | −0.13 | 2.307 | 2.305 | −0.09 |
| 6 | 8.825 | 8.814 | −0.12 | 6.890 | 6.888 | −0.03 | 4.041 | 4.038 | −0.07 |
| 7 | 11.051 | 11.057 | 0.05 | 6.997 | 6.995 | −0.03 | 4.613 | 4.609 | −0.09 |
| 8 | 14.647 | 14.719 | 0.49 | 8.890 | 8.881 | −0.10 | 4.803 | 4.712 | −1.89 |
| Order | L = 2 m | L = 4 m | L = 8 m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ANSYS | Method | Rt (%) | ANSYS | Method | Rt (%) | ANSYS | Method | Rt (%) | |
| 1 | 4.210 | 4.175 | −0.83 | 1.044 | 1.038 | −0.57 | 0.258 | 0.257 | −0.39 |
| 2 | 6.376 | 6.358 | −0.28 | 2.525 | 2.521 | −0.16 | 1.095 | 1.095 | 0.00 |
| 3 | 12.118 | 12.097 | −0.17 | 6.371 | 6.360 | −0.17 | 1.607 | 1.604 | −0.19 |
| 4 | 22.763 | 18.725 | −17.74 | 8.170 | 8.164 | −0.07 | 3.575 | 3.573 | −0.06 |
| 5 | 26.326 | 26.280 | −0.17 | 9.228 | 9.220 | −0.09 | 4.511 | 4.505 | −0.13 |
| 6 | 29.665 | 28.881 | −2.64 | 16.161 | 16.153 | −0.05 | 6.890 | 6.888 | −0.03 |
| 7 | 37.529 | 32.080 | −14.52 | 18.461 | 18.434 | −0.15 | 6.997 | 6.995 | −0.03 |
| 8 | 40.944 | 37.572 | −8.24 | 19.219 | 18.847 | −1.94 | 8.890 | 8.881 | −0.10 |
| Order | 2b = 2 m | 2b = 4 m | 2b = 8 m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Tradition | Method | Rt (%) | Tradition | Method | Rt (%) | Tradition | Method | Rt (%) | |
| 1 | 0.255 | 0.255 | 0.00 | 0.258 | 0.257 | −0.39 | 0.261 | 0.259 | −0.77 |
| 2 | 1.596 | 1.593 | −0.19 | 1.096 | 1.095 | −0.09 | 0.632 | 0.630 | −0.32 |
| 3 | 2.034 | 2.033 | −0.05 | 1.607 | 1.604 | −0.19 | 1.593 | 1.590 | −0.19 |
| 4 | 4.483 | 4.476 | −0.16 | 3.578 | 3.573 | −0.14 | 2.043 | 2.041 | −0.10 |
| 5 | 6.287 | 6.283 | −0.06 | 4.511 | 4.505 | −0.13 | 2.310 | 2.305 | −0.22 |
| 6 | 8.824 | 8.814 | −0.11 | 6.895 | 6.888 | −0.10 | 4.044 | 4.038 | −0.15 |
| 7 | 11.065 | 11.057 | −0.07 | 6.996 | 6.995 | −0.01 | 4.613 | 4.609 | −0.09 |
| 8 | 14.644 | 14.719 | 0.51 | 8.888 | 8.881 | −0.08 | 4.916 | 4.712 | −4.15 |
| Order | L = 2 m | L = 4 m | L = 8 m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Tradition | Method | Rt (%) | Tradition | Method | Rt (%) | Tradition | Method | Rt (%) | |
| 1 | 4.211 | 4.175 | −0.85 | 1.045 | 1.038 | −0.67 | 0.258 | 0.257 | −0.39 |
| 2 | 6.389 | 6.358 | −0.49 | 2.528 | 2.521 | −0.28 | 1.096 | 1.095 | −0.09 |
| 3 | 12.135 | 12.097 | −0.31 | 6.372 | 6.360 | −0.19 | 1.607 | 1.604 | −0.19 |
| 4 | 23.431 | 18.725 | −20.08 | 8.172 | 8.164 | −0.10 | 3.578 | 3.573 | −0.14 |
| 5 | 26.315 | 26.280 | −0.13 | 9.239 | 9.220 | −0.21 | 4.511 | 4.505 | −0.13 |
| 6 | 29.803 | 28.881 | −3.09 | 16.176 | 16.153 | −0.14 | 6.895 | 6.888 | −0.10 |
| 7 | 37.810 | 32.080 | −15.15 | 18.451 | 18.434 | −0.09 | 6.996 | 6.995 | −0.01 |
| 8 | 43.403 | 37.572 | −13.43 | 19.664 | 18.847 | −4.15 | 8.888 | 8.881 | −0.08 |
| Order | ANSYS | Method | Relative Tolerance (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mt = 7 nt = 3 | mt = 9 nt = 3 | mt = 11 nt = 3 | mt = 11 nt = 5 | mt = 11 nt = 7 | |||||||
| 1 | 0.255 | - | - | - | 0.255 | 0.255 | - | - | - | 0.00 | 0.00 |
| 2 | 1.595 | - | - | - | 1.593 | 1.593 | - | - | - | −0.13 | −0.13 |
| 3 | 2.031 | - | - | - | 2.035 | 2.033 | - | - | - | 0.20 | 0.10 |
| 4 | 4.482 | - | - | - | 4.476 | 4.476 | - | - | - | −0.13 | −0.13 |
| 5 | 6.278 | - | - | - | 6.297 | 6.284 | - | - | - | 0.30 | 0.10 |
| 6 | 8.825 | - | - | - | 8.814 | 8.814 | - | - | - | −0.12 | −0.12 |
| 7 | 11.051 | - | - | - | 11.102 | 11.059 | - | - | - | 0.46 | 0.07 |
| 8 | 14.647 | - | - | - | 14.720 | 14.719 | - | - | - | 0.50 | 0.49 |
| Component | Parameter | Values |
|---|---|---|
| Solar energy panel | Length L (m) | 4, 8, 20, 32 |
| Width 2b (m) | 2 | |
| Thickness 2h (m) | 0.02 | |
| Elastic modulus of aluminum E (Pa) | 6.89 × 1010 | |
| Mass density of aluminum ρ (kg∙m−3) | 2.8 × 103 | |
| Poisson ratio μ | 0.33 | |
| Center of the rigid body | Half of the side length r0 (m) | 1 |
| The moment of inertia Jx, Jy, Jz (kg∙m2) | 100, 100, 100 | |
| The mass of the rigid body mR | 150 |
| Order | mt = 9 nt = 3 | mt = 11 nt = 5 | mt = 11 nt = 7 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ref. [14] | Method | Rt (%) | Ref. [14] | Method | Rt (%) | Ref. [14] | Method | Rt (%) | |
| 1 | 0.364 | 0.364 | 0.00 | 0.363 | 0.362 | −0.28 | 0.363 | 0.362 | −0.28 |
| 2 | 0.913 | 0.914 | 0.11 | 0.912 | 0.912 | 0.00 | 0.912 | 0.911 | −0.11 |
| 3 | 2.164 | 2.165 | 0.05 | 2.160 | 2.156 | −0.19 | 2.160 | 2.156 | −0.19 |
| 4 | 2.659 | 2.660 | 0.04 | 2.652 | 2.647 | −0.19 | 2.652 | 2.646 | −0.23 |
| 5 | 2.683 | 2.683 | 0.00 | 2.683 | 2.683 | 0.00 | 2.681 | 2.680 | −0.04 |
| 6 | 2.830 | 2.831 | 0.04 | 2.830 | 2.830 | 0.00 | 2.829 | 2.827 | −0.07 |
| 7 | 5.978 | 5.981 | 0.05 | 5.966 | 5.957 | −0.15 | 5.966 | 5.957 | −0.15 |
| 8 | 6.272 | 6.277 | 0.08 | 6.258 | 6.246 | −0.19 | 6.257 | 6.246 | −0.18 |
| Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| L = 4 | Ref. [14] | 1.420 | 2.244 | 5.781 | 5.937 | 8.592 | 9.063 | 18.863 | 18.934 |
| Method | 1.414 | 2.236 | 5.773 | 5.929 | 8.573 | 9.040 | 18.840 | 18.911 | |
| Rt (%) | −0.42 | −0.36 | −0.14 | −0.13 | −0.22 | −0.25 | −0.12 | −0.12 | |
| L = 8 | Ref. [14] | 0.363 | 0.912 | 2.160 | 2.652 | 2.681 | 2.829 | 5.966 | 6.257 |
| Method | 0.362 | 0.911 | 2.156 | 2.646 | 2.680 | 2.827 | 5.957 | 6.246 | |
| Rt (%) | −0.28 | −0.11 | −0.19 | −0.23 | −0.04 | −0.07 | −0.15 | −0.18 | |
| L = 20 | Ref. [14] | 0.062 | 0.205 | 0.354 | 0.629 | 0.957 | 1.029 | 1.163 | 1.244 |
| Method | 0.062 | 0.205 | 0.354 | 0.629 | 0.956 | 1.029 | 1.163 | 1.243 | |
| Rt (%) | 0.00 | 0.00 | 0.00 | 0.00 | −0.10 | 0.00 | 0.00 | −0.08 | |
| L = 32 | Ref. [14] | 0.025 | 0.085 | 0.142 | 0.270 | 0.377 | 0.551 | 0.637 | 0.728 |
| Method | 0.025 | 0.085 | 0.142 | 0.270 | 0.377 | 0.551 | 0.637 | 0.727 | |
| Rt (%) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Zhang, X.; Cao, D.; Hao, Y. Natural Characteristics Analysis for the Spacecraft Equipped with Constructed Cantilever Solar Panels. Actuators 2023, 12, 3. https://doi.org/10.3390/act12010003
Cao Y, Zhang X, Cao D, Hao Y. Natural Characteristics Analysis for the Spacecraft Equipped with Constructed Cantilever Solar Panels. Actuators. 2023; 12(1):3. https://doi.org/10.3390/act12010003
Chicago/Turabian StyleCao, Yuteng, Xudong Zhang, Dengqing Cao, and Yuxin Hao. 2023. "Natural Characteristics Analysis for the Spacecraft Equipped with Constructed Cantilever Solar Panels" Actuators 12, no. 1: 3. https://doi.org/10.3390/act12010003
APA StyleCao, Y., Zhang, X., Cao, D., & Hao, Y. (2023). Natural Characteristics Analysis for the Spacecraft Equipped with Constructed Cantilever Solar Panels. Actuators, 12(1), 3. https://doi.org/10.3390/act12010003







