Quantifying Uncertainties in Nonlinear Dynamics of a Modular Assembly Using the Resonance Decay Method
Abstract
1. Introduction
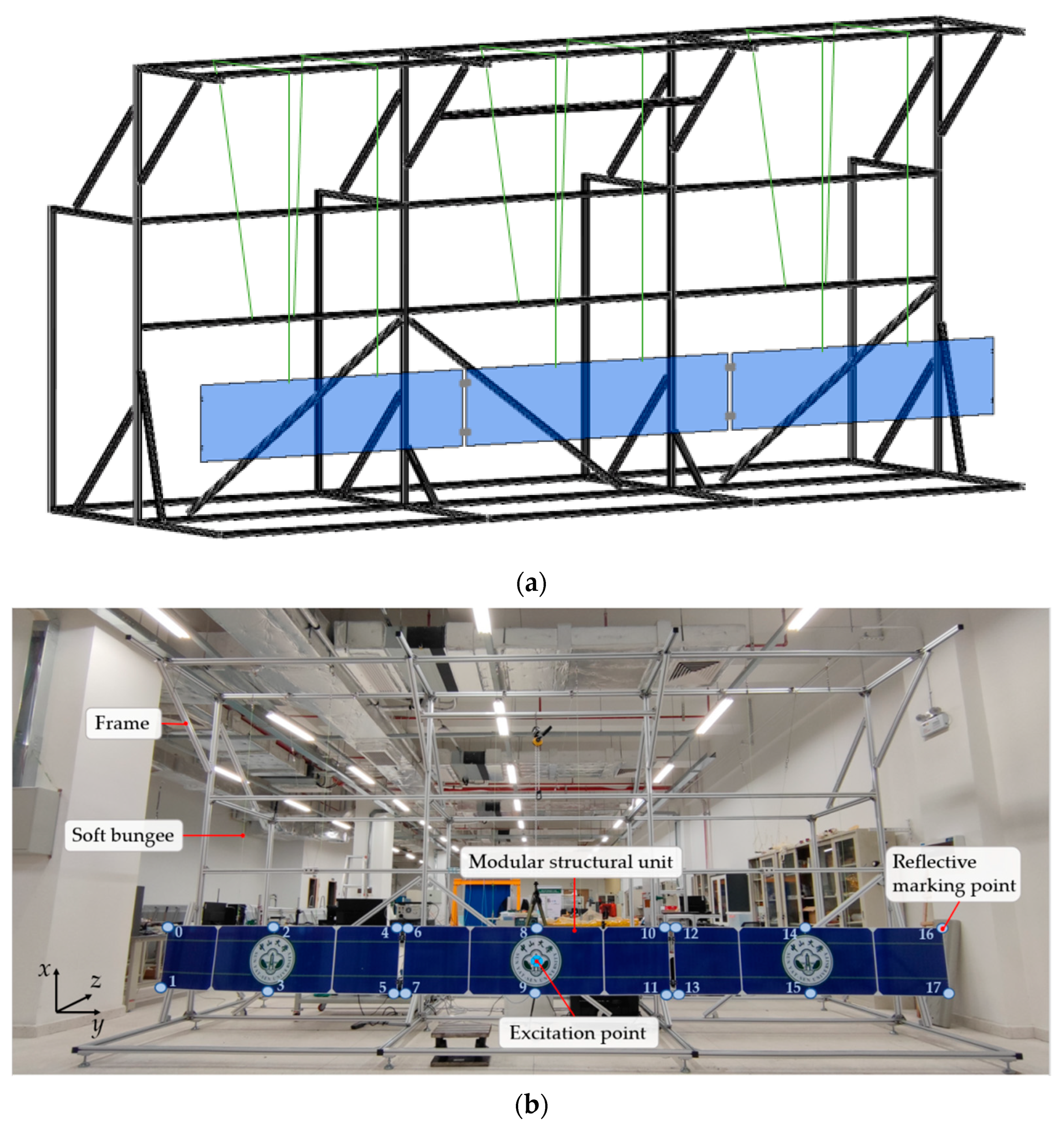
2. Ground Demonstrator of Large Structure Assembly
2.1. The Suspension Setup
2.2. The Modular Units and Joints
2.3. The Vibration Control System
2.4. The Measurement System
3. Quantification Procedure and Test Results
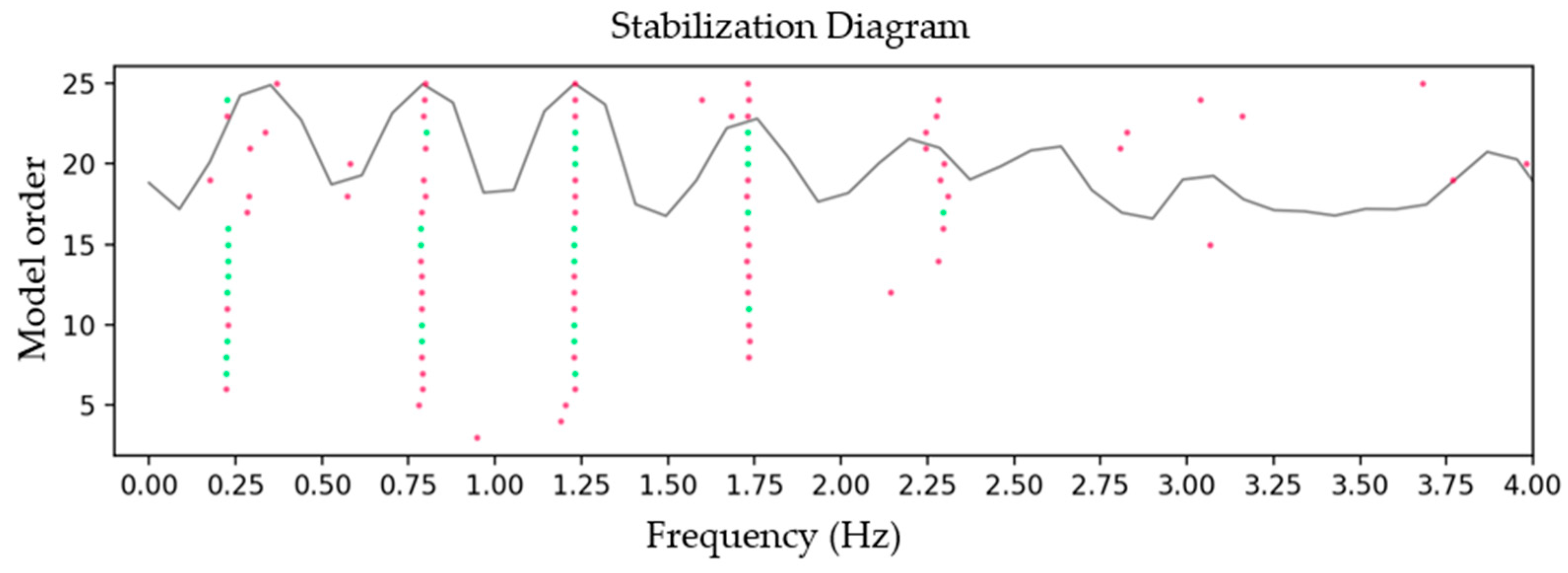
3.1. Linear Modal Survey Test
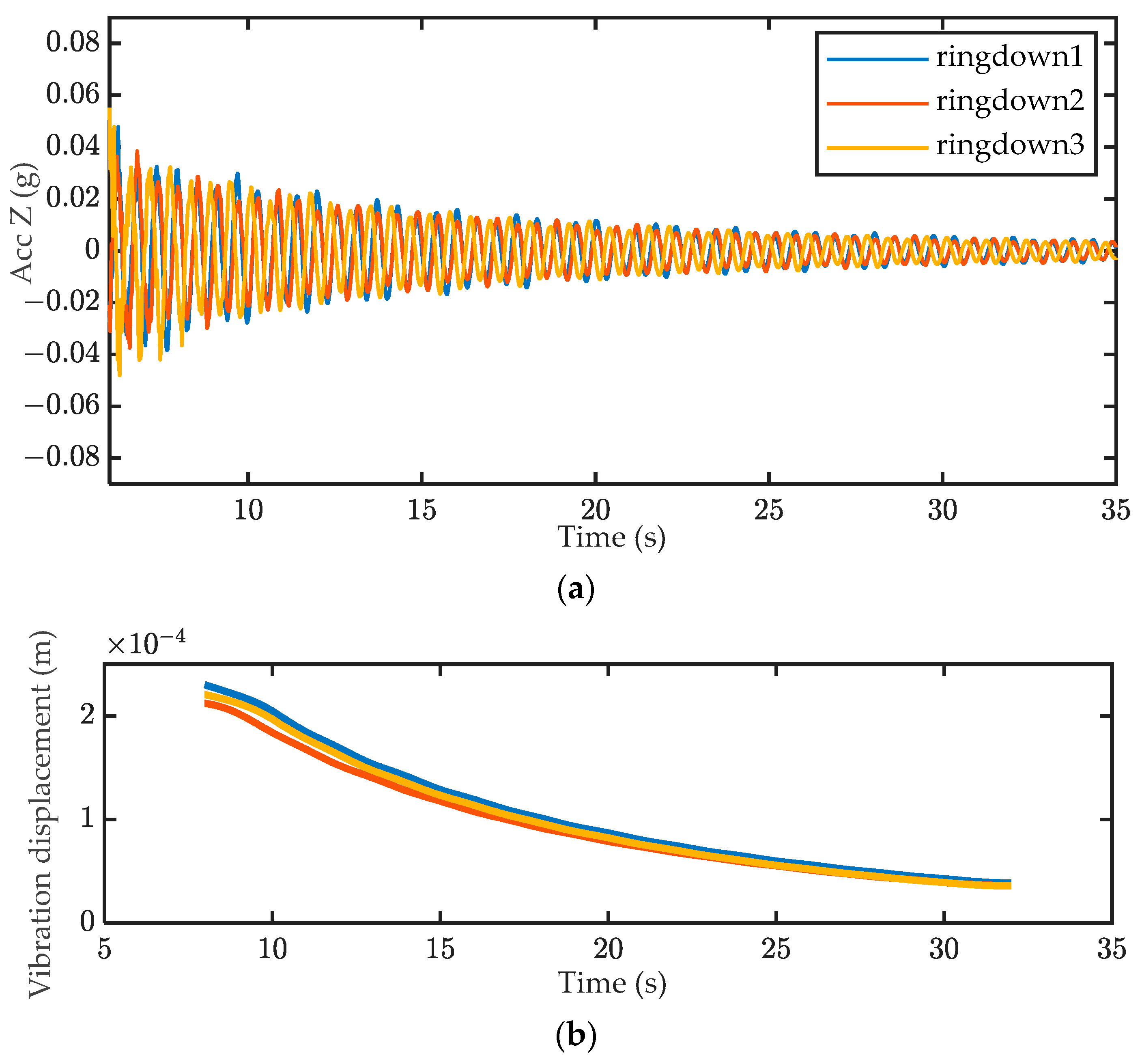
3.2. Nonlinear Resonance Decay Test
4. Conclusions
- (1)
- The proposed quantitation procedure uses backbone curves as measurement targets, which can be efficiently measured using the nonlinear resonance decay method. It is also shown that backbone curves can also accurately describe the uncertainties and nonlinearities of the assembly dynamics;
- (2)
- The modular assembly of the LSA demonstrator showed very weak stiffness nonlinearities (less than 2% softening was observed in natural frequencies), while the damping ratios varied as much as 66.7% with the vibration amplitudes. It certainly highlights the necessity of a dedicated quantification procedure for the damping nonlinearities, which cannot be identified using conventional techniques such as impact testing.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coulter, D. Beyond JWST: Future NASA Telescopes for Space and Earth Science. In Proceedings of the AIAA Space Conference, Pasadena, CA, USA, 11–13 September 2012. [Google Scholar]
- Doggett, W.R.; Teter, J.E.; Paddock, D.A.; Dorsey, J.T.; Jones, T.C.; Komendera, E.; Bowman, L.M.; Allen, B.D.; Neuhaud, J.R.; Taylor, C. Persistent assets in zero-g and on planetary surfaces: Enabled by modular technology and robotic operations. In Proceedings of the 2018 AIAA SPACE and Astronautics Forum and Exposition, Orlando, FL, USA, 15 September 2018. [Google Scholar]
- Belvin, W.K.; Dorsey, J.T.; Watson, J.J. Technology challenges and opportunities for very large in-space structural systems. In Proceedings of the International Symposium on Solar Energy from Space (Cat: No. LF99-9135), Toronto, OT, Canada, 8–10 September 2009. [Google Scholar]
- Bowman, L.M.; Belvin, W.K.; Komendera, E.; Dorsey, J.T.; Doggett, B.R. In-space assembly application and technology for NASA’s future science observatory and platform missions. In Proceedings of the Space Telescopes and Instrumentation 2018: Optical, Infrared, and Millimeter Wave, Austin, TX, USA, 6 July 2018; Volume 10698. [Google Scholar]
- Watson, J.J.; Collins, T.J.; Bush, H.G. A history of astronaut construction of large space structures at NASA Langley Research Center. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; Volume 7. [Google Scholar]
- Watson, J.J.; Heard, W.L.; Bush, H.G.; Lake, M.S.; Jensen, J.K.; Wallsom, R.E.; Phelps, J.E. Results of EVA/mobile transporter space station truss assembly tests. NASA Tech. Memo. 1988, 100661, 2–4. [Google Scholar]
- Bush, H.; Herstrom, C.; Heard, J.W.; Collins, T.; Fichter, W. Design and fabrication of an erectable truss for precision segmented reflector application. J. Spacecr. Rocket. 1991, 28, 251–257. [Google Scholar] [CrossRef]
- Doggett, W. Robotic assembly of truss structures for space systems and future research plans. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002; Volume 7. [Google Scholar]
- Rhodes, M.D.; Will, R.W.; Quach, C.C. Verification tests of automated robotic assembly of space truss structures. J. Spacecr. Rocket. 1995, 32, 686–696. [Google Scholar] [CrossRef]
- Lee, N.; Backes, P.; Burdick, J.; Pellegrino, S.; Fuller, C.; Hogstrom, K.; Kennedy, B.; Kim, J.; Mukherjee, R.; Seubert, C.; et al. Architecture for in-space robotic assembly of a modular space telescope. J. Astron. Telesc. Instrum. Syst. 2016, 2, 041207. [Google Scholar] [CrossRef]
- Karpenko, M.; Nugaras, J. Vibration damping characteristics of the cork-based composite material in line to frequency analysis. Theor. Appl. Mech. 2022, 60, 593–602. [Google Scholar] [CrossRef] [PubMed]
- Hall, D.P.; Slone, B.M.; Tobbe, P.A. Modeling and testing of docking and berthing mechanisms. In Modeling, Simulation, and Verification of Space-based Systems III, 1st ed.; Motaghedi, P., Ed.; SPIE: Kissimmee, FL, USA, 2006; Volume 6221. [Google Scholar]
- Chajec, W. Flutter calculation based on GVT-results and theoretical mass model. Aviation 2009, 13, 122–129. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, G.T. Equivalent Dynamic Stiffness Mapping technique for identifying nonlinear structural elements from frequency response functions. Mech. Syst. Signal Process. 2016, 68, 394–415. [Google Scholar] [CrossRef]
- Wang, X.; Hill, T.L.; Neild, S.A.; Shaw, A.D.; Khodaparast, H.H.; Friswell, M.I. Model updating strategy for structures with localised nonlinearities using frequency response measurements. Mech. Syst. Signal Process. 2018, 100, 940–961. [Google Scholar] [CrossRef]
- Greschik, G.; Belvin, W.K. High-fidelity gravity offloading system for free-free vibration testing. J. Spacecr. Rocket. 2007, 44, 132–142. [Google Scholar] [CrossRef]
- Sharqi, B.; Cesnik, C.E. Ground Vibration Testing on Very Flexible Aircraft. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Yu, K.P.; Zou, J.X. Dynamics of Structures, 3rd ed.; Harbin Institute of Technology Press: Harbin, China, 2015; pp. 92–95. [Google Scholar]
- Zabel, V. Operational Modal Analysis-Theory and Aspects of Application in Civil Engineering, 1st ed.; Bauhaus-Universität Weimar: Weimar, Germany, 2019; pp. 53–97. [Google Scholar]
- Brincker, R.; Andersen, P. Understanding stochastic subspace identification. In Proceedings of the 24th Conference and Ex-position on Structural Dynamics 2006 (IMAC—XXIV), St Louis, MI, USA, 30 January–2 February 2006. [Google Scholar]
- Naylor, S.; Platten, M.F.; Wright, J.R.; Cooper, J.E. Identification of multi-degree of freedom systems with nonproportional damping using the resonant decay method. J. Vib. Acoust. 2004, 126, 298–306. [Google Scholar] [CrossRef]
- Wright, J.R.; Cooper, J.E.; Desforges, M.J. Normal-mode force appropriation—Theory and application. Mech. Syst. Signal Process. 1999, 13, 217–240. [Google Scholar] [CrossRef]
- Platten, M.F.; Wright, J.R.; Cooper, J.E.; Dimitriadis, G. Identification of a nonlinear wing structure using an extended modal model. J. Aircr. 2009, 46, 1614–1626. [Google Scholar] [CrossRef]
- Londoño, J.M.; Neild, S.A.; Cooper, J.E. Identification of backbone curves of nonlinear systems from resonance decay responses. J. Sound Vib. 2015, 348, 224–238. [Google Scholar] [CrossRef]
- Feldman, M. Non-linear free vibration identification via the Hilbert transform. J. Sound Vib. 1997, 208, 475–489. [Google Scholar] [CrossRef]
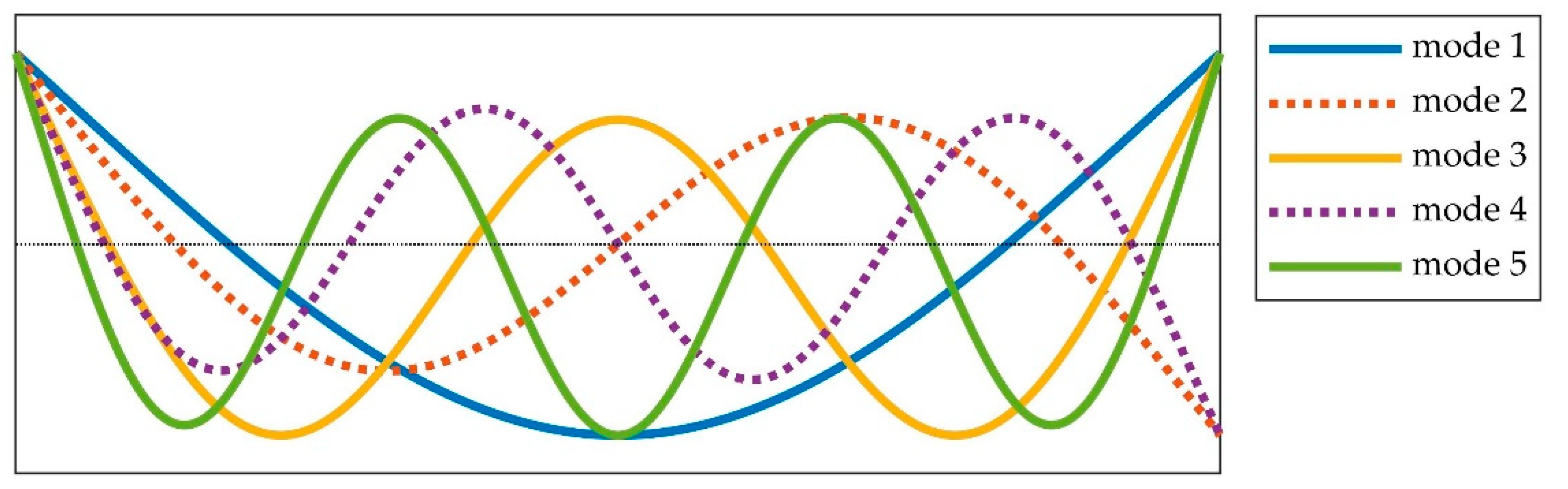




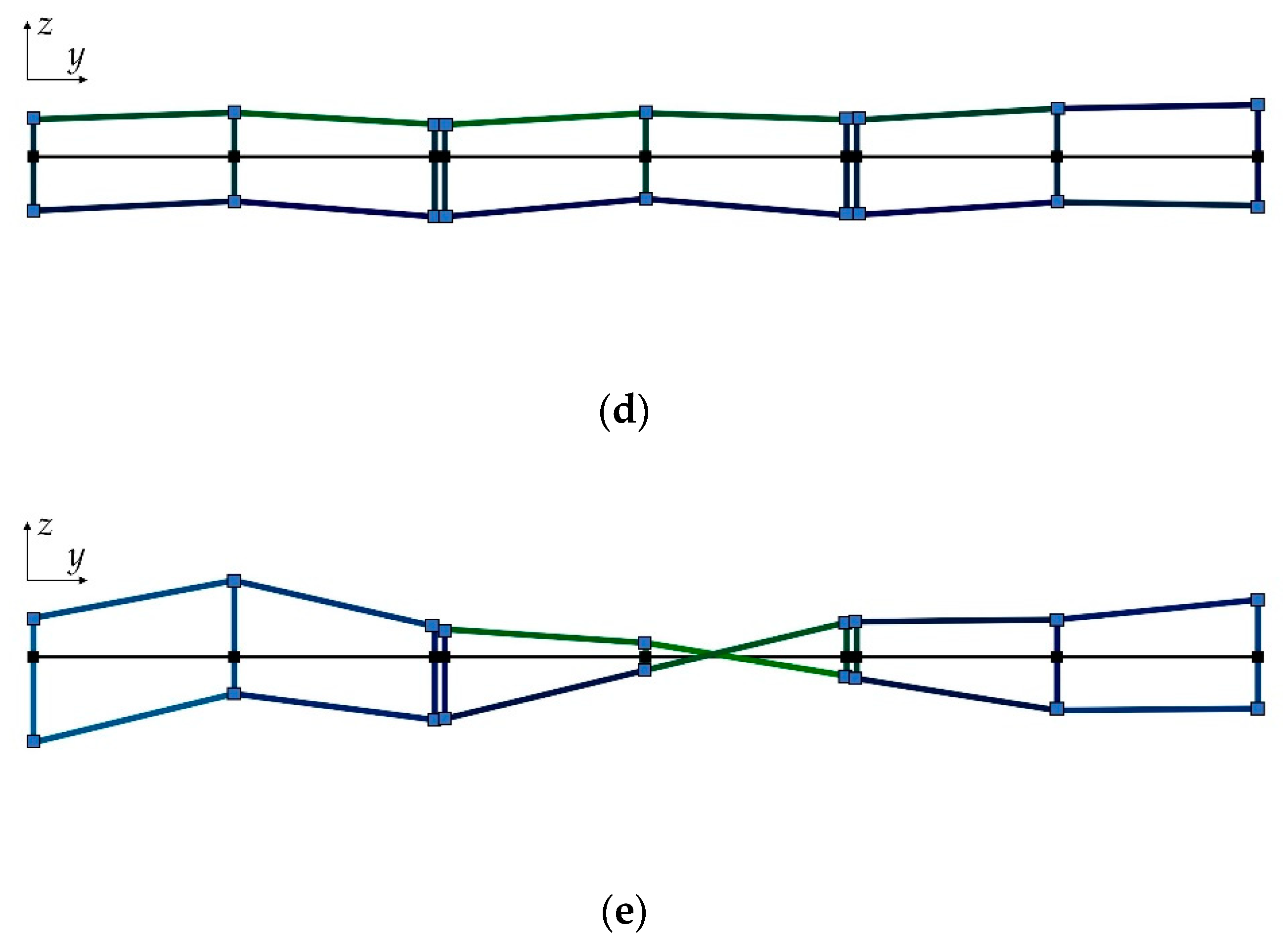
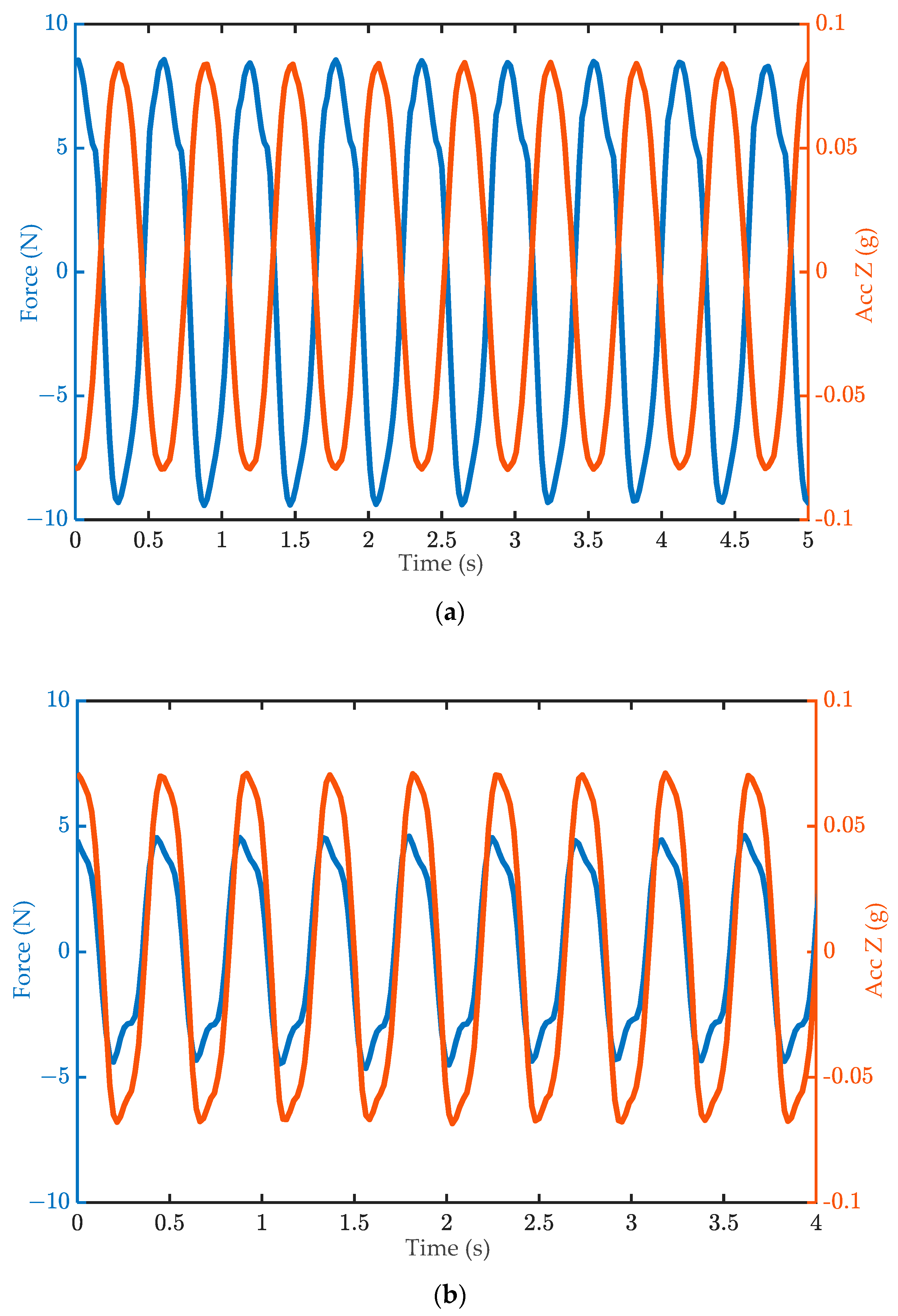
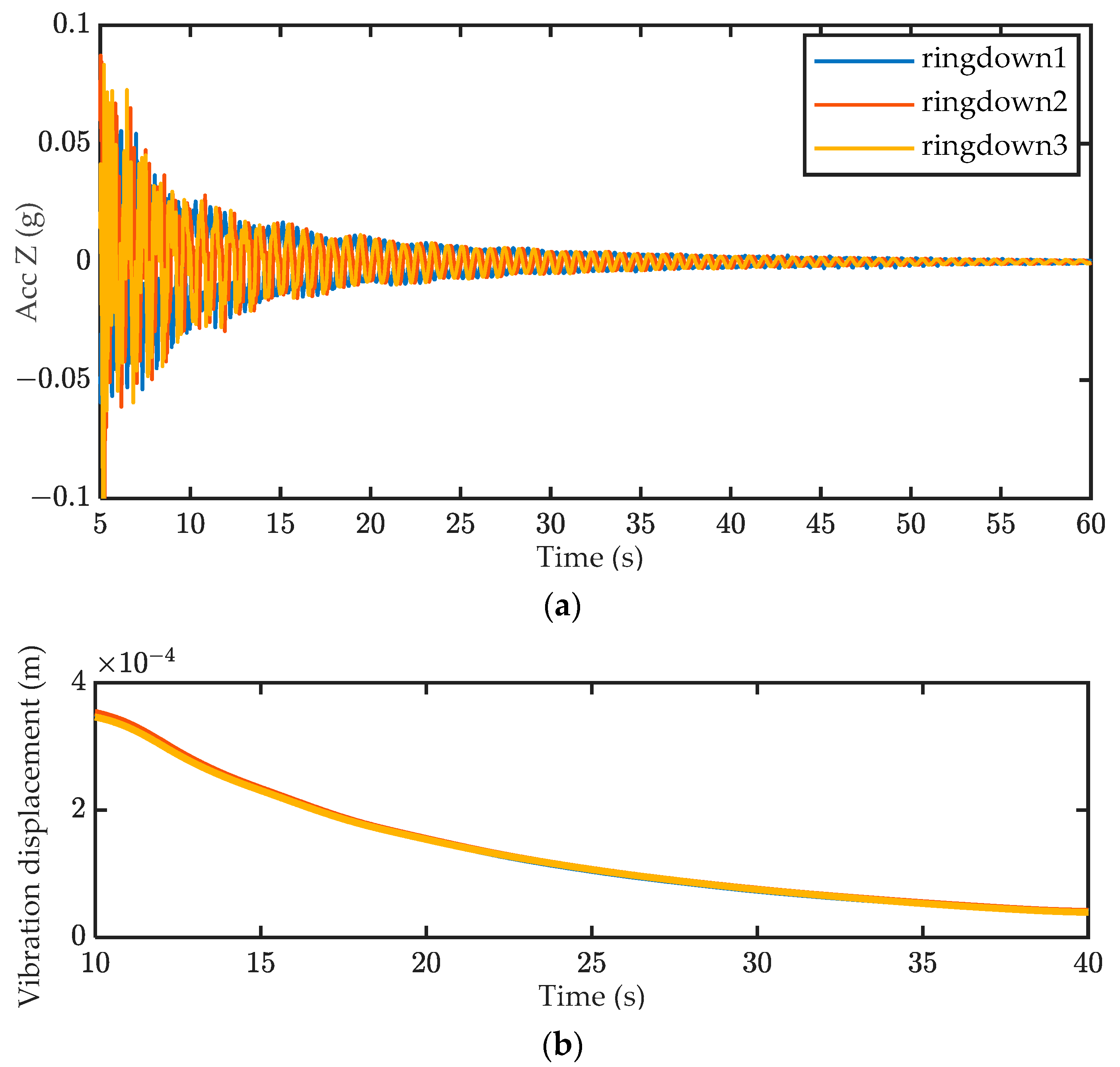
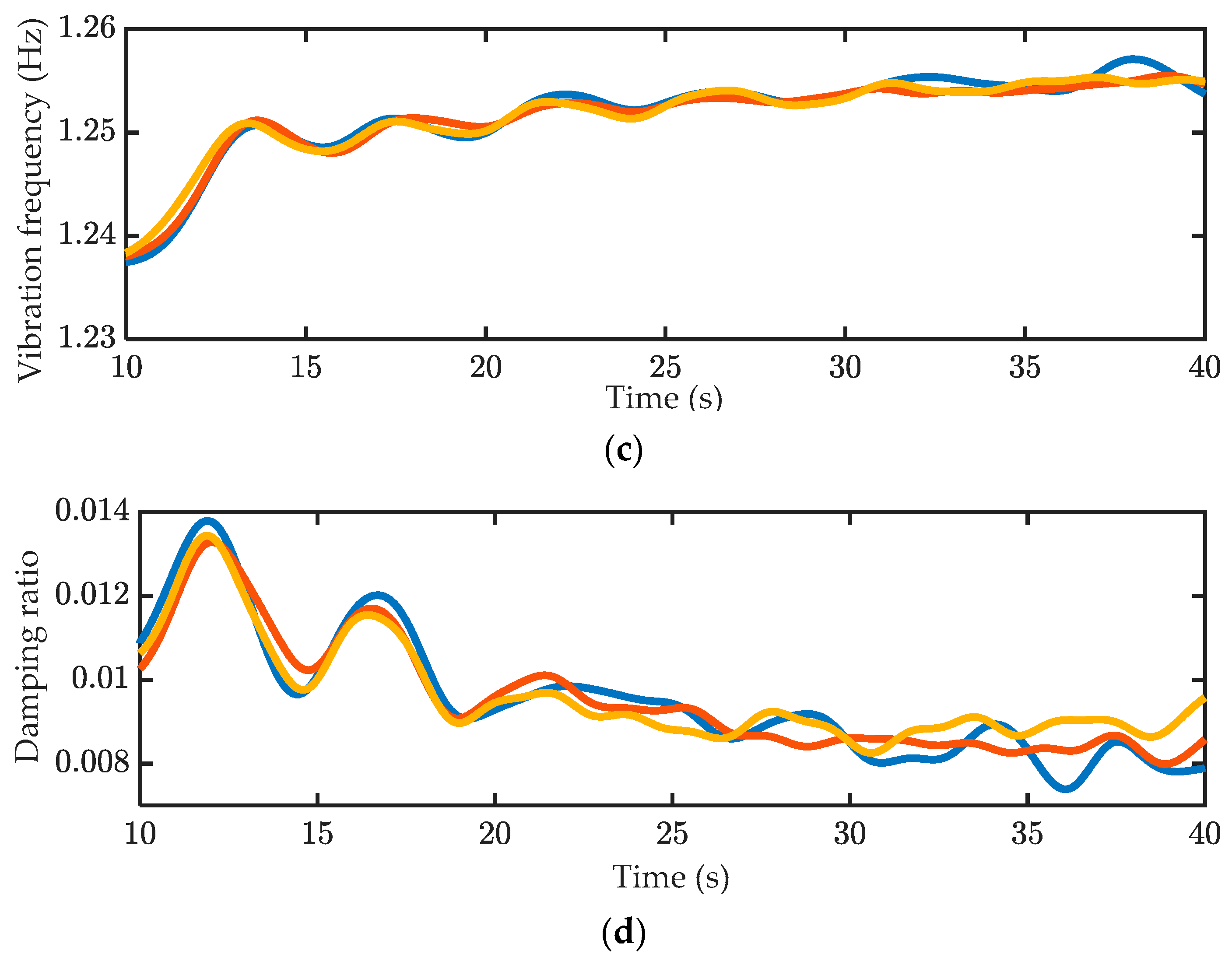



| Mode Order | Mode Shape | Theoretically Predicted Natural Frequency (Hz) |
|---|---|---|
| 1 | First bending mode | 0.29 |
| 2 | Second bending mode | 0.81 |
| 3 | Thirdbending mode | 1.59 |
| 4 | Forth bending mode | 2.63 |
| 5 | Fifth bending mode | 3.94 |
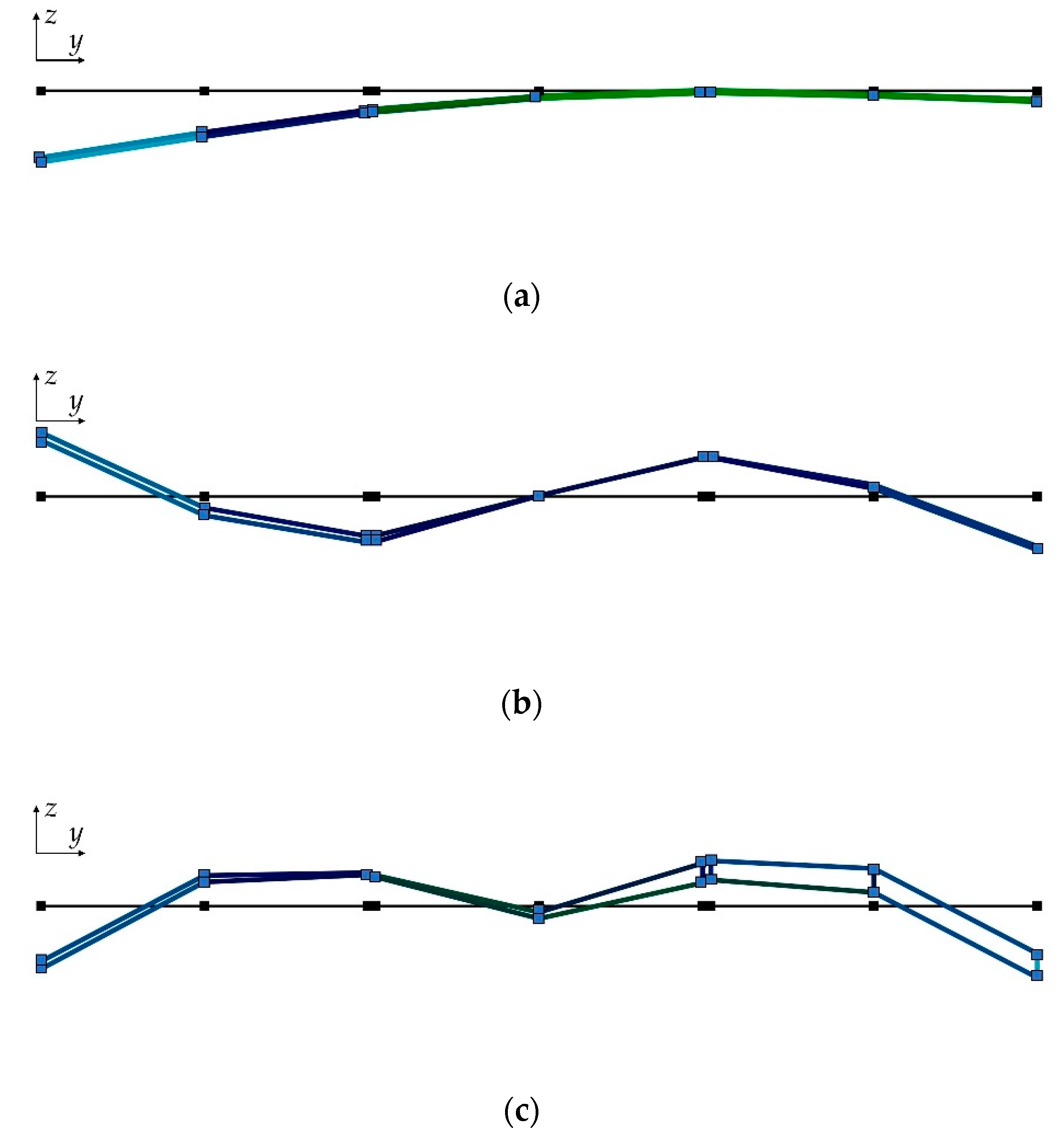
| Mode Order | Mode Shape | Natural Frequency (Hz) | Modal Damping Ratio |
|---|---|---|---|
| 1 | First bending mode | 0.23 | |
| 2 | Second bending mode | 0.80 | 1.9% |
| 3 | Third bending mode | 1.23 | 1.1% |
| 4 | First sway mode | 1.73 | 1.1% |
| 5 | First torsion mode | 2.22 | 2.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Zhao, Z.; Wang, Z.; Jiang, J.; Wu, Z.; Wang, X. Quantifying Uncertainties in Nonlinear Dynamics of a Modular Assembly Using the Resonance Decay Method. Actuators 2022, 11, 350. https://doi.org/10.3390/act11120350
Lin C, Zhao Z, Wang Z, Jiang J, Wu Z, Wang X. Quantifying Uncertainties in Nonlinear Dynamics of a Modular Assembly Using the Resonance Decay Method. Actuators. 2022; 11(12):350. https://doi.org/10.3390/act11120350
Chicago/Turabian StyleLin, Chengrong, Ziheng Zhao, Zhenyu Wang, Jianping Jiang, Zhigang Wu, and Xing Wang. 2022. "Quantifying Uncertainties in Nonlinear Dynamics of a Modular Assembly Using the Resonance Decay Method" Actuators 11, no. 12: 350. https://doi.org/10.3390/act11120350
APA StyleLin, C., Zhao, Z., Wang, Z., Jiang, J., Wu, Z., & Wang, X. (2022). Quantifying Uncertainties in Nonlinear Dynamics of a Modular Assembly Using the Resonance Decay Method. Actuators, 11(12), 350. https://doi.org/10.3390/act11120350






