Generalized Proportional Integral Observer and Kalman-Filter-Based Composite Control for DC-DC Buck Converters
Abstract
1. Introduction
- (1)
- As far as the author is concerned, this is the first opportunity to combine GPIO and KF, and solve the problem of time polynomial interference in a noisy system and successfully apply it to the system.
- (2)
- The stability of the designed controller and observer is analyzed and proven.
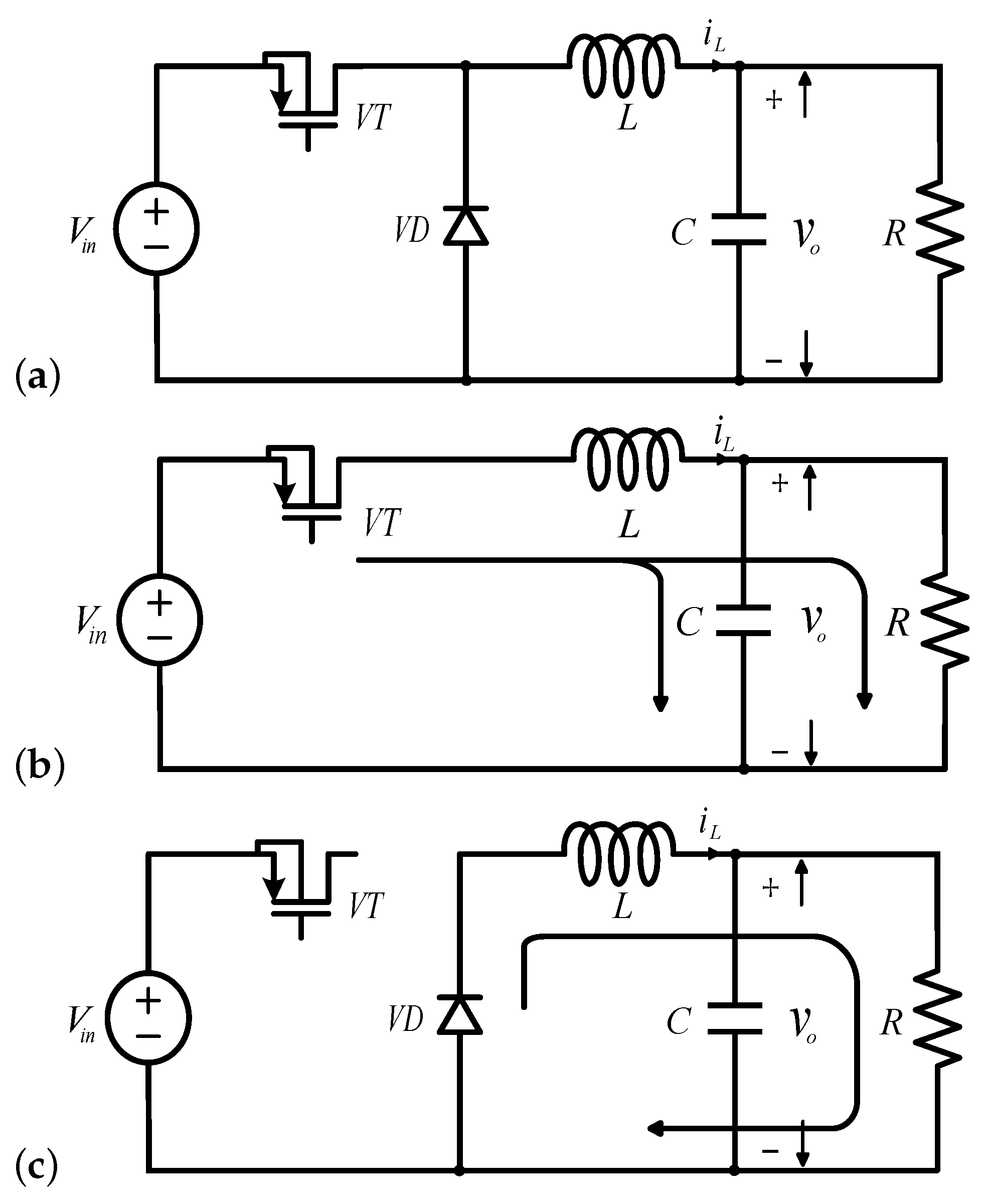
2. Modeling, Analysis, and Processing of Model
2.1. Modeling of DC-DC Buck Converter System
2.2. Analysis of Mathematical Model
2.3. Discretized Model
3. Design of the New Control Strategy (BSC + GPIO + KF) for DC-DC Buck Converter Systems
3.1. Proposed Disturbance Observer (GPIO + KF) Design
3.2. Stability Analysis of the Proposed Disturbance Observer
- (1)
- function , exists such that
- (2)
- function and a K function σ, for all , and for all exist such that:
3.3. Composite Controller Design and Analysis
4. Experimental Tests
4.1. Experimental Tests Setup
4.2. Experiment Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ESO | Extended state observer |
| GPIO | Generalized proportional integral observer |
| KF | Kalman filter |
| DOB | Disturbance observer |
| NDOB | Nonlinear disturbance observer |
| BSC | Backstepping control |
References
- Ding, S.; Liu, L.; Zheng, W. Sliding mode direct yaw-moment control design for in-wheel electric vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Sun, B.; Gao, Z. A DSP-based active disturbance rejection control design for a 1-kW H-bridge DC-DC power converter. IEEE Trans. Ind. Electron. 2005, 53, 1271–1277. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Yang, J.; Li, Q. Current sensorless sliding mode control for direct current–alternating current inverter with load variations via a usdo approach. IET Power Electron. 2018, 11, 1389–1398. [Google Scholar] [CrossRef]
- Guo, T.; Wang, Z.; Wang, X.; Li, S.; Li, Q. A simple control approach for buck converters with current-constrained technique. IEEE Trans. Control. Syst. Technol. 2017, 27, 418–425. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Wang, J.; Li, Q. Generalized proportional integral observer based backstepping control for DC-DC buck converters with mismatched disturbances. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Tehran, Iran, 25–26 January 2016. [Google Scholar]
- Alvarez-Ramirez, J.; Espinosa-Perez, G.; Noriega-Pineda, D. Currentmode control of DC-DC power converters: A backstepping approach. Int. J. Robust Nonlinear Control. 2003, 13, 421–442. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Yang, J.; Wu, B.; Li, Q. Extended state observer-based sliding mode control for PWM-based DC-DC buck power converter systems with mismatched disturbances. IET Contr. Theory Appl. 2015, 9, 579–586. [Google Scholar] [CrossRef]
- Hamed, S.; Hamed, M.; Sbita, L. Robust voltage control of a buck DC-DC converter: A sliding mode approach. Energies 2022, 15, 6128. [Google Scholar] [CrossRef]
- Mobayen, S.; Bayat, F.; Lai, C. Adaptive global sliding mode controller design for perturbed DC-DC buck converters. Energies 2021, 14, 1249. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, J.; Li, S.; Wu, B.; Qian, C. Robust control for PWM-based DC-DC buck power converters with uncertainty via sampled-data output feedback. IEEE Trans. Power Electron. 2015, 30, 504–515. [Google Scholar] [CrossRef]
- Lin, P.; Zhang, C.; Wang, P.; Xiao, J. A decentralized composite controller for unified voltage control with global system large-signal stability in DC microgrids. IEEE Trans. Smart Grid 2019, 10, 5075–5091. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, S.; Hui, S. Adaptive reference model predictive control with improved performance for voltage-source inverters. IEEE Trans. Control Syst. Technol. 2018, 26, 724–731. [Google Scholar] [CrossRef]
- Yang, J.; Wu, B.; Li, S.; Yu, X. Design and qualitative robustness analysis of an dobc approach for dc-dc buck converters with unmatched circuit parameter perturbations. IEEE Trans. Circuits Syst. I-Regul. Pap. 2016, 63, 551–560. [Google Scholar] [CrossRef]
- Choi, K.; Dong, S.; Kim, S. Disturbance observer-based offset-free global tracking control for input-constrained LTI systems with DC/DC buck converter applications. Energies 2020, 13, 4079. [Google Scholar] [CrossRef]
- Ghosh, R.; Narayanan, G. Generalized feedforward control of singlephase PWM rectifiers using disturbance observers. IEEE Trans. Ind. Electron. 2007, 54, 984–993. [Google Scholar] [CrossRef]
- Lakomy, K.; Madonski, R.; Dai, B. Active disturbance rejection control design with suppression of sensor noise effects in application to DC–DC buck power converter. IEEE Trans. Ind. Electron. 2022, 69, 819–824. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Lu, J.; Savaghebi, M.; Ghias, A. A reduced-order generalized proportional integral observer-based resonant super-twisting sliding mode control for grid-connected power converters. IEEE Trans. Ind. Electron. 2021, 68, 5897–5908. [Google Scholar] [CrossRef]
- Sira-Ramirez, C.; Nunez, A.; Visairo, N. Robust sigma-delta generalised proportional integral observer based control of a buck converter with uncertain loads. Int. J. Control 2010, 83, 1631–1640. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference (ACC), Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Prasov, A.; Khalil, H. A nonlinear high-gain observer for systems with measurement noise in a feedback control framework. IEEE Trans. Autom. Control. 2013, 58, 569–580. [Google Scholar] [CrossRef]
- Pu, Z.; Yuan, R.; Yi, J.; Tan, X. A class of adaptive extended state observers for nonlinear disturbed systems. IEEE Trans. Ind. Electron. 2015, 62, 5858–5869. [Google Scholar] [CrossRef]
- Bai, W.; Xue, W.; Huang, Y.; Fang, H. On extended state based kalman filter design for a class of nonlinear time-varying uncertain systems. Sci. China Inf. Sci. 2018, 61, 042201-1–042201-16. [Google Scholar] [CrossRef]
- Xue, W.; Bai, W.; Yang, S.; Song, K.; Huang, Y.; Xie, H. ADRC with adaptive extended state observer and its application to air-fuel ratio control in gasoline engines. IEEE Trans. Ind. Electron. 2015, 62, 5847–5857. [Google Scholar] [CrossRef]
- Sun, H.; Madonski, R.; Li, S.; Zhang, Y.; Xue, W. Composite control design for systems with uncertainties and noise using combined extended state observer and kalman filter. IEEE Trans. Ind. Electron. 2022, 69, 4119–4228. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, Y. Input-to-state stability for discrete-time nonlinear systems. Automatica 2001, 37, 857–869. [Google Scholar] [CrossRef]




| Description | Parameters | Nominal Values |
|---|---|---|
| Input voltage | 20 V | |
| Reference voltage | 9 V | |
| Inductance | H | |
| Capacitance | F | |
| Load resistance |
| Controllers | Observers | Experimental Parameters |
|---|---|---|
| BSC | GPIO | , , |
| BSC | ESO + KF | , , |
| BSC | GPIO + KF | , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, P.; Sun, H. Generalized Proportional Integral Observer and Kalman-Filter-Based Composite Control for DC-DC Buck Converters. Actuators 2023, 12, 20. https://doi.org/10.3390/act12010020
Qiao P, Sun H. Generalized Proportional Integral Observer and Kalman-Filter-Based Composite Control for DC-DC Buck Converters. Actuators. 2023; 12(1):20. https://doi.org/10.3390/act12010020
Chicago/Turabian StyleQiao, Pengyu, and Hao Sun. 2023. "Generalized Proportional Integral Observer and Kalman-Filter-Based Composite Control for DC-DC Buck Converters" Actuators 12, no. 1: 20. https://doi.org/10.3390/act12010020
APA StyleQiao, P., & Sun, H. (2023). Generalized Proportional Integral Observer and Kalman-Filter-Based Composite Control for DC-DC Buck Converters. Actuators, 12(1), 20. https://doi.org/10.3390/act12010020






