Abstract
In this study, a novel control framework is proposed to improve the tracking performance of uncertain marine vessels which work in enhanced sea states. The proposed control strategy is based on incorporating a fixed-time nonlinear disturbance observer (FTNDO) in a fixed-time convergent backstepping control. More specifically, the FTNDO is developed to reconstruct the total uncertainties due to the system uncertainty and unknown time-varying exterior disturbances. In comparison with the existing disturbance observers, the FTNDO guarantees that the estimation errors will converge to the origin within a predefined time even if the initial estimation errors tend toward infinity. This feature is quite important in the closed-loop system stability analysis as the separation principle does not hold in nonlinear systems. Besides, it does not require the restricting assumption that the upper bound of the lumped uncertainty or its time derivative has to be bounded or known. A backstepping control with a compensation control part is then designed to make the tracking errors converge to the origin within a finite time regardless of initial tracking errors. The compensation control is developed by means of the estimated signal and applied to totally reject the total uncertainty. The global fixed-time stabilization of the closed-loop system is investigated through the Lyapunov stability criterion. Numerical simulation results conducted on an uncertain marine surface vessel confirm the superior control performance and efficiency of the planned method in comparison with the existing disturbance observer-based tracking control strategies.
1. Introduction
Over the past several years, modern control strategies have been widely applied to marine surface vessels’ motion control due to their significant roles in numerous applications including transportation, maritime rescue, ocean exploration, oil harvesting, and so forth [1,2,3,4,5]. Due to the presence of marine surface vessels in a harsh ocean environment, the tracking control system development encounters a serious challenge as a result of complex uncertainties and disturbances such as ocean winds, waves and currents [6,7,8,9,10,11]. Therefore, to acquire the favorable performance of the system, numerous effective control approaches have been presented. A linear control scheme was used for tracking control for the marine surface vessels. For instance, in [12,13], the LQR control law as an optimal control strategy has been designed for tracking control of the marine surface vessels. Then, because of the highly nonlinear characteristics of the marine surface vessels, various nonlinear control approaches have been employed. In recent years, model predictive control (MPC) has been utilized to design optimal control schemes for marine surface vessels [14]. The principal drawback of the MPC is that it demands a high computational burden. A PID controller which demands less computational burden has been presented in [15]. Although the PID controller has a simple structure, its performance deteriorates if the magnitude of the external disturbance is large. As a nonlinear robust control, the well-known sliding mode control (SMC) has been utilized in surface vessels’ tracking control problems to enhance the robustness of the control system against uncertain dynamics and unknown disturbance [16,17]. Moreover, the backstepping control method has been introduced to drive the system states of the vessel to zero [18]. Despite the relatively simple design procedure of conventional backstepping control, it cannot provide fast convergence and suitable robustness against the total uncertainty. Therefore, the performance of the system would not be satisfactory.
To enhance the control performance, the finite-time control notion has been introduced due to its inherent advantages such as rapid convergence speed, improved tracking precision, and high disturbance rejection ability [19,20,21]. This concept has been extensively used in various applications such as robotic manipulators [22,23], spacecraft attitude systems [24], multi-agent systems [25], guidance systems [26], etc. This control technique has attracted the attention of many researchers and different finite-time controls for marine surface vessels have been proposed [27,28], just to name a few. The work in [27] studies the adaptive finite-time formation control problem of multiple marine surface vessels in the existence of the actuator faults, uncertainty and exterior disturbance. Introducing an integral SMC, the issue of time-varying formation control for multiple marine surface vehicles subject to actuator saturation and fault has been studied in [28]. By a combination of finite-time convergent disturbance observer and backstepping control, the problem of path-following control for underactuated surface vessels in the presence of unknown external disturbances, deviation of vessel model parameters and actuator saturation has been studied in [29]. Using a novel piecewise function, a tracking control for underactuated marine surface vessels in the existence of uncertainty and unknown disturbances has been developed in [30]. Despite the interesting property of finite-time control in providing fast and accurate convergence, the settling time of the system is directly related to the initial conditions, i.e., the larger the initial conditions, the larger the convergence time [31]. The concept of fixed-time stability guarantees that the system states converge to zero within a fixed time even if the initial condition approaches infinity [32]. In order to provide fixed-time tracking with high accuracy for marine surface vessels subject to actuator faults and uncertainties, the authors in [33] presented an innovative control framework using a mixture of a new bounding function and an approach to handling constraints. Considering actuator dead-zones, a switching control law with fixed-time convergence for marine surface vessels has been proposed in [34]. The concept of bi-limit homogeneous theory has been used in [35] to develop a fixed-time SMC law guaranteeing fast and accurate convergence for marine surface vessels with uncertainty and an unknown external disturbance.
Considering the tracking control of a marine surface vessel, the tracking performance can be attenuated in the presence of the total uncertainty which is basically composed of the system’s uncertainty as well as environmental disturbances. Although neural networks [36] and fuzzy logic systems [37] could approximate uncertainty, a large number of parameters and rules are required to be considered and a high computational burden is required. An alternative method for rejecting the lumped uncertainty has been developed through disturbance observers. In [38], an active disturbance rejection control scheme has been designed for marine surface vessels with external disturbances so that better estimation and tracking control performance can be obtained by the disturbance compensation control. Although effective, most of the existing disturbance observers can only guarantee that the errors converge to the origin as time tends to infinity. Based on the geometric homogeneity approach, a disturbance observer-based tracking control strategy with guaranteed finite-time convergence and accurate tracking performance for autonomous surface vehicles has been developed in [39]. A disturbance observer-based control based on the backstepping method has been designed in [40]. By combining two nonlinear control techniques, backstepping and variable structure control, a disturbance observer-based control with finite-time convergence for uncertain marine surface vessels has been presented in [41]. A new disturbance observer-based control strategy with a fixed-time convergence rate has been developed in [42]. However, in this work, there is a strict assumption that the upper bound of the time-derivative of lumped uncertainty should be bounded and known. In order to estimate lumped uncertainties and unmeasured velocities, an extended state observer with fixed-time convergence has been developed in [43]. Despite the better performance of this work compared to [42], the limiting assumption in [42] still exists.
This paper aims at proposing a nonlinear disturbance observer-based tracking control with fixed-time convergence for uncertain marine surface vessels. The most important innovations of this work are stated as follows:
- Compared to the existing nonlinear disturbance observers [31,32,33,34,35,36], the suggested disturbance observer provides fixed-time convergence of the estimation error without needing any restriction on the lumped uncertainties. The observer provides an accurate estimate of the total uncertainty within a finite time even if the initial estimation error approaches infinity.
- Based on the reconstructed uncertainties, a fixed-time convergent backstepping control approach is designed which ensures that the tracking errors of the marine surface vessel converge to the origin within a finite time which is regardless of the initial states. Indeed, the convergence time of the closed-loop system can be selected a priori.
The remainder of this research is arranged as follows: in the next section, the required preliminaries, problem formulation and control objectives are stated. The main outcomes are given in Section 3, in which a fixed-time disturbance observer-based backstepping control for uncertain marine surface vessels is established to realize the high-accurate control. Lastly, simulations and conclusions are provided in Section 4 and Section 5, correspondingly.
Notations: Euclidean norm of a vector is denoted by . For a vector and a positive constant , is defined where signifies the sign function. Moreover, is a cross-product matrix as . It is worth mentioning that the function is not a discontinuous function. In Figure 1, this function for has been compared with the functions , and . As can be seen, the function is continuously differentiable.
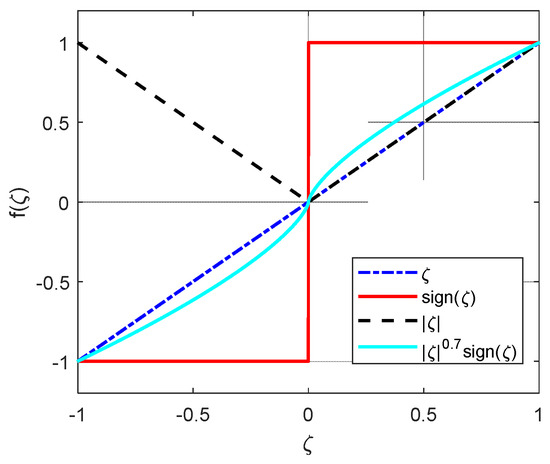
Figure 1.
Comparison with and the functions , and .
2. System Description
2.1. Mathematical Model of a Surface Vessel
Two important coordinate systems are usually utilized for marine surface vessels, i.e., the earth-fixed inertial frame and the body-fixed frame . Generally, 6 independent variables, that is, surge, sway, heave, roll, pitch, and yaw are utilized to represent vessels’ motion which includes rotation and translation. Nevertheless, due to the fact that the motion in heave, roll, and pitch axes are inherently stable in most of the vessels, a 6-DOF control issue of vessels could be converted into a 3-DOF control in surge, sway, and yaw only. Therefore, the kinematics and dynamics equations of a surface vessel are described by [44]
in which where and signify the position and heading, respectively. are the corresponding linear velocities in surge, sway, and the angular velocity in yaw. The vectors and d refer to control input and total uncertainties due to the system uncertainty and unknown and time-varying exterior disturbances, respectively. In (1), is the Jacobian matrix and it is defined as . The inertia, the Coriolis and centripetal acceleration, the damping matrices, and the vector of gravitational/buoyancy forces and moments are, respectively, denoted by , , and , and they are given as
where , , , and
where and are hydrodynamic parameters.
Because of physical restrictions on the actuator, the control input is restricted by a saturation value. Indeed, is the vector of actual control input produced by the actuators and denotes the saturation expressed as
where
where is the maximum allowed value of ith control input. The excess term of the constrained saturation is given by in which and is a positive constant.
By simple algebraic manipulations, the open-loop dynamical system (1) and (2) can be written as [44]
where
with and .
Defining new variables as and , the dynamical system (9) can be rewritten as
where , and .
2.2. Control Purpose
The main control purpose of this study is to provide a nonlinear disturbance observer for the uncertain system (13) and (14) such that the lumped uncertainties are reconstructed within a finite time which is regardless of the initial estimation error. It should be pointed out that no prior knowledge regarding the lumped uncertainties is needed, in contrast to the existing nonlinear observer frameworks for the surface vessels [42,43]. According to the estimated uncertainties, a fixed-time backstepping control is then designed to improve the convergence rate of the tracking error to zero.
3. Results
3.1. Conventional Disturbance Observer
In (14), the unknown lumped uncertainty can considerably deteriorate the control performance. In what follows, we present the design procedure for conventional as well as finite-time disturbance observers for marine surface vessels.
Let us define an auxiliary function as
in which represents a function defined by the designer. It is worth mentioning that it is defined such that its derivative with respect to is positive definite. The time-derivative of is expressed by
where . The estimation of can be obtained as
The following disturbance observer is then designed to reconstruct the total uncertainty
Taking time derivative of gives
where the estimation error is represented by . Next, the dynamics of estimation error can be calculated as
Construct a Lyapunov functional as . Differentiating it with respect to time yields.
Since the function can be selected to be positive definite, the estimation error will be asymptotically stable if the time-derivative of the total uncertainty converges to zero.
Remark 1:
To deal with the limitation of the disturbance observer, a novel finite-time disturbance observer has been proposed in [42] which is only according to the assumption that the time-derivative of the total uncertainty is bounded and known. Though, due to the complex structure of the lumped uncertainty, this assumption is also difficult to satisfy.
Remark 2.
Although the finite-time observer [42] guarantees that the estimation error converges to zeros within a finite time, the convergence time increases when the initial condition is large.
3.2. Design of Fixed-Time Nonlinear Disturbance Observer
To overcome the limitations of the conventional and finite-time disturbance observers and to guarantee that the estimation error converges to the origin in a fixed time regardless of initial conditions, a fixed-time nonlinear observer is provided in this section.
The dynamical system (24) can be rewritten in the subsequent form:
where and is a positive constant. For this system, we construct the following auxiliary system
where is the state of system (23). The discrepancy between the auxiliary system and the original one is defined by
The dynamical equation of (24) can be easily obtained as
Besides, the output of the system (25) is given as where is a positive constant.
Theorem 1.
Consider dynamical system (1) and (2). The lumped uncertainty can be estimated within a fixed time if the following nonlinear observer is applied.
where denotes estimation of , are positive constants, , and is the observer error.
Proof.
The dynamics of the estimation error are obtained as
Construct a Lyapunov function as
Then,
According to the fixed-time stability theorem [32], it can be concluded that the observer error converges to zero within a finite time which is independent of the initial estimation error. □
Remark 3.
It should be denoted that the offered fixed-time disturbance observer framework does require the lumped uncertainty to satisfy any assumption. However, for the existing disturbance observers for marine surface vessels, the upper bound of the lumped uncertainties should converge to zero [42] or it should be bounded and known [39,41,42,43]. Due to the complex structure of the lumped uncertainties, this assumption is significantly tough to satisfy.
Theorem 2.
Suppose that an estimation scheme is defined as
where . The total uncertainty will be reconstructed by in a finite time which is regardless of initial estimation error.
Proof.
Defining , one has
In light of Theorem 1, is obtained. Thus, converges to origin within a finite time and the lumped uncertainty is precisely reconstructed by . □
Remark 4.
It should be noted that included in the observer (17) is needed to implement the suggested methodology. To fulfill this requirement, the following robust uniform exact differentiator (RUED) [45] is utilized to obtain the exact fixed-time estimation of through entering into the RUED
where , and are positive parameters. The states and converge to and its time derivative within a fixed time which only depends on the , and .
3.3. Design of Fixed-Time Trajectory Tracking Control
Despite the fact that there are numerous tracking control techniques for surface vessels, they cannot satisfy that the tracking error will converge to the origin within a finite time which is regardless of initial states. In this section, based on the reconstructed lumped uncertainty, a backstepping trajectory tracking control scheme with fixed-time convergence for the marine surface vessel is developed.
Step 1: Let us define tracking error as
The time-derivative of the tracking error results in
where denotes the virtual control and is defined as
in which , and are positive gains.
Step 1: In the second step of the design, the discrepancy between the virtual control and the state is stated as
The dynamics of the error signal can be obtained as
Define a positive-definite Lyapunov candidate functional as
Differentiating with respect to time gives
We design the final control input by
in which is the estimation of and are positive gains.
Theorem 3.
Consider the dynamical system (1) and (2). If the total uncertainty is reconstructed by the nonlinear disturbance observer (26), then the control law (39) guarantees that the trajectory tracking errorsandwill converge to zero in a finite time that does not depend upon the initial states.
Proof.
If the control input (39) is substituted into (38), one has
where . Based on the fixed-time stability concept [32], it is confirmed that the tracking errors converge to the origin and the closed-loop system is fixed-time stable. The proof is ended here. □
Remark 5.
Compared to the existing backstepping controls with finite convergence time for marine surface vessels, the proposed backstepping control provides a faster convergence rate such that the settling time of the closed loop system is fixed and regardless of the initial conditions.
Remark 6.
For the proposed method implantation, the control parameters are required to be suitably selected in order to acquire superior tracking accuracy and acceptable control effort. The following points should be considered for selecting the control gains.
- Larger leads to a quicker convergence speed; however, large overshoots and more control energy consumptions result. Thus, a compromise needs to be made between the converging speed and the overshoot.
- Based on the definition of fixed-time stability, the gains are also important to determine the system’s converging rate. To be more exact, larger and smaller result in a smaller convergence time; however, they can increase the required control effort as well.
- According to the reasons given for selecting the control gains, the larger and and smaller make the estimation error converge to zero during a smaller time. However, noise enhancement can result.
Remark 7.
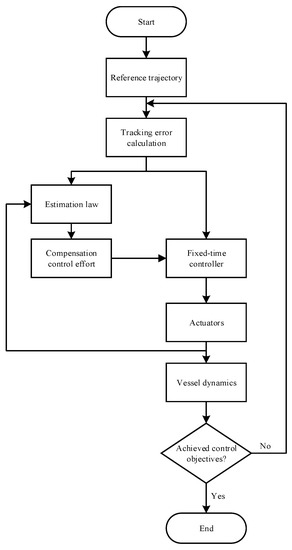
The control sequence of the suggested fixed-time disturbance observer-based tracking control scheme could be given through the flowchart depicted in Figure 2.

Figure 2.
Flow chart of the Fixed-DOTC for vessels.
4. Simulation Results
In order to evaluate the efficacy of the proposed fixed-time disturbance observer-based tracking control (denoted by FTDOBTC), a simulation study will be carried out in this section. The parameters of a surface vessel are selected from [2,3,46] and given as
where the total uncertainty which is the combination of the model uncertainty acting on the dynamics and time-varying external disturbance is given as where , , and . The total uncertainty is composed of some sinusoidal terms which are functions of time indicating ocean currents, waves (wind-generated), and wind and some terms which are functions of the system states stemming from the model uncertainties. The considered vessel is supposed to follow the following trajectory The initial condition is taken as and . The proposed control scheme is composed of two parts: the fixed-time observer (26) and the fixed-time controller (39). Based on the instruction given in Remark 6, the observer and the controller gains are selected as , , , , , , , , , , , and . The simulation results are provided in three parts.
Part 1: In this part, we are about to evaluate two main achievements of the suggested fixed-time disturbance observer-based tracking control (Fixed-DOTC) framework, that is, the fixed-time convergence of estimation error as well as the tracking errors. To this end, the control laws in (24) and (37) presented in [18] are simulated under the same conditions (the model parameters, initial conditions, uncertainty and disturbance). As can be seen in Figure 3 and Figure 4, the estimation errors under the Fixed-DOTC converge to zero within a fixed time and the total uncertainty is precisely reconstructed. Thus, Theorem 1 is verified. The position trajectory following the result can be seen in Figure 5a,b. It is further observed in Figure 6 and Figure 7 that the Fixed-DOTC achieves faster and more accurate convergence compared to the control laws in (24) and (37) in [18]. To be more exact, Fixed-DOTC only needs 2.5 s to drive the error trajectories to zero, whereas the control laws in (24) and (37) require approximately 20 and 8 s, respectively. The control inputs for the three controllers are illustrated in Figure 8. Although the Fixed-DOTC obtains much better control performance, it requires less control effort which is quite important from a practical point of view.
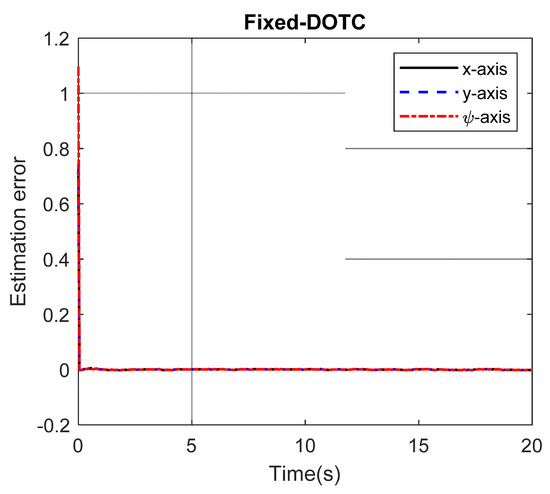
Figure 3.
The estimation errors under the Fixed-DOTC in part 1.
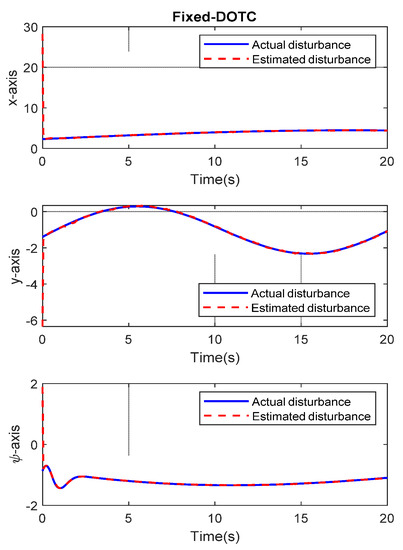
Figure 4.
The actual total uncertainty and its estimation under the Fixed-DOTC in part 1.
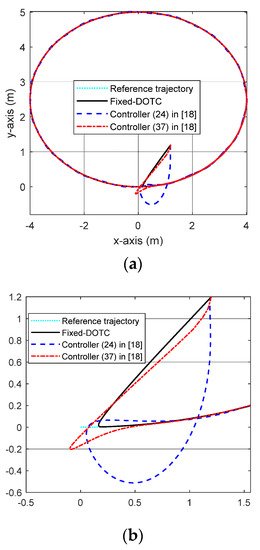
Figure 5.
The actual position trajectory and the desired position trajectory in part 1; (a) the whole trajectories, (b) zoom of the trajectories at the beginning.
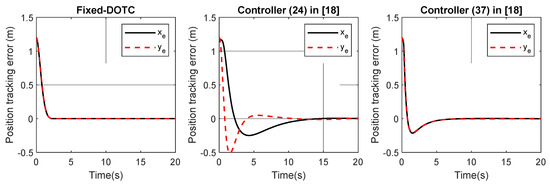
Figure 6.
The position tracking errors in part 1.
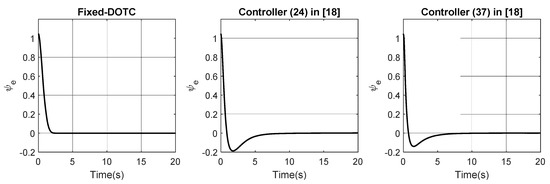
Figure 7.
The orientation tracking error in part 1.
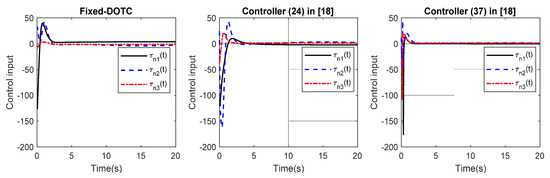
Figure 8.
The control input in part 1.
Part2: As can be seen in Figure 8, the amplitude of the control inputs is quite large. Here, we consider the actuator saturation to be 40 N for the surge force and the sway force, and 40 Nm for the yaw moment. Since the controller (24) did not show a good performance, in this part, we only compare the Fixed-DOTC with the controller (37). Moreover, the procedure of considering the actuator saturation is applied to the controller (37) to make a fair comparison. Figure 9 shows that the Fixed-DOTC is able to drive the vessel to the reference trajectory. More specifically, Figure 10 and Figure 11 depict the position and orientation tracking errors under both controllers. It is observed that the transient response of the error trajectory under the controller (37) is more deteriorated than the proposed one when the actuator saturation is taken into account. As is expected and seen in Figure 12, the maximum control input does exceed the allowable limit and the control objectives are achieved in the presence of the actuator’s physical limitations.
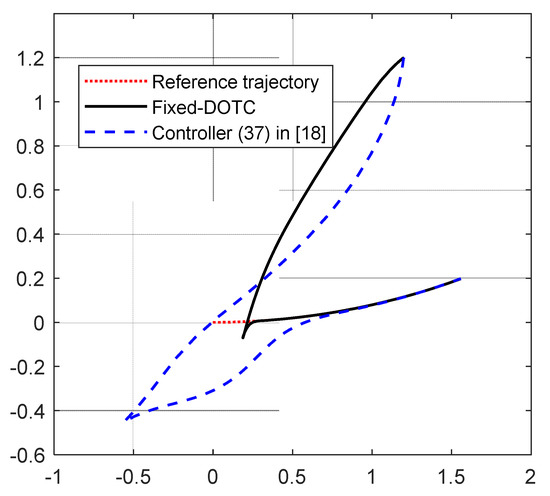
Figure 9.
The actual position trajectory and the desired position trajectory in part 2.
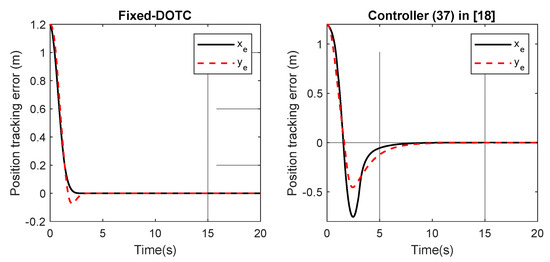
Figure 10.
The position tracking errors in part 2.
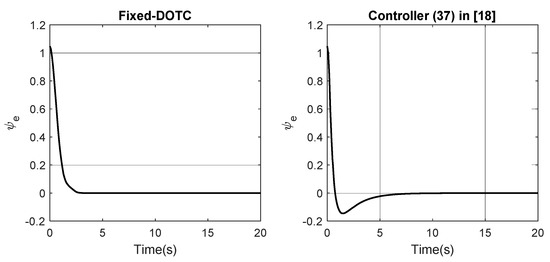
Figure 11.
The orientation tracking error in part 2.
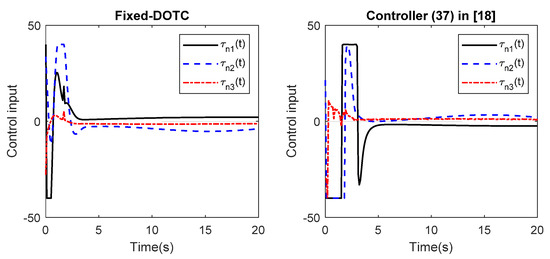
Figure 12.
The control input in part 2.
Part 3: The previous parts clearly confirmed the superior performance of the proposed Fixed-DOTC in comparison with those in [18]. In this part, the finite-time disturbance observer tracking control (Finite-DOTC) suggested in [42] is simulated. The initial condition is taken as and . The simulation outcomes are given in Figure 13, Figure 14, Figure 15 and Figure 16. Figure 13 shows the tracking performance of Fixed-DOTC and Finite-DOTC in 2D space x−y axis. Based on this figure, the system trajectory under the proposed controller reaches the reference trajectory and faster tracking error convergence is acquired. This fact is also observed in Figure 14 and Figure 15 which show that the position and orientation tracking errors converge to zero faster and more accurately. To be more exact, under the proposed law, the tracking errors approach zero at the time of 3 sec, whereas this convergence time under the Finite-DOTC is about 8 sec. Therefore, the proposed control framework improves the convergence rate by 62.5%. This means that the vessel reaches the reference path quickly. The control efforts are depicted in Figure 16. The maximum control input for both controls is the same, although Fixed-DOTC provides a faster convergence speed. By analyzing the results obtained from these figures, the superior performance of Fixed-DOTC over Finite-DOTC can be concluded.
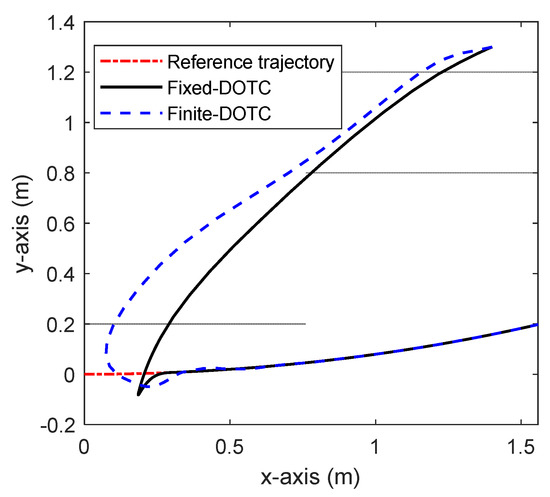
Figure 13.
The actual position trajectory and the desired position trajectory in part 3.
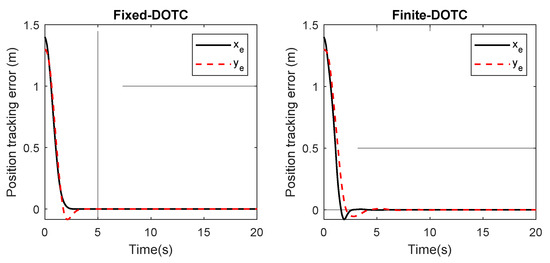
Figure 14.
The position tracking errors in part 3.
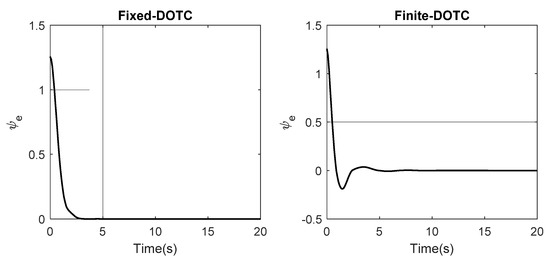
Figure 15.
The orientation tracking error in part 3.
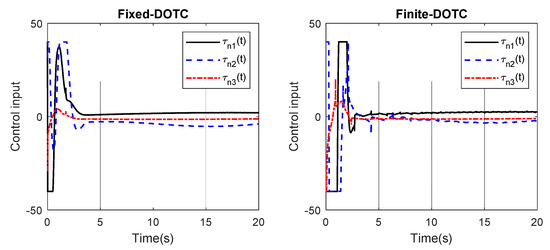
Figure 16.
The control input in part 3.
5. Conclusions
This paper deals with the challenging problem of the fixed-time disturbance observer-based tracking control for uncertain marine vessels. Based on the proposed methodology, the uncertain dynamics, as well as unknown external disturbances, are precisely reconstructed. The novel disturbance observer guarantees that the estimation error converges to origin within a finite time regardless of the initial conditions. The estimated lumped uncertainty is incorporated in the tracking control which is on the basis of fixed-time backstepping control. A rigorous analysis based on Lyapunov stability criteria shows that the closed-loop system is fixed-time stable. Finally, the simulation results confirmed that the suggested fixed-time tracking control law is able to ensure quicker convergence with more accuracy compared to the existing schemes.
Despite the good performance of the proposed disturbance observer, it is assumed that there is no uncertainty in the measurements provided by the sensors. As one of the future works, the problem of designing a disturbance observer in the presence of uncertainty on the output measurement will be studied.
Author Contributions
Conceptualization, designing, writing—original draft preparation: Y.B., K.A.A., S.M. and M.G.; Experimentation, simulation, and analysis: M.G., Y.B. and S.M.; writing—review and editing, and supervision: Y.B., K.A.A., S.M., M.G., A.I. and U.T. All authors have read and agreed to the published version of the manuscript.
Funding
The Ministry of Education in Saudi Arabia funded this research work through the project number (IF-PSAU-2021/01/17867).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available within the article.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IF-PSAU-2021/01/17867).
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Fang, M.-C.; Lin, Y.-H.; Wang, B.-J. Applying the PD controller on the roll reduction and track keeping for the ship advancing in waves. Ocean Eng. 2012, 54, 13–25. [Google Scholar] [CrossRef]
- Dai, S.-L.; Wang, C.; Luo, F. Identification and learning control of ocean surface ship using neural networks. IEEE Trans. Ind. Inform. 2012, 8, 801–810. [Google Scholar] [CrossRef]
- Qu, Y.; Xiao, B.; Fu, Z.; Yuan, D. Trajectory exponential tracking control of unmanned surface ships with external disturbance and system uncertainties. ISA Trans. 2018, 78, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, Z.; Zhang, J. Multi-under-Actuated Unmanned Surface Vessel Coordinated Path Tracking. Sensors 2020, 20, 864. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, J.; Zhou, R.; Liu, Y.; Luo, J.; Xie, S.; Peng, Y.; Pu, H. Reinforcement-Learning-Based Asynchronous Formation Control Scheme for Multiple Unmanned Surface Vehicles. Appl. Sci. 2021, 11, 546. [Google Scholar] [CrossRef]
- Zhao, Z.; He, W.; Ge, S.S. Adaptive neural network control of a fully actuated marine surface vessel with multiple output constraints. IEEE Trans. Control Syst. Technol. 2014, 22, 1536–1543. [Google Scholar]
- Cui, R.; Zhang, X.; Cui, D. Adaptive sliding-mode attitude control for autonomous underwater vehicles with input nonlinearities. Ocean Eng. 2016, 123, 45–54. [Google Scholar] [CrossRef]
- Li, D.; Du, L. AUV Trajectory Tracking Models and Control Strategies: A Review. J. Mar. Sci. Eng. 2021, 9, 1020. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Ellis-Tiew, M.-Z.; Chen, W.-C.; Wang, C.-Z. Fuzzy risk evaluation and collision avoidance control of unmanned surface vessels. Appl. Sci. 2021, 11, 6338. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Lee, C.-Y.; Tseng, S.-H.; Hu, W.-M. Nonlinear optimal control law of autonomous unmanned surface vessels. Appl. Sci. 2020, 10, 1686. [Google Scholar] [CrossRef] [Green Version]
- Xia, G.; Xia, X.; Zhao, B.; Sun, C.; Sun, X. Distributed tracking control for connectivity-preserving and collision-avoiding formation tracking of underactuated surface vessels with input saturation. Appl. Sci. 2020, 10, 3372. [Google Scholar] [CrossRef]
- Holzhuter, T. LQG approach for the high-precision track control of ships. IEE Proc.-Control Theory Appl. 1997, 144, 121–127. [Google Scholar] [CrossRef]
- Borkowski, P. Adaptive system for steering a ship along the desired route. Mathematics 2018, 6, 196. [Google Scholar] [CrossRef] [Green Version]
- Abdelaal, M.; Fränzle, M.; Hahn, A. Nonlinear Model Predictive Control for trajectory tracking and collision avoidance of underactuated vessels with disturbances. Ocean Eng. 2018, 160, 168–180. [Google Scholar] [CrossRef]
- Fang, M.-C.; Zhuo, Y.-Z.; Lee, Z.-Y. The application of the self-tuning neural network PID controller on the ship roll reduction in random waves. Ocean Eng. 2010, 37, 529–538. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C.; Soltan, R.A. Sliding-mode tracking control of surface vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Yu, R.; Zhu, Q.; Xia, G.; Liu, Z. Sliding mode tracking control of an underactuated surface vessel. IET Control Theory Appl. 2012, 6, 461–466. [Google Scholar] [CrossRef]
- Yin, S.; Xiao, B. Tracking control of surface ships with disturbance and uncertainties rejection capability. IEEE/ASME Trans. Mechatron. 2017, 22, 1154–1162. [Google Scholar] [CrossRef]
- Huang, X.; Lin, W.; Yang, B. Global finite-time stabilization of a class of uncertain nonlinear systems. Automatica 2005, 41, 881–888. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Golestani, M.; Mobayen, S.; Richter, H. Fast robust adaptive tracker for uncertain nonlinear second-order systems with time-varying uncertainties and unknown parameters. Int. J. Adapt. Control Signal Process. 2018, 32, 1764–1781. [Google Scholar] [CrossRef]
- Galicki, M. Finite-time control of robotic manipulators. Automatica 2015, 51, 49–54. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C. Global finite-time inverse tracking control of robot manipulators. Robot. Comput.-Integr. Manuf. 2011, 27, 550–557. [Google Scholar] [CrossRef]
- Esmaeilzadeh, S.M.; Golestani, M. Finite-time fault-tolerant adaptive robust control for a class of uncertain non-linear systems with saturation constraints using integral backstepping approach. IET Control Theory Appl. 2018, 12, 2109–2117. [Google Scholar] [CrossRef]
- Ghasemi, M.; Nersesov, S.G. Finite-time coordination in multiagent systems using sliding mode control approach. Automatica 2014, 50, 1209–1216. [Google Scholar] [CrossRef]
- Golestani, M.; Mohammadzaman, I.; Vali, A.R. Finite-time convergent guidance law based on integral backstepping control. Aerosp. Sci. Technol. 2014, 39, 370–376. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, X.; Zhang, G. Adaptive neural finite-time formation control for multiple underactuated vessels with actuator faults. Ocean Eng. 2021, 222, 108556. [Google Scholar] [CrossRef]
- Zhu, C.; Huang, B.; Su, Y.; Zhou, B.; Zhang, E. Finite-time time-varying formation control for marine surface vessels. Ocean Eng. 2021, 239, 109817. [Google Scholar] [CrossRef]
- Fan, Y.; Zou, X.; Wang, G.; Mu, D. Robust Adaptive Path Following Control Strategy for Underactuated Unmanned Surface Vehicles with Model Deviation and Actuator Saturation. Appl. Sci. 2022, 12, 2696. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, B.; Liao, Y.; Wang, B. Finite-time trajectory tracking control for uncertain underactuated marine surface vessels. IEEE Access 2019, 7, 102321–102330. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, B.; Golestani, M. Robust fixed-time attitude stabilization control of flexible spacecraft with actuator uncertainty. Nonlinear Dyn. 2020, 100, 2505–2519. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.-X.; Yang, G.-H. Fault-tolerant fixed-time trajectory tracking control of autonomous surface vessels with specified accuracy. IEEE Trans. Ind. Electron. 2020, 67, 4889–4899. [Google Scholar] [CrossRef]
- Zhang, P.; Guo, G. Fixed-time switching control of underactuated surface vessels with dead-zones: Global exponential stabilization. J. Frankl. Inst. 2020, 357, 11217–11241. [Google Scholar] [CrossRef]
- Yao, Q. Fixed-time trajectory tracking control for unmanned surface vessels in the presence of model uncertainties and external disturbances. Int. J. Control 2020, 1–11. [Google Scholar] [CrossRef]
- Park, B.S.; Kwon, J.-W.; Kim, H. Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica 2017, 77, 353–359. [Google Scholar] [CrossRef]
- Wang, N.; Er, M.J. Direct adaptive fuzzy tracking control of marine vehicles with fully unknown parametric dynamics and uncertainties. IEEE Trans. Control Syst. Technol. 2016, 24, 1845–1852. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, J.; Pan, Y. Active disturbance rejection control of surface vessels using composite error updated extended state observer. Asian J. Control 2017, 19, 1802–1811. [Google Scholar] [CrossRef]
- Wang, N.; Lv, S.; Er, M.J.; Chen, W.-H. Fast and accurate trajectory tracking control of an autonomous surface vehicle with unmodeled dynamics and disturbances. IEEE Trans. Intell. Veh. 2016, 1, 230–243. [Google Scholar] [CrossRef] [Green Version]
- Tomera, M.; Podgórski, K. Control of Dynamic Positioning System with Disturbance Observer for Autonomous Marine Surface Vessels. Sensors 2021, 21, 6723. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Y.; Wang, N. Nonlinear disturbance observer-based backstepping finite-time sliding mode tracking control of underwater vehicles with system uncertainties and external disturbances. Nonlinear Dyn. 2017, 88, 465–476. [Google Scholar] [CrossRef]
- Van, M.; Do, V.-T.; Khyam, M.O.; Do, X.P. Tracking control of uncertain surface vessels with global finite-time convergence. Ocean Eng. 2021, 241, 109974. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time output feedback trajectory tracking control of marine surface vessels subject to unknown external disturbances and uncertainties. ISA Trans. 2019, 93, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Yi, J.; Zhao, D. Design of a sliding mode controller for trajectory tracking problem of marine vessels. IET Control Theory Appl. 2007, 1, 233–237. [Google Scholar] [CrossRef] [Green Version]
- Cruz-Zavala, E.; Moreno, J.A.; Fridman, L.M. Uniform robust exact differentiator. IEEE Trans. Autom. Control 2011, 56, 2727–2733. [Google Scholar] [CrossRef]
- Xiao, B.; Yang, X.; Huo, X. A novel disturbance estimation scheme for formation control of ocean surface vessels. IEEE Trans. Ind. Electron. 2016, 64, 4994–5003. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).