Smooth-Switching Gain Based Adaptive Neural Network Control of n-Joint Manipulator with Multiple Constraints

Abstract

Modeling errors, external loads and output constraints will affect the tracking control of the n-joint manipulator driven by the permanent magnet synchronous motor. To solve the above problems, the smooth-switching for backstepping gain control strategy based on the Barrier Lyapunov Function and adaptive neural network (BLF-ANBG) is proposed. First, the adaptive neural network method is established to approximate modeling errors, unknown loads and unenforced inputs. Then, the gain functions based on the error and error rate of change are designed, respectively. The two gain functions can respectively provide faster response speed and better tracking stability. The smooth-switching for backstepping gain strategy based on the Barrier Lyapunov Function is proposed to combine the advantages of both gain functions. According to the above strategy, the BLF-ANBG strategy is proposed, which not only solves the influence of multiple constraints, unknown loads and modeling errors, but also enables the manipulator system to have better dynamic and steady-state performances at the same time. Finally, the proposed controller is applied to a 2-DOF manipulator and compared with other commonly used methods. The simulation results show that the BLF-ANBG strategy has good tracking performance under multiple constraints and model errors.

1. Introduction

The manipulator has been widely used in various scenarios such as medical treatment, automobile production and metal processing due to its strong safety, high precision and high efficiency [1,2,3]. The permanent magnet synchronous motor (PMSM) has the characteristics of small size, low loss and large starting torque [4,5], which is often used as the drive motor for the servo control of the manipulator [6,7]. The manipulator system driven by PMSM is a multi-variable, nonlinear and strongly coupled system. Therefore, as the production requirements increase, the rapidity, accuracy and stability of manipulator tracking have always been a research hotspot.

For manipulator tracking control, many scholars have proposed different control strategies. Traditional control strategies such as proportional integral derivative (PID) control, feedback linearization control, sliding mode control (SMC), adaptive control and backstepping control are commonly used. Intelligent control methods such as fuzzy control and neural network control are also widely used. Shojaei, Pradhan, and Kim respectively used self-tuning PID control, second-order PID control and PD control to effectively improve the steady-state tracking performance of the manipulator [8,9,10]. Feng, Yeh, and Huang respectively designed non-singular fast terminal SMC strategy [11], output feedback SMC strategy [12] and adaptive SMC strategy [13]. Each method optimizes the traditional SMC strategy, however, the chattering phenomenon still exists. Gabriele and Meng adopted the feedback linearization strategy [14,15], but this strategy requires an accurate mathematical model. In literature [16,17,18], adaptive control was designed to effectively estimate the uncertainty of the system. Kanellakopoulos proposed a recursion-based backstepping control [19], which was then widely used. Cheng and Farrell applied backstepping strategy to the control of the manipulator [20,21]. Chang, Yang and Song designed fuzzy backstepping, fuzzy adaptive and fuzzy command filter controllers to improve the stability of position tracking [22,23,24]. The neural network control has strong approximation ability, so it is used by many scholars to approximate the modeling errors and nonlinear terms [25,26,27,28].

The above methods have improved the dynamic and steady-state performances of manipulator tracking, respectively, however, it is difficult to guarantee better dynamic and steady-state performance at the same time. In addition, most of the existing strategies only consider the manipulator system and ignore the drive motor system, along with failing to consider the effects of multiple constraints, unknown loads and modeling errors at the same time. These problems often affect the safe and smooth operation of the manipulator in engineering practice. Many scholars have devised different solutions to these problems. Singh proposed the modeling concept of fractional calculus [29,30], and systematically described the fractional order model of the manipulator in the book [31]. The fractional order dynamic model can describe the system model more accurately. Meng and Liu adopted the coordination strategy of two controllers, combining the advantages of the two controllers to improve the dynamic and steady-state characteristics at the same time, but the use of two different controllers will increase the complexity of the control system [32,33]. Other studies [34,35,36] used the Barrier Lyapunov Function (BLF) to satisfy the output constraint problem. Sung and Cheng proposed a neural network strategy to approximate the model uncertainty [37,38]. Yang et al. designed a variable-gain backstepping strategy to improve the rapidity and stability of the controller [39,40,41,42].

In this paper, the smooth-switching for backstepping gain control strategy based on BLF and adaptive neural network (BLF-ANBG) is designed. Combined with the manipulator and the drive motor, the overall model of the manipulator control system is obtained. The adaptive radial basis function (RBF) neural networks are designed to approximate the modeling errors, unknown loads and unenforced inputs of the system. The gain function based on the error and the change rate of error is designed, and the Gaussian function is used as the switching function to design the method of smooth-switching for backstepping gain, which combines the advantages of the two gain functions. When the error is large, the gain function based on the error plays a major role, and the error is proportional to the gain, which shortens the rise time of the system. On the contrary, when the error is small, the gain function based on the change rate of error plays a major role, and the change rate of error is inversely proportional to the gain, which improves the stability of the steady-state of the system. The smooth-switching for backstepping gain controller is designed based on BLF (BLF-GSS) to realize the normal operation of the system under asymmetric or symmetric time-varying output limited. The BLF-ANBG strategy is proposed by combining the adaptive neural network strategy and the BLF-GSS strategy.

The main contents of this article are organized as follows. In Section 2, the overall model of the manipulator control system is provided by combining the manipulator system and the driven motor system. In Section 3, the BLF-ANBG controller based on an adaptive neural network and BLF-GSS is designed. In Section 4, the stability of the control strategy is proved by using the Lyapunov function [43]. In Section 5, the controller is applied to the 2-DOF manipulator, and the feasibility of the controller is verified by a simulation example. Some conclusions are summarized in Section 6.

2. The Overall System Model of n-Joint Manipulator Driven by PMSM

2.1. The Model of n-Joint Manipulator System

The system model of the n-joint manipulator considering the modeling error and unknown load is

$$\begin{array}{cc}& \left(M\left(q\right)+\Delta M\left(q\right)\right)\ddot{q}+\left(C(q,\dot{q})+\Delta C(q,\dot{q})\right)\dot{q}+\left(G\left(q\right)+\Delta G\left(q\right)\right)={\tau }_r-{\tau }_{{}_L}-{\tau }_f-\Delta E\end{array}$$

(1)

$$\begin{array}{cc}& {\tau }_{{}_L}=J^{\mathrm{T}}F,{\tau }_f=R_f\dot{q}+F_c\mathrm{sgn}\left(\dot{q}\right)\end{array}$$

(2)

where $q={[q_1,\cdots ,q_n]}^{\mathrm{T}}$ represents the position of each joint. $M\left(q\right)$ and $C(q,\dot{q})\in R^{n\times n}$ are the positive-definite inertia matrix and Coriolis force matrix of the nominal model, respectively. $G\left(q\right)\in R^n$ is the system gravity vector of the nominal model. ${\tau }_r$, ${\tau }_{{}_L}\in R^n$ and ${\tau }_f$ are respectively expressed as the output torque, load torque and friction torque of the manipulator system. $\Delta M\left(q\right)$, $\Delta C(q,\dot{q})$ and $\Delta G\left(q\right)$ are the modeling error. J and F are the Jacobian matrix and load force of the manipulator, respectively. $R_f$ and $F_c$ are the diagonal viscous friction and Coulomb friction matrix. $\Delta E$ is the interference signal caused by position measurement error and velocity measurement noise.

2.2. The Model of Drive Motor System

The mathematical model of PMSM with modeling errors in the $d-q$ rotating coordinate system is described by

$$\begin{array}{cc}& L_q\frac{d{i}_q}{dt}=-n_p\mathrm{\Phi }\omega -n_{p}B{L}_d{i}_d-R_s{i}_q+u_q\end{array}$$

(3)

$$\begin{array}{cc}& L_d\frac{d{i}_d}{dt}=-R_s{i}_d+n_{p}B{L}_q{i}_q+u_d\end{array}$$

(4)

$$\begin{array}{cc}& \left(J_m+\Delta J_m\right)\frac{d\omega }{dt}=\tau -{\tau }_{mL}-R_m\omega \end{array}$$

(5)

$$\begin{array}{cc}& \frac{d\theta }{dt}=\omega \end{array}$$

(6)

$$\begin{array}{cc}& \tau =n_p[(L_d-L_q)i_d{i}_q+\mathrm{\Phi }{i}_q]\end{array}$$

(7)

where $\theta$, $\omega \in R^n$ indicate the rotation angle and speed of the PMSM. $L_d$, $L_q$ is the diagonal square matrix of $d-q$ axis inductance. $B=diag\{{\omega }_1,\cdots ,{\omega }_n\}$, ${\omega }_i$ represents the ith component of the speed. $i_d$, $i_q$ and $u_d$, $u_q$ denote the $d-q$ axis stator current and voltage vector. $n_p$, $\mathrm{\Phi }$ and $R_m\in R^{n\times n}$ are pole logarithm, magnetic flux and friction matrix of PMSM, respectively. $J_m\in R^{n\times n}$ denote the diagonal inertia matrix of PMSM. $\tau$, ${\tau }_{mL}\in R^n$ are the vector of electromagnetic torque and motor load torque, respectively. $\Delta J_m$ denote the modeling error of PMSM.

Assumption 1.

The input current of PMSM is strictly three-phase symmetrical.

Assumption 2.

The core saturation of PMSM can be ignored.

Property 1.

The manipulator system and the drive system are connected by the transmission with the reduction ratio of $\mu >0$, that is $q=\mu \theta$ and ${\tau }_r={\mu }^{-1}{\tau }_{mL}$.

2.3. The Overall Model of the Manipulator Driven by PMSM

According to (1)–(7), combined with the model of the manipulator system and the PMSM system, the dynamic model of the manipulator driven by PMSM with unknown load and modeling errors can expressed as

$$\begin{array}{cc}\hfill & \overline{M}\left(q\right)\ddot{q}+\overline{C}(q,\dot{q})\dot{q}+\overline{G}\left(q\right)=\tau -\mu ({\tau }_f+{\tau }_{{}_L}+\Delta E)-\mu \left(\Delta M\left(q\right)\ddot{q}+\Delta C(q,\dot{q})\dot{q}+\Delta G\left(q\right)\right)-{\mu }^{-1}\Delta J_m\ddot{q}\end{array}$$

(8)

where $\overline{M}\left(q\right)=\mu M\left(q\right)+{\mu }^{-1}{J}_m$, $\overline{C}(q,\dot{q})=\mu C(q,\dot{q})+{\mu }^{-1}{R}_m$, $\overline{G}\left(q\right)=\mu G\left(q\right)$

Considering the input saturation of the drive motor in the project, the actual input of PMSM electromagnetic torque ${\tau }_s\left(t\right)={[{\tau }_{s1}\left(t\right),\cdots ,{\tau }_{sn}\left(t\right)]}^{\mathrm{T}}$ is defined as

$$\begin{array}{cc}& {\tau }_{si}\left(t\right)=\left\{\begin{array}{c}{\tau }_{imax},{\tau }_i\left(t\right)\ge {\tau }_{imax}\hfill \\ {\tau }_i\left(t\right),{\tau }_{imin}<{\tau }_i\left(t\right)<{\tau }_{imax}\hfill \\ {\tau }_{imin},{\tau }_i\left(t\right)\le {\tau }_{imin}\hfill \end{array}\right.\end{array}$$

(9)

where the subscript i denotes the i th element of the electromagnetic torque vector. ${\tau }_{imax}$, ${\tau }_{imin}$ are the upper and lower limit values of the electromagnetic torque input to the drive motor, respectively. The part of the control signal that cannot be executed by PMSM can be expressed as

$$\begin{array}{cc}& {\tau }_{ni}\left(t\right)={\tau }_i\left(t\right)-{\tau }_{si}\left(t\right)=\left\{\begin{array}{c}{\tau }_i\left(t\right)-{\tau }_{imax}{\tau }_i\left(t\right)\ge {\tau }_{imax}\hfill \\ 0{\tau }_{imin}<{\tau }_i\left(t\right)<{\tau }_{imax}\hfill \\ {\tau }_i\left(t\right)-{\tau }_{imin}{\tau }_i\left(t\right)\le {\tau }_{imin}\hfill \end{array}\right.\end{array}$$

(10)

Substituting (4) and (5), Equation (3) is rewritten as

$$\begin{array}{cc}& \overline{M}\left(q\right)\ddot{q}+\overline{C}(q,\dot{q})\dot{q}+\overline{G}\left(q\right)={\tau }_s-\mu {\tau }_f+f(\mu ,{\tau }_n,{\tau }_{{}_L},q,\dot{q},\ddot{q})\end{array}$$

(11)

where $f(\mu ,{\tau }_n,{\tau }_{{}_L},q,\dot{q},\ddot{q})={\tau }_n-\mu ({\tau }_{{}_L}+\Delta E)-\mu \left(\Delta M\left(q\right)\ddot{q}+\Delta C(q,\dot{q})\dot{q}+\Delta G\left(q\right)\right)-{\mu }^{-1}\Delta J_m\ddot{q}$,represents unknown modeling error, load and unexecuted input. For the convenience of the following application we use f instead of $f(\mu ,{\tau }_n,{\tau }_{{}_L},q,\dot{q},\ddot{q})$. Define the state vector as $x_1=q$, $x_2=\dot{q}$. The state equation of the manipulator system can be described as

$$\begin{array}{cc}& {\dot{x}}_1=x_2\end{array}$$

(12)

$$\begin{array}{cc}& {\dot{x}}_2={\overline{M}}^{-1}\left(x_1\right)[-\overline{C}(x_1,x_2)x_2-\overline{G}\left(x_1\right)+f+{\tau }_s-\mu {\tau }_f]\end{array}$$

(13)

$$\begin{array}{cc}& y=x_1\end{array}$$

(14)

In the actual servo tracking of the robot arm, it is necessary to ensure that the output of each joint is bounded and can normally track the desired position signal.

Assumption 3.

There exist time-varying output upper and lower bounds $y_{imax}\left(t\right)$ and $y_{imin}\left(t\right)$$(i=1,2,\cdots ,n)$, such that $y_{imin}\left(t\right)\le y_i\left(t\right)\le y_{imax}\left(t\right)$, $\forall t>0$.

Assumption 4.

There are functions $y_{dimin}\left(t\right)$ and $y_{dimax}\left(t\right)$ that satisfy the inequality $y_{imin}\left(t\right)$$\le y_{dimin}\left(t\right)$ and $y_{dimax}\left(t\right)\le y_{imax}\left(t\right)$, $\forall t>0$, so that the desired position satisfies $y_{dimin}\left(t\right)$$\le y_{di}\left(t\right)\le y_{dimax}\left(t\right)$.

Lemma 1

([34]). For any $\left|\varsigma \right|<1$, the inequality $log\frac{1}{1-{\varsigma }^2}<\frac{{\varsigma }^2}{1-{\varsigma }^2}$ is satisfied.

3. Design of Controller

In this section, the structure and approximation process of the adaptive RBF neural network are described. Then, the smooth-switching for backstepping gain method is designed. Finally, the BLF-ANBG controller is designed.

3.1. Design of Adaptive Neural Network Approximation

To estimate modeling error, external load torque and unexecuted input, an adaptive RBF neural network strategy composed of an input layer, middle layer and output layer is designed. The structure of the adaptive RBF neural network is shown in Figure 1.

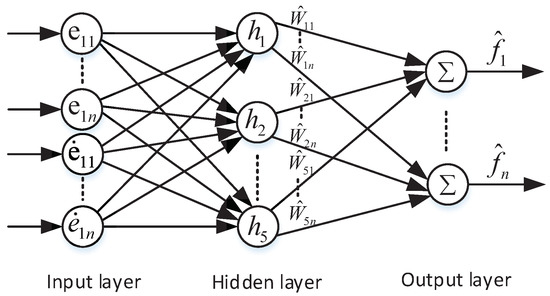
Figure 1. The structure of the Adaptive RBF Neural Network.

The middle layer is composed of five neurons, the output of each neuron is

$$\begin{array}{cc}& h_k=exp\left(-\frac{{∥z-c_k∥}^2}{b_k^2}\right)(k=1,\cdots ,5)\end{array}$$

(15)

where $z={\left[e_1,{\dot{e}}_1\right]}^{\mathrm{T}}$ is the input vector. $c_k$, $b_k$ represent the center point vector and width of the k th neuron, respectively. The output of the adaptive RBF neural network is

$$\begin{array}{cc}& \widehat{f}(·)={\widehat{w}}^{\mathrm{T}}h\left(x\right)\end{array}$$

(16)

where $h\left(x\right)={\left[h_1,\cdots ,h_5\right]}^{\mathrm{T}}$. $\widehat{w}$ is the adaptive weight, and the adaptive law is described as

$$\begin{array}{cc}& \dot{\widehat{w}}=\psi h{z}^{\mathrm{T}}PB\end{array}$$

(17)

where $\psi >0$ is the constant gain. B represents the input matrix of the closed-loop system. P is the positive definite matrix, and there exists the matrix $Q\ge 0$ such that P satisfies the stability equation $PA+A^{\mathrm{T}}P=-Q$, where A is the state matrix of the closed-loop system and the equations are given in Section 3.3. The adaptive neural network proposed in this paper recalculates the adaptive weights through the position error, velocity error of the manipulator and the output of the hidden layer of the adaptive neural network in each iteration to achieve the training of the neural network.

Property 2.

Given a continuous function $f(·)$, there is an ideal weight ${\widehat{w}}^{*}$, and the adaptive neural network approximation error $\gamma =f(·)-{\widehat{f}}^{*}(·)$ satisfies $max∥\gamma ∥\le {\gamma }_{{}_0}$. ${\gamma }_{{}_0}$ is the upper bound of error, and satisfies ${\gamma }_{{}_0}\le \epsilon$, ε is a very small positive number.

3.2. Design of Smooth-Switching for Backstepping Gain

The change in the control gain can produce the contradiction between the system dynamics characteristics and the steady-state characteristics. The larger the gain, the faster the response, the higher the accuracy, but the worse the stability [37,38]. The smaller the gain, the better the stability, but the response time will be longer and the accuracy will be lower. In addition, considering safety in engineering, the control gain is often within a certain range. In this part, a new smooth-switching for backstepping gain strategy is proposed, and the control gain is designed with the error surface and the change rate of the error surface, respectively.

3.2.1. The Variable Control Gain of the Error

Define the error surface as $e_{ij}$, where the subscript represents the j th component of the i th error surface. The variable control gain designed with error is expressed as

$$\begin{array}{cc}& \Delta k_{ij}\left(e_{ij}\right)=\frac{2{\alpha }_{ij}}{\pi }arctan{\left(\frac{e_{ij}}{{\beta }_{ij}}\right)}^2+{\delta }_{ij}\end{array}$$

(18)

where ${\alpha }_{ij}>0$ is the magnification of the gain designed with the error. ${\beta }_{ij}>0$ is the scale parameter of variable gain. ${\delta }_{ij}$ is a positive constant, ensure that $\Delta k_{ij}\left(e_{ij}\right)>0$, $\forall e_{ij}\in R$.

3.2.2. The Variable Control Gain of the Change Rate of the Error

Take the derivative of the error surface $e_{ij}$ to get ${\dot{e}}_{ij}$. The variable control gain designed with the change rate of error can be described as

$$\begin{array}{cc}& \Delta k_{ij}\left({\dot{e}}_{ij}\right)={\delta }_{ij}-\frac{2{\xi }_{ij}}{\pi }arctan{\left(\frac{{\dot{e}}_{ij}}{{\zeta }_{ij}}\right)}^2\end{array}$$

(19)

where ${\xi }_{ij}>0$ is the magnification of the gain function designed based on the change rate of error. ${\zeta }_{ij}$ is the positive scale parameter. ${\delta }_{ij}>{\xi }_{ij}$, ensure that $\Delta k_{ij}\left({\dot{e}}_{ij}\right)>0$, $\forall {\dot{e}}_{ij}\in R$.

3.2.3. Design of Smooth-Switching for Backstepping Gain

To solve the smoothness of the gain switching transition process, a smooth-switching function based on the error surface is designed as

$$\begin{array}{cc}& f\left(e_{ij}\right)=1-exp\left(-{\left(\frac{e_{ij}}{{\sigma }_{ij}}\right)}^2\right)\end{array}$$

(20)

where ${\sigma }_{ij}$ is the positive scale constant. The smooth-switching function curve with different values of ${\sigma }_{ij}$ are shown in Figure 2.

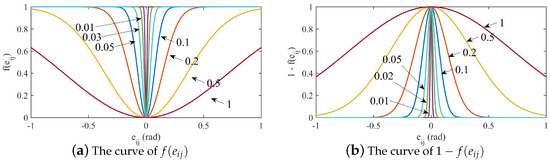
Figure 2. The smooth-switching function curve.

According to (18)–(20), the smooth-switching for backstepping gain strategy is designed as

$$\begin{array}{cc}& \Delta k_{ij}=f\left(e_{ij}\right)·\Delta k_{ij}\left(e_{ij}\right)+[1-f\left(e_{ij}\right)]·\Delta k_{ij}\left({\dot{e}}_{ij}\right)\end{array}$$

(21)

When the error is large, the control gain designed based on the error is mainly used. The greater the error, the greater the control gain, which ensures the rapid convergence of the system. When the error is small, the control gain designed by using the change rate of error is mainly used. The larger the change rate of error surface, the smaller the control gain. Thus, the jitter phenomenon caused by the large control gain of the manipulator system in the steady-state is reduced. When the error is in the middle range, the two gain functions transition in the form of smooth switching.

3.3. Design of BLF-ANBG Controller

To consider the time-varying asymmetric output limitation, the time-varying asymmetric BLF and adaptive neural network are used to design the smooth-switching for the backstepping gain controller. The block diagram of the manipulator system based on the BLF-ANBG controller is shown in Figure 3, and the design process is as follows

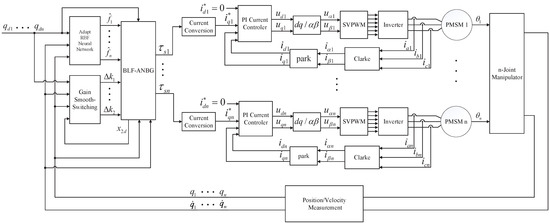
Figure 3. The Block Diagram of the Manipulator System Based on the BLF-ANBG Controller.

Step (1) Define the first tracking error surface vector as $e_1=x_1-x_d={[e_{11},\cdots ,e_{1n}]}^{\mathrm{T}}$, $x_d$ is the desired tracking position. The time-varying barrier of output is defined as

$$\begin{array}{cc}& y_{ai}\left(t\right)=x_{di}\left(t\right)-y_{imin}\left(t\right)\end{array}$$

(22)

$$\begin{array}{cc}& y_{bi}\left(t\right)=y_{imax}\left(t\right)-x_{di}\left(t\right)\end{array}$$

(23)

where $i=1,\cdots ,n$, which means the ith component of the vector. Define the time-varying asymmetric output constraints BLF as

$$\begin{array}{cc}& V_1=\sum _{i=1}^n{V}_{1i}=\sum _{i=1}^n\left[\frac{\lambda \left(e_{1i}\right)}{2}log\frac{1}{1-{\varsigma }_{i+}^2\left(t\right)}+\frac{1-\lambda \left(e_{1i}\right)}{2}log\frac{1}{1-{\varsigma }_{i-}^2\left(t\right)}\right]\end{array}$$

(24)

where

$$\begin{array}{cc}& \lambda \left(e_{1i}\right)=\left\{\begin{array}{c}1,if{e}_{1i}>0\hfill \\ 0,if{e}_{1i}\le 0\hfill \end{array}\right.\end{array}$$

(25)

$$\begin{array}{cc}& {\varsigma }_{imin}\left(t\right)=\frac{e_{1i}}{y_{ai}\left(t\right)},{\varsigma }_{imax}\left(t\right)=\frac{e_{1i}}{y_{bi}\left(t\right)}\end{array}$$

(26)

Define the coordinate transformation as

$$\begin{array}{cc}& {\varsigma }_i\left(t\right)=(1-\lambda \left(e_{1i}\right)){\varsigma }_{imin}\left(t\right)+\lambda \left(e_{1i}\right){\varsigma }_{imax}\left(t\right)\end{array}$$

(27)

Substituting (25) and (27) into (24), can obtain

$$\begin{array}{cc}& V_1=\sum _{i=1}^n{V}_{1i}=\sum _{i=1}^n\frac{1}{2}log\frac{1}{1-{\varsigma }_i^2\left(t\right)},\left|{\varsigma }_i\left(t\right)\right|\le 1\end{array}$$

(28)

It can be obtained from (28) that when $|{\varsigma }_i|\le 1$, $V_1$ is positive definite. The differential of $V_1$ as

$$\begin{array}{cc}& \begin{array}{c}{\dot{V}}_1=\sum _{i=1}^n{V}_{1i}=\sum _{i=1}^n\left[\frac{\lambda \left(e_{1i}\right){\varsigma }_{imax}\left(t\right)}{y_{bi}\left(t\right)(1-{\varsigma }_{imax}^2\left(t\right))}(e_{2i}+x_{2di}-{\dot{x}}_{di}-e_{1i}\frac{{\dot{y}}_{bi}\left(t\right)}{y_{bi}\left(t\right)})\right.\hfill \\ \left.+\frac{(1-\lambda \left(e_{1i}\right)){\varsigma }_{imin}\left(t\right)}{y_{ai}\left(t\right)(1-{\varsigma }_{imin}^2\left(t\right))}(e_{2i}+x_{2di}-{\dot{x}}_{di}-e_{1i}\frac{{\dot{y}}_{ai}\left(t\right)}{y_{ai}\left(t\right)})\right]\hfill \end{array}\end{array}$$

(29)

where $x_{2di}$ is the ith component of the virtual control vector $x_{2d}$, and the virtual control vector $x_{2d}$ is designed by using the backstepping method as

$$\begin{array}{cc}& x_{2d}=-(\Delta k_1+{\overline{k}}_1\left(t\right))e_1+{\dot{x}}_d\end{array}$$

(30)

$$\begin{array}{cc}& \Delta k_i=diag\{\Delta k_{i1},\cdots ,\Delta k_{in}\}\end{array}$$

(31)

$$\begin{array}{cc}& {\overline{k}}_1\left(t\right)=diag\{{\overline{k}}_{11}\left(t\right),\cdots ,{\overline{k}}_{1n}\left(t\right)\}\end{array}$$

(32)

where ${\overline{k}}_{1i}\left(t\right)=\sqrt{{\left(\frac{{\dot{y}}_{ai}\left(t\right)}{y_{ai}\left(t\right)}\right)}^2+{\left(\frac{{\dot{y}}_{bi}\left(t\right)}{y_{bi}\left(t\right)}\right)}^2+a}$, $a>0$ is a constant to ensure that the derivative of $x_{2di}$ is bounded. Substituting (26) and (27) and (30)–(32) into (29) can be rewritten as

$$\begin{array}{cc}& {\dot{V}}_1=\sum _{i=1}^n{\dot{V}}_{1i}\le \sum _{i=1}^n\left[-\frac{\Delta k_{1i}{\varsigma }_i^2}{1-{\varsigma }_i^2}+\left(\frac{1-\lambda \left(e_{1i}\right)}{y_{ai}^2\left(t\right)-e_{1i}^2}+\frac{\lambda \left(e_{1i}\right)}{y_{bi}^2\left(t\right)-e_{1i}^2}\right)e_{1i}{e}_{2i}\right]\end{array}$$

(33)

Step (2) The second error surface vector is defined as $e_2=x_2-x_{2d}$$={[e_{21},\cdots ,e_{2n}]}^T$. Define the stability function as $V_2={\displaystyle \sum _{i=1}^n}{V}_{2i}={\displaystyle \sum _{i=1}^n}\frac{1}{2}{e}_{2i}^2$. Substituting into (13), based on the backstepping control method, the actual control signal is selected as

$$\begin{array}{cc}& {\tau }_s=\overline{M}\left(x_1\right)\left[-\Delta k_2{e}_2+{\dot{x}}_{2d}-\eta e_1\right]+\overline{C}(x_1,x_2)x_2+\overline{G}\left(x_1\right)+\mu {\tau }_f-\widehat{f}\end{array}$$

(34)

where $\eta =diag\left\{\left(\frac{1-\lambda \left(e_{11}\right)}{y_{a1}^2\left(t\right)-e_{11}^2}+\frac{\lambda \left(e_{11}\right)}{y_{b1}^2\left(t\right)-e_{11}^2}\right),\cdots ,\left(\frac{1-\lambda \left(e_{1n}\right)}{y_{an}^2\left(t\right)-e_{1n}^2}+\frac{\lambda \left(e_{1n}\right)}{y_{bn}^2\left(t\right)-e_{1n}^2}\right)\right\}$, and $\widehat{f}$ is the adaptive RBF neural network estimate of f. Substituting (30), Equation (34) can be rewritten as

$$\begin{array}{ccc}& & {\tau }_s=\overline{M}\left(x_1\right)\left[{\ddot{x}}_d-\left(\Delta k_1+\Delta k_2+{\overline{k}}_1\left(t\right)\right){\dot{e}}_1-\left[\Delta k_2\left(\Delta k_1+{\overline{k}}_1\left(t\right)\right)+\eta \right]e_1\right]\hfill \\ & & +\overline{C}(x_1,x_2)x_2+\overline{G}\left(x_1\right)+\mu {\tau }_f-\widehat{f}\hfill \end{array}$$

(35)

Substitute (35) into (11), subtracting $\overline{M}\left(x_1\right){\dot{x}}_2+\overline{C}(x_1,x_2)x_2+\overline{G}\left(x_1\right)$ from both sides, can get

$$\begin{array}{cc}\hfill & \begin{array}{c}{\ddot{e}}_1+\left(\Delta k_1+\Delta k_2+{\overline{k}}_1\left(t\right)\right){\dot{e}}_1+\left[\Delta k_2\left(\Delta k_1+{\overline{k}}_1\left(t\right)\right)+\eta \right]e_1={\overline{M}}^{-1}\left(x_1\right)\left(f-\widehat{f}\right)\hfill \\ ={\overline{M}}^{-1}\left(x_1\right)\left(f-{\widehat{f}}^{*}+{\widehat{f}}^{*}-\widehat{f}\right)={\overline{M}}^{-1}\left(x_1\right)\left(\gamma -{\tilde{w}}^{T}h\right)\hfill \end{array}\end{array}$$

(36)

where $\tilde{w}=\widehat{w}-{\widehat{w}}^{*}$. Let $z={\left[e_1,{\dot{e}}_1\right]}^T$, the closed-loop system equation is

$$\begin{array}{cc}& \dot{z}=Az+B\left[{\overline{M}}^{-1}\left(\gamma -{\tilde{w}}^{T}h\right)\right]\end{array}$$

(37)

where $A=\left[\begin{array}{cc}{0}_n& I_n\\ -\Delta k_2\left(\Delta k_1+{\overline{k}}_1\left(t\right)\right)-\eta & -\Delta k_1-\Delta k_2-{\overline{k}}_1\left(t\right)\end{array}\right]$, $B=\left[\begin{array}{c}0\\ I_n\end{array}\right]$. $0_n$ and $I_n$ represent n dimensional zero matrix and identity matrix, respectively.

4. The Analysis of BLF-ANBG Controller

In this section, the stability of the BLF-ANBG strategy is proved. Then, the manipulator joint output constraints are verified as not violated. Finally, the tracking error convergence is proved.

4.1. Proof of BLF-ANBG Controller Stability

The Lyapunov function of the BLF- ANBG controller is defined as

$$\begin{array}{cc}& \begin{array}{c}V=V_1+V_2+\frac{1}{2}{z}^{\mathrm{T}}Pz+\frac{1}{2\psi }{∥\tilde{w}∥}^2=\sum _{i=1}^n\left[\frac{\lambda \left(e_{1i}\right)}{2}log\frac{1}{1-{\varsigma }_{i+}^2\left(t\right)}\right.\hfill \\ \left.+\frac{1-\lambda \left(e_{1i}\right)}{2}log\frac{1}{1-{\varsigma }_{i-}^2\left(t\right)}\right]+\sum _{i=1}^n\frac{1}{2}{e}_{2i}^2+\frac{1}{2}{z}^{\mathrm{T}}Pz+\frac{1}{2\psi }{∥\tilde{w}∥}^2\hfill \end{array}\end{array}$$

(38)

where $∥\tilde{w}∥=tr\left({\tilde{w}}^{\mathrm{T}}\tilde{w}\right)$ is the Frobenius norm of $\tilde{w}$, and also represents the trace of matrix ${\tilde{w}}^{\mathrm{T}}\tilde{w}$. From (38), it can be known that V is positive definite. Taking the derivative of $\tilde{w}$ and substituting (17) into $\dot{\tilde{w}}$ can obtain

$$\begin{array}{cc}& \dot{\tilde{w}}=\dot{\widehat{w}}-{\dot{\widehat{w}}}^{*}=\psi h{z}^{\mathrm{T}}PB\end{array}$$

(39)

Taking the derivative of (38) can be known that

$$\begin{array}{ccc}& & \dot{V}\le \sum _{i=1}^n\left[-\frac{\Delta k_{1i}{\varsigma }_i^2}{1-{\varsigma }_i^2}+\left(\frac{1-\lambda \left(e_{1i}\right)}{y_{ai}^2\left(t\right)-e_{1i}^2}+\frac{\lambda \left(e_{1i}\right)}{y_{bi}^2\left(t\right)-e_{1i}^2}\right)e_{1i}{e}_{2i}\right]\hfill \\ & & +\sum _{i=1}^n\left[-\Delta k_{1i}{e}_{2i}^2-\left(\frac{1-\lambda \left(e_{1i}\right)}{y_{ai}^2\left(t\right)-e_{1i}^2}+\frac{\lambda \left(e_{1i}\right)}{y_{bi}^2\left(t\right)-e_{1i}^2}\right)e_{1i}{e}_{2i}\right]\hfill \\ & & +\frac{1}{2}\left[z^{\mathrm{T}}P\dot{z}+{\dot{z}}^{\mathrm{T}}Pz\right]+tr\left(B^{\mathrm{T}}Pz{h}^{\mathrm{T}}\tilde{w}\right)\hfill \\ & & =\sum _{i=1}^n\left[-\frac{\Delta k_{1i}{\varsigma }_i^2}{1-{\varsigma }_i^2}-\Delta k_{1i}{e}_{2i}^2\right]+\frac{1}{2}\left[z^{\mathrm{T}}P\dot{z}+{\dot{z}}^{\mathrm{T}}P\dot{z}\right]+tr\left(B^{\mathrm{T}}Pz{h}^{\mathrm{T}}\tilde{w}\right)\hfill \end{array}$$

(40)

Substituting (37) into (40), it becomes

$$\begin{array}{cc}& \begin{array}{c}\dot{V}\le \sum _{i=1}^n\left[-\frac{\Delta k_{1i}{\varsigma }_i^2}{1-{\varsigma }_i^2}-\Delta k_{1i}{e}_{2i}^2\right]+\frac{1}{2}\left[z^{\mathrm{T}}PAz+z^{\mathrm{T}}PB\gamma -z^{\mathrm{T}}PB{\tilde{w}}^{T}h\right.\\ \left.+z^{\mathrm{T}}{A}^{\mathrm{T}}Pz+{\gamma }^{\mathrm{T}}{B}^{\mathrm{T}}Pz-h^{\mathrm{T}}\tilde{w}{B}^{\mathrm{T}}Pz\right]+tr\left(B^{\mathrm{T}}Pz{h}^{\mathrm{T}}\tilde{w}\right)\end{array}\end{array}$$

(41)

Noting that $h^{\mathrm{T}}\tilde{w}{B}^{\mathrm{T}}Pz=z^{\mathrm{T}}PB{\tilde{w}}^{\mathrm{T}}h=tr\left(B^{\mathrm{T}}Pz{h}^{\mathrm{T}}\tilde{w}\right)$ and ${\gamma }^{\mathrm{T}}{B}^{\mathrm{T}}Pz=z^{\mathrm{T}}PB\gamma$, (41) is rewritten as

$$\begin{array}{cc}& \dot{V}\le \sum _{i=1}^n\left[-\frac{\Delta k_{1i}{\varsigma }_i^2}{1-{\varsigma }_i^2}-\Delta k_{1i}{e}_{2i}^2\right]-\frac{1}{2}{z}^{\mathrm{T}}Qz+{\gamma }^{\mathrm{T}}{B}^{\mathrm{T}}Pz\end{array}$$

(42)

Combining Property 2 to get

$$\begin{array}{cc}\hfill & \dot{V}\le \sum _{i=1}^n\left[-\frac{\Delta k_{1i}{\varsigma }_i^2}{1-{\varsigma }_i^2}-\Delta k_{1i}{e}_{2i}^2\right]-∥z∥\left[\frac{1}{2}{\lambda }_{min}\left(Q\right)∥z∥-∥{\gamma }_{{}_0}∥{\lambda }_{max}\left(P\right)\right]\end{array}$$

(43)

where ${\lambda }_{min}(·)$ and ${\lambda }_{max}(·)$ represent the upper and lower bounds of the eigenvalues, respectively. From (43), it can be seen that all signals in the system are uniformly ultimately bounded (UUB) [44,45]. The system is semi-global and practically stable [46].

Remark 1.

To satisfy $\dot{V}\le 0$, choose appropriate controller parameters such that $∥z∥\ge \frac{2∥{\gamma }_0∥{\lambda }_{max}\left(P\right)}{{\lambda }_{min}\left(Q\right)}$. In this paper, the appropriate eigenvalues of Q are selected to satisfy the above conditions to make the system asymptotically converge to the small neighborhood of the origin. When the approximation error γ tends to 0, the system asymptotically converges to the origin.

4.2. Proof That the Manipulator Joint Outputs Constraints Are Not Violated

From (27), it can be obtained that when $e_{1i}<0$, which yields ${\varsigma }_i\left(t\right)={\varsigma }_{imin}\left(t\right)$, and because $|{\varsigma }_i|\le 1$ and $y_{ai}\left(t\right)>0$, according to (26) can be known that $-1<{\varsigma }_{imin}\left(t\right)\le 0$, then $-y_{ai}\left(t\right)<e_{1i}\left(t\right)\le 0$. Similarly, when $e_{1i}\ge 0$, $0\le e_{1i}\left(t\right)<y_{bi}\left(t\right)$ can be obtained. In conclusion, that

$$\begin{array}{cc}& -y_{ai}\left(t\right)<e_{1i}\left(t\right)<y_{bi}\left(t\right),\left|{\varsigma }_i\left(t\right)\right|<1\end{array}$$

(44)

Adding $x_{di}\left(t\right)$ to each term in the inequality, (45) can be rewritten as

$$\begin{array}{cc}& -y_{ai}\left(t\right)+x_{di}\left(t\right)<e_{1i}\left(t\right)+x_{di}\left(t\right)<y_{bi}\left(t\right)+x_{di}\left(t\right),\left|{\varsigma }_i\left(t\right)\right|<1\end{array}$$

(45)

So $y_{imin}\left(t\right)<y\left(t\right)<y_{imax}\left(t\right)$, each joint is within the given constraints.

4.3. Proof of Tracking Error Convergence

According to Lemma 1 and (38), $V\left(t\right)\le V\left(0\right)e^{-\rho t},t\ge 0$ can be obtained [34,47], where $\rho =min\left\{2\Delta k_{1j},2\Delta k_{2j}\right\}$, $j=1,\cdots ,n$. It can be obtained that

$$\begin{array}{cc}& \frac{1}{2}log\frac{1}{1-{\varsigma }_i^2\left(t\right)}\le V\left(0\right)e^{-\rho t}\end{array}$$

(46)

Hence,

$$\begin{array}{cc}& {\varsigma }_i^2\left(t\right)\le 1-e^{-2V\left(0\right)e^{-\rho t}}\end{array}$$

(47)

When $e_{1i}\le 0$, ${\varsigma }_i\left(t\right)={\varsigma }_{imin}\left(t\right)=\frac{e_{1i}}{y_{ai}\left(t\right)}$, $-y_{ai}\left(t\right)\sqrt{1-e^{-2V\left(0\right)e^{-\rho t}}}\le e_{1i}\le 0$. When $e_{1i}>0$, ${\varsigma }_i\left(t\right)={\varsigma }_{imax}\left(t\right)=\frac{e_{1i}}{y_{bi}\left(t\right)}$, $0<e_{1i}\le y_{bi}\left(t\right)\sqrt{1-e^{-2V\left(0\right)e^{-\rho t}}}$. Combining both cases, can conclude that

$$\begin{array}{cc}& -y_{ai}\left(t\right)\sqrt{1-e^{-2V\left(0\right)e^{-\rho t}}}\le e_{1i}\le y_{bi}\left(t\right)\sqrt{1-e^{-2V\left(0\right)e^{-\rho t}}}\end{array}$$

(48)

where

$$\begin{array}{cc}& \underset{t\to \infty }{lim}\left(-y_{ai}\left(t\right)\sqrt{1-e^{-2V\left(0\right)e^{-\rho t}}}\right)=0\end{array}$$

(49)

$$\begin{array}{cc}& \underset{t\to \infty }{lim}\left(y_{bi}\left(t\right)\sqrt{1-e^{-2V\left(0\right)e^{-\rho t}}}\right)=0\end{array}$$

(50)

From (49) and (50), the upper and lower bounds of $e_{1i}$ converge to 0, so $e_{1i}$ converges to 0.

5. Simulink Results and Analysis

In this section, the BLF-ANBG control strategy is applied to a 2-DOF manipulator for simulation experiments to verify the feasibility of the strategy. The simulation experiment is divided into three parts. First, to verify the effectiveness of the smooth-switching for the backstepping control method, it is compared with the two variable gains functions without the smooth-switching strategy. Second, the BLF-ANBG strategy is used to control the manipulator to track the unit-step and periodic signals without modeling error and unknown load, and compare with other commonly used control strategies. Finally, the BLF-ANBG strategy is compared with the commonly used strategies in the presence of modeling errors and unknown loads. The parameters of the manipulator system in all simulation experiments in this section are shown in Table 1.

Table 1. The parameters of the manipulator system.

Parameters	Values	Parameters	Values
Weight ($m_1$, $m_2$)	$0.5\mathrm{kg}$	Length ($l_1$, $l_2$)	$1\mathrm{m}$
$R_f$	$diag\{5,5\}$ N	$R_s$	$diag\{2.875,2.875\}\mathrm{\Omega }$
$n_p$	$diag\{4,4\}$	$L_d,L_q$	$diag\{0.0085,0.0085\}$ H
$\mathrm{\Phi }$	$diag\{0.175,0.175\}$ Wb	$J_m$	$diag\{0.0025,0.0025\}\mathrm{kg}·{\mathrm{m}}^2$
$\eta$	$diag\left\{0.01,0.01\right\}$	$R_m$	$diag\{6,6\}$ N
$F_c$	$diag\{3,3\}$ N	Sampling Period	0.0001 s

The dynamics model of the 2-DOF manipulator system can be described as (8), where the inertia matrix $M\left(q\right)$, Coriolis force matrix $C(q,\dot{q})$ and gravity matrix $G\left(q\right)$ can be defined as

$$\begin{array}{ccc}& & M\left(q\right)=\left[\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right],C(q,\dot{q})=\left[\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right],G\left(q\right)=\left[\begin{array}{c}{G}_1\\ G_2\end{array}\right]\hfill \end{array}$$

where

$$\begin{array}{cc}& \left\{\begin{array}{c}{M}_{11}=m_1{l}_1^2+m_2{l}_1^2+m_2{l}_2^2+2m_2{l}_1{l}_{2}cos{q}_2\hfill \\ M_{12}=M_{21}=m_2{l}_2^2+m_2{l}_1{l}_{2}cos{q}_2\hfill \\ M_{22}=m_2{l}_2^2\hfill \\ C_{11}=-m_2{l}_1{l}_2{\dot{q}}_{2}sin{q}_2\hfill \\ C_{12}=-m_2{l}_1{l}_2{\dot{q}}_{1}sin{q}_2--m_2{l}_1{l}_2{\dot{q}}_{2}sin{q}_2\hfill \\ C_{21}=m_2{l}_1{l}_2{\dot{q}}_{1}sin{q}_2\hfill \\ C_{22}=0\hfill \\ G_1=m_1{l}_{1}gcos{q}_1+m_2{l}_{1}gcos{q}_1+m_2{l}_{2}gcos(q_1+q_2)\hfill \\ G_2=m_2{l}_{2}gcos(q_1+q_2)\hfill \end{array}\right.\end{array}$$

(51)

The parameters of the BLF-ANBG controller are described in Table 2.

Table 2. The parameters of controller.

Parameters	Values	Parameters	Values	Parameters	Values
${\beta }_{11}$, ${\beta }_{12}$	0.5	${\zeta }_{11}$, ${\zeta }_{12}$	0.5	${\beta }_{21}$, ${\beta }_{22}$	0.05
${\zeta }_{21}$, ${\zeta }_{22}$	0.05	${\sigma }_{11}$, ${\sigma }_{12}$	0.5	${\sigma }_{21}$, ${\sigma }_{22}$	10
${\delta }_{11}$, ${\delta }_{12}$	2000	${\delta }_{21}$, ${\delta }_{22}$	270	${\alpha }_{11}$, ${\alpha }_{12}$	1000
${\alpha }_{21}$, ${\alpha }_{22}$	5	${\xi }_{11}$, ${\xi }_{12}$	1800	${\xi }_{21}$, ${\xi }_{22}$	250
$\epsilon$	0.1	$\psi$	10	Q	$diag\left\{60,60,60,60\right\}$

From Table 2, $0<{\beta }_{ij}<1$, $0<{\zeta }_{ij}<1$, the values of ${\beta }_{ij}$ and ${\zeta }_{ij}$ are obtained by trial and error within an appropriate range. When ${\beta }_{ij}$ and ${\zeta }_{ij}$ are larger, the dynamic response of the system is faster, and when ${\beta }_{ij}$ and ${\zeta }_{ij}$ are smaller, the transition process is smoother. If ${\alpha }_{ij}$ is larger, the upper bound of the variable gain function of the error is larger, and the systems response is faster, which can be appropriately increased on the premise of ensuring the safety of the system. ${\delta }_{ij}$ is the lower and upper bounds of the two gain functions, and ${\delta }_{ij}>{\xi }_{ij}$ ensures that the system is stable. Q can be appropriately increased to enhance the system convergence effect.

5.1. Simulation Comparison Results of Smooth-Switching for Backstepping Gain Strategy

In this part, the manipulator system uses the smooth-switching for backstepping gain strategy to track the unit-step signal, and compares it with two variable gain functions without the smooth-switching strategy. The initial position of each joint of the manipulator system is $q\left(0\right)={\left[0,0\right]}^{\mathrm{T}}$, the execution saturation is $\pm 20$ N·m, and the output constraints of each joint are $y_{imin}=-0.3+0.1sin(0.8t+\frac{\pi }{3})$, $y_{imax}=1.3+0.2sin(0.5t+\frac{\pi }{2})$. The tracking and error curves for the unit-step signal are provided in Figure 4.

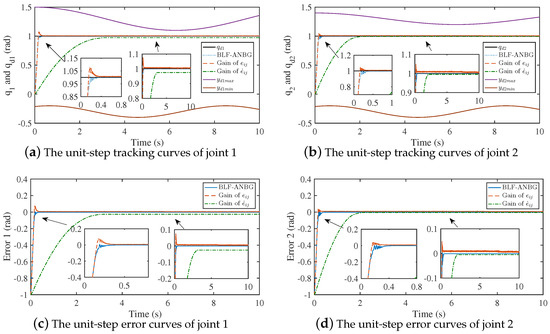
Figure 4. The unit-step tracking curves compared to two variable gain functions.

As can be seen from Figure 4, using only the gain function based on the error has a faster response speed and can reach the steady-state faster, but there will be overshoot, and large jitter will occur after reaching the steady state. Using only the gain function based on the change rate of error can improve steady-state performance but has a long response time. The smooth-switching for backstepping gain strategy combines the advantages of two gain functions and can have good dynamic and steady-state performances at the same time.

5.2. Without Modeling Error and Unknown Load

In this part, the manipulator tracks the unit-step signal and the expected periodic signal $q_d={\left[0.8sin(0.5t+\frac{\pi }{2}),0.9sin(0.8t+\frac{\pi }{3})\right]}^{\mathrm{T}}$ without modeling error and load, respectively. The input torque saturation of each joint is $\pm 20$ N·m. The joint constraints that track the unit-step signal are $y_{imin}=-0.3+0.1sin(0.8t+\frac{\pi }{3})$, $y_{imax}=1.3+0.2sin(0.5t+\frac{\pi }{2})$. The joint constraints that track the periodic signal signal are $y_{imin}=-1.1+0.1sin(0.6t+\frac{\pi }{3})$, $y_{imax}=1.2+0.2sin\left(0.5t\right)$. The proposed BLF-ANBG strategy is compared with the conventional backstepping strategy under large gain and small gain. The tracking and error curves for the unit-step signal and periodic signal are as shown in Figure 5 and Figure 6. The dynamic performance and steady-state performance of the tracking two signals are as shown in Table 3.

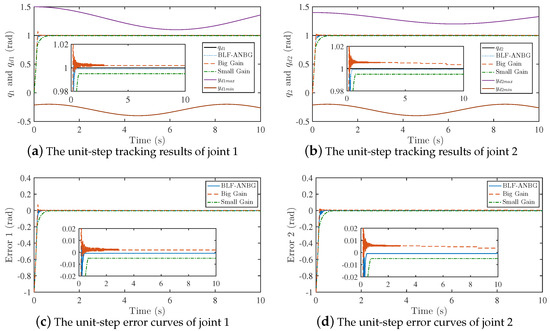
Figure 5. The unit-step tracking curves compared to traditional backstepping.

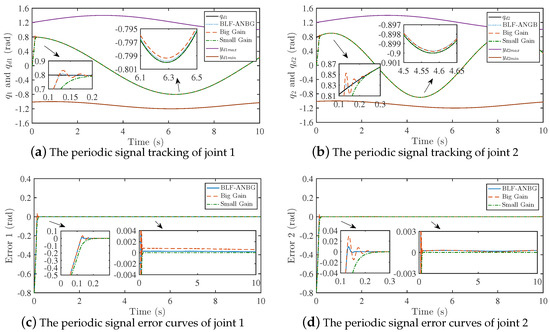
Figure 6. The periodic signal tracking curves compared to traditional backstepping.

Table 3. The rise time and error range compared to traditional backstepping.

Signal	Joint	Description	BLF-ANGB	Big Gain	Small Gain
Unit-step	joint 1	Rise Times (s)	0.1865	0.1525	0.6653
		Tracking Error (rad)	$\pm 0.0013$	$\pm 0.0095$	$\pm 0.0059$
		Jitter Range (rad)	$0.0005$	$0.032$	$0.0002$
	joint 2	Rise Times (s)	0.1894	0.1503	0.6712
		Tracking Error (rad)	$\pm 0.0011$	$\pm 0.0065$	$\pm 0.0004$
		Jitter Range (rad)	$0.00054$	$0.0035$	$0.0001$
Period	joint 1	Rise Times (s)	0.1255	0.1244	0.2312
		Tracking Error (rad)	$\pm 0.0013$	$\pm 0.0342$	$\pm 0.0011$
		Jitter Range (rad)	$0.0007$	$0.0022$	$0.0001$
	joint 2	Rise Times (s)	0.1269	0.1255	0.2716
		Tracking Error (rad)	$\pm 0.0009$	$\pm 0.0296$	$\pm 0.0005$
		Jitter Range (rad)	$0.00011$	$0.00025$	$0.00001$

From these figures and tables, it is easy to see that the joint outputs are all within the given constraints. The fixed gain of the traditional backstepping strategy without smooth-switching for gain can affect the performance of the system tracking. When the gain is large, although the system reaches the steady state in 0.1525 s and the accuracy is high, the system has a large jitter in the steady state, and the jitter range is 0.032 rad. When the gain is small, the jitter range is 0.0002 rad, which is smaller than that when the gain is large, but the system reaches the steady state at 0.6712 s and the accuracy is low. Therefore, the value of the backstepping gain will cause the contradiction between the dynamic characteristics and the steady-state characteristics of the system. When the BLF- ANBG strategy is applied, this contradiction can be effectively solved, the system can quickly reach the steady state and have better steady-state performance.

Secondly, the feasibility of this strategy is verified by comparing two commonly used SMC strategies and PD gravity compensation strategies. The tracking and error curves of the unit-step signal and periodic signal of the three strategies are presented in Figure 7 and Figure 8, respectively. The tracking performances are shown in Table 4.

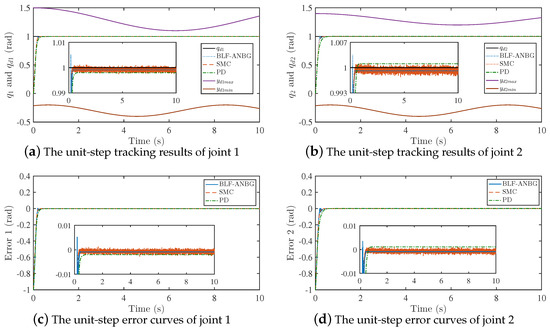
Figure 7. The unit-step signal tracking and error curves of the three strategies.

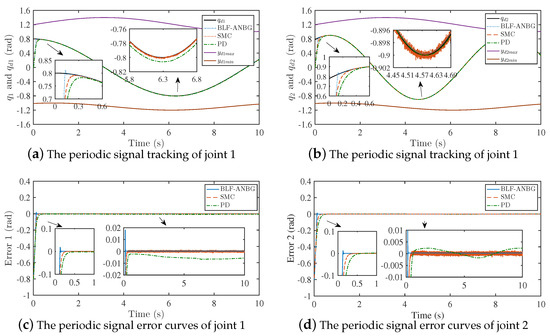
Figure 8. The expected periodic signal tracking and error curves of the three strategies.

Table 4. The rise time and error range without modeling error and load.

Signal	Joint	Description	BLF-ANGB	SMC	PD
Unit-step	joint 1	Rise Times (s)	0.1865	0.267	0.5041
		Tracking Error (rad)	$\pm 0.0013$	$\pm 0.002$	$\pm 0.0021$
	joint 2	Rise Times (s)	0.1894	0.296	0.6201
		Tracking Error (rad)	$\pm 0.0011$	$\pm 0.002$	$\pm 0.0011$
Period	joint 1	Rise Times (s)	0.1255	0.1956	0.3913
		Tracking Error (rad)	$\pm 0.0013$	$\pm 0.0023$	$\pm 0.0067$
	joint 2	Rise Times (s)	0.1269	0.2154	0.4541
		Tracking Error (rad)	$\pm 0.0009$	$\pm 0.0021$	$\pm 0.0024$

It can be seen from Figure 7 and Figure 8 and Table 4 that the SMC can quickly reach the steady-state when tracking the unit-step signal and the periodic signal, but the chattering phenomenon occurs, and the jitter range of each joint is 0.004 rad and 0.0046 rad. The jitter of the PD gravity compensation strategy is obviously reduced, yet the tracking accuracy is poor, and the tracking error is $\pm 0.0067$ rad. Compared with these two strategies, BLF-ANBG has better tracking accuracy and stability, and can reach steady state faster.

5.3. With Modeling Error and Unknown Load

In this part, time-varying modeling errors and time-varying unknown loads are added to simulate the tracking effect of the manipulator in practical engineering applications. The controller parameters are the same as in Table 2. The parameters of modeling error and unknown load are described in Table 5.

Table 5. The parameters of modeling error and unknown load.

Parameters	Values	Parameters	Values
$\Delta M\left(q\right)$	$0.15M\left(q\right)$	$\Delta C(q,\dot{q})$	$0.25C(q,\dot{q})$
$\Delta G\left(q\right)$	$0.2M\left(q\right)$	$\Delta J_m$	$0.1J_m$
${\tau }_{{}_L}$	$\left[\begin{array}{c}10sin\left(0.5t+\pi /\phantom{\pi 2}2\right)\\ 10sin\left(0.5t+\pi /\phantom{\pi 2}2\right)\end{array}\right]$	$\Delta E$	$\left[\begin{array}{c}0.1cos0.5t\\ 0.1cos0.5t\end{array}\right]$

To verify the performance of the BLF-ANBG strategy, the BLF-GSS strategy, the SMC strategy and the PD gravity compensation strategy are used for comparison. The initial position of the joint is 0. The approximation curves of the adaptive neural network strategy are shown in Figure 9.

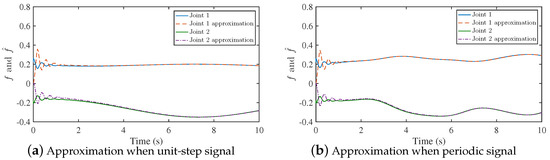
Figure 9. The approximation curves for the unit-step signal and expected periodic signal.

Figure 9 clearly shows that although the adaptive neural network has large approximation error in the initial stage, it can effectively approximate the modeling error and unknown load within 2 s. The tracking result and error curves of the unit-step signal are given in Figure 10, the tracking result and error curves of the expected periodic signal are provided in Figure 11. The controller performance is shown in Table 6.

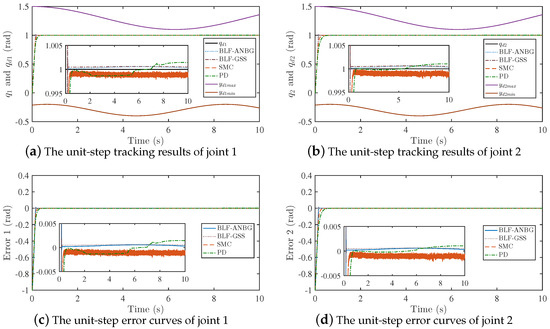
Figure 10. The unit-step signal tracking and error curves of the four strategies.

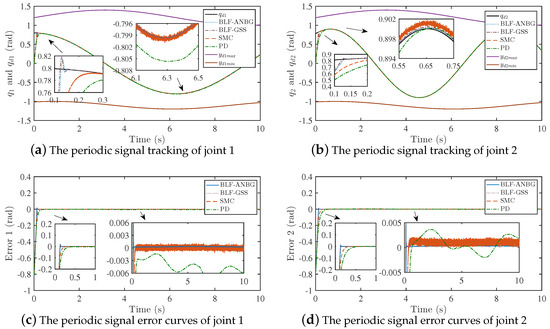
Figure 11. The expected periodic signal tracking and error curves of the four strategies.

Table 6. The tracking performance with modeling error and load.

Signal	Joint	Description	BLF-ANGB	BLF-GSS	SMC	PD
Unit-step	joint 1	Rise Times (s)	0.1562	0.1506	0.2817	0.4634
		Tracking Error (rad)	$\pm 0.0005$	$\pm 0.0006$	$\pm 0.0016$	$\pm 0.0014$
	joint 2	Rise Times (s)	0.1552	0.1496	0.2142	0.5652
		Tracking Error (rad)	$\pm 0.0005$	$\pm 0.0007$	$\pm 0.002$	$\pm 0.0012$
Period	joint 1	Rise Times (s)	0.1247	0.1235	0.2721	0.4254
		Tracking Error (rad)	$\pm 0.0002$	$\pm 0.0004$	$\pm 0.0017$	$\pm 0.0054$
	joint 2	Rise Times (s)	0.1223	0.1269	0.3256	0.4481
		Tracking Error (rad)	$\pm 0.0003$	$\pm 0.0006$	$\pm 0.0022$	$\pm 0.0047$

According to Figure 10 and Figure 11 and Table 6, it can be known that modeling errors and unknown loads have an impact on the tracking accuracy of the manipulator. In the absence of adaptive neural network compensation, the BLF-GSS strategy, the SMC strategy and the PD gravity compensation strategy all generate large tracking errors; the maximum tracking errors of the three strategies are $\pm 0.0007$ rad, $\pm 0.0022$ rad, $\pm 0.0054$ rad. The BLF-ANBG strategy can effectively reduce the modeling error and the influence of unknown loads, and can cause each joint to reach the steady-state within 0.156 s; the steady-state accuracy is also high. At the same time, the joints are all within the given constraints.

Summarizing the above results, the strategy proposed in this article can track the desired position signal quickly and stably in the presence of modeling errors and unknown loads. The contradiction between dynamic and steady-state caused by backstepping method gain is significantly improved.

6. Conclusions

This article presents a new tracking control strategy to solve the contradiction between the dynamic and steady-state characteristic caused by the control gain of the manipulator when there are uncertain interference terms. In this work, an overall model of the manipulator driven by PMSM with multiple constraints, modeling errors, and unknown loads is established. The proposed BLF-ANBG control strategy is applied to the 2-DOF manipulator. The simulation comparison shows that the proposed control strategy can effectively improve the contradiction between the dynamic and the steady-state performances of the system, and make the system take into account both excellent dynamic and steady-state characteristics. Additionally, the strategy effectively compensates for model errors, external disturbances and actuator saturation, while limiting the output of the system within the time-varying asymmetric constraint, which is more suitable for practical engineering needs. In actual engineering, the state of the speed and acceleration of the manipulator will also be constrained. In the future work, we will work hard to solve the problem of the full-state constraints of the manipulator system.