Abstract
For solving the transformation problem between the desired nonlinear control laws and installed actuators’ input commands of torpedo-like underwater vehicles, one closed-form control allocation method is proposed in this article. The goal of this study is to optimally distribute the desired nonlinear control law to each single actuator installed on the torpedo-like underwater vehicle. The first step of this proposed control allocation method is to arrange the required types, numbers, and positions of the installed actuators and then build up the thrust configuration matrix for the developed torpedo-like underwater vehicle. In this step, the desired nonlinear control law can be optimally distributed to output commands of installed actuators based on the optimization method. Next, through collecting the input and output data of each installed actuator by practical experiments, the mathematical transformation of input and output commands of each installed actuator can be found. For verifying performance of this proposed control allocation method, simulations with the robust trajectory tracking design of a torpedo-like underwater vehicle with four fins, four rudders, and one thruster are executed in this investigation.
1. Introduction
Various underwater vehicles have been developed to serve different purposes. For example, a box-shaped underwater vehicle is usually designed to perform tasks at low speed since the shape of the underwater vehicle would produce massive drag forces, while on the other hand, it is generally attached with thrusters along all the control dimensions to gain high maneuverability and precise position control. Additionally, with the above advantages, the box-shaped underwater vehicle is good at performing tasks such as seafloor mining or marine creature observation. Meanwhile, the torpedo-like underwater vehicle which is the research target of this paper has the following features. First of all, the hull of the torpedo-like underwater vehicle is streamlined allowing it to perform tasks at high speed and greatly reduce the drag force of the underwater vehicle. Secondly, in order to further reduce the drag force while moving, the torpedo-like underwater vehicle is usually mounted with thrusters along the forward direction and several fins and rudders to control the heading angle of the underwater vehicle. The last thing to mention is that the torpedo-like underwater vehicle is not controllable without speed, since the forces needed to change the heading direction are produced by fins and rudders which are not sensitive at low speed, but disadvantages such as this could be mended by adding a tunnel thruster on the hull of the underwater vehicle. As the features mentioned above, the torpedo-like underwater vehicle is suitable for performing tasks at high speed or low speed with low energy consumption, such as seafloor mapping and long-time automatic control. The realm of the autonomous underwater vehicle is very useful and prospective, and hence the guidance/control laws of the different types of the autonomous underwater vehicles have been developed through many methods. In the past decade, several nonlinear control laws based on the sliding mode control concept were proposed for the trajectory tracking problems of underwater vehicles [1,2,3]. These studies delivered satisfactory trajectory tracking performances based on the linearized model or the simplified model, with only heading and surge dynamics of underwater vehicles. In practice, the common way to guide the underwater vehicle is the line of sight (LOS) guidance method [4]. Through changing the heading way of the underwater vehicle toward the desired tracking point and using the propeller to move to the desired location, the control law derived from the LOS method reduces the desired control dimensions, which makes the derivation easier and reduces the number of actuators that the underwater vehicle needs. However, the deficiency of control dimensions would lead to inaccurate tracking results in certain directions and unexpected attitude of the underwater vehicle. To achieve precise positioning and accurate attitude control, all the degrees of freedom (surge, sway, heave, roll, pitch, yaw) must be taken into consideration. Instead, the full control of the underwater vehicle requires more actuators to be realized, and the control law derivation is much more complicated; hence, in practice, how to balance the control design and usage of actuators for controlled underwater vehicles simultaneously become an important and tricky issue. Control allocation verification perhaps is the solution of this problem because feasibility of a well-developed control law for underwater vehicles in real situations can be verified through whether distribution of the desired control command to inputs of actuators can be executed properly. To the best knowledge of the authors, limited research which investigates control law designs for underwater vehicles simultaneously take models of actuators into account in the past decade [5,6,7,8,9]. However, to put the derived control laws into practice, taking account of actuators in control designs of underwater vehicles is important and necessary. Until now, only very few control laws of vehicles integrated related control allocation methods because the complexity and difficulty are highly upgraded when integrating the control law and power allocation method. Generally, the more practical way to overcome this problem is to separate the derivation of the control law and control allocation process. Control allocation methods for vehicles have been summarized in [10,11,12,13], but no numerical simulations or practical results were delivered in these contributions. Some of these numerical searching methods, including the redistributed pseudo inverse method [14], linear programming method [15,16], and quadratic programming method [17], are roughly introduced for the designs of specific underwater vehicles. Mathematically, the redistributed pseudo inverse method has the advantage of fast calculation for the real-time realization of power allocation methods, but this is not a globally optimal design. As to the linear programming method and quadratic programming method, they currently possess support of several software programs, such as MATLAB, Mathematica, etc. Researchers and engineers of control system designs of underwater vehicles can conveniently use the well-developed tools of these two numerical searching methods to find out an optimal power allocation solution for the controlled underwater vehicle in each control moment. However, for achieving a real-time calculation for these two solution searching methods, ultra-high speed calculators are always required in practice. Based on these revealed reasons, a power allocation method which simultaneously has an easy-to-implement structure, i.e., closed-form design, and a global optimization property is proposed in this investigation for transforming the desired control commands into inputs of actuators.
2. Mathematical Model and the Desired Control Law for Torpedo-Like Underwater Vehicles
2.1. Problem Formulation
2.1.1. Dynamics of Underwater Vehicle and Robust Control Law
The proposed torpedo-like underwater vehicle with 4 fins, 4 rudders, and 1 non-rotatable thruster is shown in Figure 1.
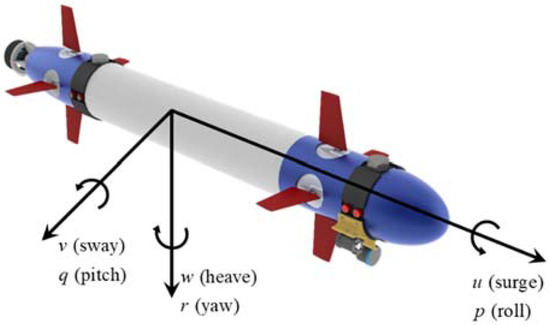
Figure 1.
The proposed torpedo-like underwater vehicle with 4 fins, 4 rudders, and 1 non-rotatable thruster.
According to Fossen [12], the mathematical model of the discussed torpedo-like underwater vehicle can be formulated as follows:
where vector η is the position and Euler angle vector of the underwater vehicle with respect to the earth frame, the vector v stands for the linear and angular velocity vector of the underwater vehicle with respect to the body-fixed frame, and the transition matrix between η = [x, y, z, φ, θ, ψ]T and v = [u, υ, w, p, q, r] T as listed in Table 1 is J(η). The matrix M represents the mass and inertia matrix of the underwater vehicle, C(v) is the Coriolis and centripetal matrix, D(v) is the hydrodynamic damping matrix, and g(η) is the gravitational and buoyancy vector. τ(e)∈R6 is the desired H∞ control law applied to control the torpedo-like underwater vehicle to track a desired trajectory, and τ(e) is also the desired target that the control allocation seeks to achieve. τd is the ocean environmental disturbances.

Table 1.
The notation for torpedo-like underwater vehicles.
By referring to [18], the desired H∞ control law τ(e), which is derived using the robust control concept, is chosen as below for the control allocation design of the torpedo-like underwater vehicle in Figure 1.
where the vector e is the trajectory tracking error vector between the torpedo-like underwater vehicle and the desired trajectory and defined as the following:
Term τe in Equation (2) is designed to eliminate the external disturbance, i.e., ocean current. As to the fuzzy logic term ζ(e)Θf, it is developed to deal with the perturbed uncertainties of the torpedo-like underwater vehicle.
where λ1, λ2, Γ, and Z are designable positive parameters or positive definite vectors, and ζ(e) is the fuzzy architecture matrix.
2.1.2. Control Allocation Design
The main design target of this investigation is to develop effective control allocation methods which can precisely and optimally convert the desired control law in Equation (1) into installed actuators’ inputs. The overall control allocation procedure for the studied torpedo-like underwater vehicle is illustrated in Figure 2. From Figure 2, it is easy to find out that the proposed method integrates optimal control allocation methods and a transformation of input and output commands of the installed actuators to generate applicable turning angles and PWM (pulse-width modulation) signal based on the H∞ control law to drive the torpedo-like underwater vehicle to precisely track desired trajectory .
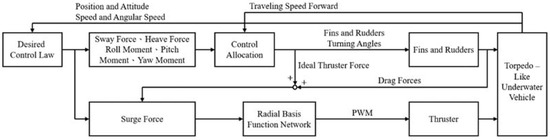
Figure 2.
The flow chart of the control allocation procedure for the torpedo-like underwater vehicle with multiple actuators.
2.2. Actuator Models
The mathematical relationship between the desired control law τ(e) and the output command vector f of the installed actuators, including turning angles of fins, turning angles of rudders, and thrust of the thruster of the controlled underwater vehicle, could be presented as follows.
where , , …, are output commands of the installed actuators.
T represents the thrust configuration matrix of the actuators, which indicates how the overall actuator control commands perform on the underwater vehicle and can be expressed as
where dypb, dysb, …, and dyT are the distances from the positions of each single installed actuator to the center of gravity of the torpedo-like underwater vehicle.
3. Control Allocation Methods for Torpedo-Like Underwater Vehicles
Based on the mathematical relationship between the desired control command τ(e) and output commands f of the installed actuators in Equation (6), an analytically optimal searching method is developed to find out the optimal output command vector f* which can precisely convert the output commands of the installed actuators into the desired control command τ(e), the method is shown in the following.
Least Squares Optimization Method
As the above mentions, the control allocation method aims to distribute the desired control law τ(e) to the installed actuators of the torpedo-like underwater vehicles and meanwhile minimizes the overall energy consumption of all the actuators. The mathematical representation of the control allocation problem of the torpedo-like underwater vehicles could be stated as follows:
where P∈R9×9 is the weighting matrix of power consumption which is positive definite. This kind of problem is called least squares optimization, and it can be solved by using the Lagrange multiplier.
Define the Lagrangian:
where λ is a vector of Lagrange multipliers, which is introduced to convert the constrained problem into an unconstrained problem. Differentiating Equation (10) with respect to f and λ, it yields
From Equation (11), it gives
From Equations (12) and (13), it yields
The vector of Lagrange multipliers λ can be derived from Equation (14):
Substituting Equation (15) into Equation (13), the analytical output command vector of the actuator f could be solved as follows:
From the mathematical derivations, the optimal solution of f*, which is the output vector of the installed actuators, can be analytically found based on Equation (16). For practical applications, the transformation between outputs and inputs of the installed actuators should be further discussed.
Remark 1:
The weighting matrix P of Equation (16) is generally set up as an identity matrix I∈R9×9 because the efficiency of all installed actuators is equal practically. However, for specific control purposes, which intend to emphasize stern control or bow control of torpedo-like underwater vehicles, adjustments of P are required. The guideline for selecting P is suggested as follows:
Assume P has the following form:
If more control forces and torques are demanded to be generated from stern rudders and fins, values of , , , and should be smaller than , , , and . Inversely, larger control forces and torques can be generated to the bow part of the controlled torpedo-like underwater vehicle based on giving smaller values to , , , and .
Assume the mapping between outputs and inputs of the installed actuators can be presented as
where K∈R9×9 is the force coefficient matrix of the installed actuators and u∈R9×1 is the actuator input command vector. The force coefficient matrix K and the actuator input command vector u will be detailed below.
Construction of the force coefficient vector of the installed actuators K depends on configuration and types of installed actuators. The main thruster, which is non-rotatable, is usually mounted on the aft of the controlled underwater vehicle to produce propulsive forces along the x axis and pushes the torpedo-like underwater vehicles forward in this study; hence, the relationship between the thruster’s input and output can be described by . Furthermore, rudders and fins are the key apparatus to steer the torpedo-like underwater vehicles. Rudders provide forces in the y axis to control sway and roll of the torpedo-like underwater vehicles; meanwhile, fins produce forces in the z axis to manipulate heave and roll of the underwater vehicles. Forces generated by rudders and fins are related to the traveling speed of the torpedo-like underwater vehicles, and the relationships between generated forces, traveling velocity, and turning angle of rudders and fins are as follows:
where L is the lift force of fins or rudders, D is the drag force of the rudders, ρ stands for the density of the water, A means the reference area of fins and rudders, and vf is the flow velocity relative to fins or rudders, and in the underwater vehicle case, it usually means the traveling speed of the vehicle, or linear velocity along the x-direction. It is clear that the fins and rudders need flow velocity or traveling speed to generate forces. CL and CD stand for the lift coefficient and drag coefficient, which could be measured through experiments, and δ is the attack angle of fins and rudders. The schematic diagrams of the fin and rudder operations are shown in Figure 3 and Figure 4 as follows.
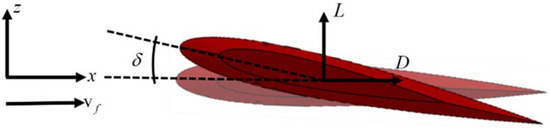
Figure 3.
The schematic diagram of fins.
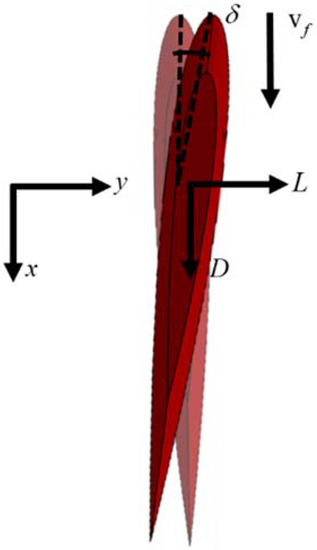
Figure 4.
The schematic diagram of rudders.
Because there are four fins, four rudders, and one non-rotatable thruster installed in this torpedo-like underwater vehicle, the vector of control forces generated by actuators, including thrusters, rudders, and fins as above mentioned can be expressed as:
where , , …, are turning angles of fins and rudders, and is the PWM command signals. We can regard these variables as inputs of actuators.
The force coefficient vector of the installed actuators K can be expressed as below:
where , ,…, and can be approximated as either a constant value or a nonlinear function.
It is worth noticing that the closed-form solution of the actuator input command vector, which implies a real-time control design is obtained, could be analytically derived for power allocation design of the trajectory tracking problem of torpedo-like underwater vehicles as follows:
4. Implementation for a Torpedo-Like Underwater Vehicle
The following figures show the prototype of the torpedo-like underwater vehicle developed and named “AUV Lab 611” by the Autonomous Vehicle Lab of National Cheng Kung University, which aims to perform underwater missions. This underwater vehicle contains one fixed thruster and one pair of fins and rudders at the stern, and one pair of fins and rudders near the bow.
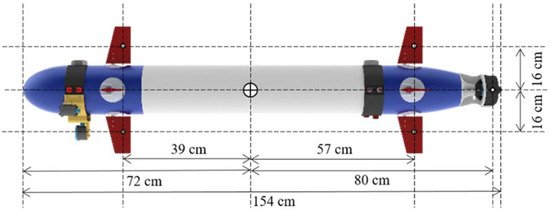
Figure 5.
Side view of the developed underwater vehicle.
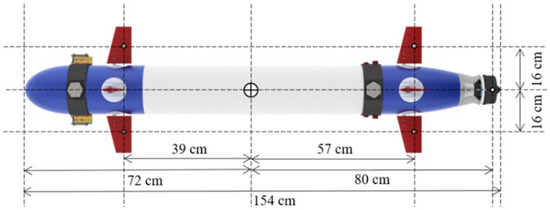
Figure 6.
Top view of the developed torpedo-like underwater vehicle.
4.1. The Specifications of the Underwater Vehicle
The following table shows the detailed specifications of this developed torpedo-like underwater vehicle. Twenty percent of modeling uncertainties were added for physical parameters: mass m, moment of inertia Ix, moment of inertia Iy, and moment of inertia Iz, listed in Table 2, during the trajectory tracking period.

Table 2.
Parameters of the controlled torpedo-like underwater vehicle.
From the specifications of the developed underwater vehicle, it is clearly noticed that the torpedo-like underwater vehicle is not in the neutral buoyancy condition since the center of gravity does not coincide with the center of buoyancy; meanwhile, the weight of the underwater vehicle is lighter than the buoyancy. In summary, when the torpedo-like underwater vehicle is put in the water, it would be tilted and float up to the surface. To avoid this problem, the proper way is to add extra weights on this developed torpedo-like underwater vehicle and adjust its center of gravity to the center of buoyancy.
4.2. The Configuration Matrix of the Torpedo-Like Underwater Vehicle
The configuration matrix of the torpedo-like underwater vehicle is related to the distance from the position of the actuators to the center of gravity.
From Figure 5 and Figure 6, it is obvious that this developed torpedo-like underwater vehicle is driven by four fins and four rudders and one fixed thruster. Considering the center of gravity as the zero point, the specifications of the actuators could be represented as Table 3.

Table 3.
The related specifications of fins and rudders of the developed torpedo-like underwater vehicle.
Following the derivations of Equations (7) and (8) above, the thrust configuration for this real developed torpedo-like underwater vehicle could be presented as
Derived from Equation (23), the thrust configuration matrix is in full rank, which means all directions of the underwater vehicle could be controlled, and meanwhile, the dimension of the generated control force vector is larger than the degrees of freedom that the desired control law wants to control, which will lead this investigation to an over-actuated control allocation problem.
4.3. The Actuator Model of the Underwater Vehicle
The discussed torpedo-like underwater vehicle in this investigation is driven by four fins, four rudders, and one fixed thruster. The mathematical presentation of these actuators could be formulated as mapping like Equation (17).
The force coefficient matrix K could be obtained by gathering input control commands and measuring generated control forces through simulations and practical tests.
4.3.1. The Hydrodynamics Model of Fins and Rudders
According to the discussion of the actuator model in Equations (18) and (19), the generated forces of the fins and rudders are expressed as
The density of water ρ was 997 kg/m and the fin and rudder reference areas A of the torpedo-like underwater vehicle prototype in our lab were 0.008 m2, and the lift coefficient CL and drag coefficient CD are related to the shape of the fin and rudder. The fins and rudders of the discussed torpedo-like underwater vehicle was designed based on the fin shape NACA−0012 type, which had a chord length of 8 cm. The lift force and the drag force of these adopted fins and rudders could be predicted precisely using a software program called Xfoil. The Xfoil software program calculation needs to input the shape of the fin and rudder along with the Reynolds number, and the Reynolds number is determined by the kinematic viscosity of the fluid, velocity of the fluid, and the chord length.
where vf is the fluid velocity, c is chord length, and υ is the kinematic viscosity. The desired traveling speed of the underwater vehicle was between 1 and 3 m/s and the kinematic viscosity of the water was 9.7937 × 10−7 m2/s.
Define the lift and drag constants as follows:
Through calculation, the Reynolds number of the fin and rudder lies around 80,000 to 245,000, and the Xfoil prediction outputs the lift and drag constants with respect to turning angles and the results are shown in Figure 7 and Figure 8.
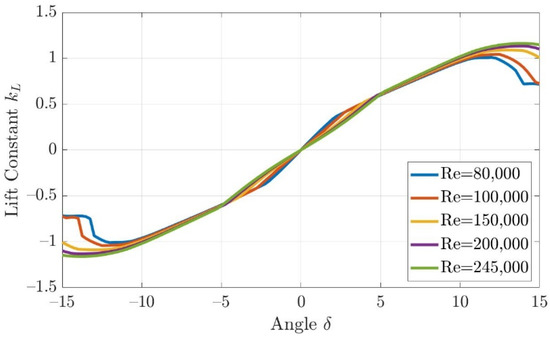
Figure 7.
The lift constant kL with respect to turning angle δ.
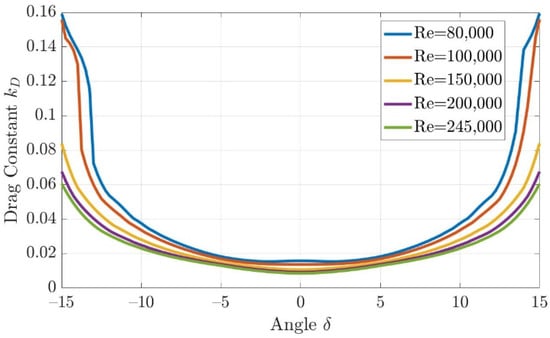
Figure 8.
The drag constant kD with respect to turning angle δ.
By using the approximation method for Figure 7 and Figure 8, the lift coefficient and drag coefficient could be estimated as
Hence, , ,…, of the force coefficient vector of the installed actuators K in Equation (21) can be all set up as 0.1090.
4.3.2. The Actuator Model of the Thruster
The fixed thruster on the discussed torpedo-like underwater vehicle is the T200 Thruster made by the Blue Robotics company. This thruster was controlled by the time interval of input square signals, and the company provides practical test data of the thruster and illustrates the relation between the input time interval and the output generated forces as in Figure 9.
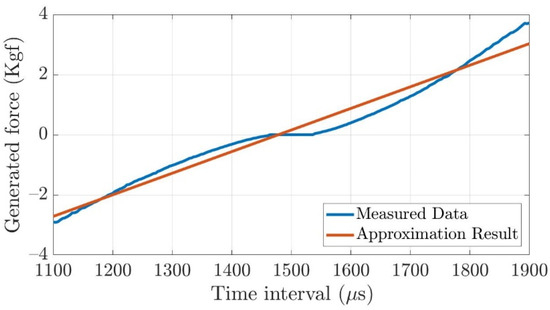
Figure 9.
The generated force with respect to time interval (PWM) using linear approximation.
The relation between PWM signals and generated forces is roughly linear, and the mathematical presentation of the thruster could be expressed as
A more precise way to approximate the thruster model is using a radial basis function network to approximate the relationship between the input PWM signals and the generated forces as . From Figure 10, it is easy to find out that the proposed radial basis function network can precisely approximate the behavior between input and output of the thruster. The detailed derivation is given in Appendix A. Through setting the inputs as measured generated forces and outputs as PWM signals, then a radial basis function network can be constructed to continuously calculate PWM signal when the control allocation gives the generated force that the thruster should produce.
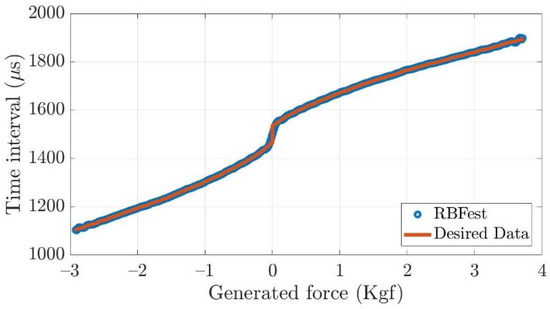
Figure 10.
The generated force with respect to time interval (PWM) using radial basis function network approximation.
4.4. Control Allocation Verification for a Torpedo-Like Underwater Vehicle
The simulation of the control allocation assumes that the torpedo-like underwater vehicle travels forward at low speed and the fluid speed on fins and rudders is equal to the traveling speed forward. Since the torpedo-like underwater vehicle travels at low speed, the small drift angle could be ignored, and furthermore, the attack angle of the fins and rudders could be regarded as the turning angle of the fins and rudders because of the neglect of drift angle [13]. Moreover, the drag forces of the fins and rudders are small compared to lift forces, so the moments produced by the drag force are ignored in this simulation. Dimensions of the desired control is 6 degrees of freedom (surge, sway, heave, roll, pitch, and yaw), and the detailed specifications of the torpedo-like underwater vehicle are presented in Table 2, and actuators are presented in Table 3. From the configuration matrix of the torpedo-like underwater vehicle in Equation (23), it is clear to see that the thruster controls only the surge way. Fins and rudders control the rest of the dimensions, so the control allocation procedures could be clarified as the following steps:
- Step 1.
- Solve the control allocation of the fins and rudders.
- Step 2.
- Calculate the angle of fins and rudders.
- Step 3.
- Calculate the drag forces of the fins and rudders by using Equation (26).
- Step 4.
- Calculate the thruster force by the desired control law and compensation of drag forces.
- Step 5.
- Calculate the PWM signal of the thruster by using the radial basis function network.
As the above arrangement, for verifying the performance of this control allocation design, a H∞ control law in Equation (2) and a sliding mode control [19] were adopted for guiding the developed torpedo-like underwater vehicle, and here one trajectory tracking case was selected to test the proposed control allocation method.
Scenario 1
In Scenario 1, the developed torpedo-like underwater vehicle starts with an initial speed 0.5 m/s forward, and the designated waypoints which will be connected as a smooth and continuous trajectory using the cubic spline method are listed in Table 4.

Table 4.
Waypoints for Scenario 1.
The initial conditions of the developed underwater vehicle are as follows:
(x, y, z, φ, θ, ψ) = (0.05, 0, 5, 0, 0, 0)
(u, υ, w, p, q, r) = (0.5, 0, 0, 0, 0, 0)
The control parameters of the nonlinear H∞ control law are chosen as Table 5.

Table 5.
The control parameters of the nonlinear H∞ control law.
The derived sliding mode control law has the following form:
where values of control parameters: λf1, λf2, ksc, and ks are listed in Table 6.

Table 6.
Control parameters of the sliding mode control law.
In this simulation, the developed torpedo-like underwater vehicle was controlled by the H∞ control law in Equation (2) and a sliding mode control, respectively. The tracking histories are illustrated in the following picture. The red dashed line is the desired trajectory, the green line is the tracking result of the nonlinear H∞ control law, and the blue line is the tracking result of the sliding mode control law. From Figure 11, the controlled torpedo-like underwater vehicle precisely tracks the desired trajectory with a steady state velocity 2 m/s.
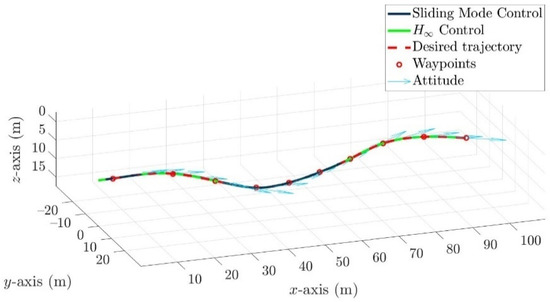
Figure 11.
Trajectory tracking history of the controlled torpedo-like underwater vehicle based on sliding mode control law (blue line) and the proposed nonlinear H∞ control law (green line) for Scenario 1.
The tracking errors of the controlled torpedo-like underwater vehicle are shown in Figure 12 and Figure 13. Obviously, there is an initial offset of −3.95 m between the first waypoint and the controlled torpedo-like underwater vehicle in the x-axis, and this position error converges to near zero exponentially. From Figure 12, the nonlinear H∞ control law outperforms the sliding mode control in position tracking ability. In addition, attitude tracking errors with respect to pitch and yaw directions of the controlled torpedo-like underwater vehicle converged quickly and bounded within ±0.5° in a steady state for two control laws, even as it was directly affected by induced forces and torques of time-varying ocean currents, and the sliding mode control law has better tracking performances in pitch and yaw directions.
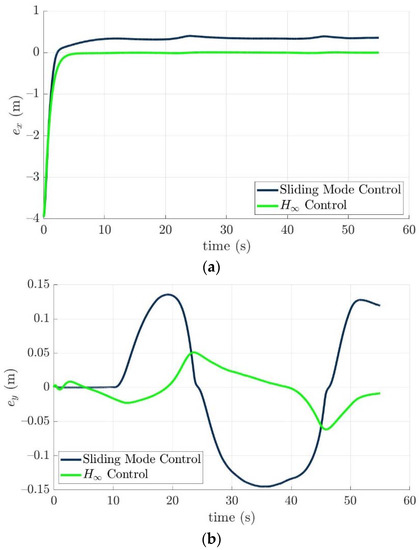
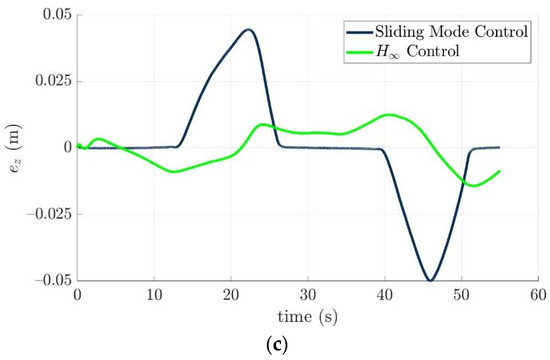
Figure 12.
Histories of the position tracking errors of the controlled torpedo-like underwater vehicle: (a) x-axis, (b) y-axis, and (c) z-axis.
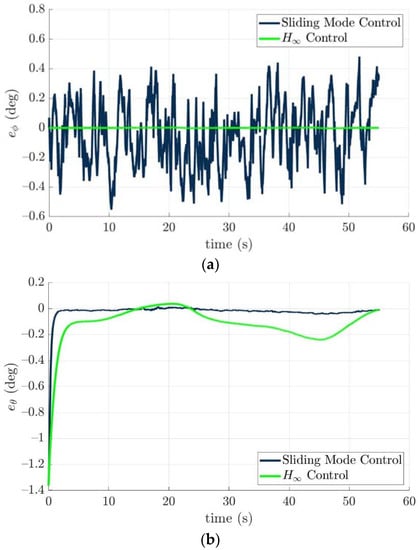
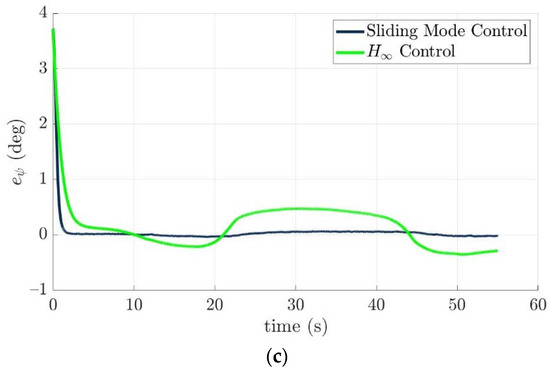
Figure 13.
Histories of the attitude tracking errors of the torpedo-like underwater vehicle: (a) roll direction, (b) pitch direction, and (c) yaw direction.
The sailing velocity of the controlled torpedo-like underwater vehicle as shown in Figure 14 based on the sliding mode control law and the nonlinear H∞ control law. It is easy to find out that the sliding mode control law possesses a quick convergence rate in the transient period.
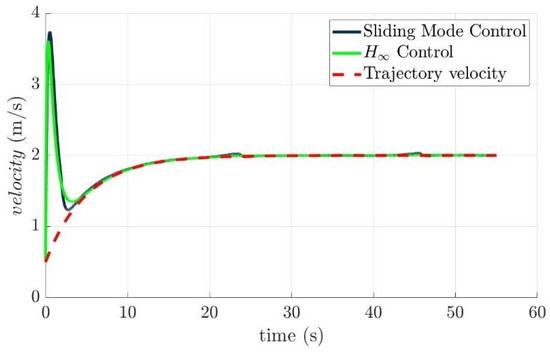
Figure 14.
The velocities of the controlled torpedo-like underwater vehicle with respect to sliding mode control and the nonlinear H∞ control law, respectively.
The desired control forces that precisely guide the developed torpedo-like underwater vehicle to track the desired trajectory based on the sliding mode control law and the nonlinear H∞ control law are illustrated as Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20. These figures reveal the facts that control forces and torques generated by the sliding mode control law to guide the torpedo-like underwater vehicle are larger than those of the nonlinear H∞ control law during the trajectory tracking period.
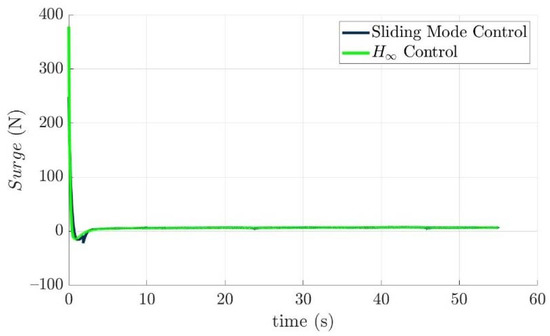
Figure 15.
Surge forces of the developed torpedo-like underwater vehicle with respect to the sliding mode control law and the nonlinear H∞ control law.
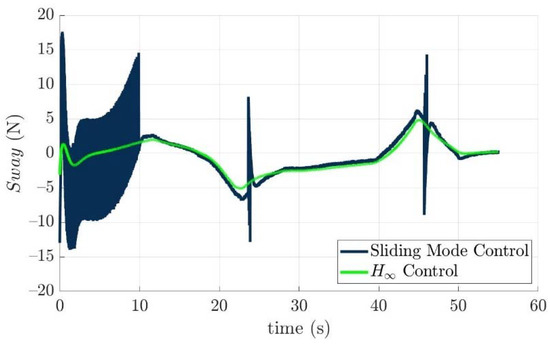
Figure 16.
Sway forces of the developed torpedo-like underwater vehicle with respect to the sliding mode control law and the nonlinear H∞ control law.
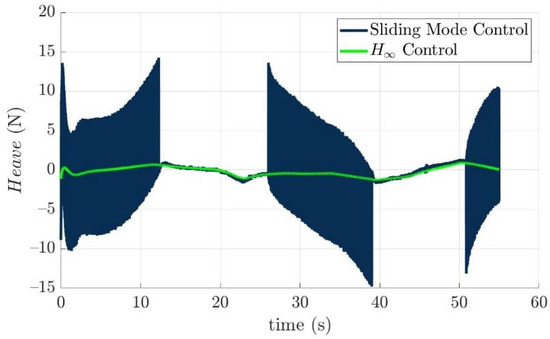
Figure 17.
Heave forces of the developed torpedo-like underwater vehicle with respect to the sliding mode control law and the nonlinear H∞ control law.
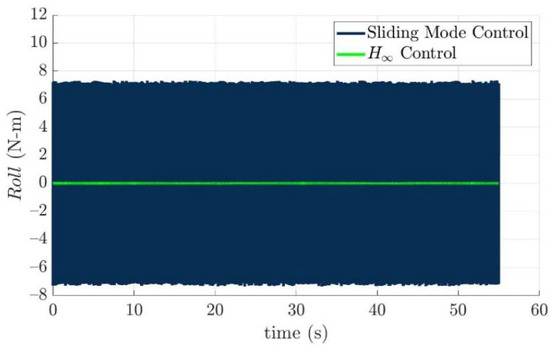
Figure 18.
Roll moments of the developed torpedo-like underwater vehicle with respect to the sliding mode control law and the nonlinear H∞ control law.
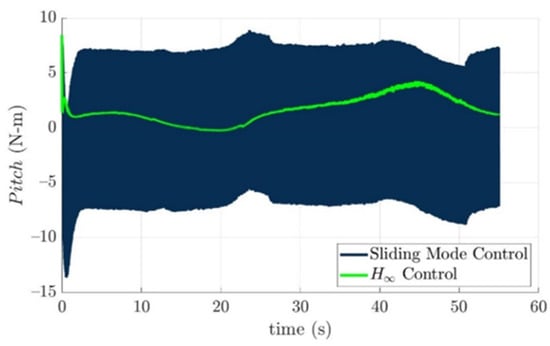
Figure 19.
Pitch moments of the developed torpedo-like underwater vehicle with respect to the sliding mode control law and the nonlinear H∞ control law.
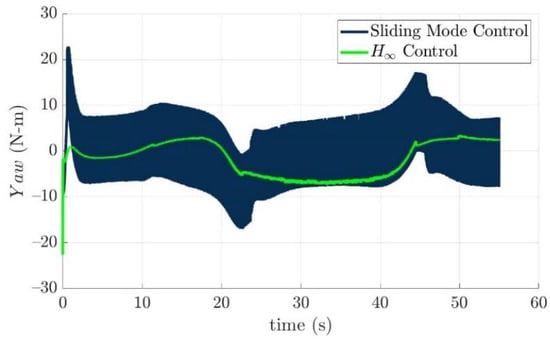
Figure 20.
Yaw moments of the developed torpedo-like underwater vehicle with respect to the sliding mode control law and the nonlinear H∞ control law.
According to the design target of this investigation, these six control forces should be converted into the input commands of actuators u. For achieving this design target, the proposed control allocation method was adopted to make the transformation of τ(e), which was generated via two adopted control laws and u for the controlled torpedo-like underwater vehicle. Based on the design procedures of the proposed optimization method, because efficiency of all installed actuators are assumed be equal, the weighting matrix P for the optimization method in Equation (22) is selected as
Through the developed control allocation method, the generated forces of each fin and rudder could be solved in real time, and the input commands could be computed using . The simulation results with respect to two adopted control laws are shown in Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28.
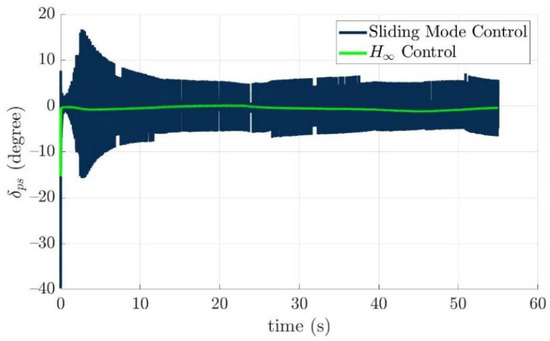
Figure 21.
The port stern fin angles of the controlled torpedo-like underwater vehicle for two control laws, respectively.
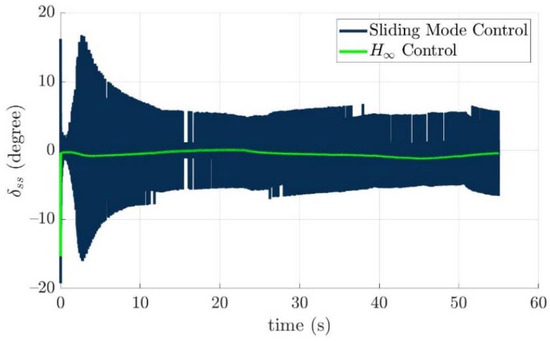
Figure 22.
The starboard stern fin angles of the controlled torpedo-like underwater vehicle for two control laws, respectively.
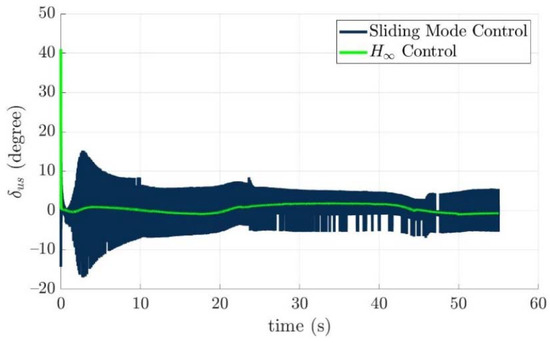
Figure 23.
The upward stern rudder angles of the controlled torpedo-like underwater vehicle for two control laws, respectively.
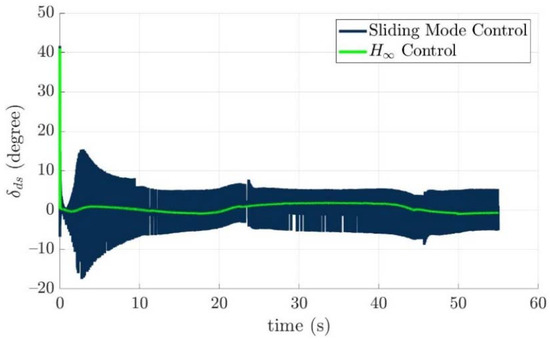
Figure 24.
The downward stern rudder angles of the controlled torpedo-like underwater vehicle for two control laws, respectively.
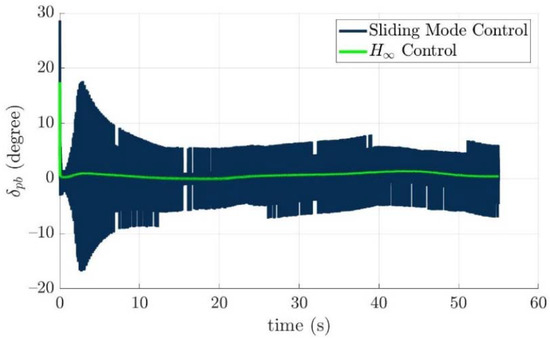
Figure 25.
The port bow fin angles of the controlled torpedo-like underwater vehicle for two control laws, respectively.
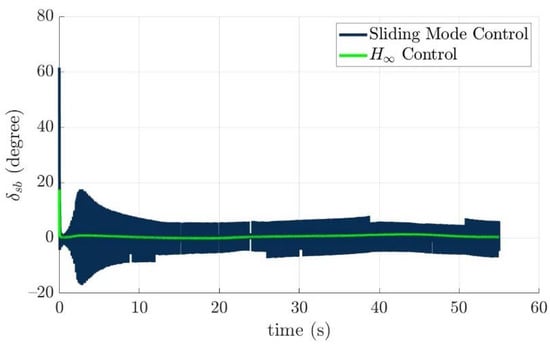
Figure 26.
The starboard bow fin angles of the controlled torpedo-like underwater vehicle for two control laws, respectively.
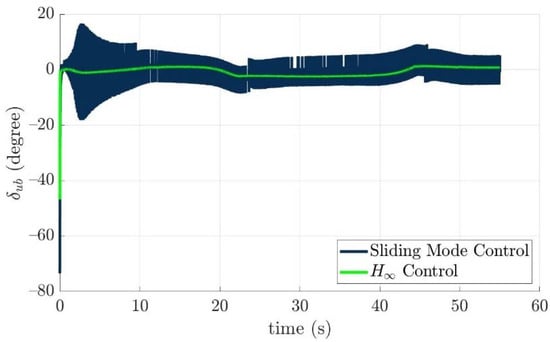
Figure 27.
The upward bow rudder angles of the controlled torpedo-like underwater vehicle for two control laws, respectively.
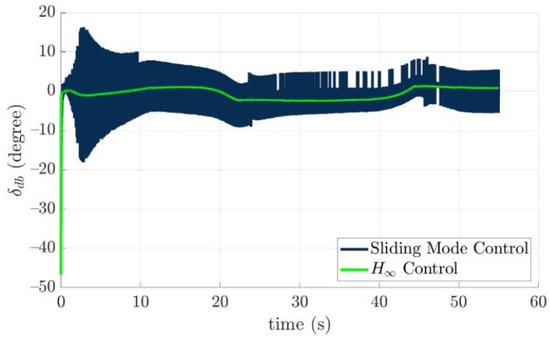
Figure 28.
The downward bow rudder angles of the controlled torpedo-like underwater vehicle for two control laws, respectively.
From simulation results of the turning angles of fins and rudders in the above, the turning angles of the fins and rudders all lie in the range of the limitations, which means the desired control commands τ(e) could be carried out by all installed actuators properly. The reason for vertically long results near 0 s of Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28 is: “The initial tracking errors, especially for x axis, and pitch and yaw directions in Figure 12 and Figure 13 are larger than others when the guided torpedo-like underwater vehicle tracks the first waypoint”.
By applying the radial basis function network to replace and using the relationship , the control commands of the thruster for two control laws could be plotted as Figure 29, respectively.
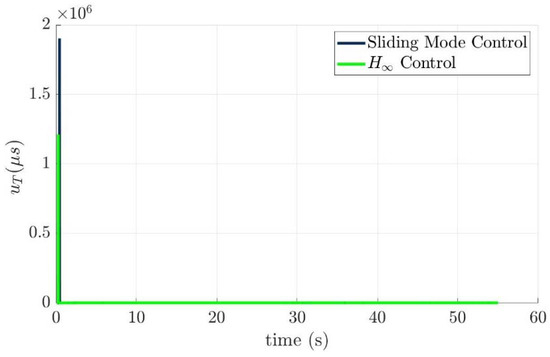
Figure 29.
The command histories of the thruster for two control laws, respectively.
5. Conclusions
In this investigation, a systematical design process for the control allocation problem of a torpedo-like underwater vehicle was proposed, and promising control allocation performances were delivered finally. In this study, the control allocation problem was formulated as an optimization problem of converting the desired control commands of a well-developed nonlinear H∞ control law and a sliding mode control law into input commands of actuators, including one thruster in the aft part, four rudders at the stern, and four fins at the forward part of the controlled torpedo-like underwater vehicle. The closed-form solutions of this control allocation problem were solved analytically. Simulations for the proposed control allocation method were examined based on a real torpedo-like underwater vehicle named “AUV Lab 611”. Simulation results reveal the fact that control commands generated by two control laws for precisely achieving the given trajectory tracking mission can be optimally and properly converted into all installed actuators of the controlled torpedo-like underwater vehicle.
Author Contributions
Conceptualization, Y.-Y.C. and C.-Y.L.; methodology, Y.-Y.C. and C.-Y.L.; software, Y.-X.H. and T.-T.Y.; validation, Y.-Y.C.; formal analysis, Y.-Y.C.; writing—original draft preparation, Y.-Y.C.; writing—review and editing, Y.-Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Derivation of Radial Basis Function Network
Give a set of input data into an unknown system:
then the unknown system generates a set of output data:
With the discrete data sets {(xi, yi), i = 1, 2, …, N}, a function could be solved to represent the unknown system by interpolation. The unknown system could be expressed as
Radial basis function is a method of interpolation, and the general form is like the below:
Term xc is the center of the radial basis function, and ||●|| represents the Euclidean 2-norm. In other words, the radial basis function stands for the relativity between the data point and the center of the radial basis function, and a common choice of the radial basis function is Gaussian function:
where σ is the radius of the Gaussian function:
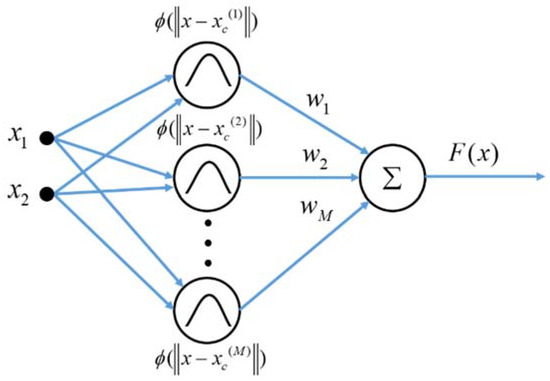
Figure A1.
The concept of the radial basis function.
The picture above shows the concept of the radial basis function interpolation, and the unknown system in Equation (A3) could be expressed as
Applying the measured input and output data sets into Equation (A6), a matrix form for presenting the relationship of input and output data is obtained as follows:
Matrix Φ is called the interpolation matrix; if N = M and Φ is non-singular then the weighting matrix could be obtained:
If N≠M, then use the pseudo-inverse instead:
By using the calculated weighting vector in Equations (A8) or (A9), a radial basis function network can be constructed.
References
- Fernandez, R.A.S.; Grande, D.; Martins, A.; Bascetta, L.; Dominguez, S.; Rossi, C. Modeling and Control of Underwater Mine Explorer Robot UX-1. IEEE Access 2019, 7, 39432–39447. [Google Scholar] [CrossRef]
- Hussain, N.A.A.; Ali, S.S.A.; Ovinis, M.; Arshad, M.R.; Al-Saggaf, U.M. Underactuated Coupled Nonlinear Adaptive Control Synthesis Using U-Model for Multivariable Unmanned Marine Robotics. IEEE Access 2019, 8, 1851–1865. [Google Scholar] [CrossRef]
- Valeriano, Y.; Fernandez, A.; Hernandez, L.; Prieto, P. Yaw Controller in Sliding Mode for Underwater Autonomous Vehicle. IEEE Lat. Am. Trans. 2016, 14, 1213–1220. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, A.; Castaneda, H. Guidance and Control Based on Adaptive Sliding Mode Strategy for a USV Subject to Uncertainties. IEEE J. Ocean. Eng. 2021, 46, 1144–1154. [Google Scholar] [CrossRef]
- Chachada, M.; Vachhani, L.; Kartik, V. Empirical waypoint navigator for over actuated autonomous underwater vehicle using novel kinematic-dynamic controller pair and control allocation techniques. In Proceedings of the 2016 Indian Control Conference (ICC), Hyderabad, India, 4–6 January 2016; pp. 354–361. [Google Scholar] [CrossRef]
- Chin, C.S.; Lau, M.W.S.; Low, E.; Seet, G.G.L. A Cascaded Nonlinear Heading Control with Thrust Allocation: An Application on an Underactuated Remotely Operated Vehicle. In Proceedings of the 2006 IEEE Conference on Robotics, Automation and Mechatronics, Bangkok, Thailand, 1–3 June 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Ji, S.; Jang, J.; Jeong, J.; Kim, Y. The H∞ controller design including control allocation for marine vessel. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, Jeju Island, Korea, 17–21 October 2012; pp. 1905–1907. [Google Scholar]
- Shen, C.; Shi, Y.; Buckham, B. Lyapunov-based model predictive control for dynamic positioning of autonomous underwater vehicles. In Proceedings of the 2017 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 27–29 October 2017; pp. 588–593. [Google Scholar] [CrossRef]
- Yu, C.; Xiang, X.; Wilson, P.; Zhang, Q. Guidance-Error-Based Robust Fuzzy Adaptive Control for Bottom Following of a Flight-Style AUV with Saturated Actuator Dynamics. IEEE Trans. Cybern. 2019, 50, 1887–1899. [Google Scholar] [CrossRef] [PubMed]
- Johansen, T.A.; Fossen, T.I. Control allocation—A survey. Automatica 2013, 49, 1087–1103. [Google Scholar] [CrossRef] [Green Version]
- Oppenheimer, M.W.; Doman, D.B.; Bolender, M.A. Control allocation for over-actuated systems. In Proceedings of the 2006 14th Mediterranean Conference on Control and Automation, Ancona, Italy, 28–30 June 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Fossen, T.I.; Johansen, T.A. A survey of control allocation methods for ships and underwater vehicles. In Proceedings of the 2006 14th Mediterranean Conference on Control and Automation, Ancona, Italy, 28–30 June 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Fossen, T.I.; Johansen, T.A. A Survey of Control Allocation Methods for Ships and Underwater Vehicles. Underw. Veh. 2009, 110–128. [Google Scholar] [CrossRef] [Green Version]
- Khan, H.Z.I.; Rajput, J.; Ahmed, S.; Sarmad, M.; Sharjil, M. Robust control of overactuated autonomous underwater vehicle. In Proceedings of the 2018 15th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 9–13 January 2018; pp. 269–275. [Google Scholar] [CrossRef]
- Soylu, S.; Buckham, B.J.; Podhorodeski, R.P. Robust Control of Underwater Vehicles with Fault-Tolerant Infinity-Norm Thruster Force Allocation. Oceans 2007, 1–10. [Google Scholar] [CrossRef]
- Yinghao, Z.; Jiangfeng, Z.; Yueming, L.; Yushan, S.; Lei, W.; Shuling, H. Research on reconstructive fault-tolerant control of an X-rudder AUV. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Tolstonogov, A.; Kostenko, V. AUV thrust allocation with variable constraints. Adv. Syst. Sci. Appl. 2017, 17, 1–8. [Google Scholar]
- Yi-Sheng, Y. Design of Adaptive Fuzzy Guidance Law for Autonomous Underwater Vehicles: Mixed H2/H∞ Approach; National Cheng Kung University: Tainan, Taiwan, 2020. [Google Scholar]
- Ke, S.; Jinchuan, Z.; Hai, W.; Xueqian, W.; Renquan, L.; Zhihong, M. Tracking Control of a Linear Motor Positioner Based on Barrier Function Adaptive Sliding Mode. IEEE Trans. Ind. Inform. 2021, 17, 7479–7488. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).