An Improved Proximal Policy Optimization Method for Low-Level Control of a Quadrotor

Abstract

In this paper, a novel deep reinforcement learning algorithm based on Proximal Policy Optimization (PPO) is proposed to achieve the fixed point flight control of a quadrotor. The attitude and position information of the quadrotor is directly mapped to the PWM signals of the four rotors through neural network control. To constrain the size of policy updates, a PPO algorithm based on Monte Carlo approximations is proposed to achieve the optimal penalty coefficient. A policy optimization method with a penalized point probability distance can provide the diversity of policy by performing each policy update. The new proxy objective function is introduced into the actor–critic network, which solves the problem of PPO falling into local optimization. Moreover, a compound reward function is presented to accelerate the gradient algorithm along the policy update direction by analyzing various states that the quadrotor may encounter in the flight, which improves the learning efficiency of the network. The simulation tests the generalization ability of the offline policy by changing the wing length and payload of the quadrotor. Compared with the PPO method, the proposed method has higher learning efficiency and better robustness.

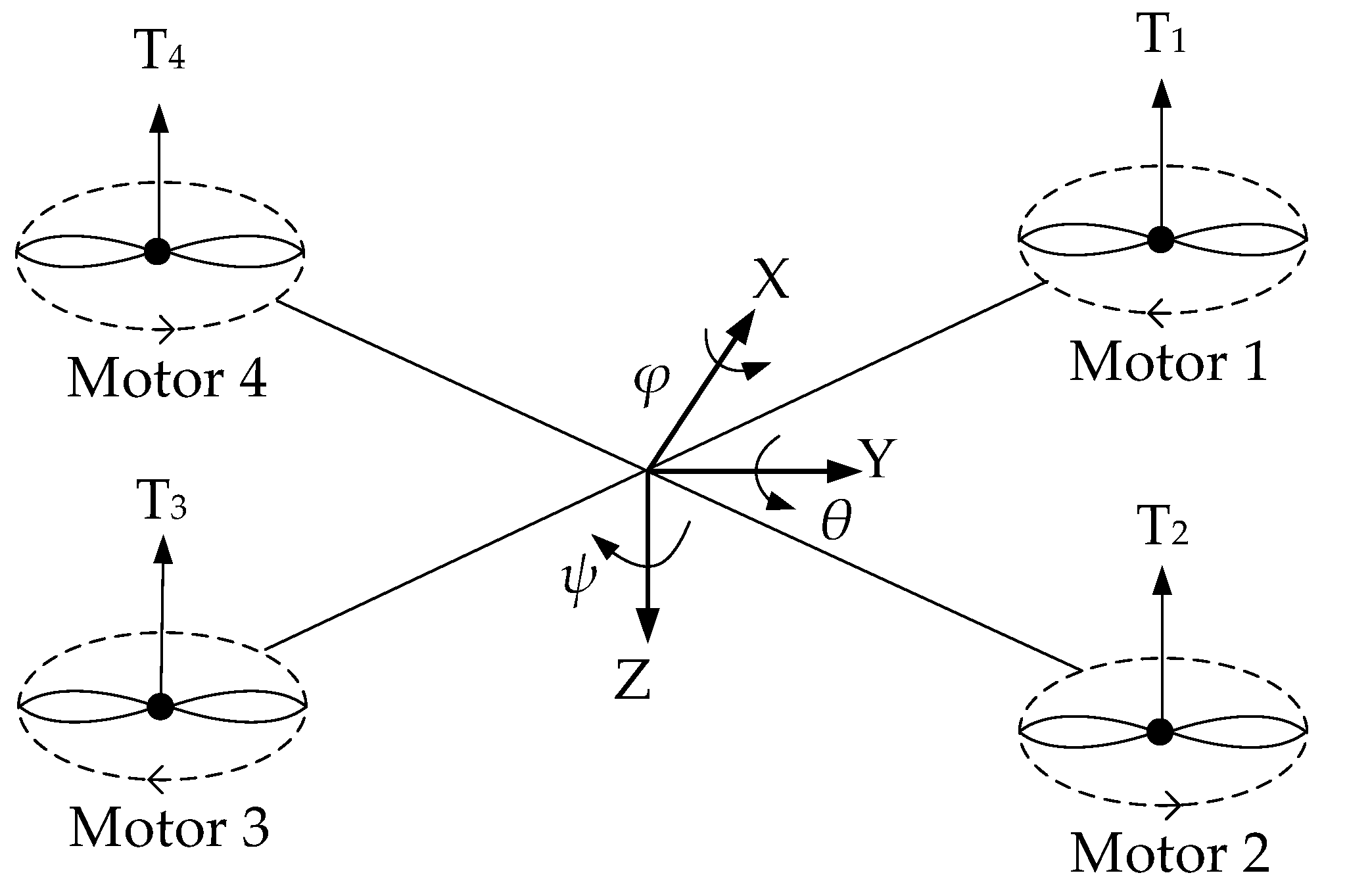
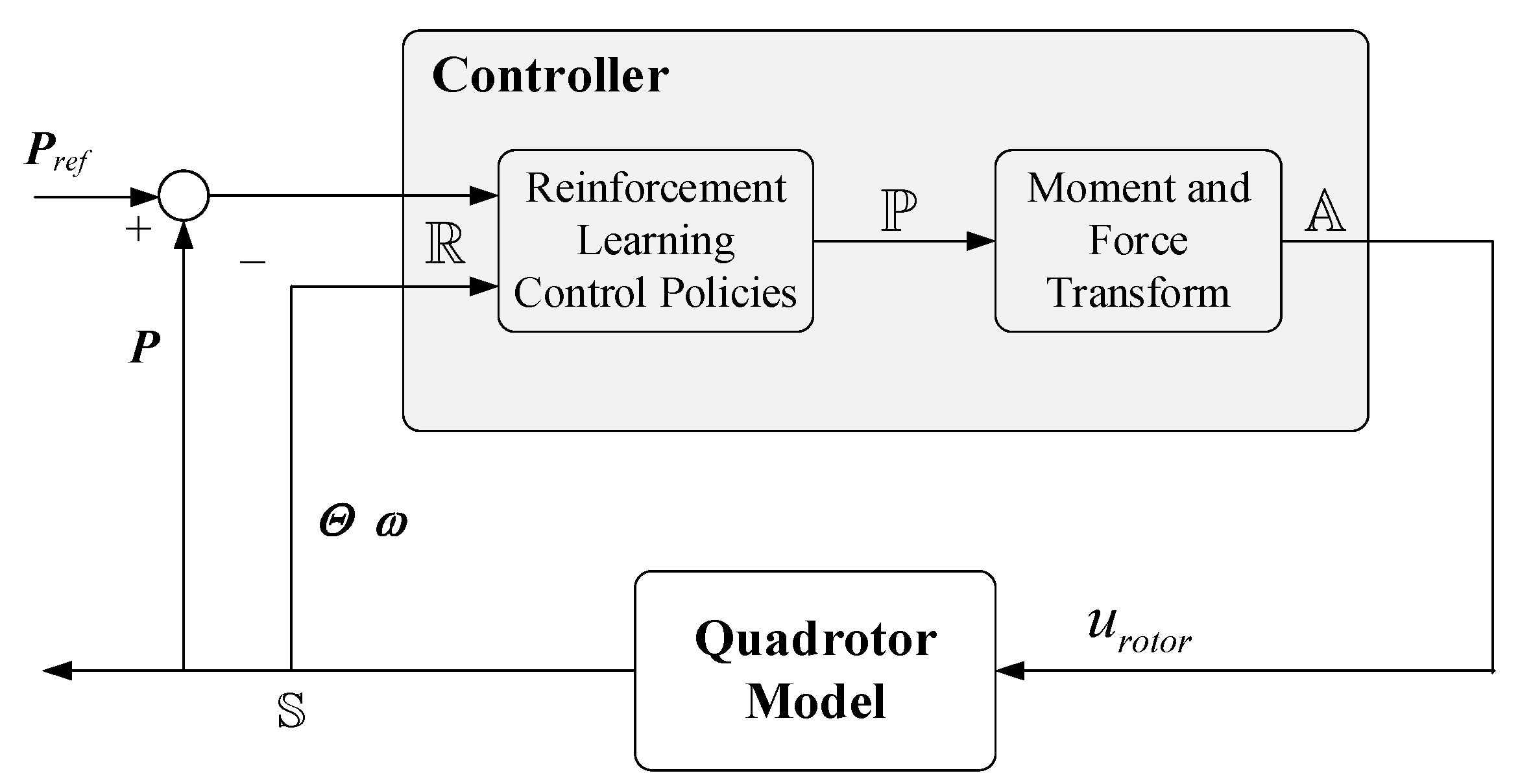
1. Introduction

Over the past decade, quadrotor unmanned aerial vehicles (UAV) have attracted considerable interest from both academic research and engineering application. With some features of vertical take-off and landing, simple structure, and low cost, they have been successfully applied in military and civil fields such as military monitoring, agricultural service, industrial detection, atmospheric measurements, and disaster aid [1,2,3,4,5]. However, the quadrotor UAV is an unstable, nonlinear, and highly coupled complex system. Furthermore, external disturbances and structure uncertainties always exist in practical quadrotors affected by wind gusts, sensor noises and unmodelled dynamics. Therefore, all these factors demand an accurate and robust controller for the quadrotor to achieve a stable flight.

An autonomous GNC system includes three subsystems of guidance, navigation and control, and it undertakes all the motion control tasks of the aerial vehicles from take-off to return. The state vector of the quadrotor usually consists of position coordinates, velocity vector and attitude angle. The navigation system is responsible for state perception and estimation. The guidance system generates state trajectory commands for the quadrotor, while the control system maintains stable control to follow the trajectory. The research on the quadrotor flight control system is usually divided into two levels, one is the low-level inner loop control layer, which is mainly used for the simple motion control and stabilization of the quadrotor, and the other is the higher-level outer loop coordination layer, such as navigation, path planning and other strategic tasks. To achieve stable control and target tracking of the quadrotor, various control policies have been developed. Traditional control theory methods, such as PID control, often have very high requirements for parameter adjustment and precise preset models. Moreover, the accuracy of the controller is greatly affected by the complex environment. Therefore, many advanced control policies are proposed to solve the control problems in complex environments, such as feedback linearization control [6] adaptive control [7], model predictive control [8], immersion and invariance control [9], sliding mode control [10], adaptive neural-network control [11,12], backstepping control [13], active disturbance rejection method [14], and so on. However, the effectiveness and robustness of most technologies mainly depend on the accuracy of the dynamic model. Although some advanced algorithms have considered the uncertainty and disturbance of the quadrotor system, they are difficult to implement in real-time due to complex control policies.

Reinforcement learning (RL) algorithms have been used with promising results in a large variety of decision-making tasks, including control problems [15]. Compared with classic control techniques, RL is a learning algorithm that directly learns from the interaction with the system and improves policies without making any assumptions on the dynamic model [16]. Many complex quadrotor decision-making problems have been solved by RL technology. In [17], an obstacle avoidance RL method combined with a recurrent neural network with temporal attention is proposed to deal with cluttered environments. In [18], UAV successfully navigate to static and dynamic formulated goals through RL method with a customized reward mechanism. In [19], line of sight and artificial potential field are introduced in the reward function to guide the UAV to perform the target tracking task. In [20], an RL path planning method based on global situational information demonstrates the excellent performance of UAVs in radar detection and missile attack environments.

In addition to high-level guidance and navigation tasks, RL has also been used for low-actuator stable motion control. At this level, the complexity of the mission lies in the complex dynamics of the quadrotor and its vulnerability to unknown dynamics such as disturbances and sensor noise [21]. In this paper, we focus more on low-level motion control of quadrotor based on a fast-response RL robust controller. In [22], the stochastic nonlinear model of helicopter dynamics was fitted and successfully applied to autonomous flight control through RL for the first time. In [23], the locally weighted linear regression method was first used to approximate the quadrotor model as a Markov Decision Process (MDP) in order to realize the continuous state-action space RL controller. In [24], deep neural networks were used in RL as a powerful value function approximator to deal with complex dynamics. In [25], a low-level controller generated by deep RL implements the basic hover control and tracking tasks of a real quadrotor firmware. In order to solve the problem of continuous state-action control decisions, the newly developed algorithms, such as Asynchronous Advantage Actor-Critic (A3C), Twin Delayed Deep Deterministic Policy Gradient (TD3), Soft Actor-Critic (SAC) and Proximal Policy Optimization (PPO), are proposed [26,27,28,29] to optimize performance on high-dimensional continuous control problems. These algorithms have also been gradually developed to solve the flight control problem of quadrotors and other complex nonlinear systems [30,31,32,33].

PPO is an advanced policy gradient algorithm, which can effectively solve the problem of low learning efficiency caused by the traditional policy gradient algorithm due to the influence of the step size. The main advantages of the PPO algorithm for training control policy are: Firstly, in [34], the hyper-parameters of PPO were proved to be robust when training various tasks, and PPO can achieve an optimal balance between control accuracy and algorithm complexity. Secondly, in [35], through the comparison of performance indicators, the training control policy of PPO was superior to other RL algorithms on every metric. It is the best performing algorithm for controlling the attitude of a quadrotor. Then, in [36], the position control of the “model-free” quadrotor was successfully realized through the PPO algorithm. In [37], considering the full six DoF system dynamics of the UAV, PPO is used to train the quadrotor control policies, which has achieved the basic control task of stable hovering. The RL integrated controller designed in [38] has solved advanced tasks such as autonomous landing in actual flight for the first time. Moreover, some improved algorithms have been presented to improve the robustness and tracking accuracy of the controller. In [39], a state integrator was introduced in the actor–critic framework, and the PPO-IC algorithm was proposed to reduce the steady-state error of the system.

However, most RL methods are only for specific control environments. Further research is still needed to design an RL algorithm with fast response and stable strategy in the flight control system. As far as RL policies on quadrotors are concerned, many problems still remain unsolved. They are summarized as follows: Firstly, the quadrotor UAV is an underactuated nonlinear system with multiple inputs and outputs. For such a complex system, PPO is prone to lacking exploration and slow convergence, especially in poor initialization policies [40]. Secondly, the reward function plays an important role in RL [41]. Most reward function settings cannot achieve effective exploration in the training control policy.

Aiming at the above problems, an improved quadrotor control policy based on PPO is proposed in this paper. Firstly, in [35], PPO has the best effect on quadrotor attitude control among all baseline RL algorithms. Inspired by this, we introduce a penalized point probability distance as the probability ratio between different policies, thereby improving the exploration efficiency. Secondly, we verify that the improved PPO algorithm has a better control performance and training rate on dimensions of attitude and position. Moreover, for the exploration of new reward signals mentioned in [36] and [39], a compound reward function is proposed to converge faster to the control requirements and minimize the steady-state error during the training process. The main contributions of this paper are summarized as follows:

In this paper, an improved quadrotor control strategy based on PPO is proposed.

(1)

In the objective function of the PPO algorithm, a penalized point probability distance based on Monte-Carlo approximation is introduced to replace KL divergence in order to eliminate the strict penalty when the action probability does not match. The strategy will optimize the decision-making of the quadrotor when training the control policy. The new policy optimization algorithm helps to stabilize the learning process of the quadrotor and promote exploration, which will be remarkably robust to model parameter variations.

(2)

For actual flight control, a compound reward function is designed to replace the single reward function to prevent the training of the decision network from falling into the local optimum. With the defined reward function, the improved PPO will be applied to the quadrotor environment to train the policy network.

The organization of this article is as follows. In Section 2, the nonlinear model of the quadrotor is established, and the theoretical overview of RL is provided. In Section 3, the algorithm and reward and punishment function are optimized after analyzing the PPO algorithm. The details and results of the simulation experiment are discussed in Section 4. The conclusion is given in Section 5.

2. System Statement

The purpose of this section is to develop an RL method that can solve the fixed-point flight control problem of the quadrotor. Moreover, the method can meet the requirements for pinpoint flying and hovering based on defined rewards.

2.1. Dynamic Model of Quadrotor

A dynamical model of the quadrotor is set up by the earth-frame I(Oxyz) and the body-frame B(Oxyz) as illustrated in Figure 1.

The position and attitude of the quadrotor expressed in the inertial frame are defined as P = [x, y, z]^T and Θ = [φ, θ, ψ]^T, where φ, θ, ψ are roll, pitch and yaw angles, respectively. $\dot{p}$, $\ddot{p}$ is the speed and acceleration of the quadrotor.

The transformation matrix R is used to transform the thrust force from the body-fixed coordinate system to the inertial coordinate system, which is

$$R=\left[\begin{array}{ccc}{C}_{\phi }{C}_{\theta }& C_{\phi }{S}_{\theta }{S}_{\phi }-C_{\phi }{S}_{\psi }& S_{\phi }{S}_{\psi }+C_{\phi }{C}_{\psi }{S}_{\theta }\\ S_{\psi }{C}_{\theta }& S_{\phi }{S}_{\theta }{S}_{\psi }+C_{\phi }{C}_{\psi }& C_{\phi }{S}_{\theta }{S}_{\psi }-C_{\psi }{S}_{\phi }\\ -S_{\theta }& C_{\theta }{S}_{\phi }& C_{\phi }{C}_{\theta }\end{array}\right],$$

(1)

where S{·} and C{·} denote sin(·) and cos(·) respectively.

The thrust generated by the four motors is defined as T_i. In the body coordinate system, the thrust of the body is vertical-upward, which can be expressed as:

$$T_i=b{u}_i, i=1, 2, 3, 4,$$

(2)

where b is the thrust gain, and u_i is the normalized control input.

The establishment of the quadrotor dynamics model is based on the dynamic characteristics of torque-driven rotational motion and force-driven translational motion. For the rotational motions, with the Euler’s equation of a rigid body, the sum of torque applied to the quadrotor can be expressed as

$$M=M_{\tau }+M_c+M_f=I\dot{w}+w\times Iw,$$

(3)

where I is the diagonal inertia matrix of the quadrotor, $w={[\dot{\phi },\dot{\theta },\dot{\psi }]}^T$ is the angular velocity of the quadrotor, and $M_{\tau }={[{\tau }_{\phi },{\tau }_{\theta },{\tau }_{\psi }]}^T$ is the control torque given by:

$$M_{\tau }=\left[\begin{array}{c}{\tau }_{\phi }\\ {\tau }_{\theta }\\ {\tau }_{\psi }\end{array}\right]=\left[\begin{array}{c}L\left(T_2-T_4\right)\\ L\left(T_1-T_3\right)\\ k\left(T_1-T_2+T_3-T_4\right)\end{array}\right],$$

(4)

where the distance from the center of mass to each rotor is L, the control torques τ_ψ along the z-axis is the sum of the reaction torques generated by the four rotors. k is the damping coefficient. The gyroscopic effect of the four rotors is $M_c={[-I_p\dot{\theta }\mathsf{\Omega },I_p\dot{\phi }\mathsf{\Omega },0]}^T$, where I_p is the moment of inertia, and Ω is the disturbance effect from each rotor. The drag torque of quadrotor flight is $M_f={[-d_{\phi }\dot{\phi },-d_{\theta }\dot{\theta },-d_{\psi }\dot{\psi }]}^T$, where d_φ, d_θ and d_ψ are the drag coefficients of the three axes.

For translational motions, the motion equation can be obtained from Newton’s second law:

$$\ddot{p}=\frac{R{F}_l}{m}-\frac{F_d}{m}-g,$$

(5)

where F_l = [0, 0, T₁ + T₂ + T₃ + T₄] is the thrust vector. $F_d={[-d_x\dot{x},-d_y\dot{y},-d_z\dot{z}]}^T$ is the aerodynamic drag, where d_x, d_y and d_z are the resistance coefficients. m is the mass of the quadrotor and g is the acceleration of gravity, $T_z=T_1+T_2+T_3+T_4$. Finally, the quadrotor dynamics equation can be expressed as:

$$\left\{\begin{array}{l}\ddot{x}=[T_z(C_{\phi }{S}_{\theta }{C}_{\psi }+S_{\phi }{S}_{\psi })-d_x\dot{x}]/m\hfill \\ \ddot{y}=[T_z(C_{\phi }{S}_{\theta }{S}_{\psi }+S_{\phi }{C}_{\psi })-d_y\dot{y}]/m\hfill \\ \ddot{z}=[T_z(C_{\phi }{C}_{\theta })-d_z\dot{z}-mg]/m\hfill \\ \ddot{\phi }=[{\tau }_{\phi }-I_p\dot{\theta }\Omega -d_{\phi }\dot{\phi }+\dot{\theta }\dot{\psi }(I_y-I_z)]/I_x\hfill \\ \ddot{\theta }=[{\tau }_{\theta }-I_p\dot{\phi }\Omega -d_{\theta }\dot{\theta }+\dot{\phi }\dot{\psi }(I_z-I_x)]/I_y\hfill \\ \ddot{\psi }=[{\tau }_{\psi }-d_{\psi }\dot{\psi }+\dot{\phi }\dot{\theta }(I_x-I_y)]/I_z\hfill \end{array}\right.$$

(6)

2.2. Quadrotor Control Based on Reinforcement Learning

The goal of RL is to find an optimal policy for an agent to interact with a certain environment to maximize the total reward over time. It uses the formal framework of the Markov Decision Process (MDP) to define the interactions between the learning agent and the environment [42]. The environment is usually modelled as an MDP described by a four-tuple ($\mathbb{S},\mathbb{A},\mathbb{P},ℝ$), where $\mathbb{S}$ and $\mathbb{A}$ are the state set and action set, respectively, $\mathbb{P}$ and $ℝ$ are the state transition probability function and reward function.

According to the interaction between the agent and the environment, the policy π_θ is updated as:

$$L({\pi }_{\theta })=\underset{s_0,s_1\cdots }{\mathbb{E}}\left[{\displaystyle \sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k}}\right]={\displaystyle {\int }_s{d}^{{\pi }_{\theta }}(s)V^{{\pi }_{\theta }}(s)ds},$$

(7)

where θ is the policy parameter, γ ∈ [0, 1) is the discount factor, π_θ is a stochastic policy, $V^{{\pi }_{\theta }}(s)=\underset{s_{t+1},s_{t+2}\cdots }{\mathbb{E}}\left[{\displaystyle \sum _{t=t}^{\infty }{\gamma }^t{r}_t\left|s_t=s\right.},{\pi }_{\theta }\right]$.

In RL, the expected reward function of the state-action (s_t,a_t) generated by policy π is called the action-value function, which is determined as:

$$Q^{\pi }(s_t,a_t)={\mathbb{E}}_{\pi }\left[R(s_t,a_t)+\gamma V^{{\pi }_{\theta }}(s_{t+1})\right].$$

(8)

Its output represents the value of taking a specific action in a specific state and following this policy thereafter. Based on the baseline function $V^{{\pi }_{\theta }}(s)$, the policy gradient can be written as:

$${\nabla }_{\theta }L({\pi }_{\theta })=\underset{s\sim {\rho }^{{\pi }_{\theta }}}{\mathbb{E}}\left[{\nabla }_{\theta }{\pi }_{\theta }(s){\nabla }_a{A}^{{\pi }_{\theta }}(s,a)\left|a\right.={\pi }_{\theta }(s)\right],$$

(9)

where $A^{{\pi }_{\theta }}(s,a)=Q^{{\pi }_{\theta }}(s,a)-V^{{\pi }_{\theta }}(s)$ is called the advantage function, and its value can represent the advantage of the value obtained by taking a certain action to the current policy π_θ(s), ${\rho }^{{\pi }_{\theta }}$ is the state distribution following the policy π_θ.

For the quadrotor control problem, the main goal is to seek an appropriate control policy to drive the quadrotor to a predefined state stably and rapidly. The quadrotor dynamics will be converted into the MDP form, and appropriate states and actions should be selected to satisfy the Markov property. The quadrotor control structure based on RL is shown in Figure 2. $\mathbb{S}$ is the current position and attitude information of the quadrotor, $\mathbb{A}$ is the control input of the quadrotor, $\mathbb{P}$ is the policy distribution of RL, and $ℝ$ is the reward function set for the task requirements. Through the interaction between the controller and the environment, the RL algorithm combined with the reward function can finally obtain the optimal policy of the quadrotor.

Among the basic RL algorithms, the policy gradient method is the most suitable because it is compatible with continuous states and actions. The parameterized random policy π_θ (a|s) directly generates the control action, which is the probability of taking action a in the given state s and parameter θ. We need to adjust the parameters to optimize the policy according to the gradient of the performance measurement value J(π_θ):

$${\nabla }_{\theta }J({\pi }_{\theta })=\underset{s\sim {\rho }^{{\pi }_{\theta }},a\sim {\pi }_{\theta }}{\mathbb{E}}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a\left|s\right.)Q^{{\pi }_{\theta }}(s,a)\right],$$

(10)

The policy gradient algorithm can find the optimal control policy without considering the accuracy of the model. However, the basic RL algorithm is difficult to effectively converge to the optimal state in the continuous state-action space of the complex environment. Many advanced RL algorithms have improved policy optimization, such as PPO. The algorithm uses a Kullback–Leibler divergence (KLD) to limit the update range of the policy, thereby improving the learning efficiency of the algorithm.

3. Proposed Approach

In this section, a policy optimization with penalized point probability distance (PPO-PPD) is firstly proposed for quadrotor control. Then, a compound reward function is adopted to promote the algorithm convergence to the desired direction.

3.1. The PPO-PPD Algorithm

In the PPO method, our goal is to maximize the following alternative objective function $L^{CPI}$ (conservative policy iteration) proposed in [43], which is constrained by the size of the policy update.

$$L^{CPI}(\theta )={\stackrel{\wedge }{\mathbb{E}}}_t\left[\frac{{\pi }_{\theta }(a_t{\left|s\right.}_t)}{{\pi }_{{\theta }_{old}}(a_t{\left|s\right.}_t)}\stackrel{\wedge }{A_t}\right],$$

(11)

where θ_old is the vector of policy parameters before the update. The objective function is maximized subject to a constraint by:

$$\stackrel{\wedge }{{\mathbb{E}}_t}\left[KL\left[{\pi }_{{\theta }_{old}}(·{\left|s\right.}_t),{\pi }_{\theta }(·{\left|s\right.}_t)\right]\right]\le \delta ,$$

(12)

where δ is the upper limit of KLD. Applying the linear approximation of the objective function and the quadratic approximation of the constraints, the conjugate gradient algorithm can be more effective to solve the problem. In the continuous domain, KLD can be defined as:

$$D_{KL}({\pi }_{{\theta }_{old}}(·\left|s\right.)‖{\pi }_{\theta }(·\left|s\right.))={\displaystyle \sum _a{\pi }_{{\theta }_{old}}(a\left|s\right.)\ln \frac{{\pi }_{{\theta }_{old}}(a\left|s\right.)}{{\pi }_{\theta }(a\left|s\right.)}},$$

(13)

where s is a given state. When choosing $D_{KL}({\pi }_{{\theta }_{old}}‖{\pi }_{\theta })$ or $D_{KL}({\pi }_{\theta }‖{\pi }_{{\theta }_{old}})$, its asymmetry results in a difference that cannot be ignored. PPO limits the update range of policy ${\pi }_{\theta }$ through KLD. It is assumed that the distribution of ${\pi }_{{\theta }_{old}}$ is a mixture of two Gaussian distributions, and ${\pi }_{\theta }$ is a single Gaussian distribution. When the learning tends to converge, the distribution of policy ${\pi }_{\theta }$ will approximate to ${\pi }_{{\theta }_{old}}$, $D_{KL}({\pi }_{{\theta }_{old}}‖{\pi }_{\theta })$ or $D_{KL}({\pi }_{\theta }‖{\pi }_{{\theta }_{old}})$ should be minimized at this moment. 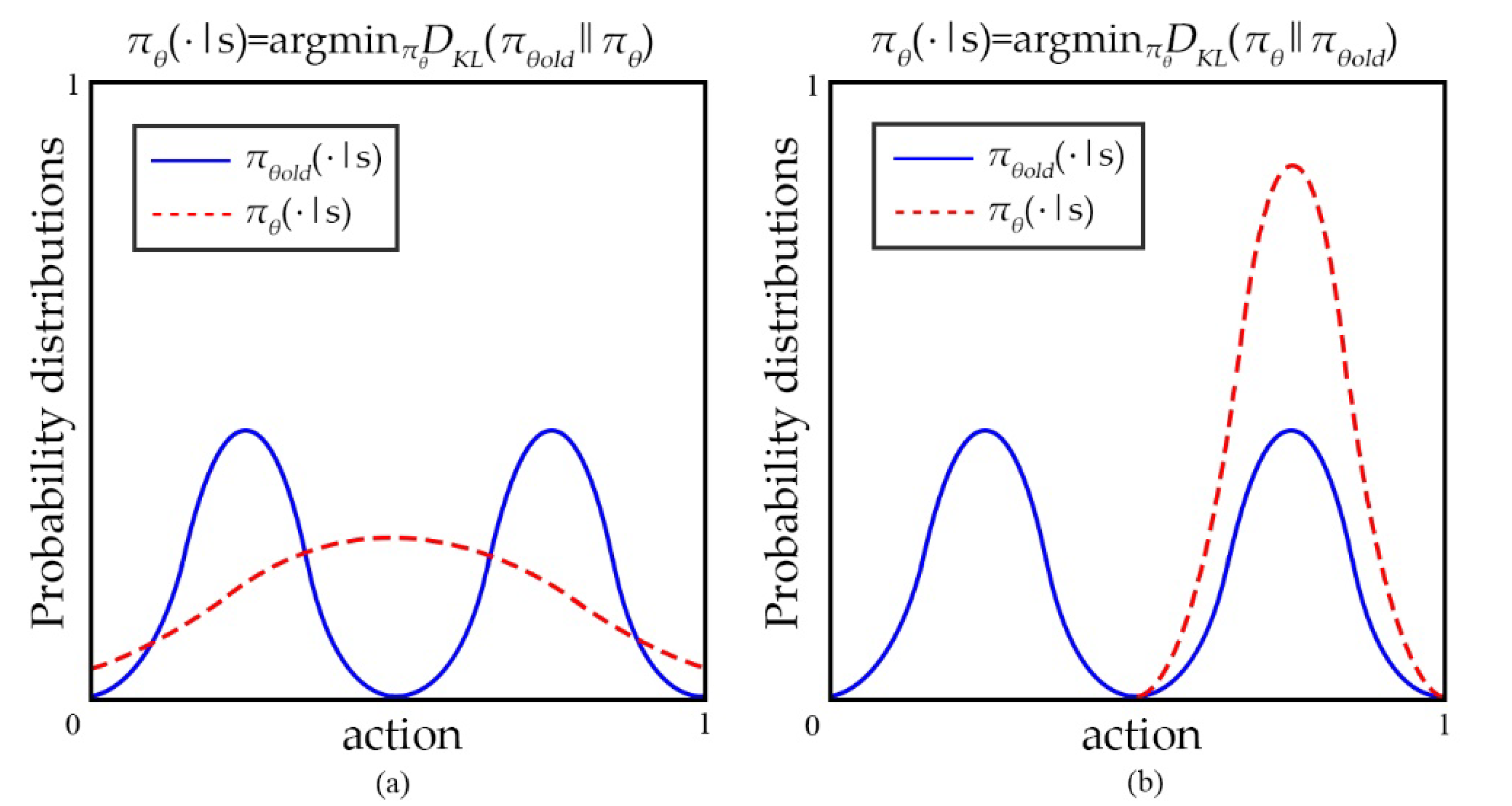Figure 3a is the effect of minimizing $D_{KL}({\pi }_{{\theta }_{old}}‖{\pi }_{\theta })$. When ${\pi }_{{\theta }_{old}}$ has multiple peaks, ${\pi }_{\theta }$ will blur these peaks together, and eventually lie between the two peaks of ${\pi }_{{\theta }_{old}}$, resulting in invalid exploration. When choosing another function, as shown in Figure 3b, ${\pi }_{\theta }$ ends up choosing to fit on a single peak of ${\pi }_{{\theta }_{old}}$.

By comparing forward and reverse KL, we argue that KLD is not an approximation or ideal limit to the expected discounted cost. Even if the θ output θ_old has the same high probability of correct action, it is still penalized for the probability mismatch of other non-critical actions.

To address the above issues, a point probability distance is introduced based on Monte Carlo approximation in the PPO objective function as a penalty for the surrogate objective. When taking action a, the point probability distance between ${\pi }_{{\theta }_{old}}(·\left|s\right.)$ and ${\pi }_{\theta }(·\left|s\right.)$ can be defined as:

$$D_{PP}\left({\pi }_{{\theta }_{old}}\left(\cdot \left|s\right.\right),{\pi }_{\theta }\left(\cdot \left|s\right.\right)\right)={\left(\mathrm{In}\frac{{\pi }_{{\theta }_{old}}\left(a\left|s\right.\right)+1}{{\pi }_{\theta }\left(a\left|s\right.\right)+1}\right)}^2.$$

(14)

In the penalty, the distance is measured by the point probability, which emphasizes the mismatch of the sampled actions in a specific state. Compared with D_KL, D_PP is symmetric, that is, $D_{PP}({\pi }_{{\theta }_{old}}‖{\pi }_{\theta })$ = $D_{PP}({\pi }_{\theta }‖{\pi }_{{\theta }_{old}})$, so when the policy is updated, D_PP is more conducive to helping the agent converge to the correct policy and avoid invalid sample learning like KLD. Furthermore, it can be found that D_PP is the lower bound of D_KL by deriving the relationship between D_PP and D_KL.

Theorem 1.

Assuming that a_i and b_i are two policy distributions with K values, then$D_{PP}(a_i‖b_i)$ ≤ $D_{KL}(a_i‖b_i)$ holds.

Proof of Theorem 1.

The total variance distance is introduced as a reference, which can be written as follows:

$$D_{TV}=\frac{{\displaystyle {\sum }_i\left|a_i-b_i\right|}}{2}.$$

(15)

From [44], $D_{TV}^2$ is the lower bound of D_KL, which is expressed as $D_{TV}^2$ ≤ D_KL. Assuming that a_x = c₁ is arbitrarily distributed in a_i, and b_x = c₂ is arbitrarily distributed in b_i, where c₁, c₂ ∈ [0, 1]. Then it can be derived:

$$\begin{array}{cc}{D}_{TV}^2\hfill & =\frac{1}{4}{\left({\displaystyle \sum _{i=1}^K\left|a_i-b_i\right|}\right)}^2\hfill \\ & =\frac{1}{4}{\left({\displaystyle \sum _{i=1,i\ne x}^K\left|a_i-b_i\right|}+\left|a_x-b_x\right|\right)}^2\hfill \\ & \ge \frac{1}{4}{\left(\left|{\displaystyle \sum _{i=1,i\ne x}^K{a}_i-}{\displaystyle \sum _{i=1,,i\ne x}^K{b}_i}\right|+a_x-b_x\right)}^2\hfill \\ & =\frac{1}{4}{\left(\left|1-c_1-\left(1-c_2\right)\right|+c_1-c_2\right)}^2\hfill \\ & ={\left(c_1-c_2\right)}^2\hfill \end{array}$$

For any real number between 0 and 1, there is ${\left(c1-c2\right)}^2\ge {\left(\mathrm{In}\left(1+c1\right)-\mathrm{In}\left(1+c2\right)\right)}^2=D_{PP}$. Therefore D_KL ≥ $D_{TV}^2$ ≥ D_PP.

Compared to D_KL, D_PP is less sensitive to the dimension of the action space. The optimization algorithm aims to improve the shortcomings of KLD. The reward function r_t(θ) only involves the probability of a given action a, the probabilities of all other actions are not activated, and this result no longer leads to long backpropagation. Based on the D_PP, a new proxy target can be obtained as:

$$\underset{\theta }{\max } \stackrel{\wedge }{{\mathbb{E}}_t}\left[\frac{{\pi }_{\theta }\left(a_t,s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t,s_t\right)}\stackrel{\wedge }{A_t}-\beta D_{PP}\left({\pi }_{{\theta }_{old}}\left(\cdot \left|s\right.\right),{\pi }_{\theta }\left(\cdot \left|s\right.\right)\right)\right],$$

(16)

where β is the penalty coefficient. Algorithm 1 shows the complete iterative process. The optimized algorithm reduces the difficulty of selecting the optimal penalty coefficient in different environments of the fixed KLD baseline from PPO. We will implement it on the quadrotor control problem.

Algorithm 1 PPO-PPD

1: Input: max iterations L, actors N, epochs K, time steps T 2: Initialize: Initialize weights of policy networks θi (i = 1, 2, 3, 4) and critic network Load the quadrotor dynamic model 3: for iteration = 1 to L do 4: Randomly initialize states of quadrotor 5: Load the desired states 6: Observe the initial state of the quadrotor s1 7: for actor = 1 to N do 8: for time step = 1 to T do 9: Run policy ${\pi }_{\theta }$ to select action at 10: Run the quadrotor with control signals at 11:  Generate reward rt and new state st+1 12:  Store st, at, rt, st+1 into mini-batch-sized buffer 13:  then 14:  Run policy ${\pi }_{\theta old}$ 15:  Compute advantage estimations $\stackrel{\wedge }{A_t}$ 16:  end for 17:  end for 18:  for epoch = 1 to K do 19:  Optimize the loss target with min-batch size $M\le NT$ 20:  then update θold ← θ 21:  Update θ w.r.t $J_{PPO}(\theta )=\underset{\theta }{\max } \stackrel{\wedge }{{\mathbb{E}}_t}\left[\frac{{\pi }_{\theta }\left(a_t,s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t,s_t\right)}\stackrel{\wedge }{A_t}-\beta D_{pp}\left({\pi }_{{\theta }_{old}}\left(\cdot \left|s\right.\right),{\pi }_{\theta }\left(\cdot \left|s\right.\right)\right)\right]$ 22:  end for 23: end for

3.2. Network Structure

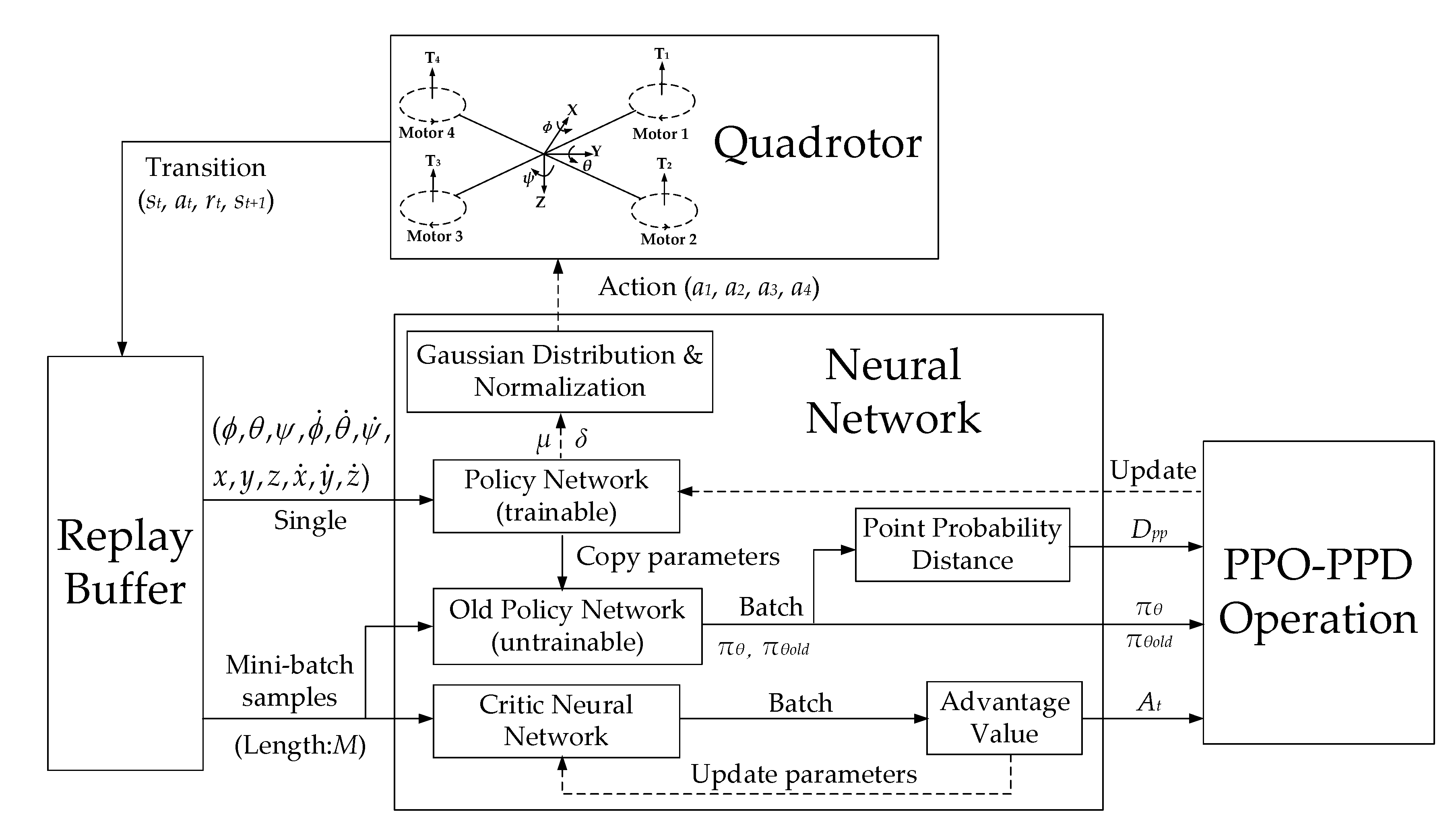
The actor–critic network structure of the algorithm is shown in Figure 4. The system is trained by a critic neural network (CNN) and a policy neural network (PNN) θ_i (i = 1, 2, 3, 4), which is formed by four policy sub-networks. The weights of the PNN can be optimized by training.

The network input of the two neural networks is the new quadrotor states $[\dot{\phi },\dot{\theta },\dot{\psi },\phi ,\theta ,\psi ,\dot{x},\dot{y},\dot{z},x,y,z]$ from the replay buffer. When the PNN collects a single state vector, the parameters of the PNN will be copied to the old PNN π_θold. In the next batch of training, the parameters of π_θold remain fixed until new network parameters are received. The output of PNN is π_θ and π_θold. The penalty D_PP is obtained by calculating the point probability distance between the two policies. When the state vector enters the CNN, according to the reward function, a batch of advantage values is generated to evaluate the quality of the action taken. Through the gradient descent method, the CNN minimizes these values to update its parameters. Finally, the policies π_θ and π_θold, penalized point probability distance D_PP and advantage value A_t are provided to update of the PNN. After the PNN is updated, its outputs μ_i and δ_i (i = 1, 2, 3, 4) correspond to the mean and variance of the Gaussian distribution. As the normalized control signals for the four rotors of the quadrotor, a set of 4-dimensional action vectors a_i (i = 1, 2, 3, 4) are randomly sampled from a Gaussian distribution.

Based on the multilayer perceptron (MLP) structure in [45], the actor-critic network structure of our algorithm is shown in Figure 5. The structure can maintain a balance between the training speed and the control performance of the quadrotor. Both networks share the same input, consisting of 12-dimensional state vectors. PNN has two fully connected hidden layers, each hidden layer contains 64 nodes with tanh function. The output layer is a 4-dimensional Gaussian distribution with mean μ and variance δ. The 4-dimensional action vector a_i (i = 1, 2, 3, 4) is obtained by random sampling and normalization, which will be used as the control signal of the quadrotor rotor. The structure of CNN is similar to that of PNN. It also has two fully connected hidden layers with the tanh activation function, and each layer has 64 hidden nodes. The difference is that its output is an evaluation of the advantage value of the current action, which is determined by the value of the reward function.

3.3. Reward Function

The goal of RL algorithm is to obtain the most cumulative rewards [46]. The existing RL reward function settings are relatively simple, most of which are presented as:

$$r=-\sqrt{x^2+y^2+z^2+{\psi }^2},$$

(17)

where r is the single-step reward value, (x, y, z) is the position observation of the quadrotor, and ψ is the heading angle. It is not enough to evaluate the pros and cons of the chosen actions of the quadrotor by relying on the efficiency of a single reward function. If (18) is used, it will make the action space update too large, and increase the ineffective exploration, making the convergence slower. A new reward function that combines multiple reward policies is introduced to solve the problem.

The quadrotor explores through a random policy. When the mainline event is triggered with a certain probability, the corresponding mainline reward should be given. Because the probability of triggering the main line reward is very low in the entire flight control, we need to design the corresponding reward function according to all possible states of the quadrotor. Therefore, in this paper, a navigation reward, boundary reward and target reward are designed. As the mainline reward, the navigation reward directly affects the position and attitude information of the quadrotor by observing the continuous state space.

• Navigation Reward;

  (a)

  Position Reward

  In order to drive the quadrotor to fly to the target point, the position reward is defined as a penalty for the distance between the quadrotor and the target point. When the quadrotor is close to the target point, the penalty should be small, otherwise the penalty should be large. Therefore, the definition of position reward is as follows:

  $$r_P=-k_P\sqrt{x_e{}^2+y_e{}^2+z_e{}^2}-k_V\sqrt{{\dot{x}}_e{}^2+{\dot{y}}_e{}^2+{\dot{z}}_e{}^2},$$

  (18)

  where x_e = x − x_d, y_e = y − y_d, z_e = z − z_d are the position errors relative to the target state, ${\dot{x}}_e$, ${\dot{y}}_e$, and ${\dot{z}}_e$ are the linear speed errors in the x, y, z-axis directions, and k_P, k_V ∈ (0, 1].

  (b)

  Attitude Reward

  The attitude reward is designed to stabilize the quadrotor flying to the target point and the large angle deflection is not conducive to the flight control of the quadrotor.

  It is found that although a simple reward function like $\sqrt{{\phi }^2+{\theta }^2+{\psi }^2}$ aims to make the attitude angle tend to 0, and the quadrotor will weigh the position reward and the attitude reward to find the local optimal policy, which is not the best control policy for quadrotor fixed-point flight. When the position is closer to the target point, the transformation function of its attitude angle also tends to 0. Without considering ψ, φ and θ can also be inversely solved to be 0. Therefore, replacing the attitude angle itself by its transformation function into the reward function will not affect the judgment of the quadrotor during position control, and can increase the stability of the inner and outer loop control. The attitude reward is defined as:

  $$r_A=-k_A\sqrt{{(C_{\phi }{S}_{\theta }{C}_{\psi }+S_{\phi }{S}_{\psi })}^2+{(C_{\phi }{S}_{\theta }{S}_{\psi }+S_{\phi }{C}_{\psi })}^2},$$

  (19)

  where $(\phi ,\theta ,\psi )$ are the attitude observation and k_A ∈ (0, 1].

  (c)

  Position-Attitude Reward

  When the distance to the target point is farther, the weight of the position reward is larger. As the quadrotor flies closer to the target point, the weight of the position reward decreases, and the weight of the attitude reward gradually increases. The specific reward function setting is as follows:

  $$r_{PA}=-k_{PA}\frac{a^2{}_{\phi ,\theta }}{\max (e_p,0.001)},$$

  (20)

  where e_p is the position error relative to the target state, a_φ and a_θ are the normalized actions of roll and pitch from 0 to 1, k_PA ∈ (0, 1] and $a_{\phi ,\theta }^2$ is the sum of the squared roll and pitch actions. It is constrained by the reciprocal of e_p to minimize the oscillation of the quadrotor near the target position. Therefore, its contrast parameter is set to 0.001.

• Boundary Reward;
  In many earlier roll-outs, when the roll angle or pitch angle of the quadrotor is over 40°, the motor will receive an emergency stop command to minimize damage [47]. In order to maintain stability, we set a boundary restriction and failure penalty to the attitude angles to prevent the quadrotor from crashing due to excessive vibration. The specific restriction is as follows:

  $$r_{BA}=\left\{\begin{array}{l}0,R_{At}\le R_{\max attitude}\\ -{\zeta }_{penalty},R_{At}>R_{\max attitude}\end{array}\right.,$$

  (21)

  where R_At is the error between the attitude angle and the target attitude at time t, R_{max attitude} is the maximum safe attitude angle, the boundary penalty ζ_penalty is a positive constant.
  For position control, the random states sampled may differ by several orders of magnitude in different flying spaces. In order to reduce the exploration time of the quadrotor, we will set a safe flight range with the target point as the center, so that the quadrotor can reduce unnecessary invalid exploration. The reward is determined as:

  $$r_{BP}=\left\{\begin{array}{l}0,R_{Pt}\le R_{boundary}\\ -\frac{R_{Pt}}{R_{boundary}},R_{Pt}>R_{boundary}\end{array}\right.,$$

  (22)

  where R_Pt is the distance between quadrotor and the target point at time t and R_boundary is the safe flight range of the quadrotor we set.
• Goal Reward;
  The mainline event of the quadrotor is to reach the target point, so in order to prompt the quadrotor to move to the target as soon as possible, a goal reward is designed. Unlike other rewards, when the quadrotor triggers a mainline event, it should be given a positive reward. When the distance between the quadrotor and the target point is less than R_reach, it is determined that the quadrotor has reached the target point. The specific reward definition is as follows:

  $$r_G=\left\{\begin{array}{l}{\zeta }_{goal},R_{Pt}\le R_{reach}\\ 0,R_{Pt}>R_{boundary}\end{array}\right..$$

  (23)
  These rewards may affect the training performance of the policy network. In this paper, when designing the quadrotor controller, all these rewards are set in combination with the corresponding tasks, and the final comprehensive reward is defined as the sum of them as follows:

  $$r=r_P+r_A+r_{PA}+r_{BA}+r_{BP}+r_G.$$

  (24)

4. Simulation

In this section, we use the proposed PPO algorithm to evaluate the quadrotor flight controller based on neural network. The simulation has been performed comparing with the PPO algorithm controller.

4.1. Simulation Settings

The quadrotor model in the simulation is constructed based on the dynamics given in (6). The parameters of the quadrotor are listed in

Table 1. Parameters of the Quadrotor Simulator.

Parameter	Description	Value
m	Mass	0.2 kg
L	Wing length	0.31 m
g	Acceleration of gravity	9.81 m/s2
b	Thrust gain	5.723
k	Reaction torque gain	0.172
Ix	X-axis moment of inertia	0.008 kg·m2
Iy	Y-axis moment of inertia	0.008 kg·m2
Iz	Z-axis moment of inertia	0.03 kg·m2
dx	X-axis air resistance coefficient	0.001
dy	Y-axis air resistance coefficient	0.001
dz	Z-axis air resistance coefficient	0.001

.

The parameter settings in the simulation model all meet the body parameters of the real quadrotor as shown in Figure 6, so as to maximize the simulation of the flight state of the real quadrotor. Considering the safety factors in actual flight, we define the safety range of the state. The range of attitude angle ϕ and θ is −45° to 45°, and the range of angular velocity $\dot{\phi }$ and $\dot{\theta }$ is −4.5 rad/s to 4.5 rad/s, which meets the limitation of the gyroscope sensor. The quadrotor is specified to operate within a range of −2.5 m to 2.5 m in the x direction, −2.4 m to 2.4 m in the y direction, and 0 m to 2.4 m in the z direction.

4.2. Training Evaluation

In the offline learning phase, the PPO-PPD is applied. The training parameters are given in

Table 2. Training parameters.

Parameter	Value
Reward discount factor γ	0.97
Learning rate	0.00025
Value function coefficient	0.01
Entropy coefficient	0.5
Mini-batch size M	128
Number of actors N	4
Maximum number of iterations L	1000
Simulation sampling time per step	0.02 s
Penalty coefficient β	0.5

.

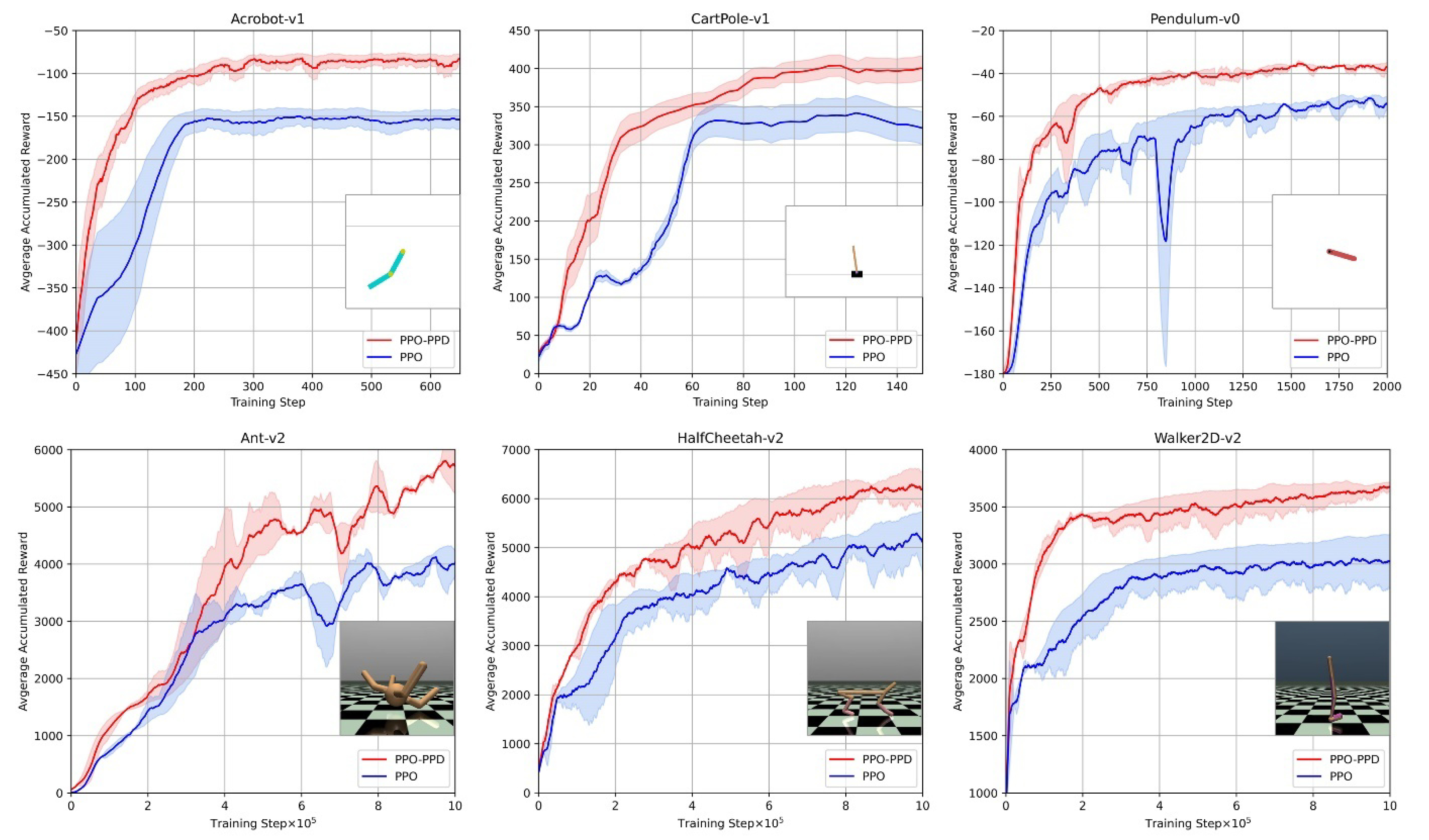
In order to verify the performance of the PPO-PPD policy, we act on multiple motion tasks in OPEN GYM [48] between PPO and PPO-PPD. The two algorithms use the same network structure and environment parameters. Motion tasks are selected from discrete action space tasks (such as Acrobot, CartPole and Pendulum), and continuous tasks (such as Ant, Half-Cheetah, and Walker2D [49]). Both PPO-PPD and PPO are initialized randomly and run five times. The comparison results are shown in Figure 7.

For an intuitive comparison of algorithm performance,

Table 3. The performance comparison between PPO-PPD and PPO.

	PPO-PPD	PPO	Comparison
Acrobot	−77.540	−150.458	+48%
CartPole	408.245	341.732	+19%
Pendulum	−38.512	−52.455	+27%
Ant	5943.459	4268.432	+39%
HalfCheetah	6337.017	5422.827	+17%
Walker2D	3672.855	3146.045	+17%

shows the best performance of PPO-PPD and PPO in different tasks. It can be observed from Figure 7 that the PPO-PPD has a faster and more accurate control policy than PPO. We then evaluate both algorithms in a quadrotor system with randomly initialized states.

In order to train a flight policy with generalization ability, the initial state of the quadrotor is random during training. The target point is set at [0, 0, 1.2]. When the policy converges, the quadrotor should be able to complete the control task of taking off and hovering to the target point at any position. We use the average cumulative reward and average value loss to measure the effect of learning and training. In each step, the greater the reward value of the feedback, the smaller the error for the desired state. The training of the quadrotor should also be carried out in the direction of smaller and smaller errors. A faster and more accurate control policy is reflected in a larger and more stable cumulative reward. In this study, we perform a calculation after every 50 sets of data are recorded, and the average cumulative reward and value loss are evaluated as the average of the 50 evaluation sets. Based on the same network and training parameters, we compare the PPO and PPO-PPD.

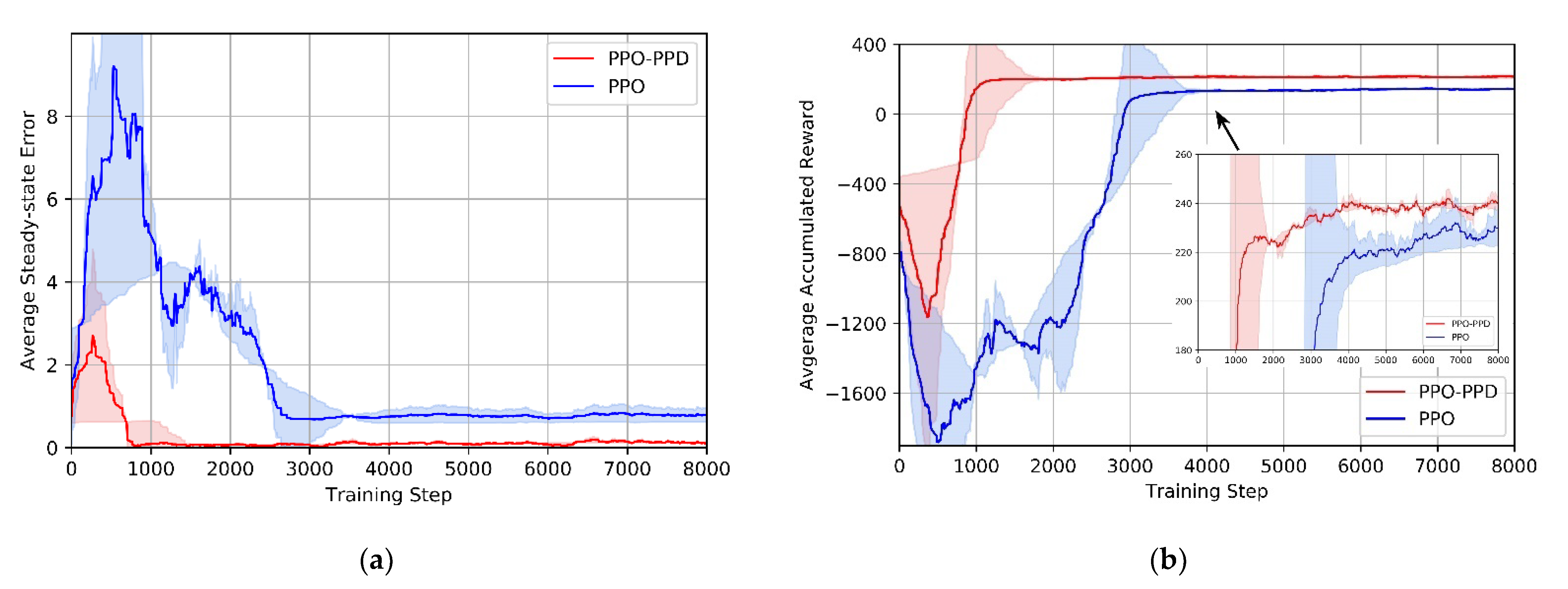
Under the initial network parameters, we conduct ten independent experiments on the two algorithms. The standard deviation of these ten experiments is indicated by the shaded part. It is shown that in the initial stage of training, both policies have obvious errors. With the continuous training of the agent, the errors of the two algorithms are gradually reduced to zero. In Figure 8a, it is very clear that the steady-state error is nearly eliminated by the PPO-PPD policy after 1000 training iterations. Although PPO policy converges after 3000 training, it is always affected by the steady-state error, and the error does not show any reduction in the next training iterations.

It can be seen from the learning progress in Figure 8b, PPO-PPD has a higher convergence rate and obtains a higher reward than PPO. In the standard deviation, PPO-PPD is more consistent with less training time. In addition, the policy begins to gradually converge when the reward value reaches 220. Therefore, a predefined threshold of 220 is set to further observe the training steps of the algorithms.

To further verify the effectiveness of compound reward function in the process of training policies, we compare the performance of PPO-PPD with compound reward, PPO-PPD with single reward, and PPO with single reward. The single reward function is taken from (17) and the compound reward function is taken from (24).

Table 4. Training steps to reach 220 threshold.

Algorithm	Training Steps
PPO-PPD with compound reward	614
PPO-PPD with single reward	1347
PPO with single reward	2875

lists the training steps required for the three algorithms to reach the threshold.

In Table 4, PPO-PPD with compound reward function takes the least number of time steps in the flight task, because the compound reward function accelerates the convergence of correct action and reduces the blind exploration of quadrotors. Comparing the PPO-PPD with a single reward function with PPO, the advantages of PPO-PPD in the algorithm structure has a better learning efficiency.

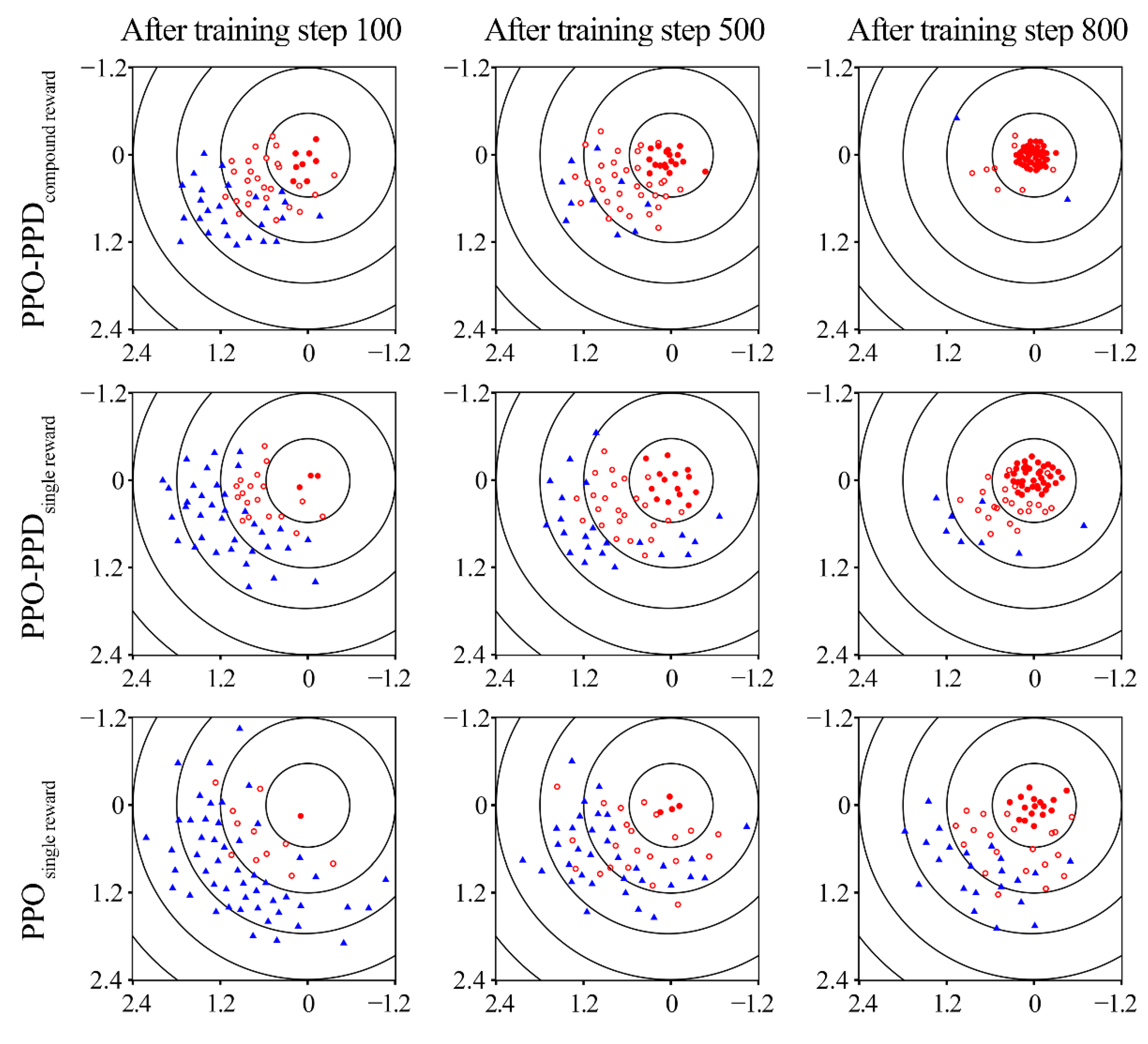
As shown in Figure 9, 60 groups of training data are sampled to obtain the final landing position of the quadrotor after the 100th, 500th and 800th training iterations of the three algorithms.

It can be drawn that the two algorithms cannot train a good policy before the 100th step. Due to the exploration efficiency, PPO-PPD has been able to sample several more rounds of good control policies than the PPO. The advantage is especially noticeable after the 500th step of training. Finally, PPO-PPD with compound reward successfully trains the control policy after the 800th training step. Because of the multi-objective reward, the PPO-PPD with compound reward can stabilize the quadrotor at the target point after completing the mainline event. However, the PPO-PPD with single reward achieves the target point with probability deflection due to its single reward. It is obvious that the quadrotor by PPO controller has not obtained a good control policy in 800th iterations. It is concluded that the PPO-PPD with compound rewards is superior to the other two methods.

The attitude control of the quadrotor at the fixed position is conducted first. This test does not consider the position information of the quadrotor, and only uses the state of the three attitude angles as the observation space. The set attitude angle state of the quadrotor model is initialized to [30, 20, 10]°, and the target attitude angle is set to [0, 0, 0]°. It can be seen from Figure 10a that PPO and PPO-PPD policies can achieve stable control. However, the PPO-PPD has smoother control performance and higher control accuracy than the PPO algorithm. On the contrary, the PPO algorithm response also has a relatively large steady-state error. Moreover, it can be observed that the quadrotor under the two control strategies can reach the steady state after 0.5 s. Comparing the mean absolute steady-state error of the two algorithms, as shown in Figure 10b, the PPO-PPD policy can achieve higher control accuracy.

Then we test the two controller performances in the fixed-point flight task under the same training iterations. The observation space for the test is the motion performance of the quadrotor on the x-axis, y-axis, and z-axis and the attitude changes of roll angle and pitch angle. A total of five observations are made. In order to maximize its flight performance, the initial position of the quadrotor is set around the boundary with the coordinates [2.4, 1.2, 0] and the desired position [0, 0, 1.2], which is assumed to be the center of the training environment point. 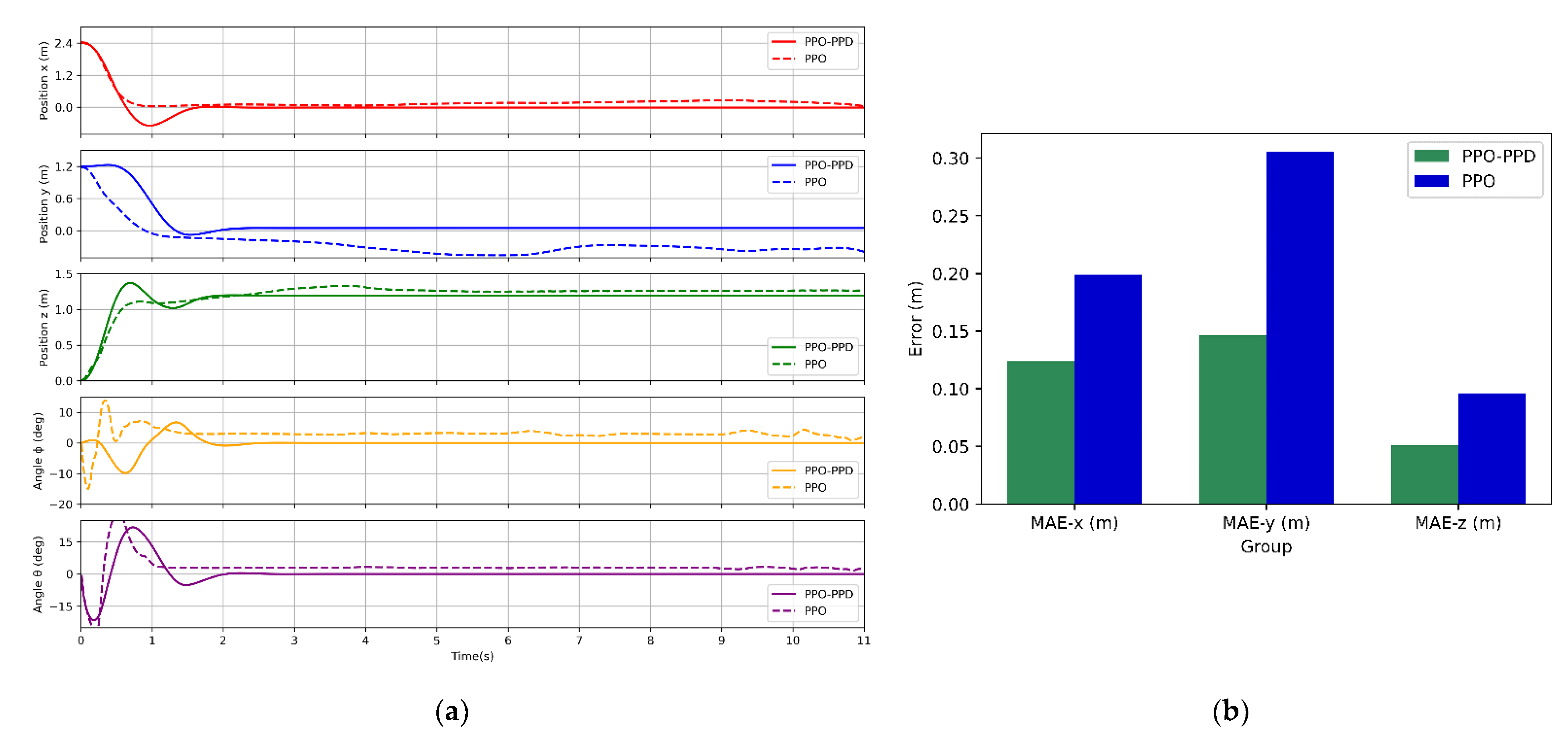Figure 11a shows the performance results of the two control policies.

It can be seen from the comparison, although both PPO-PPD and PPO converge, the PPO algorithm does not learn an effective control policy when taking off on a relatively unsafe boundary area. In terms of position control, the control policy learned by the PPO algorithm has a slow convergence with a certain steady-state error. In terms of attitude control, both policies maintain good convergence in control stability, but due to the instability of the PPO policy in the position loop, there is still a slight error in the attitude under the effect of quadrotor control. Furthermore, to compare the training results more directly, we calculate the mean absolute steady-state error on the position control loop for the two policies in steady-state at 7 s, and the comparison results are shown in Figure 11b.

In this test, both algorithms can converge to a stable policy, but PPO-PPD have the smaller steady-state error and faster convergence rate. Next, we will conduct more tests to observe the performance of the control policy trained by PPO-PPD.

4.3. Robustness Test

The main purpose of quadrotor offline learning is to learn a stable and robust control policy. In this section, we test the generalization ability of the training model, and the test is performed on the same quadrotor. In order to conduct a comprehensive robustness test to observe the learned policy, we designed two different cases.

1.

Case 1: Model generalization test under random initial state.

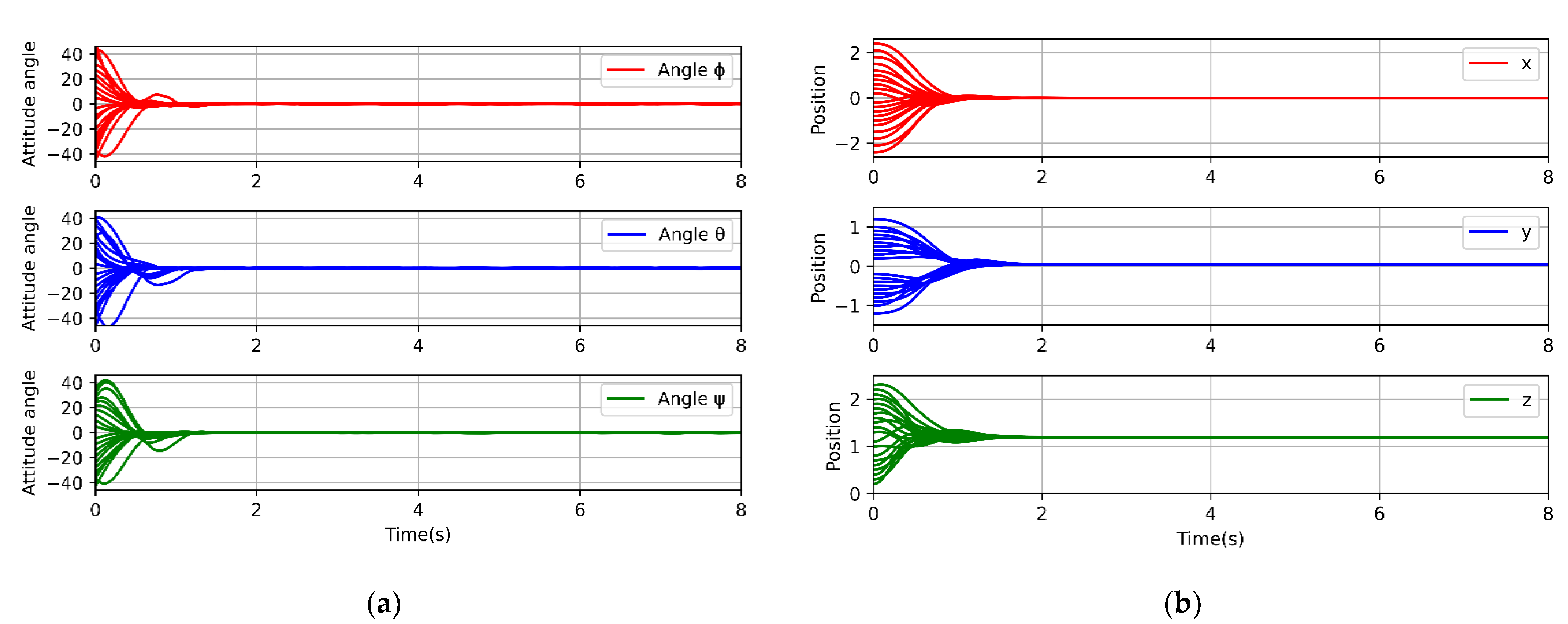
In different initial states of the quadrotor, the PPO-PPD algorithm is used to test its performance. The test is still divided into two parts. We first observe the attitude change of in the fixed-point state, that is, the control task is that the quadrotor hovers at a fixed position, randomly initializes the state within a safe range, and the attitude in the random state can be adjusted to the required steady state. We conduct the experiment 20 times, and each experiment lasts 8 s. As shown in Figure 12a, the three attitude angles start at different initial values, and the control policy can successfully converge their states.

The policy learned by the PPO-PPD algorithm can make the quadrotor stable in different states with few errors, which is enough to prove the good generalization ability of the offline policy. Next, we give the quadrotor a random initialization position within a safe range and observe its position change to test the generalization ability of the RL control policy on fixed-point flight tasks. The experiment is performed 20 times, and the duration of each group is 8 s. The results are shown in Figure 12b.

It can be seen from the results that the control policy learned by PPO-PPD has very good generalization ability. No matter what the initial position of the quadrotor is, the control policy can quickly control the quadrotor to fly to the desired target point, which is enough to prove the stability of the offline policy.

2.

Case 2: Model generalization test under different sizes.

In order to verify the robustness and generalization ability of the off-line learning control strategy, the attitude control task is carried out on quadrotor models of different sizes. The policy is tested by starting at [−15°, −10°, −5°], then flying to the attitude [0, 0, 0] in 10 s. Furthermore, a PID controller is introduced to verify the robustness of the RL control policy. In the same way as RL, PID gains are also selected by observing the system output response through trial and error. To measure the dynamic performance of the control policies, the sum of error is calculated during the flight as a metric, which is the absolute tracking error accumulated at the three attitude angles in each step. As a cascade control, the initial PID parameters are selected as follows: the position loop k_p = 0.15, k_i = 0.001, k_d = 0.5; and the attitude loop k_p = 0.25, k_i = 0.001, k_d = 0.4.

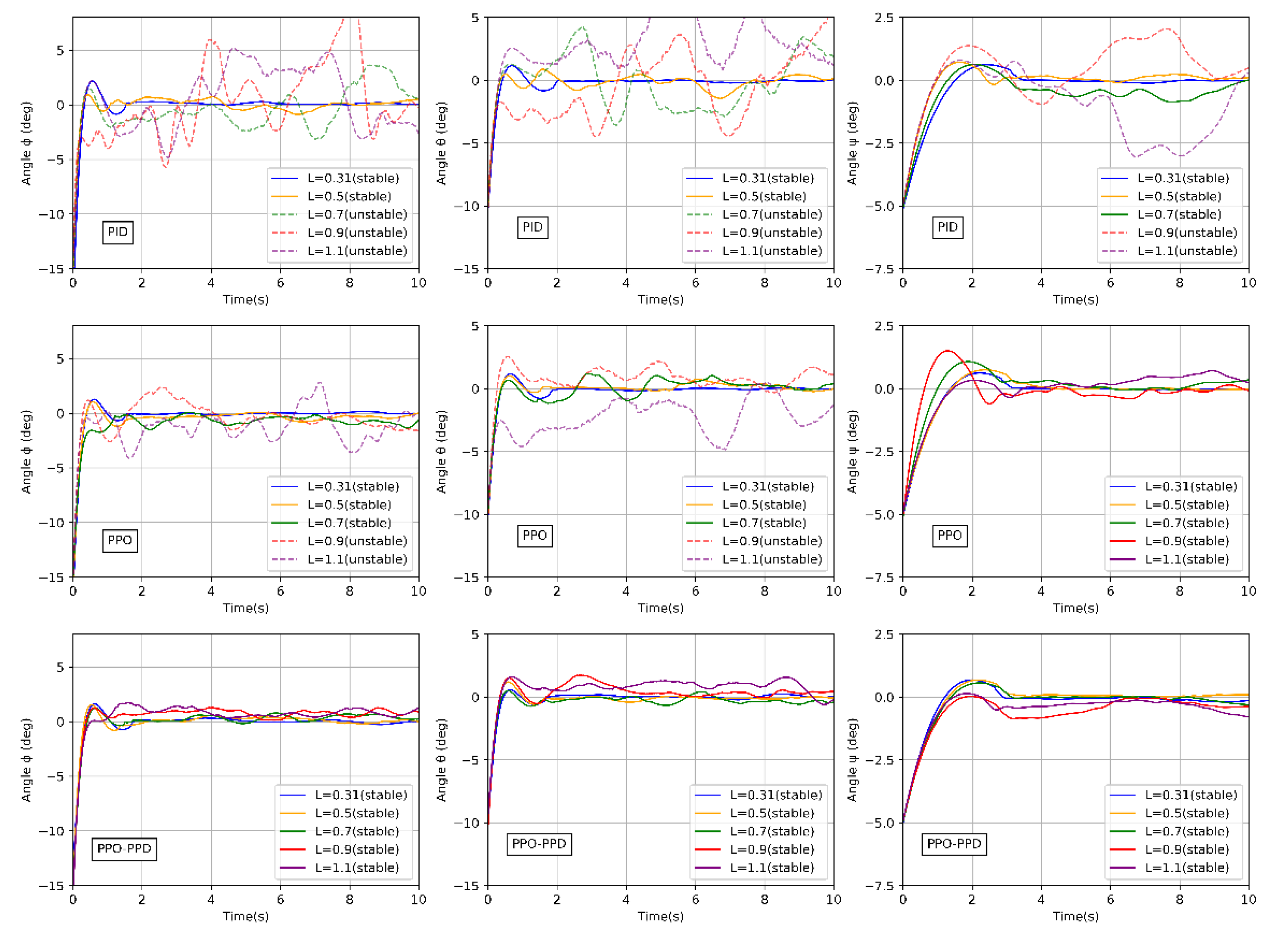
To prove the control performance of PPO-PPD under different specification models, we conducted the following simulation. The distance from the rotor of the quad-rotor model to the center of mass is 0.31 m, which is defined as the standard radius. Then we choose to test the model set radius from 0.2 m (35%) to 1.1 m (250% larger). For these model sets, the maximum thrust and mass of the quadcopter remain unchanged.

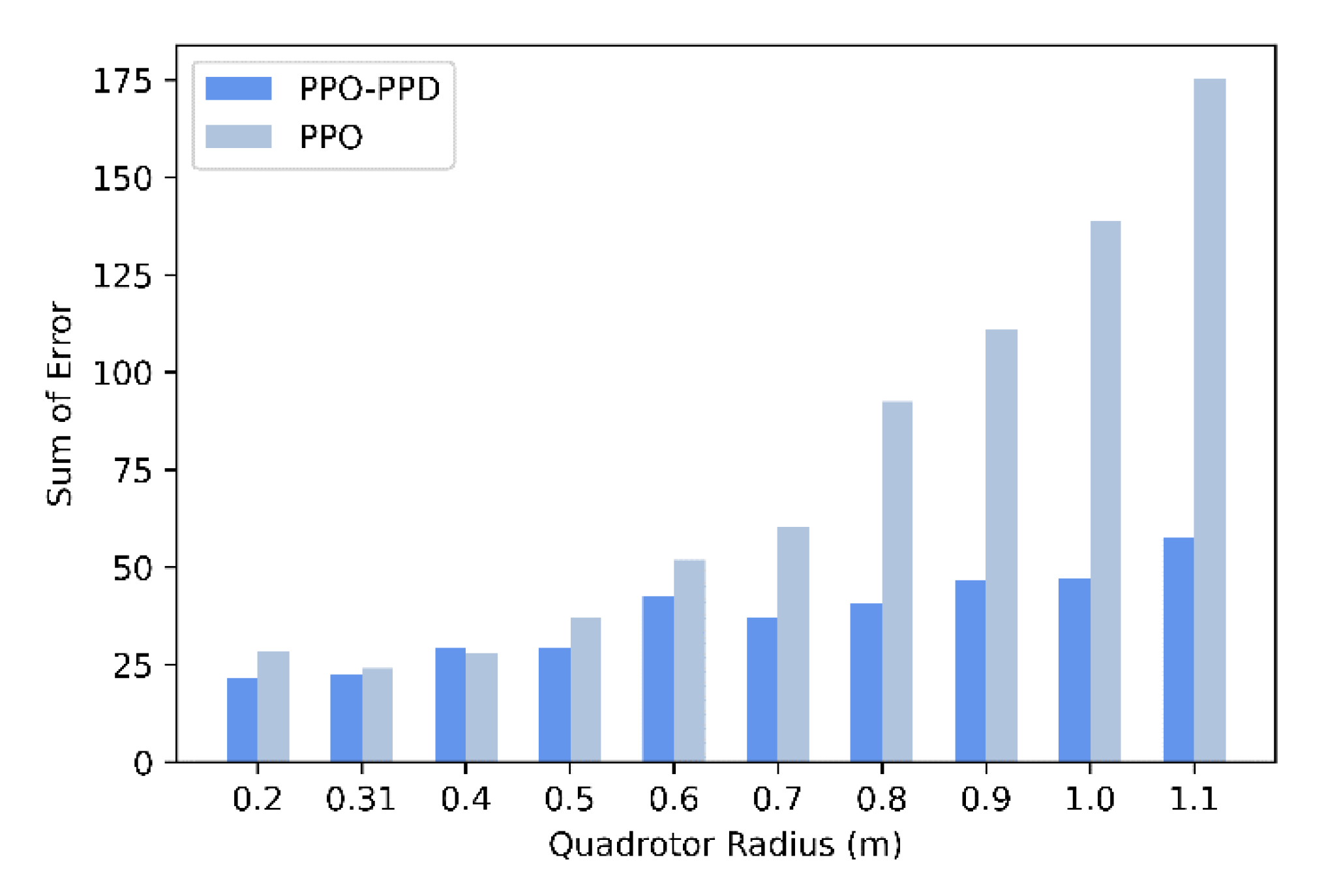
It can be seen from Figure 13 that the two RL controllers show a stable performance at radius of 0.31 m and 0.5 m. However, the attitude based on PID controller has already produced a slight oscillation. When the radius increases to 0.7 m, the PID controller has poor stability and robustness because of the parameter uncertainty. When the radius is larger than 0.9 m, the PPO policy cannot stabilize the model while the PPO-PPD policy still obtains a stable performance until 1.1 m. Figure 14 shows the sum of attitude error between the PPO-PPD and PPO algorithms at steady state. After comparison, the PPO-PPD algorithm always maintains stable, consistent, and accurate control within a large radius.

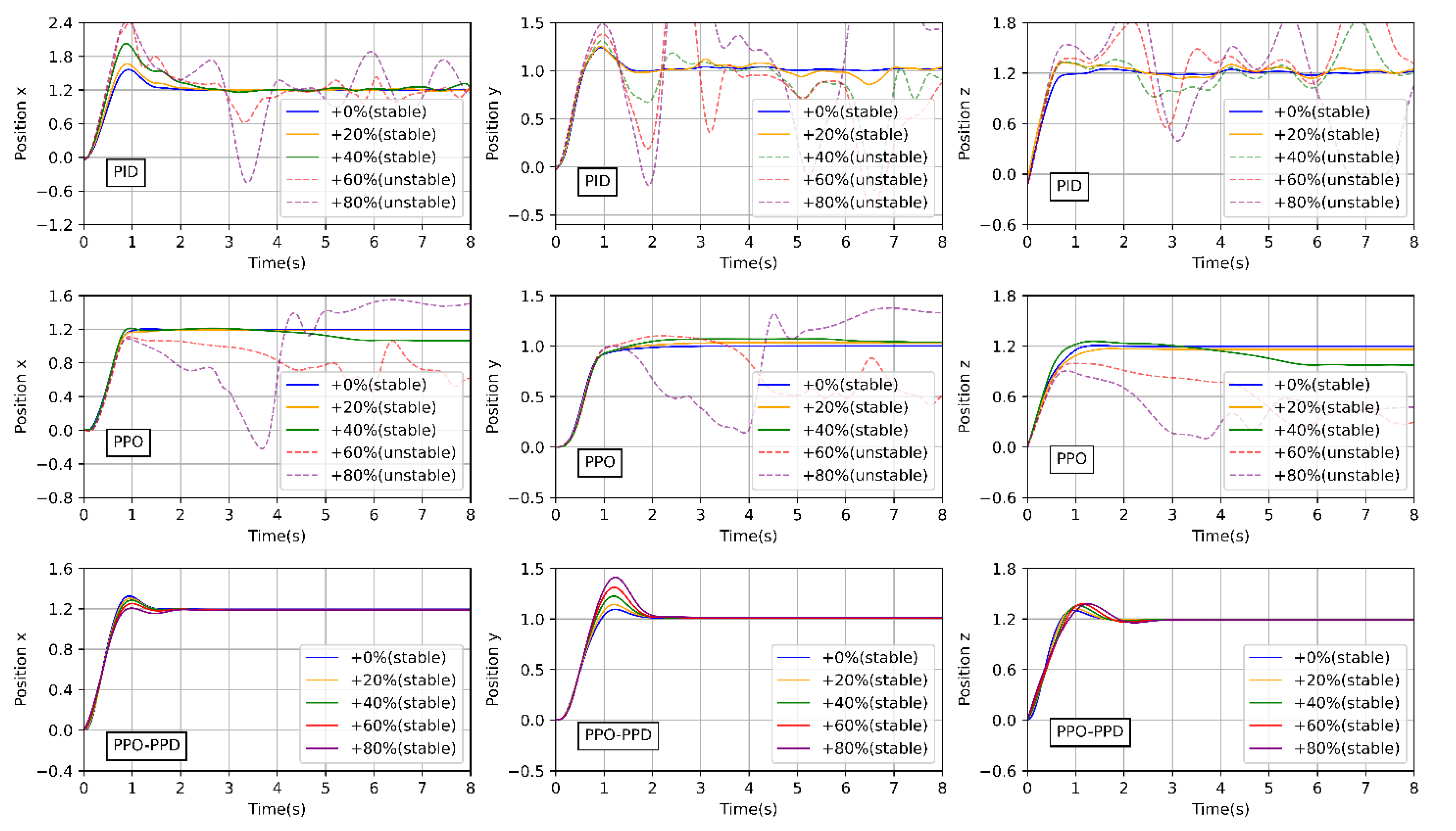
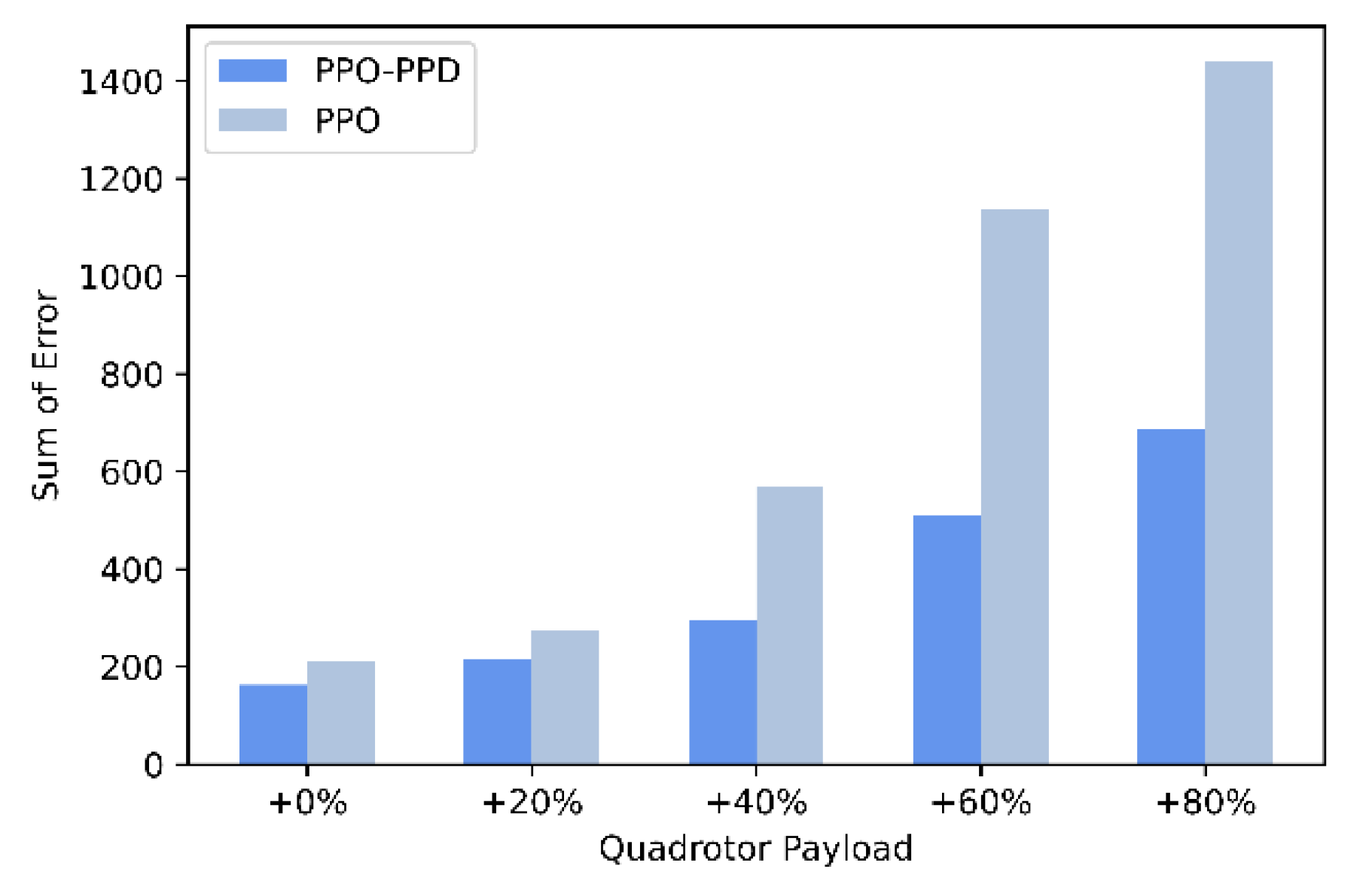
In addition, the robustness of the quadrotor of different masses are tested through a fixed-point flight mission. The mass of the quadrotor gradually increases due to the weight of payloads, which is not added in the training phase but is directly tested with the learned offline policy. The payloads are from 20% to 80% of the mass of the quadrotor, which also affects the moment of inertia of the quadrotor. After a simple test with offline training, we reduce the difficulty of fixed-point flight task to better observe the effect of load on quadrotor flight. A total of five tests are carried out. In each test, only the mass of the quadrotor is changed. The quadrotor starts from the initial point [0, 0, 0] and the desired position is [1.2, 1.0, 1.2].

The position curves of the five set tests are shown in the Figure 15. The existing PID gain can no longer meet the control requirements when the payload accounts for 40%. The PPO policy complete the task only when the mass is below 120%. When the mass is increased to 140%, there is a large position steady-state error although the quadrotor based on PPO controller is still stable. It is mainly because most of the thrust balances the gravity provided by the payloads, that the thrust acting on the position becomes small. When the payload reaches 60% to 80%, PPO cannot remain the stability of quadrotor. However, PPO-PPD can quickly reach the target position without steady-state errors in different payloads. As shown in Figure 16, the sum of position errors is compared between the PPO-PPD and PPO policy. From the comparison results, the PPO-PPD control policy has shown great robustness on different quadrotor models with different sizes or payloads.

3.

Case 3: Anti-disturbance ability test.

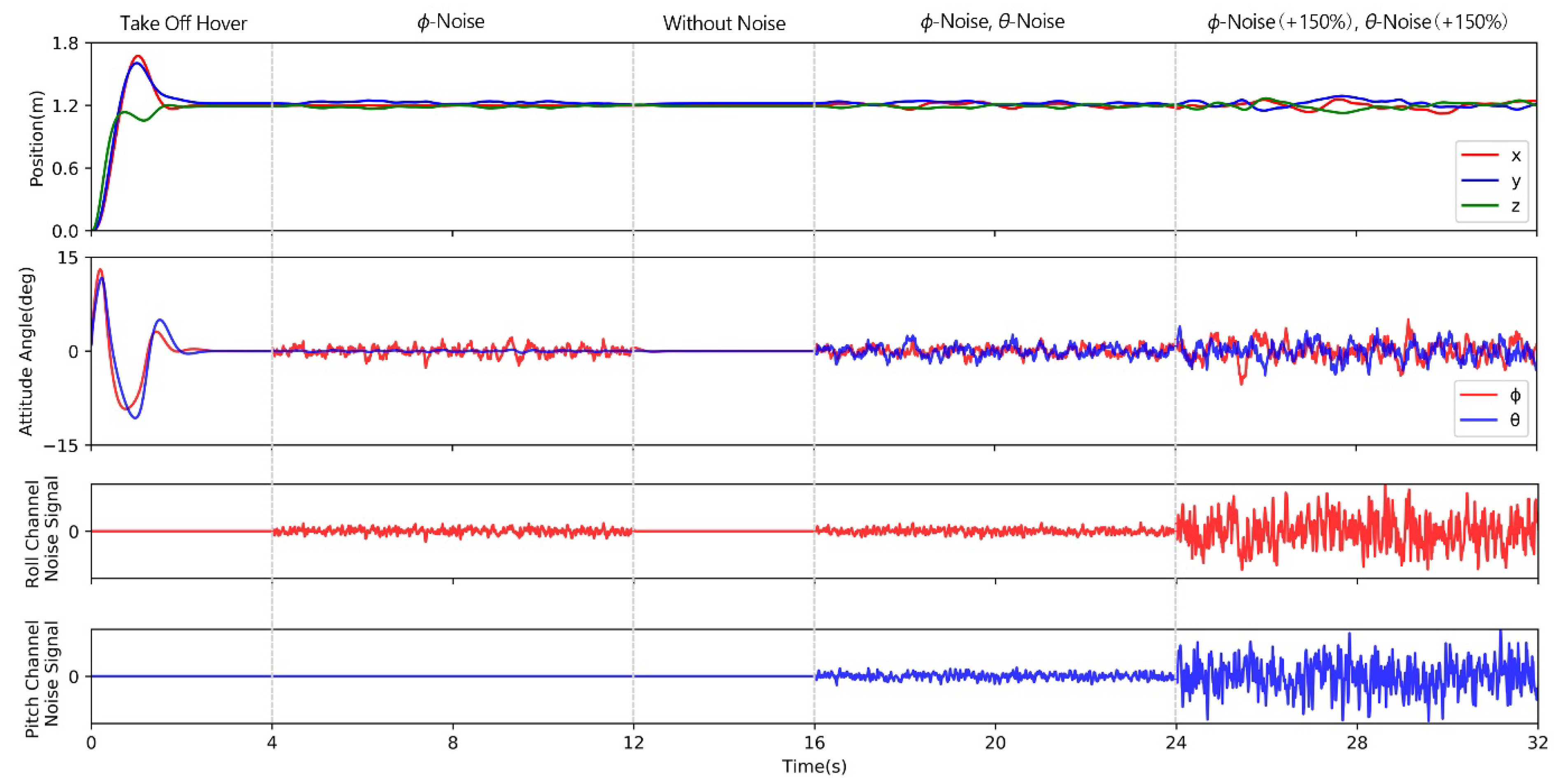
The actual quadrotor system is vulnerable to disturbances such as wind dusts and sensor noises. To verify the anti-disturbance ability of the PPO-PPD control policy, the quadrotor rotation system is added to Gaussian white noises. The test is carried out through the control task of the quadrotor hovering at a fixed point. The quadrotor flies from [0, 0, 0] to [1.2, 1.2, 1.2] using the PPO-PPD offline policy. The RL controller runs continuously for 32 s. For the first 4 s, the quadrotor takes off from the starting point and hovers at the desired position, then a noise is applied to the roll motion signal from 4 s.

The flight performance of the quadrotor is shown in Figure 17. Due to the influence of noise, the rolling channel and position of the quadrotor fluctuated slightly. The quadrotor immediately returns to the stable state when the noise disappears at t = 12 s. The noise signal is applied to the roll and pitch channels at t = 16 s, the quadrotor tends to be stable although there are slight oscillations. When the noise signal increases by 150% at the 24th second, the quadrotor has a large attitude oscillation and position deviation. In general, the control policy of PPO-PPD can successfully deal with the disturbances.

From the results of all the cases, the control policy by PPO-PPD in the offline stage shows strong robustness of quadrotor models of different sizes and payloads. Although the PPO controller has a good generalization ability, the proposed PPO-PPD method is proven to be more superior in convergence and robustness.

5. Conclusions

An improved proximal policy optimization algorithm is proposed to train the quadrotor to complete the low-level control tasks of take-off, precise flight and hover. A policy optimization method with a penalized point probability distance can provide the diversity of policy. Together with the proposed compound reward function, the new RL controller effectively reduces the training time of the control policy and improves the learning efficiency. By varying the radius and mass of the quadrotor in the test, the offline control policy is shown to have a good robustness. In addition, compared with the PPO algorithm off the shelf, the control policy learned by the proposed algorithm reduces the steady-state error of the position and attitude, and improves the control accuracy. In future work, we will focus on exploring the role of neural networks in complex nonlinear system task environments, and combine more traditional control techniques with RL to optimize the control performance of the quadrotor.