Modeling and Control Design of a Contact-Based, Electrostatically Actuated Rotating Sphere
Abstract
:1. Introduction
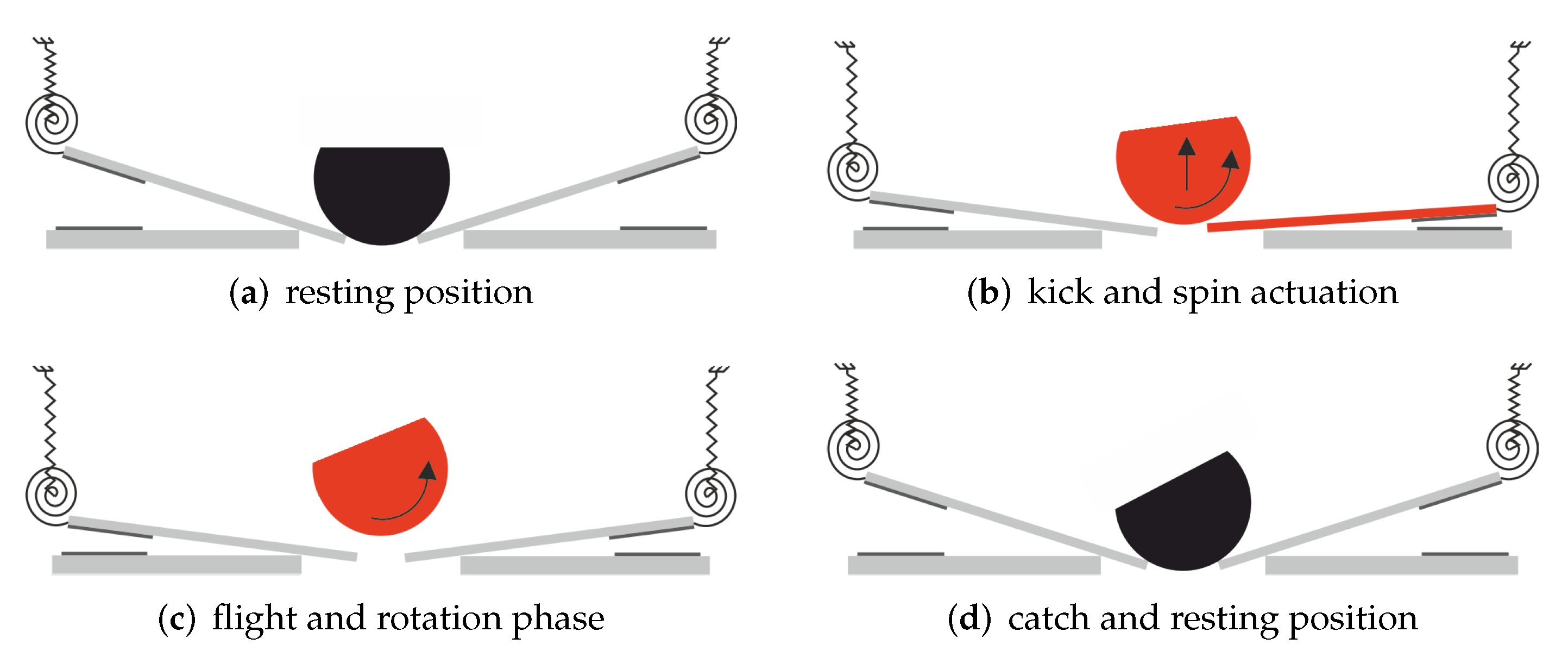
2. Actuator Design and Working Principle
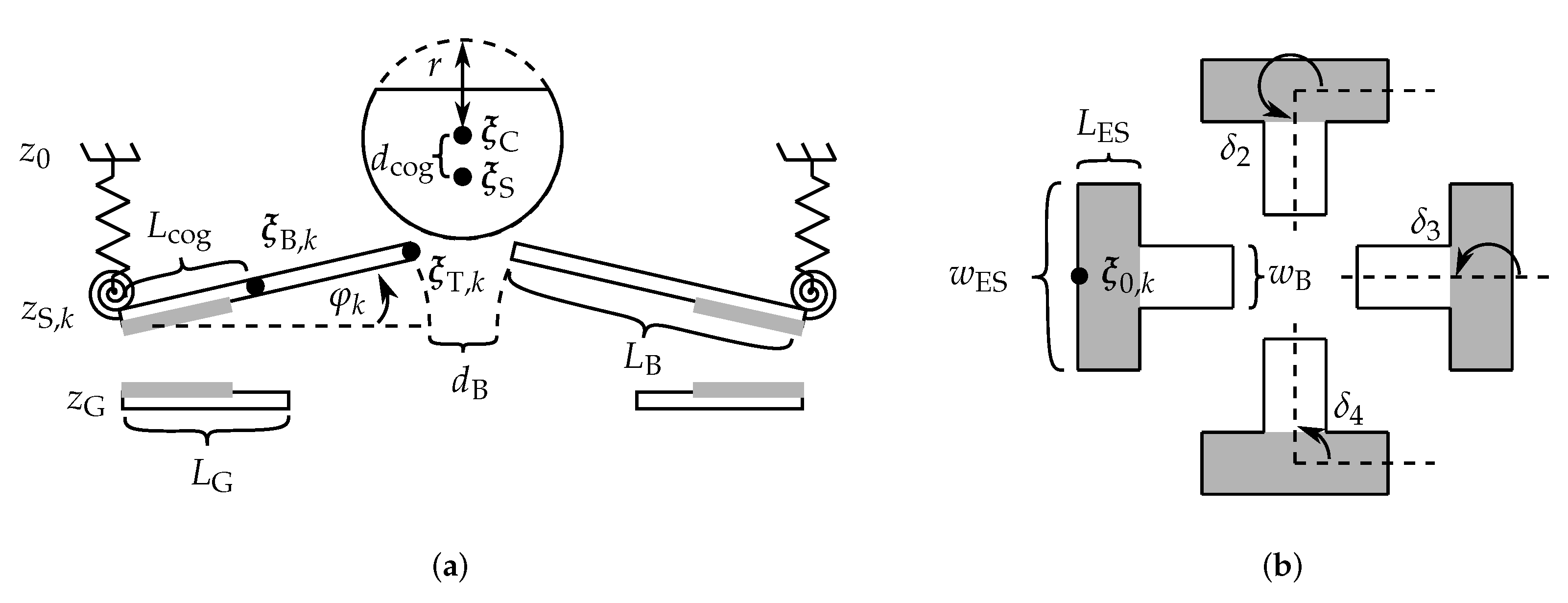
3. Modeling
3.1. Electrostatic Actuator Dynamics
3.2. Sphere Dynamics
3.3. Contact and Friction Modeling
3.3.1. Beam-Ground Contact
3.3.2. Beam-Sphere Contact
3.3.3. Beam-Sphere Friction
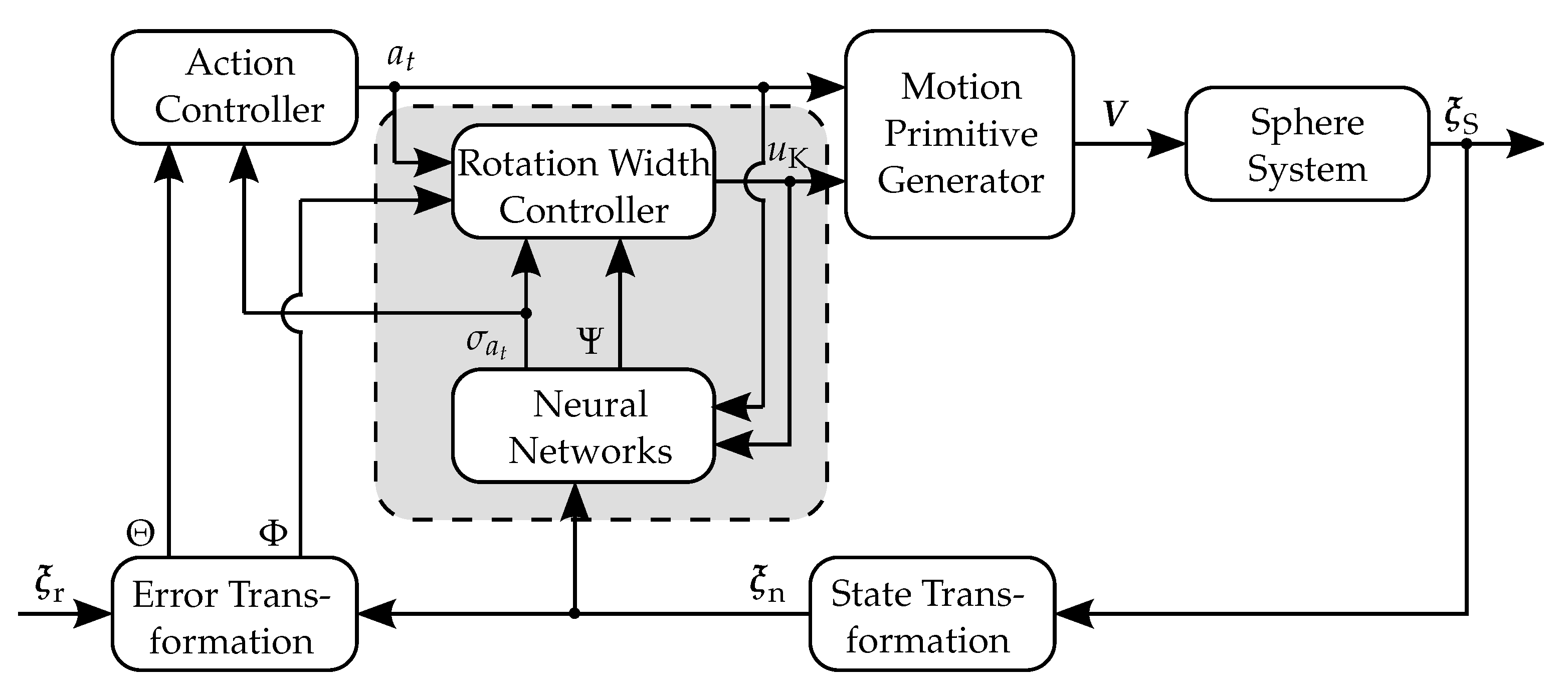
4. Control Approach
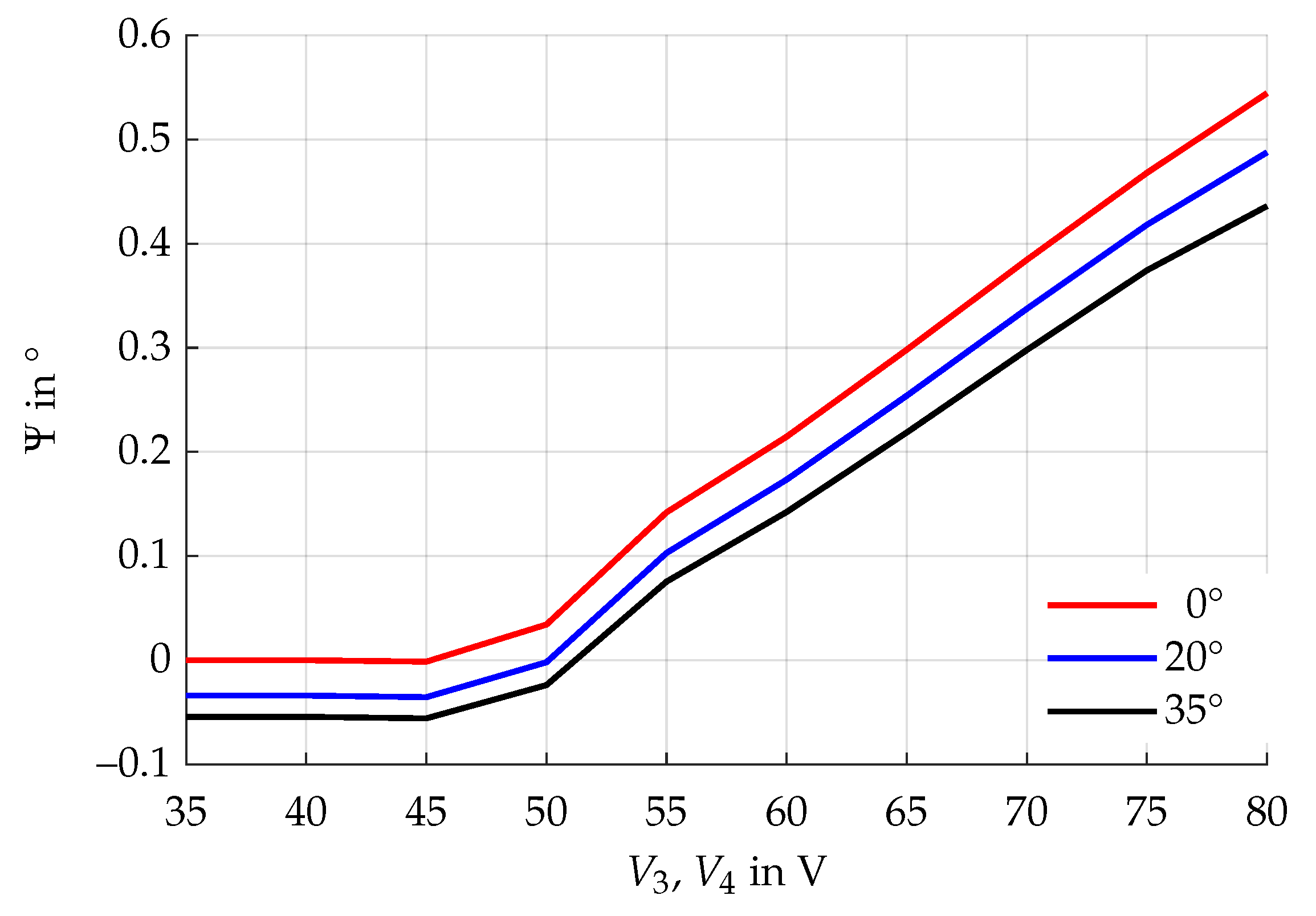
4.1. Step 1: Electrostatic Actuation
4.2. Step 2: Feedback Control
5. Results
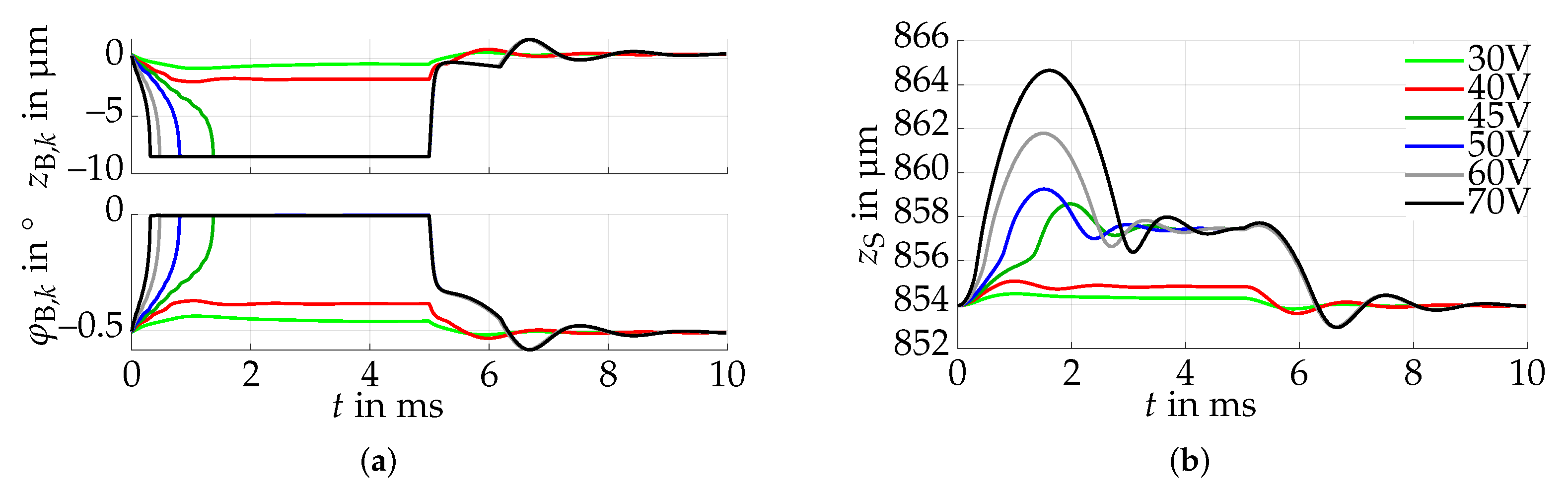
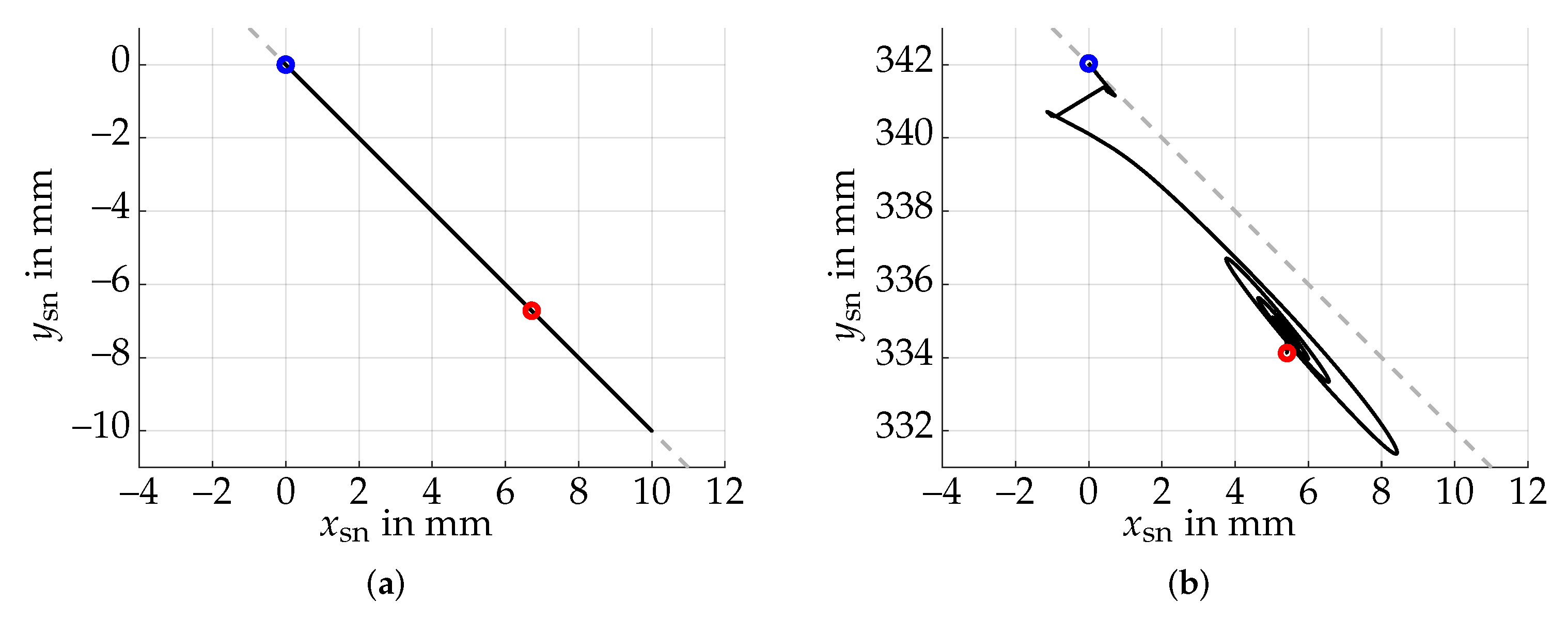
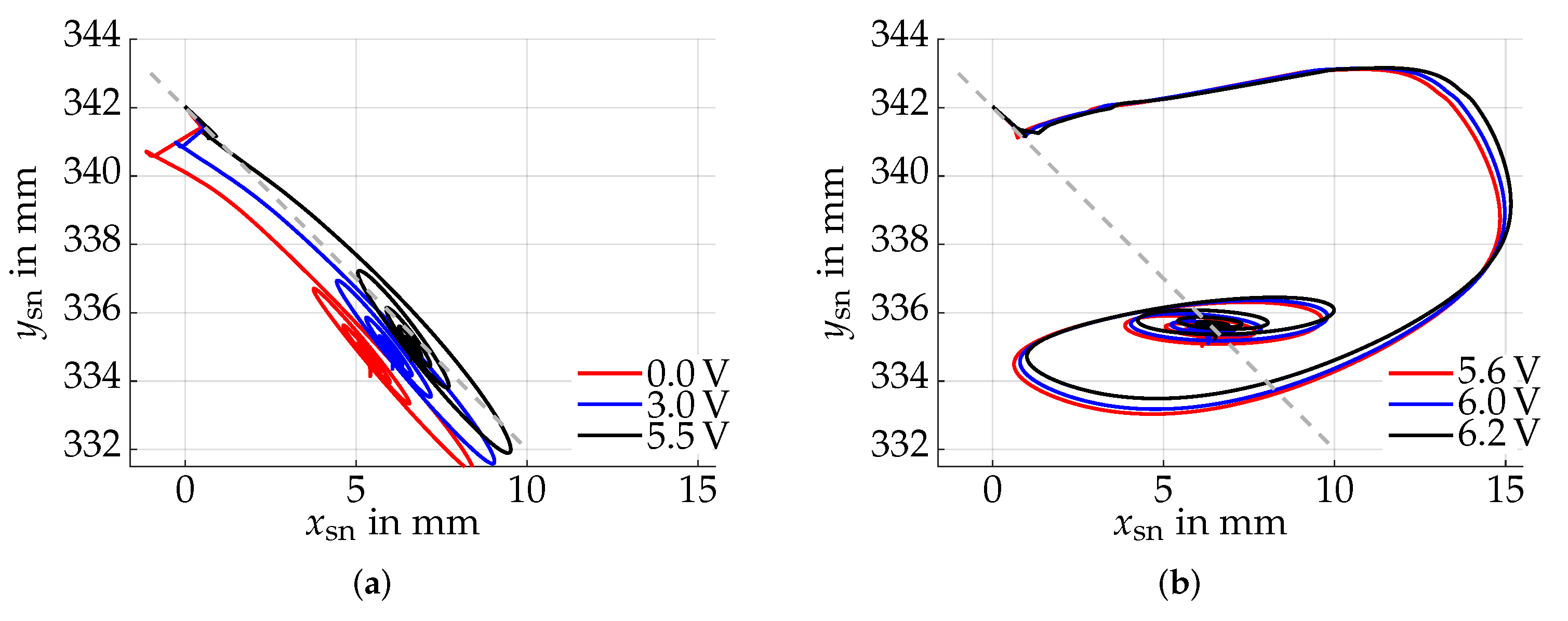
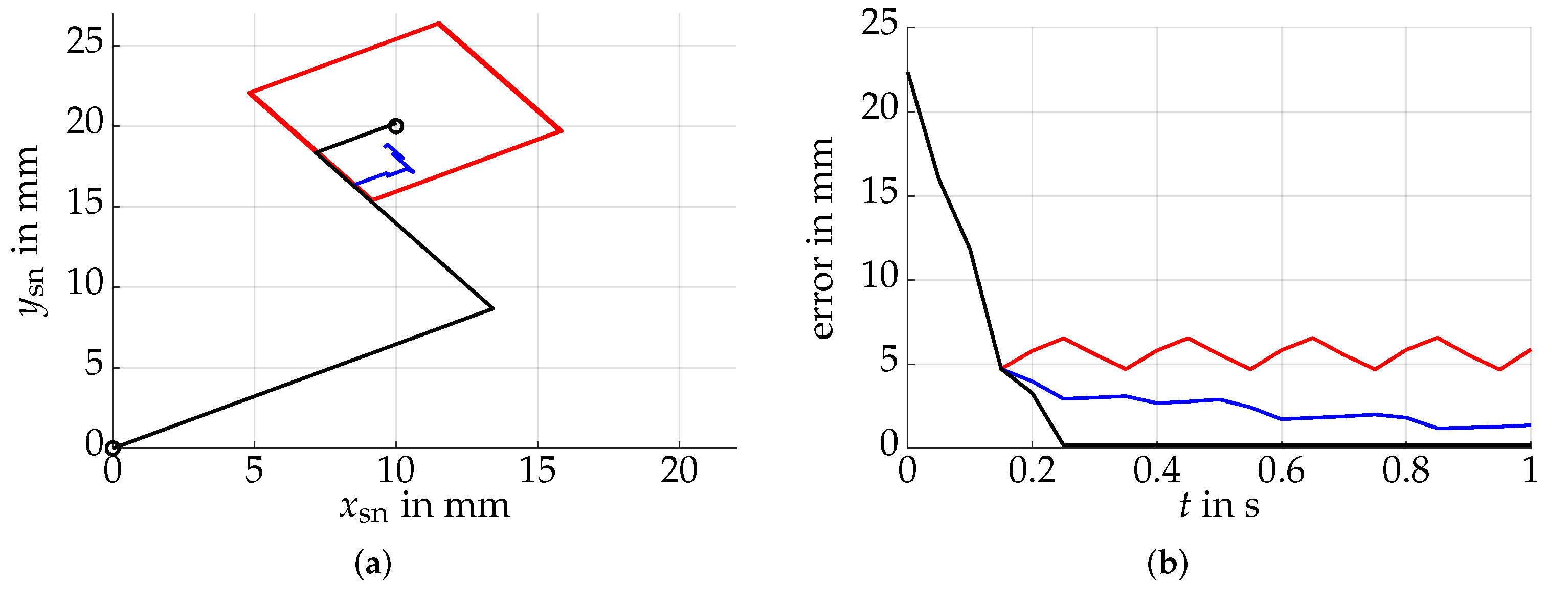
5.1. Setpoint Control
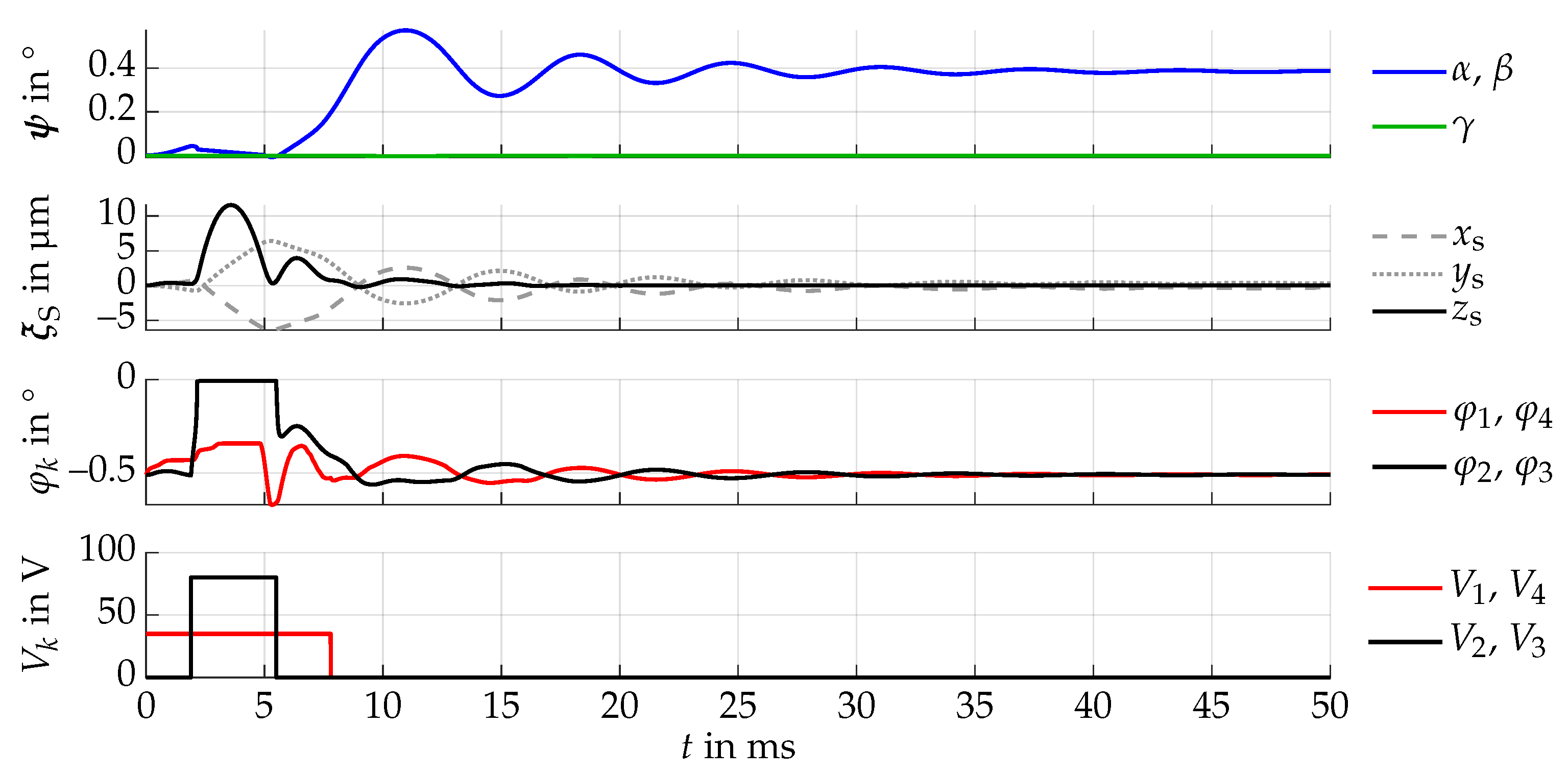
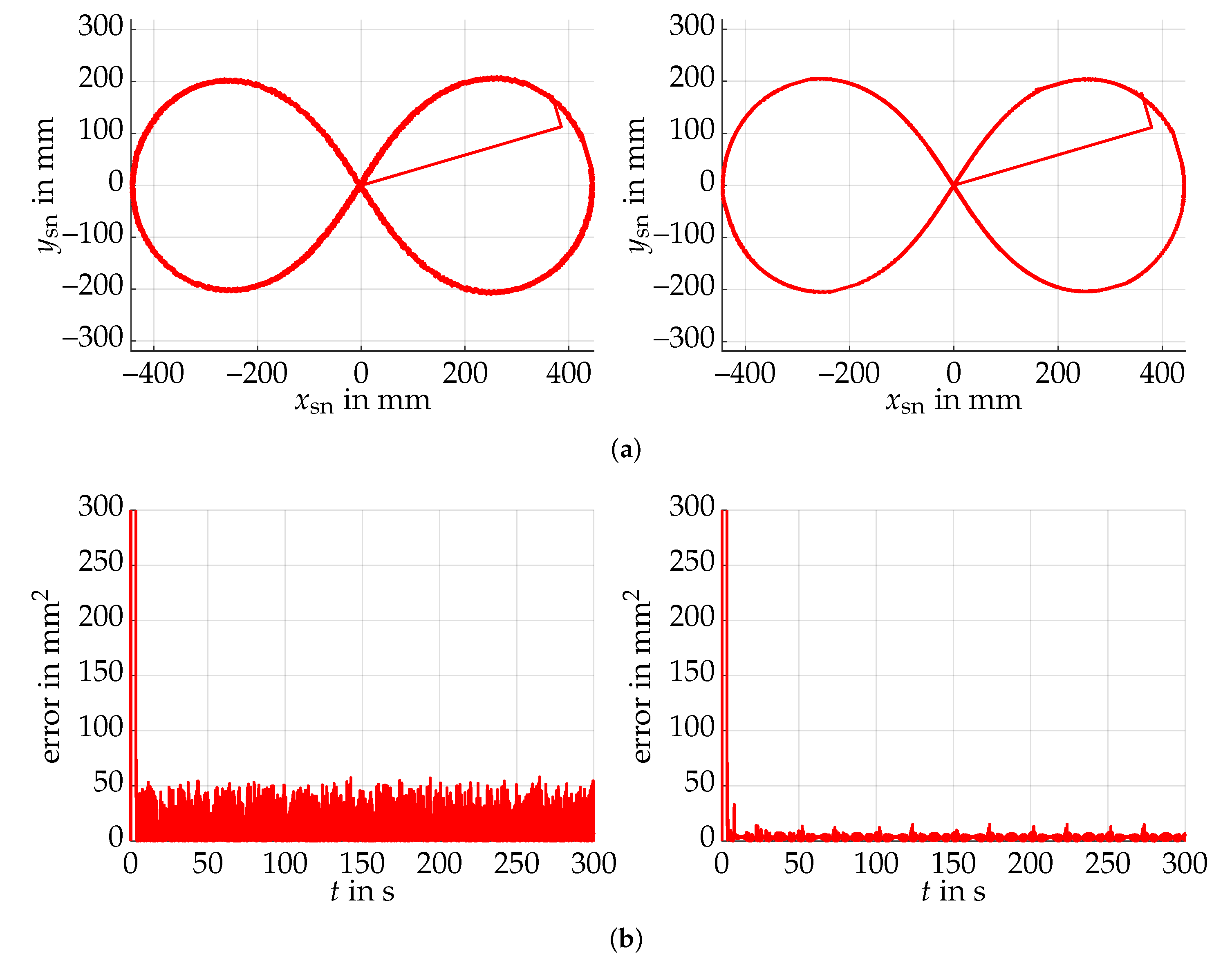
5.2. Trajectory Following Control
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Transformation Matrices
Appendix A.2. Sphere Inertia Tensor
Appendix A.3. Simulation Parameters
| Parameter | Explanation | Value |
|---|---|---|
| Beam suspension position | 0 μm | |
| Beam tip distance | 800 μm | |
| Beam length | 1400 μm | |
| Beam width | 200 μm | |
| Beam mass | 96.695 μg | |
| Beam inertia | 0.2665 g cm2 | |
| Distance to beam center of gravity | 319 μm | |
| Capacitor plate length | 500 μm | |
| Capacitor plate width | 1300 μm | |
| Virtual insulation layer thickness | 1.5 μm | |
| Vertical beam spring stiffness | 35 N | |
| Rotational beam spring stiffness | 20 μN m | |
| Vertical beam damping coefficient | 30 μN s | |
| Rotational beam damping coefficient | 5 nN m s | |
| Ground plate position | −10 μm | |
| Ground plate length | 1000 μm | |
| r | Sphere radius | 1000 μm |
| Sphere cutting angle | 90 ° | |
| Sphere mass | 30.973 mg | |
| Full sphere center and center of gravity distance | 49.7642 μm | |
| Rotational sphere damping coefficient | 0.1 nN m s | |
| Translatory sphere damping coefficient | 5 mN s | |
| Contact modeling parameter (linear stiffness) | 5 × 106 | |
| C | Contact modeling parameter (transition parameter) | |
| Contact modeling parameter (impact loss parameter) | 10 | |
| Friction parameter (viscous friction) | ||
| Friction parameter (Coulomb friction) | ||
| Friction parameter (Coulomb friction) | ||
| Friction parameter (Stribeck friction) | ||
| Friction parameter (Stribeck friction) | ||
| Learning rate (kick direction) | ||
| Learning rate (neural network bias) | ||
| Learning rate (neural network weights) |
References
- Holmström, S.T.S.; Baran, U.; Urey, H. MEMS Laser Scanners: A Review. J. Microelectromech. Syst. 2014, 23, 259–275. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Zhuang, X.; Zhou, C.; Fan, B. Development of an Electrostatic Comb-Driven MEMS Scanning Mirror for Two-Dimensional Raster Scanning. Micromachines 2021, 12, 378. [Google Scholar] [CrossRef] [PubMed]
- Chong, J.; He, S.; Ben Mrad, R. Development of a Vector Display System Based on a Surface-Micromachined Micromirror. IEEE Trans. Ind. Electron. 2012, 59, 4863–4870. [Google Scholar] [CrossRef]
- Hu, F.; Yao, J.; Qiu, C.; Ren, H. A MEMS micromirror driven by electrostatic force. J. Electrost. 2010, 68, 237–242. [Google Scholar] [CrossRef]
- Jeong, H.M.; Park, Y.H.; Jeong, H.K.; Cho, Y.C.; Chang, S.M.; Kim, J.O.; Kang, S.J.; Hwang, J.S.; Lee, J.H. Slow scanning electromagnetic MEMS scanner for laser display. In MOEMS and Miniaturized Systems VII; SPIE: Bellingham, DC, USA, 2008; Volume 6887, pp. 41–52. [Google Scholar] [CrossRef]
- Liao, W.; Liu, W.; Zhu, Y.; Tang, Y.; Wang, B.; Xie, H. A Tip-Tilt-Piston Micromirror With Symmetrical Lateral-Shift-Free Piezoelectric Actuators. IEEE Sens. J. 2013, 13, 2873–2881. [Google Scholar] [CrossRef]
- Makishi, W.; Kawai, Y.; Esashi, M. Magnetic torque driving 2D micro scanner with a non-resonant large scan angle. In Proceedings of the TRANSDUCERS 2009–2009 International Solid-State Sensors, Actuators and Microsystems Conference, Denver, CO, USA, 21–25 June 2009; pp. 904–907. [Google Scholar] [CrossRef]
- Weinberger, S.; Nguyen, T.; Lecomte, R.; Cheriguen, Y.; Ament, C.; Hoffmann, M. Linearized control of an uniaxial micromirror with electrostatic parallel-plate actuation. Microsyst. Technol. 2015, 22, 441–447. [Google Scholar] [CrossRef]
- Bunge, F.; Leopold, S.; Bohm, S.; Hoffmann, M. Scanning micromirror for large, quasi-static 2D-deflections based on electrostatic driven rotation of a hemisphere. Sens. Actuators Phys. 2016, 243, 159–166. [Google Scholar] [CrossRef]
- DFG, Kick and Catch-Cooperative Microactuators for Freely Moving Platforms: SPP 2206: Cooperative Multilevel Multistable Micro Actuator Systems (KOMMMA). Available online: https://gepris.dfg.de/gepris/projekt/424616052 (accessed on 6 March 2022).
- Barjuei, E.; Caldwell, D.; Ortiz, J. Bond Graph Modeling and Kalman Filter Observer Design for an Industrial Back-Support Exoskeleton. Designs 2020, 4, 53. [Google Scholar] [CrossRef]
- Kumbhar, S.; Sudhagar, P.; Desavale, R. An overview of dynamic modeling of rolling-element bearings. Noise Vib. Worldw. 2021, 52, 1–16. [Google Scholar] [CrossRef]
- Pustan, M.; Paquay, S.; Rochus, V.; Golinval, J.C. Modeling and finite element analysis of mechanical behavior of flexible MEMS components. Microsyst. Technol. 2011, 17, 553–562. [Google Scholar] [CrossRef]
- Schütz, A.; Olbrich, M.; Hu, S.; Ament, C.; Bechtold, T. Parametric system-level models for position-control of novel electromagnetic free flight microactuator. Microelectron. Reliab. 2021, 119, 1–9. [Google Scholar] [CrossRef]
- Yerlikaya, U.; Balkan, R. Dynamic modeling and control of an electromechanical control actuation system. In Proceedings of the Dynamic Systems and Control Conference, Tysons, WV, USA, 11–13 October 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Hurmuzlu, Y.; Marghitu, D. Rigid Body Collisions of Planar Kinematic Chains with Multiple Contact Points. Int. J. Robot. Res. 1994, 13, 82–92. [Google Scholar] [CrossRef]
- Popov, V.; Heß, M. Method of dimensionality reduction in contact mechanics and friction: A users’ handbook. Facta Univ. 2014, 12, 1–14. [Google Scholar]
- Fischer-Cripps, A. The Hertzian contact surface. J. Mater. Sci. 1999, 34, 129–137. [Google Scholar] [CrossRef]
- Specker, T.; Buchholz, M.; Dietmayer, K. Dynamical Modeling of Constraints with Friction in Mechanical Systems. In Proceedings of the 8th Vienna International Conference on Mathematical Modelling, Vienna, Austria, 18–20 February 2015; pp. 514–519. [Google Scholar] [CrossRef]
- Potocnik, B.; Music, G.; Zupancic, B. Model predictive control systems with discrete inputs. In Proceedings of the 12th IEEE Mediterranean Electrotechnical Conference, Dubrovnik, Croatia, 12–15 May 2004; Volume 1, pp. 383–386. [Google Scholar] [CrossRef]
- Asok, R.; Jinbo, F.; Constantino, L. Optimal supervisory control of finite state automata. Int. J. Control 2004, 77, 1083–1100. [Google Scholar] [CrossRef]
- Konaka, E. Controller design for discrete input control system based on machine-learning. In Proceedings of the SICE Annual Conference 2011, Tokyo, Japan, 13–18 September 2011; pp. 601–604. [Google Scholar]
- Glorennec, P.Y. Reinforcement learning: An overview. In Proceedings of the European Symposium on Intelligent Techniques, Aachen, Germany, 14–15 September 2000; pp. 14–15. [Google Scholar]
- Zhou, W.; Lan, H.; Yu, H.; Lai, L.; Peng, B.; He, X. Consideration of the fringe effects of capacitors in micro accelerometer design. Trans. Inst. Meas. Control 2018, 40, 1881–1996. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, Z.; Wang, W.; Rao, Z.; Han, Y. The 3D Capacitance Modeling of Non-parallel Plates Based on Conformal Mapping. In Proceedings of the 16th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Xiamen, China, 25–29 April 2021; pp. 1264–1267. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Koruba, Z. Classical Mechanics: Applied Mechanics and Mechatronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 30. [Google Scholar] [CrossRef]
- Olbrich, M.; Schütz, A.; Bechtold, T.; Ament, C. Design and Optimal Control of a Multistable, Cooperative Microactuator. Actuators 2021, 10, 183. [Google Scholar] [CrossRef]
- Dharmadhikari, M.; Dang, T.; Solanka, L.; Loje, J.; Nguyen, H.; Khedekar, N.; Alexis, K. Motion Primitives-based Path Planning for Fast and Agile Exploration using Aerial Robots. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 179–185. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB (R2019a); The MathWorks Inc.: Natick, MA, USA, 2019. [Google Scholar]

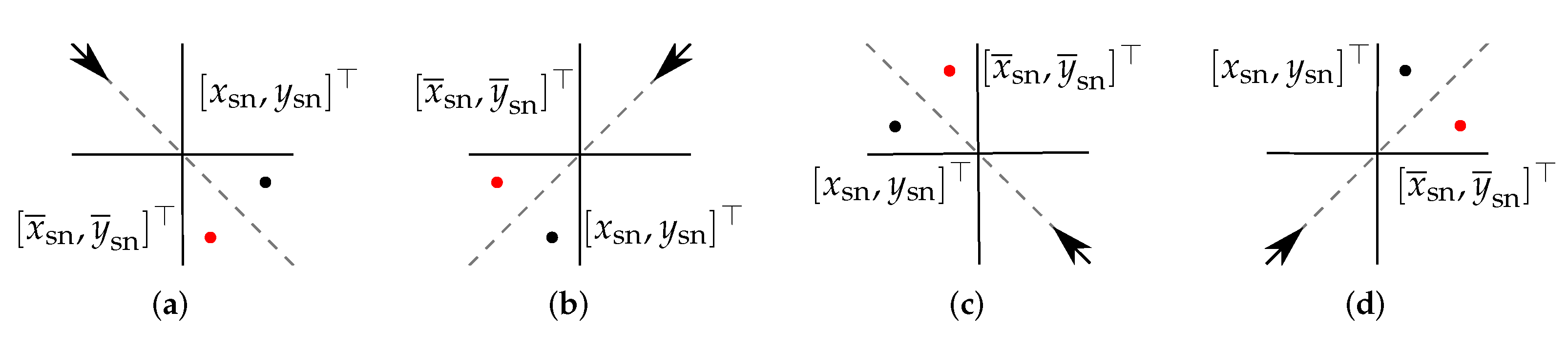



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olbrich, M.; Farny, M.; Hoffmann, M.; Ament, C. Modeling and Control Design of a Contact-Based, Electrostatically Actuated Rotating Sphere. Actuators 2022, 11, 90. https://doi.org/10.3390/act11030090
Olbrich M, Farny M, Hoffmann M, Ament C. Modeling and Control Design of a Contact-Based, Electrostatically Actuated Rotating Sphere. Actuators. 2022; 11(3):90. https://doi.org/10.3390/act11030090
Chicago/Turabian StyleOlbrich, Michael, Mario Farny, Martin Hoffmann, and Christoph Ament. 2022. "Modeling and Control Design of a Contact-Based, Electrostatically Actuated Rotating Sphere" Actuators 11, no. 3: 90. https://doi.org/10.3390/act11030090
APA StyleOlbrich, M., Farny, M., Hoffmann, M., & Ament, C. (2022). Modeling and Control Design of a Contact-Based, Electrostatically Actuated Rotating Sphere. Actuators, 11(3), 90. https://doi.org/10.3390/act11030090






