Robust Adaptive Control of Knee Exoskeleton-Assistant System Based on Nonlinear Disturbance Observer

Abstract

This study presents a control design of an angular position for the exoskeleton knee assistance system based on a model reference adaptive control (MRAC) strategy. Three schemes of the MRAC design have been proposed: the classical MRAC, MRAC with an adaptive disturbance observer, and MRAC with a nonlinear observer. The stability analysis for each scheme has been conducted and developed based on the Lyapunov theorem to prove the uniform ultimate bound of tracking and estimation errors. In addition, the adaptive laws have been developed for the proposed schemes according to the stability analysis. The effectiveness of the proposed state and output feedback controllers has been verified via computer simulation. The results based on numerical simulation have shown that the MRAC with a nonlinear observer could give better robustness characteristics and better performance in terms of tracking and estimation errors as compared to the other controllers.

1. Introduction

The reports issued by the World Health Organization (WHO) indicate that the major causes of lifelong and acute disability are neurological injuries such as spinal cord injury (SCI), brain injury equivalent of a heart attack, and strokes. Among the 15 million people worldwide who suffer strokes, 5 million are left disabled for a significant period of time, which places a burden on their communities and families [1].

Patients who suffer neurological problems and musculoskeletal lesions may lose mobility and autonomy, which in turn leads to drastic changes in their welfare. It has been shown that physical therapy and rehabilitation could effectively cure patients encountering such disorders and diseases and repeated and long-term exercises have shown fruitful results in remedy by supporting patients to achieve certain tasks [1,2].

However, these treatments may be expensive due to the requirement of physicians who supervise the treatment and who manually help disabled persons to perform the prescribed exercises. In addition, this traditional method in remedy requires many hours with a movement-supervising doctor for each patient being a further necessity in such treatment [2,3].

The existing and time-consuming exercises of rehabilitation can be replaced by actuated bio-engineering exoskeletons. These devices will alleviate the burden of the therapists and they could simultaneously assist multiple patients at once due to their repetitive and physical movements. Moreover, the robot-mediated orthoses are able to quantify, measure and record the progress of each patient by including specified sensors, which can measure variables like the angular position of the device or the exerted force, etc. Accordingly, physicians can interpret the reports and customize or modify the treatment. Therefore, based on clinical trials, these robotic exoskeletons have shown high effectiveness and efficacy [2,3].

One important issue in pursuing this type of rehabilitation is that the exoskeleton-type robot has to be designed to fit the human joint and its movement has to couple with the body of the patient so that ergonomic motion can be withstood by the wearer. This issue is very important, especially in the case of lower-limb orthoses, where these devices are responsible for reviving as many movements as possible so that the autonomy and independence of the patient can be finally regained [2,3].

The exoskeleton knee assistant system is constructed from two articulated links moving in parallel with the knee joint, by producing an amount of torque to assist the knee to move accurately and smoothly in the case of a knee disability. The exoskeleton knee assistant system depends on a brushless motor to produce the generated torque, and a control theory is a crucial need in the case of aiming for smooth and accurate movement. Modeling the exoskeleton knee assisted system and acquiring a precise model parameter is a big problem in the sense of using the system for more than one patient since patients have different physical constructions. Hence why the need for a control theory that can perform robust, adaptive, and accurate control has become the key point of this work. In what follows, a survey of relevant researches on exoskeleton motion control for lower limbs has been reviewed in brief.

Rifaï et al. presented the design of a model reference adaptive control for a shank-orthosis system subjected to online parameter variation, where asymptotic and input-to-state stabilities were proved for non-muscular effort exertion cases and for bounded torque of human exertion [4].

Kashif et al. have developed and implemented an adaptive robust integral of sign error (RISE) on an Exoskeleton Intelligently Communicating and Sensitive to Intention (EICoSI). The semi-global asymptotic stability was proved for the coupled human–exoskeleton system. It was shown that a lesser tracking error can be achieved with an adaptive RISE control as compared to a classic RISE controller [5].

Mithaq et al. presented an intelligent control design based on a combination of proportional integral derivative (PID) controller together with an adaptive neuro-fuzzy inference system (ANFIS) for position/force control of the knee joint motion in an active lower limb prosthesis. It was shown that the proposed hybrid ANFIS-PID control system outperformed that based on individual PID or ANFIS controllers [6].

Ding et al. proposed an adaptive proxy-based sliding mode control for robust and accurate tracking performance of a shank-orthosis system subjected to parameter uncertainty. This study showed that better performance in terms of robustness and tracking error could be achieved with the proposed controller as compared to the PID controller, adaptive PID control, and a traditional proxy-based sliding mode control [7].

Mefoued et al. used a high order sliding mode control (HOSMC) design for flexion/extension motion control of the knee such as to assist people with reduced mobility of the lower limb. The study showed that the HOSMC gave better performance than the PID controller in terms of robustness, tracking trajectory, finite-time convergence and stability [8].

Scandaroli et al. presented a PID and model reference adaptive control (MRAC) design for an above-knee and 3-DOF prosthesis. Based on EMG thigh signals together with a predictive trajectory generator using multi-sensorial data, the prosthesis is planned to be controlled such that the foot can be positioned accurately with respect to the floor [9]. Ajayi et al. applied a bounded control scheme for assisting patients with disorders in their lower limbs. The controller was applied to persons in a sitting position on the ankle and knee levels. The joint torques were estimated via a high gain observer to meet the requirement of the bounded human torque. The results showed good tracking of the physiotherapist trajectory is achieved by the proposed control law [10].

Sierra et al. combined two types of actuators, represented by harmonic drive-based DC motors and a pneumatic artificial muscle (PAM), for a lower limb exoskeleton in order to acquire both position accuracy and a high power/weight ratio. This developed configuration can enhance the performance of human lower limbs. This study designed PID controllers for its control purposes [11].

Lee et al. designed a sliding mode controller to address the nonlinearity and uncertainty in the Polycentric Knee Exoskeleton system. The knee system utilized an electro-hydraulic actuator (EHA) to solve the problem of the low-load capacity of other actuators. Well-performed tracking performance was shown via simulated and experimental results [12].

Rifaï et al. proposed an L1 adaptive control design to ensure trajectory tracking of the exoskeleton system at the level of the knee joint. A nonlinear proportional control was introduced to solve the delay problem due to the presence of a filter in the classical control. Both classical and augmented L1 adaptive control was implemented using an Exoskeleton Intelligently Communicating and Sensitive to Intention (EICoSI) [13].

Mefoued and Belkhiat presented a robust control design to drive a knee-exoskeleton to help people with a movement-limited knee. This study conducted dynamic modeling and parameter identification of the lower limb-exoskeleton system. Additionally, the velocity was estimated via a sliding mode observer (SMO). The proposed controller showed small tracking errors and good robustness characteristics against variation in the system parameters [14].

C. Chen presented the design of ADRC (active disturbance rejection control) based on a fast terminal sliding mode control to enhance the tracking performance of a lower limb exoskeleton system. The extended state observer (ESO) was included to estimate the lumped disturbance. It was shown that the proposed controller could perform better tracking precision and had a faster response than the PID controller [15].

J. Wang investigated finite-time and observer-based sliding mode controllers for a lower extremity exoskeleton (LEE) system actuated by artificial pneumatic muscles (PAMS). The dynamic and swinging phase models of the PAM-LEE system were analyzed based on the Lagrange principle. A finite-time ESO was used to estimate the unmeasurable velocities and lumped disturbance. Good tracking performance with high precision was achieved with the proposed control scheme [16].

A. Chevalier et al. presented the control design of a shank movement around the knee joint based on a fractional-order proportional-integral (FOPI). The proposed FOPI controller was approximated by finite-dimensional integer-order transfer functions. The controller showed better robustness against gain variations and higher disturbance rejection capabilities as compared to the integer-order PI controller [17].

S. Kaur et al. designed a fractional-order PID controller for motion control of the knee joint. The design parameters for the proposed controller were set based on an internal mode control (IMC) and a try-and-error procedure. The proposed controller showed good robustness characteristics against parameter variations [18].

S. Mefoued et al. applied a sliding mode control for a high precision motion of a knee joint orthosis in the presence of parametric and nonparametric uncertainties. The designed orthosis was used to assist or restore the movements of the knee-joint for people with reduced mobility. The proposed second-order sliding mode was showed efficacy and a satisfactory performance in terms of robustness and tracking errors as compared to conventional controllers [19].

S. Mefoued proposed a multi-layer perceptron neural network (MLPNN) control for actuating the orthosis to assist in flexion and extension motion of the knee. The proposed adaptive controller does not need a knowledge of the dynamic model and it could cope with all uncertainties due to coupling, modeling, and variation in system parameters. As compared to the PID controller, the MLPNN controller showed better tracking performance and efficiency [20].

T. K. Wang et al. proposed an adaptive motion control for the knee joint subjected to time-varying and nonlinear dynamic coupling between the prosthetic limb and the thigh. The adaptive controller could enhance the gait pattern appearance, compensate for the variation in the hip moment and adapt to walking speed [21].

Zhang Y. et al. presented a model-free adaptive controller for motion control of a knee joint exoskeleton to cope with the modeling complexity of a human–exoskeleton. The controller performed its action based on the acquisition of input and output data of the knee joint angle. It was shown that the proposed control scheme could give good tracking performance of the knee exoskeleton and good performance in waling assistance [22].

It is clear from the above literature survey that robustness with output feedback has not been addressed for the exoskeleton knee device. The problem with this system is that the adaptive controller may fail to cope with all uncertainties due to singularity problems in the change of specified system parameters. As such, an adaptive control scheme based on an observer could solve this problem to maintain the robustness of the controlled system for all potential uncertainties.

Adaptive control is a control theory that deals with totally uncertain or unknown systems parameters The Model Reference Adaptive Control (MRAC) received much interest recently due to its ability to alter its parameters in real-time environment. This enables the control system to operate in the presence of damages or failures in a highly uncertain environment. It has been shown that the MRAC can achieve good asymptotic tracking of plant states if the uncertainties can satisfy certain matching conditions. However, due to the presence of unmacted and matched disturbances, parameterization errors and unmedelled dynamics, such matching conditions usually do not hold. This could result in a deterioration of stability in terms of (UUB) Uniform Ultimate Boundedness [23,24,25,26,27,28].

The nonlinear-disturbance observer (DO) is powerful tool for estimating the unmeasurable disturbances. Disturbance presence within the adaptive control affects the adaptive gain convergence and causes what is called parameter drift. A more precise disturbance estimation can be quantized which leads to a more robust adaptive controller. Using the estimated disturbance in the control law can grant it the feature of coping with perturbation in the system [29,30].

The following points highlights the main contributions of this study:

• Design of model reference controller to robustly control the rehabilitation knee-assistant device subjected to upper bounded and unknown disturbance.
• Design of MRAC together with adaptive disturbance estimator subjected to upper bounded and unknown disturbance.
• Combining the design of nonlinear disturbance observer with MRAC controller design to robustly control the rehabilitation knee-assistant device in the presence of upper bounded and unknown disturbance.
• Conducting performance comparison among the three proposed controllers in terms of robustness, transient and control input characteristics.

It is worth to notify that the upper bound of the applied disturbance is the necessary condition to follow the control design of proposed controllers.

In addition to this section, Section 2 discusses the derivation of the mathematical modelling of the exoskeleton orthosis, Section 3 discusses the controller’s design based on a Lyapunov stability analysis, Section 4 discusses the computer simulation results and finally Section 5 delivers the conclusions.

2. Mathematical Modelling

The exoskeleton knee assisted system is constructed from two articulated links moving in parallel with the knee joint, by producing an amount of torque to assist the knee to move accurately and smoothly in the case of knee disability. Figure 1 illustrates the exoskeleton knee assisted system, configured to have an operation range of 90 degrees where 0 degree is the full extension of the knee joint, and 90 degrees represents the rest position when sitting on a high chair.

Considering the exoskeleton system as a swing pendulum, the mathematical model representation can be written assisted by Lagrangian dynamic analysis. Equation (1) describes the Lagrangian dynamic equation of motion as:

$$\frac{d}{dt} \left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=T$$

(1)

where $T$ represents the torque combination that acts on the exoskeleton system in which it consists of the generated torque and load set of torques of the solid and viscous friction and load:

$$T=u-T_u-T_s-T_v$$

(2)

where $u$ is the generated torque, $T_u$ is the load torque, $T_s=a_{s}sgn\left(\dot{\theta }\right)$ is the solid friction torque and $T_v=b_v\dot{\theta }$ is the viscous friction torque. The $L$ represents the Lagrangian operator where:

$$L=K_e-G_e$$

(3)

where $K_e=0.5 J{\dot{\theta }}^2$ represents the kinetic energy while $G_e=mgl\left(1-sin\theta \right)$ represents the gravitational energy. Where $\dot{\theta }$ represents the angular speed of the exoskeleton system, $J$ represents the moment of inertia of the leg, $m$ and $l$ tend for the leg mass in the center of gravity and the knee length, $g$ is the gravitational force and $\theta$ is the angular position of the knee.

By substituting Equations (2) and (3) into Equation (1), the dynamical model of the exoskeleton system is written as:

$$\ddot{\theta }=-\frac{b_v}{J}\dot{\theta }+\frac{1}{J}u+\frac{mgl}{J}cos\theta -\frac{a_s}{J}sgn\left(\dot{\theta }\right)-\frac{1}{J}{T}_u$$

(4)

Let ${\theta }_{des}$ be the desired knee joint behaviour or profile. In order to achieve robust tracking to the desired profile, an integral sub-dynamic will be added to the exoskeleton system by following the next analysis.

Let $e_y=\theta -{\theta }_{des}$, and its dynamics of:

$${\dot{e}}_{yi}=e_y$$

(5)

by fusing Equation (5) with Equation (4) to change the state variables as, let $x_1=e_{yi}$,$x_2=\theta$, ${\dot{x}}_2=x_3=\dot{\theta }$, and ${\dot{x}}_3=\ddot{\theta }$. Then, the dynamical system of Equations (4) and (5) can be rewritten as:

$${\dot{x}}_1=x_2-{\theta }_{des}$$

(6)

$${\dot{x}}_2=x_3$$

(7)

$${\dot{x}}_3=-\frac{b_v}{J}{x}_3+\frac{1}{J}u+\frac{mgl}{J}\mathit{cos}\left(x_2\right)-\frac{a_s}{J}sgn\left(x_3\right)-\frac{1}{J}{T}_u$$

(8)

Equations (6)–(8) can be simplified in state space representation as:

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& -\frac{b_v}{J}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]+\frac{1}{J}\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right](u+\left[\begin{array}{cc}mgl& -a_s\end{array}\right]\left[\begin{array}{c}cos(x_2)\\ sgn\left(x_3\right)\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ \frac{-1}{J}\end{array}\right]T_{u }+\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]{\theta }_{des}$$

(9)

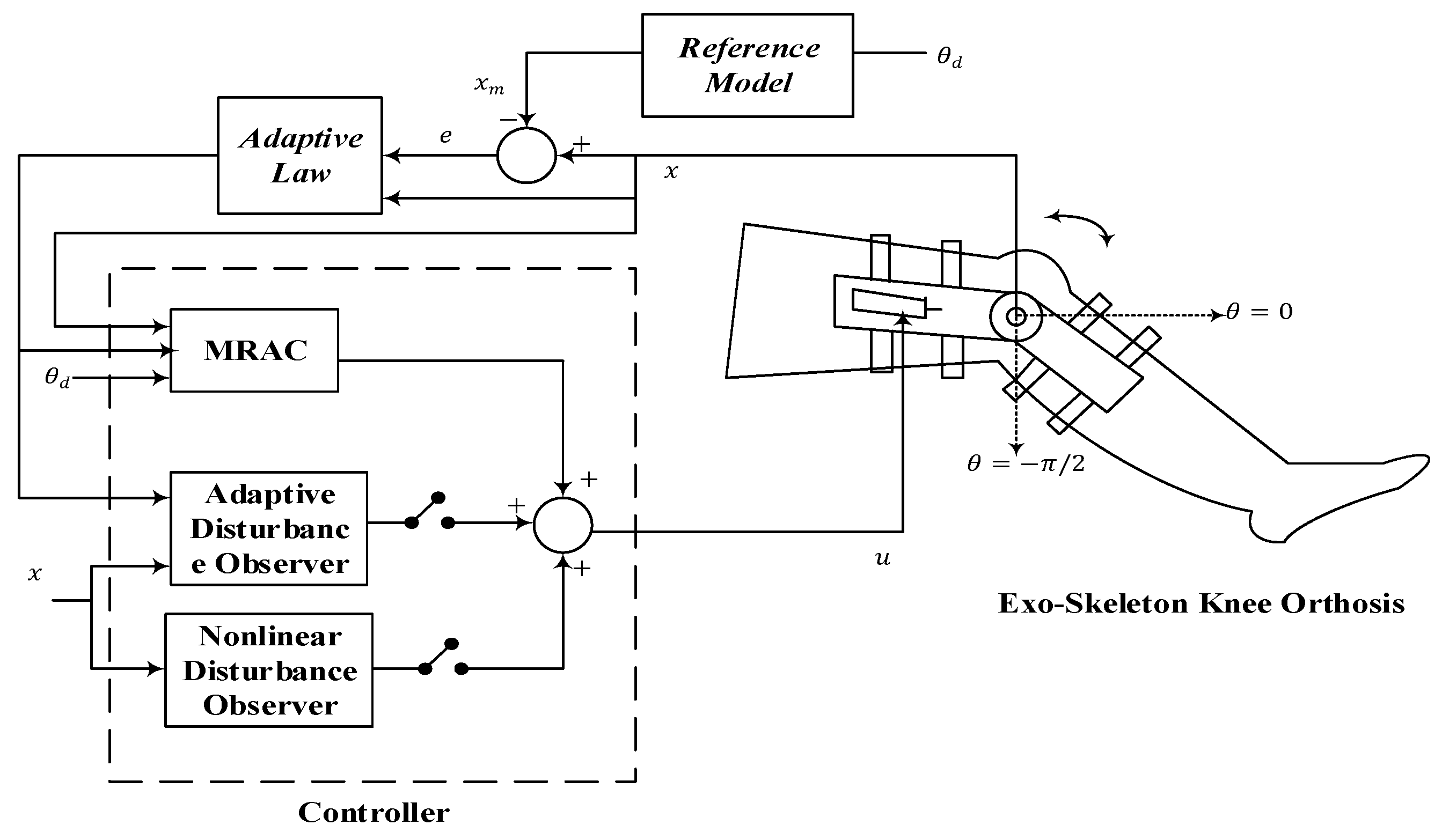
3. Controller Design

3.1. Model Reference Adaptive Control (MRAC)

For a system with dynamics [31,32,33]:

$$\dot{x}=A x+B \mathsf{\Lambda }\left(u+{\beta }^T\varphi \right)+B_m{\beta }_{des}+\zeta$$

(10)

$$y=C_{m}x$$

(11)

where:

• $A\in {ℝ}^{n\times n}$: is a matrix assumed to have totally unknown with bounded constant elements,
• $B\in {ℝ}^{n\times m}$: is the known matrix,
• $\mathsf{\Lambda }\in {ℝ}^{m\times m}$: is diagonal matrix of unknown entries,
• $\beta \in {ℝ}^{N\times m}$: is a matrix of unknown constants,
• $\varphi \in {ℝ}^{N\times m}$: is a matrix of known functions,
• $y\in {ℝ}^q$: is the vector of outputs,
• $C_m\in {ℝ}^{q\times n}$: is an output matrix of known weights,
• $\zeta \in {ℝ}^n$: is a vector of unknown upper-bounded disturbances.

The dynamic of exoskeleton knee device has to mimic in behavior as reference model,

$${\dot{x}}_m=A_m{x}_m+B_m {\beta }_{des}$$

(12)

where:

• $A_m\in {ℝ}^{n\times n}$: is the state matric of reference model,
• $B_m\in {ℝ}^{n\times m}$: is the input matrix of reference model,
• $x_m\in {ℝ}^n$: is the vector of state variables of reference model,
• ${\beta }_{des}\in {ℝ}^m$: is the commanded input.

The reference system is designed to have the desired performance characteristics of the exoskeleton knee assisted system. In order to design the reference system, the integral submerged dynamics must be designed faster than the system dynamics. The reference poles are selected to be as:

$${\lambda }_1=-250, {\lambda }_2=-123, {\lambda }_3=-20-b_v/J.$$

The reference model matrix then can be written as:

$$A_m=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ {\lambda }_1& {\lambda }_2& {\lambda }_3\end{array}\right]$$

The following duties are performed through the design of controller law $u$, which is responsible for making the system of Equations (10) and (11) to mimic the behavour of reference model:

□

To eliminate the nonlinearity described by ${\beta }^T\varphi ,$

□

To deternine the forward and feedback gains, which are necessary in the control design to satifiy its objective,

□

To address the uncertainties due to $\mathsf{\Lambda }$, $A$ and $\beta .$

The control law is chosen to have the following structure:

$$u={\widehat{K}}_x^{T}x-{\widehat{\beta }}^T\varphi$$

(13)

such that:

• $\widehat{\beta }\in {ℝ}^{N\times m}$ is the estimation matrix of unknown matrix $\theta$,
• ${\widehat{K}}_x\in {ℝ}^{n\times m}$: is the feedback gain matrix.

The matching conditions are necessary to validate the control design based on MRAC. To ensure existence of matching conditions, the following equations have to be satisfied

$$\mathrm{A}+\mathrm{B} \mathsf{\Lambda } K_x^T=A_m$$

(14)

$$\mathsf{\Delta }{\beta }^T={\widehat{\beta }}^T-{\beta }^T=0$$

(15)

where, ${\widehat{\beta }}^T$ and $K_x^T$ stands for, respectively, the matrices of estimated coefficients of parameters and the ideal feedback gains. It easy to deduce the closed-loop system,

$$\dot{x}=Ax+B\mathsf{\Lambda }\left( {\widehat{K}}_x^{T}x+{\beta }^T\varphi \right)+B_m {\beta }_{des}+\zeta$$

(16)

The following error equation defines the difference between the actual reference model states;

$$e=x-x_m$$

(17)

Taking the derivative of error equation to have

$$\dot{e}=\dot{x}-{\dot{x}}_m$$

or:

$$\dot{e}=A_{m}e+B \mathsf{\Lambda } \mathsf{\Delta }{K}_x^{T}x-\mathsf{\Delta }{\beta }^T\varphi +\zeta$$

(18)

where $\mathsf{\Delta }{K}_x^T={\widehat{K}}_x^T-K_x^T$.

The following quadratic function is a suitable choice to initiate stability analysis

$$V\left(e,\mathsf{\Delta }{K}^T\right)=e^{T}Pe+tr \left(\mathsf{\Delta }{K}^T{\mathsf{\Gamma }}_K^{-1} \mathsf{\Delta }K \mathsf{\Lambda }\right)+tr \left(\mathsf{\Delta }{\beta }^T{\mathsf{\Gamma }}_{\theta }^{-1} \mathsf{\Delta }\beta \mathsf{\Lambda }\right)$$

(19)

where $V\left(e,\mathsf{\Delta }{K}^T\right):{ℝ}^{n\times m}\to ℝ$ and $P\in {ℝ}^{n\times n} |P=P^T>0$ is a positive definite symmetric matrix. The matrix $P$ is calculated by solving the following equation:

$$P A_m+A_m^T P=-Q$$

(20)

where $Q\in {ℝ}^{n\times n}$ is the positive definite symmetric matrix, and ${\mathsf{\Gamma }}_K\in {ℝ}^{n\times n} |{\mathsf{\Gamma }}_K={\mathsf{\Gamma }}_K{}^T>0$,${\mathsf{\Gamma }}_{\beta }\in {ℝ}^{n\times n} |{\mathsf{\Gamma }}_{\beta }={\mathsf{\Gamma }}_{\beta }{}^T>0$ are diagonal matrices whose elements governing the learning or adaptation rate.

Taking the derivative of $V\left(e,\mathsf{\Delta }{K}^T\right)$ results in

$$\dot{V}=-e^{T}Qe+2 tr(\mathsf{\Delta }{K}_x^T({\mathsf{\Gamma }}_K^{-1}{\dot{\widehat{K}}}_{\mathrm{x}}+x{e}^{T}PB) \mathsf{\Lambda }+2 tr(\mathsf{\Delta }{\beta }^T({\mathsf{\Gamma }}_{\beta }^{-1}\dot{\widehat{\beta }}+\varphi e^{T}PB) \mathsf{\Lambda }+2 e^{T}P \zeta$$

(21)

Setting $\zeta$ to zero ($\zeta =0$) will enforce the trajectories of tarcking errors to reach the origin asymptotically. Accordingly, the following adaptive law can be deduced

$${\dot{\widehat{K}}}_{\mathrm{x}}=-{\mathsf{\Gamma }}_K x e^T P B$$

(22)

$$\dot{\widehat{\beta }}=-{\mathsf{\Gamma }}_{\theta } \varphi e^T P B$$

(23)

This leads to:

$$\dot{V}=-e^{T}Q e$$

(24)

which is a negative semi definite according to the fact of $-{||e||}^2\le 0$. Taking the second derivative of L. F. to have:

$$\ddot{V}=-2e^{T}Q \dot{e}$$

(25)

$\ddot{V}$ is bounded, and in Barabalt lemma sight the boundedness of $\ddot{V}$ leads to the $\underset{t\to \infty }{\lim }\dot{V}=0$. By concentrating on $\dot{V}$, its deduced $\underset{t\to \infty }{\lim }\dot{V}=0$ cannot be true unless $\underset{t\to \infty }{\lim }e=0$ which means that $\underset{t\to \infty }{\lim }||x-x_m||=0$ and the adaptive law will produce a bounded gains $\widehat{K}$, which leads to a bounded control signal $u$ (Narendra and Annaswamy 2012). According to (Lavretsky and Wise 2013), the previous procedure guarantees the asymptotic stability of the desired state variable, acting as the perspective reference model state variable and does not guarantee the controller gains converges to the calculated values, but rather produces a combination that leads to the desired results.

If $||\zeta ||\le {\zeta }_{max}$, then:

$$\dot{V}=-e^{T}Qe+d$$

(26)

where $d=2 e^{T}P \zeta$. Using the fact:

$$e^{T}Q e\le {\lambda }_{max}\left(Q\right){||e||}^2$$

(27)

If one assumes that:

$$d>{\lambda }_{\max }\left(Q\right){||e||}^2$$

(28)

Based on Equation (28), the stability will be weakened where $\dot{V}$ is no longer be negative-definite.

3.2. MRAC with Adaptive Disturbance Estimator

In the case of matched disturbance there is an opportunity to estimate that disturbance by modifying the adaptive law through some kind of disturbance compensator, namely, by adding a term to the control law to compensate the disturbance and acting as a disturbance observer. The control modification is limited to a constant and slow varying disturbance. In order to demonstrate the controller modification, the system of Equation (10) is rewritten as:

$$\dot{x}=A x+B \mathsf{\Lambda }\left(u+{\beta }^T\varphi +{\zeta }_1\right)+B_m{\beta }_{des}$$

(29)

where $\zeta =B \mathsf{\Lambda }{\zeta }_1$ and ${\zeta }_1\in R^m$ is the matched disturbance vector (unknown with upper bounded property). The control law will be:

$$u={\widehat{K}}_x^{T}x-{\widehat{\beta }}^T\varphi -{\widehat{\zeta }}_1$$

(30)

such that $\widehat{{\zeta }_1}\in R^m$ is a vector of the estimated values of ${\zeta }_1.$ Another equality will be added to the matching condition which is:

$$\mathsf{\Delta }{\zeta }_1{}^T={\widehat{\zeta }}_1{}^T-{\zeta }_1{}^T=0$$

(31)

Following the same procedure, Equations (19)–(28), the adaptive law will be modified according to the following analysis:

$$V\left(e,\mathsf{\Delta }{K}^T\right)=e^{T}Pe+tr \left(\mathsf{\Delta }{K}^T{\mathsf{\Gamma }}_K^{-1} \mathsf{\Delta }K \mathsf{\Lambda }\right)+tr \left(\mathsf{\Delta }{\beta }^T{\mathsf{\Gamma }}_{\beta }^{-1} \mathsf{\Delta }\beta \mathsf{\Lambda }\right)+tr \left(\mathsf{\Delta }{\zeta }_1{}^T{\mathsf{\Gamma }}_{\zeta }^{-1} \mathsf{\Delta }{\zeta }_1 \mathsf{\Lambda }\right)$$

(32)

The time derivative of L.F. will be:

$$\dot{V}=-e^{T}Qe+2 tr(\mathsf{\Delta }{K}_x^T({\mathsf{\Gamma }}_K^{-1}{\dot{\widehat{K}}}_{\mathrm{x}}+x{e}^{T}PB) \mathsf{\Lambda }+2 tr(\mathsf{\Delta }{\beta }^T({\mathsf{\Gamma }}_{\beta }^{-1}\dot{\widehat{\beta }}+\varphi e^{T}PB) \mathsf{\Lambda }+2 tr(\mathsf{\Delta }{\zeta }_1{}^T({\mathsf{\Gamma }}_{\zeta }^{-1}\dot{\widehat{{\zeta }_1}}+e^{T}PB) \mathsf{\Lambda }$$

(33)

In addition to the adaptive laws of Equations (22) and (23), the disturbance estimator adaptive law will be established as:

$$\dot{\widehat{{\zeta }_1}}=-{\mathsf{\Gamma }}_{\zeta } e^T P B$$

(34)

where ${\mathsf{\Gamma }}_{\mathsf{\zeta }}\in R^{\mathrm{m}\times \mathrm{m}}|{\mathsf{\Gamma }}_{\mathsf{\zeta }}={\mathsf{\Gamma }}_{\mathsf{\zeta }}{}^T>0$ and Equation (33) leads to the same result of Equation (24) as:

$$\dot{V}=-e^{T}Q e$$

(35)

and the same analysis of stability and boundedness of all the system signals.

3.3. MRAC Based on Nonlinear Disturbance Observer

This analysis includes disturbance observer as additional term to control law of Equation (30),

$$u={\widehat{K}}_x^{T}x-{\widehat{\beta }}^T\varphi -\widehat{w}$$

(36)

where $\zeta =B \mathsf{\Lambda }\mathrm{w}$ and $w\in R^m$. The estimation of disturbance by nonlinear disturbance observer will lead to improve the robustness characteristics of MRAC controller. In addition, in-cooperation of DO will enhance the capabilities of MRAC controller to cope with the upper bound of unknown disturbance.

The principle of nonlinear DO is based on the assumption that the exerted disturbance is characterized by slow-time variation; that is., $\dot{w}=0$. As such, the estimation error of disturbance can be given by

$$\tilde{w}=w-\widehat{w}$$

(37)

The observer is synthesized based on the following structure [34]:

$$\psi =\widehat{w}-p\left(x\right)$$

(38)

$$\dot{\psi }=-L\left(x\right)\psi +L\left(x\right)\left(-p\left(x\right)-f\left(x\right)-g\left(x\right)u\right)$$

(39)

where, $\psi$ is state variable of observer dynamic,$L\left(x\right)$ and $p\left(x\right)$ represent the observer gain and designed nonlinear function, respectively;

$$x^{\left(\rho \right)}=f\left(x\right)+g\left(x\right). u+w$$

(40)

where $x^{\left(\rho \right)}={\dot{x}}_n$, $g\left(x\right)=B{ \mathsf{\Lambda }}_0,$ which represents the nominal part of $\Lambda ={\Lambda }_0+{\Lambda }_d$; let:

$$L\left(x\right){\dot{x}}_n=\dot{p}\left(x\right)$$

(41)

Taking the time derivative of estimation error for disturbance to have

$$\dot{\tilde{w}}=\dot{w}-\dot{\widehat{w}}$$

(42)

Since $\dot{w}=0$, this lead to $\dot{\tilde{w}}=-\dot{\widehat{w}}$. Then, according to Equation (38), one has $\dot{\widehat{w}}=\dot{\psi }-\dot{p}\left(x\right)$, which leads to

$$\dot{\widehat{w}}=-L\left(x\right)\psi +L\left(x\right)\left(-p\left(x\right)-f\left(x\right)-g\left(x\right) u\right)-L\left(x\right) {\dot{x}}_n$$

(43)

or:

$$\dot{\tilde{w}}=L\left(x\right) \psi -L\left(x\right)\left(-p\left(x\right)-f\left(x\right)-g\left(x\right) u+{\dot{x}}_n\right)$$

(44)

Since $f\left(x\right)=-\frac{b_v}{J}{x}_3+\frac{mgl}{J}\cos \left(x_2\right)-\frac{a_s}{J}sgn\left(x_3\right)$, $g\left(x\right)=\frac{1}{J}$, and ${\dot{x}}_n={\dot{x}}_3$ Then:

$$\dot{\tilde{w}}=L\left(x\right)\zeta -L\left(x\right)\left(-p\left(x\right)+\frac{b_v}{J}{x}_3-\frac{mgl}{J}\mathit{cos}\left(x_2\right)+\frac{a_s}{J}sgn\left(x_3\right)-\frac{1}{J}u+-\frac{b_v}{J}{x}_3+\frac{mgl}{J}\mathit{cos}\left(x_2\right)-\frac{a_s}{J}sgn\left(x_3\right)+\frac{1}{J}u+w\right)$$

(45)

This leads to:

$$\dot{\tilde{w}}=L\left(x\right)\left(\zeta +p\left(x\right)\right)-L\left(x\right) w$$

(46)

That is:

$$\dot{\tilde{w}}=-L\left(x\right)\tilde{w}$$

(47)

Equation (47) means that $\tilde{w}\to 0$ or $\widehat{w}\to w$ at t$\to \infty$ asymptotically. Hence, by selecting $L\left(x\right)=L>0$ and by integrating Equation (41):

$$p\left(x\right)=L x_3$$

(48)

therefore, $\widehat{w}$ is obtained based on the observer dynamics.The following Lyapunov function is the suitable quadratic function to initiate the stability analysis:

$$V\left(e,\mathsf{\Delta }{K}^T\right)=e^{T}Pe+tr \left(\mathsf{\Delta }{K}^T{\mathsf{\Gamma }}_K^{-1} \mathsf{\Delta }K \mathsf{\Lambda }\right)+tr \left(\mathsf{\Delta }{\beta }^T{\mathsf{\Gamma }}_{\beta }^{-1} \mathsf{\Delta }\beta \mathsf{\Lambda }\right)+{\tilde{w}}^2/2$$

(49)

Taking the time derivative of Equation (49) to have:

$$\dot{V}=-e^{T}Qe+2 e^{T}P \zeta +\tilde{w}\dot{\tilde{w}}$$

(50)

Using Equation (47), one can have:

$$\dot{V}=-e^{T}Qe+2 e^{T}P \zeta -L{\tilde{w}}^2$$

(51)

Assuming that $d={\left|2 e^{T}P w\right|}_{max}$ then:

$$\dot{V}\le -e^{T}Qe+\mathrm{d}-L{\tilde{w}}^2$$

(52)

By choosing $L$ to be big enough as $L-d=\delta >0$ then:

$$\dot{V}\le -e^{T}Qe-\mathsf{\delta }{\tilde{w}}^2$$

(53)

This makes $e⟶0$ asymptotically which means that the state $x_1$ asymptotically tracks the reference model trajectory $x_m$.

The schematic diagram of the MRAC with an adaptive disturbance estimator and nonlinear disturbance observer controller to robustly control the angular position of the exoskeleton knee assisted system is illustrated in Figure 2.

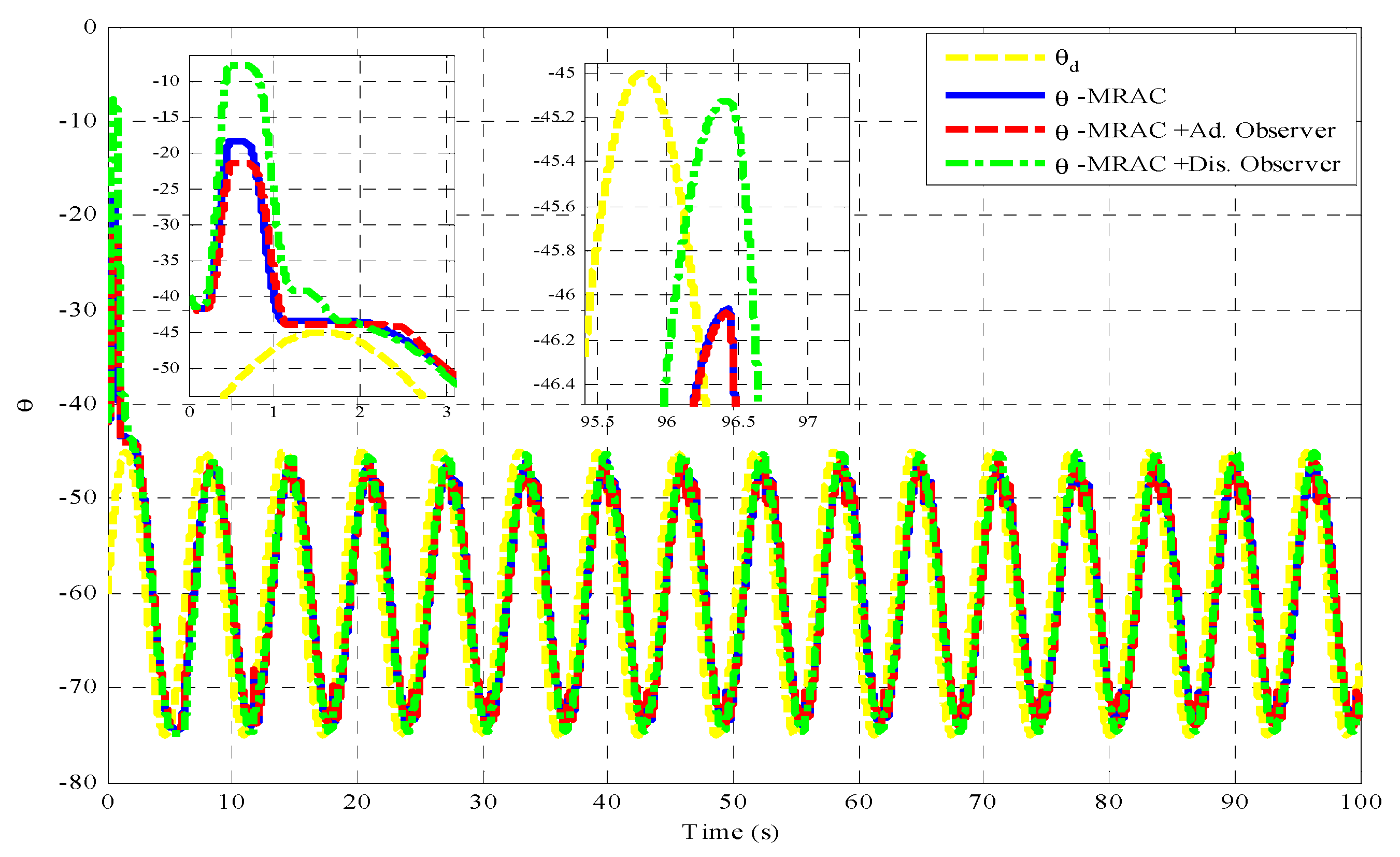
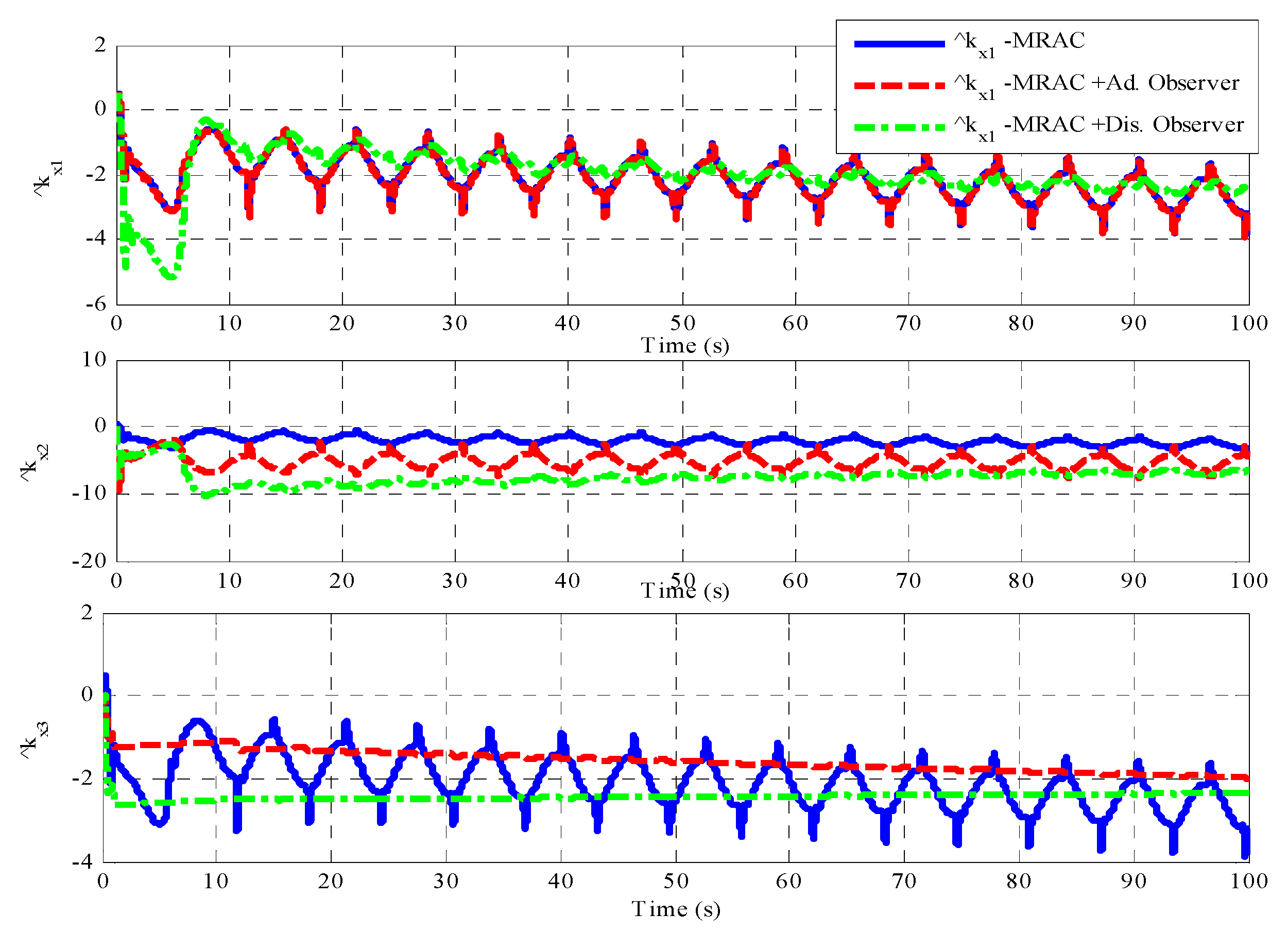
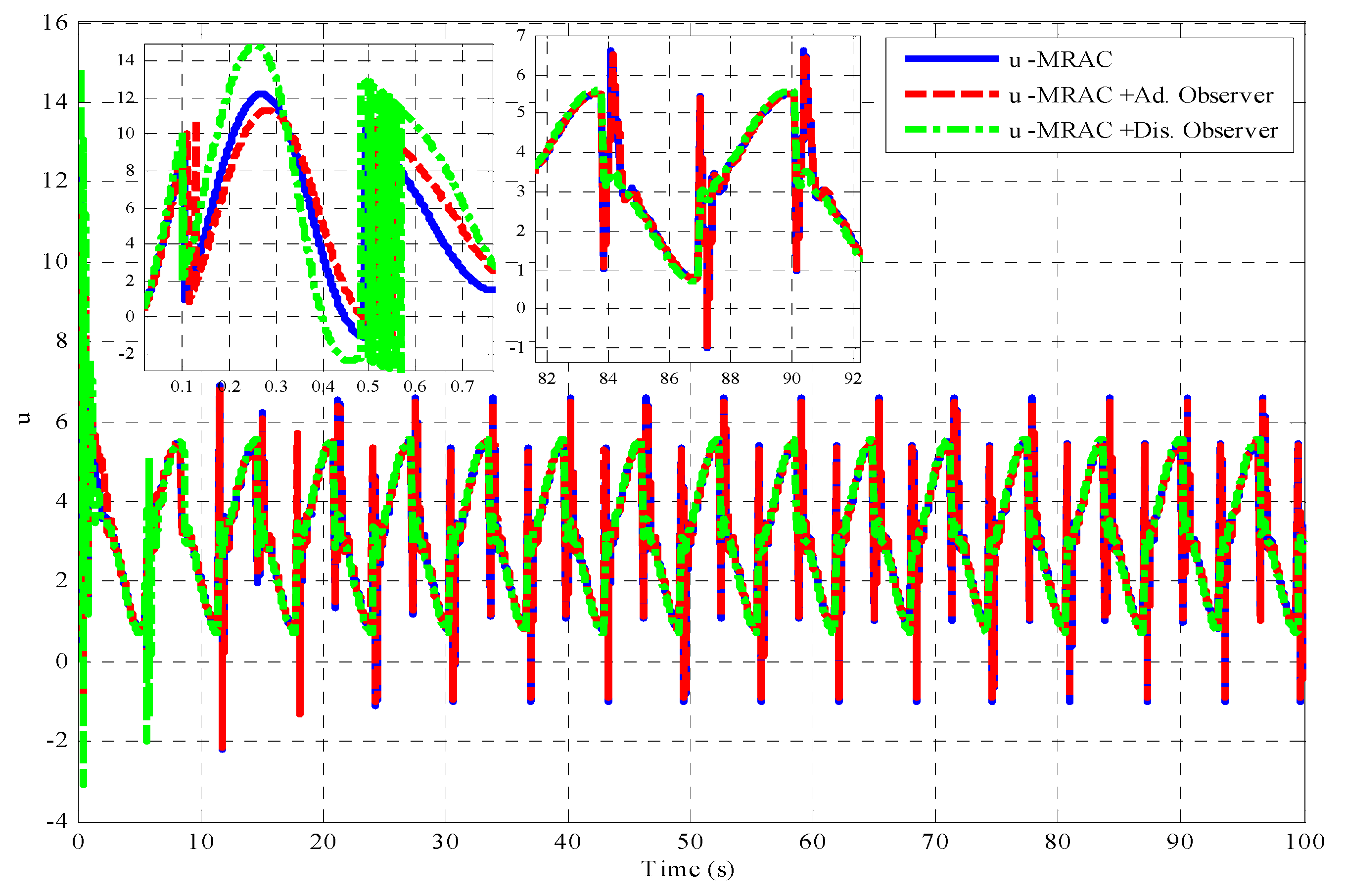
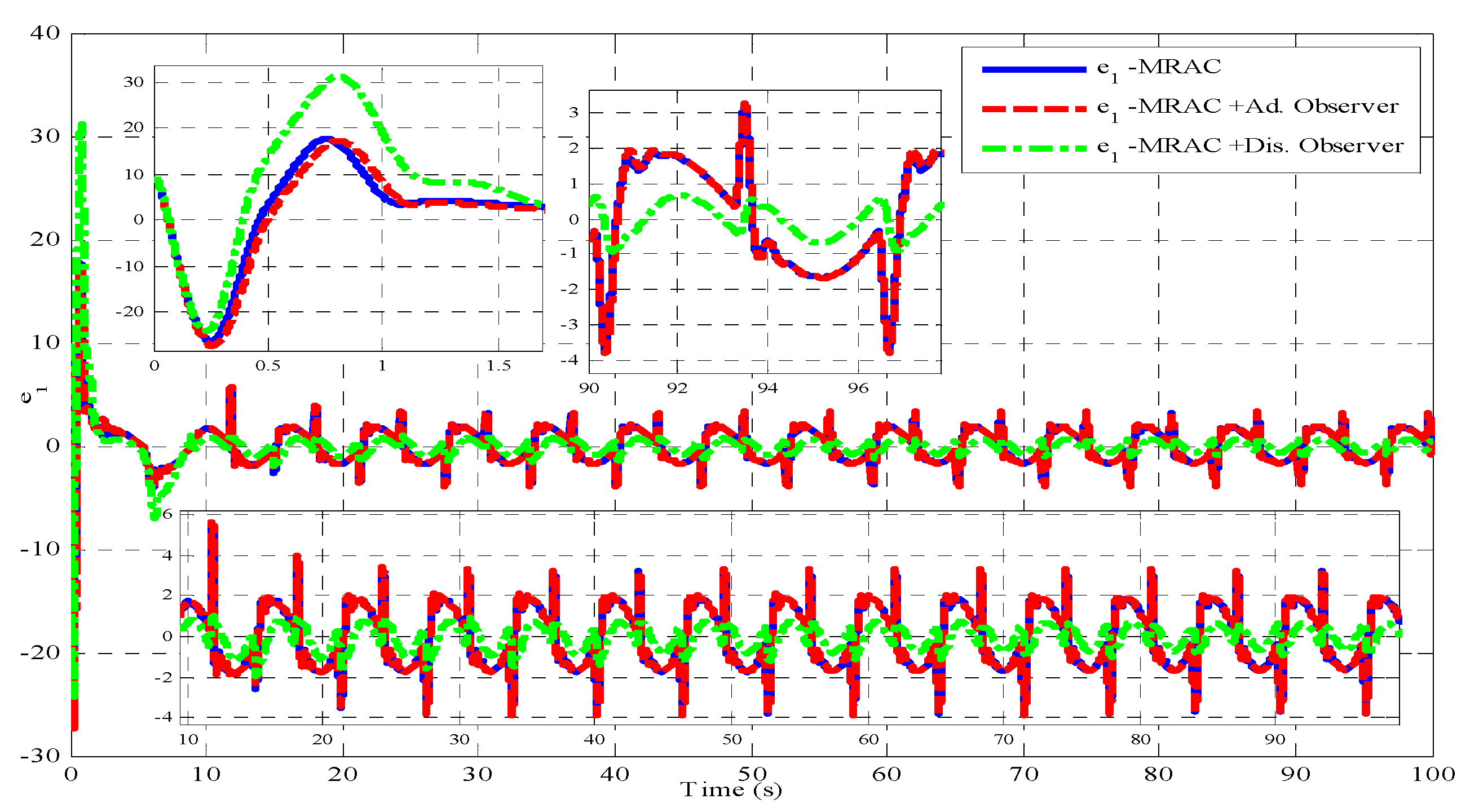
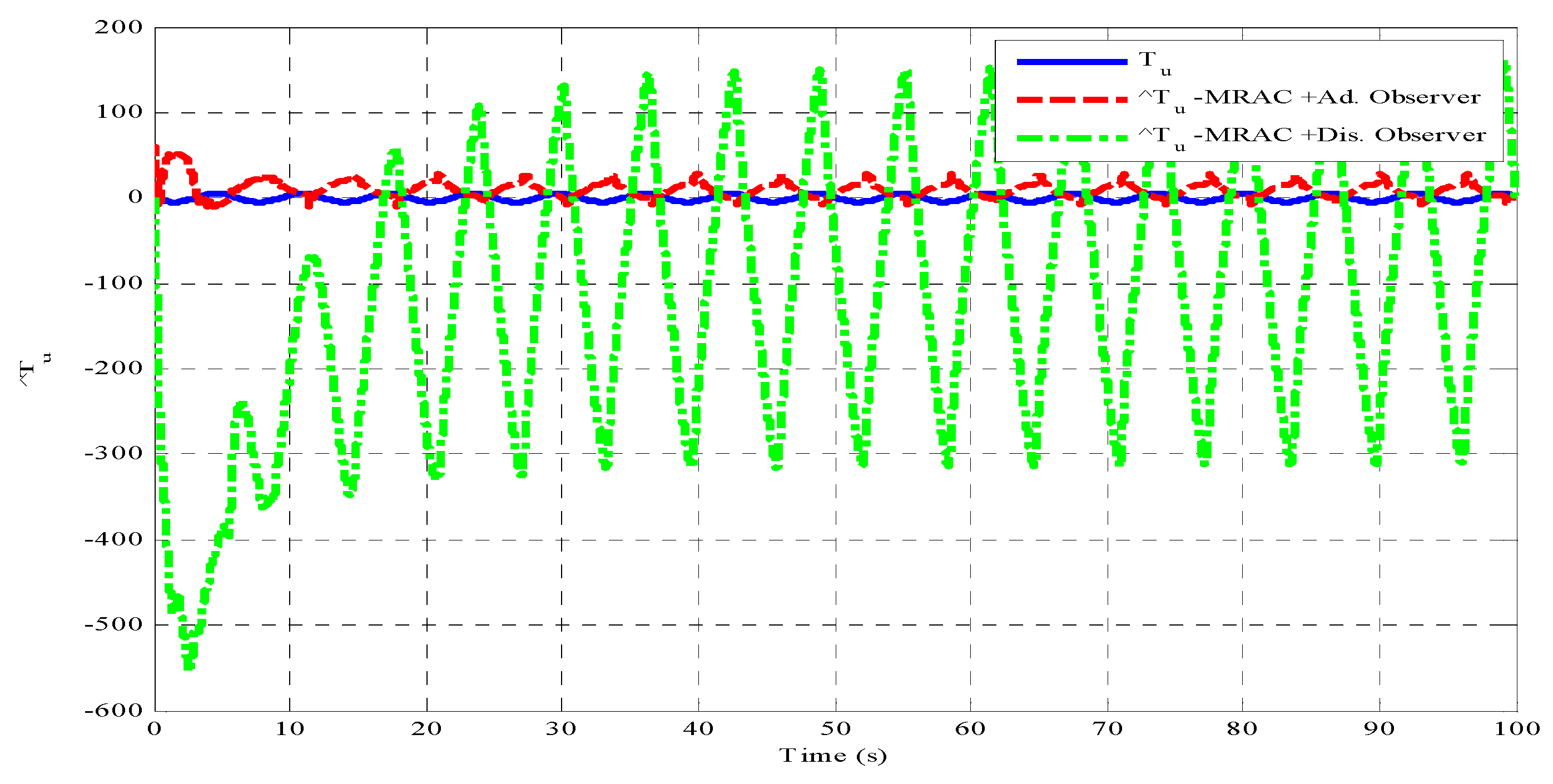
4. Simulated Results

The numerical simulation of Exoskeleton knee assisted system controlled by the three proposed controllers have been implemented within environment of MATLAB programming software. The following assumptions have to be taken into account in conducting the computer simulation,

□

The desired position trajectory is taken as sinusoidal waveform ranges between (−45 to −75 Deg.) with initial condition of −60 Deg.

□

The load torque is simulated as sinusoidal signal having the following maximum bounds:

$$-5\le T_u\le 5 (\mathrm{N}.\mathrm{m})$$

□

($\mathsf{\Lambda }=1/J$), which is entirely unknown with upper bounded limit, is treated as controller ineffectiveness.

□

A challenge of increment in inertia by 12% is added to test the totally unknown environment to the controller which avoided by most literature.

The reference model of the actual exoskeleton knee assisted system parameters used for the simulation are listed in the

Table 1. Lists of Exoskeleton Parameters.

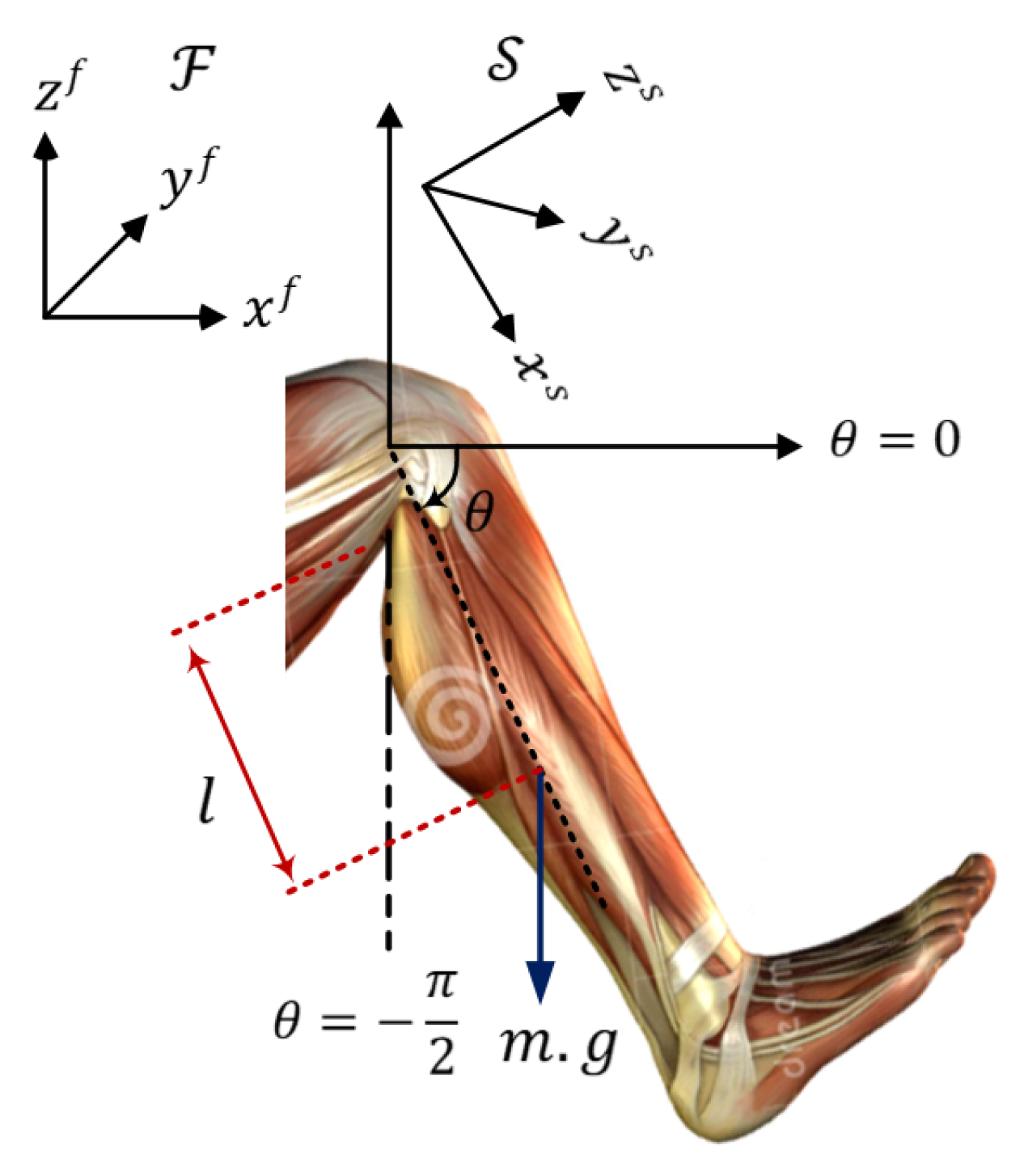
The Parameters	Value
$J$	0.323 kg.m2/rad
$m$	0.000105 Kg
$b_v$	0.35 N.m.s/rad
$a_s$	0.059 N.m/A
$l$	0.25 m
$g$	9.8 N

below [16]:

The matrices of the reference model are chosen to be:

$$A_m=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -250& -123& -18.9164\end{array}\right],B_m=\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right].$$

The following appropriate diagonal values are found for the matrices ${\Gamma }_K$,${\Gamma }_{\beta }$, ${\Gamma }_{\zeta }$ and $L$ based on a try-and-error procedure:

$${\Gamma }_K=\left[\begin{array}{ccc}100& 0& 0\\ 0& 100& 0\\ 0& 0& 100\end{array}\right], {\Gamma }_{\beta }=\left[\begin{array}{cc}500& 0\\ 0& 500\end{array} \right], {\Gamma }_{\zeta }=100,L=340$$

The position behavior of the exoskeleton knee assisted system is depicted in Figure 3. In the figure, the MRAC controller and the controller with adaptive disturbance estimator gave a better transient response than the controller with the nonlinear disturbance observer, while that situation was reversed in the steady-state response to give better performance characteristics for the MARC with the nonlinear disturbance observer than the other controllers. Figure 4 illustrates the angular velocity of the exoskeleton knee assisted system where at the transient response the MRAC with the nonlinear disturbance observer was faster than the other two controllers, which explains the faster position response of that controller in the previous figure of position response. In the rest of the velocity behavior there was a clear spike-like fluctuation in the MRAC and MRAC with an adaptive estimator while the one with the nonlinear disturbance observer acted smoothly.

Figure 5 shows the feedback adaptive gains of the three controllers; both the MRAC controller and the one with an adaptive disturbance estimator shared the same profile of oscillatory responses due to disturbance, while the controller with a nonlinear disturbance observer’s feedback adaptive gains behaved with an obviously less oscillatory response.

Figure 6 shows the unknown uncertainty parameters estimation where again the oscillatory profiles were clear in the response of both the MRAC and MRAC with adaptive response estimator, while the MRAC with a nonlinear disturbance observer showed a smoother and more stabilized action.

Figure 7 shows the unknown adaptive uncertainty parameters estimation where again the oscillatory profile was clear in the response of both the MRAC and the other controller with the adaptive disturbance estimator, while the MRAC with the nonlinear disturbance observer showed a smoother and more stabilized adaptive uncertainty parameters action.

Figure 7 shows the control action effort for the three controllers, at the transient response. The MRAC with nonlinear disturbance observer showed a slightly higher control effort and a chattering period occurred, while the two other controllers showed the same profile with slightly less effort and a smoother response along the rest of the simulation time span. The MRAC with nonlinear disturbance observer acquired less control effort to give the best performance as is seen from the previous figures and the smoother profile; however, the other two controllers showed a pulsative fluctuation at each rise and decay of their response. The spike-like fluctuation in the MRAC and MRAC with adaptive disturbance estimator came from the effect of the term of $sgn\left(x_3\right)$ in the second channel of the system model where the term was undefined in the $x_3=0$. As such, in a control sense, the behavior of the adaptive controller needed time to overcome that fluctuation.

Figure 8 shows the error between the actual angular position of the exoskeleton-assistance system and the output of the reference model system. It was shown that the MRAC with nonlinear disturbance observer showed a higher error at the transient response and considerably less error at the steady-state as compared to the other two controllers. As a measure for the performance of each controller,

Table 2. Performance indications of the proposed controllers.

Controller	Error of the Time Samples			Mean Error	Control Effort of the Time Samples			Mean Control
	t1 = 20	t2 = 60	t3 = 80		t1 = 20	t2 = 60	t3 = 80
MRAC	1 deg	2 deg	4 deg	2.33 deg	5.8 v	2.1 v	6.5 v	5.1 v
MRAC with adaptive disturbance estimator	1 deg	2 deg	4	2.33 deg	5.8 v	2.1 v	6.4 v	5 v
MRAC with nonlinear disturbance observer	0 deg	0 deg	1 deg	0.335 deg	5.76 v	2 v	3.2 v	4.3 v

shows the mean of the error of the position with the reference model and the three proposed controllers.

Figure 9 and Figure 10 show the estimation of the disturbance for the adaptive estimator and the nonlinear disturbance observer against the injected disturbance. The adaptive disturbance estimator gave less estimation error, but a phase shift or delay in estimation was noticed. On the other hand, the estimation errors based on the nonlinear disturbance observer showed in-phase tracking of disturbance but at the price of a high deviation in estimation error. That deviation or mismatch in disturbance estimation can be attributed to the principle of certainty equivalence of adaptive control theory, where the adaptive laws produce a combination of controller parameters that guarantees the best possible performance without ensuring a zero-convergence of estimation error.

5. Conclusions

This study presented three controllers based on an MRAC design for trajectory tracking of the angular position for an exoskeleton knee assistance system. Development of an MRAC controller design, MRAC with an adaptive disturbance estimator, and combining the design of a nonlinear disturbance observer with the MRAC controller to robustly control the angular position of an exoskeleton knee assisted system under unknown and upper bounded disturbance, has been argued. Making a performance comparison between the proposed three controllers in terms of transient, robustness, and control input characteristics, the stability analysis for each scheme was conducted and developed based on the Lyapunov theorem to prove the uniform ultimate bound of tracking and estimation errors. In addition, the adaptive laws were developed for the proposed schemes according to the stability analysis. The results based on numerical simulation have shown that the MRAC with a nonlinear observer could give better robustness characteristics and better performance in terms of tracking and estimation errors as compared to the other controllers. This study can be extended for future work by including other advanced control schemes to the position control of assisting devices to show their effectiveness and performances as compared to the present controller [35,36,37,38,39,40,41,42,43,44].