Exploiting Cyclic Angle-Dependency in a Kalman Filter-Based Torque Estimation on a Mechatronic Drivetrain
Abstract
:1. Introduction
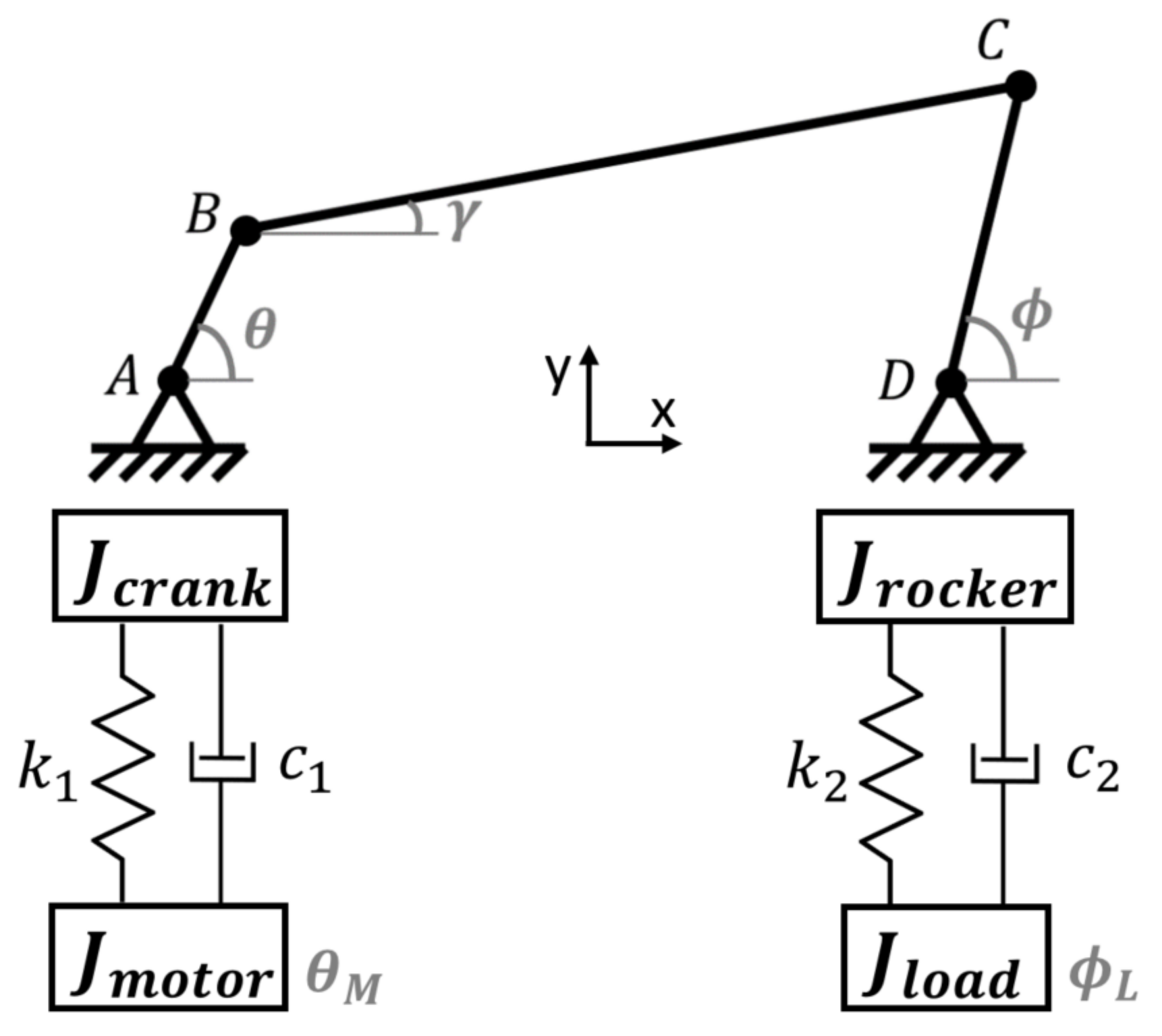
2. Mechatronic Powertrain Model
2.1. Four-Bar Linkage Model
2.2. Permanent-Magnet Synchronous Motor Model
2.3. Magnetic Spring Model
2.4. Shaft Flexibilities Model
2.5. Torsional Losses Model
2.6. Powertrain Model
3. Coupled State/Input Estimation with Exploitation of Cyclic Periodicity
3.1. State Augmentation for Magnetic Spring
3.2. Extended Kalman Filter
3.3. Exploitation of Cyclic Angle-Dependency
3.3.1. Parametrisation and Update Procedure of the Angle-Dependent Map
- A term related to the error of the torque map at cycle , quantified with a variance value .
- A term related to the difference between the two torque profiles of the consecutive cycles, quantified with a covariance term .
3.3.2. Inclusion of the Angle-Dependent Torque Map in the Estimation
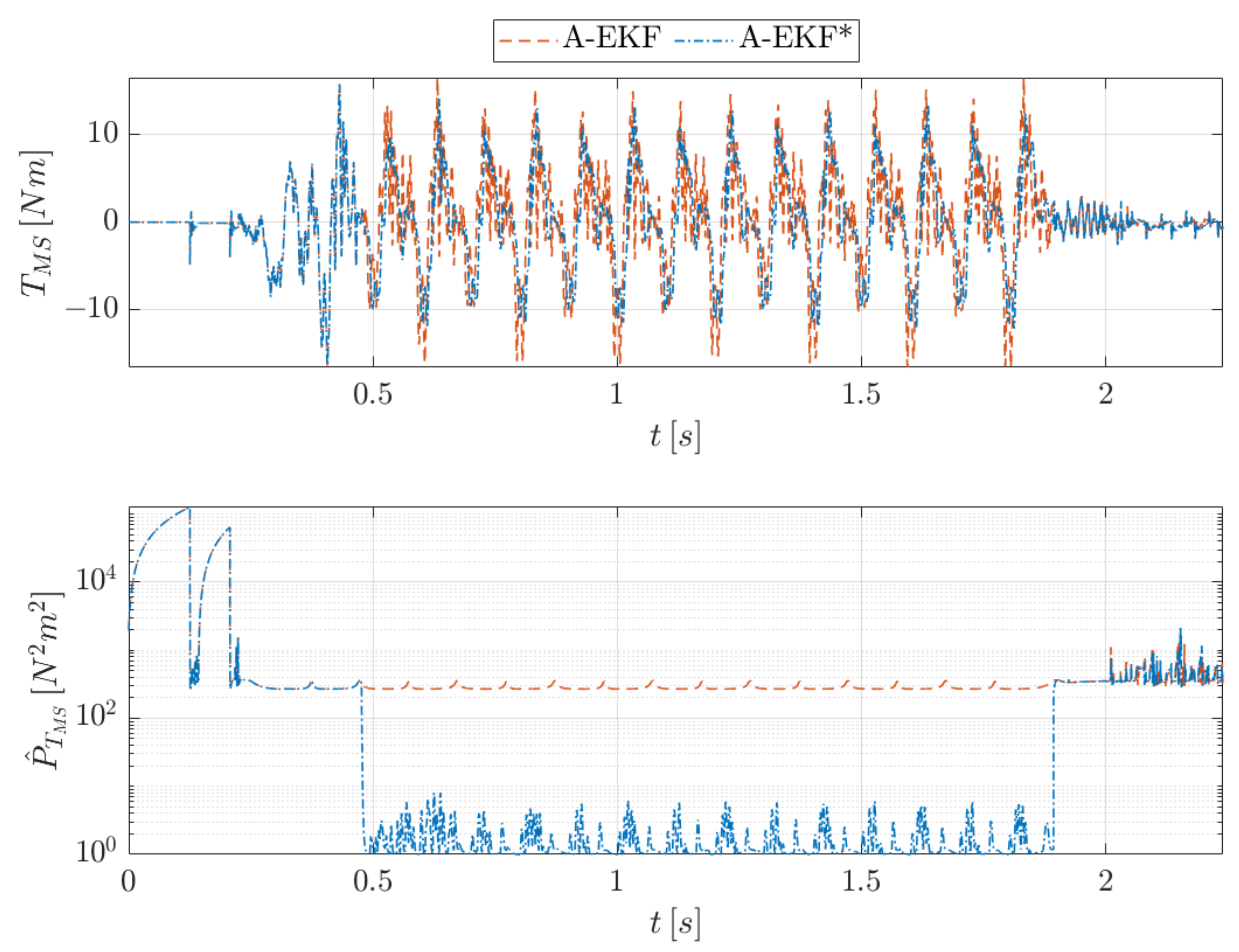
- A low-gradient regime allows a lower random walk covariance, as the torque is known to have smaller deviations each time step;
- On the contrary, a steep torque gradient at a certain angle in previous rotations demands that a higher deviation from the previous time step value is allowed this rotation.
4. Experimental Validation
4.1. Experimental Setup
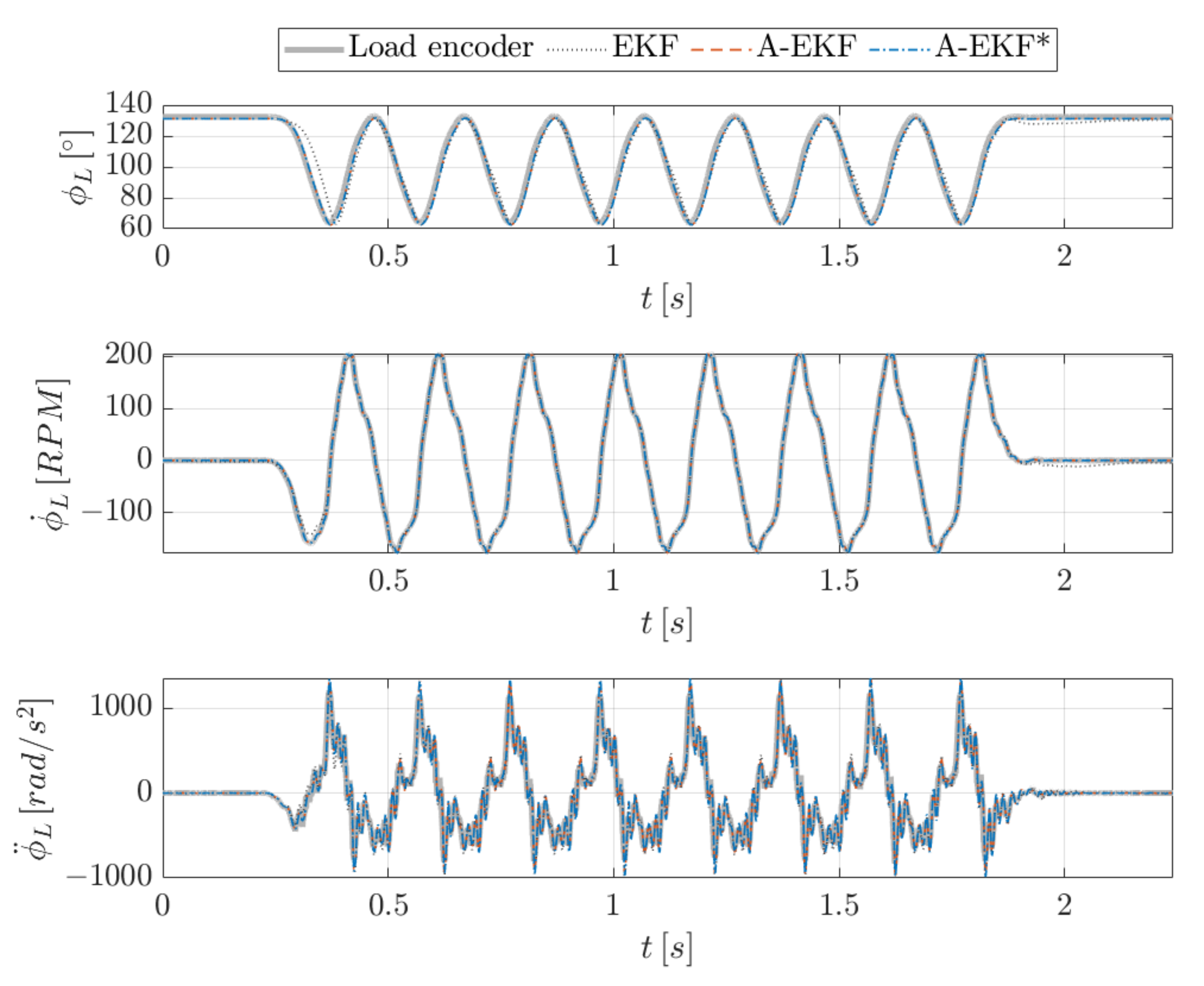
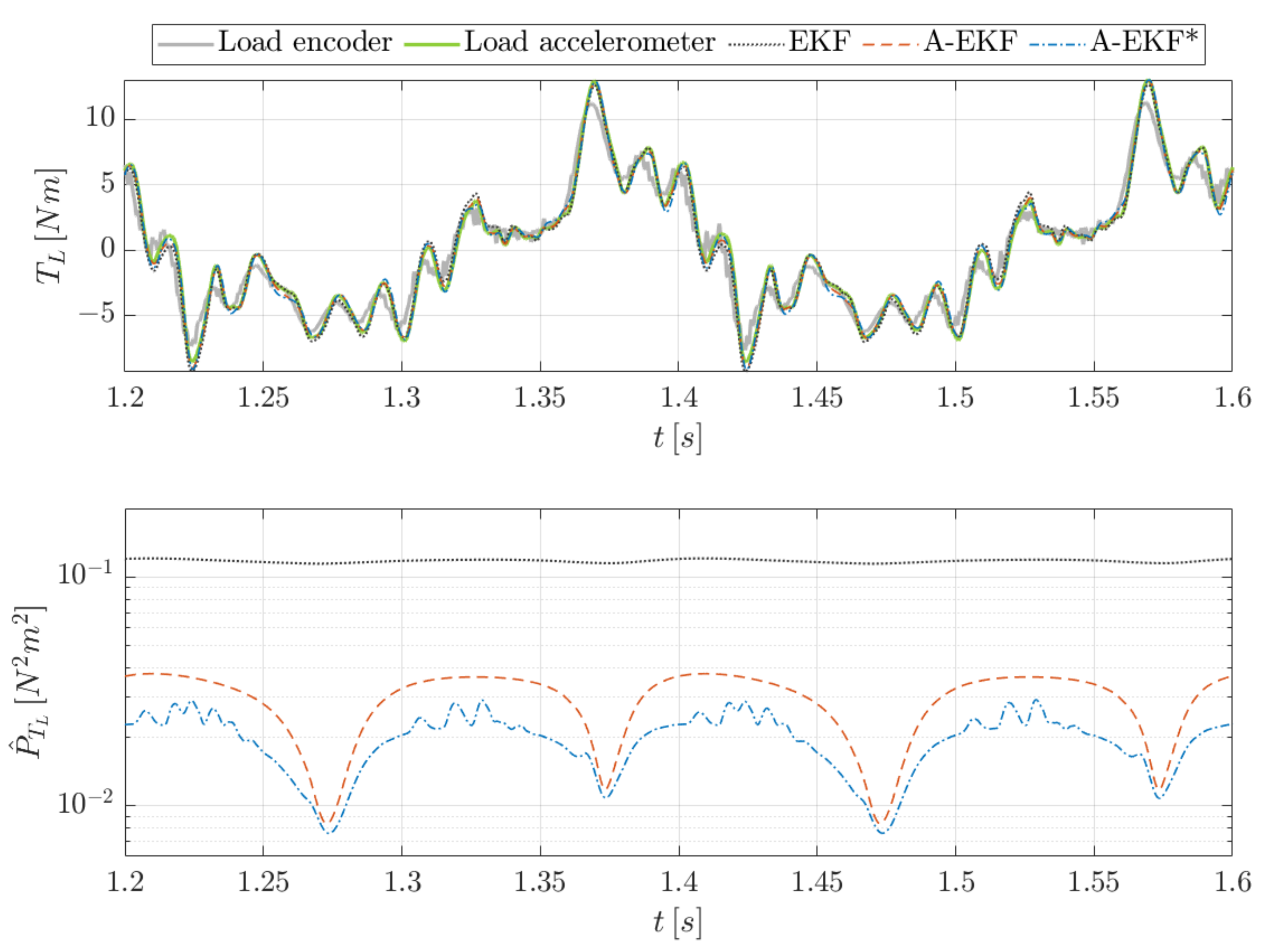
4.2. Estimation Results
- Extended Kalman filter (EKF) without augmented states where the magnetic spring torque input is modelled as an additional uncertainty. As such, the input torque is not estimated;
- Augmented extended Kalman filter (A-EKF) where the augmented state for the magnetic spring torque input is modelled using a random walk model, without exploitation of the periodicity;
- The proposed augmented extended Kalman filter, where the torque input model has an adaptive random walk covariance, depending on the gradient of the angle-dependent torque map (referred to as A-EKF*).
- (i)
- The variance reaches local minima when the load inertia reaches its reciprocating point (either minimal or maximal load angle);
- (ii)
- The variance reaches local maxima when the load inertia crosses its zero point (zero load angle).
- (i)
- The sensitivity is minimal; hence, the uncertain crank angle has only a limited influence on the uncertainty of the rocker angle;
- (ii)
- The sensitivity is maximal; hence, the uncertain crank angle has a more severe influence on the uncertainty of the rocker angle.
- The main difference between the estimation approaches is in the estimation of the magnetic spring torque at the motor side, while the comparison of the results is performed at load side. This may declare the relatively limited difference for this comparison;
- The comparison of the estimation errors relative to the independent encoder reference has a certain value. However, its value should not be overestimated as the encoder has a limited accuracy, and the comparison between the approaches may yield different results when a different validation sensor is used;
- It is assumed that the load torque is known by multiplying the acceleration value of the sensor or the estimator with the load inertia value, as it is assumed no external torques are active on the inertia. A more extensive validation using a torque sensor would allow one to validate this assumption.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nordström, L.J.L.; Nordberg, T.P. A critical comparison of time domain load identification methods. In Proceedings of the 6th International Conference on Motion and Vibration Control, Saitama, Japan, 19–23 August 2002; pp. 1151–1156. [Google Scholar]
- Klinkov, M.; Fritzen, C.P. An updated comparison of the force reconstruction methods. Key Eng. Mater. 2007, 347, 461–466. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. Trans. ASME J. Basic Eng. 1960, 82, 35–40. [Google Scholar] [CrossRef] [Green Version]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. Trans. ASME J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Lourens, E.; Reynders, E.; De Roeck, G.; Degrande, G.; Lombaert, G. An augmented Kalman filter for force identification in structural dynamics. Mech. Syst. Signal Process. 2012, 27, 446–460. [Google Scholar] [CrossRef]
- Naets, F.; Croes, J.; Desmet, W. An online coupled state/input/parameter estimation approach for structural dynamics. Comput. Methods Appl. Mech. Eng. 2014, 283, 1167–1188. [Google Scholar] [CrossRef]
- Croes, J. Virtual Sensing in Mechatronic Systems. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2017. [Google Scholar]
- Forrier, B.; Naets, F.; Desmet, W. Broadband Load Torque Estimation in Mechatronic Powertrains using Nonlinear Kalman Filtering. IEEE Trans. Ind. Electron. 2018, 65, 2378–2387. [Google Scholar] [CrossRef]
- Kirchner, M. Joint State/Input Estimation in Structural Dynamics. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2018. [Google Scholar]
- Kirchner, M.; Croes, J.; Cosco, F.; Desmet, W. Exploiting input sparsity for joint state/input moving horizon estimation. Mech. Syst. Signal Process. 2018, 101, 237–253. [Google Scholar] [CrossRef]
- Kirchner, M.; Croes, J.; Desmet, W. Joint state/input estimation with a Fourier dictionary for the input respresenation: Effect of spectral leakage. In Proceedings of the 13th International Conference on Recent Advances in Structural Dynamics, Lyon, France, 15–17 April 2019; pp. 370–381. [Google Scholar]
- Mrak, B.; Lenaerts, B.; Driesen, W.; Desmet, W. Optimal Magnetic Spring for Compliant Actuation—Validated Torque Density Benchmark. Actuators 2019, 8, 18. [Google Scholar] [CrossRef] [Green Version]
- Mrak, B.; Lenaerts, B.; Driesen, W.; Desmet, W. Optimal Design of Magnetic Springs; Enabling High Life Cycle Elastic Actuators. In Proceedings of the 16th International Symposium on Magnetic Bearings, Beijing, China, 13–17 August 2018. [Google Scholar]
- McCarthy, J.; Soh, G. Geometric Design of Linkages, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Simon, D. Optimal State Estimation, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 395–433. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R. Estimation and Tracking: Principles, Techniques, and Software, 1st ed.; Artech House: Boston, MA, USA; London, UK, 1993. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van der Veken, T.; Croes, J.; Kirchner, M.; Baake, J.; Desmet, W.; Naets, F. Exploiting Cyclic Angle-Dependency in a Kalman Filter-Based Torque Estimation on a Mechatronic Drivetrain. Actuators 2022, 11, 35. https://doi.org/10.3390/act11020035
Van der Veken T, Croes J, Kirchner M, Baake J, Desmet W, Naets F. Exploiting Cyclic Angle-Dependency in a Kalman Filter-Based Torque Estimation on a Mechatronic Drivetrain. Actuators. 2022; 11(2):35. https://doi.org/10.3390/act11020035
Chicago/Turabian StyleVan der Veken, Thijs, Jan Croes, Matteo Kirchner, Jonathan Baake, Wim Desmet, and Frank Naets. 2022. "Exploiting Cyclic Angle-Dependency in a Kalman Filter-Based Torque Estimation on a Mechatronic Drivetrain" Actuators 11, no. 2: 35. https://doi.org/10.3390/act11020035
APA StyleVan der Veken, T., Croes, J., Kirchner, M., Baake, J., Desmet, W., & Naets, F. (2022). Exploiting Cyclic Angle-Dependency in a Kalman Filter-Based Torque Estimation on a Mechatronic Drivetrain. Actuators, 11(2), 35. https://doi.org/10.3390/act11020035







